Learning Joint Twist Rotation for 3D Human Pose Estimation

from a Single Image

Chihiro Nakatsuka, Jianfeng Xu and Kazuyuki Tasaka

KDDI Research, Inc., Saitama, Japan

Keywords: 3D Human Pose Estimation, Learning Joint Twist Rotation, Swing-twist Decomposition.

Abstract: We consider monocular 3D human pose estimation with joint rotation representations because they are more

expressive than joint location representations and better suited to some applications such as CG character

control and human motion analysis in sports or surveillance. Previous approaches have encountered difficul-

ties when estimating joint rotations with actual twist rotation around limbs. We present a novel approach to

estimating joint rotations with actual twist rotations from a single image by handling joint rotations separately

decomposed into swing and twist rotations. To extract twist rotations from an image, we emphasize the joint

appearances and use them effectively in our model. Our model estimates the twist angles with an average

radian error of 0.14, and we show that estimation of twist rotations achieves a more precise 3D human pose.

1 INTRODUCTION

In recent years, monocular 3D human pose estimation

has been attracting attention in the computer vision

field. Monocular 3D human pose estimation makes it

possible to capture human motions in 3D space with-

out dedicated devices, and it is expected that it will be

used for many applications such as CG character con-

trol and human motion analysis in sports or surveil-

lance.

3D human poses are generally described in two

ways: 3D joint locations with their connections or 3D

joint rotations with a skeletal body model (Ionescu et

al., 2014). The pose representations based on joint lo-

cations are widely used and the estimation methods

have been improved in terms of robustness and run-

time efficiency (Mehta et al., 2017; Xu et al., 2020).

However, most of the representations are too ambig-

uous to express precise poses such as twist of limbs as

shown in Figure 1, and they lack the precision needed

for some applications like CG character control.

On the other hand, the representations based on

joint rotations against the template pose express more

precise poses. The pose parameters of the SMPL body

model (Loper et al., 2015) are a well-known example.

The SMPL body model reconstructs a 3D body mesh

and joint locations depending on the shape and pose

parameters. There are a variety of approaches (Bogo

et al., 2016; Kanazawa et al., 2017; Pavlakos et al.,

2019) that can be used to estimate pose parameters,

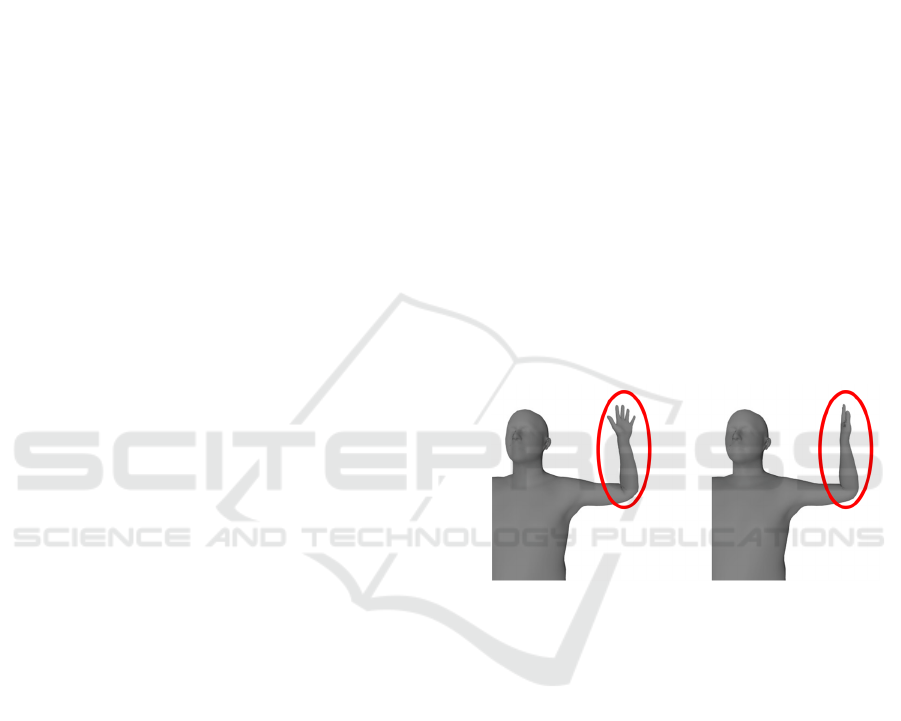
Figure 1: An example for different poses with same body

joint locations of the left elbow and left wrist. Body joint

locations have ambiguities to express a 3D body pose.

although these approaches run into difficulties when

estimating actual twist rotations, which are a compo-

nent of joint rotations around connected limbs. This

is because they mainly aim to reduce joint location

errors. Twist rotations are estimated using pose priors

such as angle limitations to avoid unusual poses with

impossible twists, or by using additional body key-

points like finger joints with longer processing time

and a clearer appearance of the whole body.

Our goal is to estimate joint rotations with actual

twist rotations from a single image with a minimal

number of calculations for real-time applications. It is

difficult to estimate twist rotations with the other

components of joint rotations because they are not

clearly visible in images compared to the other com-

ponents such as the swing rotations of limbs. In addi-

tion, it is difficult to train a model to estimate twist

rotations because there are relatively few images of

Nakatsuka, C., Xu, J. and Tasaka, K.

Learning Joint Twist Rotation for 3D Human Pose Estimation from a Single Image.

DOI: 10.5220/0010222703790386

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 5: VISAPP, pages

379-386

ISBN: 978-989-758-488-6

379

people twisting their limbs in natural scenes, and it is

difficult to get accurate ground truth for twist rota-

tions from images.

To solve these problems, we focus on estimating

twist angles around limbs by swing-twist decomposi-

tion of joint rotations and emphasizing the appearance

of limb joints because we believe important infor-

mation for twist estimation appears around the joints.

We assume that 3D joint locations are obtainable by

previous approaches (Mehta et al., 2017; Xu et al.,

2020) and they can be utilized to estimate swing rota-

tions. Furthermore, we prepare a pseudo ground truth

of joint rotations for the CMU Panoptic Dataset (Joo

et al., 2015) as the training and evaluation dataset by

using the previous approach (Pavlakos et al., 2019)

and annotating the qualities of their results.

Our model estimates twist angles around arms

with an average radian error of 0.14. Reconstructed

joint rotations with given 3D joint locations and esti-

mated twist angles are improved by an average of

0.08 radians in terms of twist rotations compared to

reconstructed joint rotations with only given 3D joint

locations. We also discuss how twist rotations affect

human body mesh reconstruction.

Our main contributions are summarized as fol-

lows.

 We reduce the difficulty of estimating joint rota-

tions with actual twist rotations by decomposing

joint rotations into swing and twist rotations.

 We present the first model for estimation of actual

twist angles from a single image directly in real

time.

 We show how estimation of twist rotations

achieves a more precise 3D human pose.

Below, we review studies related to 3D human

pose estimation with joint rotations (Section 2). Then,

we present the data preparation method and our ap-

proach (Sections 3 and 4). In the experimental section

(Section 5), we demonstrate the performance of our

approach and discuss the results. Finally, we present

our conclusion and future work (Section 6).

2 RELATED WORK

There are many 3D pose estimation approaches. Here,

we discuss the most relevant approaches for handling

3D joint rotations with a skeletal body model.

Bogo et al. (2016), Lassner et al. (2017), Xiang et

al. (2018), Pavlakos et al. (2019) and Mehta et al.

(2019) proposed model fitting approaches to estimate

pose and shape parameters for a skeletal body model

from a single image. They extract 2D landmarks or

3D features from a single image and optimize body

model parameters to fit to this geometric information

and other additional information such as pose priors

and time consistency. Pose prior has some variations,

and Murthy et al. (2019) proposed priors that de-

scribed the relationship between swing and twist ro-

tations. Such additional information is effective for

avoiding strange poses. However, it is not sufficient

for estimation of precise poses including actual twist

rotations. As shown in some previous studies (Lass-

ner et al., 2017; Xiang et al., 2018; Pavlakos et al.,

2019), more geometric information allows poses to be

estimated more precisely, however, it increases com-

putational complexity. We aim to estimate actual

twist rotations with a small number of calculations.

Another research group (Kanazawa et al., 2017;

Omran et al., 2018; Pavlakos et al., 2018; Rong et al.,

2019) proposed direct regression approaches for pose

parameters. They use 2D keypoints or body part seg-

mentation as an explicit intermediate representation

to regress pose parameters. Their approaches are

computationally rapid, but tend to be less accurate be-

cause pose parameter regression encounters problems

due to the complexity and discontinuity of 3D rota-

tions. Kolotouros et al. (2019a) attempt to integrate

these direct regression approaches with model fitting

approaches, which tend to be slow but accurate, to

compensate for the disadvantages of each approach.

However, it is still difficult to estimate precise and

accurate poses with a smaller number of calculations.

More recent approaches (Zhou et al., 2019; Varol

et al., 2018; Kolotouros et al., 2019b) avoid regress-

ing pose parameters directly. Zhou et al. (2019) re-

gress joint rotations by using 5D and 6D rotation rep-

resentations instead of pose parameters as more suit-

able representations for neural networks. Varol et al.

(2018) and Kolotouros et al. (2019b) attempt to di-

rectly regress the body mesh from a single image.

They obtained accurate and precise results with fewer

calculations. However, their method requires high

cost 3D mesh annotations for training. We regress the

twist angles as a simpler target than 5D/6D rotation

or 3D meshes without high cost annotations such as

3D meshes.

3 DATA PREPARATION

In the training and evaluation phases of our approach,

we require human images with their 3D joint rotations

including accurate twist rotations. There are several

datasets suitable for performing 3D human pose esti-

mation from images (Ionescu et al., 2014; Joo et al.,

2015; Lassner et al, 2017). We avoid datasets with

motion sensors because sensors will become noise on

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

380

the human body appearance when extracting essential

features about twist rotations that are not clearly visi-

ble in images.

We use the CMU Panoptic Dataset (Joo et al.,

2015) because it has a huge number of natural human

multiview images with camera parameters and accu-

rate 3D pose annotations. In the CMU Panoptic Da-

taset, 3D pose annotations are described in 3D joint

locations for just the body or body and hands, and

they have no twist rotation data. We predict joint ro-

tations and twist rotations from the existing annota-

tions of 3D body and hands joint locations using the

SMPLify-x method (Pavlakos et al., 2019), which is

able to estimate pose parameters of the SMPL body

model accurately and precisely. We customize the

SMPLify-x method by fitting the body model to 3D

joint locations instead of 2D joint locations. Then, we

select high-quality predictions manually. “High qual-

ity” means the body joint locations and the palm ori-

entations of the reconstructed SMPL model are visu-

ally consistent with the pose of the person in the im-

age. Twist rotations are extracted as pseudo ground

truth from the selected predictions and 3D joint loca-

tions. Note that we create annotations of twist rota-

tions solely around the arms and we ignore pose pa-

rameter errors for the lower body because there are

few high-quality results for the whole body due to the

relatively sparse annotations for the lower body in the

original CMU Panoptic dataset.

Here, we explain SMPL pose parameters and our

settings. The SMPL body model defines the kinematic

tree with the pelvis as the root (e.g. the child joint of

the shoulder is the elbow.) As shown in Figure 2, joint

rotations of SMPL pose parameters mean the relative

rotation for their child joints and the connected limbs

around them, and they can be decomposed to swing

and twist rotations. Joint rotations of the SMPL pose

parameters are described by angle-axis representations.

The 3D mesh of the SMPL model is controlled by the

pose and shape parameters, and 3D joint locations are

regressed from the mesh. For simplicity, we assume

that the shape parameter is always set to zero; meaning

a normal body shape. We refer to the pose with zero

pose parameters as the “T pose”.

Figure 2: Left sphere is the parent joint and right sphere is

the child joint. There is a limb between both joints. The joint

rotation for the parent joint is decomposed into swing and

twist rotations.

For extraction of twist rotations, we follow the

swing-twist decomposition formula of Dobrowolski

(2015) as the direct method. First, we convert the

joint rotations adopted as the pose parameters to qua-

ternion representations from axis-angle representa-

tions. Let 𝑅



be the rotation of joint 𝐽



(𝑗=0,…,3 for

right/left shoulder and right/left elbow). For the fol-

lowing explanations, we designate the conversion

from axis-angle representation to quaternion repre-

sentation as 𝜑 and inverse conversion as 𝜓. We as-

sume that 𝑅



can be decomposed to the swing rotation

𝑆



and the twist rotations 𝑇



as formula (1).

𝑅



=𝑇



∙𝑆



(1)

Let 𝑣



be the direction vector from joint 𝐽



to its child

joint 𝐽





on T pose, and rotate 𝑣



by 𝑅



or 𝑆



; then we

obtain rotated direction vector 𝑤



as formula (2).

𝑤



=𝑅



∙

𝑣



∙𝑅





=𝑆



∙

𝑣



∙𝑆





(2)

𝑆



can be calculated from 𝑣



and 𝑤



by formula (3).

𝑆



=𝜑cos



𝑣



∙𝑤



∙

𝑣



𝑤



𝑣



𝑤







(3)

Here, we get the twist rotation 𝑇



and the twist angle

𝜃



around its rotation axis.

𝑇



=𝑅



∙𝑆





(4)

𝜃



=

𝜓𝑇



, 𝑖𝑓

𝜓𝑇





𝜓𝑇





=𝑤



𝜓𝑇



, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

(5)

Finally, we convert the range of angles 𝜃



from

2𝜋,2𝜋 to



𝜋,𝜋



. The twist angle is a simpler

representation than the other representations. In our

method, we represent twist rotations by twist angles

expressed in radians.

Learning Joint Twist Rotation for 3D Human Pose Estimation from a Single Image

381

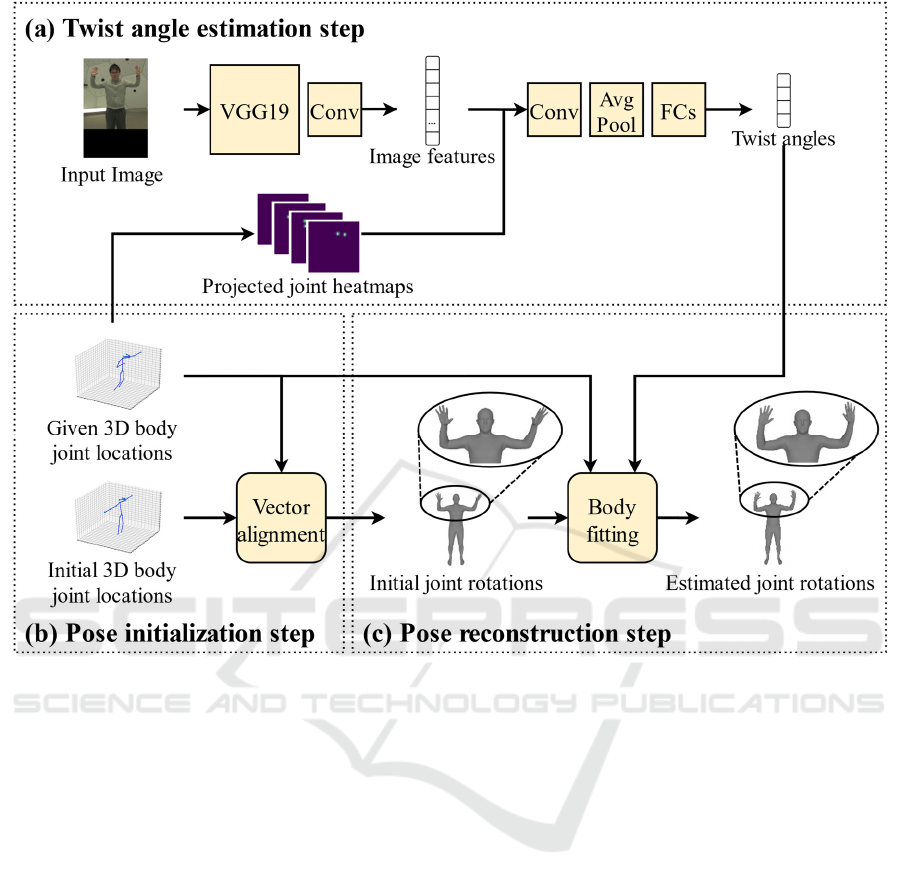
Figure 3: (a)Twist angle estimation step. Our model estimates twist angles around arms from a single RGB image and the

heatmaps for projecting the parent joint and child joint locations on the input image. (b) Pose initialization step. Initial 3D

body joint locations (T pose) and given 3D body joint locations undergo vector alignment to calculate the rotations between

the direction vectors for each limb, and the skeletal body model is initialized by the calculated joint rotations. (c) Pose recon-

struction step. The initialized skeletal body model undergoes body fitting so that its 3D body joint locations correspond more

closely to the given locations and its twist angles around the arms correspond more closely to estimated angles.

4 APPROACH

We propose an approach to estimate twist angles

around arms from a single RGB image and recon-

struct the skeletal body pose by using given 3D

body joint locations and estimated twist angles

around arms. Our approach has 3 steps: twist angle

estimation step (Section 4.1), pose initialization

step (Section 4.2) and pose reconstruction step

(Section 4.3). An overview is shown in Figure 3.

4.1 Twist Angle Estimation

Our model estimates twist angles around arms from

a single RGB image and the heatmaps for the pro-

jected parent joint and child joint locations on the

input image as shown in Figure 3(a).

First, we extract image features 𝐹 from a single

RGB image 𝐼∈ℝ



by using the first 10 lay-

ers of the pretrained VGG19 from the ImageNet

dataset (Simonyan & Zisserman, 2014) and one

convolutional layer. In our approach, the input im-

age 𝐼 is assumed to contain a single person. We

consider that the twist rotation around a limb

mainly affects the appearance of its parent and

child joint. Thus, we also create the heatmaps

𝐻

,



∈ℝ



for the locations of the parent joint 𝐽



and child joint 𝐽





on the input image 𝐼. The joint

locations on the image are projected from given 3D

body joint locations and given camera parameters.

Here, the heatmap 𝐻

,



is calculated by formulas

(6) and (7).

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

382

𝐻





𝑝



=exp

𝑝  𝑙





𝜎





(6)

𝐻

,





𝑝



=max 𝐻



𝑝,𝑙



,𝐻



𝑝,𝑙







(7)

Where 𝐻



∈ℝ



is the heatmap of the joint 𝐽



loca-

tion, 𝑝∈ℝ



is any location on heatmaps, 𝐻



∙



is the

value of the heatmap on the input location, 𝑙



∈ℝ



the location of 𝐽



and 𝜎



controls the spread of the

peak on the heatmap. These heatmaps 𝐻

,



and image

features 𝐹 are concatenated to emphasize the image

features around the parent and child joints effectively,

and then they are passed to the convolutional layer,

average pooling layer, and three fully connected lay-

ers.

Thereby, we obtain the set of twist angles 𝜃

∗

. The

range of these twist angles is



𝜋,𝜋



, however, the

valid range for human joints is limited around zero.

Therefore, we do not need to consider the singularity

around 𝜋 and 𝜋. For this reason, we simply adopt

the mean squared error as the loss function for 𝜃

∗

The 𝜃

∗

and the ground truth 𝜃 are the normalized

range from



𝜋,𝜋





0,1



by formula (8) for sim-

plicity of training, and our model is trained by mini-

mizing the loss function ℒ𝑜𝑠𝑠





defined by for-

mula (9).

𝜃

𝜃𝜋

𝜋

(8)

ℒ𝑜𝑠𝑠





=𝜃

𝜃

∗







(9)

4.2 Pose Initialization

In the pose initialization step, the skeletal body model

is initialized to make the following pose reconstruc-

tion step easier as shown in Figure 3(b). We make the

relative joint locations of the skeletal body model

closer to given 3D body joint locations. We call the

joint locations of the skeletal body model with T pose

as the initial 3D body joint locations. The vector from

a specific joint location to its child joint location is

called as a limb direction vector. The pair of limb di-

rection vectors for the initial joint locations and given

joint locations are applied to the vector alignment.

Vector alignment means calculating a rotation be-

tween the pair of direction vectors in the same manner

as expressed in the formula (3). The skeletal body

model is initialized by the obtained joint rotations.

Figure 4: The distributions for twist angles around the arms

of (a) training and (b) evaluation dataset. The title of each

graph is the parent joint name of the target limb.

4.3 Pose Reconstruction

In the pose reconstruction step, the skeletal body

model is optimized to fit the given 3D body joint lo-

cations and estimated twist angles as shown in Figure

3(c). We seek to minimize the objective function

ℒ𝑜𝑠𝑠



defined in formula (10) to (12) by using the

Levenberg-Marquardt algorithm.

ℒ

𝑜𝑠𝑠



=𝐿



𝐿







(10)

ℒ

𝑜𝑠𝑠



=𝜃



𝜃

∗





(11)

ℒ

𝑜𝑠𝑠



ℒ

𝑜𝑠𝑠



𝜀ℒ𝑜𝑠𝑠



(12)

Where 𝐿



and 𝐿



are the 3D body joint loca-

tions of the current skeletal body pose and given pose.

𝜃



is the twist angles around arms calculated from

the current skeletal body pose by formulas (1) to (5).

The 𝜀 controls the weight for ℒ𝑜𝑠𝑠



. Finally, we

obtain the prediction of the joint rotations.

Learning Joint Twist Rotation for 3D Human Pose Estimation from a Single Image

383

Figure 5: Body meshes reconstructed by the ground truth joint rotations (GT), initial joint rotations at the pose initialization

step (Initialized), estimated joint rotations without twist angle estimation (Estimated w/o twist angle) and estimated joint

rotations with twist angle estimation (Ours). Our approach improves the twist of arms (solid line circle) compared to the result

without twist angle estimation (dotted line circle).

Table 1: The mean error of estimated twist angles (radian)

for the evaluation dataset (623 poses) with some of them

having a large twist angle around any limb (96 poses).

parent joint

name

LSho RSho LElb RElb

eval data 0.06 0.17 0.18 0.15

w large twist 0.06 0.20 0.17 0.17

5 EXPERIMENTS

We present the performance of our approach by eval-

uating the accuracy of the twist angle estimated at the

first step and the poses reconstructed at the final step

and the computational efficiency. Reconstructed

poses are evaluated in terms of twist angle errors,

joint rotation errors and vertex errors. First, we show

our dataset and training details, and then each result

is described and discussed.

5.1 Dataset and Training Details

Our dataset prepared in Section 3 provides the human

body images with the ground truth joint rotations and

locations. It has 2,042 poses with 61,539 images from

multiple views and 7 video sequences for training,

and 623 poses with 623 images from a single view

and 2 video sequences for evaluation. These 9 video

sequences are the same as the sequences used in the

experiments conducted by Xiang et al. (2019). Figure

4 shows the distributions for twist angles around arms

of a (a) training and (b) evaluation dataset. Twist an-

gles are concentrated on small values, and it makes

training difficult.

Our model requires an input image size of

368x368 (single person cropped). We train our model

for 19.7K iterations with 8 images in a batch.

5.2 Twist Angle Estimation Accuracy

We evaluate our model at the twist angle estimation

step. Our approach requires 3D body joint locations

as input. We use the ground truth locations for our all

evaluation to focus on twist of arms. Table 1 shows

the mean error of estimated twist angles in radians for

the evaluation dataset with 623 poses and some of

them with 96 poses including a large twist angle (over

0.35 radians) around any limb. The estimated twist

angles for the evaluation dataset has small errors from

0.06 to 0.18 with an average of 0.14 radians. There

are few poses with a large twist angle in the training

dataset as shown in Figure 4(a), however, the errors

for the evaluation dataset with large twist angles are

still relatively small from 0.06 to 0.20 with an average

of 0.15 radians. It means our model makes it possible

to capture the magnitude of the twist around arms ro-

bustly from a whole-body image and the heatmaps of

joint locations.

5.3 Pose Reconstruction Accuracy

We evaluate reconstructed joint rotations at the final

step of our approach and show the effect of the twist

angles estimated at the first step by comparing with

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

384

the poses reconstructed without twist angles. The 𝜀 in

formula (12) is 0.02 for reconstruction with twist an-

gles and the 𝜀 is zero for reconstruction without twist

angles. Table 2(a) shows the mean error of twist an-

gles in radians calculated from the reconstructed joint

rotations in the same manner as formulas (1) to (5).

Results were obtained for the entire evaluation data

and part of the data having a large twist angle around

any limb. For the entire evaluation data, estimated

twist angles improve the results by a max of 0.15 and

an average of 0.08 radians, and for the data with a

large twist angle, a greater effect was observed for

most joints, improving by a max of 0.33 and an aver-

age of 0.12 radians.

We also evaluate the result by the quaternion error

of joint rotations. Quaternion error 𝐸



shows the

magnitude of rotation between two rotations, and it is

defined by formula (13).

𝐸



‖

𝜓



𝑄



∙𝑄





‖

(13)

Where 𝑄



and 𝑄



are respectively the esti-

mated and ground truth joint rotations in quaternion

representation. The mean quaternion errors

with/without estimated twist angles for the entire/part

of the evaluation data are shown in Table 2(b). The

estimated twist angles improve the results especially

for elbow rotations. Table 2(a) and Table 2(b) show

that the errors for right shoulder rotations for the data

with a large twist angle are increased by estimated

twist angles. Estimated twist angles around the limb

connected to the right shoulder are relatively inaccu-

rate as shown in Table 1, and it makes the optimiza-

tion around the right shoulder difficult. We consider

that the lower accuracy of estimated twist angles for

the right shoulder is caused by data bias. The evalua-

tion dataset includes the rare right shoulder postures

for training data.

In Table 2(c), we present the vertex-to-vertex

(v2v) error of the reconstructed body mesh. The v2v

error is the mean error of the reconstructed mesh ver-

tex locations. They are usually used for evaluation of

reconstructed joint rotations. There are negligible dif-

ferences between the v2v error results. It is not suita-

ble for evaluation of twist estimation because the dis-

placement of limb meshes caused by a twist rotation

is minor in comparison with whole body meshes. In

addition, these v2v errors are much smaller than pre-

vious approaches in general because the precise 3D

body joint locations are given as input unlike previous

ones.

Finally, we show that the estimated twist angles

improve the quality of body mesh reconstruction

around arms in Figure 5. It’s highly effective against

body meshes with large twist angles.

5.4 Runtime and Model Size

On a NVIDIA TITAN V GPU, our model at the twist

angle estimation step is small with 41.98 MB param-

eters, and it performs very rapidly at 5 msec/person.

It shows our model estimates twist angles from a sin-

gle image directly in real time. However, the pose re-

construction step takes 139 msec/person on 12 CPUs

(Intel(R) Core(TM) i7-8700K CPU @ 3.70GHz) and

the total processing time is 189 msec/person. Alt-

hough it is difficult to make a direct comparison due

to differences in input and output data, SMPLify-x

method (Pavlakos et al., 2019), which is able to esti-

mate the poses accurately and precisely, takes much

longer time in our environment.

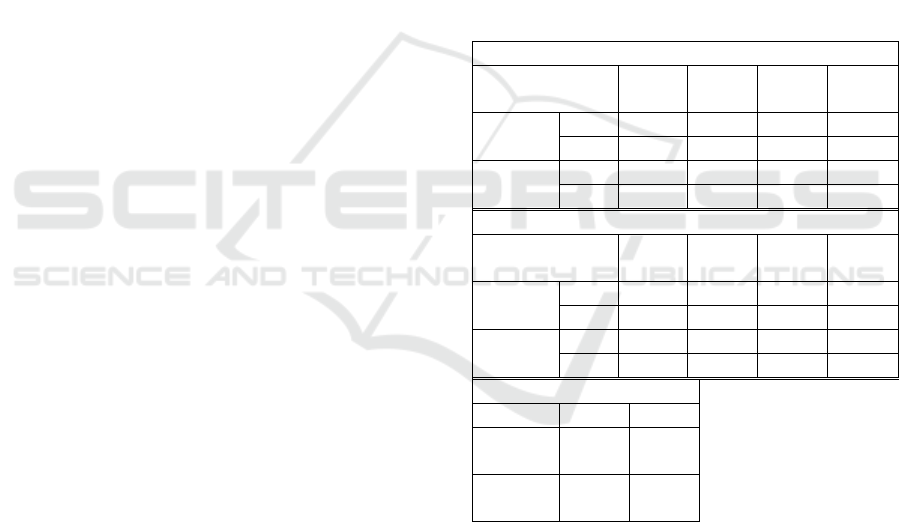
Table 2: The mean error of (a) twist angles (radian)/(b) qua-

ternions (radian)/(c) v2v (mm) calculated from the recon-

structed joint rotations with/without estimated twist angles

for entire/part of the evaluation data.

(a)

parent joint

name

LSho RSho LElb RElb

eval

data

w 0.29

0.23 0.15 0.20

w/o 0.29 0.32 0.30 0.27

w large

twist

w 0.23 0.42

0.28 0.30

w/o 0.25 0.25 0.61 0.60

(b)

parent joint

name

LSho RSho LElb RElb

eval

data

w 0.42 0.37

0.50 0.50

w/o 0.39 0.39 0.64 0.65

w large

twist

w 0.33 0.52

0.56 0.59

w/o 0.32 0.34 0.87 0.91

(c)

w w/o

eval

data

20.74 20.13

w large

twist

26.34 25.67

6 CONCLUSION

We proposed a novel approach to estimate twist rota-

tions around limbs to improve 3D human pose esti-

mation from a single RGB image. Previous vision-

based approaches did not handle twist rotations

around limbs directly because of their ambiguity. Our

experiments demonstrated the feasibility of estimat-

ing twist rotations from an image and its effect on

pose reconstruction using a skeletal body model.

Learning Joint Twist Rotation for 3D Human Pose Estimation from a Single Image

385

There is no enough dataset which includes 3D

joint rotations on images, so we focus on normal twist

rotations around the arms. As future work, we will

create a larger dataset to evaluate our model in more

detail and estimate twist rotations around the other

limbs including variety of poses. We also believe cre-

ating a larger dataset for training and applying data

balancing to twist angles bias would be effective

strategies to improve the robustness and accuracy of

our model. We will also tackle the problems of pose

reconstruction from noisy 3D body joint locations and

make a performance comparison between previous

approaches and ours.

REFERENCES

Bogo, F., Kanazawa, A., Lassner, C., Gehler, P., Romero,

J., & Black, M. J. (2016). Keep It SMPL: Automatic

Estimation of 3D Human Pose and Shape from a Single

Image. ECCV, 561–578.

Dobrowolski, P. (2015). Swing-twist decomposition in

Clifford algebra. In arXiv [cs.RO]. arXiv.

http://arxiv.org/abs/1506.05481

Ionescu, C., Papava, D., Olaru, V., & Sminchisescu, C.

(2014). Human3.6M: Large Scale Datasets and Predic-

tive Methods for 3D Human Sensing in Natural Envi-

ronments. TPAMI/PAMI, 36(7), 1325–1339.

Joo, H., Liu, H., Tan, L., Gui, L., Nabbe, B., Matthews, I.,

Kanade, T., Nobuhara, S., & Sheikh, Y. (2015). Panop-

tic studio: A massively multiview system for social mo-

tion capture. ICCV, 3334–3342.

Kanazawa, A., Black, M. J., Jacobs, D. W., & Malik, J.

(2018). End-to-end recovery of human shape and pose.

CVPR, 7122–7131.

Kolotouros, N., Pavlakos, G., Black, M. J., & Daniilidis, K.

(2019a). Learning to reconstruct 3D human pose and

shape via model-fitting in the loop. ICCV, 2252–2261.

Kolotouros, N., Pavlakos, G., & Daniilidis, K. (2019b).

Convolutional mesh regression for single-image human

shape reconstruction. CVPR, 4501–4510.

Lassner, C., Romero, J., Kiefel, M., Bogo, F., Black, M. J.,

& Gehler, P. V. (2017). Unite the people: Closing the

loop between 3d and 2d human representations. CVPR,

6050–6059.

Loper, M., Mahmood, N., Romero, J., Pons-Moll, G., &

Black, M. J. (2015). SMPL: a skinned multi-person lin-

ear model. TOG, 34(6), 1–16.

Mehta, D., Sotnychenko, O., Mueller, F., Xu, W., Elgharib,

M., Fua, P., Seidel, H.-P., Rhodin, H., Pons-Moll, G.,

& Theobalt, C. (2020). XNect: Real-time Multi-Person

3D Motion Capture with a Single RGB Camera. TOG,

39(4), 82:1–82:17.

Mehta, D., Sridhar, S., Sotnychenko, O., Rhodin, H.,

Shafiei, M., Seidel, H.-P., Xu, W., Casas, D., & Theo-

balt, C. (2017). VNect: real-time 3D human pose esti-

mation with a single RGB camera. TOG, 36(4), 1–14.

Murthy, P., Butt, H. T., Hiremath, S., Khoshhal, A., &

Stricker, D. (2019). Learning 3D joint constraints from

vision-based motion capture datasets. IPSJ Transac-

tions on Computer Vision and Applications, 11(1), 5.

Omran, M., Lassner, C., Pons-Moll, G., Gehler, P., &

Schiele, B. (2018). Neural Body Fitting: Unifying Deep

Learning and Model Based Human Pose and Shape Es-

timation. 3DV, 484–494.

Pavlakos, G., Choutas, V., Ghorbani, N., Bolkart, T., Os-

man, A. A., Tzionas, D., & Black, M. J. (2019). Expres-

sive Body Capture: 3D Hands, Face, and Body From a

Single Image. CVPR, 10967–10977.

Pavlakos, G., Zhu, L., Zhou, X., & Daniilidis, K. (2018).

Learning to estimate 3D human pose and shape from a

single color image. CVPR, 459–468.

Rong, Y., Liu, Z., Li, C., Cao, K., & Loy, C. C. (2019).

Delving deep into hybrid annotations for 3d human re-

covery in the wild. ICCV, 5340–5348.

Simonyan, K., & Zisserman, A. (2015). Very Deep Convo-

lutional Networks for Large-Scale Image Recognition.

ICLR.

Varol, G., Ceylan, D., Russell, B., Yang, J., Yumer, E., Lap-

tev, I., & Schmid, C. (2018). Bodynet: Volumetric in-

ference of 3d human body shapes. ECCV, 20–36.

Xiang, D., Joo, H., & Sheikh, Y. (2019). Monocular total

capture: Posing face, body, and hands in the wild.

CVPR, 10965–10974.

Xu, J., Yu, Z., Ni, B., Yang, J., Yang, X., & Zhang, W.

(2020). Deep Kinematics Analysis for Monocular 3D

Human Pose Estimation. CVPR, 899–908.

Zhou, Y., Barnes, C., Lu, J., Yang, J., & Li, H. (2019). On

the Continuity of Rotation Representations in Neural

Networks. CVPR, 5738–5746.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

386