Detection of Error Correlates in the Motor Cortex in a Long Term

Clinical Trial of ECoG based Brain Computer Interface

Vincent Rouanne

, Maciej Śliwowski

1,2 b

, Thomas Costecalde

, Alim Louis Benabid

1,3 d

and Tetiana Aksenova

Univ. Grenoble Alpes, CEA, LETI, Clinatec, F-38000 Grenoble, France

CEA, LIST, Gif-sur-Yvette, France

CHU Grenoble Alpes, Grenoble, France

Keywords: Brain Computer Interface, Error Correlates, Sensory-motor Cortex, Machine Learning, Clinical Trial,

Tetraplegic Subject.

Abstract: Error correlates are thought to be promising for BCIs as a way to perform error correction or prevention, or

to label data in order to perform online adaptation of BCIs’ control models. Current state-of-the-art BCIs are

motor-imagery-based invasive BCIs and thus have no access to neural data apart from sensory-motor cortices.

We investigated at the single trial level the presence and detectability of error correlates in the primary motor

cortex during observation or motor imagery (MI) control of a BCI with two discrete classes by a tetraplegic

user. We show that error correlates can be detected using a broad range of classifiers, namely Support Vector

Machine (SVM), logistic regression, N-way Partial Least Squares (NPLS), Multilayer Perceptron (MLP) and

Convolutional Neural Network (CNN) with respective mean AUC of the ROC curve of 0.645, 0.662, 0.642,

0.680 and 0.630 in the observation condition, and 0.623, 0.605, 0.603, 0.626 and 0.580 in the MI-control

condition. We also suggest that these error correlates are stable in time. These findings suggest that error

correlates could be used in clinical trials using invasive motor-imagery-based BCIs for error correction or

prevention.

1 INTRODUCTION

Brain computer interfaces (BCI) are promising tools

that use neural signal recordings to directly control

effectors. However, BCIs are currently mostly used in

research laboratories due to several limitations,

including their often too low performances and their

requirement to be calibrated in specific conditions

with the assistance of a researcher. Both of these

issues can be alleviated using a biomimetic strategy

of learning for the training of the decoder of the BCI.

In humans, brain signals that generate correct actions

can be reinforced, while action recognized as

erroneous can be corrected and may have also

reduced probability of being performed in the future.

This learning requires feedback in order to know if a

given action was correct or erroneous. In the case of



https://orcid.org/0000-0001-7708-8176

https://orcid.org/0000-0001-6744-1714

https://orcid.org/0000-0003-2216-4447

https://orcid.org/0000-0002-4479-1807

https://orcid.org/0000-0003-4007-2343

an action performed by a human controlled BCI, the

human receives feedback (e.g. visual) regarding the

success of the action, whereas the machine does not.

Having the user consciously (e.g. orally or physically)

transferring this feedback to the BCI may be tiring,

impractical or even impossible depending on the

condition of the user. However, the feedback received

by the user may produce specific brain activity. A

BCI able to detect such brain activity would thus have

access to learning-enabling feedback. Brain activity

correlated to errors was recorded as early as 1991 in

the experiments of Falkenstein et al. (1991).

Detection of error correlates during BCI operation

can provide a way to either correct mistakes after they

have been performed or train or update the models

used to control the BCI (Chavarriaga, Sobolewski, &

Millan, 2014). The ability to reliably detect error

Rouanne, V.,

Sliwowski, M., Costecalde, T., Benabid, A. and Aksenova, T.

Detection of Error Correlates in the Motor Cortex in a Long Term Clinical Trial of ECoG based Brain Computer Interface.

DOI: 10.5220/0010227800260034

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 26-34

ISBN: 978-989-758-490-9

correlates in brain signals is thus valuable for the

development of BCIs.

Although error correlates can be used directly as

control signals to operate a BCI (Chavarriaga,

Iturrate, & Millan, 2016), we are interested here in

their use as a secondary signal acquired to improve

the performance of BCIs. Notably, error correlates

have been used in simulations and online experiments

to automatically correct errors during BCI operation

(Even-Chen et al., 2018; Parra, Spence, Gerson, &

Sajda, 2003) or to update control models without the

use of new externally labeled data (Blumberg et al.,

2007; Spüler, Rosenstiel, & Bogdan, 2012).

The error correlate discovered by Falkenstein et

al. (1991) is the error-related signal mostly used in

BCI applications. This waveform called the error-

related potential (ErrP) is composed of a negative

potential deflection over the fronto-central scalp area

roughly 50 to 100ms after the event that induced it,

followed by a centro-parietal positive deflection

(Chavarriaga, Sobolewski, & Millan, 2014).

Conveniently for BCI, ErrPs are relatively stable

across time and tasks (Chavarriaga & Millan, 2010;

Ferrez & del R. Millan, 2008), are elicited when an

error is performed by a BCI controlled or observed by

a user (Ferrez & del R. Millan, 2008; Schalk,

Wolpaw, McFarland, & Pfurtscheller, 2000) and are

detectable at the single-trial level (Parra, Spence,

Gerson, & Sajda, 2003). However, the localization of

these ErrPs is a drawback for current state-of-the-art

BCIs. The BCIs best in terms of performance are

invasive and thus often have access to limited

recording areas over or in the brain (Benabid et al.,

2019; Wodlinger et al., 2014). The primary sensory-

motor cortex is the best candidate for the recording

area of an invasive BCI due to its ability to generate

motor imagery signals. In such circumstances, ErrPs

cannot be recorded when using these BCIs. We focus

hereafter on the specific case of BCIs that acquire

brain signals from the sensory-motor cortex only.

ErrPs are not the only error correlates that can be

recorded from brain signals. Error correlates have

been reported in the primary motor and

somatosensory cortex. In a MEG study, Koelewijn et

al. (2008) reported a stronger beta rebound after an

outcome error than after a correct task outcome, both

when observing or performing a motor task. Previous

work by van Schie et al. (2004) demonstrated the

existence of error correlates in the motor cortex by

showcasing the variability of the lateralized readiness

potential between correct and erroneous response in

an Eriksen flanker task. Although their experiment

was performed on non-human primates and using

intracortical electrodes, Inoue et al. (2016)

successfully showed that end-point errors during

reaching tasks are encoded in the primary motor

cortex. Maybe more importantly, they provided

evidence that these error signals are necessary for

adaptation in reaching movements. In an EEG-ECoG

combined study, Völker et al. (2018) showed that

error processing in the human brain involved

modulation of brain activity in the high gamma

frequency band (60-90Hz), including modulations in

the precentral gyrus and post central gyrus. These

findings are consistent with the more recent study by

Wilson et al. (2019), in which they also found an

increase in the high gamma frequency band (70-

100Hz) after erroneous BCI task outcomes with

respect to correct ones. Finally, Milekovic et al.

(2012, 2013) reported detection of errors at the single

trial-level using ECoG in the motor region

(accuracy76%) during motor execution by able-

bodied subjects. Apart from Milekovic et al., no

single-trial detection of error correlates in the motor

cortex have been reported. However, Milekovic et

al.’s studies have the drawbacks of being performed

with overt movement tasks instead of BCI operation

by tetraplegic user with motor imagery. Additionally,

these studies were performed with subjects implanted

with large ECoG grids due to intractable epilepsy.

Although they report detectability using electrodes

located over the motor cortex, this does not insure the

detectability using electrodes positioned with motor

imagery for BCI in mind.

In this study, we perform an experiment where a

tetraplegic user receives erroneous feedback from a

BCI while observing or controlling its actions. Neural

data are acquired using chronic ECoG implants

located over the left and right primary sensory-motor

cortex. The BCI is controlled using motor imagery

and errors should be detected on a single trial basis

using the brain data recorded from the motor cortex.

Several decoding models are trained for the purpose

of detecting error correlates.

2 METHODS

2.1 Data Recording

The subject in this experiment was a 28-year-old male

who had tetraplegia following a C4-C5 spinal cord

injury (ASIA scale levels of the subject are presented

in Benabid et al. (2019)). The subject was implanted

with two WIMAGINE (Mestais et al., 2015) ECoG

implants 24 months prior to the experiments in this

study, as a participant in the clinical trial “BCI and

Tetraplegia”. The “BCI and Tetraplegia” clinical trial

Detection of Error Correlates in the Motor Cortex in a Long Term Clinical Trial of ECoG based Brain Computer Interface

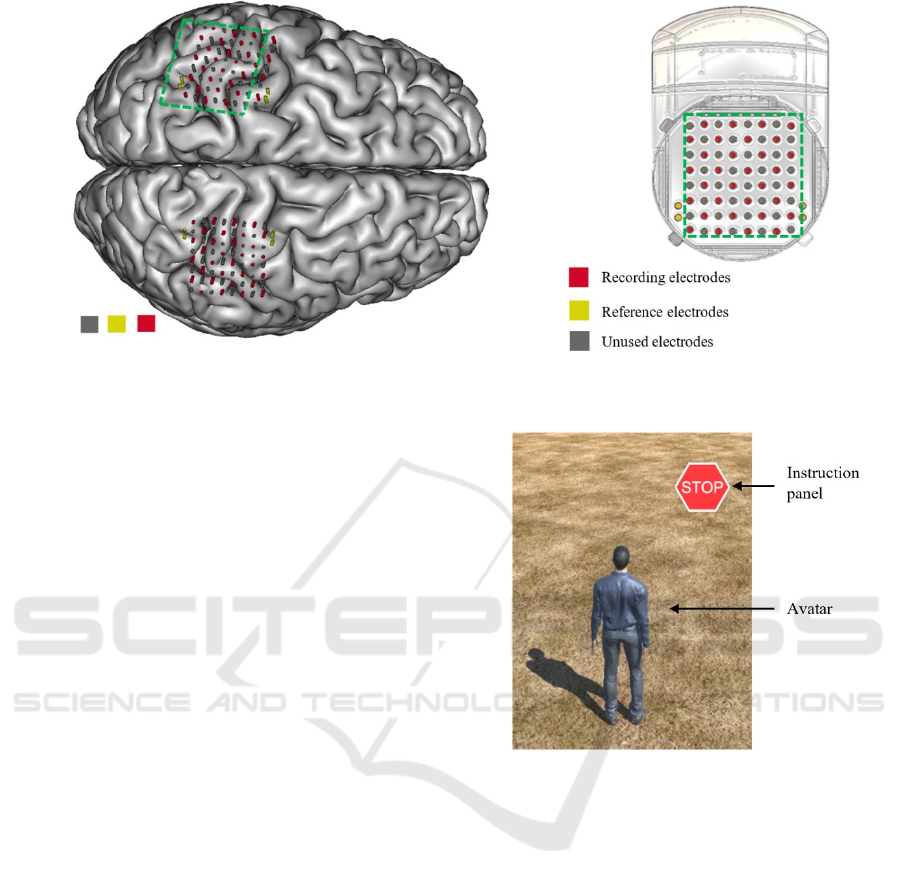
Figure 1: A. Position of the electrodes of each WIMAGINE implant over the right and left sensory-motor areas on a

reconstruction of the subject’s brain from MRI. B. Schematic view of a WIMAGINE implant.

(ClinicalTrials.gov identifier: NCT02550522) was

approved by French authorities: Agence nationale de

sécurité du médicament et des produits de santé

(ANSM) with the registration Number: 2015-

A00650-49 and the ethical committee (Comité de

Protection des Personnes - CPP) with the Registration

number: 15-CHUG-19. The implants were

positioned over the left and right sensory-motor

cortex (Figure 1). Experimental data was recorded at

a sampling rate of 586Hz from 32 out of the 64

electrodes of each implant because of limited data

rates.

2.2 Experimental Setup

The subject was sited in front of a computer screen

where a human avatar was represented from a third

person perspective. An instruction panel that either

displayed a GO or STOP label was also displayed

(Figure 2). The avatar could either stand still or walk

forward at a fixed speed. Two conditions of control

were designed. In the first condition (condition 1), the

subject had no control over the avatar, which was

controlled by the computer. In the second condition

(condition 2), the avatar was controlled by the subject

using leg motor imagery. The subject was already

trained to control a similar avatar using leg motor

imagery prior to this experiment (Benabid et al.,

2019).

In condition 1, the subject was instructed to focus

on the avatar and to expect the avatar to follow the

instructions displayed on the instruction panel as if he

was controlling the avatar’s actions through motor

imagery. In this condition, the instruction panel

switched its instruction every 5 to 15 seconds. The

Figure 2: The environment is similar to the one in Benabid

et al. (2019). The subject either watched the avatar move

automatically (condition 1), or controlled it using leg motor

imagery (condition 2). When the instruction panel showed

“STOP” the avatar was supposed to stay idle, whereas when

it showed “GO” the avatar was supposed to walk.

avatar followed the change in instruction with a

random reaction speed between 200ms and 500ms.

Additionally, error periods were automatically

introduced in this condition. During error periods, the

avatar switched its state to the opposite of the one

required from the instruction panel. Error and correct

periods always lasted at least two seconds, and error

periods never lasted more than three seconds. Error

periods were introduced at random following the

previous restrictions with an error rate of

approximately two to three errors per minute.

Nineteen sessions of eleven minutes of recording

were acquired over 268 days in condition 1.

In condition 2, the subject controlled the avatar

using leg motor imagery. Walking was triggered by

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

performing both legs motor imagery, while standing

still was performed by not performing motor imagery.

In this condition, the duration of error and correct

periods as well as the error rate were entirely

determined by the control of the subject over the BCI.

Since the subject was already trained for such a task

and had achieved high control of the BCI, a new

control model was built specifically for the

experiment using a purposely-reduced dataset as

training set. This was performed in order to ensure

that errors would still occur in this simple control

paradigm. Thirteen sessions of on average eleven

minutes of recording were acquired over 141 days in

condition 2.

Condition 1 was designed to ensure that error

correlates could be recorded in the motor cortex with

the present electrode setup, without any interference

from motor imagery signals. It also ensured that error

correlates detected in condition 2 were not due to

motor imagery confounds. Condition 2 was designed

to assess if error correlates could be detected while

the BCI was used.

2.3 Data Labelling

In both conditions, the goal of the experiment was to

distinguish correct from erroneous events. Events

were defined as moments when the avatar changes its

state. Specifically, correct events were defined as the

avatar changing its state to the one required by the

instruction panel, and error events were defined as the

avatar changing its state to the opposite of the one

required by the instruction panel. We expected error

correlates to appear after such erroneous events, as

was the case in Milekovic et al. (2013).

Epochs of one second and spaced by 100ms (90%

overlap) were considered for the classification of

correct or erroneous events. The first six full epochs

after an event were labeled according to the event

type. The first such epoch contained temporal data

from the event onset to one second after the event.

The last epoch contained temporal data from 0.5s

after the event to 1.5s after the event (Figure 3).

Additionally, epochs that were too close to another

event were discarded. The inclusion of several epochs

for each event was performed with two goals in mind.

The first one is to counterbalance the issue of

synchronization. Indeed the timing of the brain

response to the erroneous or correct events may vary

depending on several conditions, such as the attention

level, the tiredness of the subject, or the workload as

is the case in classical ErrPs paradigms (Iturrate,

Chavarriaga, Montesano, Minguez, & Millán, 2012).

Additionally, there was some jitter in the reaction

Figure 3: Example of an error event where the avatar starts

walking when it is supposed to stay idle. Red dots indicate

epochs belonging to the error class. The first epoch included

contains neural data from the onset of the error to one

second after.

time of the avatar itself to a change of command (e.g.

the avatar must finish a step before stopping), which

was estimated to be up to 300ms. Adding several

epochs for each event increased the probability of

having the desired brain signal in one of them at the

cost of some label uncertainty.

2.4 Feature Extraction

Time-frequency decomposition of brain signals is

classically performed in the literature for the

detection of error correlates in the motor cortex

(Milekovic, Ball, Schulze-Bonhage, Aertsen, &

Mehring, 2012; Wilson et al., 2019). Therefore, time-

frequency information was extracted for each 1s

epoch and for the 64 electrodes. Continuous complex

wavelet transform was applied using a family of

fifteen Morlet wavelets of central frequencies from

10Hz to 150Hz. For each 1s epoch, the absolute value

of this time-frequency data was averaged over the

temporal dimension into ten non-overlapping

windows of 100ms. The resulting feature tensor for

each epoch was thus of shape 10  15  64,

respectively along the temporal, frequential and

spatial dimensions.

2.5 Data Balance

Due to the design of the experiment, there was an

imbalance in the class repartition of the data in both

condition 1 and 2 (Table 1). Additionally, error

epochs and correct epochs could each be of two

separate types. Error epochs could be due to the

avatar starting to walk when expected to stand idle, or

due to the avatar stopping when expected to walk.

Similarly, correct epochs could be due to the avatar

starting to walk when expected to walk or due to the

Detection of Error Correlates in the Motor Cortex in a Long Term Clinical Trial of ECoG based Brain Computer Interface

avatar stopping when expected to stop. The existence

of these sub-classes could potentially create strong

confounds for the error correlate detection if they

were not balanced (e.g. a motor imagery confound in

condition 2). The training dataset was balanced by

oversampling the three sub-classes with the least

number of epochs to the same number of epochs as

the most populated sub-class. Oversampling was

performed by repetition of the epochs present in the

sub-classes.

Table 1: Number of epoch in each class for each condition.

2.6 Decoders

Several decoder types were trained and compared on

both condition 1 and 2. We trained classical decoders

used in BCI studies, namely support vector machine

(SVM), logistic regression, multilayer perceptron

(MLP), convolutional neural networks (CNN) and N-

way partial least squares (NPLS). These decoders

share a characteristic of simplicity as the dataset in

this problem is of high dimensionality (9600 input

features), and with a relatively low amount of samples

(~9000 and ~8000 in condition 1 and 2 respectively).

For various example of use of these decoders for BCI,

the interested reader may refer to Lotte et al. (2018).

2.6.1 SVM & Logistic Regression

SVM and logistic regression are considered as state-

of-the-art methods for binary classification. These

methods are most often used in combination with

kernels, which can act as nonlinear projections of the

input data into high dimensional spaces without

having to specify the transformed input data. Regular

kernels (Gaussian and polynomial) were not used as

in preliminary studies they tended to strongly overfit

the training datasets, even with strong regularization

parameters and low Gaussian kernel scale (<10-5) or

low polynomial kernel order (order of 2 or 3).

Since we have more features in our input dataset

than sample points, regularization was used for both

SVM and logistic regression. For both methods, ridge

regularization was applied. After preliminary results,

lambda was set to one.

2.6.2 NPLS

NPLS is a less known method in the field of BCIs. It

is a linear method that is particularly suitable for

tensor-based high dimensional datasets. It also has the

advantage of being updatable using low

computational power and without requiring to save

the full original training dataset (Eliseyev et al.,

2017).

2.6.3 MLP

MLP is a fully connected feedforward artificial neural

network. It may be interpreted as a logistic regression

model preceded by a nonlinear transformation which

increases predictive power of the model. Proposed

MLP model consisted of one hidden layer with 100

neurons (with learnable weights) followed by a ReLU

activation. As all neurons are connected to each input

component and produce linear combination of input

features, it results in a huge number of parameters to

train. Considering the size of the dataset and number

of parameters we decided to regularize the model by

applying batch normalization, dropout with

probability of a neuron being zeroed 0.5, L2

regularization on model’s weights with lambda equal

0.1 and early stopping on validation set.

2.6.4 CNN

CNNs take advantage of data structure. They are

capable of capturing invariant patterns that may occur

in different parts of the signal. They have less

trainable parameters than similar MLP because of

filters weight sharing which means that the same set

of small filters is applied all over the data. We decided

to use CNN as there is a possible shift in error

correlates synchronization inside epochs. By sliding

convolutional filter over the signal in the time domain

we expected network to recognize error correlates

(which we expect to be time invariant) occurring in

different epoch’s moment with the same filter. It

results in lower number of parameters and possible

higher performance in detecting time invariant

patterns. Proposed CNN used 128 filters of shape

51564 respectively in time, frequency and

channels dimension. Each filter was slid only over

time dimension with stride equal 1. We applied the

same regularization methods as for the MLP.

2.7 Decoder Application and

Performance Evaluation

We report the performance of each model regarding

the desired task, which is the detection of error or

correct events. Up to 6 epochs were used for each

event but the signal corresponding to an error may not

be found in all of these epochs. Events were classified

och t

e Condition 1 Condition 2

Number of

ochs

Correct 7539 4412

Erro

2307 3580

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

as errors as soon as one of their associated epochs was

classified as an error. The number of correct and error

events in each fold are summarized in Table 2 and 3.

The performance of the event decoder was

assessed over a five-fold cross-validation performed

across sessions, which means that an equal number of

sessions was presented in each of the five data splits.

Each split was used as a testing fold once, with the

corresponding other four splits used as training fold.

The performance of each decoder was evaluated

using the area under the curve (AUC) of the receiver

operating characteristic (ROC) curve for each test

fold of the cross-validation, for the task of event

classification.

Table 2: Repartition of error and correct events in each fold

for condition 1 (observation).

Event

Fold

Train

Correct 1006 992 985 981 1072

Erro

283 308 316 317 332

Test

Correct 253 267 274 278 187

Erro

106 81 73 72 57

Table 3: Repartition of error and correct events in each fold

for condition 2 (control with motor imagery).

Event

Fold

Train

Correct 633 554 558 590 609

Erro

519 457 464 469 483

Test

Correct 103 182 178 146 127

Erro

79 141 134 129 115

3 RESULTS

In the first condition the avatar was not controlled by

the subject and the subject monitored only the actions

taken by the BCI. In the second condition the state of

the avatar was controlled by the user through leg

motor imagery. The results for each decoder and

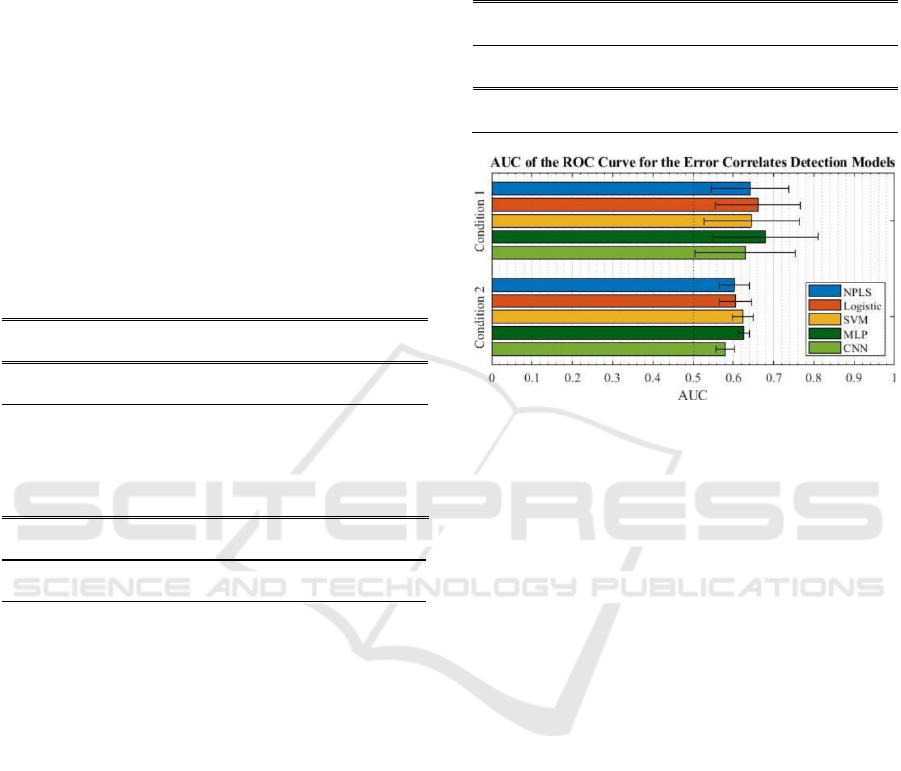
condition are summarized in Table 4 and Figure 4. A

Friedman test was performed to compare model

performances within each condition group. No

significant differences was found between models in

condition 1 (p-value = 0.13) or between models in

condition 2 (p-value = 0.08).

The results we report show that MLP achieved the

best performance in both the observation and MI-

control conditions. CNN and MLP were the two

models that allowed for the most complex

representations, such as nonlinear relationships.

Taking into account that regularization would limit

the drawbacks associated to their high number of

parameters, we expected these models to perform the

Table 4: Mean and standard deviation over five test folds of

the area under the curve of the receiver operating

characteristic curve for the classification of error vs correct

events.

Condition 1 NPLS Logistic SVM MLP CNN

AUC mean 0.642 0.662 0.645 0.680 0.630

AUC st

0.096 0.106 0.119 0.131 0.124

Condition 2 NPLS Logistic SVM MLP CNN

AUC mean 0.603 0.605 0.623 0.626 0.580

AUC st

0.037 0.040 0.027 0.014 0.022

Figure 4: Mean area under the curve of the receiver

operating characteristic curve for each model and each

condition. Error bars on the left and right of the mean each

represent one time the standard deviation.

best. CNN had less parameters than MLP and was

also more adapted to the task of re-synchronizing the

error correlates. However, the performances of CNN

models were the worst across all decoders. A possible

explanation for this is that both neural network

architectures (and neural networks in general) had a

high number of hyperparameters and we did not

perform an exhaustive search of these

hyperparameter spaces (e.g. learning rate, number of

filters, regularization weight).

In each condition, the three other decoders

performed similarly, with small variabilities

demonstrating better performances for logistic

regression in the first condition and for SVM in the

second condition. NPLS always performed slightly

worse than SVM and logistic regression.

Performance across different folds was

represented by the standard deviation of the AUC.

Since cross-validation was performed session-wise,

this standard deviation can be used to predict the

generalization capabilities of each model over

different datasets. In the observation condition, the

standard deviations of the AUC for each decoder

were close to one another, with NPLS having the

lowest. In the MI-control condition MLP had the

lowest standard deviation, close to twice lower than

the standard deviation of other decoders.

Detection of Error Correlates in the Motor Cortex in a Long Term Clinical Trial of ECoG based Brain Computer Interface

On average, the AUC of the decoders in condition

1 decreased by 6.8% for condition 2. This was

expected since the motor imagery signals used to

control the BCI in the MI-control condition can be

regarded as noise for the classification of error and

correct events. However, the standard deviation of the

AUC was up to ten times larger in the observation

condition than in the MI-control condition. We

suggest that the higher variability in the observation

condition was due to a higher variability in the

attention level of the subject than in the MI-control

condition. Indeed, in the MI-control condition the

subject was more engaged in the task since he had

active control over the avatar’s actions. In the

observation condition, the subject was more

vulnerable to distractions due to the lack of

interaction required by the condition. We hypothesize

that the attention level modulated the strength of the

error correlates in the motor cortex, similarly to how

it modulates classical ErrPs (Yeung, Holroyd, &

Cohen, 2005).

4 DISCUSSION

4.1 Impact of Event Latency

We hypothesize that the error correlate reported here

could be modulated by the length of correct or error

periods prior to an event. Although the duration of

these periods, or latency before each event, was partly

controlled in condition 1 there was no inclusion or

exclusion criterion based on it in condition 2. We

suggest that this latency may influence the brain

response to events. For example, correct events after

a long erroneous period may elicit a stronger brain

response than after a short erroneous period. Due to

the relatively small dataset acquired in this

experiment, separating the events based on latency

was not possible, but larger studies should take it into

account when possible.

4.2 Inter-session Stability of Error

Correlates

It should be noted that the different sessions of this

experiment were recorded over the course of several

months. The cross-validation was performed session-

wise, which means that the models were partly trained

on data recorded far away temporally from the data

they were tested on. This leads us to suggest that the

error correlates we report in the motor cortex may

exhibit a certain temporal stability, similarly to ErrPs.

4.3 Single Trial Detection of Error

Correlates

Although the AUCs reported in this study are not

considerably high, these are still above chance levels

for each algorithm tested here. We therefore suggest

that there effectively is an error correlate detectable at

the single trial level in the motor cortex when either

observing or controlling a BCI that performed an

erroneous action. Additionally, although the AUC

decreased between the observation and MI-control

condition, the ability to detect error correlates in the

motor cortex during operation of the BCI using motor

imagery is valuable not only from a neuroscience

perspective where it could provide some additional

insight on the motor learning mechanisms, but also

for potential applications in state-of-the-art BCIs for

which it is a requirement.

4.4 Decoders for Online BCIs

Although SVM, logistic regression and neural

networks are recognized as powerful methods, it is

not easy to update these classifier online without

retraining them on the full training dataset. This

property can be a drawback for some BCI

applications, including online training which is

considered as better than classical training with

feedback that is not generated by the control of the

BCI. More investigation would be required if these

decoders were to be trained or updated in online BCI

paradigms. In such cases, one should preferably use

NPLS over these decoders, as NPLS demonstrated

only slightly lower performances (up to 3.7% lower)

than the other decoders while being easily trainable

and updatable online.

5 CONCLUSION

Like previous independent studies reported, we found

error correlates in the time-frequency decomposition

of brain signals recorded in the sensory-motor cortex

using ECoG. However, to our knowledge this study

is the first to report the possibility to detect at the

single-trial-level error correlates in the sensory-motor

cortex during operation of a BCI. This study is also

the first one to report error correlates in the sensory-

motor cortex of a tetraplegic subject. Additionally, in

this study the operation of the BCI is performed using

motor imagery, further highlighting the value of these

results since a BCI with access to neural data from the

motor cortex only (such as invasive state-of-the-art

motor-imagery-based BCIs) could still be able to

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

detect error correlates and potentially use them for

error correction or model adaptation. The fact that the

detection accuracy of the NPLS was close to other

model is also a strong point for potential online model

adaptations, as it is computationally fast to update in

real time compared to the other models presented.

The main limitation of this study is that it was

restricted to the first subject of the clinical trial.

However, this clinical trial is expected to have a total

of 5 subjects, who could later be added to this study.

Other perspective future studies include

implementing automatic error correction for this

binary BCI, as well as error correlate detection during

control of more complex BCI effectors using multiple

degrees of freedom.

AUTHOR CONTRIBUTIONS

VR and MS performed the analyses and wrote the

manuscript. VR and TA designed the task. ALB and

TA provided input and mentorship through the

analysis and writing. TC collected the data.

ACKNOWLEDGMENTS

Clinatec is a Laboratory of CEA-Grenoble and has

statutory links with the University Hospital of

Grenoble (CHUGA) and with University Grenoble

Alpes (UGA). This study was funded by CEA

(recurrent funding) and the French Ministry of Health

(Grant PHRC-15-15-0124), Institut Carnot, Fonds de

Dotation Clinatec.MS was supported by the CEA

NUMERICS program, which has received funding

from the European Union's Horizon 2020 research

and innovation program under the Marie

Sklodowska-Curie grant agreement No 800945.

Fondation Philanthropique Edmond J Safra is a major

founding institution of the Clinatec Edmond J Safra

Biomedical Research Center.

REFERENCES

Benabid, A. L., Costecalde, T., Eliseyev, A., Charvet, G.,

Verney, A., Karakas, S., … Chabardes, S. (2019). An

exoskeleton controlled by an epidural wireless brain–

machine interface in a tetraplegic patient: A proof-of-

concept demonstration. The Lancet Neurology.

https://doi.org/10.1016/S1474-4422(19)30321-7

Blumberg, J., Rickert, J., Waldert, S., Schulze-Bonhage, A.,

Aertsen, A., & Mehring, C. (2007). Adaptive

Classification for Brain Computer Interfaces. 2007 29th

Annual International Conference of the IEEE

Engineering in Medicine and Biology Society, 2536–

2539. https://doi.org/10.1109/IEMBS.2007.4352845

Chavarriaga, R., Iturrate, I., & Millan, J. del R. (2016, May

30). Robust, accurate spelling based on error-related

potentials.

Chavarriaga, R., & Millan, J. d R. (2010). Learning From

EEG Error-Related Potentials in Noninvasive Brain-

Computer Interfaces. IEEE Transactions on Neural

Systems and Rehabilitation Engineering, 18(4), 381–

388. https://doi.org/10.1109/TNSRE.2010.2053387

Chavarriaga, R., Sobolewski, A., & Millan, J. d R. (2014).

Errare machinale est: The use of error-related potentials

in brain-machine interfaces. Frontiers in Neuroscience,

8. https://doi.org/10.3389/fnins.2014.00208

Eliseyev, A., Auboiroux, V., Costecalde, T., Langar, L.,

Charvet, G., Mestais, C., … Benabid, A.-L. (2017).

Recursive Exponentially Weighted N-way Partial Least

Squares Regression with Recursive-Validation of

Hyper-Parameters in Brain-Computer Interface

Applications. Scientific Reports, 7(1), 1–15.

https://doi.org/10.1038/s41598-017-16579-9

Even-Chen, N., Stavisky, S. D., Pandarinath, C.,

Nuyujukian, P., Blabe, C. H., Hochberg, L. R., …

Shenoy, K. V. (2018). Feasibility of Automatic Error

Detect-and-Undo System in Human Intracortical

Brain–Computer Interfaces. IEEE Transactions on

Biomedical Engineering, 65(8), 1771–1784.

https://doi.org/10.1109/TBME.2017.2776204

Falkenstein, M., Hohnsbein, J., Hoormann, J., & Blanke, L.

(1991). Effects of crossmodal divided attention on late

ERP components. II. Error processing in choice

reaction tasks. Electroencephalography and Clinical

Neurophysiology, 78(6), 447–455.

https://doi.org/10.1016/0013-4694(91)90062-9

Ferrez, P. W., & del R. Millan, J. (2008). Error-Related

EEG Potentials Generated During Simulated Brain–

Computer Interaction. IEEE Transactions on

Biomedical Engineering, 55(3), 923–929.

https://doi.org/10.1109/TBME.2007.908083

Inoue, M., Uchimura, M., & Kitazawa, S. (2016). Error

Signals in Motor Cortices Drive Adaptation in

Reaching. Neuron, 90(5), 1114–1126.

https://doi.org/10.1016/j.neuron.2016.04.029

Iturrate, I., Chavarriaga, R., Montesano, L., Minguez, J., &

Millán, J. d R. (2012). Latency correction of error

potentials between different experiments reduces

calibration time for single-trial classification. 2012

Annual International Conference of the IEEE

Engineering in Medicine and Biology Society, 3288–

3291. https://doi.org/10.1109/EMBC.2012.6346667

Koelewijn, T., van Schie, H. T., Bekkering, H., Oostenveld,

R., & Jensen, O. (2008). Motor-cortical beta

oscillations are modulated by correctness of observed

action. NeuroImage, 40(2), 767–775.

https://doi.org/10.1016/j.neuroimage.2007.12.018

Lotte, F., Bougrain, L., Cichocki, A., Clerc, M., Congedo,

M., Rakotomamonjy, A., & Yger, F. (2018). A review

of classification algorithms for EEG-based brain-

computer interfaces: A 10 year update. Journal of

Detection of Error Correlates in the Motor Cortex in a Long Term Clinical Trial of ECoG based Brain Computer Interface

Neural Engineering, 15(3). Scopus.

https://doi.org/10.1088/1741-2552/aab2f2

Mestais, C. S., Charvet, G., Sauter-Starace, F., Foerster, M.,

Ratel, D., & Benabid, A. L. (2015). WIMAGINE:

Wireless 64-Channel ECoG Recording Implant for

Long Term Clinical Applications. IEEE Transactions

on Neural Systems and Rehabilitation Engineering,

23(1), 10–21.

https://doi.org/10.1109/TNSRE.2014.2333541

Milekovic, T., Ball, T., Schulze-Bonhage, A., Aertsen, A.,

& Mehring, C. (2012). Error-related

electrocorticographic activity in humans during

continuous movements. Journal of Neural Engineering,

9(2), 026007. https://doi.org/10.1088/1741-

2560/9/2/026007

Milekovic, T., Ball, T., Schulze-Bonhage, A., Aertsen, A.,

& Mehring, C. (2013). Detection of Error Related

Neuronal Responses Recorded by Electrocorticography

in Humans during Continuous Movements. PLOS

ONE, 8(2), e55235.

https://doi.org/10.1371/journal.pone.0055235

Parra, L. C., Spence, C. D., Gerson, A. D., & Sajda, P.

(2003). Response error correction-a demonstration of

improved human-machine performance using real-time

EEG monitoring. IEEE Transactions on Neural

Systems and Rehabilitation Engineering, 11(2), 173–

177. https://doi.org/10.1109/TNSRE.2003.814446

Schalk, G., Wolpaw, J. R., McFarland, D. J., &

Pfurtscheller, G. (2000). EEG-based communication:

Presence of an error potential. Clinical

Neurophysiology: Official Journal of the International

Federation of Clinical Neurophysiology, 111(12),

2138–2144. https://doi.org/10.1016/s1388-

2457(00)00457-0

Schie, H. T. van, Mars, R. B., Coles, M. G. H., &

Bekkering, H. (2004). Modulation of activity in medial

frontal and motor cortices during error observation.

Nature Neuroscience, 7(5), 549–554.

https://doi.org/10.1038/nn1239

Spüler, M., Rosenstiel, W., & Bogdan, M. (2012). Online

Adaptation of a c-VEP Brain-Computer Interface(BCI)

Based on Error-Related Potentials and Unsupervised

Learning. PLoS ONE, 7(12), e51077.

https://doi.org/10.1371/journal.pone.0051077

Völker, M., Fiederer, L. D. J., Berberich, S., Hammer, J.,

Behncke, J., Kršek, P., … Ball, T. (2018). The

dynamics of error processing in the human brain as

reflected by high-gamma activity in noninvasive and

intracranial EEG. NeuroImage, 173, 564–579.

https://doi.org/10.1016/j.neuroimage.2018.01.059

Wilson, N. R., Sarma, D., Wander, J. D., Weaver, K. E.,

Ojemann, J. G., & Rao, R. P. N. (2019). Cortical

Topography of Error-Related High-Frequency

Potentials During Erroneous Control in a Continuous

Control Brain–Computer Interface. Frontiers in

Neuroscience, 13, 502.

https://doi.org/10.3389/fnins.2019.00502

Wodlinger, B., Downey, J. E., Tyler-Kabara, E. C.,

Schwartz, A. B., Boninger, M. L., & Collinger, J. L.

(2014). Ten-dimensional anthropomorphic arm control

in a human brain-machine interface: Difficulties,

solutions, and limitations. Journal of Neural

Engineering, 12(1), 016011.

https://doi.org/10.1088/1741-2560/12/1/016011

Yeung, N., Holroyd, C., & Cohen, J. (2005, May). ERP

correlates of feedback and reward processing in the

presence and absence of response choice. Cerebral

Cortex (New York, N.Y. : 1991).

https://doi.org/10.1093/cercor/bhh153.

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing