
Deep Convolutional Second Generation Curvelet Transform-based MR
Image for Early Detection of Alzheimer’s Disease
Takrouni Wiem
1
and Douik Ali
2
1
University of Sousse, ISITCom, 4011, Sousse, Tunisia, Networked Objects Control and Communication Systems
Laboratory (NOCCS-ENISO), 4054, Sousse, Tunisia
2
University of Sousse, ENISO, Networked Objects Control and Communication Systems Laboratory (NOCCS),
Keywords:
Second-Generation Curvelet (SGC), Mild Cognitive Impairment (MCI), Multiclass Classification.
Abstract:
Merging neuroimaging data with machine learning has an important potential for the early diagnosis of
Alzheimer’s Disease (AD) and Mild Cognitive Impairment (MCI). The applicability of multiclass classifi-
cation and the prediction to define the progress of different stages of the disease have been relatively under-
studied. This paper presents a short review of the deep learning history and introduces a new solution for
delineating changes in each stage of AD. Our Deep Convolutional Second-Generation Curvelet Transform
Network (SGCTN) is divided into both levels: The feature learning level is the first task that can combine a
Second-Generation Curvelet (SGC) with autoencoder trained features. Then, for each hidden layer, a pool-
ing is used to obtain our convolutional neural network. This network is used to learn predictive information
for binary and multiclass classification. Our experiments test uses a different number of Cognitively Normal
(CN), AD, early EMCI, and Later LMCI subjects from the AD Neuroimaging Initiative (ADNI). Magnetic
Resonance Imaging (MRI) information modalities are considered as input. The proposed DSGCCN achieves
98.1% accuracy for delineating the early MCI from CN. Furthermore, for detecting the distinctive level of
AD, a multiclass classification test realizes the global accuracy of , and it more particularly differentiates MCI
and AD groups from the CN group with 96% accuracy. Compared to the state-of-the-art deep approach, our
results indicate that our architecture can achieve better performance for the same databases. Model analysis
based (SGC) can improve the classification performance via comparison experiments.
1 INTRODUCTION
Recent research by Alzheimer’s Statistics reports that
for Alzheimer’s Disease (AD) in the world, almost
50 million people have Alzheimer’s or related de-
mentia with only one in four people with AD have
been diagnosed. AD and other dementia are the top
reason for disabilities in later life. Seventy-two per-
cent of the projected rise in the global burden of de-
mentia and pervasiveness by 2050 will take place in
low and middle-income countries (Ryu et al., 2017).
AD is neuropathologically identified by grievous cell
loss and cortical atrophy along with an elevated de-
mentia index as calculated by numbers of neuritic
plaques and neurofibrillary tangles in the hippocam-
pus and the neocortex. This disease gets worse with
time and later declines cognitive functions and behav-
ioral impairments that touch memory, language and
thought, including forgetfulness. Cure strategies for
AD are concentrating on preventing the AD evolu-
tion or speeding up the clearance of these aggregates.
AD, composed of different neurodegenerative levels,
which represent the mutation from one stage to an-
other and identifies each one by the specificity of the
biomarker. It is indicated that 15-25% of people aged
60 or older have a prodromal stage of AD that can be
related to Mild Cognitive Impairment (MCI), which is
a transitional stage between dementia and the normal
cognitive function. A patient diagnosed with MCI can
either have later MCI (LMCI) or Early MCI (EMCI)
due to age-linked memory degradation, hence the ac-
cent on the importance of early diagnosis of the dis-
ease. Thus, accurate and early diagnosis of MCI can
help path disease progression, supply better treatment
paradigms for patients, and decrease medical costs.
Nevertheless, neuroimaging and clinical studies have
exposed differences between MCI and Cognitively
Normal (CN) (Scheltens and Korf, 2000), (Silverman,
2009). To identify pathological biomarkers to under-
Wiem, T. and Ali, D.
Deep Convolutional Second Generation Curvelet Transform-based MR Image for Early Detection of Alzheimer’s Disease.
DOI: 10.5220/0010228902850292
In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages
285-292
ISBN: 978-989-758-488-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
285

stand the mechanism causes and monitor early brain
changes for each stage of the disease, the quantitative
prognosis of AD/MCI by analyzing different types of
neuroimaging modalities is necessary for the early
classification of AD. Magnetic Resonance Imaging
(MRI) allows measuring spatial patterns of atrophy
and their growth with disease evolution. It also sup-
plies visual information concerning the macroscopic
tissue atrophy, which results from the cellular changes
and detects neuronal injury and degeneration under-
lying AD/MCI (Davatzikos et al., 2011). Positron
Emission Tomography (PET) (Nozadi et al., 2018)
can be used for the examination of the cerebral glu-
cose metabolism which indicates the functional brain
activity. Thereby, a trustworthy diagnosis from brain
modalities is necessary, and a sturdy Computer-Aided
Diagnosis (CAD) by the data anatomization of neu-
roimaging will enable for a more reliable and infor-
mative approach and can increase potentially diag-
nostic accuracy. A classical interpretation process for
exploring biomarkers for the neuropsychiatric analy-
sis disorders has been founded on the univariate mass
statistics within the assumption that various regions
of the brain act independently. Nevertheless, this as-
sumption (Fox et al., 2005) is not suitably specified
for our present comprehensive brain functioning.
2 RELATED WORK
Machine Learning (ML) methods, which can lay hold
of the correlation between regions into account, have
become the basic integration and attraction of CAD
techniques (Davatzikos et al., 2008), (Suk et al., 2017)
and have been broadly used for the automated diag-
nosis and interpretation of brain disorders. Further-
more, various ML classification models have been
used to develop automated neurological disorder pre-
diction. Both major research orientations include
Support Vector Machine (SVM) (Pinaya et al., 2016)
and Deep Learning (DL) based diagnostic models
(Greenspan et al., 2016), (Litjens et al., 2017). SVM-
based models of brain disorders have been criticized
for their poor performance on raw data and for re-
quiring the expert use of design techniques to ex-
tract informative handcrafted features. In contrast,
DL models enable a system to use raw data as in-
put, thus allowing them to automatically find highly
discriminating features in the training dataset (Shen
et al., 2017). As a recent successful category of unsu-
pervised learning models, autoencoders, such as con-
volutional (Masci et al., 2011), variational (Kingma
and Welling, 2013), k-sparse (Makhzani and Frey,
2013), contractive (Rifai et al., 2011) and denois-
ing ones (Vincent et al., 2008), perform an impor-
tant role in feature extraction, dimension reduction
and generative tasks. Higher data dimensionality is
an endemic characteristic of medical data, and learn-
ing efficient coding for image classification is the
goal of these autoencoders. It is crucial to note that
these approaches distort spatial locality (neighbor re-
lations) in brain-imaging data (Suk et al., 2017), (Liu
et al., 2019), (Payan and Montana, 2015) over the fea-
ture extraction level. Many automated systems have
been developed in the last years for binary classi-
fication (normal or abnormal) of brain MRI, which
have made remarkable progress. However, multi-
class classification into a specific grade of brain dis-
eases is comparatively more challenging and has great
clinical significance. Numerous methods have been
utilized to analyze using the wavelet or its variants
to extract features for the task of binary and multi-
class brain MRI, despite their defeat to capture direc-
tional features at numerous levels of resolution (Gudi-
gar et al., 2019), (Jia et al., 2019), (Nayak et al.,
2017). In the last mentioned references, the em-
ployed classifiers, like the SVM, the fuzzy neural net-
work, and Least-squares SVM endure critical issues
such as high computational complexity, poor scala-
bility and slow learning speed. In (Zhang and Sug-
anthan, 2016), the random vector functional link net-
work was a classifier that afforded great generaliza-
tion performance at the speed learning property. The
hybrid approach (Gao et al., 2018) combined the MRI
texture features of the contourlet-based hippocampal,
the regional CMgl measurement based on fluorine-
18 fluorodeoxyglucose-positron emission tomogra-
phy, medical history, the morphometric volume, the
neuropsychological tests of symptoms with the multi-
variant models to enhance the AD classification and
the prediction of MCI conversion, and to appraise
whether the partial least squares and the Gaussian
process were realizable in developing multivariate
models in such a situation. Hence, this situation had
various limitations, only hippocampal MRI texture
features were explored, the size was approximately
modest, and the power statistical might be restricted.
Thus, this model was insensitive to high-dimensional
data, and dimensionality reduction might upgrade the
predictive achievement of this model. However, very
few studies have been announced up to now concern-
ing multiclass AD classification, predicting MCI con-
version and precision detection. Even more, it re-
mains unknown which method is more appropriate
for processing high-dimensional data in this context.
To address the above problems, in the present study,
we propose a new combination of a Second Genera-
tion Curvelet Transform Network (SGCTN) and Deep
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
286
Convolutional Autoencoder (DCA) for early detec-
tion of AD and prediction of MCI conversion. A DCA
consists of operating the classification of a particu-
lar class against all the other classes of the dataset by
the reconstruction of Deep Convolutional (SGCTN).
This reconstruction is achieved using a sequence of
a stacked autoencoder and a linear classifier. The re-
maining part of this paper is composed of four sec-
tions. The Deep Convolutional (SGCTN) is proposed
in section III. An overview of the dataset utilized in
the classification test is given in section IV. Section V
includes the experiments and the results of the test.
Finally, Section VI summarizes and concludes this
paper.
3 PROPOSED DEEP
CONVOLUTIONAL (SGCTN)
To improve the rate of convergence and classification
performance, a new approach called Deep Convolu-
tional (SGCTN) is constructed. In this section, we
describe the theoretical background steps that lead to
our approach.
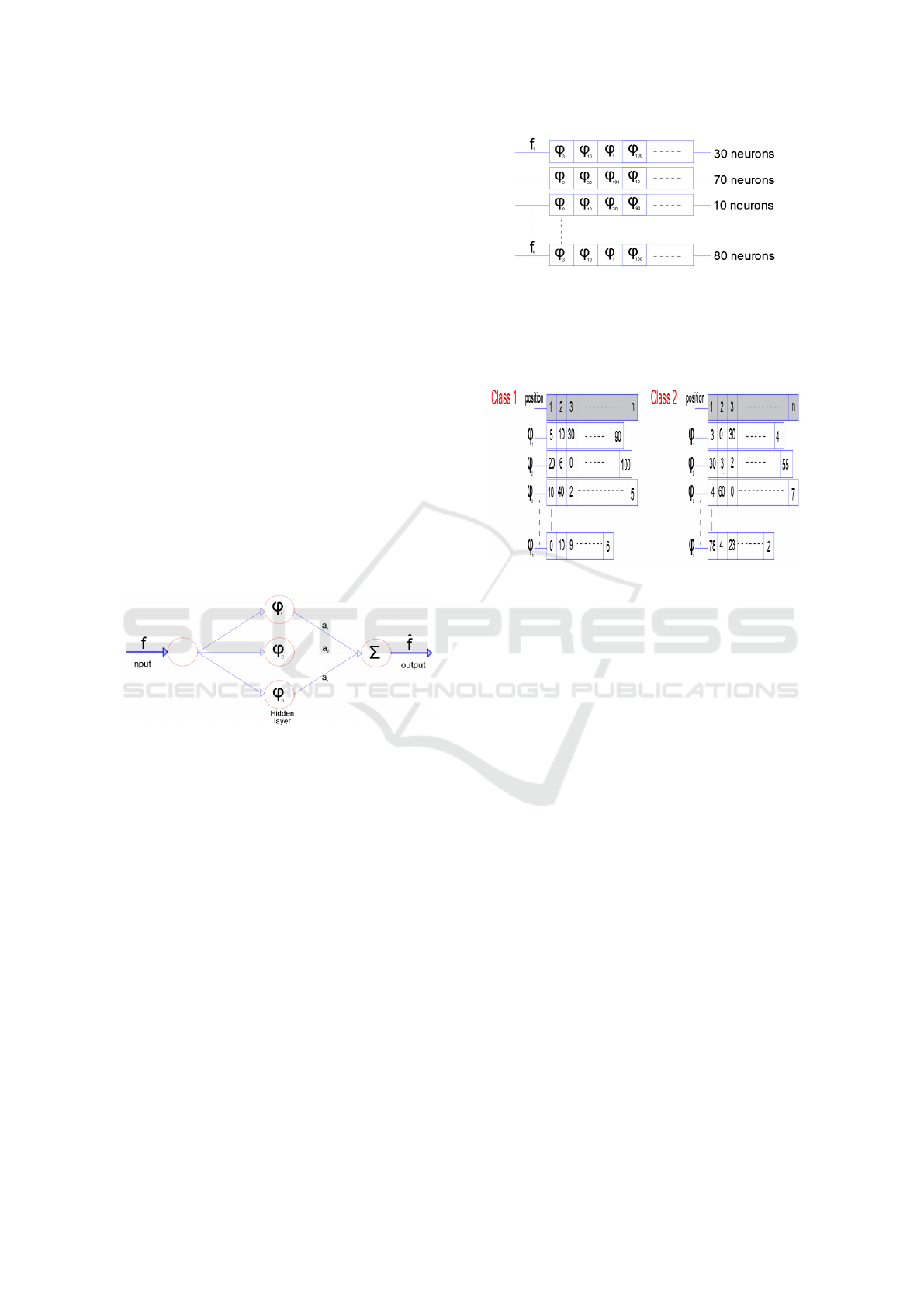
Figure 1: The SGCTN for one element of class.
• Step 1: We construct the SGCTN for each object
of a class using the best algorithm (Dubois et al.,
2015), (Ma and Plonka, 2010). Figure 1 is consti-
tuted for three layers. The SGCTN is defined by a
much simpler and more natural indexing structure
with three parameters: scale, orientation (angle)
and location, so curved singularities can be well
approximated with very few coefficients and in a
non-adaptive manner. We define an SGCTN by
pondering a series of second generation curvelets
(SGC) interpreted and widened from one mother
SGC atom with weight values to approximate a
determined signal f:
ˆ
f =
n
∑
i=1
(a
i
ϕ
i
) (1)
• Step 2: Every SGCTN is shown in the form of a
table (Figure 2). The neuron number that contains
a SGC can vary for each SGCTN created in step
1.
Figure 2: Tables of each SGCTN for a class.
• Step 3: In this stage, we select the best SGC (cho-
sen in step 2) to produce an SGCTN for a class.
Thereby, we account that our brain dataset is com-
posed of two classes:
Figure 3: Tables of the number of appearance of each SGC
for a class.
- Class 1 which we will represent in a SGCTN.
- Class 2 which includes all the other classes of
the dataset.
We build tables for all the SGC in the dataset of
SGC for the two classes (Class 1 and Class 2).
The tables hold the number of emergences of each
SGC in each position in all the SGCTN utilizing
the tables in step 2 (Figure 3). Subsequently, we
calculate a coefficient for every SGC in that man-
ner: for ϕ
i
in class 1, the coefficient is determined
by the sum of all the values of ϕ
i
that are multi-
plied by (1+ (n - i)) in each position (i) and the
identical operation is used for ϕ
i
in class 2. This
is indicated as follows
Class1
coe f
ϕ
i
=Class2
coe f
ϕ
i
=
n
∑
i=1
(V
i
∗(1+(n−i)))
(2)
Whence, the global coefficient for ϕ
i
is defined as
follows
Glob
coe f
ϕ
i
= Class1
coe f
ϕ
i
−Class2
coe f
ϕ
i
(3)
Next, we calculate all global coefficients of all
SGC and arrange them on a table ordered from the
biggest to the smallest (Figure 4). The method of
coefficient calculation for all SGC enables penal-
izing the SGC frequently utilized in other classes
(in our instance, the classes are combined in one
class: class 2) and the preferred SGC used in the
Deep Convolutional Second Generation Curvelet Transform-based MR Image for Early Detection of Alzheimer’s Disease
287

Figure 4: Tables of the global coefficient for each SGC.
working class (Class1). For example, if ϕ
i
is the
ideal SGC utilized in class 1 in the first position
with 30 emergences and the ideal SGC in class 2
in the second position with 200 emergences, we
calculate the ϕ
i
coefficient to punish it and avert it
in the first position.
Figure 5: SGCTN for a class.
• Step 4: We construct a novel SGCTN for a class
(Figure 5) utilizing the ideal SGC from the table in
step 3. The total of the SGC utilized for the overall
SGCTN is the average of the SGC numbers used
in step 2.
• Step 5: In this stage, we construct a network (with
the use of the SGC in our SGCTN that produces
a class in step 4) using an autoencoder algorithm.
It is important to note that an encoder level gener-
ates a feature vector (hidden layer) from the input
vector with a primal SGC and a decoder level that
reconstructs the input vector from the vector of a
feature with a dual SGC. In this phase, the neurons
of the hidden layer incorporate a linear function.
We take into consideration that:
f = x
1
, x
2
, x
3
, ..., x
n
ˆ
f = ˆx
1
, ˆx
2
, ˆx
3
, ..., ˆx
n
ϕ
i
= w
1i
, w
2i
, w
3i
, ..., w
ni
ˆ
ϕ
i
= ˆw
1i
, ˆw
2i
, ˆw
3i
, ..., ˆw
ni
(4)
Then,
a
i
=≺ f , ϕ
i
=⇒ a
i
=
n
∑
j=1
(w
ji
x
j
) (5)
ˆx
i
=
n
∑
j=1
ˆw
ji
a
j
(6)
• Step 6: The hidden layer is used to construct our
SGCTN and it is considered for the second train-
ing of the input layer. The hidden layer is used to
construct our deep convolutional SGCTN and it
is considered for the second training of the input
layer. The construction of an SGCTN with both
hidden layers and a linear classifier is displayed
in Figure 6. This process is enforced for all ele-
Figure 6: A deep SGCTN with both hidden layers.
ments of a class until the creation of our deep con-
volutional SGCTN, which figures the entire class.
After that, we replace the linear function by the
sigmoid function in the hidden layers to enforce
fine-tuning. The choice of using the sigmoid func-
tion is to promote the significant features and to
derivate an activation function in the backpropa-
gation step. A few new components are shown
to be very effective when connected to a convolu-
tional neural network:
*Local Contrast Normalization (LCN): This com-
ponent is an efficient technique that makes a
deep architecture more sturdy to illumination
changes that have not been seen under training.
It adapts local subtractive and divisive normaliza-
tions, which impose a kind of local competition
between features at the identical spatial position
in various feature maps and adjacent features in a
feature map. It is determined by this function:
X
i+1,x,y
=
X
i,x,y
− m
i,N(x,y)
σ
i,N(x,y)
(7)
*Geometric Lp-norm Pooling (GLP): Pooling is
the reducing step of spatial resolution, which ag-
gregates local features over the region of inter-
est into a statistic through a certain spatial pool-
ing operation. The GLP method can preserve
the specific-class spatial/geometric information
on the pooled features and appreciably boosts the
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
288

Figure 7: Geometric Lp-norm pooling of adjacent SGC.
discriminating ability of the resultant features for
image classification. It is determined by this func-
tion:
Out = (
∑∑
I(i, j)
GLP
∗ G
k
(i, j))
1
GLP
(8)
where I is the input feature map, Gk is a Gaus-
sian kernel, and Out is the output feature map. In
our contribution, we achieve intelligence pooling.
We operate it if and only if the SGC that are dis-
covered in the neurons are adjacent, whether of an
identical type or an identical scale (Figure 7). For
that reason, for each hidden layer, GLP and LCN
are employed of our SGCTN and will be consid-
ered as one step (Figure 8). In addition, our deep
convolutional SGCTN will be created.
Figure 8: Typical architecture of Deep convolutional
SGCTN.
• Step 7: For the last stage, a linear weak classifier
is applied, which is defined to be a classifier that
is only slightly correlated with true classification.
It plainly classifies data with a unique threshold
on a certain data dimension.
4 DATASET OVERVIEW
In this work, we use the ADNI http://adni.loni.
usc.edu/ dataset including various phases (ADNI-1,
ADNI-2, and ADNI-GO) which is preprocessed by
Freesurfer (v5.3). The ADNI has gathered 1167 scans
of adults aged between 55 and 90, composed of cog-
nitively normal older persons, individuals with early
AD, and individuals with early or late MCI. The
demographic details of subjects are provided in Ta-
ble I. In this paper, we analyze the performance of
our architecture on both T1 and T2 weighted MRI
images collected from the same set of subjects and
evaluate different parameters under both binary and
multi class classification. To train our data, parallel
processing is needed, so we use open source pack-
age python 3.0 to perform the training and valida-
tion of the classifier (GPU: 1xTesla K80, having 2496
CUDNN cores, compute 3.7, 24GB(23.439GB Us-
able) GDDR5 VRAM). We use Keras library over
Tensorflow modules to design our proposed architec-
ture.
5 EXPERIMENTS AND RESULT
We compare the performance of our model while
training and testing with brain MRI together
with (Original Features Curvelet Network (OFCN),
SGCTN), and segmented hippocampal regions.
5.1 Devising Training and Test Set
We augment the MRI data to resist the model from ge-
ometry changes and noise. We use 5482 MRI slides in
our experiment. We split the data into 85:15 training
and testing sets based on subjects to defeat the intra
relation amid the split data to carry out the classifica-
tion without biasing.
5.2 Classification Results and
Discussion
The focus of this work is established on demonstrat-
ing how the proposed approach can resolve the most
discriminating elements related to the progression of
MCI and ameliorate binary and multiclass classifica-
tion performance. After the selection of features, we
train the initial SGCTN to learn the fundamental vec-
tor of features. Those features are connected to the
other input of the autoencoder to learn secondary fea-
tures in order to discriminate the various levels of the
disease. Our network includes seven hidden layers
and a softmax layer for output. We test the classi-
fication performance in both cases, which is OFCN
and SGCTN. In this latter, we choose five scales and
eighteen orientations. The results provide the confu-
sion matrix to perform the quality of our architecture,
Deep Convolutional Second Generation Curvelet Transform-based MR Image for Early Detection of Alzheimer’s Disease
289

Table 1: Demoghraphic details about the participant study.
Categories Age MMSE CDR CDR GS
AD (284 sc) 75.85 ± 7.94 23.4±2.1 4.5 to 9 0.7±0.3
LMCI (169 sc) 72.99±7.67 27.1± 1.9 2.5 to 4.5 0.5±0.2
EMCI (328 sc) 72.62±7.33 28.4±1.5 0.5 to 2.5 0.5±0.0
Contols (371 sc) 75.68±8.01 29.1±0.9 0 to 0.5 0.0±0.0
which contains actual and predicted class informa-
tion. The following five metrics are considered:
Accuracy(ACC) =
T P + T N
T P + T N + FP + FN
(9)
Sensitivity(SEN) =
T P
T P + FN
(10)
Speci f icity(SPEC) =
T N
T N + FP
(11)
PositivePredictiveValue(PPV ) =
T P
T P + FP
(12)
Table II proves the results of our network, witch al-
lows distinguishing between CN/AD, CN/EMCI and
EMCI/LMCI. The results are more accurate with
99.1%, 98.1% and 93.3 % in the tasks of CN vs AD,
CN vs EMCI and EMCI vs LMCI, respectively for
the deep convolutional SGCTN using whole image
compared with the OFCN in the same tasks with hip-
pocampal patch are 92.4% 90.8 % and 89.7% is more
accurate than the OFCN using whole image. On the
Figure 9: ROC curves to multiclass classification.
other hand, the OFCN model achieves good perfor-
mance in both tasks. This can be explained by the au-
toencoder selecting only each class and separating the
approximation to the components of the other class.
The selection based on the principal contribution of
each best SGC to the construction of the SGCTN for
each component of a class. We note that the SGC
stays unchanged and that the weight changes from
one slide to another for both classes. Then, based on
a SGC, which, in fact includes an extension of the
isotropic multiresolution analysis concept to include
anisotropic scaling and angular dependence (direc-
tionality) while preserving rotational invariance. The
SGC is also faster and less redundant compared to its
original features curvelet (OFC), It does not exhibit
blocking artefacts due to special partitioning.
We use the learning curve of the multiclass
classification using the proposed deep convolutional
SGCTN (Figure 9). The classifier can more accu-
rately differentiate CN, AD and LMCI from an EMCI
class, so the overall classification performance is ame-
liorated significantly. It can be noted that the learning
curve related to the test is closer to the learning curve
of validation. As there are three classes instead of
both classes, the model can learn more generic dis-
criminative elements through all three classes. Then,
the confusion matrix evaluates the performance with
each line corresponding to a true class. The com-
ponents of the diagonal of the confusion matrix de-
pict the point number for the predicted label which
is equal to the true label, whereas the components of
the off-diagonal are those that are misclassified by the
classifier (Figure 10). Compared with the deep learn-
Figure 10: AD vs. LMCI vs. EMCI vs. CN classification
confusion matrix.
ing classification model and geometric transform-
based feature extraction pattern analysis based on
ADNI data (Fang et al., 2020), (Wee et al., 2019),
(Ramzan et al., 2020), it should be noted that in Ta-
ble III our proposed architecture still achieves bet-
ter performance in the terms of classification accu-
racy for the two tasks (EMCI vs. LMCI and, CN vs.
EMCI). This can be considered for the use of autoen-
coder based SGC, which gives better feature extrac-
tion than other method based on a deep model with
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
290

Table 2: Binary classification performance comparison of OFCN features and SGCTN features.
Task Features OFCN SGCTN
ACC SEN SPEC PPV ACC SEN SPEC PPV
CN/AD
hippocampal 92.4 % 93.4% 90.2% 90.4% 97.3% 98.3% 96.1% 96.5%
whole slide 91.2% 91.9% 89.9% 90.2% 99.1% 99.8% 98.2% 98.6%
CN/EMCI
hippocampal 90.8% 91.3% 89.3% 89.7% 96.9% 97.2% 95.2% 95.6%
whole slide 90.6% 92.1 % 88.8% 88.9% 98.1% 98.8% 97.2% 97.6%
LMCI/EMCI
hippocampal 89.7% 90.1% 87.9% 88.0% 91.9% 93.2% 90.8% 90.9%
whole slide 86.8% 88.1% 85.8% 85.9% 93.3% 94.5% 92.7% 92.9%
Table 3: Accuracy CN vs. EMCI and EMCI vs. LMCI classification comparison.
CN vs. AD CN vs. EMCI EMCI vs. LMCI
(Fang et al., 2020) - 79.25% 83.33%
(Wee et al., 2019) 81.0% - -
(Ramzan et al., 2020) - 96.85% 88.6%
Proposed 99.1% 98.1% 93.3%
or without a transform based on multiresolution anal-
ysis(Gao et al., 2018), (Hofer et al., 2020), (Swain
et al., 2020).
6 CONCLUSIONS
In this study, a novel deep convolutional SGCTN for
brain disease image classification, which combines
the flexibility of SGC with autoencoder technique to
extract and reduce these features. By this method, a
series of trained autoencoders are accomplished by a
linear classifier and are stacked to build a deep con-
volutional neural network. The obtained classifica-
tion CN vs. EMCI results indicate that our architec-
ture can perform well the delineation of the fluffiest
changes associated with the EMCI group. After the
reconstruction of deep convolutional SGCTN layers,
high accuracy of 98.2% is obtained, which display the
potential of the proposed approach for clinical diag-
nosis of the early level of AD. Also, the deep convo-
lutional SGCTN achieves high accuracy in the task of
EMCI vs. LMCI of 93.3 % , as well as an AUC score
of 96.1 % CN vs. EMCI and EMCI vs. LMCI clas-
sification results are considered as the best classifica-
tion performance obtained so far. A future work, we
aim to focus on considering the advantage of the pro-
posed approach to build a computer-aided diagnosis
system that can help in the EMCI delineating group
in the process of multiclass classification, which can
be helpful in the planning of early therapy and ame-
liorative interventions.
REFERENCES
Davatzikos, C., Bhatt, P., Shaw, L. M., Batmanghelich,
K. N., and Trojanowski, J. Q. (2011). Prediction
of mci to ad conversion, via mri, csf biomarkers,
and pattern classification. Neurobiology of aging,
32(12):2322–e19.
Davatzikos, C., Fan, Y., Wu, X., Shen, D., and Resnick,
S. M. (2008). Detection of prodromal alzheimer’s dis-
ease via pattern classification of magnetic resonance
imaging. Neurobiology of aging, 29(4):514–523.
Dubois, S., P
´
eteri, R., and M
´
enard, M. (2015). Character-
ization and recognition of dynamic textures based on
the 2d+ t curvelet transform. Signal, Image and Video
Processing, 9(4):819–830.
Fang, C., Li, C., Forouzannezhad, P., Cabrerizo, M., Curiel,
R. E., Loewenstein, D., Duara, R., Adjouadi, M., Ini-
tiative, A. D. N., et al. (2020). Gaussian discriminative
component analysis for early detection of alzheimer’s
disease: A supervised dimensionality reduction algo-
rithm. Journal of Neuroscience Methods, 344:108856.
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M.,
Van Essen, D. C., and Raichle, M. E. (2005). The
human brain is intrinsically organized into dynamic,
anticorrelated functional networks. Proceedings of the
National Academy of Sciences, 102(27):9673–9678.
Gao, N., Tao, L.-X., Huang, J., Zhang, F., Li, X.,
O’Sullivan, F., Chen, S.-P., Tian, S.-J., Mahara, G.,
Luo, Y.-X., et al. (2018). Contourlet-based hip-
pocampal magnetic resonance imaging texture fea-
tures for multivariant classification and prediction
of alzheimer’s disease. Metabolic Brain Disease,
33(6):1899–1909.
Greenspan, H., Van Ginneken, B., and Summers, R. M.
(2016). Guest editorial deep learning in medical imag-
ing: Overview and future promise of an exciting new
technique. IEEE Transactions on Medical Imaging,
35(5):1153–1159.
Gudigar, A., Raghavendra, U., San, T. R., Ciaccio, E. J., and
Acharya, U. R. (2019). Application of multiresolution
analysis for automated detection of brain abnormality
using mr images: A comparative study. Future Gen-
eration Computer Systems, 90:359–367.
Hofer, C., Kwitt, R., H
¨
oller, Y., Trinka, E., and Uhl, A.
(2020). An empirical assessment of appearance de-
scriptors applied to mri for automated diagnosis of
Deep Convolutional Second Generation Curvelet Transform-based MR Image for Early Detection of Alzheimer’s Disease
291

tle and mci. Computers in Biology and Medicine,
117:103592.
Jia, W., Muhammad, K., Wang, S.-H., and Zhang, Y.-
D. (2019). Five-category classification of patho-
logical brain images based on deep stacked sparse
autoencoder. Multimedia Tools and Applications,
78(4):4045–4064.
Kingma, D. P. and Welling, M. (2013). Auto-encoding vari-
ational bayes. arXiv preprint arXiv:1312.6114.
Litjens, G., Kooi, T., Bejnordi, B. E., Setio, A. A. A.,
Ciompi, F., Ghafoorian, M., Van Der Laak, J. A.,
Van Ginneken, B., and S
´
anchez, C. I. (2017). A survey
on deep learning in medical image analysis. Medical
image analysis, 42:60–88.
Liu, M., Zhang, J., Lian, C., and Shen, D. (2019). Weakly
supervised deep learning for brain disease prognosis
using mri and incomplete clinical scores. IEEE Trans-
actions on Cybernetics.
Ma, J. and Plonka, G. (2010). A review of curvelets and re-
cent applications. IEEE Signal Processing Magazine,
27(2):118–133.
Makhzani, A. and Frey, B. (2013). K-sparse autoencoders.
arXiv preprint arXiv:1312.5663.
Masci, J., Meier, U., Cires¸an, D., and Schmidhuber, J.
(2011). Stacked convolutional auto-encoders for hi-
erarchical feature extraction. In International con-
ference on artificial neural networks, pages 52–59.
Springer.
Nayak, D. R., Dash, R., Majhi, B., and Prasad, V. (2017).
Automated pathological brain detection system: A
fast discrete curvelet transform and probabilistic neu-
ral network based approach. Expert Systems with Ap-
plications, 88:152–164.
Nozadi, S. H., Kadoury, S., Initiative, A. D. N., et al.
(2018). Classification of alzheimer’s and mci patients
from semantically parcelled pet images: a compari-
son between av45 and fdg-pet. International journal
of biomedical imaging, 2018.
Payan, A. and Montana, G. (2015). Predicting alzheimer’s
disease: a neuroimaging study with 3d convolutional
neural networks. arXiv preprint arXiv:1502.02506.
Pinaya, W. H., Gadelha, A., Doyle, O. M., Noto, C., Zug-
man, A., Cordeiro, Q., Jackowski, A. P., Bressan,
R. A., and Sato, J. R. (2016). Using deep belief net-
work modelling to characterize differences in brain
morphometry in schizophrenia. Scientific reports,
6:38897.
Ramzan, F., Khan, M. U. G., Rehmat, A., Iqbal, S., Saba,
T., Rehman, A., and Mehmood, Z. (2020). A deep
learning approach for automated diagnosis and multi-
class classification of alzheimer’s disease stages using
resting-state fmri and residual neural networks. Jour-
nal of Medical Systems, 44(2):37.
Rifai, S., Mesnil, G., Vincent, P., Muller, X., Bengio, Y.,
Dauphin, Y., and Glorot, X. (2011). Higher order
contractive auto-encoder. In Joint European confer-
ence on machine learning and knowledge discovery
in databases, pages 645–660. Springer.
Ryu, C., Jang, D. C., Jung, D., Kim, Y. G., Shim, H. G.,
Ryu, H.-H., Lee, Y.-S., Linden, D. J., Worley, P. F.,
and Kim, S. J. (2017). Stim1 regulates somatic
ca2+ signals and intrinsic firing properties of cere-
bellar purkinje neurons. Journal of Neuroscience,
37(37):8876–8894.
Scheltens, P. and Korf, E. S. (2000). Contribution of
neuroimaging in the diagnosis of alzheimer’s disease
and other dementias. Current opinion in neurology,
13(4):391–396.
Shen, D., Wu, G., and Suk, H.-I. (2017). Deep learning in
medical image analysis. Annual review of biomedical
engineering, 19:221–248.
Silverman, D. (2009). PET in the Evaluation of Alzheimer’s
Disease and Related Disorders. Springer.
Suk, H.-I., Lee, S.-W., Shen, D., Initiative, A. D. N., et al.
(2017). Deep ensemble learning of sparse regression
models for brain disease diagnosis. Medical image
analysis, 37:101–113.
Swain, B. K., Sahani, M., and Sharma, R. (2020). Auto-
matic recognition of the early stage of alzheimer’s dis-
ease based on discrete wavelet transform and reduced
deep convolutional neural network. In Innovation in
Electrical Power Engineering, Communication, and
Computing Technology, pages 531–542. Springer.
Vincent, P., Larochelle, H., Bengio, Y., and Manzagol, P.-
A. (2008). Extracting and composing robust features
with denoising autoencoders. In Proceedings of the
25th international conference on Machine learning,
pages 1096–1103.
Wee, C.-Y., Liu, C., Lee, A., Poh, J. S., Ji, H., Qiu, A.,
Initiative, A. D. N., et al. (2019). Cortical graph
neural network for ad and mci diagnosis and transfer
learning across populations. NeuroImage: Clinical,
23:101929.
Zhang, L. and Suganthan, P. N. (2016). A comprehensive
evaluation of random vector functional link networks.
Information sciences, 367:1094–1105.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
292
