Elliptical Fitting as an Alternative Approach to Complex Nonlinear Least

Squares Regression for Modeling Electrochemical Impedance

Spectroscopy

Norman Pfeiffer

1 a

, Toni Wachter

, J

urgen Frickel

, Christian Hofmann

, Abdelhamid Errachid

and

Albert Heuberger

Fraunhofer IIS, Fraunhofer Institute for Integrated Circuits, Am Wolfsmantel 33, 91058 Erlangen, Germany

Lehrstuhl f

ur Informationstechnik mit dem Schwerpunkt Kommunikationselektronik (LIKE),

Friedrich-Alexander Universit

at Erlangen-N

urnberg, Am Wolfsmantel 33, 91058 Erlangen, Germany

Institut des Sciences Analytiques, Universit

e de Lyon, 5 rue de la Doua, 69100 Villeurbanne, France

Keywords:

Electrochemical Impedance Spectroscopy, Elliptical Fitting, Randles Circuit, Least Squares Fitting, Charge

Transfer Resistance, Complex Nonlinear Least Squares.

Abstract:

Electrochemical impedance spectroscopy is an important procedure with the ability to describe a wide range of

physical and chemical properties of electrochemical systems. The spectral behavior of impedimetric sensors

is mostly described by the Randles circuit, whose parameters are determined by regression techniques on the

basis of measured spectra. The charge transfer resistance as one of these parameters is often used as sensor

response. In the laboratory environment, the regression is usually performed by commercial software, but

for integrated, application-oriented solutions, separate approaches must be pursued. This work presents an

approach for elliptical ﬁtting of the curve in the Nyquist plot, which is compared to the complex nonlinear

least squares (CNLS) regression technique. For this purpose, artiﬁcial spectra were generated, which were

considered both with and without noise superposition. Although the average error in calculating the charge

transfer resistance from noisy signals using the elliptical ﬁtting of −2.7% was worse than the CNLS with

2.4 ·10

−2

%, the former required only about

/225 of the computing time compared to the latter. Following

application-oriented evaluations of the achievable accuracies, the elliptical approach may turn out to be a

resource saving alternative.

1 INTRODUCTION

Electrochemical impedance spectroscopy (EIS) is a

common measurement technology for the analysis of

biosensors, such as FET-based structures (Kharitonov

et al., 2001). Its advantage is the description of chem-

ical and physical phenomena of an electrochemical

system, thus allows the characterization of the electri-

cal properties of the sensor surface and the investiga-

tion of interfacial reaction mechanisms (Macdonald,

1990). Furthermore, impedimetric biosensors have

other advantages such as label-free measurements,

miniaturization capability, low production costs etc.

(Prodromidis, 2010). In research EIS is used in vari-

ous chemical and medical applications for the analy-

sis of biosensors, e.g. for the diagnosis of heart dis-

https://orcid.org/0000-0002-6839-3002

eases (Halima et al., 2019) or of Alzheimer’s disease

(Rushworth et al., 2014), for the detection of bacte-

ria as Escherichia coli or viruses (Leva-Bueno et al.,

2020) or for detection of cancer cells (Chowdhury

et al., 2018).

The application-oriented interpretation of the

impedance spectra of biosensors is usually done by

modeling the biofunctionalized sensor area. For

this purpose an equivalent circuit diagram is ap-

plied, which describes the electrochemical and phys-

ical phenomena. As a model for an electrode in con-

tact with an electrolyte, the so called Randles circuit is

used, which describes a one-step charge transfer pro-

cess involving the diffusion of reactants to the inter-

face (Barsoukov and Macdonald, 2005). In the ma-

jority of published EIS studies, different interface pa-

rameters such as charge transfer resistance R

or dou-

ble layer capacitance C

are determined by modeling

Pfeiffer, N., Wachter, T., Frickel, J., Hofmann, C., Errachid, A. and Heuberger, A.

Elliptical Fitting as an Alternative Approach to Complex Nonlinear Least Squares Regression for Modeling Electrochemical Impedance Spectroscopy.

DOI: 10.5220/0010231600420049

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 42-49

ISBN: 978-989-758-490-9

(Pejcic and De Marco, 2006). Within the scope of sci-

entiﬁc publications, commercial software is usually

used to realize the modeling, which is performed by

a complex nonlinear least squares (CNLS) regression

technique (Kauffman, 2009) with the electrical equiv-

alent circuit diagram. Alternatively, R

is determined

manually at the second extrapolated intersection with

the real axis on the low-frequency side of the Nyquist

plot, thus by a geometric approach. This method for

estimating R

is used extensively in the electrochem-

ical ﬁeld (Randviir and Banks, 2013).

Electrochemical biosensors can be used in a vari-

ety of applications, such as the examination of sweat,

saliva, blood or urine as part of a wearable sensor

(Sun et al., 2016) (Dang et al., 2018) (Sgobbi et al.,

2016). Apart from medical applications, also small

and energy-efﬁcient devices for gas monitoring or en-

vironmental analysis are considered (Cimafonte et al.,

2020) (Willa et al., 2017). Especially as soon as EIS

is used in a mobile scenario, it must be determined

where the evaluation of recorded spectra will be car-

ried out. On the one hand, raw data can be sent to a

computing unit, which, however, results in greater de-

pendencies on the overall system architecture. An ex-

ample of this are alarm systems, which have a higher

risk of errors due to the communication link to the

computing unit. On the other hand, modelling can be

carried out directly on the (low-power) electronics. In

the latter case the efﬁciency of algorithms plays an

important role.

This work proposes an approach that uses ellipti-

cal ﬁttings to provide an automated, geometric esti-

mation of R

. Thus, reproducibilities and accuracies

should be increased compared to manual methods, but

lower computational times than CNLS are expected.

Therefore both the elliptical ﬁtting and CNLS were

implemented in Python and evaluated by simulated

data with and without noise.

2 MATERIALS AND METHODS

2.1 Generation of Simulation Data

As usual for FET-based biosensors, the Randles cir-

cuit was used to simulate the artiﬁcial impedance

spectra. Its equivalent circuit consists of an elec-

trolyte resistance R

in series with a parallel circuit

of the double layer capacitance C

and an impedance

of the Faraday charge exchange. The latter is a serial

connection of the charge transfer resistance R

and

the Warburg impedance Z

. The Faraday impedance

has its origin in the ion exchange between the elec-

trolyte and the ions in the metallic conducting elec-

trode (Yuan et al., 2010). In many cases the dou-

ble layer capacitance C

is replaced by a constant

phase element CPE due to non-ideal conditions such

as porous electrodes. The impedance of the CPE is

deﬁned by

CPE

( f ) =

Q(i2π f )

n ∈ [0,1]. (1)

Here, Q is a pre-factor of the CPE and n its exponent.

For n = 1, Equation 1 represents the behaviour of

an ideal capacitor with the capacitance C = Q (Shoar

Abouzari et al., 2009).

A special case of the CPE is Z

with a constant

phase of 45°. It describes the contribution of diffusion

from or to an electrode. A theoretical electrode with

an inﬁnitely large area and thus unlimited diffusion

can be described as follows

( f ) =

(i2π f )

. (2)

The used equivalent circuit for providing a Ran-

dles circuit and therefore simulating the electrical

behaviour of a FET-based biosensor is shown in

Figure 1.

CPE

Figure 1: Equivalent circuit of the Randles circuit. R

the electrolyte resistance, R

charge transfer resistance, Z

Warburg impedance, CPE constant phase element.

In order to achieve the expected shape of the Ran-

dles circuit in a Nyquist plot with a semicircle be-

haviour at higher frequencies and the impact of the

Warburg impedance only in the lower-frequency half

of the semicircle, the ranges for the parameter values

were selected as presented in Table 1.

To simulate spectra for test purposes, random

numbers for a factor a and an exponent b were drawn,

resulting in a parameter β = a ·10

within the men-

tioned range of values for each component. These pa-

rameters are ﬁnally used to generate the artiﬁcial Ran-

dles circuit. However, depending on the relative ratio

between the parameters of the spectrum, its Nyquist

plot can assume the form of a simple line, since in this

case Z

can dominate the spectra. Based on the prac-

tical irrelevance of this case, such simulations are dis-

carded by checking the change of its phase and com-

paring it with a threshold angle.

Elliptical Fitting as an Alternative Approach to Complex Nonlinear Least Squares Regression for Modeling Electrochemical Impedance

Spectroscopy

Table 1: Range of values for each parameter of the Randles

circuit used to simulate artiﬁcial spectra. R

electrolyte re-

sistance, R

charge transfer resistance, Q

pre-factor of the

Warburg impedance Z

, Q pre-factor of the CPE, n expo-

nent of the CPE.

Parameter Min Max Unit

Ω

9 ·10

Ω

−8

−6

S ·

√

Q 10

−11

−6

S ·s

n 0.5 1 -

Each simulation was run twice, once without and

once with noise. For the latter a Gaussian noise was

superimposed to the argument (µ = 0, σ

= 1%) and

the phase (µ = 0, σ

= 1

◦

). In total, 100 spectra were

simulated, each without and with noise.

2.2 Complex Nonlinear Least-squares

Regression

To determine the parameter R

, the parameters B of

the equivalent circuit are calculated using the acquired

values Z

acq

. This was realised by using the method

of least squares (LS). The LS is a mathematical stan-

dard procedure for the calculation of the parameters

B = (β

,β

,...,β

) ∈ R

of a system of equations.

The goal of the procedure is to minimize the resid-

uals r

between the values of the model curve z

mod

and the acquired data z

acq

in respect to the measuring

frequency f

(B) = z

acq

( f

) −z

mod

(B, f

) (3)

Therefore the sum of the error squares R is deﬁned

as the sum of the least squares for all frequencies

= ( f

, f

,..., f

) ∈ R

R(B) =

∑

m=1

(B)

(4)

Those parameters B are to be found, which minimize

the sum of the quadratic residuals:

min

= min

B∈R

∑

m=1

(B)

(5)

The solution of this minimization problem depends

on the type of model function (Papageorgiou et al.,

2015). In the present case there is a nonlinear

optimization problem, for which the Gauss-Newton

method is a suitable procedure for the calculation of

optimal parameters B. The method is a numerical ap-

proach to solve nonlinear minimization problems ac-

cording to the LS. The basic idea is to linearize the

nonlinear cost function R and subsequently optimize

it with the help of the LS. To achieve the linearization

the ﬁrst order Taylor expansion is used. For the resid-

ual r

with the parameters B

(k)

∈ R

in iteration step

k a linearization to

˜r

(B,B

(k)

) = r

(k)

) + ∇r

(k)

)

(B −B

(k)

) (6)

with the Jacobi matrix J = ∇r

(k)

)

results. This

leads to the minimization problem:

(k+1)

= min

B∈R

∑

m=1

˜r

(B,B

(k)

)

(7)

= B

(k)

−((J|

(k)

·(J|

(k)

)

−1

(J|

(k)

) ·R(B

(k)

)

This iteration step is repeated until the result converts

(Bertsekas, 1999). To guarantee a minimization and

to treat the case of a singular matrix JJ

, the Gauss-

Newton step can be optimized to

(k+1)

= B

(k)

−α

(k)

((J|

(k)

) ·(J|

(k)

)

+ ∆

(k)

)

−1

(J|

(k)

) ·R(B

(k)

)

(8)

with α(k) ≥ 0. Thereby ∆

(k)

is selected so that

(J|

(k)

) · (J|

(k)

)

+ ∆

(k)

is positive deﬁnite. If ∆

(k)

is chosen as a positive multiple of the unit matrix

∆

(k)

= λ

I,λ ≥ 0 the Levenberg-Marquardt algorithm

(LMA) is obtained (Bertsekas, 1999), which is ap-

plied in the present work to determine the component

values of the equivalent cirucit shown in Figure 1.

Since the ﬁrst derivative of the equation describing

the equivalent circuit is not known, the Jacobi matrix

must be determined during the regression by numer-

ical differentiation. Furthermore, due to the use of

capacitors and resistors, the parameters of the equiva-

lent circuit diagram have extreme differences in size,

so that derivation is not straightforwardly possible.

This is explained by the fact that the existing differ-

ences in the magnitude of the parameter values have

an unequal strong inﬂuence on the numerical differ-

entiation.

Furthermore, parameters of different magnitudes

lead to problems during regression with the LMA.

Within each iteration, the error between the mea-

sured value and the calculated value is evaluated and

the inﬂuence of changing a single parameter is as-

sessed. Accordingly the step size for each parame-

ter is adapted within an iteration. However, a small

step size of a resistor may have little to no inﬂuence

on the calculated impedance value, whereas the same

step size may be quite signiﬁcant for a capacitance.

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

For these reasons, all parameters are normalized to

a uniform value range. In a ﬁrst step, each parameter

β is divided into a factor a and an exponent b:

β = a ·10

(9)

Consequently, the number of parameters is doubled.

Then the parameters are scaled to the same value

range W ∈ [t

scaled

= t

β −min(β)

max(β) −min(β)

·(t

−t

) (10)

These parameters are then used to perform the regres-

sion.

The acquired impedances Z

acq

and the calculated

impedances Z

cal

are also standardized, whereby these

are separated into the real and imaginary parts. Thus

the real and imaginary part have the same inﬂuence

on the calculated error. This step is performed using

a z-score:

standard

z −z

(11)

with the mean value z and the standard deviation σ.

For both impedances Z

acq

and Z

cal

, z and σ are calcu-

lated from Z

acq

. The z-score is chosen because it does

not show signiﬁcant differences in empirical compar-

ison to the min-max normalization using simulated

data. However, it is generally better at handling out-

liers, which is relevant for real measured spectra.

Since CNLS is based on the LMA algorithm, the

success of the procedure is strongly dependent on the

used start parameters. By using unfavorable start pa-

rameters the algorithm could get stuck in a local opti-

mum and does not ﬁnd a satisfying result. In the ideal

case, values close to the actual parameter sizes are

chosen as start parameters. However, since the value

ranges for each parameter are quite large, it is not pos-

sible to make a generally valid preselection. To ad-

dress this issue, a pre-ﬁt method that allows the esti-

mation of favorable start values for CNLS has already

been published (Barsukov and Macdonald, 2012).

In general, the approach of the pre-ﬁt is to perform

a CNLS with a circuit that contains a series connec-

tion of two RC elements (R

, C

for m = 1,2) and a

series resistor R

(see Figure 2). The result of the pre-

ﬁt is then used as the start value for the actual CNLS

with the Randles circuit. Therefore, the components

from the pre-ﬁt have to be assigned to the components

from the Randles circuit and can then be used as start

values for the CNLS. For this purpose, the time con-

stants of the determined RC elements are calculated

according to τ

= R

and sorted by size in ascend-

ing order.

CPE

m=1 m=2

Figure 2: Equivalent circuit diagram of the pre-ﬁt approach

(top) with the corresponding assignment of the component

values to the parts of the Randles circuit (bottom). The as-

signment is done by means of the time constant τ

Using the τ

sorted by size, the elements of the

pre-ﬁt can be assigned to the components of the Ran-

dles circuit. It is now exploited that τ for diffusion is

much larger than that of a charge exchange. First, R

is given by the series resistance R

. The remaining

components of the Randles circuit are then assigned

an ordinal number m. CPE and R

form m = 1 and Z

is assigned m = 2. This ordinal number corresponds

to the time constants of the pre-ﬁt, sorted by size.

Thus, the smaller time constant from the pre-ﬁt

is assigned to the CPE and its capacitor value C

used as start value for Q (See Equation 1). Because

the exponent of the CPE cannot be assigned, it is al-

ways set to n = 0.75. The component R

receives the

resistance value R

from the same RC element. The

Figure 3: Exemplary illustration of a simulated spectrum

(green) with the result of the pre-ﬁt (blue) and the corre-

sponding result of the CNLS (red) in the Nyquist and Bode

plot.

Elliptical Fitting as an Alternative Approach to Complex Nonlinear Least Squares Regression for Modeling Electrochemical Impedance

Spectroscopy

second RC element and Z

are handled in the same

way.

In the investigations of this work, a normal CNLS

is performed ﬁrst, whose start values are the loga-

rithmic means of the deﬁned ranges. If this does

not lead to a satisfying result, the same is done with

a former pre-ﬁtting, which is exemplarily shown in

Figure 3.

2.3 Elliptical Fitting

In case only the parameter R

is of interest for sen-

sor analysis, a geometric approach based on ellipti-

cal ﬁtting was developed. Here it is taken into ac-

count that the inﬂuence of the Warburg impedance

is only effective at comparably low frequencies. In

higher frequency ranges, the equivalent circuit results

in the parallel circuit R

||CPE shifted by the series

resistor R

. Since this parallel circuit leads to a semi-

circle or a depressed semi-circle (Orazem and Tribol-

let, 2008) (Shoar Abouzari et al., 2009) with charac-

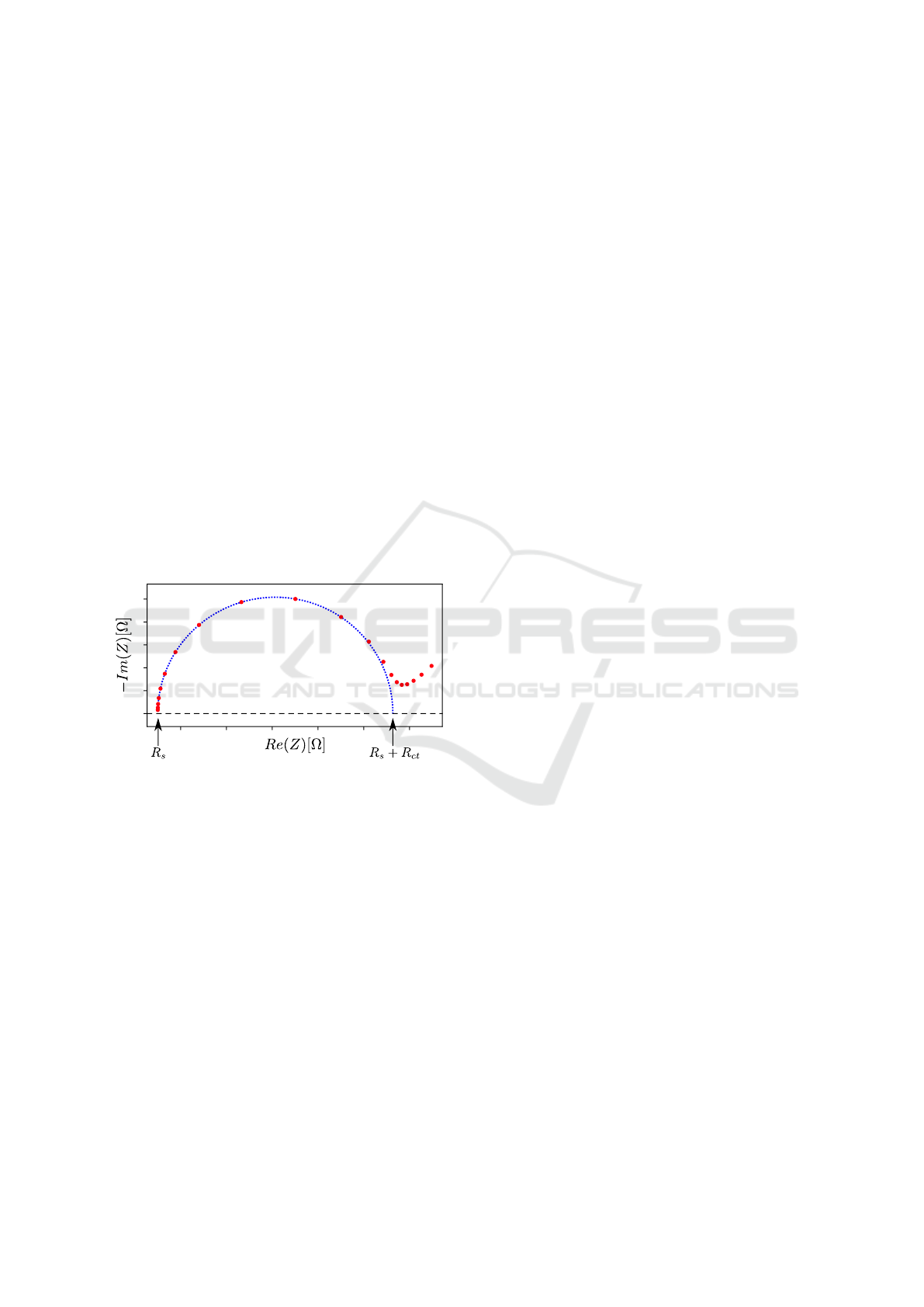
teristic points in the Nyquist plot (see Figure 4), an

elliptical ﬁtting can be used to extract the value of R

Figure 4: Exemplary Nyquist plot of a simulated data set

from a Randles circuit (red) with a ﬁtted semicircle (blue).

The left zero crossing of the semicircle represents the R

the remaining zero crossing describes R

+ R

In order to suppress the inﬂuence of the War-

burg impedance at lower measuring frequencies and

thus not to distort the ﬁtting of the ellipse, a pre-

selection of measuring points is made. Only measur-

ing points on the semicircle at the Nyquist plot should

be used. The turning point between semicircle and

Warburg impedance is used as the cut-off point. To

ﬁnd this point a 5th degree polynomial is ﬁtted to the

impedance values of the Nyquist plot. This polyno-

mial degree has proven to be a good value to avoid

overﬁtting, but still to reproduce the curve as accu-

rately as possible. Starting from the polynomial, the

ﬁrst and second derivatives are formed. The inﬂection

point now results from the zero point of the second

derivative, as far as the ﬁrst derivative is positive. All

points to the left of this point are used for the ellipse

ﬁt.

When a cone is cut on a plane that does not contain

the apex or is perpendicular to the axis of rotation, an

ellipse is obtained. A circle is only a special case of

an ellipse with half axes of equal size. For this reason

the basis for the ﬁt is the general cone equation

F(~a,~x) = ax

+ bxy + cy

+ dx + ey + f = 0. (12)

Hereby, ~a =



a b c d e f



and

~x =



xy y

x y 1



(Fitzgibbon et al.,

1999). The algebraic distance F(a,x) is the dis-

tance of a point (x,y) from the intersection edge

F(a, x) = 0. Using the method of least squares this

distance shall be minimized for given data points. To

avoid trivial solutions like ~a = 0 additional conditions

have to be set to the solution. A simple approach

is the consideration as an eigenvalue problem. For

this a quadratic condition matrix C is set up. The

eigenvalue problem thus results in

Da = λCa (13)

with the design matrix D =



c... x



(Bookstein, 1979). C has the condition that the vec-

tor ~a must describe an ellipse. Fitzgibbon et al. de-

scibed that this can be achieved with a negative dis-

criminant b

−4ac (Fitzgibbon et al., 1999). This is

generally difﬁcult to solve, but this application leaves

the freedom to scale the parameters arbitrarily. Thus

the equality constraint 4ac −b

= 1 is obtained. In

matrix notation the constraint can be written as

C~a = 1 (14)

where

C =







0 0 2 0 0 0

0 −1 0 0 0 0

2 0 0 0 0 0

0 0 0 0 0 0







. (15)

The minimization problem can then be solved by cal-

culating the eigenvectors of the Equation 13. If now a

pair of eigenvalue and eigenvector (λ

,~u

) solves the

equation system, so does also (λ

,µ~u

) with each value

of µ. With the condition from Equation 14 we can

now ﬁnd a value for µ thus resulting in

C~u

= 1. (16)

Accordingly, it applies that

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

C~u

. (17)

The parameters for an ellipse, which solves the opti-

mization problem, now result from

ˆa

= µ

. (18)

3 RESULTS

Both approaches, the CNLS and the elliptical ﬁtting

were applied to the simulated spectra. An exemplary

data set is shown in Figure 5.

Figure 5: Example of simulated data points of a Ran-

dles circuit with superimposed noise (blue; R

= 1.72 ·

, R

= 2.10 ·10

, Q

= 2.83 ·10

−7

, Q = 3.13 ·10

−10

n = 0.88), the appropriate result of the model ﬁtting (black;

−0.05% error of the R

calculation) and of the elliptical

ﬁtting (red, 0.26% error of the R

calculation).

The calculated value of the parameter R

were ex-

tracted and compared to the original value of the sim-

ulation. They were used to calculate the mean rela-

tive error E

and the coefﬁcient of determination R

The simulated spectra, which could not be ﬁt by one

of the presented approaches, were discarded for fur-

ther investigation. The raw and noisy data were con-

sidered separately. To compare the performance of

both approaches, the required calculation times were

measured for each ﬁtting procedure. All methods are

implemented in the Python programming language.

The simulations were performed on a 1.90 GHz Intel

Core™ i7-8650U Prozessor with 16 GB of RAM.

The achieved results for both methods are shown

in Table 2. The relative Error E

represents the differ-

ence between the calculated value R

ct,c

and the true

value R

ct,t

, referred to R

ct,t

. The linear relationship

ct,c

= mR

ct,t

+b with its coefﬁcient of determination

were calculated and is exemplary shown in

Figure 6 for the noisy spectra. Table 2 also shows the

number of discarded spectra N

which could not be

ﬁtted with the presented approaches.

Figure 6: Linear relationship between the calculated values

ct,c

of the CNLS (red) or the elliptical ﬁtting (blue) and the

true value R

ct,t

The calculation time for each approach was mea-

sured, whereby all steps depending on the method

(e.g. preselection of measuring points, normalization,

ﬁtting) were included. The distribution of the calcu-

lation times is shown as boxplot for the raw spectra in

Figure 7.

Figure 7: Distribution of the calculation time for CNLS and

the elliptical ﬁtting. 100 raw spectra without noise were

used.

Elliptical Fitting as an Alternative Approach to Complex Nonlinear Least Squares Regression for Modeling Electrochemical Impedance

Spectroscopy

Table 2: Results of the simulation of the CNLS and the elliptical ﬁting EF. Raw signals (CNLS

,EF

) and noisy signals

(CNLS

,EF

) were observed. The parameters mean relative error E

, slope m, intercept b, coefﬁcient of determination R

number of discarded spectra N

, median calculation time t

cal

were determined.

[%] m b[Ω] R

cal

[s]

CNLS

1.5 ·10

−6

±1.5 ·10

−5

1.00000 1.2 ·10

−3

1.00000 1 4.6 ·10

−1

−2.7±4.2 1.01027 5.6 ·10

0.99957 2 2.0 ·10

−3

CNLS

2.4 ·10

−2

±4.6 ·10

−1

0.99934 5.3 ·10

0.99997 0 4.5 ·10

−1

−2.7±4.3 1.00965 5.6 ·10

0.99950 2 2.0 ·10

−3

4 DISCUSSION AND OUTLOOK

By using the CNLS, low error in the calculation of R

is achieved and also the linear relationship to the real

value is better compared to the elliptical ﬁtting at least

for non-noisy spectra. However, this difference in

performance is smaller when considering noisy spec-

tra. This observation leads to the assumption that for

very noisy signals the difference between the two ap-

proaches could become even smaller. However, this

has to be investigated and evaluated in the following

work, preferably by using real measured spectra from

FET-based biosensors. Besides the consideration of

different noise overlays, the analysis of artifact inﬂu-

ences would also be relevant.

The results of the time measurements show that

the elliptical ﬁtting is more resource efﬁcient than

CNLS. However, these results have to be interpreted

in the context of the normalization that has been car-

ried out for the CNLS. In this process, all components

of the equivalent circuit diagram are replaced by a

factor a and an exponent b (see Equation 9), which

in turn makes the regression more time-consuming.

Nevertheless, the elliptical ﬁtting might be more suit-

able to be implemented on low-power embedded sys-

tems. In this respect, further concepts have to be de-

veloped how this approach can be efﬁciently imple-

mented on an embedded system. Thus an investiga-

tion of the power consumption would be applicable

as well.

Although the elliptical ﬁtting requires less com-

putational time than the CNLS, it is also able to ﬁt

the majority of the spectra within the data set consid-

ered in this work, which in turn stands for a high ro-

bustness of the algorithm. However, the CNLS with

the pre-ﬁt algorithm achieves even better results but

with a greater computational effort. It should be em-

phasized that the pre-ﬁt was mainly responsible for

achieving these good values, since without the pre-

ﬁt the CNLS would have had to reject 33 spectra

(without noise) or respective 31 spectra (with noise).

It is also striking that the superimposed noise has a

positive effect on the modeling ability of the CNLS,

although a strong vulnerability to noise has already

been described in the literature (Kauffman, 2009).

The results also conﬁrm that start values of the com-

ponents are decisive for the error obtained with CNLS

and demonstrate the effectiveness of the pre-ﬁt algo-

rithm. However, the disadvantage of a high depen-

dency on the start values applies less strongly to the

elliptical ﬁtting. Nevertheless, further optimizations

of the elliptical ﬁtting should be implemented, allow-

ing to reliably ﬁt more spectra. This can be achieved

by intercepting cases where the Warburg impedance

already dominates at the imaginary maximum of the

semicircle, causing the pre-selection of measurement

points to be erroneous.

For a real application scenario, the presented ap-

proaches should be adapted in order to optimize their

performance. For example, due to smaller min-max

limits of the individual parameters, particular expo-

nents can be ﬁxed so that the regression is less com-

putationally demanding. However, the presented ap-

proaches allow the modelling of a wide range of pa-

rameter combinations without the need to specify ap-

proximate initial values or narrower limits for extreme

values. They thus represent generic modelling tech-

niques.

In cases where C

can be applied instead of CPE,

the semicircle of the Randles circuit is not depressed.

For this purpose, further research is needed to deter-

mine the accuracy and computational effort that can

be achieved by a circular ﬁtting.

5 SUMMARY

With an average error of −2.7%, the elliptical

ﬁtting cannot achieve the accuracy of the CNLS

(2.4 ·10

−2

%) for the determination of R

, at least

when using ideal spectra. Thereby it could be shown

that pre-ﬁt is a suitable method to reduce the depen-

dence of CNLS on the start value. Preliminary data

indicate that the results of elliptical ﬁtting are less de-

pendent on noise than CNLS, but in any case, the lat-

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

ter has lower errors and a lower number of rejected

spectra for the data used in this work. However, this

behavior needs further investigation. The measure-

ments of the computation time showed that the el-

liptical ﬁtting needs only about

/225 of the compu-

tational effort compared to the CNLS. This leads to

the assumption that this approach might be suitable

for implementations on embedded systems. For this

purpose the accuracy of the elliptical ﬁtting has to be

estimated depending on the application, the measure-

ment and/or the sensor.

ACKNOWLEDGEMENTS

This research was funded by EU H2020 research and

innovation program entitled KardiaTool with grant

768686.

REFERENCES

Barsoukov, E. and Macdonald, J. R. (2005). Impedance

Spectroscopy: Theory, Experiment, and Applications.

Barsukov, Y. and Macdonald, J. R. (2012). Electrochemi-

cal Impedance Spectroscopy, pages 1–17. American

Cancer Society.

Bertsekas, D. P. (1999). Nonlinear programming, Second

Edition.

Bookstein, F. L. (1979). Fitting conic sections to scattered

data. Computer Graphics and Image Processing.

Chowdhury, A. D., Ganganboina, A. B., Park, E. Y., and

an Doong, R. (2018). Impedimetric biosensor for de-

tection of cancer cells employing carbohydrate target-

ing ability of Concanavalin A. Biosensors and Bio-

electronics.

Cimafonte, M., Fulgione, A., Gaglione, R., Papaianni, M.,

Capparelli, R., Arciello, A., Censi, S. B., Borriello,

G., Velotta, R., and Ventura, B. D. (2020). Screen

printed based impedimetric immunosensor for rapid

detection of Escherichia coli in drinking water. Sen-

sors (Switzerland).

Dang, W., Manjakkal, L., Navaraj, W. T., Lorenzelli, L.,

Vinciguerra, V., and Dahiya, R. (2018). Stretchable

wireless system for sweat pH monitoring. Biosensors

and Bioelectronics.

Fitzgibbon, A., Pilu, M., and Fisher, R. B. (1999). Direct

least square ﬁtting of ellipses. IEEE Transactions on

Pattern Analysis and Machine Intelligence.

Halima, H. B., Zine, N., Gallardo-Gonzalez, J., Aissari,

A. E., Sigaud, M., Alcacer, A., Bausells, J., and Er-

rachid, A. (2019). A Novel Cortisol Biosensor Based

on the Capacitive Structure of Hafnium Oxide: Appli-

cation for Heart Failure Monitoring. In 20th Interna-

tional Conference on Solid-State Sensors, Actuators

and Microsystems and Eurosensors.

Kauffman, G. B. (2009). Electrochemical Impedance Spec-

troscopy. By Mark E. Orazem and Bernard Tribollet.

Angewandte Chemie International Edition.

Kharitonov, A. B., Wasserman, J., Katz, E., and Willner,

I. (2001). The use of impedance spectroscopy for

the characterization of protein-modiﬁed ISFET de-

vices: Application of the method for the analysis of

biorecognition processes. Journal of Physical Chem-

istry B.

Leva-Bueno, J., Peyman, S. A., and Millner, P. A. (2020). A

review on impedimetric immunosensors for pathogen

and biomarker detection. Medical Microbiology and

Immunology.

Macdonald, D. D. (1990). Some advantages and pitfalls of

electrochemical impedance spectroscopy. Corrosion.

Orazem, M. E. and Tribollet, B. (2008). Electrochemical

Impedance Spectroscopy. Wiley.

Papageorgiou, M., Leibold, M., Buss, M., Papageorgiou,

M., Leibold, M., and Buss, M. (2015). Methode der

kleinsten Quadrate. In Optimierung.

Pejcic, B. and De Marco, R. (2006). Impedance spec-

troscopy: Over 35 years of electrochemical sensor op-

timization. Electrochimica Acta.

Prodromidis, M. I. (2010). Impedimetric immunosensors-A

review. Electrochimica Acta.

Randviir, E. P. and Banks, C. E. (2013). Electrochemi-

cal impedance spectroscopy: An overview of bioan-

alytical applications. Analytical Methods, 5(5):1098–

1115.

Rushworth, J. V., Ahmed, A., Grifﬁths, H. H., Pollock,

N. M., Hooper, N. M., and Millner, P. A. (2014).

A label-free electrical impedimetric biosensor for

the speciﬁc detection of Alzheimer’s amyloid-beta

oligomers. Biosensors and Bioelectronics.

Sgobbi, L. F., Razzino, C. A., and Machado, S. A. (2016).

A disposable electrochemical sensor for simultaneous

detection of sulfamethoxazole and trimethoprim an-

tibiotics in urine based on multiwalled nanotubes dec-

orated with Prussian blue nanocubes modiﬁed screen-

printed electrode. Electrochimica Acta.

Shoar Abouzari, M. R., Berkemeier, F., Schmitz, G., and

Wilmer, D. (2009). On the physical interpretation of

constant phase elements. Solid State Ionics, 180(14-

16):922–927.

Sun, A., Venkatesh, A. G., and Hall, D. A. (2016). A Multi-

Technique Reconﬁgurable Electrochemical Biosen-

sor: Enabling Personal Health Monitoring in Mobile

Devices. IEEE Transactions on Biomedical Circuits

and Systems.

Willa, C., Schmid, A., Briand, D., Yuan, J., and Koziej,

D. (2017). Lightweight, Room-Temperature CO2 Gas

Sensor Based on Rare-Earth Metal-Free Composites

- An Impedance Study. ACS Applied Materials and

Interfaces.

Yuan, X.-Z., Song, C., Wang, H., and Zhang, J. (2010).

Electrochemical Impedance Spectroscopy in PEM

Fuel Cells. Springer, London.

Elliptical Fitting as an Alternative Approach to Complex Nonlinear Least Squares Regression for Modeling Electrochemical Impedance

Spectroscopy