A Retinex Inspired Bilateral Filter for Enhancing Images under Difﬁcult

Light Conditions

Michela Lecca

Fondazione Bruno Kessler, via Sommarive 18, Trento, Italy

Keywords:

Retinex, Bilateral Filter, Spatial Color Algorithm, Image Enhancement.

Abstract:

This paper presents SuPeR-B, a novel, Retinex inspired color spatial algorithm to enhance images acquired

under difﬁcult light conditions, such as pictures containing dark and bright regions caused by backlight and/or

local, not diffused spotlight. SuPeR-B takes as input a color image and improves its readability by processing

its color channels independently in accordance with some principles of the Retinex theory. Precisely, SuPeR-

B re-works the channel intensity of each pixels accounting for differences computed both in the spatial and

intensity domains. In this way, SuPeR-B acts as a bilater ﬁlter. The experiments, carried out on a real-world

dataset, shows that SuPeR-B ensures good enhancement results, also in comparison with other state-of-the-art

algorithms: SuPeR-B improves the overall content of the image, making the dark regions brighter and more

contrasted, while lowering possible chromatic dominants of the light.

1 INTRODUCTION

An image enhancer is an algorithm that improves the

visibility of the content and of the details of an in-

put image. Such an algorithm is particularly needed

each time an image has been acquired under difﬁcult

light conditions, like low-light, back-light and/or mul-

tiple light sources, which cause noise, color distor-

tions and strong shadows and make hard to under-

stand what the image depicts. Improving the image

quality is essential not only for human observers but

also for all the machine vision algorithms requiring

an accurate detail visibility, such as key-point detec-

tors for robust and illumination invariantimage/object

recognition (Lecca et al., 2019). Many methods for

enhancing pictures captured under bad illuminations

have been proposed in the literature. Some exam-

ples are global and local image methods exploiting

statistical analysis, e.g. (Zuiderveld, 1994), (Gianini

et al., 2014), Retinex inspired algorithms and variants,

e.g. (Morel et al., 2010), (Bani´c and Lonˇcari´c, 2013),

(Lecca et al., 2018), (Lecca and Messelodi, 2019),

(Bani´c and Lonˇcari´c, 2015), illuminance/reﬂectance

decomposition approaches, e.g. (Guo et al., 2017),

(Wang et al., 2013), (Fu et al., 2016), machine learn-

ing techniques, e.g. (Jiang et al., 2019), (Wei et al.,

2018), (Lv et al., 2018), (Li et al., 2020).

https://orcid.org/0000-0001-7961-0212

Despite the huge efforts made till now, image en-

hancement is still an open issue. In fact, the most

enhancers rely on speciﬁc hypotheses about illumina-

tion, reﬂectance and spectral properties of the acqui-

sition device. These assumptions limit the enhancer

applicability to speciﬁc contexts. For instance, many

algorithmsassume that the illumination varies slightly

across the image, but this preventsthe enhancementof

images with abrupt changes of light, as for instance

strong shadows. In this respect, the enhancement of

images with very dark and very bright regions has

been poorly investigated. These images are usually

generated by capturing scenes with backlight or local,

brilliant but not diffused spotlights (see ﬁg. 1).

This work contributes to the state of the art on the

enhancement of such images by presenting SuPeR-B,

a novel spatial color algorithm obtained as a variant of

the Retinex inspired image enhancer SuPeR (Lecca

and Messelodi, 2019). Both SuPeR and SuPeR-B

take as input a color image, process their channels

separately, and partition each channel by regular, not

overlapping tiles, which are treated as super-pixels

and processed according to some principles of the

Retinex theory. The acronym SuPeR comes from

Italic letters marked above. SuPeR rescales the in-

tensity I(x) of any pixel x by a value, which is com-

puted as the average of the tile maximum intensities

greater than I(x), where each intensity is weighted

by a function inversely proportional to the distance

Lecca, M.

A Retinex Inspired Bilateral Filter for Enhancing Images under Difﬁcult Light Conditions.

DOI: 10.5220/0010235900760086

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages

76-86

ISBN: 978-989-758-488-6

Figure 1: Examples of images captured with backlight and

with local, not diffuse spotlight and their versions enhanced

by SuPeR-B (α = 0, a,b = -1). In the backlight image (top,

left), the subject is displayed against a brilliant sky and ap-

pears dark. In the spotlight image (top, right), the monitor

of the notebook positioned in a dark room acts as a local,

not diffused spotlight, that cannot illuminate sufﬁciently the

near-by regions. In both the cases, the image content with-

out enhancement is unreadable.

of the tile barycenter from x. The resulting image is

an enhanced version of the input one: it is brighter

and more contrasted, has a lower color distribution

entropy, while shadows and color casts possibly due

to the light are smoothed or even removed. The

experiments show that SuPeR provides an accurate

image enhancement of the most of real-world, low-

light images with very fast computational times, but

its performance decreases in case of backlight and

spotlight images. SuPeR-B (where ’B’ stands for

’back-light’ but also indicates that this is a second,

improved version of SuPeR) overcomes this prob-

lem by implementing a novel function weighting the

tile intensities involved in the enhancement of I(x).

This function, modeled by a Coon patch, accounts

not only for the distance between the tile barycen-

ters and x but also for the amount of the difference

between the tile maximum intensity and I(x). In this

way, SuPeR-B acts like a bilateral ﬁlter which pro-

cesses pixelwise the image based both on intensity

and spatial features, brightening dark regions within

edge preservation. The experiments carried out on

a dataset of real-world back-light and spotlight im-

ages show that SuPeR-B outperforms SuPeR as well

as other algorithms at the state of the art, in particular

the multi-scale Retinex algorithm (Petro et al., 2014),

the channel-division approach (Ramirez Rivera et al.,

2012), the image fusion-based enhancer for single

backlit images (Wang et al., 2016) and the learning

based approach for image restoration (Li and Wu,

2018). In this framework, the performance of SuPeR-

B have been evaluated by comparing the brightness,

the contrast and the color distribution entropy of the

test images before and after the enhancement. The

results show that SuPeR-B increases the brightness

and contrast, lowers the color distribution entropy and

preserves the important edges, meaning that the en-

hanced image has more visible details and a more

readable content than the input one.

2 RELATED WORK

The enhancement of images with dark and bright re-

gions due to the light has been scarcely addressed

in the literature. From the hardware point of view,

the high dynamic range (HDR) devices attempt to

deal with the root of the problem, by capturing multi-

exposure images of the same scene and merging them

via tone mapping functions in order to generate a high

quality pictures. Nevertheless, the HDR tone map-

ping functions often introduce in the ﬁnal image un-

pleasant distortions and artifacts, and thus they them-

selves are subject of current research. In addition,

HDR imaging cannot solve the problem of enhancing

an existing image where the light conditions hamper

the visibility of the content of some regions.

The image enhancers working globally, such as

histogram equalization, generally perform scarcely

because they do not account for the variability of the

light across the scene. Better performance is reached

by spatial adaptive enhancers, such as many Retinex

inspired algorithms. These latter basically process the

image channels separately and re-work the channel

intensity of each pixel x based on the intensity (and

sometimes also on other visual features like gradient)

of pixels sampled from a neighborhood of x. The out-

put image is brighter and more contrasted than the

input one, possible shadows and color casts due to

the illumination are smoothed or even removed, the

dynamic range of the image is stretched. In other

Retinex inspired algorithms, the local spatial informa-

tion is modeled through a function of the distance of

x from the pixels selected as relevant for the enhance-

ment, e.g. (Jobson et al., 1997), (M. Lecca, A. Rizzi,

and R.P. Serapioni, 2017), (Lecca, 2018), (Lecca and

Messelodi, 2019). For all the Retinex inspired meth-

ods, the deﬁnition of the locality, i.e. of the neighbor-

hood of x to be processed or of the distance function,

is a key point. For instance, when the all the pix-

els around x are considered, these algorithms tends

to behave like the Max-RGB algorithm. This latter

rescales the intensity of each pixel by the maximum

intensity over the image, but this leads to unsatis-

factory results on most real world and noisy images.

When the neighborhood of x is very small, the ﬁnal

A Retinex Inspired Bilateral Filter for Enhancing Images under Difﬁcult Light Conditions

image is close to an edge map, where chromatic in-

formation and some details are lost. A priori knowl-

edge about image content and/or light sources may

greatly help to choose the neighborhood or distance

function maximizing the algorithm performance, but

such a knowledge is often unavailable.

Retinex algorithms at multiple resolution allow to

simulate the effects of HDR imaging (Jobson et al.,

1997), (Petro et al., 2014): the input image is pro-

cessed sequentially by a Retinex algorithm with in-

creasing neighborhood (or support for the distance

function) and the obtained images are averaged to-

gether. This approach avoids the user to select a spe-

ciﬁc extent of the pixel neighborhood while stretches

the dynamic range of the image, brightening the dark

regions. Nevertheless, the prize to pay is a longer

computational time, a less accurate removal of the

light effects and sometimes the generation of artifacts.

Other algorithms, e.g. (Tsai and Yeh, 2010),

(Li and Wu, 2018), (Ramirez Rivera et al., 2012),

speciﬁcally address the problem of enhancing back-

light/spotlight images. To this purpose, they segment

the input image in backlight/frontlight regions and re-

work them with different enhancing functions. In par-

ticular, the work in (Tsai and Yeh, 2010) segments

the image by thresholding, then linearly stretches and

shifts separately the dark and bright regions in order

to brighten the ﬁrst one and darken the second one. A

variant of this computational scheme is proposed by

(Li and Wu, 2018) (hereafter denoted as Backlit), that

replaces the thresholding based segmentation with a

region growing approach and introduces guided ﬁl-

ters for improving the results. Speciﬁcally, the im-

age is partitioned in backlight and frontlight regions

through support vector machines and conditional ran-

dom ﬁelds, and each segmented region is enhanced

by a tone mapping function which maximizes the We-

ber contrast while minimizes tone distortions. Region

borders are processed by a linear combination of the

tone mapping functions estimated before to avoid ar-

tifacts. For all these approaches, the use of differ-

ent functions for enhancing the dark and bright re-

gions enables good results, which however strongly

depend on the segmentation accuracy. The work in

(Ramirez Rivera et al., 2012), here called Channel di-

vision, enhances edges and ﬂat regions with different

approaches considering image texture. The enhance-

ment results obtained on edges and ﬂat regions are

blended together to highlight details while maintain-

ing the smoothness of ﬂat regions. This method pro-

vides good results for a wide range of images, but it

poorly works in extreme conditions, as for instance

on pictures with near-black portions, where the con-

trast computation is affected by noise. The work in

(Wang et al., 2016), here shortly named Fusion, pro-

poses a fusion method, that processes the input image

I in the HVS space and computes from I an image I

with over-enhanced dark regions, an image I

where

the dynamic range of bright regions has been com-

pressed, and image I

with enhanced contrast. Each

image I

is smoothed by a Laplacian operator to re-

move undesired halos, then it is pixel-wise multiplied

to a weight that controls its overall exposure. The re-

sulting images are averaged and the result is the en-

hanced version of I.

The difﬁculty in deﬁning the spatial locality of the

image processing, the generation of artifacts along the

edges, the low quality of the image signal in dark re-

gions, the lack of a priori knowledge about the image

content are issues that make hard and challenging the

enhancement of a bad illuminated image and this jus-

tiﬁes the research of new methods.

3 THE PROPOSED APPROACH

This Section presents SuPeR (3.1) and its variant

SuPeR-B (Subsection 3.2).

3.1 SuPeR

Among the many Retinex implementations and in par-

ticular among the algorithms of the Milano Retinex

family (Rizzi and Bonanomi, 2017), the Retinex in-

spired spatial color algorithm SuPeR is of interest not

only for its enhancement performance, but also for

its fast computational times, requiring less than 0.2

seconds to process an image with size 640 × 480

with 100 tiles on a standard PC with CPU Intel(R)

Xeon(R) CPU E3-1245 v6 at 3.70 GHz (see (Lecca

et al., 2019)).

SuPeR takes as input a color image

I and an inte-

ger parameter n > 0. It enhances

I by implementing

some principles which are at the basis of the Retinex

theory, i.e. 1) independent processing of the three im-

age channels; 2) channel processing based on local

spatial and intensity information; 3) image enhance-

ment with smoothing/removal of light effects.

Let us introduce some notation. Let I be a chan-

nel of

I and let S be the domain of I, i.e. the set of

the spatial coordinates of the pixels composing I (and

thus I). Let D denote the length of the diagonal of S.

Here, the channel I is regarded as a function from S

to the intensity range (0, 1], where zero has been ex-

cluded to enable the computation of intensity ratios.

Let L indicate the enhanced version of I.

SuPeR enhances

I by implementing sequentially a

global and a pixel-wise image processing.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

Figure 2: Examples of images (on left) enhanced by SuPeR

(on right) with n = 25.

In the global processing, SuPeR partitions S in n rect-

angular, not overlapping tiles T

,. ..,T

by a regular

grid superimposed on S. According to the principle

1 reported above, SuPeR processes each channel in-

dependently. Speciﬁcally, given the channel I, SuPeR

computes the set B = {(b

) : i = 1,.. .,n}, where

∈ S is the barycenter of T

and m

is the maximum

channel intensity over T

In the pixel-wise processing, SuPeR maps the inten-

sity I(x) of any x ∈ S on a new value L(x) deﬁned as

follows:

L(x) =







∑

(b,m)∈B

(1−d(x,b))

I(x)

∑

(b,m)∈B

(1−d(x,b))

if B

1 otherwise

(1)

where B

= {(b,m) ∈ B : I(x) < m} and d is the Eu-

clidean distance between x and b, normalized to range

between 0 and 1:

d(x,b) =

k x − b k

. (2)

According to Equation (1), given the point x, Su-

PeR selects from B the subset B

composed by the

pairs (b,m) corresponding to tiles whose maximum

intensity exceeds I(x). If B

is empty, then the inten-

sity I(x) is mapped onto one, otherwise it is rescaled

by the values ms and each ratio I(x)/m is averaged

with a weight d depending on the distance of b from

x. This weight models the spatial locality of the al-

gorithm and decreases by increasing the distance of

b from x. This behaviour is in line with the Retinex

principle stating that the intensities close to x inﬂu-

ence the perception of I(x) more than those located

further (principle 2).

The ﬁnal enhanced image is obtained by packing

the L’s into an RGB image, which is robust to changes

of light (principle 3). In fact, the division of I(x)

by other intensity values enables smoothing or even

discounting light effects, such as shadows or color

dominants of the illumination. This is in line with

the von Kries model (Finlayson et al., 1994), (Lecca,

2014), stating that the change of any pixel RGB triplet

caused by a light variation can be approximated by

a linear diagonal transform of the RGB triplet. In

the original paper of SuPeR, the authors suggest to

smooth the input image by a median ﬁlter so that to

make the method robust to salt and pepper noise.

The experiments on SuPeR, conducted on real-

world images, showed good performance, both in

terms of enhancement and of computational time.

The images were improved by increasing their bright-

ness and their contrasts and by ﬂattening their color

distribution. Some examples are shown in Fig. 2.

Nevertheless, in case of images with extreme con-

ditions, such as backlight and spotlight, the perfor-

mance of SuPeR decreases, as illustrated in Fig. 3

and discussed in the next Subsection.

3.2 SuPeR-B

Figure 3 shows an example of image with extreme

backlight, depicting a giraffe against a brilliant, red-

dish sky. The enhancement by SuPeR smooths the

effects of the light changing the colors of the sky, but

the giraffe appears still dark and its details are unde-

tectable. Regarding the results of the other algorithms

speciﬁcally designed to cope with backlight, the algo-

rithm Channel Division (Ramirez Rivera et al., 2012)

performs poorly, while the others (i.e. the multi-scale

Retinex MSR described in (Petro et al., 2014), Fusion

(Wang et al., 2016) and Backlit (Li and Wu, 2018))

work a little better, but the visibility of the giraffe re-

mains low.

The bad result by SuPeR is due to the fact that the

intensity values of the pixels inside the dark regions

are divided by much greater intensity values sampled

from the sky. Although penalized by the distance

function, these sky intensities contribute heavily to

the image enhancement and make the values of L de-

creasing on the giraffe region. As already mentioned

in Section 3, multi-resolution Retinex inspired algo-

rithms, as MSR, tend to generate artifacts and they do

not ensure a good removal/smoothing of the light ef-

fects. This discourages the application of SuPeR at

multiple scales. Thresholding the distance function in

Equation (1) to exclude the high sky intensities from

the enhancement of the dark region may appear a pos-

sible way to increase the giraffe intensities, but it may

cause the loss of important edges, as those on the bor-

ders. A novel solution is proposed by SuPeR-B.

A Retinex Inspired Bilateral Filter for Enhancing Images under Difﬁcult Light Conditions

(a)

(b)

Figure 3: (a) Image enhancement of a backlight image by SuPeR and by SuPeR-B for different values of the parameters a,b

and α. For SuPeR-B the weighting function is also shown. (b) Image enhancement of the input image in (a) by the algorithms

compared with SuPeR-B.

SuPeR-B inherits from SuPeR the general work-

ﬂow, i.e. it processes the image channels separately

by the two global and local routines of SuPeR, but

introduces in Equation (1) a novel function f that

weights the contribution of the intensities in B

not

only upon their spatial distance from x but also upon

their difference from I(x). Speciﬁcally, SuPeR-B re-

places the equation (1) with the following one:

(x) =







∑

(b,m)∈B

f(δI(x,b),d(x,b))

I(x)

∑

(b,m)∈B

f(δI(x,b),d(x,b))

if B

1 otherwise

(3)

where δI(x,b) = I(b) − I(x) and f weights the inten-

sities close to x and to I(x) more than the other values.

While on bright regions the values of f is almost ir-

relevant, on dark regions they are set to increase the

brightness and the detail visibility.

There exist many expressions for f and differ-

ent expressions produce different enhancement lev-

els. In the current implementation of SuPeR-B, f

is modeled by a Coon patch, i.e. a compact surface

in 3D space whose borders are described by paths in

2D space intersecting two by two at the four patch

corners (see Figure 4 for an example). Precisely,

let c

: [0,1] → R be four continuous paths

with c

(0) = d

(0), c

(1) = d

(0), c

(0) = d

(1)

and c

(1) = d

(1). The equation of the Coon patch

bounded by these paths is:

C(s,t) = S(s,t) + T(s,t) −U(s,t) (4)

where

S(s,t) = (1−t)c

(s) + tc

(s)

T(s,t) = (1− s)d

(t) + sd

(t)

U(s,t) = c

(0)(1− s)(1− t) + c

(1)s(1− t) +

(0)(1− s)t + c

(1)st.

Pictorially, we can imagine that the endpoints of the

path c

, which belongs to the xz plane, move respec-

tively along the paths d

and d

modifying the shape

of c

accordingly until c

rests (and coincides) with

. The same representation holds for d

, whose end-

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

points are initially overc

(0) and c

(0) and go respec-

tively to d

(0) and d

(1) until d

reaches (and coin-

cide with) d

. Moving the corners and/or changing

the path equations allows to model a lot of surfaces.

Figure 4: Example of Coon surface in 3D space.

In the current version of SuPeR-B, the paths c

, d

and d

are lines deﬁned as follows:

(s) = s(α− 1) + 1

(s) = s(b− a) + a

(t) = t(a− 1) + 1

(t) = t(b− α) + α

where α, b, a are real-world user parameters and s,t ∈

[0,1]. In order to ensure positivity of the weights, the

function f is deﬁned as

f(s,t) = max(C(s,t), 0), (5)

where the parameters s and t represent respectively

the variation of intensity δI and the value of d between

two image pixels.

The values of α,a,b must be chosen so that (i)

to satisfy the Retinex principle stating that the contri-

bution of the sampled pixels to the enhancement de-

creases with their distance from x, and (ii) to improve

the visibility of the image content in the dark regions

by weighting more the items of B

closest to I(x) in

the intensity space. As a general condition, for α,a,b

such that

α ≤ 1,a < 1, b ≤ min{a,α} (6)

the requirements (i) and (ii) are satisﬁed. In fact,

when a ≥ 1, the intensities spatially located far from

x become more relevant than those close to x in the

computation of L(x) and this violates the requirement

(i). On the contrary, values of a < 1 enables the im-

plementation of (i). The parameter α acts in the in-

tensity domain similarly to d in the spatial domain:

α controls the contribution of δI to L(x), making the

intensities of B(x) closer to I(x) in the intensity do-

main more important than the others. The value α = 1

is in this case admitted and used to weight equally

the intensity variations at a given distance, regardless

of their amount, since c

(δI(x, b)) = 1 for any value

of δ(x,b). When α < 1, the relevance of δI(x,b) de-

creases proportionally to the value δI(x, b). The pa-

rameter b controls the value of f as d and δI grow

away: the lower b, the lower the effects of high val-

ues of d and δI are on L(x). Values of b greater than

a and α make f increasing when d and δI grow and

this trend has to be prevented because in contrast with

both the requirements (i) and (ii). Therefore, b must

be smaller than min{a,α}. Finally, we note that for

some choices of α,a,b, the values of C may become

smaller than zero: these valuesmust be excluded from

the computation of f, therefore C is cast to zero as

described by Equation (1). This operation extends the

range of variability of the parameters α,a, b deﬁned

by the inequalities (6), cutting down values of f for

which the requirements (i) and (ii) are not fulﬁlled.

Examples of f obtained for different values of

α,a,b are shown in Fig. 3 along with the correspond-

ing enhancement by SuPeR-B. For all the parameter

values used here, the yellowish color due to the light

has been removed. In particular, for α = 0,−1, the

input image has been remarkably improved. A more

deep analysis of the enhancement results of SuPeR-B

is provided in the next Section.

3.3 Experiments

The performance of SuPeR-B has been measured on

a database of 60 images with dark and bright regions

at different proportions. These images have been

taken from Pixabay (https://pixabay.com/), from pri-

vate collections of the author and from databases pub-

lished on the net and used to test and illustrate en-

hancement methods, e.g. (Wang et al., 2016), (Fu

et al., 2016), (Li and Wu, 2018), (Ramirez Rivera

et al., 2012). Some examples of such images are

shown in Figures 3 and 4.

The results of SuPeR-B have been compared with

the four enhancers brieﬂy described in Section 2,

i.e. Channel Division (Ramirez Rivera et al., 2012)

Fusion (Wang et al., 2016)

, Backlit (Li and Wu,

2018)

along with an implementation of the multi-

scale Retinex implementation (Petro et al., 2014)

The evaluation has been carried out by comparing

three objective measures of image quality before and

after applying the enhancement procedures. These

measures, that are widely used to judge the perfor-

Code: http://vision.khu.ac.kr/?page

id=551

Code: https://xueyangfu.github.io/

Code: https://github.com/7thChord/backlit

Code: https://it.mathworks.com/matlabcentral/

ﬁleexchange/71386-multiscale-retinex

A Retinex Inspired Bilateral Filter for Enhancing Images under Difﬁcult Light Conditions

(a) Enhancement of a Backlight Image

(b) Enhancement of a Spotlight Image

Figure 5: Comparison of enhancement results on a (a) backlight, (b) spotlight, (c) dark image.

mance of an enhancer,are computed on the brightness

Br of any color image

I. Br is the gray-levelimage de-

ﬁned on S and obtained by averaging pixel-wise the

channel intensities of

I, i.e.:

Br(x) =

∑

i=0

(x) ∀ x ∈ S, (7)

where the I

s denote the color channels of

The evaluation measures are deﬁned as follows:

1. Flatness of the luminance probability density (f

i.e. the L

distance between the probability den-

sity function of Br and the uniform probability

density function. The lower f

, the lower the en-

tropy of Br is. An image enhancer is expected to

decrease the value of f

measured on the input im-

age. In fact, this means that in the enhanced image

the dynamic range of the colors is wider than in

the input image, meaning that strong changes of

light and brightness have been smoothed or even

removed;

2. Mean value of the brightness (f

), i.e. the aver-

age of the intensities of Br. Enhancement usually

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

increases the value of f

, since it makes the input

image brighter;

3. Mean value of the multi-resolution luminance

contrast (f

), i.e. a measure of the local varia-

tions of the Br values at multiple scales proposed

in (Rizzi et al., 2004). f

is computed as follows.

The image Br is sequentially half-scaled. For each

rescaled version Br

of Br, a pixel wise contrast

cBr

(x) and a global contrast cBr

are computed.

Precisely, cBr

(x) is the average value of the ab-

solute differences between the luminance Br(x) at

x ∈ S and its 8-neighboring values, while cBR

the mean value of the cBr

(x)’s. The measure f

is deﬁned as the mean value of the cBr

’s over the

number of scale factors. Any enhancer is expected

to improve the visibility of the details, and thus to

increase the value of f

with respect to that of the

input image.

It is to note that the exact amount of the f

, f

and

depend on the image content. Images with already

clear (unreadable, resp.) content have usually a low

(high, resp.) value of f

and high (low, resp.) val-

ues of f

and f

. What is important to evaluate an

enhancer is the variation of the f

s after the enhance-

ment: the less readable the image, the more relevant

this variation is. Therefore, in this work the evalu-

ation of the performances of the enhancers has been

conducted by comparing the values of the f

s on the

input and on the enhanced images. In addition, in or-

der to provide more detailed information about the en-

hancement of the dark and bright regions, each input

image has been segmented in two parts P

and P

The f

s are thus computed on P

and P

instead of

the whole image and indicated respectively with f

and f

. The segmentation has been performed by a

thresholding procedure such that:

= {x ∈ S : Br(x) > τ} (8)

= {x ∈ S : Br(x) ≤ τ} (9)

and τ = (max

x∈S

Br(x) − min

x∈S

Br(x))/2. Basically,

this segmentation partitions the input image in two re-

gions with different luminance, with P

darker than

. Despite naive, this segmentation allows to sepa-

rate the frontlight and backlight regions of the input

images in a sufﬁciently reliable way.

The current implementation of SuPeR-B is written

in C++. The parameter n has been set to 100. The ex-

periments have been repeated for different triplets of

(a,b,α) obtained by varying a,b in {−1,0} and α in

{-1, 0, 1} within the inequalities in formula (6). For

α = 1 and a = b = 0, SuPeR-B behaves like SuPeR.

The function f, that is computed in the global pro-

cessing phase, is discretized and represented as a ma-

trix with size 100×100 to speed up the computational

time for the enhancement, that is on average less than

1 second (on a notebook with Intel CORE i5 and op-

erating system Windows 10). In these experiments,

no median ﬁlter has been applied.

Table 1 reports the mean values of the perfor-

mance evaluation measures computed on the whole

image (f

s), on the bright region P

s) and on the

dark region ( f

s). Precisely, these values have been

averaged over the number of dataset images.

All the enhancers improve the image content, by

increasing the values of f

and f

, while decreasing

that of f

. MSR achieves the best results in term of

and f

, but as already observed in the paper MSR

suffers for halos generation (see Fig. 5(a) for an ex-

ample). Channel Division outputs the worst results in

terms of f

and f

, returning an image still dark and

with a remarkable difference between dark and bright

regions, as proved by the gap between f

s and f

(see for instance, Fig. 5(b) and (c)). In particular,

Channel Division yields the highest value of f

and

the lowest value of f

. For α = −1, SuPeR-B out-

puts the highest values of f

and very low values of

, while in general, for any choice of the parameters

α,a,b, it obtains values of f

close to those of Chan-

nel Division, SuPeR, Fusion and Backlit.

A similar trend is observed for the dark regions

. Again, the readability of the P

s is improved

by all the enhancers, MSR grants the lowest f

and

the highest f

, Channel Division reports the lowest

and SuPeR-B performs similar to SuPeR, Fusion,

Backlit and Channel Division in terms of contrast

while reports for α = −1 very high values of f

and

very low values of f

The results on the P

s could appear quite surpris-

ing: in fact, here, apart from Channel Division, all the

enhancers increase the brightness, but decrease the

contrast, while the histogram ﬂatness remains high

and in many cases exceeds that measured on the in-

put images. This behaviour is justiﬁed as follows. On

the bright regions, enhancement is usually not neces-

sary since the content is already clear. Anyway, the

brightness of the P

s, that is on average very high on

the input, is further increased by the enhancers, al-

though much less than that of the P

s. The point is

that in the enhanced images, the brightness is very

close to its maximum value (i.e. 255) and conse-

quently its histogram is peaked on right and thus far

from an uniform probability density function (i.e. f

is high). Moreover, in the dataset considered here,

the bright regions are often almost uniform or present

few or slight edges. The main contribution to the

contrast of the P

s comes from their boundaries with

the dark regions P

s. Despite the enhancers preserve

these boundaries, they diminish their magnitude be-

A Retinex Inspired Bilateral Filter for Enhancing Images under Difﬁcult Light Conditions

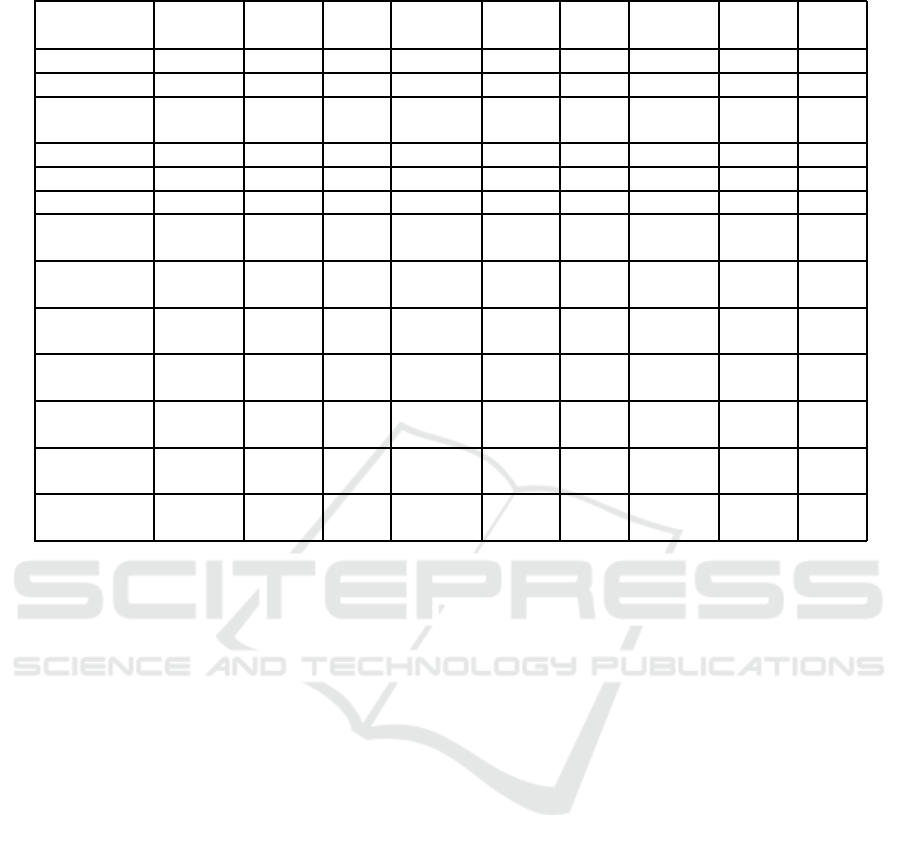
Table 1: Evaluation of SuPeR-B in comparison with other enhancers. For SuPeR-B the triplet (α,a, b) is reported.

Algorithm f

[×10

−3

] [×10

−3

] [×10

−3

]

INPUT 4.17 67.79 16.56 4.92 179.33 33.07 5.26 29.74 14.58

MSR 2.21 118.12 28.66 4.69 185.23 30.51 2.35 97.24 31.66

CHANNEL 4.04 89.45 21.60 5.86 228.30 36.03 4.53 41.49 20.97

DIVISION

FUSION 3.23 89.54 20.52 4.84 189.51 32.27 4.22 56.82 19.82

BACKLIT 2.78 100.65 22.79 4.68 189.30 28.35 3.47 73.26 23.55

SuPeR 3.41 104.95 19.95 5.40 210.54 29.78 4.25 65.56 19.63

SuPeR-B 3.34 106.64 20.06 5.40 210.78 29.61 4.17 67.71 19.31

(1, 0, -1)

SuPeR-B 3.31 105.32 20.17 5.37 210.51 30.07 4.15 66.16 19.87

(1, -1, -1)

SuPeR-B 3.17 119.31 20.05 5.51 213.03 26.53 3.95 84.12 20.46

(0, 0, 0)

SuPeR-B 3.02 123.13 20.19 5.53 213.47 25.84 3.75 89.81 20.83

(0, 0, -1)

SuPeR-B 2.89 123.48 20.48 5.50 213.43 26.14 3.61 90.02 21.15

(0, -1, -1)

SuPeR-B 2.92 141.15 20.08 5.88 218.83 20.42 3.26 113.97 22.17

(-1, 0, -1)

SuPeR-B 2.78 142.35 20.33 5.87 219.29 20.28 3.05 115.44 22.55

(-1, -1, -1)

cause they increase the brightness of P

: this causes

the decrease of f

. Channel Division represents an

exception, since the trend of the f

s is the same of

those of the f

and of the f

s. Nevertheless, as al-

ready mentioned above, among the enhancers, this al-

gorithm achieves unsatisfactory results, with still dark

images characterized by high gap between f

and f

Regarding SuPeR-B, it is to note that the values of

s it reports are in general smaller than those of the

other enhancers. This is because, in line with Retinex

theory and as well as SuPeR, SuPeR-B tends to re-

move slight edges, that are often present in the bright

regions but that are considered to be irrelevant for un-

derstanding the main content of the scene. In particu-

lar, the low values of f

indicate a scarce presence of

edges on P

, and this justiﬁes the high values of f

Figure 3 shows that different values of α,a,b pro-

vide very different enhancement results. In accor-

dance with Equation (3), the parameters α and a tune

respectively the contributions to L

(x) of the intensity

differences and of the spatial differences, while the

parameter b controls both these contributions when

the intensity and spatial differences are large. In par-

ticular, lowering α increases the weight of the small

intensity differences and this generally higher the val-

ues of f

and f

, especially in dark areas. For any

ﬁxed value of α, low values of a increase the spa-

tial locality of the algorithm, yielding again high val-

ues of f

and f

. Low values of b further decreases

the weight of high intensity and spatial differences.

Therefore, the lower α, a,b, the higher the locality of

the algorithm in spatial and intensity domains is.

According to such observations, when α = 1,

SuPeR-B behaves similarly to SuPeR: in fact, in this

case the contribution to L

(x) of the intensity varia-

tions does not depend on their amount and the Coon

patch is close to a stepway, whose slope is determined

by the spatial terms. As already mentioned before,

for α = 1,a = b = 0, SuPeR-B implements SuPeR,

where the locality of the image processing depends

exclusively on the spatial features. Figure 3(a) show

an example of image enhancement obtained by tuning

only the contribution of the spatial differences with

α = 1,a = b = −20: the details of the giraffe be-

come a little more visible, but the giraffe is still quite

dark and its borders are very tick, so that the results

is unsatisfactory. Better results are obtained by tun-

ing the algorithm locality also in the intensity domain,

as shown by the enhanced pictures of Figure 3(a) ob-

tained for α = −1,−2.

In general, the experiments show that for backlight

and spotlight images the best performance is achieved

by tuning the differences in both the spatial and inten-

sity domains.

Finally, differently from the algorithms consid-

ered here exept for SuPeR, SuPeR-B exhibits the im-

portant property of lowering the color cast due to the

illumination, returning an enhanced image robust to

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

changes of light. This property is clearly illustrated in

Figure 5(c) and it is of great importance for many ma-

chine vision algorithms, such as illumination invari-

ant feature matching and people/object recognition in

real-world scenarios.

4 CONCLUSIONS

Figure 6: Examples of usage of SuPeR-B as a pre-

processing step of the key-point detector in (Lowe, 2004):

the enhancement of the input images (on left) grants a better

detection of key-points (in green color, on right) in the dark

regions.

The Retinex inspired spatial color algorithm SuPeR-

B proposes a novel and efﬁcacious technique to en-

hance images captured under difﬁcult light, in partic-

ular under backlight and local, not diffused spotlights

that hamper understandingthe image content. SuPeR-

B basically implements a bilateral processing of the

channel intensities of the image pixels that enable

brightening dark regions, smoothing color casts due

to the light, while preserving important edges. The

bilateral processing is modeled by the weighting func-

tion f, that here has been expressed as a Coon surface

bounded by lines. The experiments proved that this

choice of f provides a satisfactory level of enhance-

ment, also in comparison with other algorithms at the

state-of-the-art. The input images are remarkably im-

proved by SuPeR-B, which increase their brightness

and detail visibility, especially in the dark areas, while

decrease the overall color distribution entropy.

As mentioned in Section 3, there are many expres-

sions for f: determining the equation of f and the

values of its parameters most suitable for enhancing

an image within a given task is a critical point for

a reliable and aware usage of SuPeR. In general, in

the current implementation of SuPeR-B, the choice

of the values of α,a,b to be input to SuPeR-B should

be guided by the applications at the hand as well as by

the image content. For instance, for human inspection

of the content of the giraffe image in Figure 3, the val-

ues (α,a, b) = (0, 0, 0) and (1, 0, -1) perform poorly

in comparison with the others. In other cases, like for

(α,a, b) = (-1, -1, -1), the brightness of the enhanced

image is too high and the image content is washed out

or over-enhanced. As a conclusion, the set-up of f is

an open issue to be investigated in the future.

Future work will also include the usage of SuPeR-

B within computer vision tasks that require to process

high quality images, as for instance image descrip-

tion and matching. In this respect, as pointed out in

(Lecca et al., 2019) and as illustrated by the examples

in Figure 6, the improvement of visual characteris-

tics such as brightness, contrast and color distribution

does not only grant a better visibility and readability

of the image content for humans, but it is also funda-

mental to improve the detection of image key-points

(here performed by SIFT (Lowe, 2004)) and thus to

increase the performance of algorithms for descrip-

tion and matching of images regardless of their illu-

mination conditions.

REFERENCES

Bani´c, N. and Lonˇcari´c, S. (2013). Light Random Sprays

Retinex: exploiting the noisy illumination estimation.

IEEE Signal Processing Letters, 20(12):1240–1243.

Bani´c, N. and Lonˇcari´c, S. (2015). Fireﬂy: A hardware-

friendly real-time local brightness adjustment method.

In 2015 IEEE International Conference on Image Pro-

cessing (ICIP), pages 3951–3955.

Finlayson, G. D., Drew, M. S., and Funt, B. V. (1994).

Color constancy: generalized diagonal transforms suf-

ﬁce. JOSA A, 11(11):3011–3019.

Fu, X., Zeng, D., Huang, Y., Liao, Y., Ding, X., and Pais-

ley, J. (2016). A fusion-based enhancing method

for weakly illuminated images. Signal Processing,

129:82–96.

Gianini, G., Manenti, A., and Rizzi, A. (2014). QBRIX: a

quantile-based approach to Retinex. J. Opt. Soc. Am.

A, 31(12):2663–2673.

Guo, X., Li, Y., and Ling, H. (2017). Lime: Low-light

image enhancement via illumination map estimation.

IEEE Transactions on Image Processing, 26(2):982–

993.

Jiang, Y., Gong, X., Liu, D., Cheng, Y., Fang, C., Shen, X.,

Yang, J., Zhou, P., and Wang, Z. (2019). Enlighten-

gan: Deep light enhancement without paired supervi-

sion. arXiv preprint arXiv:1906.06972.

Jobson, D. J., Rahman, Z., and Woodell, G. A. (1997).

Properties and performance of a center/surround

retinex. IEEE Transactions on Image Processing,

6(3):451–462.

Jobson, D. J., Rahman, Z.-u., and Woodell, G. A. (1997). A

multiscale retinex for bridging the gap between color

A Retinex Inspired Bilateral Filter for Enhancing Images under Difﬁcult Light Conditions

images and the human observation of scenes. IEEE

Transactions on Image processing, 6(7):965–976.

Lecca, M. (2014). On the von Kries Model: Estimation,

Dependence on Light and Device, and Applications,

pages 95–135. Springer Netherlands, Dordrecht.

Lecca, M. (2018). STAR: A segmentation-based approx-

imation of point-based sampling Milano Retinex for

color image enhancement. IEEE Transactions on Im-

age Processing, 27(12):5802–5812.

Lecca, M. and Messelodi, S. (2019). SuPeR: Milano

Retinex implementation exploiting a regular image

grid. J. Opt. Soc. Am. A, 36(8):1423–1432.

Lecca, M., Simone, G., Bonanomi, C., and Rizzi, A. (2018).

Point-based spatial colour sampling in milano-retinex:

a survey. IET Image Processing, 12(6):833–849.

Lecca, M., Torresani, A., and Remondino, F. (2019). On im-

age enhancement for unsupervised image description

and matching. In Ricci, E., Rota Bul`o, S., Snoek, C.,

Lanz, O., Messelodi, S., and Sebe, N., editors, Image

Analysis and Processing – ICIAP 2019, pages 82–92,

Cham. Springer International Publishing.

Li, S., Cheng, Q. S., and Zhang, J. (2020). Deep multi-path

low-light image enhancement. In 2020 IEEE Confer-

ence on Multimedia Information Processing and Re-

trieval (MIPR), pages 91–96.

Li, Z. and Wu, X. (2018). Learning-based restoration of

backlit images. IEEE Transactions on Image Process-

ing, 27(2):976–986.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International journal of computer

vision, 60(2):91–110.

Lv, F., Lu, F., Wu, J., and Lim, C. (2018). MBLLEN: Low-

light image/video enhancement using cnns. In BMVC,

page 220.

M. Lecca, A. Rizzi, and R.P. Serapioni (2017). GREAT: a

gradient-based color-sampling scheme for Retinex. J.

Opt. Soc. Am. A, 34(4):513–522.

Morel, J. M., Petro, A. B., and Sbert, C. (2010). A PDE

formalization of Retinex theory. IEEE Transactions

on Image Processing, 19(11):2825–2837.

Petro, A. B., Sbert, C., and Morel, J.-M. (2014). Multiscale

retinex. Image Processing On Line, pages 71–88.

Ramirez Rivera, A., Byungyong Ryu, and Chae, O.

(2012). Content-aware dark image enhancement

through channel division. IEEE Transactions on Im-

age Processing, 21(9):3967–3980.

Rizzi, A., Algeri, T., Medeghini, G., and Marini, D. (2004).

A proposal for contrast measure in digital images. In

CGIV 2004 - 2nd European Conference on Color in

Graphics, Imaging, and Vision and 6th Int. Sympo-

sium on Multispectral Color Science, pages 187–192,

Aachen.

Rizzi, A. and Bonanomi, C. (2017). Milano retinex family.

Journal of Electronic Imaging, 26(3):031207.

Tsai, C.-M. and Yeh, Z.-M. (2010). Contrast compensation

by fuzzy classiﬁcation and image illumination analy-

sis for back-lit and front-lit color face images. IEEE

Transactions on Consumer Electronics, 56(3):1570–

1578.

Wang, Q., Fu, X., Zhang, X., and Ding, X. (2016). A fusion-

based method for single backlit image enhancement.

In 2016 IEEE International Conference on Image Pro-

cessing (ICIP), pages 4077–4081.

Wang, S., Zheng, J., Hu, H.-M., and Li, B. (2013). Nat-

uralness preserved enhancement algorithm for non-

uniform illumination images. IEEE Transactions on

Image Processing, 22(9):3538–3548.

Wei, C., Wang, W., Yang, W., and Liu, J. (2018). Deep

retinex decomposition for low-light enhancement. In

BMVC.

Zuiderveld, K. (1994). Contrast limited adaptive histogram

equalization. In Graphics gems IV, pages 474–485.

Academic Press Professional, Inc.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications