Fiducial Points-supported Object Pose Tracking on RGB Images

via Particle Filtering with Heuristic Optimization

Mateusz Majcher and Bogdan Kwolek

AGH University of Science and Technology,

30 Mickiewicza, 30-059 Krakow, Poland

Keywords:

6D Object Pose, Object Segmentation, Pose Tracking.

Abstract:

We present an algorithm for tracking 6D pose of the object in a sequence of RGB images. The images are

acquired by a calibrated camera. A particle ﬁlter is utilized to estimate the posterior probability distribution

of the object poses. The probabilistic observation model is built on the projected 3D model onto image and

then matching the rendered object with the segmented object. It is determined using object silhouette and

distance transform-based edge scores. A hypothesis about 6D object pose that is calculated on the basis of

object keypoints and the PnP algorithm is included in the probability distribution. A k-means++ algorithm

is then executed on multi-modal probability distribution to determine modes. A multi-swarm particle swarm

optimization is executed afterwards to ﬁnd ﬁnest modes in the probability distribution together with the best

pose. The object of interest is segmented by an U-Net neural network. Eight ﬁducial points of the object are

determined by a neural network. A data generator employing 3D object models has been developed to syn-

thesize photorealistic images with ground-truth data for training neural networks both for object segmentation

and estimation of keypoints. The 6D object pose tracker has been evaluated both on synthetic and real images.

We demonstrate experimentally that object pose hypotheses calculated on the basis of ﬁducial points and the

PnP algorithm lead to considerable improvements in tracking accuracy.

1 INTRODUCTION

It is expected that in the near future, robots will per-

form routine tasks that they are not able to perform

today. Estimating the 6-DoF pose (3D rotations + 3D

translations) of an object with respect to the camera

is crucial to realize such tasks. Delivering robust esti-

mates of the object pose on the basis of RGB images

is a difﬁcult problem. The discussed task has many

important aspects that should be resolved to achieve

robust object grasping, including object classiﬁcation,

object detection, object tracking, object segmentation

and ﬁnally, estimation of the 6D object pose. A lot of

successful researches have been done in these direc-

tions (He et al., 2017; Deng et al., 2019).

The most simple way for camera pose estimation

consists in using squared markers, for instance ArUco

markers (Garrido-Jurado et al., 2014). However, hav-

ing on regard that the marker detection is based on

high contrast edges in the image as well as overall

high intensity contrast between the black and white

areas of the marker, such methods are prone to mo-

tion blur caused by fast marker or camera movement,

mainly due to unsharp or blurred edges (Marchand

et al., 2016). In Perspective-n-Point (PnP) algorithm

(Fischler and Bolles, 1981) the pose of a calibrated

camera is estimated on the basis of a set of 3D points

in the world and their corresponding 2D projections

in the image. However, the correspondence-based ap-

proaches require rich texture features. They calculate

the pose using the PnP and recovered 2D-3D corre-

spondences, often in a RANSAC (Fischler and Bolles,

1981) framework to support outlier rejection. While

PnP algorithms are usually robust when the object is

well textured, they can fail when it is featureless or

when in the scene there are multiple objects occlud-

ing each other.

A large variety of object pose estimation ap-

proaches relying on natural point features have been

proposed in the past, e.g. (Lepetit et al., 2004; Vidal

et al., 2018), to enumerate only some of them. In gen-

eral, features can either encode image properties or be

a result of learning.

Recently, great progress has been made on esti-

mating 6D object pose from the 2D image via deep

learning-based architectures. A ﬁrst attempt to use

Majcher, M. and Kwolek, B.

Fiducial Points-supported Object Pose Tracking on RGB Images via Particle Filtering with Heuristic Optimization.

DOI: 10.5220/0010237109190926

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 5: VISAPP, pages

919-926

ISBN: 978-989-758-488-6

919

a convolutional neural network (CNN) for direct re-

gression of 6DoF object poses was PoseCNN (Xiang

et al., 2018). For example, in (Kehl et al., 2017) the

authors treat the pose estimation as a classiﬁcation

problem and train neural networks to classify the im-

age features into a discretized pose space. In general,

two main CNN-based approaches to 6D pose object

pose estimation have emerged: either regressing the

6D object pose from the image directly (Xiang et al.,

2018) or predicting 2D key-point locations in the im-

age (Rad and Lepetit, 2017), from which the object

pose can be determined by the PnP algorithm. In (Rad

and Lepetit, 2017) the whole process is divided into

two stages. In the ﬁrst stage the authors determine

the centres of objects of interest, and afterwards they

use deep neural networks to determine the rotation of

the object. In (Peng et al., 2019), a Pixel-wise Voting

Network (PVNet) to regress pixel-wise unit vectors

pointing to the keypoints and then using these vec-

tors to vote for keypoint locations via RANSAC has

been proposed. Instead of directly regressing image

coordinates of keypoints, their method predicts unit

vectors that represent directions from each pixel of

the object towards the keypoints, then these directions

vote for the keypoints locations based on RANSAC.

There are several publicly available datasets for

benchmarking the performance of algorithms for 6D

object pose estimation, including OccludedLinemod

(Brachmann et al., 2014), YCB-Video (Xiang et al.,

2018). However, the current datasets do not focus

on 6D object tracking using RGB image sequences.

They are mainly designed for single-frame based pose

estimation. The data do not contain distortions (e.g.

motion blur caused by fast object motions) and free-

style object motions, which are common in real-world

scenarios.

In this work we investigate the problem of 6-DOF

object pose estimation and tracking on RGB images

acquired from a calibrated camera. U-Net neural net-

work is used to segment the object of interest. The

segmented object is then fed to a neural network esti-

mating the 2D position of eight ﬁducial points of the

object. Afterwards, the 6D object pose is estimated

using the PnP algorithm and then used as a pose hy-

pothesis during the pose inference. A particle ﬁlter

(PF) combined with a particle swarm optimization

(PSO) is utilized to estimate the posterior probabil-

ity distribution of the object poses as well as the best

pose. The observation model and objective function

are calculated on the basis of the projected 3D model

onto images and then matching the rendered object

with the segmented object. It is determined using

object silhouette and distance transform-based edge

scores. A hypothesis about 6D object pose that is cal-

culated on the basis of eight ﬁducial keypoints and

the PnP algorithm is included in the probability dis-

tribution of the object poses. A k-means++ algorithm

is then executed on multi-modal probability distribu-

tion. A particle swarm optimization is executed af-

terwards to ﬁnd the modes in the probability distribu-

tion. The ﬁducial points of the object are determined

by a neural network. A data generator employing 3D

object models has been developed to synthesize pho-

torealistic images with ground-truth data for training

neural networks both for object segmentation and es-

timation of keypoints. The 6D object pose tracker

has been evaluated both on synthetic and real images

with six objects. In order to capture real images each

of six objects has been placed on top of an electric

turntable and then captured from four camera eleva-

tions. We demonstrate experimentally that object hy-

potheses calculated on the basis of ﬁducial points and

the PnP algorithm permit achieving considerable im-

provements in tracking accuracies.

2 OBJECT SEGMENTATION

The architecture of neural network for object seg-

mentation has been based on the U-Net (Ronneberger

et al., 2015). The architecture of U-Net resembles the

letter U, which is why it is called so. In such networks

we can distinguish a contracting path (encoding) path

and an expansive (decoding) path. In the contraction

path, each block consists of a series of 3×3 convo-

lution layers followed by a 2×2 max pooling, where

the number of cores after each block doubles. A char-

acteristic feature of the U-Net architecture is the ex-

pansive path, which also, by analogy with the con-

tracting path, consists of several expansion blocks.

In this path, the 2×2 max pooling is replaced by a

2×2 upsampling layer. Each step in the expanding

path consists of the upsampling operation followed

by a 2×2 convolution, combining with an appropri-

ately cropped property map, and this is completed

by two 3×3 convolutions, followed by ReLU. Skip

connections used in U-Net directly connects the fea-

ture maps between encoder and decoder. The neural

network was trained on RGB images. To reduce the

training time, prevent overﬁtting and to increase per-

formance of the U-Net we added Batch Normalization

(BN) (Ioffe and Szegedy, 2015) after each Conv2D.

As it improves gradient ﬂow through the network, it

reduces dependence on initialization and higher learn-

ing rates are achieved. Data augmentation has also

been applied during the network training. The pixel-

wise cross-entropy has been used as the loss function.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

920

3 6D OBJECT POSE

ESTIMATION

The 6D pose is estimated using a CNN, which deliv-

ers 2D locations of eight ﬁducial points of the object.

The 2D locations of such points are then fed to a PnP

algorithm, that delivers the 6D pose of the object. A

segmented image of size 128×128 pixels is delivered

from the U-Net CNN to the ﬁducial CNN as input,

which determines 2D locations of eight keypoints.

Figure 1 shows a schematic architecture of ﬁducial

CNN. The network architecture has been designed in

such a way as to obtain, on the one hand, sufﬁcient

precision in the estimation of the position of keypoints

in the images, and on the other hand, to avoid intro-

ducing unnecessary delays in the estimation of the

position of the points during the pose tracking. The

ﬁrst part consists of 2 blocks, where each one con-

tains convolutional layer with 3×3 kernels, followed

by max-pooling with kernel of size 2×2, respectively.

The layers are completed by the batch normalization

and ReLU activation function. The next part con-

sists of 3 consecutive convolutional layers with 3×3

kernels followed by max-pooling with kernel of size

2×2. In the MLP part, in the ﬁrst two layers there

are 512 neurons in each layer, and in the last there are

16 neurons that deliver the positions of 8 pairs of key-

points of the object. The loss function was mean abso-

lute error (MAE). This network is a result of several

experiments aiming at ﬁnding possibly small neural

network, while still achieving pose estimates with ac-

curacy sufﬁcient for object grasping. For each object

a separate network has been trained. Given class in-

formation determined by segmentation networks like

mask-RCNN (He et al., 2017), the network for pose

estimation can be selected automatically.

Figure 1: Neural network for estimation of ﬁducial points.

The discussed neural network requires input im-

ages of size 128 × 128 with the segmented object of

interest. During pose tracking a ROI containing the

object can be extracted easily using information from

the previous frame and then scaled to desirable size.

3.1 PF-PSO with PnP-based Hypotheses

The algorithm extends the algorithm for 6D pose

tracking (Majcher and Kwolek, 2020), which com-

bines particle ﬁltering and particle swarm optimiza-

tion as well as effectively utilizes the k-means++

(Arthur and Vassilvitskii, 2007) for better dealing

with multimodal distributions. Given the particle

set representing the posterior probability distribu-

tion in the previous frame, the particles are propa-

gated according to a probabilistic motion model, the

pose likelihoods on the basis of probabilistic observa-

tion model are calculated, and afterwards the particle

weights are determined and a resampling is executed,

see also Fig. 2, as in ordinary particle ﬁlters. A par-

ticle with a small weight is replaced in such a resam-

pled particle set by a particle with pose determined on

the basis of keypoints and the PnP algorithm, see line

#2 in below pseudo-code. Next, samples are clustered

using k-means++ algorithm (Arthur and Vassilvitskii,

2007), which applies a sequentially random selection

strategy according to a squared distance from the clos-

est center already selected. Afterwards, a two-swarm

PSO is executed to ﬁnd the modes in the probability

distribution. The number of the iterations executed by

the PSO is set to three. Next, ten best particles are se-

lected to form a sub-swarm, see lines #6-7 in below

pseudo-code. Twenty iterations are executed by such

a sub-swarm to ﬁnd better particle positions. The best

global position returned by the discussed sub-swarm

is used in visualization of the best pose. Finally, an

estimate of the probability distribution is calculated

by replacing the particle positions determined by the

PF with corresponding particle positions, which were

selected to represent the modes in the probability dis-

tribution, see lines #6-7, and particles reﬁned by the

sub-swarm, see line #9. The initial probability distri-

bution is updated by ten particles with better positions

found by the PSO algorithms and ten particles with

better positions found by the sub-swarm, see lines

#9-11. The probabilistic motion model, observation

model and objective function in the PSO are the same

as in (Majcher and Kwolek, 2020).

1 function select(n best, X)

2 X

sorted

= quicksort(X) using f ()

3 return X

sorted

[1. .. n best]

1 X

= PF(X

t−1

)

2 x

PnP

= PnP(), replace worst x ∈ X

with x

PnP

3 X

= k-means++(X

)

4 ∼,X

= PSO(X

,3)

5 ∼,X

= PSO(X

,3)

6 X

c1 best

= select(5,X

)

7 X

c2 best

= select(5,X

)

8 X

best

= X

c1 best

c2 best

9 g

best

= PSO(X

best

,20)

10 substitute 5 x ∈ X

with corresp. x ∈ X

c1 best

11 substitute 5 x ∈ X

with corresp. x ∈ X

c2 best

13 substitute 10 x ∈ X

with corresp. x ∈ X

best

14 return g

best

Fiducial Points-supported Object Pose Tracking on RGB Images via Particle Filtering with Heuristic Optimization

921

Figure 2: PF-PSO supported with pose hypotheses, which

are determined on the basis of keypoints and the PnP.

4 DATASET

To evaluate and compare pose estimation algorithms,

a number of benchmark datasets have been pro-

posed, including: Linemod (Hinterstoisser et al.,

2013), Linemod-Occluded (Brachmann et al., 2014),

T-LESS (Hodan et al., 2017), YCB-Video (Xiang

et al., 2018), HomebrewedDB (Kaskman et al., 2019).

The datasets are mainly designed for single-frame

based pose estimation. They do not contain distor-

tions (e.g. motion blur caused by fast object mo-

tions) and free-style object motions, which are im-

portant for experiments and performance evaluation

in real-world scenarios. A recently proposed dataset

(Wu et al., 2017) has been designed for pose track-

ing and addresses issues mentioned above. In partic-

ular, it contains binary masks for real objects. How-

ever, this dataset has not been designed for algorithms

based on deep learning. For instance, it does not con-

tain keypoints data and therefore neural networks for

6D pose estimation on the basis of keypoints (Zhao

et al., 2018) can not be trained. Moreover, in 3D

object sub-dataset only objects generated by a 3D

printer are available. This means that it does not per-

mit a comparison of results obtained for frequently

used objects in popular datasets, like power drill from

YCB-Video dataset. This motivated us to utilize an

extended dataset for 6D object tracking (Lopatin and

Kwolek, 2020).

Our dataset contains six objects: drill, multime-

ter, electrical extension, duck, frog and piggy. The

extension, duck, frog, and piggy are texture-less or

almost texture-less. 3D models of the objects were

prepared manually using Blender, which is a 3D com-

puter graphics software toolset (Blender Online Com-

munity, 2020). The diameter of the ﬁrst object is

228 mm and the 3D model consists 417777 vertices,

the diameter of the second object is 138 mm and 3D

model contains 119273 vertices, the diameter of third

object is 103 mm and 3D model contains 216233 ver-

tices, the diameter of the fourth object is 117 mm

and 3D model contains 140148 vertices, the diame-

ter of the ﬁfth object is 108 mm and 3D model con-

tains 135072 vertices, and the diameter of the sixth

object is equal to 116 mm and its 3D model con-

sists of 132620 vertices. The 3D models of the ob-

jects have been designed using 2.81 software version

of Blender. Figure 3 depicts rendered images, which

were obtained on the basis of our 3D models. The

images were rendered using Python scripts (Lopatin

and Kwolek, 2020) with Blender’s engine support. As

we can observe, our 3D models permit photo-realistic

rendering of the objects in the requested poses.

(a) Duck

(b) Piggy

(d) Extension

(e) Multimeter

(f) Power drill

Figure 3: Samples of real images.

We generated images for training neural networks

both for object segmentation/detection and tracking.

For object detection and object segmentation the ob-

ject masks are stored both in images with binary

masks as well as .json ﬁles, which are compatible with

coco data format (Lin et al., 2014). The binary masks

are stored in .png images with alpha (transparency)

channel. The .jsn ﬁles contain also 3D positions of

eight ﬁducial points. Even if a ﬁducial point is oc-

cluded, it is generated on the image. Thus, the num-

ber of ﬁducial points is constant despite occlusions

or self-occlusions. This means that neural networks

like mask-RCNN can be trained easily not only for

object detection or segmentation, but also after small

modiﬁcation of the code for estimation of position of

ﬁducial points on the RGB images. The information

about 6D pose of the objects is also stored in the .json

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

922

ﬁles. It is worth noting that popular datasets for 6D

object pose estimation do not contain data on object

keypoints, i.e. ﬁducial points of the objects, and usu-

ally contain only information on the 3D positions of

the rectangular corners describing the object of inter-

est, and thus automatically determined from the posi-

tion of the camera or ArUco markers. The tracking

sub-dataset contains images with three types of mo-

tion: (i) object moves from left to right and then from

right to left, (ii) object moves and simultaneously ro-

tates from 0 . . . 180

◦

and then makes full rotation and

(iii) object moves, simultaneously rotates and changes

distance to the camera.

In addition to the synthetic data mentioned above,

the dataset contains also real data. The camera has

been calibrated using the OpenCV library (Bradski

and Kaehler, 2013). The ground truths of the object

poses have been determined using measurements pro-

vided by a turntable. Each object has been observed

from four different camera views, see Fig. 4. The

objects were rotated in range 0

◦

.. .360

◦

. During ob-

ject rotation, every ten degrees an image has been ac-

quired with corresponding rotation angle. This means

that for each object the number of images acquired in

such a way is equal to 144.

Figure 4: Camera setting.

For training the object segmentation models the

objects were rotated and observed by the camera from

different views. For each considered object, 150 im-

ages with manual delineations of the objects (Lopatin

and Kwolek, 2020) were prepared and stored in the

dataset. Additionally, 2D locations of ﬁducial points

are stored in corresponding ﬁles. This subset con-

sisting of real RGB images with the corresponding

ground truth data can be employed for training as well

as evaluation of neural networks for 6D object pose

estimation and tracking. The data are stored in the

format that is identical with data format utilized in the

synthetic subset.

5 EXPERIMENTAL RESULTS

At the beginning of this Section we discuss evaluation

metric for 6D pose estimation, Afterwards, we present

experimental results.

5.1 Evaluation Metric for 6D Pose

Estimation

We evaluated the quality of 6-DoF object pose esti-

mation using ADD score (Average Distance of Model

Points) (Hinterstoisser et al., 2013). ADD is deﬁned

as average Euclidean distance between model vertices

transformed using the estimated pose and the ground

truth pose. This means that it expresses the average

distance between the 3D points transformed using the

estimated pose and those obtained with the ground-

truth one. It is deﬁned as follows:

ADD = avg

x∈M

||(Rx + t) − (

Rx +

t)||

(1)

where M is a set of 3D object model points, t and R

are the translation and rotation of a ground truth trans-

formation, respectively, whereas

t and

R correspond

to those of the estimated transformation. This means

that it expresses the average distance between the 3D

points transformed using the estimated pose and those

obtained with the ground-truth one. The pose is con-

sidered to be correct if average distance e is less than

d, where d is the diameter (i.e., the largest distance

between vertices) of M and k

is a pre-deﬁned thresh-

old (normally it is set to ten percent).

We determined also the rotation error on the basis

of the following formula:

err

rot

= arccos((Tr(

−1

) − 1)/2) (2)

where Tr stands for matrix trace,

R and R denote ro-

tation matrixes corresponding to ground-truth and es-

timated poses, respectively.

5.2 Evaluation of Pose Tracking

At the beginning we evaluated a basic version of the

algorithm (Majcher and Kwolek, 2020), i.e. without

PnP-based hypotheses to support PF-PSO on freely

available OPT benchmark dataset (Wu et al., 2017),

which has been recorded for tracking of 6D pose

of the objects. In discussed dataset the image se-

quences were recorded under various lighting con-

ditions, different motion patterns and speeds using

a programmable robotic arm. Table 1 presents the

tracking scores achieved in 6D pose tracking of House

and Ironman objects in FreeMotion scenario.

Fiducial Points-supported Object Pose Tracking on RGB Images via Particle Filtering with Heuristic Optimization

923

Table 1: Tracking scores [%] achieved by basic version of

our algorithm in tracking 6D pose of House and Ironman in

FreeMotion scenario.

tracking score [%] House Ironman

Behind, ADD 10% 88 41

Behind, ADD 20% 100 66

Left, ADD 10% 82 32

Left, ADD 20% 98 61

Right, ADD 10% 60 51

Right, ADD 20% 86 83

Front, ADD 10% 56 28

Front, ADD 20% 89 51

Average, ADD 10% 72 38

Average, ADD 20% 93 65

Table 2 contains AUC scores achieved by recent

methods in 6D pose tracking of House and Iron-

man objects in FreeMotion scenario. As we can ob-

serve, our algorithm in basic version achieves better

results in comparison to results achieved by PWP3D,

UDP and ElasticFusion. In comparison to results in

(Bugaev et al., 2018) it achieves slightly worse results

on House object and worse results on the Ironman.

Table 2: AUC scores achieved in tracking 6D pose of House

and Ironman in FreeMotion scenario, compared to results

achieved by recent methods.

AUC score [%] House Ironman

(Prisacariu and Reid, 2012) 3.58 3.92

(Brachmann et al., 2016) 6.04 5.16

(Whelan et al., 2016) 2.83 1.75

(Bugaev et al., 2018) 14.48 14.71

Our method 12.12 5.16

Since the OPT benchmark dataset does not con-

tain enough data to train and evaluate of neural net-

works for ﬁducial point estimation, we conducted ex-

periments on our dataset. For evaluation of 6D pose

tracking we selected the sequences #2 in which the

objects move from left to right, simultaneously make

rotations from 0 to 180

◦

, and after reaching the right

side of the image, the objects move back from right

to left, simultaneously make full rotation about axis.

The training of neural networks both for object seg-

mentation/detection and 6D pose estimation was done

on synthetic images only. Table 3 presents experi-

mental results that were obtained by our algorithm.

Table 4 compares results achieved by our algo-

rithm with and without the PnP algorithm. As we

can observe, thanks to employing in the PF-PSO al-

gorithm an additional information about object poses,

far better tracking scores can be achieved for all con-

sidered objects.

Figure 5 depicts ADD scores over time that were

obtained by the PF-PSO with neural network esti-

mating position of ﬁducial points and the PnP algo-

rithm. As we can observe, slightly bigger errors were

Table 3: Tracking scores [%] achieved by our algorithm in

tracking 6D pose of objects.

^,ADD [%] drill frog pig duck ext. mult.

◦

, 10 84 67 48 58 15 17

◦

, 20 93 78 73 90 22 28

◦

, 10 77 76 49 86 63 72

◦

, 20 96 93 77 90 83 91

◦

, 10 67 63 61 83 65 73

◦

, 20 94 78 87 87 90 99

◦

, 10 50 35 42 91 80 87

◦

, 20 75 53 71 99 98 100

Av., 10 69 60 50 79 56 62

Ave, 20 89 75 77 91 73 80

achieved for 0

◦

camera view. In discussed camera

view the pose tracking was done using side-view im-

ages of the objects.

Figure 6 depicts rotation errors over time on real

images, which have been obtained by the PF-PSO

with neural network estimating 2D location of ﬁdu-

cial points and the PnP algorithm. As we can ob-

serve, the largest errors were obtained for the ex-

tension, which is symmetric and texture-less object.

Somewhat larger errors were observed for 30

◦

cam-

era view.

In order to segment the House and Ironman ob-

jects we trained a single U-Net on 660 images from

the OPT benchmark. A single U-Net has been trained

on 1800 images in order to segment all six objects

from our dataset. The Dice scores were higher than

95% for all objects. The neural networks for estima-

tion of positions of keypoints were trained on 300 im-

ages and evaluated on 50 images.

The complete system for 6D pose estimation has

been implemented in Python and Keras framework.

On the basis of keypoint positions the object poses

were calculated using solvePnPRansac (Lepetit et al.,

2009) from OpenCV library. The system runs on an

ordinary PC with a CPU/GPU. On PC equipped with

i5-8300H CPU 2.30 GHz the segmentation time us-

ing U-Net is about 0.3 sec., whereas the 6D pose is

estimated in about 0.03 sec. About ten times short-

ening of time has been observed on TitanX graph-

ics card. Initial experiments conducted with Franka-

Emika robot, which has been equipped with Xtion

RGB-D sensor demonstrated usefulness of the pro-

posed approach to estimation of 6D pose of objects

held in hand. The images for training and evaluating

the segmentation algorithm as well as extracted ob-

jects with corresponding ground-truth for evaluating

the 6D object pose tracking are freely available for

download at: http://agh.edu.pl/

∼

bkw/src/pose6d.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

924

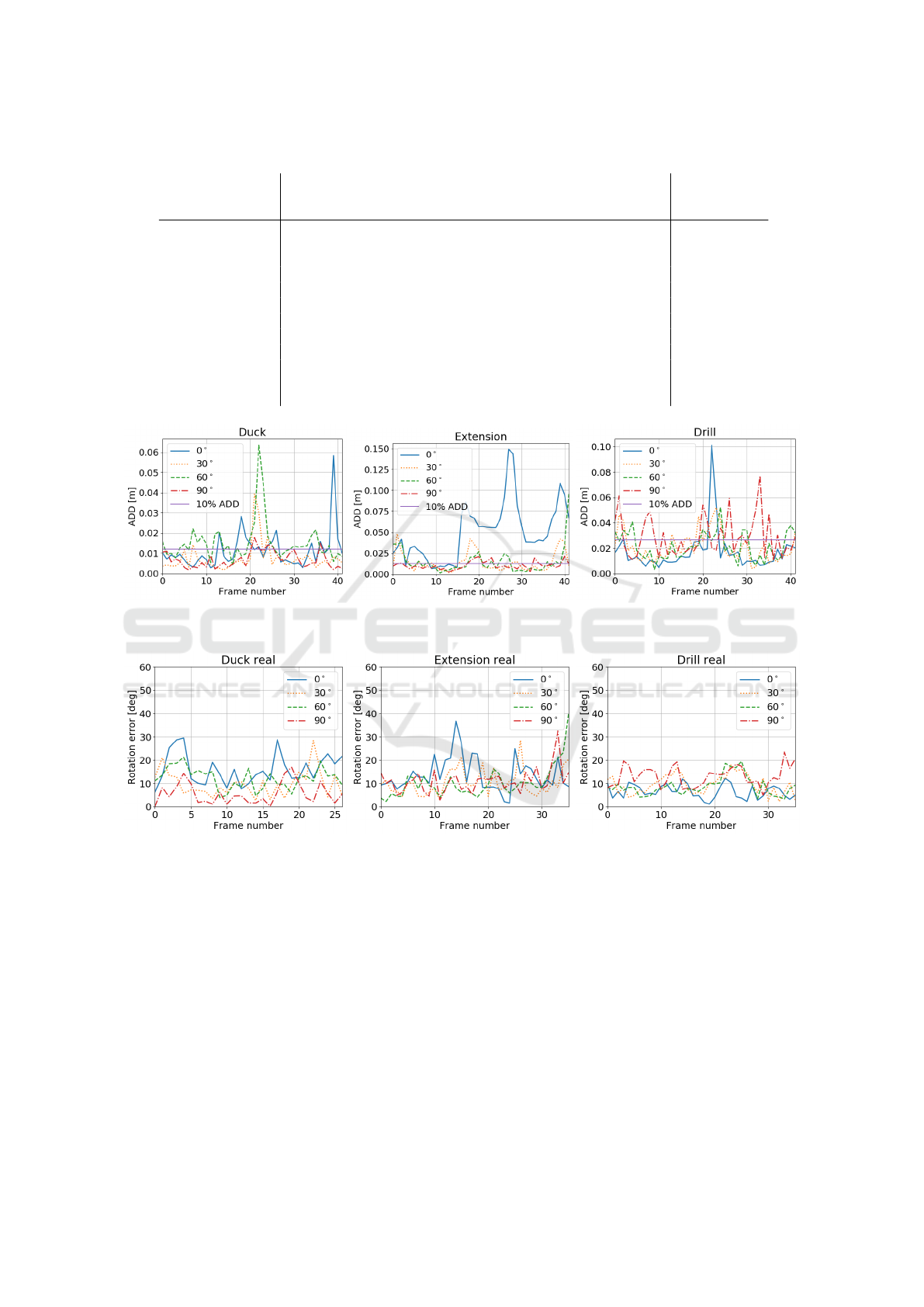
Table 4: Tracking scores [%] achieved by our algorithm with and without PnP.

tracking score [%]

◦

ADD

10%

◦

ADD

20%

◦

ADD

10%

◦

ADD

20%

◦

ADD

10%

◦

ADD

20%

◦

ADD

10%

◦

ADD

20%

Avg.,

ADD

10%

Avg,

ADD

20%

drill w/o PnP 79 88 60 86 54 74 31 59 56 77

drill with PnP 84 93 77 96 67 94 50 75 69 89

frog w/o PnP 31 33 33 37 37 49 12 24 28 36

frog with PnP 67 78 76 93 63 78 35 53 60 75

pig w/o PnP 50 63 44 49 51 59 48 52 48 56

pig with PnP 48 73 49 77 61 87 85 88 61 81

duck w/o PnP 41 71 76 79 61 78 82 100 65 82

duck with PnP 58 90 86 90 83 87 91 99 79 91

ext. w/o PnP 18 33 55 82 52 73 70 100 49 72

ext. with PnP 15 22 63 83 65 90 80 98 56 73

mult. w/o PnP 1 7 61 93 67 96 77 88 51 71

mult. with PnP 17 28 72 91 73 99 87 100 62 80

Figure 5: ADD scores over time for images from sequence #2, obtained by PF-PSO and neural network estimating 2D location

of ﬁducial points and PnP algorithm (plots best viewed in color).

Figure 6: Rotation errors over time for real images, obtained by PF-PSO using poses that were obtained by the PnP algorithm.

6 CONCLUSIONS

In this paper, a framework for tracking 6D pose of the

object in a sequence of RGB images has been pro-

posed. In this segmentation-driven approach the ob-

ject of interest is delineated by a single U-net neural

network, trained to segment a set of considered ob-

jects. A basic PF-PSO algorithm has been evaluated

on freely available OPT benchmark dataset for track-

ing 6D pose of objects. Promising results were ob-

tained on discussed dataset. This basic algorithm has

been extended by including in the probability distri-

bution maintained by the PF-PSO a hypothesis about

6D object pose. Such a hypothesis about the object

pose is calculated on the basis of object keypoints

and the PnP algorithm. The location of ﬁducial key-

points on images is determined by a neural network,

trained separately for each object. The evaluations

were done on our dataset that contains both real and

synthesized images of six texture-less objects and has

been recorded to perform tracking of 6D object pose

on RGB images. A separate neural network has been

trained to segment all considered objects. Thanks to

3D location of ﬁducial points on synthetic objects and

Fiducial Points-supported Object Pose Tracking on RGB Images via Particle Filtering with Heuristic Optimization

925

2D location of such points on real images, various

keypoint-based deep neural network can be trained

for object pose estimation in end-to-end framework.

ACKNOWLEDGEMENTS

This work was supported by Polish National

Science Center (NCN) under a research grant

2017/27/B/ST6/01743.

REFERENCES

Arthur, D. and Vassilvitskii, S. (2007). K-means++: The

Advantages of Careful Seeding. In Proc. ACM-SIAM

Symp. on Discrete Algorithms, pages 1027–1035.

Blender Online Community (2020). Blender - a 3D mod-

elling and rendering package. Blender Foundation,

Stichting Blender Foundation, Amsterdam.

Brachmann, E., Krull, A., Michel, F., Gumhold, S., Shotton,

J., and Rother, C. (2014). Learning 6D object pose es-

timation using 3D object coordinates. In ECCV, pages

536–551. Springer.

Brachmann, E., Michel, F., Krull, A., Yang, M., Gumhold,

S., and Rother, C. (2016). Uncertainty-driven 6D pose

estimation of objects and scenes from a single RGB

image. In CVPR, pages 3364–3372.

Bradski, G. and Kaehler, A. (2013). Learning OpenCV:

Computer Vision in C++ with the OpenCV Library.

O’Reilly Media, Inc., 2nd edition.

Bugaev, B., Kryshchenko, A., and Belov, R. (2018). Com-

bining 3D model contour energy and keypoints for ob-

ject tracking. In ECCV, pages 55–70, Cham. Springer.

Deng, X., Mousavian, A., Xiang, Y., Xia, F., Bretl, T., and

Fox, D. (2019). PoseRBPF: A Rao-Blackwellized

Particle Filter for 6D Object Pose Tracking. In

Robotics: Science and Systems (RSS).

Fischler, M. A. and Bolles, R. C. (1981). Random Sample

Consensus: A Paradigm for Model Fitting with Ap-

plications to Image Analysis and Automated Cartog-

raphy. Commun. ACM, 24(6):381–395.

Garrido-Jurado, S., Munoz-Salinas, R., Madrid-Cuevas,

J. J., Mar

ın-Jimenez, M. J. (2014). Automatic gener-

ation and detection of highly reliable ﬁducial markers

under occlusion. Pattern Rec., 47(6):2280–2292.

He, K., Gkioxari, G., Dollar, P., and Girshick, R. (2017).

Mask R-CNN. In IEEE Int. Conf. on Computer Vision

(ICCV), pages 2980–2988.

Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski,

G., Konolige, K., and Navab, N. (2013). Model based

training, detection and pose estimation of texture-less

3D objects in heavily cluttered scenes. In Computer

Vision – ACCV 2012, pages 548–562. Springer.

Hodan, T., Haluza, P., Obdrzalek, S., Matas, J., Lourakis,

M., and Zabulis, X. (2017). T-LESS: An RGB-D

dataset for 6D pose estimation of texture-less objects.

In WACV, pages 880–888.

Ioffe, S. and Szegedy, C. (2015). Batch Normalization: Ac-

celerating deep network training by reducing internal

covariate shift. In ICML - vol. 37, pages 448–456.

Kaskman, R., Zakharov, S., Shugurov, I., and Ilic, S.

(2019). HomebrewedDB: RGB-D dataset for 6D pose

estimation of 3D objects. In IEEE Int. Conf. on Com-

puter Vision Workshop (ICCVW), pages 2767–2776.

Kehl, W., Manhardt, F., Tombari, F., Ilic, S., and Navab, N.

(2017). SSD-6D: Making RGB-Based 3D Detection

and 6D Pose Estimation Great Again. In IEEE Int.

Conf. on Computer Vision, pages 1530–1538.

Lepetit, V., Moreno-Noguer, F., and Fua, P. (2009). EPnP:

An accurate O(n) solution to the PnP problem. Int. J.

Comput. Vision, 81(2):155–166.

Lepetit, V., Pilet, J., and Fua, P. (2004). Point matching as a

classiﬁcation problem for fast and robust object pose

estimation. In CVPR, pages 244–250.

Lin, T.-Y., Maire, M., Belongie, S., Hays, J., Perona, P.,

Ramanan, D., Dollar, P., and Zitnick, C. L. (2014).

Microsoft COCO: Common Objects in Context. In

ECCV, pages 740–755. Springer.

Lopatin, V. and Kwolek, B. (2020). 6D pose estimation of

texture-less objects on RGB images using CNNs. In

The 19th Int. Conf. on Artiﬁcial Intelligence and Soft

Computing, pages 180–192. Springer.

Majcher, M. and Kwolek, B. (2020). 3D Model-Based 6D

Object Pose Tracking on RGB Images Using Particle

Filtering and Heuristic Optimization. In 15th Int. The

Int. Conf. on Computer Vision Theory and Applica-

tions (VISAPP), pages 690–697, vol. 5. SciTePress.

Marchand, E., Uchiyama, H., and Spindler, F. (2016).

Pose estimation for augmented reality: A hands-on

survey. IEEE Trans. on Vis. and Comp. Graphics,

22(12):2633–2651.

Peng, S., Liu, Y., Huang, Q., Zhou, X., and Bao, H. (2019).

PVNet: Pixel-Wise Voting Network for 6DoF Pose

Estimation. In IEEE Conf. on Comp. Vision and Patt.

Rec., pages 4556–4565.

Prisacariu, V. A. and Reid, I. D. (2012). PWP3D: Real-

Time Segmentation and Tracking of 3D Objects. Int.

J. Comput. Vision, 98(3):335–354.

Rad, M. and Lepetit, V. (2017). BB8: A scalable, accurate,

robust to partial occlusion method for predicting the

3D poses of challenging objects without using depth.

In IEEE Int. Conf. on Comp. Vision, pages 3848–3856.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-

Net: Convolutional networks for biomedical image

segmentation. In MICCAI, pages 234–241. Springer.

(Vidal), J., (Lin), C., and (Mart

ı), R. (2018). 6D pose esti-

mation using an improved method based on point pair

features. In Int. Conf. on Control, Automation and

Robotics, pages 405–409.

Whelan, T., Salas-Moreno, R. F., Glocker, B., Davison,

A. J., and Leutenegger, S. (2016). ElasticFusion. Int.

J. Rob. Res., 35(14):1697–1716.

Wu, P., Lee, Y., Tseng, H., Ho, H., Yang, M., and Chien,

S. (2017). A benchmark dataset for 6DoF object pose

tracking. In IEEE Int. Symp. on Mixed and Aug. Real-

ity, pages 186–191.

Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2018).

PoseCNN: A Convolutional Neural Network for 6D

Object Pose Estimation in Cluttered Scenes. In

IEEE/RSJ Int. Conf. on Intel. Robots and Systems.

Zhao, Z., Peng, G., Wang, H., Fang, H., Li, C., and Lu,

C. (2018). Estimating 6D pose from localizing desig-

nated surface keypoints. ArXiv, abs/1812.01387.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

926