
Efficient Image Registration with Subpixel Accuracy using a Hybrid
Fourier-based Approach
Jelina Unger and Klaus Brinker
Hamm-Lippstadt University of Applied Sciences, Marker Allee 76-78, 59063 Hamm, Germany
Keywords:
Image Registration, Fourier-based Cross Correlation, Image Projections, Subpixel Accuracy.
Abstract:
In many fields like medical imaging and remote sensing, it is necessary to register images with subpixel accu-
racy. A general problem is the tradeoff between accuracy and efficiency. This paper presents a highly accurate
and efficient algorithm for subpixel image registration using Fourier-based cross correlation to determine the
translation between two images. Therefore a coarse to fine strategy is used. It combines a fast method using
image projections with an accurate approach using matrix multiplication for refined computation. The results
show that the new approach has almost the same level of accuracy as the accurate method, but with reduced
computational complexity. Compared to the fast method, the computational complexity of the new approach
is slightly higher, but achievs a higher level of accuracy. Overall the hybrid approach achieves an efficient
registration with a relatively short runtime.
1 INTRODUCTION
Image registration is the process of aligning two or
more images of the same object on top of each other.
For this purpose the transformation between those im-
ages is determined. Typical transformation types are
rotation, scaling, and translation. In this paper we
focus on translations which is suitable, e.g. for mi-
croscopic applications among others. Many applica-
tions require calculation of the transformation down
to a fraction of a pixel, i.e. with subpixel accuracy.
In medical imaging, this allows monitoring changes
in the human body of one patient but also facilitates
comparing different patients. For this purpose images
of different times or modalities are registered (Farn-
combe and Iniewski, 2014).
Fourier-based methods have gained increasing at-
tention in recent years. The basic method is to com-
pute an upsampled version of the cross correlation be-
tween two images using the discrete Fourier Trans-
form (DFT) and locate its peak. In general, the main
problem is to exhibit high accuracy and low com-
putational time simultaneously (Tong et al., 2019).
Guizar-Sicairos et al. (2008) present a highly accu-
rate approach. A coarse to fine strategy is imple-
mented using matrix multiplication to be more effi-
cient. Still, this approach yields a high computational
complexity. A fast approach is presented by Yang et
al. (2012). They only use image projections which
reduces the runtime but also decreases the level of ac-
curacy. The aim of the present work is to combine
both approaches to one highly efficient and accurate
hybrid algorithm.
Section 2 presents the basic methods of Fourier-
based image registration and outlines the three al-
gorithms. In Section 3, an evaluation of the algo-
rithms and different relevant influencing factors are
presented. The results are discussed in Section 4. Fi-
nally a conclusion is given in Section 5.
2 REGISTRATION METHODS
In the following, we first introduce the definitions of
the DFT, explain the basic method for subpixel image
registration, and lastly present the three algorithms.
The DFT and its inverse can be calculated by dif-
ferent methods. In this paper the transformation for-
mula and matrix multiplication are used. The trans-
formation formula for 1D-DFT of a signal f(x) with
length N is shown in Equation 1 (McAndrew, 2016).
F(u) =
N−1
∑
x=0
f (x)exp
n
−2πi
xu
N
o
(1)
The inverse 1D-DFT of the Fourier-Spectral F(u) can
be calculated using Equation 2.
f (x) =
1
N
N−1
∑
u=0
F(u)exp
n
2πi
xu
N
o
(2)
Images can be described as a two-dimensional func-
tion F(x,y) with dimensions N × M. Therefore, the
136
Unger, J. and Brinker, K.
Efficient Image Registration with Subpixel Accuracy using a Hybrid Fourier-based Approach.
DOI: 10.5220/0010242901360143
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 2: BIOIMAGING, pages 136-143
ISBN: 978-989-758-490-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

generalized 2D-DFT formula is necessary, which is
shown in Equation 3.
F(u, v) =
N−1
∑
x=0
M−1
∑
y=0
f (x, y)exp
n
−2πi
ux
N
+
vy
M
o
(3)
The inverse 2D-DFT is calculated by Equation 4.
f (x, y) =
1
MN
N−1
∑
u=0
M−1
∑
v=0
F(u, v)exp
n
2πi
xu
N
+
yv
M
o
(4)
Matrix multiplication is another method to calcu-
late the (inverse) 2D-DFT of images (Soummer et al.,
2007). It can be expressed as
F(u, v) = w
XU
· f (x, y) · w
YV
(5)
and
f (x, y) =
1
N
w
∗
XU
· F(u, v) ·
1
M
w
∗
YV
(6)
where w
XU
and w
YV
are the transformation matrices
and * indicates the complex conjugation. They are
defined by Equation 7 and 8.
w
XU
= exp
{
−2πiXU
}
(7)
w
YV
= exp
{
−2πiYV
}
(8)
The vectors X and U are defined as
X =
(
[0, 1, ..., N − 1] −
N
2
for even N
[0, 1, ..., N − 1] −
N−1
2
for odd N
(9)
and
U =
(
1
N
· [0, 1, ...,
N
2
− 1, −
N
2
, ..., −1] for even N
1
N
· [0, 1, ...,
N−1
2
, −
N−1
2
, ..., −1] for odd N
(10)
where N describes the height of the image. Y and V
are computed analogously but with the exception that
image width M replaces height N.
2.1 Subpixel Image Registration
In general, the translation between two images f(x,y)
and g(x,y) can be described as
f (x, y) = g(x − ∆x, y − ∆y) (11)
where ∆x and ∆y are the vertical and the horizontal
shifts (Tong et al., 2019). We define f as the refer-
ence image and g as the image to be registered. To
compute these translations, Fourier-based cross cor-
relation is computed by Equation 12 and its peak has
to be located (Anuta, 1970).
CC(x, y) = F
−1
(F(u, v)G
∗
(u, v)) (12)
G and F denote the Fourier-Transform of images g
and f, * indicates the complex conjugation and F
−1
the inverse DFT. For achieving subpixel accuracy, an
upsampled version of the cross correlation is required.
Therefore, the number of data points is increased by
a factor of κ, allowing a theoredical accuracy of
1
κ
of
a pixel. A common method to achieve upsampling is
zero-padding (Shin et al., 2017). For this, the prod-
uct F(u, v)G
∗
(u, v) with size N × M is embedded in
a larger array of zeros with size κN × κ M. Calculat-
ing the inverse DFT of this array results in an upsam-
pled version of the cross correlation. Finally the peaks
are located and the shifts are converted to the original
pixel units (Yang et al., 2012).
Another method to perform upsampling is to cal-
culate the inverse DFT by using matrix multiplication.
For this, the transformation matrices must be adjusted
by increasing the value range of the vectors X, Y, U
and V by the upsampling factor κ. Furthermore, the
upsampling can be limited to a specific image region.
The vector X is computed by
X =
(
[0, 1, ..., Dκ − 1] −
Dκ
2
+ sκ for even Dκ
[0, 1, ..., Dκ − 1] −
Dκ−1
2
+ sκ for odd Dκ
(13)
where D denotes the image region height and s the
vertical center. Y is computed analogously with the
exception that the width replaces the height and the
horizontal replaces the vertical center. To calculate
the vector U Equation 14 is used.
U =
(
1
κN
· [0, 1, ...,
N
2
− 1, −
N
2
, ..., −1] for even N
1
κN
· [0, 1, ...,
N−1
2
, −
N−1
2
, ..., −1] for odd N
(14)
To compute V, the same approach can be used by
replacing the height N with the width M (Soummer
et al., 2007).
Due to the increase of data points, the upsampling
is always related to a higher computational complex-
ity. The advantage of the matrix multiplication is that
the upsampling can be localized to a specific image
region (Tong et al., 2019).
2.2 Matrix Multiplication DFT
Approach
A highly accurate algorithm to register images by us-
ing Fourier-based cross correlation is presented by
Guizar-Sicairos et al. (2008). A coarse to fine strat-
egy is used. The first step is to compute the Fourier-
based cross correlation over the entire image using
zero-padding with an upsampling factor of κ
0
= 2 and
to locate its peak. In the second step, an upsampled
version of the 1.5 × 1.5 pixel neighborhood around
the rough estimation is computed by matrix multi-
plication. At this point the upsampling factor is ad-
justable. The peak is located in the output array and
Efficient Image Registration with Subpixel Accuracy using a Hybrid Fourier-based Approach
137

converted into units of original pixels. The last step
is to combine the rough and refined estimation to the
final translation vector. We refer to this algorithm as
MM.
2.3 Image Projections DFT Approach
A high-speed algorithm for subpixel image registra-
tion is presented by Yang et al. (2012). To reduce
computational time, one-dimensional image projec-
tions are used to compute the upsampled Fourier-
based cross correlations.
First, vertical and horizontal image projections are
calculated by taking the sum of each row respectively
column, using Equation 15 and 16 for an image f(x,y)
with height N and width M.
f
row
(x) =
M−1
∑
y=0
f (x, y) (15)
f
col
(y) =
N−1
∑
x=0
f (x, y) (16)
The information of edges can influence the cross cor-
relation. To reduce this effect a filter is applied, which
is shown in Equation 17 and 18.
f
row, f ilt
(x) = f
row
(x) −
"
1
N
N−1
∑
i=0
f
row
(i)
#
(17)
f
col, f ilt
(y) = f
col
(y) −
"
1
M
M−1
∑
j=0
f
col
( j)
#
(18)
This preprocessing step is performed for both
images f(x,y) and g(x,y). All filtered projections
are transformed in the frequency domain by using
the transformation formula. Hence, two products
F
row
(u)G
∗
row
(u) and F
col
(v)G
∗
col
(v) are computed. In
order to achieve subpixel accuracy, zero-padding is
used. For this purpose both products are embedded in
larger arrays of zeros with size κN respectively κM.
Computing the inverse 1D-DFT with the transforma-
tion formula of these arrays results in upsampled ver-
sions of cross correlations. Finally peaks are located
and converted into units of original pixels to receive
vertical and horizontal translations. We refer to this
algorithm as IP.
2.4 Combination of Image Projections
and Matrix Multiplication DFT
In this paper we present a novel efficient algorithm
which combines the MM algorithm from (Guizar-
Sicairos et al., 2008) and the IP algorithm from (Yang
f
g
Horizontal & vertical
image projections
f
row
, f
col
, g
row
, g
col
Filter projections
1D DFT of projections
F
row
, F
col
, G
row
, G
col
Projections product
F
row
G
row
* and F
col
G
col
*
Zero padding with �
0
= 2
1D cross correlations
by computing inverse DFT
Locate peaks
Rough estimation of translation
2D DFT of images
F and G
Image product
FG*
Upsampled 2D cross correlation
over rough translation estimation
by computing inverse DFT
using matrix multiplication
Locate peak
Refined translation
Combine rough and refined
translation values
Images
Figure 1: Computational process of the proposed combina-
tion approach.
Figure 2: Filtered image projections for the reference image
f and the image to be registered g.
et al., 2012). The main idea is to keep the high ac-
curacy of MM, but with low computational time like
IP. Therefore, we consider a coarse to fine strategy.
For the first rough estimation, the IP approach is used
with an upsampling factor of κ
0
= 2. MM is used for
the refined estimation of translation. A more detailed
computational process visualization is given in Fig-
ure 1 and explained in the following. This steps are
performed for two images f(x,y) and g(x,y):
1. Rough shift estimation
(a) compute and filter vertical and horizontal pro-
jections of both images
(b) compute upsampled Fourier-based cross cor-
relations of vertical and horizontal projections
BIOIMAGING 2021 - 8th International Conference on Bioimaging
138
100 50 0 50 100
Translation (pixel)
0.0
0.2
0.4
0.6
0.8
1.0
Cross correlation
1e10
horizontal
vertical
(a)
Vertical translation
(pixel)
0.8
0.4
0.0
0.4
0.8
Horizontal translation
(pixel)
0.8
0.4
0.0
0.4
0.8
Cross correlation
(b)
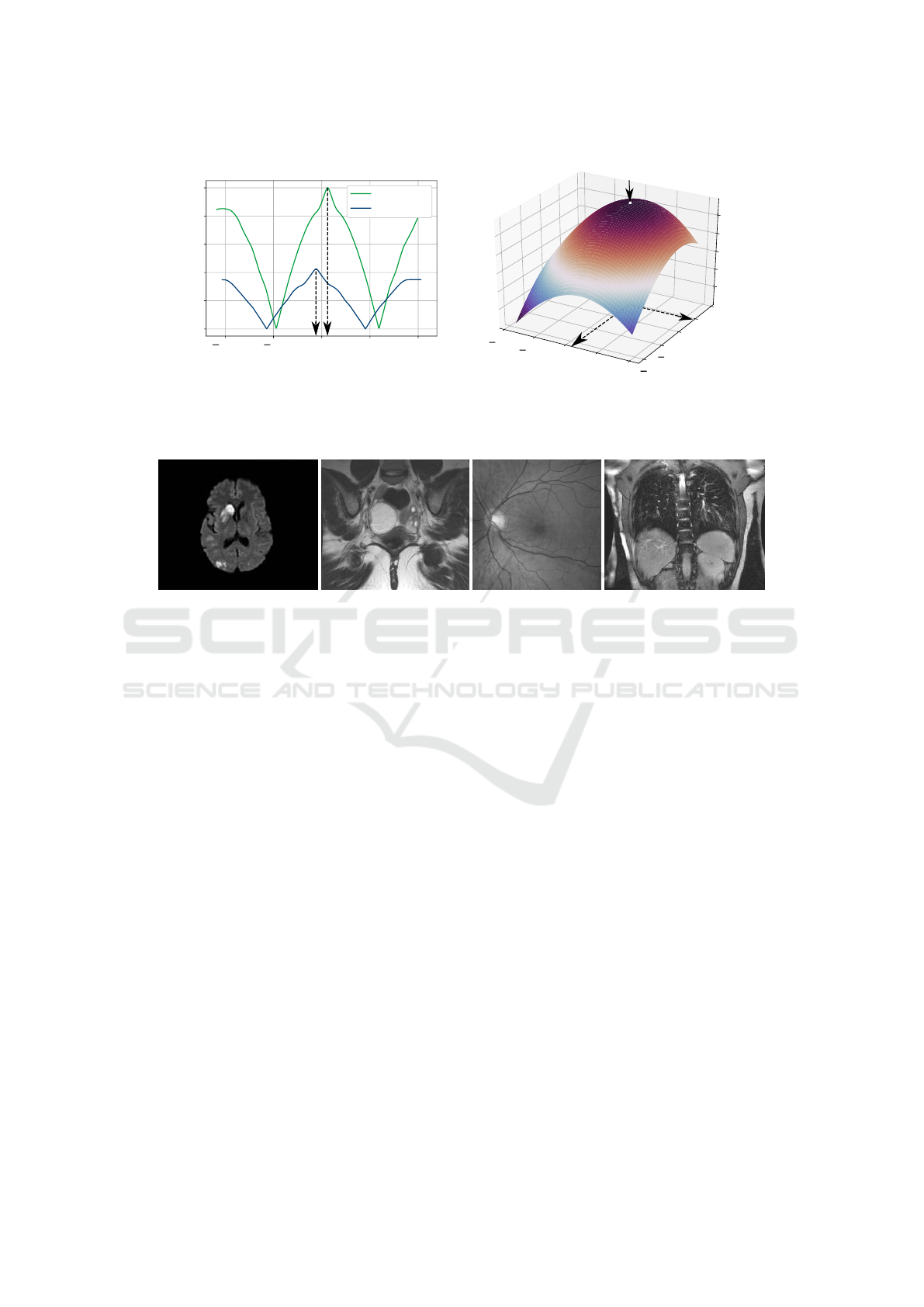
Figure 3: Visualization for the main steps of combination algorithm: (a) 1D rough cross correlations and (b) 2D refined cross
correlation around the rough estimation, where the locations of peaks are marked by arrows.
Figure 4: Four examples of test images from (He et al., 2020), (Budai et al., 2013) and (Cohen, 2020).
with an upsampling factor of κ
0
= 2 by using
zero-padding and transformation formula
(c) locate the peak and convert it into original pixel
units
2. Refined shift estimation
(a) compute the product F(u, v)G
∗
(u, v) and define
transformation matrices w
XU
and w
YV
for im-
age region centered over the rough estimated
peak with a region size of 1.5κ × 1.5κ pixel in
upsampled pixel units
(b) compute the upsampled cross correlation by
multiplying these three matrices
(c) locate the peak and convert into original pixel
units
3. Add rough and refined estimation for receiving
the total translation vector
The filtered image projections are visualized in
Figure 2. It can be seen that projections of the image g
have the same shape as the reference image f, but are
shifted slightly. Figure 3 shows the cross correlations
for the first rough and the refined estimation. The
rough estimation consists of two one-dimensional
cross correlations for the vertical and horizontal di-
rection. Their peaks can clearly be determined for -6
and 6 pixels. The refined cross correlation over the
rough estimation has a peak at (0.32, 0.10). For both
cross correlation plots, peaks and their corresponding
position are marked by arrows. In total a translation
of (−5.68, 6.10) is determined for this sample image
pair by adding rough and refined estimation.
2.5 Implementation
All three algorithms were implemented in Python
(version 3.7.1). Standard libraries especially NumPy
(version 1.18.1) and its modul numpy.fft for discrete
Fourier Transform were used. The library Scikit-
image (version 0.16.2) was only used for loading im-
ages. For the MM approach the implementations from
(Guizar, 2016) and (Fezzani et al., 2020) were used.
Evaluation is performed on a HP 250 G5 Notebook
with Intel(R) Core Processor 2.40 GHz, 8 GB RAM
and 64-bit-operating-system.
3 EVALUATION
In this section, we evaluate all three algorithms with
respect to accuracy and runtime. First, the methods
for conducting the evaluation are described. Further
on, the general performance for accuracy and runtime
is evaluated. Additionally, we analyze performance
for different image sizes and under the presence of
Efficient Image Registration with Subpixel Accuracy using a Hybrid Fourier-based Approach
139

(a) (b) (c) (d)
Figure 5: Visualization of different noise variances for a test image (He et al., 2020): (a) 0, (b) 0.05 (c) 0.1 and (d) 0.3.
(a)
(b)
(c)
Figure 6: Visualization of the pixel error versus mean translation for (a) MM, (b) combination algorithm and (c) IP.
noise. The final part of the evaluation includes an
analysis of the influence of different upsampling fac-
tors.
3.1 Methods
For the evaluation, a dataset of 300 medical images
from (He et al., 2020), (Budai et al., 2013) and (Co-
hen, 2020) is used for the reference images. Four
sample images are shown in Figure 4. In order to
obtain an image to be registered for each reference
image, a random translation is performed which is be-
tween 0.5 % and 3 % of the corresponding image side.
Additionally, noise is added to slightly change the im-
age information in contrast to the reference image.
To evaluate the accuracy, the mean value is calcu-
lated from the absolute vertical and horizontal error
for each image pair. Additionally, the mean absolute
error (MAE) is calculated over the entire dataset in or-
der to assess general performance. Furthermore, the
runtime is measured and the mean value is calculated
over the dataset to evaluate the efficiency. The tol-
erances are given by the doubled standard deviation
(Std).
For the first three parts of evaluation, an upsam-
pling factor of κ = 100 is used. In order to ana-
lyze the performance with noisy images, the dataset
is extended. The same translations as for the first
three parts are used, but six images to be registered
with different noise levels for every reference im-
age are created. A multiplicative Gaussian noise is
used. The noisy image is defined as image
noise
=
image + n ∗ image, where n is Gaussian noise with
zero mean and different variances in the range of 0
to 0.3. In Figure 5, four noise levels are shown by a
sample test image.
3.2 General Performance
The results for the general performance of all algo-
rithms are shown in Table 1. The MM and combina-
tion algorithm have the same high level of accuracy of
0.005 ± 0.011 pixel for the MAE. The MAE of the IP
approach is more than three times as large. But the IP
method has the shortest runtime with 0.019 ± 0.029 s.
The combination algorithm is just slightly slower, but
MM requires significantly more time. Accordingly,
the combination algorithm reduces the MAE in con-
trast to the IP approach by over 70 % and runtime in
contrast to the MM approach by over 75 %.
Table 1: General performance for all algorithms.
Algorithm MAE (pixel) Runtime (s)
MM 0.005 ± 0.011 0.324 ± 0.562
Combination 0.005 ± 0.011 0.079 ± 0.125
IP 0.017 ± 0.029 0.019 ± 0.029
The results for the error in dependence on trans-
lation are visualized in Figure 6. Besides, the MAE
the limit of tolerance for the dataset is given. It is
shown that most error samples for MM and combina-
BIOIMAGING 2021 - 8th International Conference on Bioimaging
140

Figure 7: MAE depending on image size.
tion are within this limit. For the IP, the tolerance limit
is larger and error samples spread more. Furthermore,
the error is equally distributed over the translation size
for all algorithms, therefore, no dependence between
error and size of translation is visible here.
3.3 Dependency on Image Size
In the following, we analyze whether image size in-
fluences accuracy and runtime. To visualize accu-
racy, the images were grouped by size and the MAE
were calculated for each group (Figure 7). As already
shown in Section 3.2, the MAE for the IP approach is
clearly higher than for the other two algorithms. The
MAE for the MM and combination approach is ex-
actly the same. However, for all algorithms the MAE
is about the same for all sizes. There are only minor
fluctuations that don’t indicate a clear trend. Hence,
no dependency can be determined.
Though, a clear dependency on the image size
for the runtime can be determined, which is shown
in Figure 8. The runtime increases with larger im-
age size. For small images around 200 pixel im-
age dimension, all algorithms have a low runtime
under 0.04 s. But the runtime of the MM approach
is already slightly higher. Additionally it shows the
sharpest increase with a quadratic trend up to 1.2 s.
The runtime of the combination approach also shows
a quadratic trend, but the curve progression is much
flatter though, reaching a maximum of only 0.26 s
which is almost 80 % less than the MM. The IP ap-
proach shows only a slight linear increase in time up
to 0.045 s.
3.4 Dependency on Noise
In the following we analyze the performance for im-
ages with different noise levels. Figure 9 shows the
MAE at different noise levels. The MM and combina-
tion approach achieve low MAE. The MM approach
has a slight linear increase of the MAE from 0.005
Figure 8: Runtime depending on image size.
Figure 9: MAE depending on noise variance.
up to 0.015 pixel. For low noise levels the combina-
tion algorithm has the same accuracy as MM. Though
starting from the noise variance of 0.1, the MAE in-
creases slightly more up to 0.03 pixel. In contrast,
the MAE of IP already rises steeply for low noise lev-
els from 0.009 to 0.106 pixel. For the highest noise
level, the MAE of the combination algorithm is twice
as large as of the MM, but still 70 % less than of the
IP approach.
Table 2: MAE for general performance and noisy images.
Algorithm MAE (pixel)
normal images noisy images
MM 0.005 ± 0.011 0.010 ± 0.018
Combination 0.005 ± 0.011 0.013 ± 0.052
IP 0.017 ± 0.029 0.051 ± 0.172
In comparison to the general performance, which
is presented in Section 3.2, the MAE of subpixel ac-
curacy increases for all algorithms (Table 2). For MM
and combination the MAE doubles, but for the com-
bination the increase is slightly more. For the IP a
steep increase can be observed. Moreover, the MAE
is tripled. For normal images the error of the combi-
nation algorithm is 70 % less compared to IP and even
75 % for noisy images.
Efficient Image Registration with Subpixel Accuracy using a Hybrid Fourier-based Approach
141

Figure 10: MAE depending on upsampling factor.
Figure 11: Runtime depending on upsampling factor.
3.5 Dependency on the Upsampling
Factor
In the following, the influence of different upsampling
factors to subpixel accuracy and runtime is evaluated.
If the upsampling factor is increased by a factor of
10, the registration is theoretically more accurate by
a factor of 10. However, Figure 10 shows that this is
not always the case. For the IP, the decrease of MAE
becomes less and from upsampling factor 100 to 1000
it totally stagnates. The MAE for MM and combina-
tion is exactly the same. In the beginning it decreases
almost by a factor of 10. But for κ = 1000 it also stag-
nates.
At values of κ = 1, which means there is no up-
sampling, IP is slightly more accurate. But for higher
values, the MAE of MM and the combination ap-
proach is significantly less. For the κ = 10, it is al-
ready 20 % and for κ = 100 and κ = 1000 it is more
than 70 %.
Taking runtime into account, it can be observed
that there are only slight changes for the first three
upsampling factors 1 to 100, but for the highest fac-
tor runtime increases rapidly (Figure 11). Gener-
ally, the IP approach has the shortest runtime with
0.008 ± 0.03 s for an upsampling with the factor 1 to
100 and increases by 0.18 s for the highest factor. The
MM approach has a considerably longer runtime with
0.315 ± 0.648 s for lower upsampling factors and in-
creases more rapidly for the highest upsampling by
0.517 s. The runtime for the combination algorithm is
slightly higher than for the IP, but significantly lower
than for the MM with 0.060 ± 0.126 s for the lower
upsampling factors. Though it increases by 0.516 s
for the highest upsampling as the MM approach.
4 DISCUSSION
The purpose of this paper was to combine two image
registration algorithms so that the translation between
images can be determined with high accuracy and low
computational requirements. The results have shown
that our combination algorithm fulfills these two cri-
teria. The MM approach is always the most accurate
one, but the combination algorithm achieves almost
the same level of accuracy. In contrast, the IP has al-
ways a significantly higher error. However, regarding
runtime it is the most efficient. The combination al-
gorithm can’t achieve the same low runtime, but it is
still in a very low range of a few milliseconds. Espe-
cially compared to the MM approach, runtime can be
reduced significantly. Additionally, the combination
algorithm isn’t as sensitive to large image sizes. As
seen in Figure 8, the runtime of the combination in-
creases significantly less than for the MM approach.
Hence, the dependency on the image size is low and
therefore it is applicable to scenarios with large image
dimensions.
We conclude that accuracy of all algorithms
doesn’t depend on translation and image size. As we
only conducted limited experiments regarding the im-
age and translation size, it can not be ruled out that the
accuracy is dependent on translations, especially large
ones. Because the larger the translation, the smaller
the matching image regions. Thus, the similarity be-
tween both images is reduced, which could compli-
cate the registration process. However as such large
translation are rare in medicine, we choose this set-
ting.
Guizar-Sicairos et al. (2008) states that the MM
approach is robust to noise, because the whole image
information is used for the rough estimation and all
data points from the upsampled cross correlation as
well. Our results confirm these findings as seen in
Figure 9. The IP doesn’t use the whole image infor-
mation, because due to image projections the data is
reduced. Hence, it is highly sensitive to noise. The
combination algorithm is to a similar degree as MM
robust to noise. Just for high noise levels it is slightly
more sensitive. Conducting the first rough estimation
by the projection method is mostly accurate enough.
BIOIMAGING 2021 - 8th International Conference on Bioimaging
142

If the real peak is still within proximity to the first es-
timation, the refined estimation can still recover it. If
the rough estimation is very imprecise, an unavoid-
able error will occur in the refined determination. To
improve the algorithm in this respect, the rough esti-
mation can be refined by using a higher upsampling
factor or to enlarge image region for the refined esti-
mation. For this reason, it must be clarified whether
the gain in accuracy is worth the increase in runtime.
The upsampling factor is a tool to achieve higher
accuracy. For a factor κ translation can be determined
by
1
κ
of a pixel. Results have shown that this factor
is limited to 100. Higher factors don’t achieve higher
accuracy. Additionally, a higher upsampling results in
a longer runtime, because there are more data points
to be processed. For low factors the increase in run-
time isn’t significant, because it’s just a slight increase
of data. However, for large factors like 1000 run-
time increases rapidly. This property was observed
for all algorithms. Finally an upsampling factor of
κ = 100 is a suitable choice, because best accuracy
can be achieved without rapid increase of runtime.
The combination algorithm is limited to determine
translation between images. Therefore, our evalua-
tion only focuses on paraxial translation between im-
ages. For most image registration problems, rotation
and scaling has to be considered as additional trans-
formations between images. In order to generalize our
algorithm it can be extended to determine also other
transformations: The Fourier-Mellin-Transformation
can be used for computing rotation and scaling, and
afterwards determining the translation (Tong et al.,
2019).
5 CONCLUSIONS
This paper presents an efficient algorithm for image
registration with subpixel accuracy. More precisely,
we propose a hybrid approach consisting of a coarse
to fine strategy. For the first rough estimation image
projections are used, while for the refined estimation
the method of matrix multiplication is performed only
on a small region around the first estimation center.
Experimental results have shown that the algorithm
is very accurate and computationally highly efficient.
The MAE can be reduced by over 70 % compared to
the IP approach and runtime by over 75 % compared
to the MM approach. It is robust with respect to noise
and can handle large images. To improve the algo-
rithm in further work, it can be extended to consider
generalized transformation models, such as including
rotation and scaling.
REFERENCES
Anuta, P. (1970). Spatial registration of multispectral and
multitemporal digital imagery using fast fourier trans-
form techniques. IEEE Transactions on Geoscience
Electronics, 8(4):353–368.
Budai, A., Bock, R., Maier, A., Hornegger, J., and Michel-
son, G. (2013). Robust vessel segmentation in fundus
images: High-resolution fundus image dataset. Inter-
national Journal of Biomedical Imaging.
Cohen, J. (2020). Covid chest x-ray dataset. Avail-
able: https://github.com/ieee8023/covid-chestxray-
dataset. (visited on July 22, 2020).
Farncombe, T. and Iniewski, K. (2014). Medical imaging:
Technology and applications. Devices, circuits, and
systems. CRC Press, Boca Raton, Fla.
Fezzani, R., Nunez-Iglesias, J., Lee, G. R., and Boulogne,
F. (2020). scikit-image phase cross correlation.
Available: https://github.com/scikit-image/scikit-
image/blob/v0.17.2/skimage/registration/ phase
cross correlation.py. (visited on August 08, 2020).
Guizar, M. (2016). Effizient subpixel image registration by
cross-correlation. Available: https://www.mathworks.
com/matlabcentral/fileexchange/18401-efficient-
subpixel-image-registration-by-cross-correlation.
(visited on August 08, 2020).
Guizar-Sicairos, M., Thurman, S. T., and Fienup, J. R.
(2008). Efficient subpixel image registration algo-
rithms. Optics letters, 33(2):156–158.
He, X., Zhang, Y., Mou, L., Xing, E., and Xie, P. (2020).
Pathvqa: 30000+ questions for medical visual ques-
tion answering: Medical dataset. arXiv preprint
arXiv:2003.10286.
McAndrew, A. (2016). A computational introduction to dig-
ital image processing. CRC Press, Boca Raton, FL,
second edition.
Shin, J. G., Kim, J. W., Lee, J. H., and Lee, B. H. (2017).
Accurate reconstruction of digital holography using
frequency domain zero padding. In Chung, Y., Jin, W.,
Lee, B., Canning, J., Nakamura, K., and Yuan, L., ed-
itors, 25th International Conference on Optical Fiber
Sensors, SPIE Proceedings, page 103235H. SPIE.
Soummer, R., Pueyo, L., Sivaramakrishnan, A., and Van-
derbei, R. J. (2007). Fast computation of lyot-
style coronagraph propagation. Optics express,
15(24):15935–15951.
Tong, X., Luan, K., Stilla, U., Ye, Z., Xu, Y., Gao,
S., Xie, H., Du, Q., Liu, S., Xu, X., and Liu, S.
(2019). Image registration with fourier-based image
correlation: A comprehensive review of developments
and applications. IEEE Journal of Selected Topics
in Applied Earth Observations and Remote Sensing,
12(10):4062–4081.
Yang, Y., Zhilong, Z., Xin, X., and ZhaoLin, S. (2012). An
upsampling approach to subpixel registration based on
gray scale projection. In 2012 Third International
Conference on Digital Manufacturing & Automation,
pages 210–213. IEEE.
Efficient Image Registration with Subpixel Accuracy using a Hybrid Fourier-based Approach
143
