Mesh Animation Compression using Skinning and Multi-chart

Displacement Texture

Andrej F

usek

1 a

, Adam Rie

cick

2,3 b

, Martin Stuchl

ık

3 c

and Martin Madaras

1,2,3 d

Faculty of Informatics and Information Technologies, Slovak University of Technology in Bratislava, Slovakia

Faculty of Mathematics, Physics and Informatics, Comenius University in Bratislava, Slovakia

Skeletex Research, Slovakia

Keywords:

Computers and Graphics, Animation, Compression, Skeleton.

Abstract:

Realistic animations of 3D models are currently very complex, and to stream them over a network in real-time,

it is necessary to use compression. Currently, many different methods can be used. Some of them use skeleton

transformation as an approximation of the animation, others use remeshing for decreasing mesh complexity. In

this paper, a novel method of 3D animation compression is presented. It is based on reconstructing a 3D mesh

from a 2D displacement texture and subsequent skeletal skinning enhanced by a surface tuning. The tuning

is performed by displacing the skinned vertices according to high-frequency details encoded in a Differential

Texture since the output of the skinning is just an approximation of the original animation. Skinning weights

are encoded in another new texture type - Skinning Map. In each frame of the streaming animation, just a new

skeleton pose and the Differential Texture are needed to be sent. The proposed method has a high compression

ratio for various animations because the pose is a small data structure and the Differential Texture contains just

high-frequency details and on top of that, it can be compressed as video. Furthermore, differences between

original and reconstructed animation are minimal, as evidenced by visual and numerical comparisons.

1 INTRODUCTION

Skeletal animation of 3D models is commonly used

in many animated movies or games. However, to

contain more details in the animation, the skeleton is

not sufﬁcient. The other extreme, a mesh animation,

deﬁnes the position of each vertex of the model for

each animation frame. This way, high-quality anima-

tions can be achieved. However, the amount of data

is very large, so actually, it is a problem to stream

it in real-time (e.g. in an online game). There are

some compression methods that address these prob-

lems and they are analyzed in this paper. Two main

approaches

are suitable for the animation compres-

sion: remeshing and skinning.

The ﬁrst approach converts a mesh from each an-

imation frame into a format that is either better for

compression or just contains fewer vertices. The

https://orcid.org/0000-0002-2685-8692

https://orcid.org/0000-0002-1546-0048

https://orcid.org/0000-0001-8556-8364

https://orcid.org/0000-0003-3917-4510

Also PCA-based methods can be used, but they are not

listed because of their poor properties (Brice

no et al., 2003).

second one uses skinning as an approximation of

the complicated animation and some algorithms ex-

tend this method by corrections to this approximation.

There are also methods that are a combination of these

two, and they use a texture for deﬁning the mesh it-

self. However, the mesh surface is stretched to the

whole texture, and therefore it is not optimal.

We propose a novel method of mesh animation

compression, based on a combination of state-of-the-

art methods for representing the mesh by texture and

for skinning. In general, skinning produces just an

approximation of the input mesh animation. There-

fore, high-frequency details, that cannot be contained

in skeletal animation, are stored in a Differential Tex-

ture. All the textures are generated using a parame-

terization with near-optimal stretch and consequently,

the reconstruction quality is high. Due to skinning,

the Differential Texture contains just high-frequency

details, so the compression ratio achieves also high

values. Further, the proposed method offers an option

to set the level of detail so that the user can choose a

trade-off between the quality and compression ratio.

Properties of our proposed method are evaluated on

several mesh animations and with different levels of

Fúsek, A., Rie

cický, A., Stuchlík, M. and Madaras, M.

Mesh Animation Compression using Skinning and Multi-chart Displacement Texture.

DOI: 10.5220/0010244302010208

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 1: GRAPP, pages

201-208

ISBN: 978-989-758-488-6

201

detail.

The high compression ratio makes this method

suitable for streaming high-detail animations for var-

ious VR applications, games, or other entertainment.

For example, human animation, along with facial an-

imations (like mouth or wrinkles movement) can be

effectively compressed by our method.

2 RELATED WORK

There are already several different approaches to

mesh animation compression. However, for better

understanding them and also our method, we ﬁrstly

analyze two problems related to the mesh animation,

static mesh representation, and skeletal animation.

2.1 Static Mesh Representation

Each frame of the mesh animation is basically a static

mesh which usually consists of triangles and it repre-

sents the surface of some 3D object. The triangle is

deﬁned by three indices to a vertex list. However, the

meshes are mostly irregular and the representation is

relatively difﬁcult to compress efﬁciently.

Since the mesh deﬁnes just the 2D surface of the

3D model, it is possible to represent the mesh by a 2D

image which could be compressed by some classic

techniques, e.g. wavelet compression. This idea was

ﬁrst presented by Gu et al. (Gu et al., 2002). In such a

representation, some parameterization of the surface

needs to be deﬁned and its quality can be measured

as L

stretch, deﬁned by Sander et al. (Sander et al.,

2001). This value also predicts the quality of a mesh

reconstructed from the image (Sander et al., 2002),

since the conversion causes remeshing and subse-

quently a lossy compression of the original model.

For optimizing the parameterization, there are

many stretch-minimization methods. They can be

divided into two groups, based on the boundary of

the 2D domain. From commonly used methods,

Yoshizawa et al. (Yoshizawa et al., 2004) ﬁx the

boundary to a convex shape (circle or square) and

methods by Smith and Schaefer (Smith and Schaefer,

2015) and Rabinovich et al. (Rabinovich et al., 2017)

let the boundary free during the minimization.

Bijectivity is also an important property of the pa-

rameterization, because if it is not bijective, some sur-

face details, like corners or other extremes, cannot be

preserved. Fortunately, there are some parameteriza-

tion methods that guarantee bijectivity. The ﬁrst of

them was presented by Tutte (Tutte, 1960) where the

bijective parameterization of any topological disk can

be obtained by solving a linear system.

Currently, many parameterization methods can be

used to represent the mesh by a texture. For ex-

ample, Tarini et al. (Tarini et al., 2004) designed a

PolyCube-Maps, where the mesh was simpliﬁed to

a set of aligned cubes and a vertex of the mesh was

mapped to a point on the surface of the nearest cube,

similarly to classic cube-map. Usai et al. (Usai et al.,

2015) designed a method which divides the mesh sur-

face according to a curve-skeleton and maps segments

created this way onto rectangles which were placed

into the ﬁnal texture.

Geometry Images (GIM) (Gu et al., 2002) cuts the

model surface to reach a topological disk with low-

est possible stretch. The surface is then mapped onto

a square texture according to Floater (Floater et al.,

1997). Thus obtained parameterization is bijective,

however, has a high L

stretch value, which is sub-

sequently minimized using the method of Yoshizawa

et al. (Yoshizawa et al., 2004). As the last step, the

colors of the texture pixels are set according to the

mapped 3D position (red = X, green = Y, blue = Z). In

reconstruction, each 2 by 2 quad of neighboring pixels

form two triangles and therefore, full texture forms a

mesh which is similar to the original one. Since the

full surface of the arbitrary model is mapped onto the

single square, low stretch values cannot be achieved

and so the reconstruction quality of more complex

models is poor.

Multi-Chart Geometry Images (MCGIM) (Sander

et al., 2003) is also based on the idea of represent-

ing the whole mesh by a single image, however, un-

like GIM, this method divides the surface into several

segments, called also charts. L

stretch of each chart

parameterization is then minimized, leaving bound-

aries of the charts free during the optimization. This

way, values of L

stretch are near ideal and therefore,

the reconstruction quality is also higher. All parame-

terized charts are placed onto a single rectangular tex-

ture and their rasterized boundaries are overwritten to

guarantee a watertight mesh after the reconstruction.

As a ﬁnal step, mesh optimization is performed in or-

der to achieve even higher quality, especially in areas

with sharp features of the represented model.

2.2 Skeletal Skinning

Most common animations express the movement of a

human or some animal. This kind of animation can

be approximated by a skeleton transformation. The

skeleton itself deﬁnes a topology of the model, it con-

sists of bones connected in a hierarchy, and by rota-

tion (and translation) of them, a simple animation can

be achieved (Jacobson and Sorkine, 2011).

Skinning of the mesh is a process, where the mesh

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

202

is deformed according to the skeleton pose. Each

vertex of the mesh has deﬁned weights which de-

scribe how much each bone inﬂuences that vertex

and the bones themselves have deﬁned transforma-

tion matrices computed from the rotations and trans-

lations (Lander, 1998).

The simplest skinning method, called Linear

Blend Skinning (LBS) (Lander, 1998) uses the weight

to linearly interpolate between vertex position trans-

formed by each bone independently. This approach

results in smooth deformation of the mesh, but also

signiﬁcant artifacts, like volume collapse near skele-

ton joints, if extreme rotation (near 180 degrees twist)

is performed. This method is very simple, but the

animation in these extreme cases looks very unnatu-

ral. Fortunately, several improvements to this method

were designed later.

First automatic method (without need to manu-

ally change the skeleton), Spherical Blend Skinning

(SBS) (Kavan and

ara, 2005), interpolates quater-

nions instead of the transformation matrices. This ap-

proach prevents the collapse of volume and requires

just a few more operations in rendering than LBS.

There are many newer methods, e.g. Skinning

with Dual Quaternions (Kavan et al., 2007), but we

would like to pay special attention to the state-of-the-

art method (Le and Hodgins, 2016), called Real-time

Skeletal Skinning with Optimized Centers of Rotation

(ORCS). The basic idea of this method is to rotate

vertices around optimized centers, not just joints of

the skeleton as in other skinning methods. The cen-

ters are pre-computed in an initialization step, as av-

erage positions of vertices with similar weights, and

the real-time algorithm is similar to SBS. The output

of this method looks more realistic and preserves the

same volume near joints during the whole animation,

even at extreme rotations.

2.3 Current Methods of Mesh

Animation Compression

Currently, there are many different approaches to an-

imation compression. The ﬁrst group of algorithms is

based on Principal component analysis (PCA), for ex-

ample, a method by Sattler et al. (Sattler et al., 2005)

or Lee et al. (Lee et al., 2007). These methods are

based on the fact that in all common mesh animations,

many vertices are moved very similarly between the

frames and therefore use PCA for extracting the main

components of this information.

Geometry Videos (Brice

no et al., 2003) converts

a mesh from each frame of the animation to a 2D

image using the GIM method and encodes result-

ing images as MPEG video. Multi-chart Geome-

try Video (Mamou et al., 2006) is very similar, but

uses MCGIM instead of GIM. These methods pro-

duce representations with higher quality than PCA-

based methods.

Although none of these methods takes the advan-

tage that most mesh animations can be approximated

by skeleton transformation, there are several different

methods based on that idea. In Skinning Mesh Ani-

mations (SMA) (James and Twigg, 2005), the mesh

animation is automatically converted into a skeleton-

based animation, and differences from the original

one are encoded using a method similar to Eigen-

Skin (Kry et al., 2002). However, compression is not

a primary goal of this method so it does not support

mesh simpliﬁcation (level of detail).

There is also Skeletex representation (Madaras

et al., 2018) where the mesh is represented by a skele-

ton and several vector-displacement textures, one for

each bone of the skeleton. It could be used for ani-

mation compression as well, but the resulting anima-

tion does not guarantee C

continuity (there are visi-

ble edges in segment boundaries).

The method by Feng et al. (Feng et al., 2010) uses

an approach similar to GIM to represent the rest-pose

mesh and the animation is performed by skinning of

the reconstructed mesh. Skinning weights and bone

indices are encoded with the same parameterization

as vertex positions.

2.4 Quality Metrics

To decide whether some compression method is

good or not, existing evaluation metrics will be used

to evaluate the animation reconstructed from com-

pressed representation.

If reconstructed mesh in each frame has the same

connectivity as the original one, a metric deﬁned by

Karni and Gotsman (Karni and Gotsman, 2004) could

be used. It considers also how much the vertices move

on average during the whole animation.

However, many methods convert the original

mesh from the animation to a representation with dif-

ferent connectivity. Therefore, a metric that is able

to compare two surfaces has to be used. Most com-

mon is Hausdorff distance which measures the dis-

tance from each vertex of the ﬁrst mesh to the near-

est point on the second mesh surface (Rockafellar and

Wets, 2009). One can compute a mean or max value

of these measured distances (Cignoni et al., 1998).

Payan et al. (Payan et al., 2008) compute the average

of the max Hausdorff distances for the entire anima-

tion to measure the distortion of the reconstruction.

Mesh Animation Compression using Skinning and Multi-chart Displacement Texture

203

Figure 1: Overview diagram of our method for animation compression and reconstruction.

3 ANIMATION

REPRESENTATION

The basic idea of our proposed compression method

is to represent a static 3D model in a rest pose and its

movement separately. To enable real-time streaming

of highly detailed animation, the movement deﬁnition

is designed to be as small as possible.

Our designed method of animation compression

itself is based on skeletal skinning of mesh recon-

structed from MCGIM and subsequently applying

corrections from a texture stream. Therefore, the

static model must contain also skinning weights and

the skeleton, and the movement consists of skeleton

poses and textures with the corrections. All proper-

ties of vertices (positions, skinning weights, normals,

corrections, etc.) are encoded in 2D textures with

the same parameterization. An overview diagram ex-

pressing the whole method and inside processes is in

Figure 1.

3.1 Conversion

Within a conversion of input mesh animation, there

are two processes: an initial conversion of the static

3D model in a rest pose and a real-time conversion of

the animation frames.

3.1.1 Static Model Conversion

The input of the initial conversion is an arbitrary mesh

in a rest pose along with its skeleton and skinning

weights. These structures could be generated using an

existing method for conversion the mesh animation to

a skeletal one (James and Twigg, 2005). The output

is a representation of the static model which consists

of one main ﬁle that contains model dimensions, po-

sition, skeleton, and several textures. These ﬁles need

to be sent just once, at the start of the streaming pro-

cess. An example of them can be seen in Figure 2.

The main part of this conversion is to generate

the geometry image and it is inspired mostly by the

MCGIM method by Sander et al. (Sander et al., 2003).

Firstly, the surface of the input mesh is segmented

and each segment is parameterized using the bijec-

tive stretch minimizing method by Smith and Schae-

fer (Smith and Schaefer, 2015). This way, a set of 2D

charts with near-ideal stretch is created. The follow-

ing steps are placing them onto a single rectangular

image, sampling of the image, and zippering in order

to guarantee a water-tight mesh after reconstruction.

In addition to the image, we preserve also a pa-

rameterization as the output of the MCGIM creation,

because it is necessary for exporting also all other im-

ages. To enable skeletal skinning of a mesh recon-

structed from the MCGIM, we design two new texture

types. Index Skinning Map (ISM) encodes the indices

of bones and Weight Skinning Map (WSM) encodes

amounts of bone inﬂuences.

Figure 2: Example ﬁles of the static model representation

(bear model). From left: the main ﬁle, MCGIM, ISM,

WSM and optional normal map.

Since each vertex of the input mesh has a skinning

weights, exporting them to the skinning maps are rel-

atively simple. In most cases, the vertex has a limited

number of inﬂuencing bones to 4, but because of the

parameterization, some output texture pixels can be

related to more bones. However, the amount of in-

ﬂuence by the ﬁfth and next bones is practically very

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

204

small and can be neglected. A similar approach was

used in the method by Feng et al. (Feng et al., 2010).

The bone indices are encoded during exporting

ISM by simple bit-wise operations - since four bone

indices need to be encoded in three channels (red,

green, blue). For WSM export, the weights encoding

are based on the fact that a sum of all weights for each

vertex is equal to 1.0. Therefore, one of the weights,

the highest one, is not encoded. Other weights (3 or

less) are written directly to color channels of corre-

sponding pixels. They are sorted in descending order

and to improve the precision of the quantization, each

weight is multiplied by its order in the original weight

list.

3.1.2 Real-time Conversion

During the processing of each frame in real-time

streaming of animation, an input is a new mesh with

the same connectivity as the rest-pose mesh and new

pose of the skeleton that could be obtained using a

method for extraction pose from current frame (James

and Twigg, 2005).

To generate a texture used to correct errors from

skinning approximation, the skinning of the recon-

structed mesh is performed and thus deformed mesh

is compared with the new input mesh. Differences

between these two surfaces are computed for each re-

constructed vertex using the nearest point on the sur-

face of the original mesh and they are just exported

to a new Differential Texture (DT) using the parame-

terization computed in the initial conversion. For ac-

celeration of this process, just a small triangles subset

of the original mesh is considered while ﬁnding the

nearest point.

Therefore, just the new pose and this texture need

to be sent in streaming. In addition, classic video en-

coders can be used to compress the texture stream,

since it forms a 2D video during the animation. For

example, MPEG compression was used in this paper.

3.2 Reconstruction

Reconstruction of the animation can be divided

into an initial and a real-time algorithm as well.

Within initialization, the rest-pose mesh is recon-

structed from the MCGIM just like in the original

method (Sander et al., 2003) and both skinning maps

are decoded by simple applying inverse operations to

the encoding.

Since the ORCS method by Le and Hodgins (Le

and Hodgins, 2016) is used to skin the reconstructed

mesh, the centers of rotation must be computed in

the initialization step as well. This computation is

performed according to the procedure in the origi-

nal method, but the center positions are stored in a

texture, similar to the way how vertex positions are

stored in the MCGIM. The output of the initial recon-

struction is used in a shader for a real-time rendering

of the animation.

For the reconstruction of one animation frame

in real-time, transformation matrices for ORCS are

computed from the skeleton and its new pose. The

rest-pose mesh is skinned as in ORCS and its sur-

face is then displaced by currently received Differen-

tial Texture in order to tune the errors.

Algorithm 1: Real-time rendering of the repre-

sentation.

Input:

• global variables: transformation matrices for

all bones MAT S, model offset o, model size s,

DT scale s

• global textures: MCGIM, IS M, WSM,

CoR (optimized centers of rotation), DT

(differential texture with corrections)

• for each vertex: UV coordinate u

Output: Deformed position v

Algorithm:

= MCGIM[u] ∗ s +o; //rest position

= MAT S[ISM[u]]; //4 matrices

= W SM[u]; //4 skinning weights

c = CoR[u] ∗ s +o; //center of rotation

= ORCS(v

, M

, W

, c); //skinned position

= v

+ (DT [u]− 0.5) ∗ s

;

For a better understanding of the real-time ren-

dering algorithm, a pseudo-code of a vertex shader is

stated in Algorithm 1. Although this code just recon-

structs and deforms the vertex, for ﬁnal rendering in

the fragment shader, normal mapping or color textur-

ing can be added using the original UV coordinates.

4 RESULTS

In this section, there is an evaluation of a compression

ratio and a reconstruction quality for different input

animations and levels of detail. Also, a visual and nu-

meric comparison with alternative methods is listed.

4.1 Level of Detail

The proposed method enables a level of detail (LoD)

setting since the output texture resolution can be set

Mesh Animation Compression using Skinning and Multi-chart Displacement Texture

205

arbitrarily. The dependence of average reconstruction

error on texture width for different input animations is

shown in Figure 3. The error is computed as an aver-

age value of mean Hausdorff error through the whole

animation using MeshLab (Cignoni et al., 1998).

Figure 3: An evaluation of average reconstruction error de-

pending on texture resolution.

Visual comparison of reconstruction with differ-

ent levels of detail can be seen in Figure 4. All recon-

structions are ﬂat-shaded.

Figure 4: Detail of reconstructed frame of SMPL Male an-

imation (Loper et al., 2015) with different levels of detail.

MCGIM texture width from left: 64, 128 and 256 pixels. In

the last image, there is the original input mesh.

Achieved compression ratios along with max and

mean average error (computed as normalized Haus-

dorff distance) are in Table 1. To compute the ratio,

the size of one original frame (340 kB for mesh in bi-

nary PLY format) is divided by the size of the same

frame in our representation.

Table 1: Achieved compression ratios along with aver-

age errors for the snake animation. In this table, there is

noted also the resolution of textures and the stream speed

which expresses the minimum needed bandwidth of real-

time streaming to achieve 30 FPS during the animation.

4.2 Impact of Difference Texture

The course of reconstruction error (mean Hausdorff

distance) during whole snake animation is in Figure 5.

Notice the improvement in quality when using the dif-

ferential texture as opposed to the case of a skinning

algorithm only. The lowest error is in the ﬁrst frame

because it is used as bind-pose.

Figure 5: The course of mean Hausdorff distance during the

SMPL Male Hopping animation (Loper et al., 2015) recon-

structed from textures with resolution 128 x 190 pixels. The

average compression ratio in streaming was 405:1 for raw

skinning and 62:1 for case with DT.

4.3 Comparison with Alternative

Representations

If we use the Skeletex method (Madaras et al., 2018)

to represent the mesh animation, it would cause vis-

ible lightning artifacts, especially in animation with

extreme joints rotation. A visual comparison with our

method is in Figure 6. Notice the differences around

joints of the bear rear legs. Our method deforms the

rest-pose model smoothly since it uses skinning and

therefore has a C

continuity.

Figure 6: Comparison of extreme joints rotation performed

on bear model by Skeletex (top) and by our method (bot-

tom).

In Table 2, there is a numerical comparison

of our method with Skinning Mesh Animations

(SMA) (James and Twigg, 2005). We set the level

of detail for each animation independently so that the

reconstruction error was similar to the one in SMA.

Therefore, the compression ratio can be compared

easily. The error is computed as a Percent distortion,

similarly to the error in the SMA article with one edit.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

206

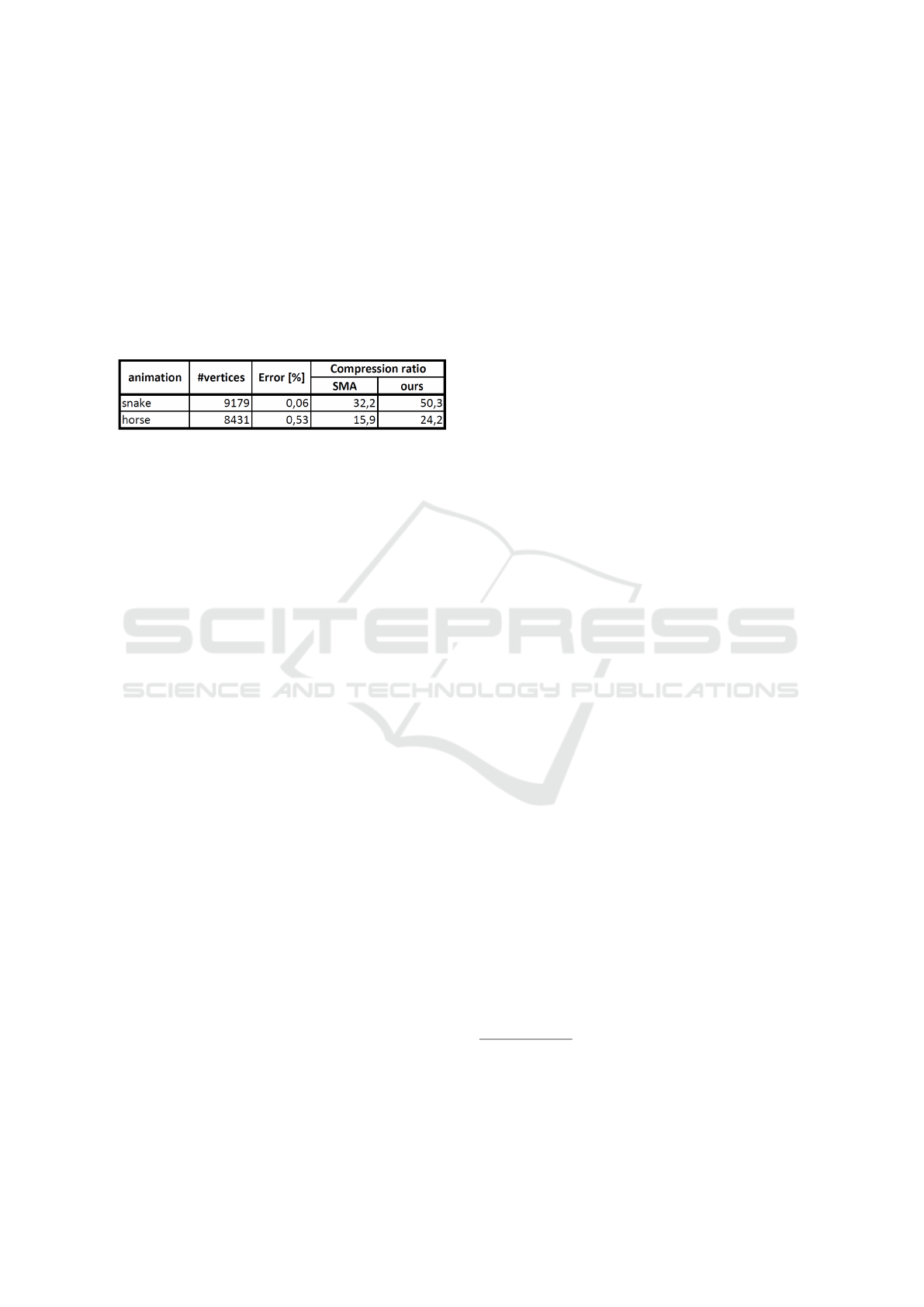
Since our method changes the geometry, the error is

computed as Hausdorff distance divided by the same

normalization factor as in the original metric. The im-

provement in the compression ratio is not big, how-

ever, note the ability to set the level of detail in our

method. If high quality is not needed (e.g. if the cam-

era in rendering is not close to the object), the LoD

can be lowered which causes a signiﬁcant increase of

the compression ratio (see Table 1).

Table 2: Comparison of compression ratios with SMA

method.

5 DISCUSSION

The proposed animation representation enables com-

pression of the input mesh animation and real-time

rendering directly using the generated textures. How-

ever, along with the mesh animation, the skeleton and

skinning weights are required. For automatic extrac-

tion of them, some existing methods, like (James and

Twigg, 2005), can be used.

5.1 Advantages

The main advantage of the representation is param-

eterization properties. It is bijective in all cases due

to segmentation and the L

stretch is for most cases

less than 1.01, and that implicates high reconstruc-

tion quality which was conﬁrmed within the evalua-

tion. Also, good compression ratios can be achieved

if a PNG encoding for rest-pose texture and MPEG

encoding for differential textures was used.

5.2 Limitations

The proposed representation is not suitable for anima-

tions that cannot be approximated by a skeleton, e.g.

building demolition or other animation with extreme

deformations. The vertices movement would have to

be captured just in the DT which is designed to con-

tain just little differences.

Another limitation is that the input meshes for all

animation frames need to have the same number of

vertices in the same order. This constraint makes it

hard to integrate our method with the fusion of some

moving object recorded by a 3D camera (Newcombe

et al., 2015). If the meshes do not satisfy this condi-

tion, our compression algorithm needs to be modiﬁed

to compare all pairs of input and reconstructed ver-

tices.

6 CONCLUSION

In this paper, a new method of mesh animation com-

pression was presented. Designed representation con-

sists of a skeleton and several textures where different

properties of a model in the rest pose are encoded.

Animation reconstructed from the representation was

evaluated and reasonable reconstruction quality was

measured. By setting the output texture resolution,

a compression ratio and the quality can be affected.

This trade-off can be affected also by changing the

video codec. In the evaluation, we used MPEG en-

coder. All textures consist of several disconnected

charts, nevertheless there were no visible holes or

cracks in the reconstructed mesh animation.

6.1 Future Work

There are several ideas to improve the proposed

method, but they are out of the scope.

During encoding surface differences in Differen-

tial Texture, they were multiplied by a manually esti-

mated scale so there is a limit, how big the difference

can be to be yet contained in the texture. However, it

could be automated and optimal value could be sent

for each frame. Furthermore, the user could specify if

he wants a higher compression ratio or rather higher

quality and the scale would be set according to this

requirement.

ACKNOWLEDGMENTS

We would like to express many thanks to Jason Smith

(the main author of the paper Bijective parameteriza-

tion with free boundaries) for help in the implemen-

tation of his method.

Mesh animations used in evaluation our method

are downloaded from different webpages

and

skinned rest poses from the SMA webpage

http://people.csail.mit.edu/sumner/research/deftransfer/

data.html (horse), http://www710.univ-lyon1.fr (snake),

http://graphics.cs.cmu.edu/projects/sma/textData/chicken

Crossing.zip (chicken)

http://graphics.cs.cmu.edu/projects/sma/textData

Mesh Animation Compression using Skinning and Multi-chart Displacement Texture

207

REFERENCES

Brice

no, H. M., Sander, P. V., McMillan, L., Gortler, S., and

Hoppe, H. (2003). Geometry videos: a new represen-

tation for 3d animations. In Proceedings of the 2003

ACM SIGGRAPH/Eurographics symposium on Com-

puter animation, pages 136–146. Eurographics Asso-

ciation.

Cignoni, P., Rocchini, C., and Scopigno, R. (1998). Metro:

measuring error on simpliﬁed surfaces. In Computer

graphics forum, volume 17, pages 167–174. Wiley

Online Library.

Feng, W.-W., Kim, B.-U., Yu, Y., Peng, L., and Hart, J.

(2010). Feature-preserving triangular geometry im-

ages for level-of-detail representation of static and

skinned meshes. ACM Transactions on Graphics

(TOG), 29(2):1–13.

Floater, M. S. et al. (1997). Parametrization and smooth

approximation of surface triangulations. Computer

aided geometric design, 14(3):231–250.

Gu, X., Gortler, S. J., and Hoppe, H. (2002). Geometry im-

ages. In Proceedings of the 29th annual conference on

Computer graphics and interactive techniques, pages

355–361.

Jacobson, A. and Sorkine, O. (2011). Stretchable and

twistable bones for skeletal shape deformation. In

Proceedings of the 2011 SIGGRAPH Asia Confer-

ence, pages 1–8.

James, D. L. and Twigg, C. D. (2005). Skinning mesh

animations. ACM Transactions on Graphics (TOG),

24(3):399–407.

Karni, Z. and Gotsman, C. (2004). Compression of soft-

body animation sequences. Computers & Graphics,

28(1):25–34.

Kavan, L., Collins, S.,

ara, J., and O’Sullivan, C. (2007).

Skinning with dual quaternions. In Proceedings of

the 2007 symposium on Interactive 3D graphics and

games, pages 39–46.

Kavan, L. and

ara, J. (2005). Spherical blend skinning: a

real-time deformation of articulated models. In Pro-

ceedings of the 2005 symposium on Interactive 3D

graphics and games, pages 9–16.

Kry, P. G., James, D. L., and Pai, D. K. (2002). Eigen-

skin: real time large deformation character skinning

in hardware. In Proceedings of the 2002 ACM SIG-

GRAPH/Eurographics symposium on Computer ani-

mation, pages 153–159.

Lander, J. (1998). Skin them bones: Game programming

for the web generation. Game Developer Magazine,

5(1):10–18.

Le, B. H. and Hodgins, J. K. (2016). Real-time skeletal

skinning with optimized centers of rotation. ACM

Transactions on Graphics (TOG), 35(4):1–10.

Lee, P.-F., Kao, C.-K., Tseng, J.-L., Jong, B.-S., and Lin,

T.-W. (2007). 3d animation compression using afﬁne

transformation matrix and principal component analy-

sis. IEICE TRANSACTIONS on Information and Sys-

tems, 90(7):1073–1084.

Loper, M., Mahmood, N., Romero, J., Pons-Moll, G., and

Black, M. J. (2015). SMPL: A skinned multi-person

linear model. ACM Trans. Graphics (Proc. SIG-

GRAPH Asia), 34(6):248:1–248:16.

Madaras, M., Rie

cick

y, A., Mes

aro

s, M., Stuchl

ık, M.,

and Piovar

ci, M. (2018). Skeletex: Skeleton-texture

co-representation for topology-driven real-time inter-

change and manipulation of surface regions. In Com-

puter Graphics Forum, volume 37, pages 325–336.

Wiley Online Library.

Mamou, K., Zaharia, T., and Preteux, F. (2006). Multi-

chart geometry video: A compact representation for

3d animations. In Third International Symposium on

3D Data Processing, Visualization, and Transmission

(3DPVT’06), pages 711–718. IEEE.

Newcombe, R. A., Fox, D., and Seitz, S. M. (2015). Dy-

namicfusion: Reconstruction and tracking of non-

rigid scenes in real-time. In Proceedings of the IEEE

conference on computer vision and pattern recogni-

tion, pages 343–352.

Payan, F., Kamoun, A., and Antonini, M. (2008). Remesh-

ing and spatio-temporal wavelet ﬁltering for 3d an-

imations. In 2008 IEEE International Conference

on Acoustics, Speech and Signal Processing, pages

1081–1084. IEEE.

Rabinovich, M., Poranne, R., Panozzo, D., and Sorkine-

Hornung, O. (2017). Scalable locally injective

mappings. ACM Transactions on Graphics (TOG),

36(4):1.

Rockafellar, R. T. and Wets, R. J.-B. (2009). Variational

analysis, volume 317. Springer Science & Business

Media.

Sander, P. V., Gortler, S., Snyder, J., and Hoppe, H. (2002).

Signal-specialized parameterization.

Sander, P. V., Snyder, J., Gortler, S. J., and Hoppe, H.

(2001). Texture mapping progressive meshes. In Pro-

ceedings of the 28th annual conference on Computer

graphics and interactive techniques, pages 409–416.

Sander, P. V., Wood, Z. J., Gortler, S., Snyder, J., and

Hoppe, H. (2003). Multi-chart geometry images.

Sattler, M., Sarlette, R., and Klein, R. (2005). Simple and

efﬁcient compression of animation sequences. In Pro-

ceedings of the 2005 ACM SIGGRAPH/Eurographics

symposium on Computer animation, pages 209–217.

Smith, J. and Schaefer, S. (2015). Bijective parameteri-

zation with free boundaries. ACM Transactions on

Graphics (TOG), 34(4):1–9.

Tarini, M., Hormann, K., Cignoni, P., and Montani, C.

(2004). Polycube-maps. ACM transactions on graph-

ics (TOG), 23(3):853–860.

Tutte, W. T. (1960). Convex representations of graphs.

Proceedings of the London Mathematical Society,

3(1):304–320.

Usai, F., Livesu, M., Puppo, E., Tarini, M., and Scateni,

R. (2015). Extraction of the quad layout of a triangle

mesh guided by its curve skeleton. ACM Transactions

on Graphics (TOG), 35(1):1–13.

Yoshizawa, S., Belyaev, A., and Seidel, H.-P. (2004). A

fast and simple stretch-minimizing mesh parameteri-

zation. In Proceedings Shape Modeling Applications,

2004., pages 200–208. IEEE.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

208