Estimation of Movement Speed in Monitoring

Systems based on Sensors of Multiple Types

Jakub Wagner

and Paweł Mazurek

Institute of Radioelectronics and Multimedia Technology, Warsaw University of Technology, Warsaw, Poland

Keywords: Healthcare, Monitoring, Data Fusion, Numerical Differentiation, Regularisation, Total Variation.

Abstract: The research reported in this paper is related to the differentiation and fusion of measurement data in systems

for healthcare-oriented unobtrusive monitoring of elderly persons. Two methods for regularised numerical

differentiation – suitable for different shapes of trajectories of the monitored person’s movement – are con-

sidered. A technique for the fusion of data from sensors of different types – which involves weighting those

data according to the available a priori information about the variances of errors corrupting those data – is

presented. Guidelines on the usage and optimisation of that technique are provided according to the results of

numerical experimentation based on synthetic data.

1 INTRODUCTION

1.1 Motivation for Monitoring

The life expectancy at birth, estimated for the global

population in 2019, is ca. 73 years; it has been rising

during the last decades and is predicted to reach 77

years by the half of the twenty-first century, while the

global fertility rate – i.e. the number of live births per

woman over a lifetime – is decreasing (United

Nations, 2019). For these reasons, the global popula-

tion is ageing, i.e. the share of people aged at least 65

years is growing. Taking into account these predic-

tions, several global institutions involved in the pro-

tection and management of public health have point-

ed out the necessity to take actions aimed at improv-

ing the quality of life of elderly people and at ensuring

that the public expenditures, related to the healthcare

services addressed to those people, remain affordable

(see, for example, WHO, 2017). That necessity has

inspired the development of diverse technological

means, designed to facilitate the accomplishment of

various healthcare-related objectives such as the re-

duction of the number of admissions to nursing

homes, the optimisation of the processes of treatment

or rehabilitation, or the social integration of elderly

people. For instance:

https://orcid.org/0000-0002-2739-4578

https://orcid.org/0000-0002-8239-4589

 Alerting devices – such as those worn on the body

or clothes, which send out an emergency signal

when a button is pressed – reduce the delay of in-

tervention after dangerous events such as falls,

and enhance the sense of safety of elderly people

who live independently in their households, thus

encouraging them to stay active (Fleming and

Brayne, 2008).

 Robots support elderly people in tasks which they

are unable to complete without aid, and may

relieve them from the sense of loneliness (Wada

et al., 2004, Sharkey and Sharkey, 2012).

 Sensors and actuators ensuring the safe function-

ing of household appliances protect elderly people

from dangerous accidents (Al-Shaqi et al., 2016).

 Video games which involve players in physical

activity may be used to promote such activity

among elderly people and gather information

about their health status (Garcia Marin, 2015).

 Social-networking websites and systems based on

ambient-display screens – designed to help elder-

ly people maintain contact with their relatives and

friends – help prevent their social isolation

(Campos et al., 2016).

 Monitoring systems provide data representative of

the behaviour and physiological parameters of in-

dependently-living elderly people, help in identi-

fying progressive changes in those people’s health

Wagner, J. and Mazurek, P.

Estimation of Movement Speed in Monitoring Systems based on Sensors of Multiple Types.

DOI: 10.5220/0010249300690079

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 69-79

ISBN: 978-989-758-490-9

status and enable quick reactions to dangerous ac-

cidents (Peetoom et al., 2015).

This study is focused on technological solutions

belonging to the last category, viz. on monitoring

systems which enable the acquisition of data repre-

sentative of the monitored person’s movement tra-

jectory. Such data can be used to obtain information

useful for the healthcare practitioners, in particular –

to estimate the monitored person’s walking speed.

Walking is a complex task which requires the interac-

tion of several organs and the proper functioning of

multiple parts of the brain (Kikkert et al., 2016). The

analysis of gait can provide information about the so-

called functional mobility, i.e. a set of abilities related

to balance and gait manoeuvres used in everyday life

– abilities which partially reflect the overall health

status (Shumway-Cook et al., 2000). Some quantities

characterising the gait – such as the stride length, the

stride frequency, or the variability of the stride time –

are correlated with the risk of falling and are useful as

indicators of conditions such as Parkinson’s disease,

osteoarthritis or diabetes (Hodgins, 2008). On the

other hand, the speed with which a person walks com-

fortably during every-day activities – the so-called

self-selected walking speed – has been recently recog-

nised as a versatile, informative and easily measur-

able indicator of functional mobility and general

health status (Lusardi, 2012):

 its values smaller than 0.6 m/s indicate a high risk

of fall and hospitalisation;

 its increase of at least 0.1 m/s is a useful predictor

of well-being;

 its similar decrease is correlated with the deterio-

ration of the health status or the decline in overall

functioning.

In clinical settings, self-selected walking speed

can be estimated by using a stopwatch to measure the

time which the examined person needs to walk along

a path of a predefined length; however, the in-home

use of monitoring systems may prove to be more re-

liable, convenient and affordable than clinical assess-

ment sessions (Hagler et al., 2010).

Apart from the estimation of the self-selected

walking speed, the data representative of the monitor-

ed person’s two- or three-dimensional movement tra-

jectory – together with the estimates of velocity and

acceleration, obtained on the basis of those data – can

be used in other healthcare-oriented applications,

such as the detection of falls (Khan and Hoey, 2017)

or the analysis of that person’s behavioural patterns

(Baldewijns et al., 2016), which may enable the early

detection of the onset of dementia.

1.2 Techniques for Monitoring

In the practice of healthcare-oriented monitoring, the

solutions based on wearable sensors – i.e. sensors

attached to the body or clothes of the monitored per-

son, including accelerometers, gyroscopes and sen-

sors of physiological parameters – are the most wide-

spread ones (Majumder et al., 2017). The most im-

portant drawback of such techniques is the fact that

the need to wear devices may be considered inconve-

nient by the people subject to monitoring; further-

more, a system based on wearable devices becomes

useless if the monitored person forgets to wear the

device or decides not to do it. For these reasons, it

seems desirable to develop monitoring systems which

do not require any action from the monitored persons.

Other monitoring techniques, already applied in

healthcare practice, include those based on video

cameras, passive-infrared detectors of motion and

pressure sensors. There are also two emerging cate-

gories of monitoring techniques which attract grow-

ing attention of researchers, viz. techniques based on

depth sensors and impulse-radar sensors. The recent

attempts to apply them for monitoring of elderly per-

sons are mainly motivated by the conviction that they

may be less intrusive, invasive and cumbersome than

the above-mentioned, better explored techniques.

This study is devoted to the monitoring techniques

which – like those based on depth sensors and im-

pulse-radar sensors – involve the estimation of the

position of the monitored person’s centre of mass

with high temporal resolution (i.e. several to several

dozen estimates per second), followed by the analysis

of the sequences of those estimates. Such techniques

require numerical differentiation in order to estimate

the monitored person’s movement speed. The posi-

tion estimates are corrupted with measurement errors,

so their numerical differentiation is an ill-posed prob-

lem, i.e. if no remedies are applied, small errors cor-

rupting the data may cause large errors in the speed

estimates. Therefore, the problem of numerical differ-

entiation needs to be regularised, i.e. redefined in

such a way as to ensure a kind of “regularity” of the

speed estimates, at the cost of limiting their attainable

fidelity to the measurement data, in order to reduce

their sensitivity to the measurement errors.

Sensors which operate according to different phy-

sical principles tend to have specific complementary

advantages and disadvantages; for example, impulse-

radar sensors offer a broad field of view and the ca-

pacity of through-the-wall monitoring, but provide

estimates of the monitored person’s position corrupt-

ed with larger errors than depth sensors, which – on

the other hand – cannot detect occluded persons and

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

whose field of view is limited. This study is devoted

to monitoring systems which employ sensors of mul-

tiple types and thus require the application of an ade-

quate method for the fusion of data acquired by means

of those sensors.

Despite the generally recognised need for devel-

oping technological solutions aimed at improving the

quality of life of elderly people and contributing to

the efficiency of public health management, health-

care-oriented monitoring systems are still not being

commonly used in healthcare facilities and house-

holds. This may be explained by the difficulties relat-

ed to the development of technological solutions

which can be both widely accepted among elderly

people and – at the same time – capable of providing

healthcare practitioners with useful information

(Debes et al., 2016). Solutions aimed at combining

the complementary advantages of several types of

sensors seem to have a promising potential for

achieving a satisfactory compromise between the two

above-mentioned qualitites.

1.3 Scope of Study

Two methods of numerical differentiation have been

considered in this study (cf. Subsection 2.2):

 a method based on Tikhonov regularisation, suit-

able for the analysis of smooth movement trajec-

tories;

 a method based on total-variation regularisation,

suitable for the analysis of piecewise-linear move-

ment trajectories.

In both cases, the fusion of data from different sensors

has been performed by adopting an adequate indicator

of the fidelity of the speed estimates to the measure-

ment data (cf. Subsection 2.3). The aim of this study

is the analysis of the properties and applicability of

that indicator – the analysis based on the results of

experiments performed using synthetic data.

2 ESTIMATION OF MOVEMENT

SPEED

2.1 Mathematical Formulation of

Research Problem

Let’s assume that the time-dependence of the mon-

itored person’s position in a given direction can be

modelled using a scalar, real-valued function

𝑓: ℝ → ℝ of a scalar variable

modelling time,

differentiable on the interval





0,T

. The analytic

form of

is unknown. The available data





are its error-corrupted values, resulting from mea-

surements performed at time instants

tt

such

that

ttT





. Those data are modelled as

follows:





nnn

xft









for

1, ,nN 

(1)

where





are realisations of independent ran-

dom variables





modelling measurement er-

rors. Since it is assumed that those data may have

been acquired by means of different types of sensors,

the distributions of the variables





may dif-

fer; in this study, it is assumed that those variables are

zero-mean, normally distributed and that their vari-

ances are





. Those variances are unknown,

but their estimates

ˆˆ



 are available; in prac-

tice, these estimates may be obtained as a result of

prior calibration experiments.

The time-dependence of the monitored person’s

speed in the given direction is modelled with





, i.e.

the first derivative of

. Speed estimates





,,x 





are sought such that:













ft

for

1, ,nN 

(2)

2.2 Numerical Differentiation

The procedure for numerical differentiation, i.e. de-

termination of the sequence









ˆˆ

x

on the basis

of the sequence





, involves the following

operations:

 approximation of the function

 computation of the first derivative





of the re-

sult of approximation

 evaluation of





at the time instants

tt

The approximation of

requires the determination

of a set of admissible approximating functions and the

selection of one of them on the basis of the data



In this study, it is assumed that the admissible approx-

imating functions are polynomial splines of degree 2.

Such functions are defined as quadratic polynomials

in each subinterval







1, , 1nN

; hence,

it can be easily checked that the following equality is

satisfied for each such function

Estimation of Movement Speed in Monitoring Systems based on Sensors of Multiple Types

(3)

Thus:

(4)

for

The

1N 

equations obtained by evaluating Eq. (4)

for

2, ,nN 

– the equations specifying the linear

relation between the values of the approximating

function and the values of its first derivative – may be

supplemented by adopting an additional assumption

regarding the movement of the monitoring person;

here, it has been assumed that the speed of the moni-

tored person is constant at the beginning of the time

interval under analysis, i.e.:

















ˆˆ

0ft ft

(5)

Eq. (4) and Eq. (5) may be collected in the following

way:





ˆˆ





Qx x

(6)

where



is the vector of values of the approximating

function, shifted by





t

      

1121 1

ˆˆˆˆ ˆ ˆ

ft ft ft ft ft ft





  



x 





is the vector of estimates of the first derivative:

   



111 1 1

ˆˆ

ˆˆˆ

x x ft ft















x 

and the matrix

is defined as follows:

21 21

31 32

31 1

21 4 2

222

222 2

110

tt tt

tt t t

tt tt































If the measurement errors are negligible and – conse-

quently – one may assume that the best approximat-

ing function is the one which interpolates the mea-

surement data,

i.e.







for

1, ,nN 

, then

Eq. (6) can be used directly to obtain the vector





of speed estimates,

viz.:







xQx



(7)

where





is the vector of measurement data shifted







112 1 1N

xx x x x



  x

 



However, the condition number of

tends to be

very large even for relatively small

N, and thus the

speed estimates obtained this way are unacceptably

inaccurate even when the errors corrupting the data

are small. The remedy for this is regularisation, which

consists in imposing an additional constraint on the

set of admissible approximating functions. Such a

constraint should be based on a realistic

a priori as-

sumption regarding the movement of the monitored

person, in particular – an assumption about the shape

of the function

modelling the trajectory of that

movement. In this study, constraints on the following

two quantities are considered:

 the squared 2-norm of the vector of values of the

second derivative of the approximating function,

denoted with



hereinafter:

(8)

where and:

 the squared 1-norm of the vector of values of the

second derivative of the approximating function,

denoted with



hereinafter:

 



22 1

ˆˆ







 







xDx

(9)

The imposition of a constraint on



– being a va-

riant of the regularisation technique commonly re-

ferred to as Tikhonov regularisation (Stickel, 2010) –

is suitable when the monitored person’s movement

trajectory is adequately modelled with a smooth func-

tion, i.e. a function whose several derivatives are con-

tinuous. Such an assumption about the shape of the

modelling function seems reasonable when human

movement is analysed in a relatively short time inter-

val; for example, during gait, the position of the mon-

itored person’s centre of mass along the direction or-

thogonal to the walking direction fluctuates smoothly

with a period corresponding to the stride duration.

  



ˆˆ ˆ ˆ

nn n n

ft ft f t f t









 



2, ,nN 

 



111

ˆˆˆ ˆ

tt t t

ft ft f t f t













  













2, ,nN 

 



22 1

ˆˆ





 



xDx

 



22 2

ˆˆ

ft ft











x 



21 21

32 32

NN NN

tt tt

































BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

On the other hand, the imposition of a constraint



– being a variant of the regularisation technique

commonly referred to as total-variation (TV) regu-

larisation (Rudin et al., 1992) – is suitable when the

movement trajectory is adequately modelled with a

piecewise-linear function. Such an assumption seems

reasonable when the walking trajectory is modelled in

a time interval of several seconds or minutes, since

people tend to walk with approximately piecewise-

constant speed.

The effects of both considered regularisation tech-

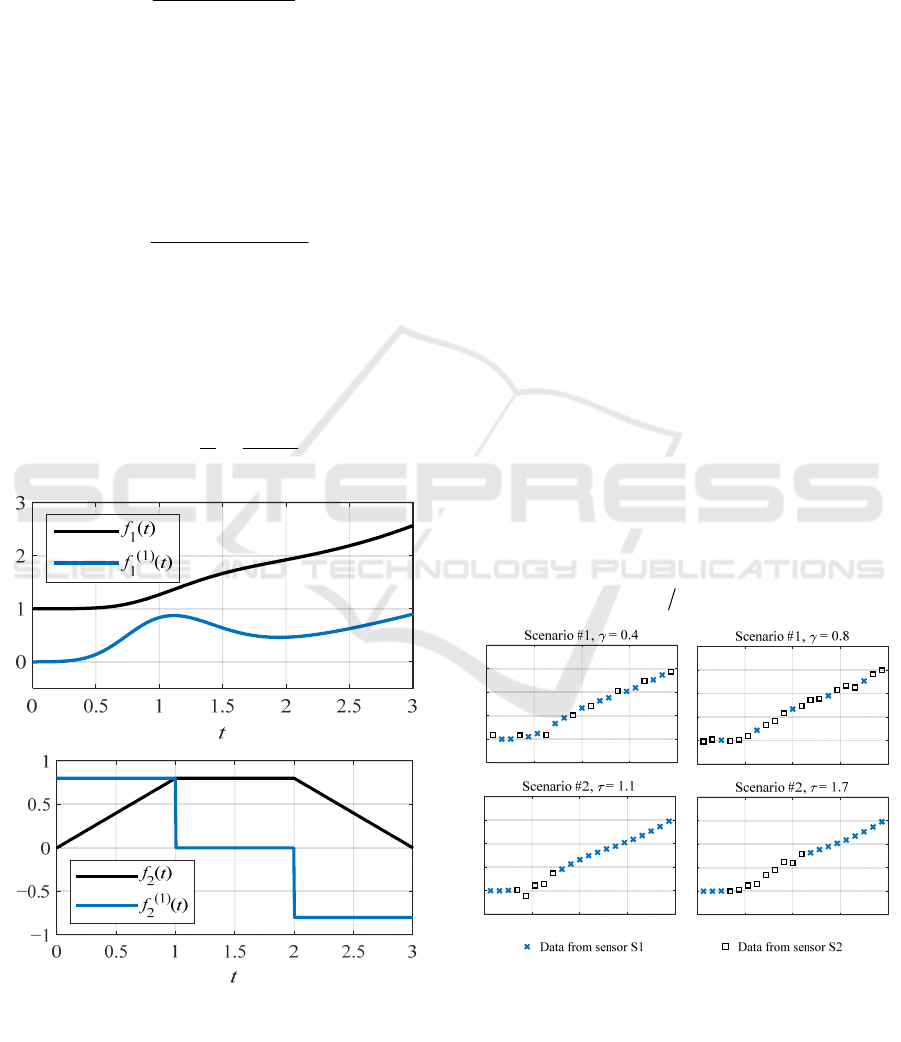
niques are illustrated in Figure 1, which presents the

shapes of some arbitrarily selected, exemplary func-

tions, characterised by different values of



and



Figure 1: Exemplary functions, characterised by different

values of



and



, together with their first derivatives;

the functions presented in the left column have been

obtained by imposing decreasing constraints on



(note

that



also decreases); the functions presented in the right

column have been obtained by imposing decreasing con-

straints on



(note that in this case



increases).

For practical choices of the constraints

max



and

max



, it is unlikely that there exists an admissible ap-

proximating function which satisfies such a constraint

and – at the same time – interpolates the measurement

data. Therefore, the vector of speed estimates needs

to be determined by minimising an indicator of the

fidelity of the results to the measurement data, denot-

ed hereinafter with

; in the case of Tikhonov regu-

larisation, this minimisation problem can be formu-

lated in the following way:







max

arg inf ,





xξξDξR

(10)

and, analogously, in the case of TV regularisation:







max

arg inf ,





xξξDξR (11)

Various choices for the indicator

are viable; the

one studied here is described in the next subsection.

2.3 Fusion of Data from Different

Sensors

In order to quantify the discrepancy between the

results of estimation and the measurement data, one

may evaluate the vector of approximation residuals,

computed in the following way:





ˆˆ





xx Qx x



(12)

The a priori information about the accuracy of the

employed sensors – the information contained in the

estimates

ˆˆ





– can be incorporated in the

procedure for estimation of movement speed by al-

lowing for larger approximation residuals at the time

instants which correspond to the data acquired using

sensors with lower accuracy. This can be done by de-

fining the indicator

in Eq. (10) and Eq. (11) as a

weighted norm of the vector





, with weights se-

lected on the basis of the estimates

ˆˆ





(13)

where



W R

is a diagonal weighting matrix

whose nth element is defined as follows:





ˆˆ

max 1, ,









 (14)

with





R

being a parameter controlling the

amount of weighting. For





, all the data are

taken into account with equal weights; for larger



the data corresponding to smaller



(i.e. the data ac-

quired using more accurate sensors) have more influ-

ence on the estimates of speed. The division by the

maximum element in Eq. (14) ensures that



so that the values of

are in approximately the same

range regardless of the value of



The experiments described in Section 3 are aimed

at assessing the influence of the value of



and of



ˆˆ





  

xx Qx x











ˆˆ



 Qx x W Qx x



Estimation of Movement Speed in Monitoring Systems based on Sensors of Multiple Types

the accuracy of the estimates



on the quality of the

estimates of speed.

2.4 Computational Formulae

Equation (10), defining the vector of speed estimates

obtained using Tikhonov regularisation, can be

reformulated using the Lagrange multiplier technique

in the following way:





arg inf







xQξxDξξ



R (15)

where



is a regularisation parameter (related to the

constraint

max



) whose value may be selected empi-

rically. The analytic solution of Eq. (15) yields:



TTT







xQWQDDQWx



(16)

In the case of TV regularisation, the correspond-

ing minimisation problem – defined by Eq. (11) – can

be reformulated in an analogous way, viz.:





arg inf







xQξxDξξ



R (17)

but the dependence of









cannot be ex-

pressed in closed form, because the term

is not

differentiable. However,





can be determined us-

ing the following iterative algorithm, being a general-

ised version of the algorithm described in (Chartrand,

2011) (which corresponds to

being the identity

matrix):





x 

(18)

  

11 1

ˆˆ ˆ

ii i

xx x

for

0,1, 2,i  

(19)

where





x

is the solution of the following set of

linear algebraic equations:





Hx g

(20)



HQWQ DED

(21)



ˆˆ

ii ii





gQWQx x DEDx



(22)

with









11NN

 

E R

being a diagonal matrix whose

nth element is defined as follows:

(23)

The value of the regularisation parameter may significant-

ly influence the quality of the estimates of speed; however,

the problem of its selection remains outside the scope of this

The term 0𝜀≪1 is introduced to prevent the di-

vision by zero, whereas



is a regularisation param-

eter – related to the constraint

max



– whose value

may be selected empirically

3 NUMERICAL EXPERIMENTS

3.1 Methodology of Experimentation

The synthetic data, used for experimentation, have

been generated according to the formula:

for ,

(24)

where:













3330

1exp



  

for





0,3t 

is a smooth test function, well suited to be differ-

entiated using Tikhonov regularisation;





0.8 for 1

0.8 for 1 2

0.8 3 for 2

ft t















 



is a piecewise-linear test function, better suited to

be differentiated using TV regularisation;







tn t





for

1, , 51nN





0.06t



,nr





are pseudorandom numbers following zero-

mean normal distributions whose variances are



;



is the number of generated sequences of syn-

thetic data, each corresponding to a different set

of pseudorandom numbers

,nr





for

1, ,nN 

and

1, ,rR





The functions

and

, together with their first

derivatives:













3310

16 exp



  

(25)



0.8 for 1

0for1 2

0.8 for 2

ft t



















(26)

are depicted in Figure 2.

paper. The interested reader may refer to, e.g., (Hansen,

2010, Chapter 5), (Bauer and Lukas, 2011) and (Reichel

and Rodriguez, 2013).

 



,1 ,

ˆˆ

in in













,,nr k n nr

ft x



1, ,nN 

1, ,rR





1, 2k 

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

The level of disturbances in the data has been

characterised by the signal-to-noise ratio, defined in

the following way:

(27)

The signal-to-noise ratio corresponding to the esti-

mates of the derivative





has been determined in

the analogous way:

(28)

The performance of the studied methods of numerical

differentiation has been compared in terms of the

relative signal-to-noise ratio, defined as:

SNR

RSNR





(29)

Figure 2: Functions used for the generation of synthetic data

and their first derivatives.

The numerical experiments have been designed in

such a way as to emulate a monitoring system em-

ploying two sensors – called S1 and S2 hereinafter –

which provide position estimates corrupted with er-

rors whose variances are



and



, respectively,

such that:

S2 S1







with





1, 10





(30)

Two scenarios have been considered:

 According to the first one – called scenario #1

hereinafter – S1 and S2 are acquiring data simul-

taneously; approximately



data points, uni-

formly distributed over the time interval under an-

alysis, with





0.4,0.8





, are acquired by means

of S2, whereas the remaining data – by S1.

 According to the second one – called scenario #2

hereinafter – S2 is only acquiring data for





0.5,t





, with





1.1, 1.7





, and S1 – only dur-

ing the remaining fragments of the time interval

under analysis. This scenario corresponds to the

configuration in which a sensor with low accuracy

is used only when the monitored person is outside

the field of view of another, more accurate sensor.

Exemplary data, generated according to both above-

described scenarios, are shown in Figure 3.

The sequences

1, ,

rNr







have been normal-

ised in order to ensure that

0,r

SNR

remains approxi-

mately constant throughout the experimentation, re-

gardless of the ratio

S2 S1



Figure 3: Exemplary data generated according to scenario

#1 (first row) and scenario #2 (second row) for different

values of



and





0, 10

10log

nr n

SNR

xft











1, ,rR 



 



1, 10

10log

nr n

SNR

xft









1, ,rR 

Estimation of Movement Speed in Monitoring Systems based on Sensors of Multiple Types

with

(31)

The value

0.021





results in

SNR 

and is

roughly consistent with the authors’ previous experi-

ences with impulse-radar sensors and depth sensors

(Wagner et al., 2017).

It has been assumed that



is known accurately,

i.e. that its perfect estimate

S1 S1





is available; on

the other hand, the uncertainty of the estimate



has been modelled in the following way:

S2 S2











0.1, 10





(32)

For both test functions

and

and for both

scenarios, the following experiments have been per-

formed:

 experiments aimed at assessing the influence of

the weighting of data on the quality of the speed

estimates for different ratios

S1 S2



, with



and



being known perfectly and the values of

all other parameters having been fixed;

 experiments aimed at assessing the influence of

the weighting of data on the quality of the speed

estimates for different fractions of the data having

been acquired by means of sensor S2, with



and



being known perfectly and the values of

all other parameters having been fixed;

 experiments aimed at assessing the influence of

the ratio

S1 S2



on the quality of the speed esti-

mates for different fractions of the data having

been acquired by means of sensor S2, with



and



being known perfectly and the values of

all other parameters having been fixed;

 experiments aimed at assessing the influence of

the error corrupting the estimate



the quality of the speed estimates for different

ratios

S1 S2



, with the values of all other param-

eters having been fixed.

The sequences of data, generated using the test

function

, have been differentiated using Tikhonov

regularisation, whereas those generated using the test

function

– using TV regularisation; such a choice

is justified by the shapes of those functions. For each

sequence of data, the value of the regularisation pa-

rameter



has been selected in such a way as to max-

imise RSNR; it is only possible in the synthetic setting

of the numerical experiments reported here. This pos-

sibility has been exploited in order to study the influ-

ence of other parameters on the quality of the speed

estimates independently from the influence of the re-

gularisation parameters, although – in practice – the

optimisation of regularisation parameters is an impor-

tant and complex task which, nevertheless, remains

outside the scope of this paper.

3.2 Results of Experiments

Figures 4–7 present the results of the numerical

experiments described in the previous subsection. In

order to facilitate the interpretation of these figures,

the symbols of selected parameters, together with

their descriptions, are collected in Table 1. The ob-

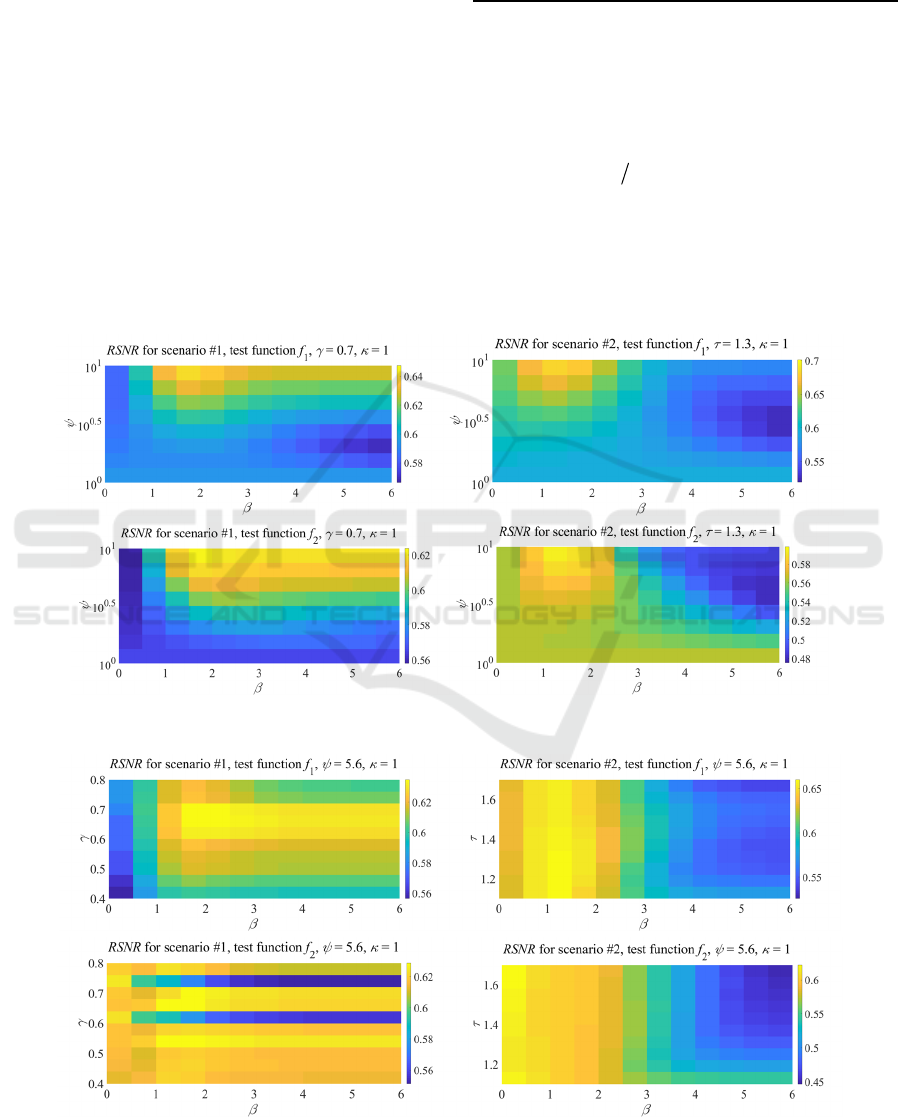
tained results indicate that:

 The studied method for weighting the data on the

basis of the available information about the vari-

ances of errors corrupting those data yields an

improvement in the quality of the speed estimates

when the ratio

S2 S1



is sufficiently large, viz.

larger than ca. 2 (cf. Figure 4); when that ratio is

smaller, the use of





does not yield any sig-

nificant benefit.

 The weighting of data is more advantageous in the

case of scenario #2 – i.e., when less accurate data

are acquired within a continuous fragment of the

time interval under analysis – than in the case of

scenario #1 – i.e., when less accurate data are

mixed uniformly with more accurate data (cf.

Figure 4, note the differences in the colour scales).

 In most cases, the values provide the

best results (cf. Figure 4).

 In the case of scenario #1, setting too large

yields only modest negative effects (cf. Figure 4,

left column). On the other hand, in the case of

scenario #2, setting too large may yield results

worse than setting – i.e., ignoring the

available information about the ratio (cf.

Figure 4, right column).

 In the case of scenario #2, the dependencies of the

quality of the speed estimates on and on

are not significantly affected by the length of the

time interval in which the data are acquired by

sensor S2 (cf. the right columns of Figure 5 and

Figure 6).

 In the case of scenario #1 with test function ,

no systematic dependency of the quality of the

speed estimates on the fraction of data acquired













0.021





1, ,rR 





1, 3









S1 S2







BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

using sensor S2 can be observed in the obtained

results (cf. the lower-left panels of Figure 5 and

Figure 6).

 The quality of the speed estimates is sensitive to

the error corrupting the estimate of the variance

. In the case of scenario #1 with test function

, overestimation of that variance does not in-

crease the errors corrupting the speed estimates as

much as its underestimation. On the other hand, in

all the other cases, for larger values of that vari-

ance the best results are obtained, surprisingly,

when it is slightly underestimated (cf. Figure 7).

The results presented here are representative ex-

amples of the results of a more exhaustive set of ex-

periments, in which other values of the fixed param-

eters have also been taken into account.

Table 1: Symbols and descriptions of parameters presented

in Figures 4–7.

Symbol Description

the amount of weighting of the data according to the

estimates of the sensors’ accuracy; cf. Eq. (14) in

Subsection 2.3

in scenario #1, the fraction of the data acquired using

sensor S2; cf. Subsection 3.1

in scenario #2, the end of the time interval in which data

have been acquired using sensor S2; cf. Subsection 3.1

the ratio ; cf. Subsection 3.1

the relative error corrupting the estimate of ;

cf. Eq. (32) in Subsection 3.1

RSNR

the signal-to-noise ratio in the speed estimates, relative

to the signal-to-noise ratio in the measurement data; cf.

Eq. (29) in Subsection 3.1

Figure 4: Dependence of RSNR on



and



for both scenarios, both test functions and fixed values of





and



Figure 5: Dependence of RSNR on



and





for both scenarios, both test functions and fixed values of



and













S2 S1







Estimation of Movement Speed in Monitoring Systems based on Sensors of Multiple Types

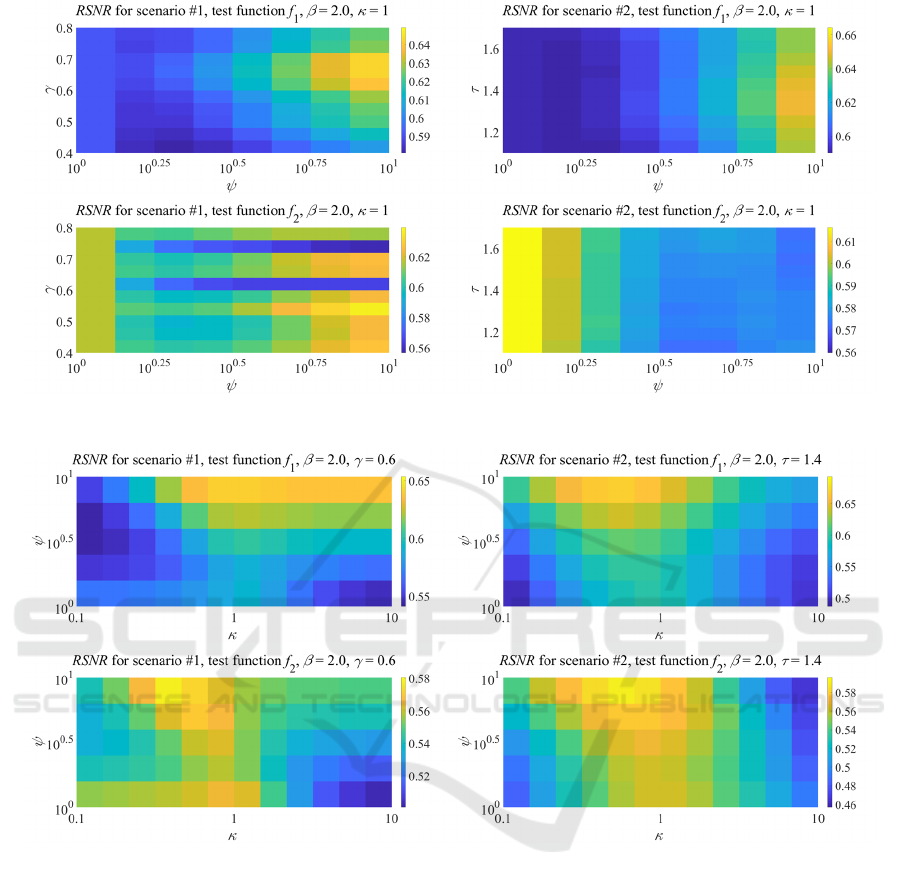
Figure 6: Dependence of RSNR on and or for both scenarios, both test functions and fixed values of and .

Figure 7: Dependence of RSNR on and for both scenarios, both test functions and fixed values of , and .

4 SUMMARY

AND CONCLUSIONS

Healthcare-oriented monitoring systems based on the

fusion of data from sensors of various types, which

allow for estimating the monitored person’s move-

ment speed, may assist healthcare practitioners in

their efforts to ensure good quality of life of elderly

persons and can contribute to the reduction of the

public expenditures related to the healthcare services

addressed to those persons.

The technique for fusion of measurement data ac-

quired by means of different sensors, presented in this

paper, may be used for improving the accuracy of the

estimates of speed obtained using such systems when

some a priori information about those data is avail-

able. Guidelines on the selection of the parameters

characterising that technique, based on numerical ex-

perimentation, are also provided. These results may

turn out to be useful in the development of monitoring

systems based on depth sensors and impulse-radar

sensors.

The prospects for future studies involve – above

all – experiments aimed at testing the described meth-

ods on the basis of real-world data.



















BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

ACKNOWLEDGEMENT

The work reported in this paper has been

accomplished within the project 2017/25/N/ST7/

00411 financially supported by the National Science

Centre, Poland.

REFERENCES

Al-Shaqi, R., M. Mourshed and Y. Rezgui, 2016. Progress in

ambient assisted systems for independent living by the

elderly. SpringerPlus, vol. 5, no. 1, p. 624.

Baldewijns, G., et al., 2016. Automated in-home gait transfer

time analysis using video cameras. Journal of Ambient

Intelligence and Smart Environments, vol. 8, no. 3, pp.

273–286.

Bauer, F. and M. A. Lukas, 2011. Comparing parameter

choice methods for regularization of ill-posed problems.

Mathematics and Computers in Simulation, vol. 81, no.

9, pp. 1795–1841.

Campos, W., A. Martinez, W. Sanchez, H. Estrada, N. A.

Castro-Sánchez and D. Mujica, 2016. A systematic

review of proposals for the social integration of elderly

people using ambient intelligence and social networking

sites. Cognitive Computation, vol. 8, no. 3, pp. 529–542.

Chartrand, R., 2011. Numerical differentiation of noisy,

nonsmooth data. ISRN Applied Mathematics, vol. 2011,

pp. 1–11.

Debes, C., A. Merentitis, S. Sukhanov, M. Niessen, N.

Frangiadakis and A. Bauer, 2016. Monitoring activities

of daily living in smart homes: understanding human

behavior. IEEE Signal Processing Magazine, vol. 33, no.

2, pp. 81–94.

Fleming, J. and C. Brayne, 2008. Inability to get up after

falling, subsequent time on floor, and summoning help:

prospective cohort study in people over 90. BMJ, vol.

337, p. a2227.

Garcia Marin, J., 2015. The use of interactive game

technology to improve the physical health of the elderly:

a serious game approach to reduce the risk of falling in

older people. Ph.D. thesis, Faculty of Engineering and

Information Technology, University of Technology,

Sydney.

Hagler, S., D. Austin, T. L. Hayes, J. Kaye and M. Pavel,

2010. Unobtrusive and ubiquitous in-home monitoring: a

methodology for continuous assessment of gait velocity

in elders. IEEE Transactions on Biomedical

Engineering, vol. 57, no. 4, pp. 813–820.

Hansen, P. C., 2010. Discrete Inverse Problems: Insight and

Algorithms, Society for Industrial and Applied

Mathematics.

Hodgins, D., 2008. The importance of measuring human gait.

Medical Device Technology, vol. 19, no. 5, pp. 42–47.

Khan, S. S. and J. Hoey, 2017. Review of fall detection

techniques: a data availability perspective. Medical

Engineering and Physics, vol. 39, pp. 12–22.

Kikkert, L. H. J., N. Vuillerme, J. P. van Campen, T.

Hortobágyi and C. J. Lamoth, 2016. Walking ability to

predict future cognitive decline in old adults: a scoping

review. Ageing Research Reviews, vol. 27, pp. 1–14.

Lusardi, M., 2012. Is walking speed a vital sign? Topics in

geriatric rehabilitation, vol. 28, no. 2, pp. 67–76.

Majumder, S., et al., 2017. Smart homes for elderly

healthcare—recent advances and research challenges.

Sensors, vol. 17, no. 11, p. 2496.

United Nations, Department of Economic and Social Affairs,

Population Division, 2019. World population prospects

2019: Highlights. ST/ESA/SER.A/423. Available:

https://population.un.org/wpp/publications (as of

October 5, 2020).

Peetoom, K. K. B., M. A. S. Lexis, M. Joore, C. D. Dirksen

and L. P. De Witte, 2015. Literature review on

monitoring technologies and their outcomes in

independently living elderly people. Disability and

Rehabilitation: Assistive Technology, vol. 10, no. 4, pp.

271–294.

Reichel, L. and G. Rodriguez, 2013. Old and new parameter

choice rules for discrete ill-posed problems. Numerical

Algorithms, vol. 63, no. 1, pp. 65–87.

Rudin, L. I., S. Osher and E. Fatemi, 1992. Nonlinear total

variation based noise removal algorithms. Physica D:

Nonlinear Phenomena, vol. 60, no. 1, pp. 259–268.

Sharkey, A. and N. Sharkey, 2012. Granny and the robots:

ethical issues in robot care for the elderly. Ethics and

Information Technology, vol. 14, no. 1, pp. 27–40.

Shumway-Cook, A., S. Brauer and M. Woollacott, 2000.

Predicting the probability for falls in community-

dwelling older adults using the Timed Up & Go test.

Physical Therapy, vol. 80, no. 9, pp. 896–903.

Stickel, J. J., 2010. Data smoothing and numerical

differentiation by a regularization method. Computers &

Chemical Engineering, vol. 34, no. 4, pp. 467–475.

Wada, K., T. Shibata, T. Saito and K. Tanie, 2004. Effects of

robot-assisted activity for elderly people and nurses at a

day service center. Proceedings of the IEEE, vol. 92, no.

11, pp. 1780–1788.

Wagner, J., et al., 2017. Comparison of two techniques for

monitoring of human movements. Measurement, vol.

111, pp. 420–431.

World Health Organization, 2017. Integrated care for older

people: guidelines on community-level interventions to

manage declines in intrinsic capacity. Available:

https://apps.who.int/iris/handle/10665/258981 (as of

June 14, 2019).

Estimation of Movement Speed in Monitoring Systems based on Sensors of Multiple Types