A Human Ear Reconstruction Autoencoder

Hao Sun

1 a

, Nick Pears

1 b

and Hang Dai

2 c

Department of Computer Science, University of York, York, U.K.

Mohamed bin Zayed University of Artiﬁcial Intelligence, Abu Dhabi, U.A.E.

Keywords:

Ear, 3D Ear Model, 3D Morphable Model, 3D Reconstruction, Self-supervised Learning, Autoencoder.

Abstract:

The ear, as an important part of the human head, has received much less attention compared to the human

face in the area of computer vision. Inspired by previous work on monocular 3D face reconstruction using

an autoencoder structure to achieve self-supervised learning, we aim to utilise such a framework to tackle

the 3D ear reconstruction task, where more subtle and difﬁcult curves and features are present on the 2D ear

input images. Our Human Ear Reconstruction Autoencoder (HERA) system predicts 3D ear poses and shape

parameters for 3D ear meshes, without any supervision to these parameters. To make our approach cover the

variance for in-the-wild images, even grayscale images, we propose an in-the-wild ear colour model. The con-

structed end-to-end self-supervised model is then evaluated both with 2D landmark localisation performance

and the appearance of the reconstructed 3D ears.

1 INTRODUCTION

Three-dimensional (3D) face modelling and 3D face

reconstruction from monocular images have drawn

increasing attention over the last few years. Espe-

cially with deep learning methods, 3D face recon-

struction models are empowered to have more com-

plexity and better feature extraction ability. However,

as an important part of the human head, the human

ear has received signiﬁcantly less attention. Our 3D

ear reconstruction approach establishes a dense cor-

respondence between 2D ear input image pixels and

3D vertices of a 3D Morphable Model (3DMM) of the

ear, thus enabling both 2D and 3D ear landmark local-

isation. Furthermore, 3D ear recognition is enabled

(Zhou and Zaferiou, 2017; Emer

c et al., 2017b;

Emer

c et al., 2019) using the 3D shape encoding

provided by the ﬁtted 3DMM.

A detailed 3D ear reconstruction can be a vital

part of constructing a high quality 3D model of the

full human head (Dai et al., 2020a; Dai et al., 2019;

Ploumpis et al., 2020; Dai et al., 2020b). In this con-

text it is desirable to model the ears as separate entities

and then fuse them to the head. The reason is that it

is difﬁcult to control the spatially high frequency as-

pects of the ear (such as the skin folds) with parame-

https://orcid.org/0000-0003-2062-127X

https://orcid.org/0000-0001-9513-5634

https://orcid.org/0000-0002-7609-0124

ters that simultaneously control the whole head shape.

Such 3DMM head parameters are better at capturing

the low frequency shape variances across an aligned

human head 3D dataset.

With the detailed ear shape modelled by the ﬁt-

ted ear 3DMM, a number of applications are pos-

sible, such as the design of ear wear (headphones,

earphones, hearing aids), eye wear (since eye wear

frames usually require ear support) and other head

wear used in virtual and augmented reality applica-

tions.

(1)

(2) (3)

Figure 1: (1) 55 landmarks and their semantics from ITWE-

A dataset (Zhou and Zaferiou, 2017) (2) Rendered densely

corresponded coloured 3D ear mesh projected onto the orig-

inal image (3) Original image marked with predicted land-

marks.

Most modern approaches for 3D face or 3D ear

reconstruction from monocular images fall into three

categories: generation based, regression based and

the combination of both (Tewari et al., 2017). Gen-

eration based methods require a parametric model for

the 3D object and 3D landmarks to optimise a set of

136

Sun, H., Pears, N. and Dai, H.

A Human Ear Reconstruction Autoencoder.

DOI: 10.5220/0010249901360145

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 5: VISAPP, pages

136-145

ISBN: 978-989-758-488-6

parameters for optimal alignment between projected

3D models and 2D landmarks. For 3D ear reconstruc-

tions, two approaches can be found in literature (Dai

et al., 2018; Zhou and Zaferiou, 2017). Regression-

based methods usually utilise neural networks to

regress a parametric model’s parameters directly, as

proposed by (Richardson et al., 2016; Zollh

ofer et al.,

2018) for 3D face reconstruction. Generation-based

methods are often more computationally costly, due

to their non-convex optimisation criteria and the re-

quirement for landmarks. Regression-based methods

require ground truth parameters to be provided, which

is only accessible when using synthetic data (Richard-

son et al., 2016). Otherwise other 3D reconstruction

algorithms are required to obtain ground truth param-

eters beforehand (Zhu et al., 2017). Therefore, Tewari

et al. proposed a self-supervised 3D face reconstruc-

tion method named Model-based Face Autoencoder

(MoFA) that combines both generation and regression

based methods. This aims to mitigate the negative as-

pects of the two categories of method, by using an

autoencoder composed of a regression-based encoder

and a generation-based decoder (Tewari et al., 2017).

However, there are no regression-based or autoen-

coder structured approaches for 3D ear reconstruction

in the literature. Whether this self-supervised autoen-

coder approach can tackle the complexity of the ear

structure remains an open question that we address

here.

The core idea of the self-supervised learning ap-

proach is to synthesise similar colour images from

original colour input images in a differentiable man-

ner. For such an approach, a parametric ear model

is needed. Dai et al. propose a 3D Morphable

Model (3DMM) of the ear, named the York Ear Model

(YEM). Its 3D ear mesh has 7111 vertex coordi-

nates, so 21333 vertex parameters, reduced to 499

shape parameters using PCA. However, to enable

self-supervised learning, the 3D ear meshes require

colour/texture, which is not included in the YEM

model.

In this context, we present a Human Ear Recon-

struction Autoencoder (HERA) system, with the fol-

lowing contributions:

• A 3D ear reconstruction method that is completely

trained unsupervised using in-the-wild monocular

ear colour 2D images.

• An in-the-wild ear colour model that colours the

3D ear mesh to minimise its difference with the

2D ear image in appearance.

• Evaluations that demonstrate that the proposed

model is able to predict a densely corresponded

coloured 3D ear mesh (e.g. Figure 1 (2)) and 2D

landmarks (e.g. Figure 1 (3)).

2 RELATED WORK

In this section, we discuss a range of 3D face recon-

struction methods that utilise an autoencoder structure

to achieve self-supervised learning. The method this

paper proposes obtains 3D ear shapes by employ a

strong prior provided by an ear 3DMM, thus the two

existing 3D parametric ear models will be discussed.

Finally, two methods that evaluate their methods us-

ing normalised landmark error are discussed, since we

evaluate landmark prediction accuracy on the same

dataset, using the same metric.

2.1 Self-supervised Learning for 3D

Dense Face Reconstruction

The self-supervised learning approach to 3D face

reconstruction builds an end-to-end differentiable

pipeline that takes the original colour images as input,

predicts and reconstructs the 3D face mesh, then uses

a differentiable renderer to reconstruct colour images

as output. The goal of such a self-supervised learn-

ing approach is to minimise the difference between

input colour images and output colour images. Sev-

eral novel 3D face reconstruction approaches have re-

cently been proposed. Improvements include using a

face recognition network to contribute to a loss func-

tion, using a Generative Adversarial Network (GAN)

for texture generation (Gecer et al., 2019) and re-

placing the linear 3DMM structure with a non-linear

3DMM (Tran and Liu, 2018). The aim of all of those

approaches is to achieve better performance more in-

tuitively, particularly in terms of minimising the ap-

pearance difference between generated output images

and real input images.

2.2 In-the-wild Ear Image Dataset

There are numerous in-the-wild ear image datasets

built for various purposes, here we focus on Collec-

tion A from the In-the-wild Ear Database (ITWE-A)

since it has 55 manually-marked landmarks. All

the landmarks have semantic meaning, as shown in

Figure 1 (1). This dataset contains 500 images in its

training set and 105 images in its test set, where each

image is captured in-the-wild and contains a clear ear.

The dataset has a large variation in ear colours, as is

the nature of in-the-wild images, and it even contains

several grayscale images. Traditional 3DMM colour

models, such as that of the Basel Face Model 09

(BFM09) (Blanz and Vetter, 1999), often fail to gen-

erate a highly-similar appearance to the input. How-

ever, the in-the-wild ear colour model proposed here,

A Human Ear Reconstruction Autoencoder

137

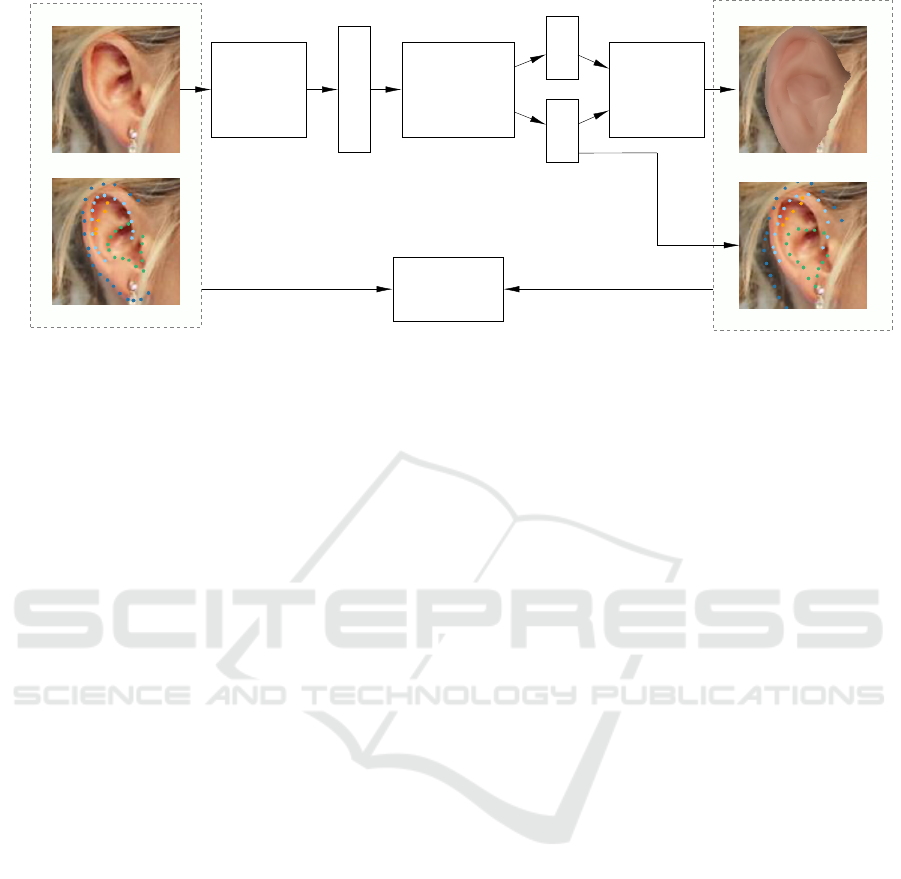
Input Ear Image

Encoder

(ResNet-18)

Intermediate

Code Vector v

Ear 3DMM

Ear Colour Model

Shape S

Colour C

Differentiable

Renderer

Synthesised Image

Predicted Landmarks

Ground Truth Landmarks

Pixel Loss

Landmark Loss

Figure 2: Overview of the autoencoder architecture.

can cover such colour variance, since it models

directly from the in-the-wild images themselves.

2.3 Parametric Ear Models

Zhou and Zaferiou build their parametric ear model

using an Active Appearance Model (AAM), which is

a linear model that aims to model the 2D ear’s shape

and colour simultaneously(Cootes et al., 1998). A

3D Morphable Model (3DMM) is a closely-related

model that models objects’ shapes and colours in 3D

instead of 2D. Blanz and Vetter ﬁrst proposed a 3D

Morphable Model (3DMM) for human faces (Blanz

and Vetter, 1999), which builds a linear system that

allows different 3D face meshes to be described by

199 shape parameters. Similarly, Dai et al. (Dai

et al., 2018) proposed a 3D morphable model for the

human ear named the York Ear Model (YEM), also

based on a linear system, but with 499 parameters.

Here, we utilise this ear 3DMM for its strong 3D ear

shape prior. Meanwhile, the reduced dimension of

the parameters allows the neural network to perform

a much easier regression task using 499 shape param-

eters rather than 21333 raw vertex parameters.

2.4 2D Ear Detection

Ear detection or localisation in 2D images aims to

ﬁnd the region of interest bounding the ear, from im-

ages of the human head that contain ears; for exam-

ple, proﬁle-view portraits. It is a vital preprocessing

step in the 3D ear reconstruction pipeline. Object de-

tection has been studied for decades and there exists

a number of algorithms that speciﬁcally perform the

2D ear detection task. Zhou and Zaferiou (Zhou and

Zaferiou, 2017) use the histogram of oriented gradi-

ents with a support vector machine (HoG+SVM) to

predict a rectangular region of interest. Emer

c et

al. (Emer

c et al., 2017a) and Bizjak et al. (Bizjak

et al., 2019) propose deep learning methods to tackle

the 2D ear detection task by predicting a pixel-level

segmentation of the 2D ear image directly.

2.5 2D Ear Landmark Localisation

2D ear landmark localisation is a task for ﬁnding spe-

ciﬁc key points on 2D ear images. It is an intuitive

method of quantitative evaluation of this work where

the shape and alignment of the reconstructed 3D ear

mesh can be evaluated precisely. In 2D face landmark

localisation, numerous approaches obtain 2D land-

marks by reconstructing 3D models ﬁrst (Zhu et al.,

2017; Liu et al., 2016; McDonagh and Tzimiropou-

los, 2016). Being able to achieve competitive results

against a specialised 2D landmark predictor is neces-

sary for the success of a 3D dense ear reconstruction

algorithm. Zhou and Zaferiou’s approach comes with

the ITWE-A dataset and is considered as a baseline.

They use Scale Invariant Feature Transform (SIFT)

features and an AAM model to predict 2D landmarks

(Zhou and Zaferiou, 2017). Hansley and Segundo

(Hansley et al., 2018) propose a CNN-based approach

to regress 2D landmarks directly and they also evalu-

ate on the ITWE-A dataset. Their approach proposes

two CNNs that both predict the same set of landmarks

but with different strengths. The ﬁrst CNN has bet-

ter generalisation ability for different ear poses. The

resulting landmarks of the ﬁrst CNN are used to nor-

malise the ear image. The second CNN predicts im-

proved normalised ear images based on the results of

the ﬁrst CNN.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

138

3 THE HERA SYSTEM

Our proposed Human Ear Reconstruction Autoen-

coder (HERA) system employs an autoencoder struc-

ture that takes ear images as input and generates syn-

thetic images. Therefore, it is trained by minimising

the difference between input images and the ﬁnal syn-

thesised images. An illustration of our end-to-end ar-

chitecture is shown in Figure 2. The encoder is a CNN

predicting intermediate code vectors that are then fed

to the decoder, where coloured 3D ear meshes are re-

constructed and rendered into 2D images.

The decoder is comprised of: (1) the YEM ear

shape model and our in-the-wild ear colour model that

reconstruct ear shapes and ear colours respectively;

(2) PyTorch3D (Ravi et al., 2020) that renders im-

ages with ear shapes and colours in a differentiable

way. The comparison of the input and synthesised

images is implemented by a combination of loss func-

tions and regularisers. The essential loss function is

a photometric loss, with an additional landmark loss

that can be included for both faster convergence time

and better accuracy. The whole autoencoder structure

is designed to be differentiable and so can be trained

in an end-to-end manner. Each part of the architec-

ture (i.e. encoder CNN, ear 3DMM, scaled orthogo-

nal projection and loss functions) is differentiable by

default, thereby using a differentiable renderer to ren-

der 3D meshes to 2D images makes the whole archi-

tecture differentiable. The core part of the decoder is

described in Section 3.1. The whole end-to-end train-

able architecture and the necessary training methods

are then described in Section 3.4.

3.1 Ear 3D Morphable Model

Preliminaries

This section describes the 3DMM part of the decoder

which comprises an ear shape model derived from the

YEM, an ear colour model, and the projection model.

With this 3DMM, the shape parameters α

can be

reconstructed to an 3D ear vertex coordinate vector

S ∈ R

N×3

where N is the number of vertices in a sin-

gle 3D ear mesh. The colour parameters α

are then

reconstructed to a vertex colour vector C

C ∈ R

N×3

colour each vertex. The pose parameters p

p are used

in the projection model that aligns 3D ear meshes with

2D ears’ pixels.

3.1.1 Ear Shape Model

We employ YEM model (Dai et al., 2018), which

supplies the geometric information necessary for re-

construction. It is constructed using PCA from 500

3D ear meshes and thus provides a strong statistical

prior. The 3D ear vertex coordinate vector (i.e. 3D

ear shape) S

S is reconstructed from shape parameter

vector α

by:

S =

S (α

) =

S +U

, (1)

where

S ∈ R

is the mean ear shape, U

∈ R

3N×499

the ear shape variation components and the resulting

matrix is rearranged into a N × 3 matrix, where each

row represents a vertex coordinate in 3D space.

The projection model employed is the scaled or-

thogonal projection (SOP) projecting 3D shape to 2D.

Given the 3D ear shape S

S from Equation 1, the pro-

jection function,

V , is deﬁned as:

V =

V (S

S, p

p) = f P

R(r

r) S

S + T

T , (2)

where P



1 0 0

0 1 0



is the orthogonal projection

matrix, V

V ∈ R

N×2

are the projected 2D ear vertices

and

R(r

r) is the function that returns the rotation ma-

trix. Since scaled-orthogonal projection is used, V

provides sufﬁcient geometric information for the dif-

ferentiable renderer and no additional camera param-

eters are needed.

In addition, 2D landmarks can be extracted from

the projected vertices V

V by manually selecting 55 se-

mantically corresponding vertices. Thus we can de-

ﬁne a vector of 2D landmarks of a projected ear shape

V as:

= V

V (L

L), (3)

where X

∈ R

55×2

are the landmark’s x and y coordi-

nates indexed by L

L in the projected ear vertices V

V .

3.1.2 In-the-wild Ear Colour Model

The YEM model contains an ear shape model only.

However, the decoder in our architecture requires the

3D ear meshes to be coloured to generate plausible

synthetic ear images. To solve this problem, we build

an in-the-wild ear colour model using PCA whiten-

ing.

Firstly, for each ear image from of the 500 images

from the training set of the ITWE-A dataset, a set of

whitened ear shape model parameters α

and ear pose

p is ﬁtted using a non-linear optimiser to minimise 2D

landmark distances. Using the reconstruction Equa-

tions 9 ∼ 3, the optimisation criteria E

can be formed

as follow:

X (α

, p

p) =



S (

α(α

)), p



, (4)

(α

, p

p, X

) =





X (α

, p



L) − X



, (5)

A Human Ear Reconstruction Autoencoder

139

0 -2SD

0 +2SD

1 -3SD

1 +3SD

2 -3SD

2 +3SD

3 -3SD

3 +3SD

4 -3SD

4 +3SD

Mean Colour

Figure 3: In-the-wild Ear Colour Model. The mean colour

and ﬁrst 5 parameters ± standard deviations (SD) are

shown. The mean 3D ear mesh is used.

where

X is the whole reconstruction and projection

function, N

= 55 is a constant representing the num-

ber of landmarks and X

∈ R

55×2

is the ground truth

2D landmarks provided by the ITWE-A dataset.

After the shapes are ﬁtted, the colour for each

vertex is obtained by selecting the corresponding 2D

pixel colour. This process ends up in 500 vertex

colour vectors, which can then be used to build the in-

the-wild ear colour model using PCA whitening. The

vertex colour vectors are parameterised by 40 param-

eters and cover by 86.6% of the colour variation. The

reconstruction coverage rate is not proportional to the

quality of the model building, since setting a moder-

ate coverage rate can implicitly ignore some occlu-

sions (e.g. hair and ear piercings). This colour model

is shown in Figure 3.

The reconstruction of the vertex colour vector C

is:

C =

C (α

) =

C +U

, (6)

where α

∈ R

40×1

is the colour parameter vector.

is average vertex colour vector, U

is vertex colour

variance component matrix and both are calculated by

the PCA whitening algorithm.

3.2 Intermediate Code Vector

The intermediate code vector

v =

{

p, α

, α

}

(7)

connects the encoder and the decoder and has seman-

tic meaning. Where

p =

{

r, T

T , f

}

(8)

deﬁnes the pose of the 3D ear mesh. r

r ∈ R

is the

azimuth, elevation and row which map to the rotation

matrix through function

R(r

r) : R

→ R

3×3

. T

T ∈ R

2×1

deﬁnes the translation in X-axis and Y-axis. The

translation in z-axis is not necessary since scaled or-

thogonal projection is used. f is a fraction num-

ber that deﬁnes the 3D mesh’s scale. α

∈ R

40×1

are the PCA whitened shape parameters and will be

recovered to the shape parameters β

∈ R

499×1

and

then proceeded by the YEM 3DMM. α

∈ R

40×1

are

the colour parameters for the in-the-wild ear colour

model built by this paper.

3.3 PCA Whitening

To ease the optimisation process in training, we use

PCA whitening to transfer the YEM ear model param-

eters into the format that is more favourable for deep

learning frameworks. Firstly, the variances of the pa-

rameters can differ in a very large scale from 8 × 10

for the most signiﬁcant parameter to 5 × 10

−7

for the

least important parameter. It is difﬁcult to train a neu-

ral network to effectively regress such large variance

data. Secondly, the large number of the parameters

slow the neural networks’ training speed and worse

the optimisation process. This could be mitigated by

trimming a portion of the less important parameters

out. But this has potential to lose the shape and color

information from the trimmed part. To overcome this,

we perform PCA whitening (Kessy et al., 2018) over

the full set of parameters. PCA whitening aims to

generate zero-mean parameters with reduced dimen-

sions in unit-variance. In our experiment, YEM’s

original parameters β

of 499 dimensions are trans-

formed to α

of 40 dimensions while covering 98.1%

of the variance associated with the original parame-

ters. Each original parameter vector β

can be recov-

ered from α

by:

α(α

) = U

, (9)

where U

∈ R

499×40

is a constant matrix of variation

components calculated by the PCA whitening pro-

cedure. The original parameters’ mean is not added

since they are zero-mean already.

3.4 Ear Autoencoder

We now combine the intermediate code vector and

decoder components, described in previous sections,

with the encoder, the differentiable renderer and the

loss functions, to build the end-to-end autoencoder

As illustrated in Figure 2, we build an self-

supervised architecture that consists of an encoder,

an intermediate code vector, the decoder components,

the differentiable renderer and the loss for back-

propagation.

The encoder is an 18-layer residual network

(ResNet-18) which is a CNN that performs well on

regression from image data (He et al., 2016). We use

PyTorch3D (Ravi et al., 2020) as a differentiable im-

age renderer developed using PyTorch (Paszke et al.,

2019). It is a differentiable function that maps a set

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

140

of vertex coordinate vector and vertex colour vector

to a 2D image. The encoder Q and decoder W can be

formed as follows:

pred

= Q (I

, θ

θ), (10)

pred

= W



pred



, (11)

pred

= Render



pred



, (12)

pred

= S

pred

L), (13)

where I

is the input image and θ

θ are the weights of

the encoder network Q. In the decoder W , the pre-

dicted 3D mesh (i.e. shape with pose S

pred

and colour

pred

) are reconstructed from the predicted interme-

diate code vector v

pred

. The reconstructed 3D mesh

is then fed to the differential image render for cap-

turing the rendered image I

pred

. The L

L indexes the

x and y coordinates of the 55 ear landmarks in the

ear shape S

S. The predicted landmarks X

pred

∈ R

55×2

can be derived from the predicted ear shape by index-

ing the x and y coordinates of the 55 ear landmarks

in the predicted 3D ear shape from L

L. The encoder

ResNet-18 is initialised using the weights pre-trained

on ImageNet (Deng et al., 2009). The trained encoder

network can be used for the shape and color parame-

ters regression.

3.4.1 Loss Function

Our loss function follows the common design of

loss functions in differentiable renderer based self-

supervised 3D reconstruction approaches. The pro-

posed loss function is a combination of four weighted

losses as:

loss

= λ

pix

) + λ

, X

)

+ λ

reg1

) + λ

reg2

), (14)

where λ

are the weights for the losses E

Pixel Loss. The core idea of the self-supervised ar-

chitecture is that the model can generate synthetic im-

ages from input images and are compared with input

images. Thus to form such comparison, the Mean

Square Error (MSE) is used on all pixels:

pix

) = L

MSE

(Render (W (Q (I

, θ

θ))), I

(15)

Where L

MSE

is a function that calculates the mean

square error. A pixel mask is used to compare the ren-

dered ear region only, since the rendered ear images

have no background.

Landmark Loss. The optional landmark loss is

used to speed up the training process and help the

network learn 3D ears with better accuracy. Zhou and

Zaferiou (Zhou and Zaferiou, 2017) propose the mean

normalised landmark distance error as their shape

model evaluation metric. Here, we employ it as a part

of the loss function. It can be formed as:

, X

) =

(W(Q(I

,θ

θ)))(L

L)−X

(

)

(16)

where X

is the ground truth landmarks and D

)

is a function gets the diagonal pixel length of the

ground truth landmarks’ bounding box. Since this

loss is optional, setting λ

= 0 can enable the whole

model to be trained on 2D image data I

only, mak-

ing the use of very large-scale unlabelled training data

possible.

Regularisers. Two regularisers are used to con-

strain the learning process and are weighted sepa-

rately. The ﬁrst regulariser is the statistical plausi-

bility regulariser. The regulariser is formed by:

reg1

) =

∑

j=1

s j

∑

j=1

c j

, (17)

where α

and α

are ear shape and colour parameters

predicted by the encoder network. Therefore this pe-

nalises the Mahalanobis distance from the mean shape

and colour.

During our experiments, we found that an addi-

tional restriction on the scale parameter f has to be

applied for the model to be successfully trained with-

out landmarks. The restriction is formed by:

reg2

) =











(0.5 − f )

if f < 0.5

( f − 1.5)

if f > 1.5

0 otherwise

, (18)

We employed two sets of weights, λ, depending on

whether or not landmark loss is used when training.

• Training with landmarks: λ

pix

= 10, λ

= 1,

reg1

= 5 × 10

−

2 and λ

reg2

= 0

• Training without landmarks: λ

pix

= 2, λ

= 0,

reg1

= 5 × 10

−

2 and λ

reg2

= 100

3.4.2 Dataset Augmentation

Since the ITWE-A dataset used to train our model

contains only 500 landmarked ear images, having lim-

ited variance on ear rotations, we perform data aug-

mentation on the original dataset. An ear direction of

a 2D ear image is deﬁned by a 2D vector from one

of the ear lobe landmark points to one of the ear he-

lix landmark points. For each 2D ear image, 12 ran-

dom rotations around its central point are applied such

that the angles between their ear directions and the Y-

axis of the original image are uniformly distributed

A Human Ear Reconstruction Autoencoder

141

between −60

◦

and 60

◦

. The augmented ear image

dataset contains 6, 000 images in total. With this aug-

mentation, we ﬁnd that test set landmark error drops

signiﬁcantly.

4 RESULTS

In this section, both quantitative evaluation results and

qualitative evaluation results are discussed. Quanti-

tative evaluation focuses on comparing landmark ﬁt-

ting accuracy with different approaches. While the

qualitative evaluation focuses on evaluating the vi-

sual results of this 3D ear reconstruction algorithm.

Furthermore, an ablation study is conducted to anal-

yse the improvement that various optimisations of this

work has proposed, including the PCA whitening on

the YEM model parameters, the statistical plausibil-

ity regulariser and the dataset augmentation. The ab-

breviation Human Ear Reconstruction Autoencoder

(HERA) is used to represent the ﬁnal version of this

work.

4.1 Quantitative Evaluations

Table 1: Normalised landmark distance error statistics on

ITWE-A.

Method mean ± std median ≤ 0.1 ≤ 0.06

Zhou & Zaferiou 0.0522 ± 0.024 0.0453 95% 78%

HERA 0

8 ±

± 0

9 0

1 1

0% 9

HERA-W/O-AUG-LM 0.0591 ± 0.014 0.0567 99% 64.7%

The main quantitative evaluation method applied is

the mean normalised landmark distance error pro-

posed by (Zhou and Zaferiou, 2017) formed in Equa-

tion 16 which also forms the landmark loss that trains

our system. Projecting the 3D ear meshes’ key points

to 2D and comparing them with the ground truth can

assess the accuracy of the 3D reconstruction. There

are two approaches that predict the same set of land-

marks using the same dataset in the literature , there-

fore comparisons can be formed. Zhou & Zaferiou’s

work (Zhou and Zaferiou, 2017) is considered as

a baseline solution and Hansley & Segundo’s work

(Hansley et al., 2018) is a speciﬁcally designed 2D

landmark localisation algorithm that has the lowest

landmark error in the literature. To interpret the land-

mark error, it is stated that for an acceptable predic-

tion of landmarks, the mean normalised landmark dis-

tance error has to be below 0.1 (Zhou and Zaferiou,

2017). This is a dimensionless metric that is the ra-

tio of the mean Euclidean pixel error to the diagonal

length of the ear bounding box.

As this paper stated in Section 3.4.1, HERA can

be trained without landmarks or data augmentation

in a self-supervised manner. The HERA version that

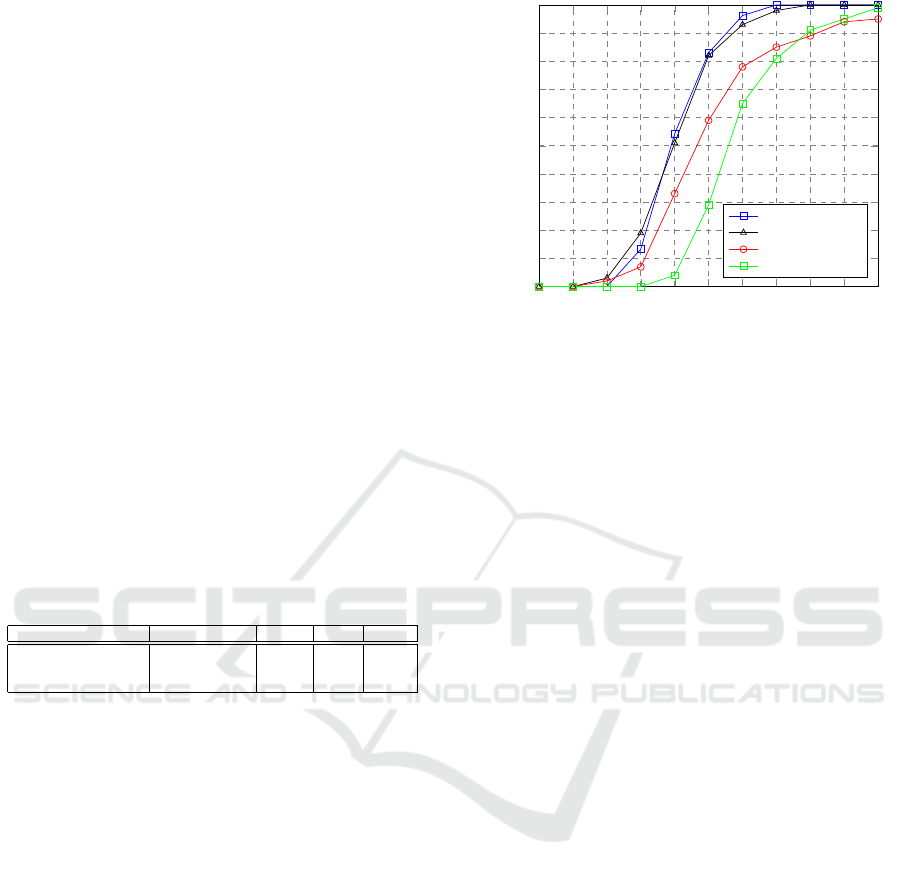
0 0.01 0.02 0.03 0.04

0.05 0.06

0.07 0.08 0.09 0.1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Landmark error

Percentage of images

HERA

Hansley & Segundo

Zhou & Zaferiou

HERA-W/O-AUG-LM

Figure 4: Cumulative error distribution curve compari-

son among different landmark detection algorithms and our

work.

uses no landmark loss during training and trains on

the original 500 ear images is named HERA-W/O-

AUG-LM.

Our HERA system is now compared with Zhou

& Zaferiou’s and Hansley & Segundo’s work regard-

ing the normalised landmark error’s mean, standard

deviation, median and cumulative error distribution

(CED) curve evaluated on the test set of ITWE-A

which contains 105 ear images. The numerical results

are shown in Table 1 and the CED curve is shown in 4.

Additionally, the percentage of predictions that have

error less than 0.1 and 0.6 are given in Table 1.

From Table 1 and Figure 4, it can be concluded

that HERA outperforms Zhou & Zaferiou’s work by

a large margin in terms of 2D landmark localisation

task. When compared with Hansley & Segundo’s 2D

landmark localisation work, similar results are shown.

This is considered acceptable when comparing a 3D

reconstruction algorithm with a 2D landmark local-

isation algorithm. Hansley & Segundo’s landmark

localiser is comprised of two speciﬁcally designed

CNNs for landmark regressions while HERA uses

only one CNN to regress a richer set of information

(i.e. pose, 3D model’s parameters and colour param-

eters). Regarding the threshold of 0.1 proposed by

(Zhou and Zaferiou, 2017), both HERA and Hansley

& Segundo’s work are 100% below 0.1, and HERA

trained without landmarks achieves 99% below 0.1.

The CED curves show that, although HERA-W/O-

AUG-LM performs worse than Zhou & Zaferiou’s

work in the error region below around 0.077, our per-

formance is better at the 0.1 error point. In other

words, HERA-W/O-AUG-LM can predict landmarks

with less than 0.1 error more consistently than the

baseline.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

142

Figure 5: Test set prediction results with different ear

colours. Top row: original ear images marked with pre-

dicted 2D landmarks. Bottom row: predicted 3D ear meshes

projected onto original ear images.

Table 2: Normalised landmark distance error statistics on

ITWE-A for ablation study.

Method mean ± std median ≤ 0.1 ≤ 0.06

HERA 0.0398 ± 0.009 0.0391 100% 96.2%

HERA-W/O-WTN 0.0401 ± 0.009 0.0384 100% 96.2%

HERA-W/O-PIX 0.0392 ± 0.009 0.0387 100% 96.2%

HERA-W/O-AUG 0.0446 ± 0.011 0.0437 100% 92.4%

HERA-W/O-AUG-LM 0.0591 ± 0.014 0.0567 99% 64.7%

4.2 Qualitative Evaluations

Qualitative evaluations of this work focus on visually

showing the 3D reconstruction results on ITWE-A’s

test set. In Figure 5, three images with large colour

variation are predicted, the top row shows the 2D

landmark predictions look reasonable. The compar-

ison between the top row and the bottom row shows

that the quality of the reconstructed 3D meshes are

reasonable in geometric aspect, while the in-the-wild

colour model can reconstruct a large variation of in-

the-wild ear colours even from grayscale images.

In Figure 6, two images with different head poses

are selected for 3D ear reconstruction. The top row

shows the results from a near-ideal head pose (i.e.

near-proﬁle face) and the bottom row shows the re-

sults from a large head pose deviation from the ideal

(i.e. front facing, tilted head). The ﬁgure shows that

HERA works well with different head poses. For the

front facing images, the model predicts the correct

horizontal rotation rather than narrowing the 3D ear

mesh’s width to match the 2D image.

4.3 Ablation Study

We now study how each component can affect

HERA’s performance and we evaluate on several sys-

tem variations including HERA-W/O-WTN (with-

out PCA whitening on 3D ear shape parameters β

HERA-W/O-PIX (without pixel loss), HERA-W/O-

Figure 6: Test set prediction results with different head

poses. Each row represents a distinct subject. 1

column:

Original uncropped images. 2

column: Predicted 3D ear

meshes. 3

column: Predicted 2D landmarks. Ear pose is

successfully predicted when difﬁcult head pose involves.

(2)(1) (3)

Figure 7: Appearance comparison between the recon-

structed 3D ear meshes of (1) Ground truth input image, (2)

HERA and (3) HERA-W/O-PIX (without using the pixel

error). Although the landmark errors are similar, not using

pixel error results in a rendered image with more appear-

ance difference.

AUG (without data augmentation) and HERA-W/O-

AUG-LM (without landmark loss).

Table 2 shows the statistics for all the variations of

HERA. When training without PCA whitening on 3D

ear shape parameters and without pixel loss, perfor-

mance on 2D landmark localisation is similar to the

ﬁnal proposed method. However, using PCA whiten-

ing balances the parameters for the neural network to

predict and therefore acts as a better underlying de-

(1) (2) (3)

Figure 8: 2D landmark localisation comparison between

the prediction results of (1) HERA, (2) HERA-W/O-AUG

(without data augmentation) and (3) HERA-W/O-AUG-LM

(without data augmentation or landmark error). Data aug-

mentation enables better ear rotation prediction and land-

mark loss is vital to accurate alignment especially for the

ear contour part.

A Human Ear Reconstruction Autoencoder

143

sign choice. The major contribution of applying PCA

whitening in this work is that it speeds up the training

process by more than 30% per epoch on a GPU. In

the meantime, a balanced design of intermediate code

vector with similar variance for each parameter can

beneﬁt the performance of the neural network. The

proposed HERA system then takes ∼ 70 seconds to

train one epoch on an NVIDIA RTX 2080 and takes

∼ 350 epochs to train the whole network. After train-

ing, the network predicts a single image in 6 ms.

For training without pixel loss, as shown in Figure

7, the overall appearance of the rendered ear image

differs from the input ear image especially for the he-

lix part. Training without pixel loss makes the model

focus on lowering the landmark alignment error re-

gardless of the overall appearance of the ear. There-

fore it is necessary to utilise the pixel loss. This set of

ﬁgures also illustrates the pose ambiguity of this sys-

tem caused by orthogonal projection. For a distinct

set of ear 3DMM parameters, there exists two differ-

ent rotations that result in the same projected 2D land-

marks. In one case, such as Figure 7 (1), the external

auditory canal part of the ear is visible and in the other

case such as the other rendered images in this paper,

the external auditory canal is covered by itself. This

ambiguity may affect further applications that relate

the reconstructed 3D ear and other 3D objects, such

as the 3D head, but a simple 3D registration task can

be carried out to solve the rotational ambiguity, if re-

quired. Restrictions on the rotations during the train-

ing phase can be applied to allow the results to fall

into desired range.

When training without data augmentation, the 2D

landmark localisation performance drops by a small

amount mainly due to its lack of variety in ear rota-

tion, shown in Figure 8. When training without land-

mark loss, the predicted landmarks is not accurate

enough, shown in Figure 8. As a result, the recon-

structed 3D ears are not accurately aligned with the

2D ears especially for the ear contours.

5 CONCLUSION

As a large proportion of human-related 3D recon-

struction approaches focus on the human face, 3D ear

reconstruction, as an important human-related task,

has much less related work. In this paper, we propose

a self-supervised deep 3D ear reconstruction autoen-

coder from single image. Our model reconstructs the

3D ear mesh with a plausible appearance and accurate

dense alignment, as witnessed by the accurate align-

ment compared to ground truth landmarks. The com-

prehensive evaluation shows that our method achieves

state-of-the-art performance in 3D ear reconstruction

and 3D ear alignment.

REFERENCES

Bizjak, M., Peer, P., and Emer

Z. (2019). Mask r-cnn for

ear detection. In 2019 42nd International Convention

on Information and Communication Technology, Elec-

tronics and Microelectronics (MIPRO), pages 1624–

1628. IEEE.

Blanz, V. and Vetter, T. (1999). A morphable model for

the synthesis of 3d faces. In Proceedings of the 26th

annual conference on Computer graphics and inter-

active techniques, pages 187–194.

Cootes, T. F., Edwards, G. J., and Taylor, C. J. (1998). Ac-

tive appearance models. In European conference on

computer vision, pages 484–498. Springer.

Dai, H., Pears, N., Huber, P., and Smith, W. A. (2020a).

3d morphable models: The face, ear and head. In 3D

Imaging, Analysis and Applications, pages 463–512.

Springer.

Dai, H., Pears, N., and Smith, W. (2018). A data-augmented

3d morphable model of the ear. In 2018 13th IEEE In-

ternational Conference on Automatic Face & Gesture

Recognition (FG 2018), pages 404–408. IEEE.

Dai, H., Pears, N., and Smith, W. (2019). Augmenting a 3d

morphable model of the human head with high resolu-

tion ears. Pattern Recognition Letters, 128:378–384.

Dai, H., Pears, N., Smith, W., and Duncan, C. (2020b). Sta-

tistical modeling of craniofacial shape and texture. In-

ternational Journal of Computer Vision, 128(2):547–

571.

Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-

Fei, L. (2009). Imagenet: A large-scale hierarchical

image database. In 2009 IEEE conference on com-

puter vision and pattern recognition, pages 248–255.

Ieee.

Emer

Z., Gabriel, L. L.,

Struc, V., and Peer, P. (2017a).

Pixel-wise ear detection with convolutional encoder-

decoder networks. arXiv preprint arXiv:1702.00307.

Emer

Z.,

Struc, V., and Peer, P. (2017b). Ear recognition:

More than a survey. Neurocomputing, 255:26–39.

Emer

Z., SV, A. K., Harish, B., Gutfeter, W., Khiarak,

J., Pacut, A., Hansley, E., Segundo, M. P., Sarkar, S.,

Park, H., et al. (2019). The unconstrained ear recog-

nition challenge 2019. In 2019 International Confer-

ence on Biometrics (ICB), pages 1–15. IEEE.

Gecer, B., Ploumpis, S., Kotsia, I., and Zafeiriou, S. (2019).

Ganﬁt: Generative adversarial network ﬁtting for high

ﬁdelity 3d face reconstruction. In Proceedings of the

IEEE Conference on Computer Vision and Pattern

Recognition, pages 1155–1164.

Hansley, E. E., Segundo, M. P., and Sarkar, S. (2018). Em-

ploying fusion of learned and handcrafted features

for unconstrained ear recognition. IET Biometrics,

7(3):215–223.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

144

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Kessy, A., Lewin, A., and Strimmer, K. (2018). Optimal

whitening and decorrelation. The American Statisti-

cian, 72(4):309–314.

Liu, F., Zeng, D., Zhao, Q., and Liu, X. (2016). Joint

face alignment and 3d face reconstruction. In Euro-

pean Conference on Computer Vision, pages 545–560.

Springer.

McDonagh, J. and Tzimiropoulos, G. (2016). Joint face de-

tection and alignment with a deformable hough trans-

form model. In European Conference on Computer

Vision, pages 569–580. Springer.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., et al. (2019). Pytorch: An imperative

style, high-performance deep learning library. In

Advances in neural information processing systems,

pages 8026–8037.

Ploumpis, S., Ververas, E., O’Sullivan, E., Moschoglou,

S., Wang, H., Pears, N., Smith, W., Gecer, B., and

Zafeiriou, S. P. (2020). Towards a complete 3d mor-

phable model of the human head. IEEE Transactions

on Pattern Analysis and Machine Intelligence.

Ravi, N., Reizenstein, J., Novotny, D., Gordon, T., Lo, W.-

Y., Johnson, J., and Gkioxari, G. (2020). Accelerating

3d deep learning with pytorch3d. arXiv:2007.08501.

Richardson, E., Sela, M., and Kimmel, R. (2016). 3d

face reconstruction by learning from synthetic data.

In 2016 fourth international conference on 3D vision

(3DV), pages 460–469. IEEE.

Tewari, A., Zollhofer, M., Kim, H., Garrido, P., Bernard,

F., Perez, P., and Theobalt, C. (2017). Mofa: Model-

based deep convolutional face autoencoder for unsu-

pervised monocular reconstruction. In Proceedings of

the IEEE International Conference on Computer Vi-

sion Workshops, pages 1274–1283.

Tran, L. and Liu, X. (2018). Nonlinear 3d face morphable

model. In Proceedings of the IEEE conference on

computer vision and pattern recognition, pages 7346–

7355.

Zhou, Y. and Zaferiou, S. (2017). Deformable models of

ears in-the-wild for alignment and recognition. In

2017 12th IEEE International Conference on Auto-

matic Face & Gesture Recognition (FG 2017), pages

626–633. IEEE.

Zhu, X., Liu, X., Lei, Z., and Li, S. Z. (2017). Face align-

ment in full pose range: A 3d total solution. IEEE

transactions on pattern analysis and machine intelli-

gence, 41(1):78–92.

Zollh

ofer, M., Thies, J., Garrido, P., Bradley, D., Beeler, T.,

erez, P., Stamminger, M., Nießner, M., and Theobalt,

C. (2018). State of the art on monocular 3d face re-

construction, tracking, and applications. In Computer

Graphics Forum, volume 37, pages 523–550. Wiley

Online Library.

A Human Ear Reconstruction Autoencoder

145