Extending StructureNet to Generate Physically Feasible 3D Shapes

Jannik Koch

1,2

, Laura Harak

, Alisa Jung

and Carsten Dachsbacher

Fraunhofer Institute of Optronics, System Technologies and Image Exploitation IOSB, Ettlingen, Germany

Karlsruhe Institute of Technology, Karlsruhe, Germany

Keywords:

Generative Models, Shape Synthesis, Graph Neural Networks, Physical Constraints, Measure of Infeasibility.

Abstract:

StructureNet is a recently introduced n-ary graph network that generates 3D structures with awareness of

geometric part relationships and promotes reasonable interactions between shape parts. However, depending

on the inferred latent space, the generated objects may lack physical feasibility, since parts might be detached

or not arranged in a load-bearing manner. We extend StructureNet’s training method to optimize the physical

feasibility of these shapes by adapting its loss function to measure the structural intactness. Two new changes

are hereby introduced and applied on disjunctive shape parts: First, for the physical feasibility of linked parts,

forces acting between them are determined. Considering static equilibrium, compression and friction, they are

assembled in a constraint system as the Measure of Infeasibility. The required interfaces between these parts

are identiﬁed using Constructive Solid Geometry. Secondly, we deﬁne a novel metric called Hover Penalty that

detects and penalizes unconnected shape parts to improve the overall feasibility. The extended StructureNet

is trained on PartNet’s chair data set, using a bounding box representation for the geometry. We demonstrate

ﬁrst results that indicate a signiﬁcant reduction of hovering shape parts and a promising correction of shapes

that would be physically infeasible.

1 INTRODUCTION

Tools that automate the generation of 3D shapes are

an important aid for creators of entertainment media,

like video games or ﬁlm, and researchers using physi-

cal simulations. Due to this demand, various procedu-

ral modeling techniques trying to provide results that

are both diverse and available in vast quantities have

been proposed before.

Early grammar-based methods are able to produce

a large variety of shapes by relying on sets of gen-

erative descriptions. While these usually work well

for simple shapes, the underlying rules become more

complex or even contradictory the more detailed the

shapes to be generated are. The difﬁculty of describ-

ing the detailed makeup of complex shapes as gram-

mars encouraged alternative methods that infer the

synthesis rules from exemplary data.

In the context of shape analysis and (part-based)

shape synthesis, advanced methods like (Ma et al.,

2014) capture geometric properties for mapping an

exemplary source model to a target model at various

levels of complexity. More generally, inferring com-

plex behavior from data is a core component in the

ﬁeld of artiﬁcial neural networks.

Recent generative models leverage Variational

Autoencoders (VAEs) or Generative Adversarial Net-

works (GANs) to create 3D shapes without using

heuristics for detecting the underlying object struc-

ture, but rather learning it (Goodfellow et al., 2016).

The StructureNet (Mo et al., 2019a) framework used

in this paper not only considers the geometry, but also

the part relationships in the learning process by rep-

resenting shapes as hierarchical graphs. This allows

for the generation of shapes of novel structure and ge-

ometry, as well as editing shapes or shape parts while

preserving the structural hierarchy.

While the generated objects mostly maintain a vi-

sual plausibility, the assembled latent space the new

shapes are drawn from may still hold non-functional

or defective shapes with asymmetrical or missing

parts. Physically correct interactions with such shapes

are often impractical. A possible reason for the gener-

ation of defective shapes is an underrepresentation of

the respective shape family in the training data. Since

gathering additional data is not always possible, this

paper aims to extend the training to explicitely pro-

mote physically feasible shapes in the training.

Our approach views the task as an inverse statics

problem. We provide two additional metrics in Struc-

tureNet’s training: For detached parts we present a

novel metric called the Hover Penalty that promotes

Koch, J., Haraké, L., Jung, A. and Dachsbacher, C.

Extending StructureNet to Generate Physically Feasible 3D Shapes.

DOI: 10.5220/0010256702210228

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 1: GRAPP, pages

221-228

ISBN: 978-989-758-488-6

221

parts being in contact with each other. Furthermore

we apply a linear constraint system to calculate the

Measure of Infeasibility introduced by (Whiting et al.,

2009) to evaluate the overall physical feasibility.

2 RELATED WORK

Generative Models: Various attempts at generating

3D geometry by inferring a generative model have

been made prior to StructureNet (Mo et al., 2019a).

(Kalogerakis et al., 2012) train a probabilistic

model on a set of compatibly segmented shapes.

The VAE (Kingma and Welling, 2013) used by

StructureNet is a common approach to achieve this

goal. 3D-GAN (Wu et al., 2016) uses Generative

Adversarial Networks (GANs) and achieves results

of similar quality. While both architectures generate

novel shapes that successfully imitate the original

input, neither implementation currently considers

physical limitations. This paper attempts to mitigate

that.

Static Analysis: Since StructureNet uses an

approach based on neural networks, we achieve the

consideration of physical feasibility by extending the

total loss for which the network adjusts its weights.

These new components of the loss function are

based on previous research about physical feasibility.

(Whiting et al., 2009) present an approach to optimize

masonry shapes, like cathedrals or unreinforced con-

crete dams, for physical feasibility. While focusing

on buildings, their approach works well with arbitrary

3D geometry and provides the means for automatic

adjustments of massive shapes.

Further research in the ﬁeld of structural sound-

ness focuses on 3D printing. For example, (Pr

evost

et al., 2013) tackle balancing a 3D shape before

printing. Furthermore, (Stava et al., 2012) optimize

3D printable shapes for physical feasibility and

additionally try to maximize robustness for subse-

quent cleaning and transportation. While providing

impressive results, both optimization approaches

hollow out shapes, which does not translate well to

our use case as we want to focus on massive shapes

that are often found in real life. This makes the

approach by (Whiting et al., 2009) the more sensible

choice. Additionally, the ﬁndings by (Pr

evost et al.,

2013) focus on a solution that assists a human

designer. Since the ﬁndings by (Whiting et al., 2009)

tune shapes in a fully automatic fashion, they lend

themselves more to a machine learning approach as

employed by us.

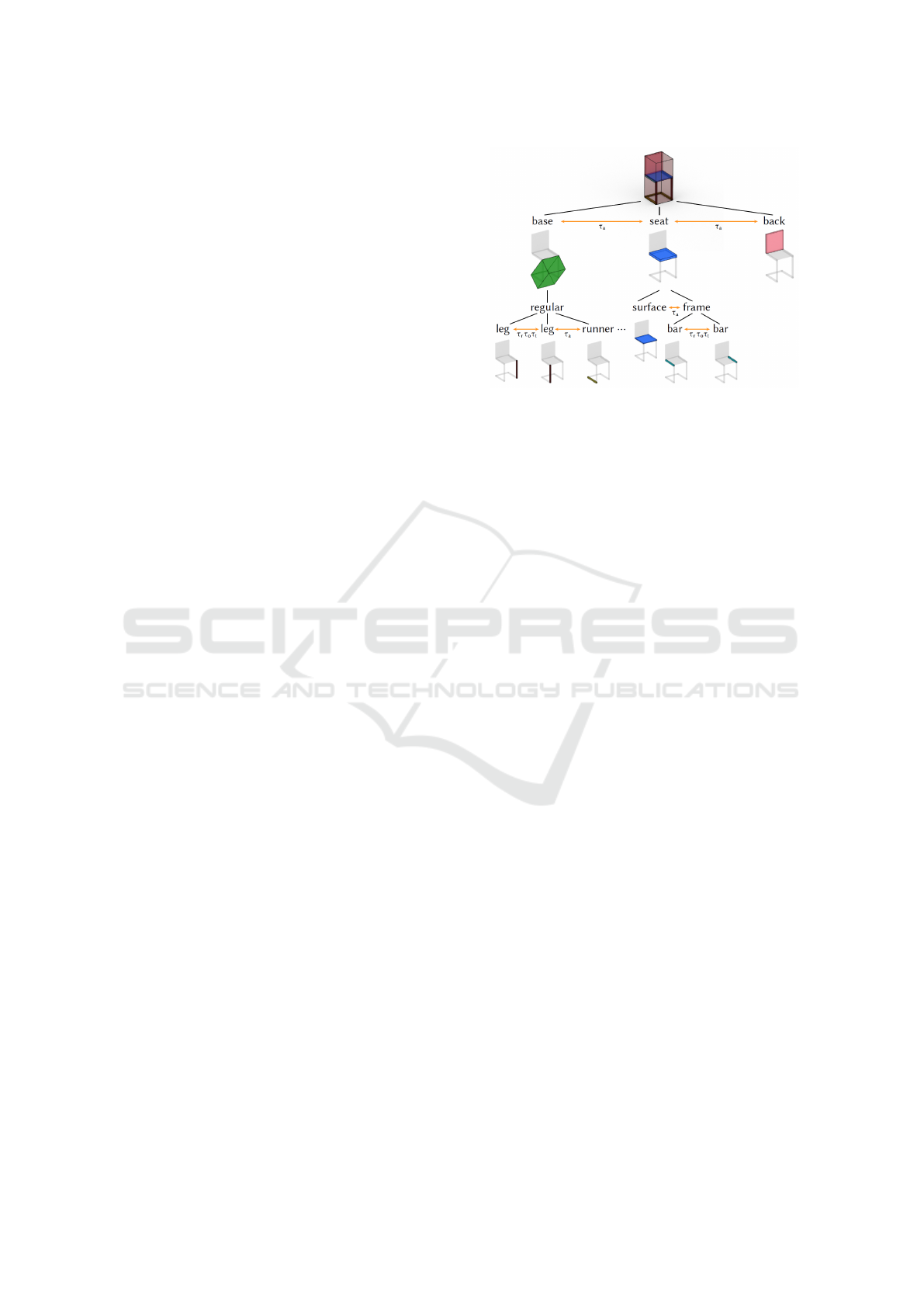
Figure 1: The representation of a chair from the Part-

Net (Mo et al., 2019b) data set as an n-ary graph created

by (Mo et al., 2019a). The shape parts are hierarchically or-

dered (black edges), geometrically represented as oriented

bounding boxes and semantically labeled accordingly (col-

ors). The orange horizontal edges describe geometric re-

lationships between parts, speciﬁcally adjacency (τ

) and

translational, reﬂective or rotational symmetries (τ

, τ

Constructive Solid Geometry: In order to eval-

uate the physical feasibility of a shape we need to

compute the contact surfaces between the shape’s

parts. We achieve this by employing intersection op-

erations provided through Constructive Solid Geome-

try (CSG) (Laidlaw et al., 1986) on the part geometry.

The choice of CSG is due to the fact that it works on

arbitrary geometry and computes a geometrical repre-

sentation of the interactions.

3 STRUCTURENET

FRAMEWORK

StructureNet is a graph neural network that generates

multi-part 3D models (shapes) with varying structure

and geometry. Its essential component is an n-ary

graph that represents the overall structure of a shape

and thus allows to organize its parts hierarchically

as nodes. Additionally, geometric relationships like

adjacencies or symmetries between part siblings are

considered as horizontal edges within that graph as

shown in Figure 1.

StructureNet is a generative approach in the

context of both shape analysis and shape synthesis of

graph structured shape data. It is trained and tested

with the PartNet data set (Mo et al., 2019b) which

already classiﬁes shapes into model categories and

contains hierarchically ordered and semantically

labeled shape part geometries. The geometry is either

represented as point clouds or oriented bounding

boxes and fed into a Variational Autoencoder (VAE).

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

222

Figure 2: Examples of incorrectly generated chairs by the

original StructureNet (Mo et al., 2019a): Hovering parts

(left), asymmetrical shape parts (middle) or overlapping

shape parts (right) are addressed by the Measure of Infeasi-

bility and Hover Penalty introduced in this paper.

The VAE consists of two hierarchical graph networks

that convolve a shape’s graph. In the following para-

graphs we brieﬂy recap StructureNet’s architecture

and training workﬂow.

Architecture: The VAE is composed of a group

of two encoders (e) and a group of two decoders (d)

that learn a mapping from a shape S to a feature vec-

tor z and the shape’s reconstruction S

from z with

= d(e(S)). Both groups trace the graph of S recur-

sively in a bottom-up (e) and top-down (d) order, each

encoder and decoder handling either the geometry of

a shape part (leaf node) itself or a child graph of a

part. Here, a geometry encoder induces a feature vec-

tor from the leaf nodes by processing the geometric

representation of the corresponding shape parts (point

clouds or bounding boxes) differently. A graph en-

coder then encodes these intermediate feature vectors

of each part and each part relationship recursively to

get z for the entire input shape S.

Starting with z as the latent code of the root node,

a graph decoder recursively transforms it into child

graphs, where each node (shape part) and its edges

to other nodes (geometric relationships) are assigned

a probability predicting their (non-)existence. Nodes

and edges that are not predicted to exist are discarded,

existing nodes are decoded into their geometry rep-

resentation using a geometry decoder. Additionally,

the semantic label of a part and a probability of it

being a leaf node for ending recursion are determined.

Training: StructureNet’s training stage only con-

siders shapes with a limited number of child parts.

Fine-grained shapes with a hierarchy containing an

exceeding number of child parts are refused. The total

loss for learning a reversible mapping of a shape S to

z is minimized using Mini-Batch Gradient Descent:

total

= E

S ∼ S

(S) + L

(S) + βL

(S)]. (1)

S ∼ S

is the expected value of the summed losses for

a shape S to be drawn from a distribution of a certain

shape category S, such as tables, chairs or cabinets.

(S) is the loss function for learning to reconstruct

the shape S

= d(e(S)) from the ground truth shape

S. The correspondence between both shapes’ parts is

determined by solving a linear assignment problem,

matching their parts separately for each child graph.

For the exact composition of this reconstruction loss

see (Mo et al., 2019a). L

(S) is the loss function for

structure consistency between the reconstructed part

geometries and edges, which aims at making parts

structurally consistent with their relationships, where

a relationship between two parts should also hold for

their subtrees. βL

(S) is a weighted variational regu-

larization loss for handling the distribution density of

shapes in the inferred latent space.

The total loss L

total

is calculated as a forward

propagation function, where batches with a certain

number of shapes from one category are fed into the

network to obtain the loss of each batch by summing

up the individual losses of each shape after encoding

and decoding. Since StructureNet still might produce

failure cases (Figure 2), we extend its total loss to ac-

count for the physical feasibility for every batch in

Section 5.

4 PHYSICAL FEASIBILITY

Physical feasibility is deﬁned as the ability of a shape

to support its own weight. (Whiting et al., 2009)

model this as a system of constraints based on the

forces acting between shape parts. Determining

whether a shape is physically feasible is therefore

a task of ﬁnding a set of forces that satisfy these

constraints.

Constraints: All forces act on the vertices of

the contact surfaces between parts (“interfaces”). A

shape is considered physically feasible if a set of

forces exists that negates the gravitational forces of

every part while each force points in a “plausible”

direction. The situation in which all contact forces

negate each other and all gravitational forces is

referred to as static equilibrium. A plausible di-

rection of a force lies in a cone around the surface

normal, which limits the directions due to friction.

Furthermore, forces need to provide compression,

meaning they need to point away from the interface

in order to model parts pushing each other away.

This compression constraint prevents the presence of

“tension forces” which point in the opposite direction

and act as glue holding physically infeasible shapes

together. Figure 3 shows an example of the tension

and compression forces.

Measure of Infeasibility: The constraint system

only provides binary answers to the question of

Extending StructureNet to Generate Physically Feasible 3D Shapes

223

Figure 3: Visualization of the active forces at an exemplary

part interface. From the perspective of the chair leg, F

the tension force and F

the compression force. The di-

rection of the forces swaps when observing from the seat’s

perspective. In reality, only the compression force is needed

here as the seat presses down on the leg, satisfying the com-

pression constraint.

physical feasibility, since there either is or is not

a set of forces that satisﬁes the constraint system.

Therefore, (Whiting et al., 2009) soften the com-

pression constraint to allow for tension forces that

hold the shape together where necessary. Tension

forces are penalized, resulting in an optimization

problem where the squared sum of tension forces is

minimized. The minimum is the metric describing

the overall physical feasibility of the shape, called

the Measure of Infeasibility. The system of equations

describing the Measure of Infeasibility is shown in

Equation 2.

Extension: In order to extend StructureNet to ac-

count for physical feasibility, we include the Measure

of Infeasibility into the training stage. The new met-

ric serves as an additional element of the loss func-

tion and promotes the generation of physically feasi-

ble shapes. Our approach is comprised of the individ-

ual steps shown in Figure 4 and described further in

the following section.

5 EXTENSIONS

Graph Representation: The geometry generated by

StructureNet is arranged as a tree graph. In order to

assess the physical feasibility of a shape generated by

StructureNet, only the graph leaves are of concern as

they store the geometry of the individual parts. The

relationships between parts stored in the graph are

ignored: While adjacency relationships play a role in

later steps, they are not reliably provided in newly

generated data during training. Instead of relying

on the information stored in the graph, adjacency

relationships are therefore detected using intersection

checks during interface generation.

Figure 4: Visualization of the process by which the Measure

of Infeasibility and Hover Penalty is calculated from a graph

object.

Geometry Pre-processing: The original Struc-

tureNet implementation supports both point cloud and

bounding box representations, including semantic la-

bels. Instead of differentiating between these, we fo-

cus on the latter and support the former by approx-

imating point clouds with bounding boxes using the

ﬁndings by (Barequet and Har-peled, 2001). The re-

sults of the approximation are shown in Figure 5.

This avoids further case differentiations in subsequent

steps of our method. The tradeoff, however, is addi-

tional overhead and a loss of detail when using the

point cloud representation, which is discussed further

in Section 7. Last, we add a bounding box represent-

ing the ground to the overall geometry, so we can treat

the ground like any other shape part during interface

calculations.

Figure 5: Converting a point cloud shape into a bounding

box representation, including the addition of a ground part.

Interface Generation: We generate part inter-

faces using Boolean operations. Note that parts of

generated shapes not only share a polygonal contact

plane, but often intersect signiﬁcantly. Therefore, in-

terfaces are deduced from the intersection volume.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

224

First, every possible pair of parts is checked for ad-

jacency by testing whether their Boolean intersection

volume is zero using CSG. If that is not the case, this

intersection volume is cut out from one of the two

parts chosen at random. The new triangles created by

this operation are then used as the interfaces between

the parts as shown in Figure 6.

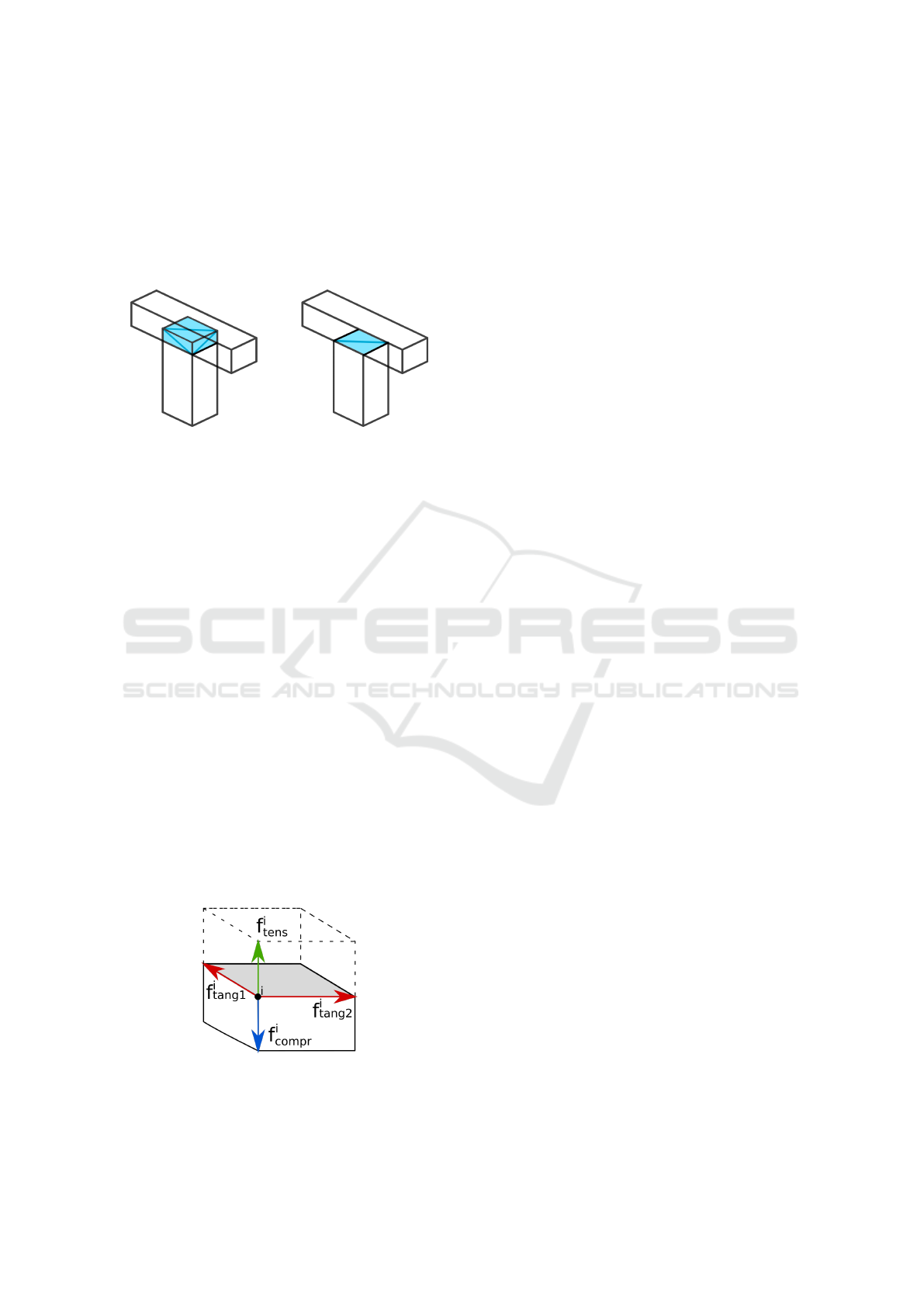
Figure 6: Exemplary removal of an intersection volume,

yielding two new triangles used as part interfaces.

Hover Penalty: Since the Measure of Infeasibil-

ity requires a ground part to push back against the

shape for static equilibrium, it can only account for

parts with direct or indirect ground contact. We in-

troduce an additional penalty for parts or clusters of

parts hovering in mid-air. By keeping track of the

pairwise adjacencies found when calculating the in-

terfaces, we check parts for direct or indirect ground

contact. Direct contact with the ground is given if a

direct adjacency relationship with the ground part ex-

ists. Indirect contact with the ground is characterized

by a chain of adjacencies that lead to a part that is

in direct contact with the ground. For every part that

is not in direct or indirect contact with the ground, we

take the smallest possible Euclidean distance between

the centers of gravity to any part with direct or indirect

ground contact. The sum of these distances makes up

the additional Hover Penalty loss. The rationale be-

hind this is that parts should be nudged towards each

other until they can all be adjusted using the Measure

of Infeasibility.

Constraint System: Once the interfaces and the

Hover Penalty are calculated, the constraint system

Figure 7: Visualization of the force components that make

up any force acting on a vertex i. Note that the choice which

force is the compression force and which one is the tension

force is based on the perspective of the bottom part.

for the Measure of Infeasibility (Whiting et al., 2009)

shown in Equation 2 can be applied:

y(S) = min

∑

( f

tens

)

(2)

s.t. A

· f + w = 0

f r

· f ≤ 0

compr

· f ≥ 0

with y being the Measure of Infeasibility of a shape

S. f is the concatenation of every force vector f

placed on an interface vertex i in the shape. Each

of these force vectors is further subdivided into four

components with respect to the basis vectors of

the local coordinate system of the interface. There

are two tangential components f

tang1

, f

tang2

for the

tangential basis vectors lying within the plane of the

interface and both the compression f

compr

and tension

components f

tens

along the normal. An overview

of the force components is shown in Figure 7. The

constraints on the vector f are imposed using the

constraint matrices A

, A

f r

, A

compr

and the weight

vector w. A

contains the local coordinate systems

of every part interface. A multiplication with the

force vector yields the acting forces of every interface

in global coordinate space. The weight vector w

represents the weight, and thereby gravitational force,

of every part. Static equilibrium is therefore reached

when the acting forces of the shape and the weight

vector cancel each other out. The volume of each part

is used as its respective weight, assuming all parts

are made of the same material with a uniform density

of 1. A

f r

and A

compr

enforce the aforementioned

friction and compression constraints. Further details

about the system of equations and its construction

can be found in the original work by (Whiting et al.,

2009).

Optimization: We optimize the force vector to

ﬁnd the Measure of Infeasibility using a trust region

optimization routine (Conn et al., 2000). The initial

guess randomly distributes force vectors across the

interface vertices such that they already lie within

the friction cone along the respective normal. Every

component of the initial guess respective to the ten-

sion force basis vector is set to zero, since we assume

initially that a physically feasible solution exists.

Loss Extension: Both the resulting Measure

of Infeasibility and the overall Hover Penalty are

weighted individually and added to the overall loss

function, as shown in Equation 3. Initial testing re-

sulted in 1.0 being chosen for both weights, which al-

lows the additional losses to have roughly the same

impact as the pre-existing loss functions used by

Extending StructureNet to Generate Physically Feasible 3D Shapes

225

StructureNet. Note that the range of the Hover

Penalty is inﬂuenced by the overall scale of the shape.

This means that other data sets using shapes of a

different scale need to tune the weight of the Hover

Penalty accordingly. We model the new total loss of

a shape S including the Measure of Infeasibility loss

moi

and the Hover Penalty loss L

as:

total

= E

S ∼ S

(S) + L

(S) + β L

(S) (3)

+ L

moi

(S) + L

(S)]

under the assumption that each loss weight is already

multiplied onto each loss as was the case in the origi-

nal formulation.

Note that this total loss is calculated using the av-

erages of the individual losses across an entire batch

of shapes. This means that the Measure of Infeasibil-

ity and Hover Penalty would need be calculated for

all shapes in the batch. Due to their signiﬁcant com-

putational cost, we chose to approximate the actual

average by only averaging both losses for a smaller,

random subset of each batch. In our case, this subset

only contained an eighth of each batch.

6 RESULTS

We trained the StructureNet implementation provided

by (Mo et al., 2019a) including the additional losses

for 35 epochs instead of the 200 epochs used in the

original StructureNet implementation. The reduced

epoch count is due to changes in the training duration

which are elaborated upon at the end of this section

and in Section 7. Furthermore, we used the PartNet

chair data set for ease of comparison to the original

results.

Impact on Pre-existing Losses: We observe no

signiﬁcant change in the development of pre-existing

losses used in Equation 1 when comparing the origi-

nal StructureNet implementation to the one using our

additions. This implies no relevant interplay between

the new and old losses, e.g. increasing the physical

feasibility at a loss of realistic part relationships.

Development of New Losses: The development

of both new losses is shown in Figure 8. We observe

that both new losses are delayed in their manifes-

tation. This is possibly caused the fact that early

generated shapes are too simple to be physically

infeasible in a signiﬁcant way. Once sufﬁcient shape

complexity is reached after around 5 epochs (50 to

75 steps), the Hover Penalty rapidly increases before

gradually decreasing. While the Hover Penalty

converges, the Measure of Infeasibility behaves much

more erratically and spikes occasionally. Further

training for more epochs is required to assess the

overall behavior of the Measure of Infeasibility.

Visual Results: 100 samples were taken from

both the original StructureNet implementation and the

one with the added losses after 35 epochs of training.

The Measure of Infeasibility and the Hover Penalty

have been computed for the samples in each set, the

results of which are shown in Figure 9. Figure 10

compares the sample with the highest Measure of In-

feasibility of each set. Both samples constitute the

cases with the highest Measure of Infeasibility from

their respective set. The sample taken from the ex-

tended version of StructureNet has a negligible Mea-

sure of Infeasibility, which might be the result of an

improved placement and tilt of the chair legs and the

back rest. Likewise, we must take into account in-

consistencies regarding the computation of part inter-

faces, the limitations of which are discussed in the

next section. Note that the addition of arm rests did

not cause the shape to have a signiﬁcant Measure of

Infeasibility. This suggests that the interface calcula-

tion resulted in two holes being carved into the back

rest into which the arm rests are inserted. While this

allows for a more physically feasible solution than

shortening the arm rests, it is a random decision.

Only 5 shapes were found to have hovering parts

after introducing the additional losses compared to

27 shapes before. The few shapes that still exhibited

hovering parts also produced signiﬁcant Hover Penal-

ties. This suggests that extreme outliers still have to

be attached to the main shape, while the occurrence

of barely detached parts was already corrected.

Figure 11 shows examples of an extreme case before

and after introducing the additional losses.

Training Duration: The new loss calculations re-

sulted roughly in a nine-fold increase of the training

time. Around 75% of the additional loss computation

time is spent on minimizing the system of equations

shown in Equations 2 and 3 in Section 5. Another

11% of the additional loss computation time is spent

on interface calculation. The remaining time spent on

the additional loss computations is mainly used for

preparing the geometry and the constraint system.

7 LIMITATIONS, FUTURE WORK

The current state of our approach serves as a pilot

study that needs to be explored further to assess the

overall effect on the generated shapes. Additional

training with more epochs and different data sets is a

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

226

Figure 8: Loss development of the Measure of Infeasibility (left) and the Hover Penalty (right). The total loss is denoted on

the y-axis while the x-axis denotes training steps, with 500 steps corresponding to roughly 35 epochs. The range of each axis

spans to the maximum value found. Mild smoothing has been applied to the graphs, with the original data being hinted at in

the background.

Figure 9: Histograms comparing the Measure of Infeasibil-

ity and Hover Penalty of 100 samples taken before and after

applying the additional losses. The absolute Measure of In-

feasibility or Hover Penalty is shown on the x-axis and the

number of affected samples is shown on the y-axis.

Figure 10: Comparison of two cases of a high Measure of

Infeasibility. The sample in the top row is a result of the

original, unaltered implementation of StructureNet and re-

ceives a Measure of Infeasibility of 17.21. The sample in

the bottom row is a result of the implementation of Struc-

tureNet that includes the new losses and receives a Measure

of Infeasibility of 4.45 · 10

−4

. Both samples were taken af-

ter 35 epochs of training.

primary necessity. An ablation study could also help

to clarify the effects of the individual losses.

Training Duration: Due to additional overhead

caused by the new losses, the training duration

Figure 11: Comparison of two cases of a high Hover

Penalty. The left case is a result of the original, unal-

tered implementation of StructureNet and receives a Hover

Penalty of 4.79. The right case is a result of including the

new losses and receives a Hover Penalty of 3.03. Both

samples were taken after 35 epochs of training. Note that

what can be considered a high Hover Penalty depends on

the overall scale of the shape.

increased signiﬁcantly. Reducing the performance

impact of the changes is a crucial venue for future

work. This includes more sophisticated initial guess

and faster minimization routines. An improved

interface calculation routine could also help.

Interface Computation: Further necessary

improvements to the interface calculation routine are

related to interface quality. The interfaces resulting

from the current algorithm are arbitrary due to the

random selection of which part to cut into. An

example of three possible outcomes resulting from

the same intersecting geometry is given in Figure 12.

This can have a drastic impact on the Measure of

Infeasibility. An improved solution should provide

deterministic, consistent results and better reﬂect

human intent. Additionally, it should also try to

minimize the number of triangles used to represent

the interfaces to reduce the optimization time.

Point Clouds: The current handling of point

clouds causes a loss of geometric detail. By separat-

ing the implementation into a bounding box version

and a point cloud version, the geometric data could

be exploited more efﬁciently.

Materials: We do not support parts of varying

materials. Respecting material properties when

Extending StructureNet to Generate Physically Feasible 3D Shapes

227

Figure 12: Three possible sets of interfaces resulting from

the same geometry. The result depends on which part the

intersection volume is cut out of. Since this is a random

decision, the results are arbitrary. Note that the Measure of

Infeasibility of the leftmost case is lower than the rest due

to neither of the top parts resting on the bottom part.

calculating part weights and friction properties

would yield more realistic results. This includes the

assumption that materials have a uniform density,

which is not always the case in the real world. Our

implementation also ignores deformable parts.

Support Structures: The current solution does

not account for parts being held together by support

structures like screws or bolts, which are common

in the real world. Optimally, a certain amount of

tension forces that could be provided this way should

be granted without reducing the physical feasibility.

Data Sets: Lastly, our extended approach has

only been tested on the PartNet chair data. Further

testing on different data sets is necessary to assess the

general applicability of the method.

8 CONCLUSIONS

In this paper, we have shown an initial step towards

including physical feasibility in the generation of 3D

shapes using StructureNet. While the demonstrated

effects of the Measure of Infeasibility are small, likely

due to the limited training time, signiﬁcant improve-

ments due to the Hover Penalty are already notice-

able. Further work needs to focus on additional train-

ing, reducing training duration and making the Mea-

sure of Infeasibility more predictable.

REFERENCES

Barequet, G. and Har-peled, S. (2001). Efﬁciently approxi-

mating the minimum-volume bounding box of a point

set in three dimensions. In In Proc. 10th ACM-SIAM

Sympos. Discrete Algorithms, pages 38–91.

Conn, A. R., Gould, N. I. M., and Toint, P. L. (2000). Trust

Region Methods. Society for Industrial and Applied

Mathematics.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press.

Kalogerakis, E., Chaudhuri, S., Koller, D., and Koltun, V.

(2012). A Probabilistic Model of Component-Based

Shape Synthesis. ACM Transactions on Graphics,

31(4).

Kingma, D. P. and Welling, M. (2013). Auto-Encoding

Variational Bayes.

Laidlaw, D. H., Trumbore, W. B., and Hughes, J. F. (1986).

Constructive Solid Geometry for Polyhedral Objects.

In Computer Graphics (Proceedings of SIGGRAPH

’86), volume 20, pages 161–170.

Ma, C., Huang, H., Sheffer, A., Kalogerakis, E., and Wang,

R. (2014). Analogy-Driven 3D Style Transfer. In Eu-

rographics 2014, pages 175–184.

Mo, K., Guerrero, P., Yi, L., Su, H., Wonka, P., Mi-

tra, N., and Guibas, L. (2019a). Structurenet: Hi-

erarchical graph networks for 3d shape generation.

ACM Transactions on Graphics (TOG), Siggraph Asia

2019, 38(6):Article 242.

Mo, K., Zhu, S., Chang, A. X., Yi, L., Tripathi, S., Guibas,

L. J., and Su, H. (2019b). PartNet: A large-scale

benchmark for ﬁne-grained and hierarchical part-level

3D object understanding. In The IEEE Conference on

Computer Vision and Pattern Recognition (CVPR).

evost, R., Whiting, E., Lefebvre, S., and Sorkine-

Hornung, O. (2013). Make It Stand: Balancing Shapes

for 3D Fabrication. ACM Trans. Graph., 32(4).

Stava, O., Vanek, J., Benes, B., Carr, N., and M

ech, R.

(2012). Stress Relief: Improving Structural Strength

of 3D Printable Objects. ACM Trans. Graph., 31(4).

Whiting, E., Ochsendorf, J., and Durand, F. (2009). Proce-

dural Modeling of Structurally-Sound Masonry Build-

ings. ACM Trans. Graph., 28(5).

Wu, J., Zhang, C., Xue, T., Freeman, W. T., and Tenenbaum,

J. B. (2016). Learning a Probabilistic Latent Space of

Object Shapes via 3D Generative-Adversarial Model-

ing. In Advances in Neural Information Processing

Systems, pages 82–90.

APPENDIX

The source code is available on GitHub: https://

github.com/Novare/structurenet physf.

GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications

228