
An Effective 3D ResNet Architecture for Stereo Image Retrieval
E. Ghodhbani
1 a
, M. Kaaniche
2 b
and A. Benazza-Benyahia
1 c
1
University of Carthage SUP’COM, LR11TIC01, COSIM Lab., 2083, El Ghazala, Tunisia
2
Institut Galil
´
ee, L2TI, Universit
´
e Sorbonne Paris Nord, France
Keywords:
Image Retrieval, Color Stereo Images, Disparity Maps, Deep Learning, Residual Neural Networks.
Abstract:
While recent stereo images retrieval techniques have been developed based mainly on statistical approaches,
this work aims to investigate deep learning ones. More precisely, our contribution consists in designing a two-
branch neural networks to extract deep features from the stereo pair. In this respect, a 3D residual network
architecture is first employed to exploit the high correlation existing in the stereo pair. This 3D model is then
combined with a 2D one applied to the disparity maps, resulting in deep feature representations of the texture
information as well as the depth one. Our experiments, carried out on a large scale stereo image dataset, have
shown the good performance of the proposed approach compared to the state-of-the-art methods.
1 INTRODUCTION
3D sensing mechanisms have witnessed a rapid
evolution in recent years. A particular attention has
been paid to the stereoscopic imaging paradigm.
The main advantage of this technique is the ability
to recover the depth information of the target scene
by simply capturing two images with two slightly
different viewing angles, mimicking in such way
the human visual system. This particular 3D image
representation has been widely integrated in several
active applications such as augmented reality displays
(Kim et al., 2014), obstacle detection for autonomous
vehicle navigation (Bernini et al., 2014), and laparo-
scopic surgeries (Sdiri et al., 2019). This growing
deployment has led to an expanding generation of
large-scale Stereo Image (SI) databases. Hence,
efficient retrieval systems that grant both fast and
accurate access to these repositories is of major
concern. The core objective of retrieval systems is to
extract discriminating features in order to accurately
characterize the rich content of the images.
Regarding SI retrieval, different approaches have
been developed in the literature. 1 For instance, the
first proposed approach (Feng et al., 2011) performs
the SI retrieval using MPEG-7 edge histograms ex-
tracted from the left image. Then, the selected image
a
https://orcid.org/0000-0002-6685-7117
b
https://orcid.org/0000-0003-1874-3243
c
https://orcid.org/0000-0002-4562-2757
candidates are further refined through a re-ranking
procedure based on the disparity cues. Peng et
al. (Peng et al., 2015) proposed to retrieve optical
satellite SI using features extracted from digital
surface models and ortho-images. Other works have
relied on a statistical modeling framework in the
wavelet domain to generate salient features (Chaker
et al., 2015; Ghodhbani et al., 2019). The main
idea behind these works is to resort to an adequate
parametric modeling to fit the distributions of the
wavelet coefficients.
Recently, Deep Neural Networks (DNN) (LeCun
et al., 2015) have received considerable attention
in the retrieval community. The common objective
of the proposed DNN-based approaches is to train
deep architectures to capture high-level features that
efficiently abstract image attributes. Although this
research area has rapidly evolved towards developing
more efficient retrieval systems, it is important to
note here that most deep learning based retrieval
methods have been devoted to the context of single
views (Babenko et al., 2014; Tolias et al., 2015), and
very few works have been developed for multi-view
images (Su et al., 2015; Ma et al., 2018).
Therefore, we propose in this paper to investigate
deep learning methods for the stereo image retrieval.
In this respect, a 3D residual network architecture
is first developed to exploit the high correlations
existing between the left and right views of the stereo
pair. Moreover, another 2D architecture is applied
to the disparity maps. Finally, the resulting texture
380
Ghodhbani, E., Kaaniche, M. and Benazza-Benyahia, A.
An Effective 3D ResNet Architecture for Stereo Image Retrieval.
DOI: 10.5220/0010261103800387
In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages
380-387
ISBN: 978-989-758-488-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
and depth features are combined by a fusion
DNN for the retrieval purpose.
The rest of this paper is organized as follows. In
Section 2, we introduce the basic concept of resid-
ual networks. In Section 3, the proposed residual net-
works based retrieval methods are described. Exper-
imental results are provided and discussed in Section
4, and some conclusions are drawn in Section 5.
2 BACKGROUND ON RESIDUAL
NETWORKS
2.1 Motivation of Residual Networks
Convolutional Neural Networks (CNNs) are a promi-
nent category of artificial neural networks thanks to
their ability to capture local spatial coherence of im-
ages. They have shown a notable success in abstract-
ing semantic features, useful in a wide range of com-
puter vision tasks, including object detection (Ji et al.,
2018), action recognition (Zhang et al., 2018), seman-
tic segmentation (Long et al., 2015) and face identifi-
cation (Zheng et al., 2019).
However, very deep CNNs have been frequently
exposed to the notorious problem of vanishing gra-
dient during the training phase (He et al., 2016). For
this reason, several attempts were made to build novel
CNNs that cope with this shortcoming. Residual net-
works (ResNet) are ones of the effective alternatives
(He et al., 2016). These networks make use of short-
cut connections that allow flow of information to shal-
lower layers without attenuation frequently caused by
successive non-linear transformations. The intuition
behind this reformulation is that nonlinear layers are
unlikely to approximate an identity mapping that en-
ables to propagate larger gradients to initial layers,
which could potentially alleviate the vanishing gra-
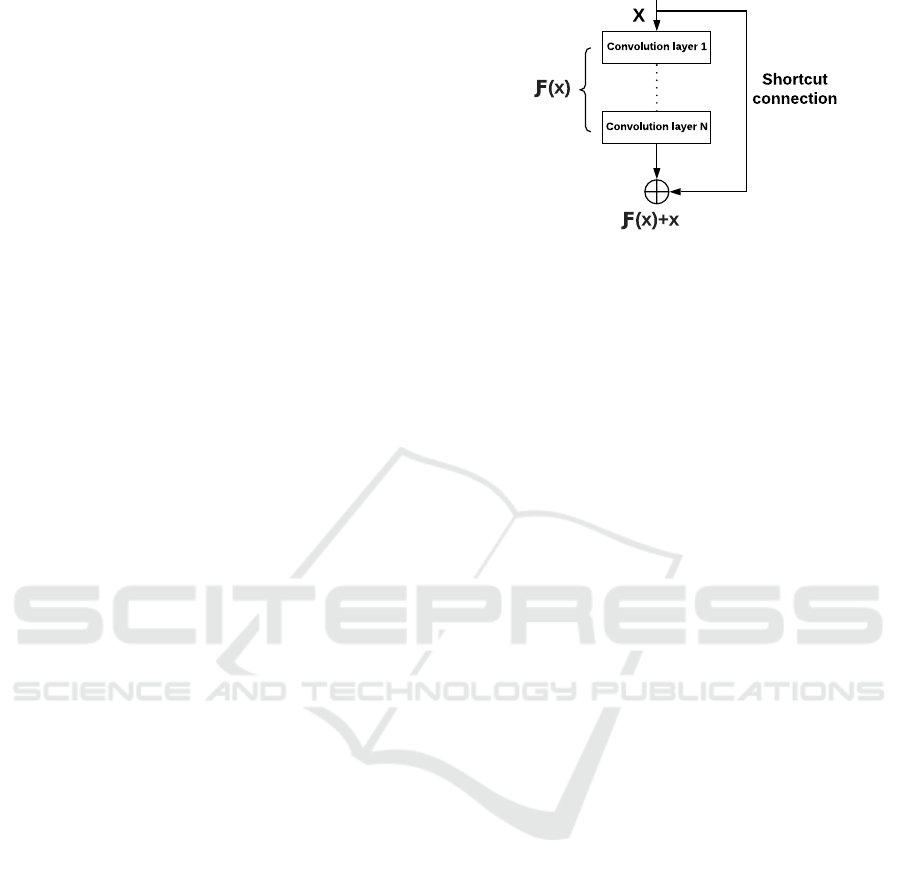
dient issue. Formally, denoting by H (x) the under-
lying mapping to learn from a set of stacked layers
whose input is x. The mapping H (x) should be an
identity operator in order to alleviate the degradation
issue. The residual learning consists in fitting a differ-
ence mapping (namely residual mapping) defined as:
F (x) = H (x) − x instead of fitting the conventional
H (x). Hence, it is much easier to optimize the resid-
ual mapping F (x) than fitting an identity mapping.
Fig. 1 displays a residual block (also called an
identity block) of a ResNet.
Empirical attainment of this paradigm is threefold.
First, extremely deep residual networks converge
faster than their plain counterparts. Secondly, in-
Figure 1: A basic residual block architecture.
creasing the depth of residual networks improves the
accuracy gain unlike conventional very deep CNNs.
Finally, residual networks with very high depth still
have low complexity than conventional deep CNNs
as VGG nets (Simonyan and Zisserman, 2015).
ResNets consist of three main parts. The first
part involves a series of stacked residual blocks, each
block has 3 convolution layers with different number
of filters. The feature maps resulting from the last
residual block is then abstracted in a compact vector
using a global average pooling layer. Finally, a fully
connected (FC) layer followed by a softmax activa-
tion function is used to perform a categorical classifi-
cation task.
For the retrieval task, the feature vector obtained
at the global average pooling layer could serve as an
efficient semantic representation of each input image.
Indeed, a forward pass over the ResNet is firstly per-
formed to both query and database images. Then, an
adequate similarity measure is retained to assess the
closeness between the query image and each of the
candidate ones using their related feature vectors.
2.2 3D Residual Networks
In the conventional 2D residual networks, only the
spatial correlations are captured. However, using
only 2D kernels may ignore other kinds of correla-
tion like those existing in multi-component images
and video sequences. To this end, multi-dimensional
CNNs present a suitable alternative to resolve this is-
sue. These networks perform joint convolutions on
feature maps instead of operating in a separate man-
ner as conventional spatial 2D based CNNs.
Driven by the compelling advantages of exploit-
ing residual networks, researchers have focused on
extending such networks to the spatio-temporal do-
main. For this purpose, three-dimensional residual
networks (namely 3D ResNet) have been introduced
(Hara et al., 2018). These networks perform 3D con-
volution and pooling operations in order to model the
spatial information and simultaneously capture tem-
An Effective 3D ResNet Architecture for Stereo Image Retrieval
381

poral connections across frames. They were mainly
devoted to process multiple video frames. For in-
stance, authors in (Tran et al., 2017; Hara et al., 2017)
have proved the outperformance of 3D ResNets in
the task of action recognition, compared to the first
proposed 3D CNN (Karpathy et al., 2014). For the
same task, Hara et al. (Hara et al., 2018) have empiri-
cally demonstrated that 3D ResNets trained on large-
scale video datasets, have reached competitive accu-
racy rates outperforming several 2D CNNs. While
such ResNet architecture has been mainly exploited
in the context of recognition and classification, and
to the best of our knowledge, this current work is the
first one exploring ResNets for stereo image retrieval.
3 RESNET-BASED STEREO
IMAGE RETRIEVAL
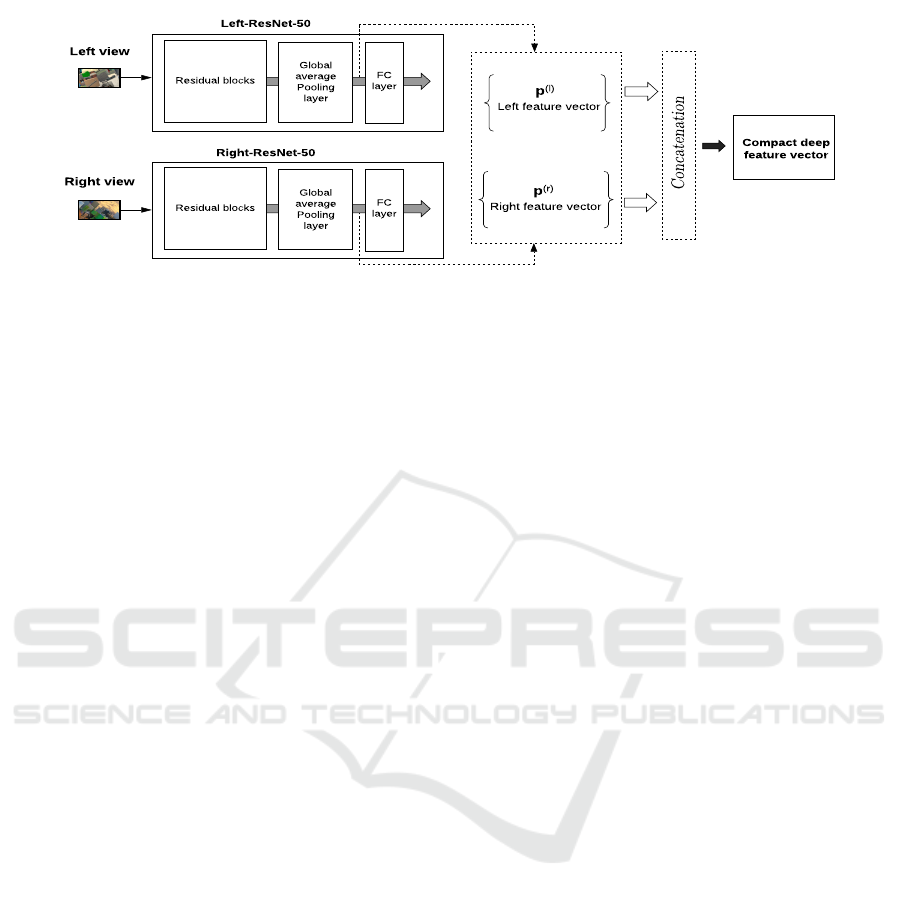
3.1 ResNet-based Independent Stereo
Image Representation
A straightforward deep learning-based SI retrieval
method may consist in applying a conventional single
view retrieval method to each view of the stereo pair.
This approach could be considered as a univariate SI
representation in the sense that each view is processed
independently from the other. Fig. 2 illustrates this
approach. Formally, for each input view (for example
the left one), the resulting feature vector is given by:
p
(l)
= [v
(l)
1
,v
(l)
2
,...,v
(l)
K
]
>
,with v
(l)
k
=
H
∑
i=1
W
∑
j=1
X
(l)
k
(i, j)
H ×W
.
(1)
where X
(l)
k
is the k-th feature map of size W × H, and
K denotes the whole number of maps at the last resid-
ual block. In a similar way, the deep feature vector
p
(r)
is defined. As a result, the final feature vector of
the stereo pair is given by:
p =
p
(l)
,p
(r)
. (2)
Afterwards, the similarity between a query SI
(I
(q,l)
,I
(q,r)
) and each database SI (I
(db,l)
,I
(db,r)
) is
measured using the sum of the Euclidean distances
between their associated feature vectors. It is ex-
pressed as follows:
˜
D(I
(q)
k I
(db)
) = D(I
(q,l)
k I
(db,l)
) + D(I
(q,r)
k I
(db,r)
),
= kp
(q,l)
− p
(db,l)
k
2
+ kp
(q,r)
− p
(db,r)
k
2
,
(3)
where p
(q)
= (p
(q,l)
,p
(q,r)
) and p
(db)
= (p
(db,l)
,p
(db,r)
)
represent respectively the global feature vector of the
query and the database SI.
3.2 Joint SI Representations using 3D
ResNet
While 3D CNNs attempt to capture temporal correla-
tions across consecutive inputs, we are interested in
using such network to fully exploit the correlations
existing between the RGB channels of the left and
right views of the input color SI. More precisely, the
first proposed approach consists in using simultane-
ously the resulting six channels of both views as an
input of our 3D ResNet architecture. Thus, as shown
in Fig. 3, the main difference of the latter with respect
to the previous 2D ResNet architecture is that the 3D
convolution steps are updated to take into account the
correlations between the two views. Besides, contrary
to the straightforward approach which outputs two
separate feature vectors (one vector per view), this ar-
chitecture enables to represent both stereo views in a
single compact feature vector.
During the training stage, the network learns to
encode the semantics of the color stereo components
in a joint fashion. Denoting by (I
(l)
i
,I
(r)
i
) the i-th train-
ing SI and its corresponding class y
i
, the categorical
cross-entropy loss is used to backpropagate gradients.
It is expressed as follows:
L = −
C
∑
c=1
y
(i,c)
log(p
(i,c)
), (4)
where C is the total number of classes in the training
dataset, y
(i,c)
is a binary indicator of value 1 if the
class label c is the corresponding exact label y
i
) for
the i-th SI sample, and 0 if not. p
(i,c)
is the network
predicted probability that the i-th SI sample is of class
c.
Later on, and similarly to the straightforward ap-
proach, the global average pooling layer of the trained
network is used as a feature extractor to generate rep-
resentative features for each SI. Finally, given p
(q)
and
p
(db)
the feature vectors of the query SI and the can-
didate SI, the Euclidean distance is used to measure
their similarity as follows:
˜
D(I
(q)
k I
(db)
) = kp
(q)
− p
(db)
k
2
. (5)
3.3 Fusion with Depth Maps-based
Representation
Driven by the compelling benefits of the depth infor-
mation in the SI retrieval task (Chaker et al., 2015;
Ghodhbani et al., 2019), we propose an improved ap-
proach that takes into account both texture and depth
attributes of the SI. In this regard, the proposed archi-
tecture consists of two branches. The first branch is
a 3D ResNet used to extract relevant cues from both
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
382
Compact deep
feature vector
Left-ResNet-50
p
(l)
Left feature vector
Left view
Concatenation
Right view
Residual blocks
Global
average
Pooling
layer
FC
layer
Residual blocks
Global
average
Pooling
layer
FC
layer
p
(r)
Right feature vector
Right-ResNet-50
Figure 2: SI representation using two ResNets.
stereo views as described in the previous proposed
approach, while the second branch is a 2D ResNet,
adopted to learn how to analyze and abstract depth
data properties. The proposed architecture undergoes
a two-stage learning process. The first stage aims
at learning a distinctive high-level cues associated to
texture and color in the SI. It has a 3D input shape
consisting of the six color channels of the stereo pair.
The second stage aims at training the second branch,
i.e. the 2D ResNet on the disparity maps of the train-
ing set. Both training are performed using the cate-
gorical cross-entropy loss function to back-propagate
gradients and adjust the network weights. Conse-
quently, the resulting two-branch architecture is used
to extract salient features from each SI and its corre-
sponding disparity map. Indeed, a couple of feature
vectors is generated for each stereo pair, reflecting in
such formulation both texture and depth attributes. It
could be expressed as:
p =
p
(c)
,p
(d)
. (6)
The similarity measurement between a query and
database SI characterized by their feature vectors
p
(q)
= (p
(q,c)
,p
(q,d)
) and p
(db)
= (p
(db,c)
,p
(db,d)
) re-
spectively, is performed using the Euclidean distance
as follows:
˜
D(I
(q)
k I
(db)
) = kp
(q,c)
− p
(db,c)
k
2
+ kp
(q,d)
− p
(db,d)
k
2
.
(7)
4 EXPERIMENTS
4.1 Training Setup
The proposed approaches have been conducted using
a ResNet-50. This network mainly consist of 5 stages.
The first one involves a convolutional layer with 64
filters of size 7 × 7 and a stride of 2, a ReLu activa-
tion, followed by a max-pooling layer. The remaining
stages are a stack of identity and convolution blocks
as illustrated in Fig. 4. When input and output tensors
of an identity block do not have the same dimensions,
a 1 × 1 convolution operation is added to the shortcut
connection in order to match the dimensions before
performing the element-wise adding operation. The
modified identity block is referred to as a convolu-
tional block.
During all training stages, both 2D and 3D
ResNets are fed with inputs of size 480×270. Be-
sides, the batch size and learning rate are set to 16
and 10
−4
, respectively. Moreover, the Adam opti-
mizer (Kingma and Ba, 2014) is retained to update
the network weights. All experiments have been con-
ducted using a Nvidia Quadro P5000 GPU with 16
GB of memory.
4.2 Dataset Overview
To evaluate the retrieval performance of the proposed
approaches, a database with a large-scale training set
is crucial for training deep ResNets. However, to the
best of our knowledge, the only color SI dataset sat-
isfying the large scale criteria is the FlyingThings3D
dataset (Mayer et al., 2016). It consists of 25,000 SI
of size 960×540 and their associated ground truth dis-
parity maps. Since this database is not mainly dedi-
cated neither for classification nor for retrieval tasks,
we propose to build upon it to generate our appro-
priate dataset as follows. The training dataset is ini-
tially partitioned into 10-frame subsets rendered from
small clips. Images in the same subset share visual
content, and are considered as a class of similar im-
ages. It is obvious that training deep CNNs such as
ResNets requires largely higher number of samples
in each subset. To this end, we resort to an offline
data augmentation framework in order to enlarge the
training subsets, and help the network to better gen-
eralize and prevent overfitting. We have considered
300 subsets and have performed 20 affine data trans-
formations such as rotation, translation, shearing and
An Effective 3D ResNet Architecture for Stereo Image Retrieval
383

State
State
Training stereo views
Database SI
Retrieved SI
Query SI
3D ResNet-50
. . . .
Traning stage
Test stage
Query SI
representation
Database SI
representation
Similarity
measurement
Training disparity maps
2D ResNet-50
. . .
Residual block 1
Pooling Layer
300-d FC Layer
Conv. layer
Pooling Layer
Residual block 16
300-d FC Layer
. . .
Pooling Layer
Conv. layer
Pooling Layer
Text
Residual block 1
Text
Residual block 16
. . .
Trained 3D ResNet-50 on texture data
Trained 2D ResNet-50 on disparity data
. . .
Residual block 1
Pooling Layer
300-d FC Layer
Conv. layer
Pooling Layer
Residual block 16
300-d FC Layer
. . .
Pooling Layer
Conv. layer
Pooling Layer
Text
Residual block 1
Text
Residual block 16
Figure 3: Flowchart of the proposed joint SI representation using a two-branch architecture.
Convolution layer
x 2 x 3
Max-pooling layer
Stage_2
Input data
Convolutional
block
Identity block
Convolutional
block
Identity block
Average pooling
layer
FC layer
x 5
Convolutional
block
Identity block
x 2
Convolutional
block
Identity block
Stage_3 Stage_4
Stage_5
Stage_1
Figure 4: A ResNet-50 architecture.
flipping over each stereo pair. The new dataset is com-
posed of 63,000 SI, split into 80% for training (i.e.
50,400 stereo pairs), and 20% for test (i.e. 12,600
stereo pairs). Some class samples of this new dataset
are shown in Fig. 5. Note that the same transforma-
tions are carefully performed for both stereo pairs and
their associated disparity maps in order to preserve
their spatial correlation.
4.3 Comparison Methods
We will consider the following proposed and state-of-
the-art methods:
• GC-MGG-7-LRD (Ghodhbani et al., 2019): A
statistical-based approach to retrieve color SI.
This method considers a Gaussian copula-based
modelling in the wavelet domain in order to em-
phasize different dependencies between the stereo
pair, as well as those existing between the stereo
views and their associated depth maps. Note that
this approach has reached the best retrieval perfor-
mance relatively to other proposed methods, and
several state-of-the art statistical methods as well.
• CroW (Kalantidis et al., 2016): A deep learning-
based retrieval approach devoted for mono-view
images. This approach mainly relies on a cross-
dimensional weighting pipeline, followed by an
aggregation scheme in order to abstract output
tensors derived from the last convolutional layer
of the used network. The aggregated outputs are
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
384

Figure 5: Some class samples of the generated database.
considered as salient features to perform the re-
trieval task. We propose to test this approach in
the context of SI through joining convolutional
output tensors of both left and right views before
performing the weighting and aggregation proce-
dures.
• ResNet-LR: This method relies on an indepen-
dent stereo view representation by separately ap-
plying the conventional ResNet architecture to the
left and right views. It should be noted that this
method can also be seen as a direct application
of a conventional ResNet-based state-of-the-art
method.
• ResNet-3D-LR: The proposed joint representa-
tion that highlights texture correlations among the
stereo pair using a 3D ResNet.
• ResNet-3D-LR+ResNet-D: The proposed
method that aims at characterizing texture and
depth data using a two-branch network.
Regarding deep learning based approaches, Table 1
illustrates the number of trainable parameters as well
as the length of the resulting feature vectors used for
the retrieval task.
4.4 Results
In order to evaluate the performance of the retrieval
task, several objective metrics were defined. The most
commonly used metrics are:
• The precision PR versus recall RC ratios. The pre-
cision PR = N
r
/N is the ratio between the number
of relevant images in the returned ones N
r
and the
number of returned images N, whereas the recall
RC = N
r
/N
t
is the ratio between N
r
and the num-
ber of relevant images in the database N
t
. These
two metrics are commonly used to plot PR-RC
curve in order to illustrate the exhaustive retrieval
performance of the target algorithm.
• The mAP presents the mean over all queries of
average precision associated to each query. It is
expressed as follows:
mAP =
1
N
N
∑
q=1
AP(q)
!
(8)
where N is the total number of images in the test
set, and AP is the average precision of each query,
defined as:
AP =
1
N
t
N
∑
i=1
R
index(i)
i
. (9)
Given the ordered candidate images relatively to
the query, and N
t
the number of relevant images
in the database, let NR(i) is the number of rele-
vant images till the i-th position in the ranked list.
Thereafter, R
index(i) is defined as:
R index(i) =
NR(i) if the i-th ranked image
is relevant,
0 otherwise.
(10)
Note that a retrieved image is considered as rele-
vant if it shares the same class of the query one.
To evaluate the retrieval performance of deep
features obtained using the proposed architectures
for both independent and joint SI representations as
well as the above described state-of-the-art methods,
Tab. 2 outlines the reached mAP rates of each method
on the generated database. This table shows that the
different tested deep learning based approaches sig-
nificantly outperform the classical statistical based re-
trieval method. Besides, we remark that the proposed
approaches, even the ResNet-LR that relies on an in-
dependent SI representation, outperform the CroW
method. This could confirm the performance of the
ResNet relatively to the VGG network retained in
the CroW approach. For this reason, we propose
An Effective 3D ResNet Architecture for Stereo Image Retrieval
385
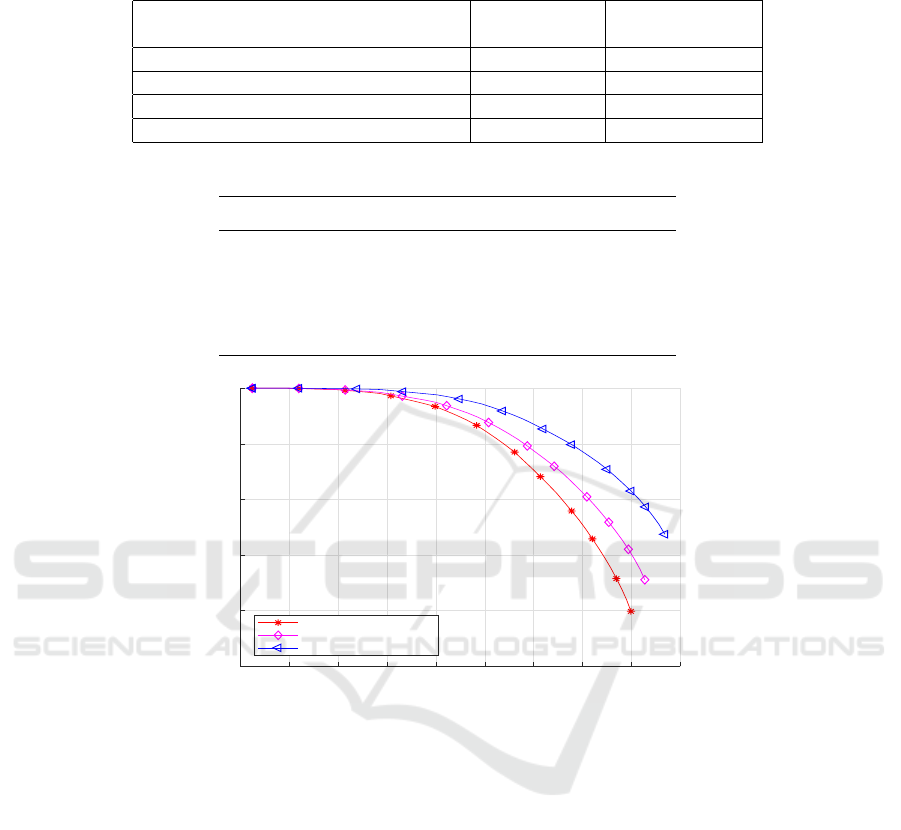
Table 1: The proposed approaches wih the number of trainable parameters (in millions) and the length of the final feature
vector.
Model Number of Length of
parameters feature vector
CroW-SI (Kalantidis et al., 2016) 138M 1,024
ResNet-LR 25.7M 4,096
ResNet-3D-LR 46.8M 2,048
ResNet-3D-LR+ResNet-D 72.5M 4,096
Table 2: mAP rates of the state-of-the-art and proposed methods.
Methods mAP
GC-MGG-7-LRD (Ghodhbani et al., 2019) 0.23
CroW-SI (Kalantidis et al., 2016) 0.52
ResNet-LR 0.84
ResNet-3D-LR 0.87
ResNet-3D-LR+ResNet-D 0.91
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
RC
0.75
0.8
0.85
0.9
0.95
1
PR
ResNet-LR
ResNet-3D-LR
ResNet-3D-LR+ResNet-D
Figure 6: PR-RC curves of the independent and joint-based SI representations.
now to focus on the t3D ResNet-based retrieval meth-
ods and study their performance in terms of PR-RC.
Thus, as it can be seen from Fig. 6, the proposed 3D
ResNet architecture leads to better precision-recall re-
sults compared to the conventional ResNet architec-
ture applied separately to each view of the stereo pair.
This confirms the interest of the joint feature extrac-
tion method compared to the independent one. It is
important to note here, as shown in Table 1, that an-
other main advantage of the joint method is that the
size of its resulting output feature vector is half of
that generated by the independent process of the two
views. This allows to accelerate the retrieval pro-
cess, especially for large scale databases. Moreover,
further improvements are obtained by combining the
previous deep features of the texture information with
those of the depth information.
5 CONCLUSION AND
PERSPECTIVES
In this paper, a two-branch neural network is proposed
for color stereo image retrieval. More precisely, a 3D
ResNet is employed to exploit the high correlations
existing between the left and right views of the stereo
pair. Then, a 2D ResNet architecture is added to ex-
tract deep feature from the depth information. Ex-
perimental results have shown the benefits of the pro-
posed methods compared to state-of-the-art image re-
trieval methods. In future work, we propose to extend
this architecture by designing a multi-modal feature
learning framework.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
386

REFERENCES
Babenko, A., Slesarev, A., Chigorin, A., and Lempitsky,
V. (2014). Neural codes for image retrieval. In Euro-
pean Conference on Computer Vision, pages 584–599.
Springer.
Bernini, N., Bertozzi, M., Castangia, L., Patander, M., and
Sabbatelli, M. (2014). Real-time obstacle detection
using stereo vision for autonomous ground vehicles:
A survey. In 17th International IEEE Conference on
Intelligent Transportation Systems (ITSC), pages 873–
878.
Chaker, A., Kaaniche, M., and Benazza-Benyahia, A.
(2015). Disparity based stereo image retrieval through
univariate and bivariate models. Signal Processing:
Image Communication, 31:174–184.
Feng, Y., Ren, J., and Jiang, J. (2011). Generic framework
for content-based stereo image/video retrieval. Elec-
tronics Letters, 47(2):97–98.
Ghodhbani, E., Kaaniche, M., and Benazza-Benyahia, A.
(2019). Depth-based color stereo images retrieval us-
ing joint multivariate statistical models. Signal Pro-
cessing: Image Communication, 76:272–282.
Hara, K., Kataoka, H., and Satoh, Y. (2017). Learning
spatio-temporal features with 3d residual networks for
action recognition. In Proceedings of the IEEE Inter-
national Conference on Computer Vision Workshops,
pages 3154–3160.
Hara, K., Kataoka, H., and Satoh, Y. (2018). Can spa-
tiotemporal 3d CNNs retrace the history of 2d cnns
and imagenet. In Proceedings of the IEEE conference
on Computer Vision and Pattern Recognition, pages
6546–6555.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition, pages 770–778.
Ji, Y., Zhang, H., and Wu, Q. J. (2018). Salient object detec-
tion via multi-scale attention CNN. Neurocomputing,
322:130–140.
Kalantidis, Y., Mellina, C., and Osindero, S. (2016). Cross-
dimensional weighting for aggregated deep convolu-
tional features. In European conference on computer
vision, pages 685–701. Springer.
Karpathy, A., Toderici, G., Shetty, S., Leung, T., Suk-
thankar, R., and Fei-Fei, L. (2014). Large-scale video
classification with convolutional neural networks. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition, pages 1725–1732.
Kim, M., Lee, J., and Whon, K. (2014). Sparogram:
the spatial augmented reality holographic display for
3d visualization and exhibition. In IEEE VIS In-
ternational Workshop on 3DVis, pages 81–86, Paris,
France.
Kingma, D. P. and Ba, J. (2014). Adam: A
method for stochastic optimization. arXiv preprint
arXiv:1412.6980.
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-
ing. Nature, 521(7553):436–444.
Long, J., Shelhamer, E., and Darrell, T. (2015). Fully con-
volutional networks for semantic segmentation. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition, pages 3431–3440.
Ma, C., Guo, Y., Yang, J., and An, W. (2018). Learn-
ing multi-view representation with lstm for 3-d shape
recognition and retrieval. IEEE Transactions on Mul-
timedia, 21(5):1169–1182.
Mayer, N., Ilg, E., Hausser, P., Fischer, P., Cremers, D.,
Dosovitskiy, A., and Brox, T. (2016). A large dataset
to train convolutional networks for disparity, optical
flow, and scene flow estimation. In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition, pages 4040–4048.
Peng, F., Wang, L., Gong, J., and Wu, H. (2015). Devel-
opment of a framework for stereo image retrieval with
both height and planar features. IEEE Journal of Se-
lected Topics in Applied Earth Observation and Re-
mote Sensing, 8(2):800–815.
Sdiri, B., Kaaniche, M., Cheikh, F. A., Beghdadi, A., and
Elle, O. J. (2019). Efficient enhancement of stereo
endoscopic images based on joint wavelet decompo-
sition and binocular combination. IEEE Transactions
on Medical Imaging, 38(1):33–45.
Simonyan, K. and Zisserman, A. (2015). Very deep con-
volutional networks for large-scale image recognition.
In International Conference on Learning Representa-
tions.
Su, H., Maji, S., Kalogerakis, E., and Learned-Miller, E.
(2015). Multi-view convolutional neural networks for
3d shape recognition. In Proceedings of the IEEE
International Conference on Computer Vision, pages
945–953.
Tolias, G., Sicre, R., and J
´
egou, H. (2015). Particular object
retrieval with integral max-pooling of cnn activations.
arXiv preprint arXiv:1511.05879.
Tran, D., Ray, J., Shou, Z., Chang, S.-F., and Paluri, M.
(2017). Convnet architecture search for spatiotempo-
ral feature learning. arXiv preprint arXiv:1708.05038.
Zhang, B., Wang, L., Wang, Z., Qiao, Y., and Wang, H.
(2018). Real-time action recognition with deeply
transferred motion vector cnns. IEEE Transactions on
Image Processing, 27(5):2326–2339.
Zheng, L., Huang, Y., Lu, H., and Yang, Y. (2019). Pose-
invariant embedding for deep person re-identification.
IEEE Transactions on Image Processing, 28(9):4500–
4509.
An Effective 3D ResNet Architecture for Stereo Image Retrieval
387
