Segmented ECG Bio Identification using Fréchet Mean Distance

and Feature Matrices of Fiducial QRS Features

Abdullah Biran

and Aleksandar Jeremic

Department of Biomedical Engineering, McMaster University, Hamilton, Canada

Department of Electrical Engineering, McMaster University, Hamilton, Canada

Keywords: Biomedical Signal Processing, Biometrics, Electrocardiogram, QRS Segmentation, Short Time Fourier

Transform, Feature Lags.

Abstract: In this paper, we present a new segmented based method for human identification using Fréchet distances and

the characteristics of the lag-feature matrices of six fiducial based QRS features. We examined the

applicability of our methodology on 124 ECG records of 62 subjects from the publicly available ECG ID data

base. Our experiments show that the Fréchet distance can identify majority of the subjects (44 individuals)

using the feature matrix of QRS segment lagged by one beat with an identification accuracy ranging from

80% to 100%. Our preliminary results indicate that identifying humans using segmented approaches can be

potentially useful.

1 INTRODUCTION

One of the potential applications of wearable sensing

devices is human identification using biometric

signals. Historically, biometric has been using

fingerprinting and more recently iris scans. In

addition to identification accuracy issues some of the

currently used techniques can be either spoofed

and/or stolen. To this purpose, the identification using

in vivo signals has gained considerable research

interest in recent years. One of the most promising

techniques is based on the electrocardiography (ECG)

measurements. In addition to its in vivo

characteristics, ECG has robust advantages including

universality, hidden nature and simple acquisition

(Joao, S. Cardoso, & Lourenco, 2018). Generally,

ECG based human identification is done in two

different ways: fiducial points based and non-fiducial

feature based (Joao, S. Cardoso, & Lourenco, 2018).

The fiducial techniques relay on locating heartbeat

waveform points, onsets and offsets followed by

extracting different temporal, morphological and

amplitude features. The non-fiducial methods are

based on extracting features without relying on

segmentation algorithms such as using

autocorrelation and wavelet coefficients algorithms

(Chun Chi , Peng Tzu, & Pie Lun, 2019).

Many methods have been applied for personal

identification using ECG. Adrian et al. have

proposed a method using wavelet-based distance

measure for human identification (D.C. Chan, M.

Hamdy, Badre, & Badee, 2008). Saiful et al.

developed another method using the heartbeat

morphology features (Islam, Alajlan, Bazi, & S.

Hichri, 2012). Lin et al presented an algorithm by

applying non-linear Lyapunov exponents, root mean

square (RMS) and support vector machine (SVM)

(Lin, Chen, Lin, Yang, & Chiang, 2014).

Furthermore, Gutta and Cheng proposed discrete

cosine transform (DCT) and autocorrelation

techniques for extracting non-fiducial ECG features

(Gutta & Cheng, 2016). In contrast, Arteaga-Falconi

et al presented a numerical algorithm to extract

fiducial based time and amplitude features (Arteaga-

Falconi, Al Osman, & El Saddik, 2016). Moreover,

Biran et al. have developed segmented and non-

segmented techniques based on Short Time Fourier

Transform (STFT), Euclidian distance and Fréchet

distance to test the feasibility of using ECG as

biometric modality (Biran & Jeremic, Non-

Segmented ECG bio-Identification using Short Time

Fourier Transform and Frecht Mean Distance, 2020).

Liu et al. developed a multi scale autoregressive

model method (MSARM) for personal identification

using ECG (Liu, et al., 2018). Moreover, Sidek et al.

investigated the feasibility of ECG signal as biometric

Biran, A. and Jeremic, A.

Segmented ECG Bio Identiﬁcation using Fréchet Mean Distance and Feature Matrices of Fiducial QRS Features.

DOI: 10.5220/0010262302230227

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 223-227

ISBN: 978-989-758-490-9

223

modality in abnormal cardiac conditions (Sidek,

Khalil, & F. Jelinek, 2014). Furthermore, Odinaka et

al. proposed a multibiometric identification system

based on combining both the electrical originating

signal, the ECG, and the laser Doppler vibrometry

(LDV) (Odinaka, A. O’Sullivan, J. Sirevaag, & W.

Rohrbaugh, 2015).

In this study, we present a fiducial based method

using electrocardiogram (ECG) by creating four

feature matrices of QRS segments. We segment the

ECG signal using our results in (Biran & Jeremic,

Automatic QRS Detection and Segmentaion using

Short Time Fourier Transfrom and Feature Fusion,

2020). We randomize the training/testing procedures

and calculate feature matrices using four different

lags. We identify the subjects using the Fréchet

distance of feature matrices. In Figure 1 we illustrate

the outline of the methodology.

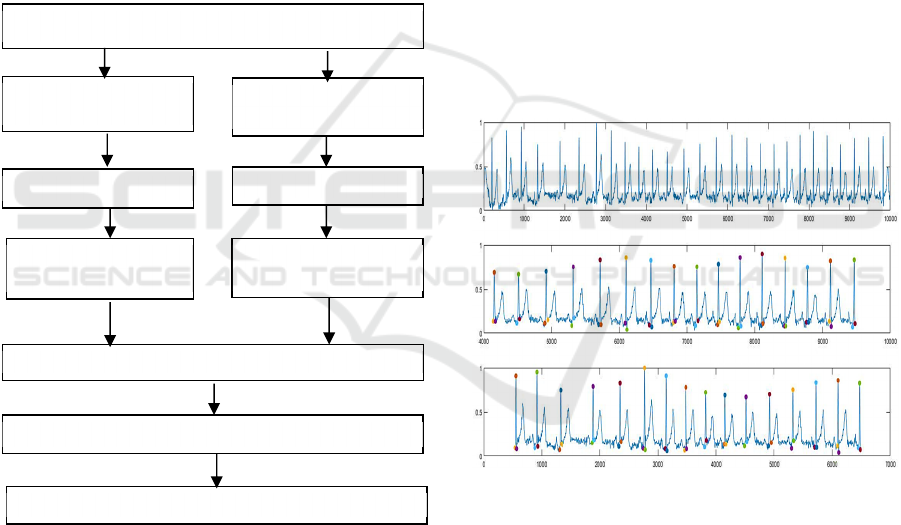
Figure 1: Block Diagram.

2 PROPOSED METHODOLOGY

2.1 ECG Database

In this study, we use filtered ECGs of 62 subjects

from the publicly available ECG ID database. The

ECG signals were measured using single lead at 500

sampling frequency and for a duration of 20 seconds.

The data record for each subject consists of two

measurements obtained at different times/days. In the

remainder of the paper, we use the normalized data as

it is commonly used procedure in many of the

machine learning based algorithms in order to

account for possible variability in signal range. In this

stage, we apply our previous work techniques on

automatically segmenting QRS peaks using

windowed STFT and QRS feature fusion. The

previously proposed method correctly and accurately

locates and segments the Q, R and S peaks. (Biran &

Jeremic, Automatic QRS Detection and Segmentaion

using Short Time Fourier Transfrom and Feature

Fusion, 2020).

Following majority of the methods that are used

for individual identification, we create two sets of

ECG data which are used for training \ referencing

and testing. To illustrate, we randomize the process

of selecting the QRS peaks in order to evaluate the

performance of the proposed algorithm. We

arbitrarily set the number of selected beats for both

test and reference ECG to 16. In Fig. 2 we show an

example of the randomization in the training and test

data selection.

Figure 2: An example of randomly selecting the training\

referencing and testing QRS waves.

2.2 QRS Feature Extraction

Using the results from our previous work we extract

the following features after aligning the

corresponding QRS segments: R-Q peak interval

( 𝑃



, S-R peak interval 𝑃



, R-Q amplitude

difference 𝑃



, R-S amplitude difference 𝑃



, QRS

wave distances 𝑃



, and slope distances of the QRS

wave𝑃



. Note that since the last two features are

calculated using the difference between the waves the

number of the feature measurements will be smaller

than the number of available heart beats.

Automatic QRS Segmentation using Windowed STFT

Randomly Selecting 16

training QRS Waves

Randomly Selecting 16

test QRS Waves

QRS Feature Extraction

Calculating feature

matrices.

Calculating feature

matrices

Applying Fréchet Mean distances

Finding the Fréchet based decisions

Calculating the identification accuracies

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

224

In order to perform the identification task, we propose

to calculate the feature matrices using the training set

and then to identify unknown subject by calculating

the distances between the testing data and training

data and select a subject with the smallest distance.

Let 𝐹



∊𝑅



and 𝐹



∊𝑅



be the feature

vectors for any two QRS waves, then we define the

cross-feature ( 𝐶𝐹 ) matrix between any two QRS

waves using equation (1).

𝐶𝐹 𝐹



𝐹





(1)

By utilizing equation (1), multiple cross-feature

matrices can be calculated by applying particular lags

between QRS waves. Accordingly, we apply

equation (2) to calculate the QRS feature matrices

from both the training and testing data sets.

𝐶𝐹





∑

















(2)

Where 𝐿 the lag coefficient, 𝐹 is the QRS feature

vector and 𝑛1 to 𝑐𝐿 is the index of QRS wave

where c is the number of segments.

Since we are using 4 different lags and we have two

set of QRS data (training and testing), by applying

equation (2), we define four training matrices and

four examining matrices of QRS features for each

subject.

2.3 Identification based on Fréchet

Distance

In this study, we apply the findings of Joromi’s work;

specifically, the Fréchet distance of covariance

matrices using Riemannian distances (Jahromi, 2014

). Technically, for any cross-feature matrix, we use

equation (3) to define the feature matrix

𝑅 𝐶𝐹



𝐶𝐹





(3)

Using equation (3) we first calculate the feature

matrix using training set and label them 𝐸



where L

is the lag coefficient and 𝑗1,2,….,𝑁 is the subject

number. Similarly, 𝑇



corresponds to lag l matrix

calculated using the test data. Then, we use the

following Fréchet distances between 𝑇



and 𝐸



𝐹𝑀𝐷1



𝑇𝑟



𝑇





 𝑇𝑟𝐸



2𝑇𝑟𝑇







𝐸



𝑇













(4)

𝐹𝑀𝐷2



𝑇𝑟



𝑇





 𝑇𝑟𝐸



2𝑇𝑟𝑇







𝐸







 (5)

where 𝑇𝑟 is trace of the matrix.

3 RESULTS

We have applied our algorithm on 124 ECGs of 62

subjects from the ECG ID database. We test the

performance of the proposed algorithm in terms of the

average personal identification accuracy, which is

computed using equation (6)

𝐴









∑

𝐹𝐵𝐷



 100





(6)

where is 𝐾 is the total number of experiments.

Consequently, to obtain the average performance,

we repeated the training and testing 10 times. Then

we use equation (13) to find the average personal

identification accuracy. As a result, Table 1 shows

that majority of the subjects (44 from record 1 and 43

from record 2 using FMD2) are correctly identified

with an average identification accuracy ranging from

80% to 100% at lag coefficient L = 1. In comparison,

40 subjects are correctly identified in the same

accuracy range by using FMD1. This shows that

FMD2 identifier has significantly better performance

compared to FMD1 as seen in Table 1, Figure 3 and

Figure 4. In addition, these findings indicate that

personal QRS features for most subjects remain stable

over one lag. However, for larger lag values, the

identification accuracy is fluctuating and is highly

dependent on the personal QRS properties. Figures 5

and 6 show examples of the fluctuating in the average

personal identification accuracy over the remaining

three lag coefficients.

4 CONCLUSIONS

In this paper, we proposed an automated fiducial

algorithm based on Fréchet distance and features of

QRS waves to identify subjects using their ECG. Our

preliminary results indicate that by measuring the

FMD2 distance between randomly created cross

feature matrices calculated by one beat lag, majority

of the individuals can be identified with high

accuracy range. Furthermore, applying different lag

coefficients can support the identification process

when the personal QRS feature remain stable over

time. Most importantly, our results indicate that the

ECG based human identification using fiducial

algorithms can achieve acceptable accuracy levels

Segmented ECG Bio Identiﬁcation using Fréchet Mean Distance and Feature Matrices of Fiducial QRS Features

225

Figure 3: The average personal accuracy for all subject after

10 experiments using FMD2 and lag coefficient L =1 of

randomly selected QRS waves from record 1. We can see

that majority of the subjects (44 subjects) have an

identification accuracy ranging from (80 % to 100%).

Figure 5: The personal identification accuracy (Y-axis) of

different subjects using FMD2 over 4 lag coefficients (X-

axis) after 10 experiments. The top two are from record 1

and the bottom two are from record 2.

Figure 4: The Average Personal Accuracy for All Subject

after 10 Experiments using FMD2 and Lag Coefficient L

=1 of Randomly Selected QRS Waves from Record 2. We

See Can That Majority of the Subjects (43 Subjects) Have

an Identification Accuracy Ranging from (80 % to 100%).

Figure 6: The personal identification accuracy (Y-axis) of

different subjects using FMD1 over 4 lag coefficients (X-

axis) after 10 experiments. The top two are from record 1

and the bottom two are from record 2.

50 60 70 80 90 100

SubjectNumber

PersonalIdentificationAccuracy(100%)

FMD2basedIdentificationusingQRSfromrecord

1atL=1

50 60 70 80 90 100

Subject Number

PersonalIdentificationAccuracy(100%)

FMD2basedIdentificationusingQRSfromrecord

2atL=

1

Subject 62 Subject 10

Subject 4 Subject 18

100

1234

100

1234

100

1234

100

1234

Subject 17 Subject 38

Subject 1 Subject 19

100

1234

100

1234

100

1234

100

1234

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

226

Table 1: The total number of subjects identified per

accuracy range over all the distance measurements and data

records.

Accuracy 50% 60% 70% 80% 90% 100%

FMD2,

record 1

2 8 8 15 15 14

FMD2,

record 2

2 2 15 23 11 9

FMD1,

record 1

2 6 14 20 8 12

FMD1,

record 2

5 6 11 11 10 19

REFERENCES

Arteaga-Falconi, J., Al Osman, H., & El Saddik, A. (2016,

March). ECG Authentication for Mobile Devices. IEEE

Transactions onInstrumentation and Mesurement, 65,

591-600.

Biran, A., & Jeremic, A. (2020). Automatic QRS Detection

and Segmentaion using Short Time Fourier Transfrom

and Feature Fusion. 33rd Canadian Conference on

Electrical and Computer Engineering. London.

Biran, A., & Jeremic, A. (2020). ECG Based Human

Identification using Short Time Fourier Transform and

Histograms of Fiducial QRS Features. 13th

International Joint Conf. on Biomedical Engineering

Systems and Technologies, (pp. 324-329). Malta.

Biran, A., & Jeremic, A. (2020). Non-Segmented ECG bio-

Identification using Short Time Fourier Transform and

Frecht Mean Distance. 42nd Annual International

Conference of the IEEE Engineering in Medicine and

Biology Society, (pp. 5506-5509). Montreal.

Chun Chi , W., Peng Tzu, C., & Pie Lun, H. (2019, May).

Cancelable Biometric Recognition With ECGs:

Subspace-Based Approaches. IEEE Transactions on

Forensics and Security, 14, 1323-1336.

D.C. Chan, A., M. Hamdy, M., Badre, A., & Badee, V.

(2008, February). Wavelet Distance Measure for

Person IdentificationUsing Electrocardiograms. IEEE

Transactions on Instrumentation, 57, 248-253.

David, C., Silva, H., Gamboa, H., Fred, A., & Figueiredo,

M. (2013, February). Novel fiducial and non-fiducial

approaches to electrocardiogram-based biometric sys-

tems. Institution of Engineering Technology, 2, 64-75.

Gutta, S., & Cheng, Q. (2016, March). Joint Feature

Extraction and Classifier Design for ECG-Based

Biometric Recognition. IEEEJournal of Biomedical

and Health Informatics, 20, 460-468.

Islam, S., Alajlan, N., Bazi, Y., & S. Hichri, H. (2012,

May). HBS: A Novel Biometric Feature Based

onHeartbeat Morphology. IEEEtransactions on

Information Technology in Biomedicine, 16, 445-453.

Jahromi, M. (2014 ). Frechet Means with Respect to the

Riemannian Distances: Evaluations and Applications .

McMaster University .

Joao, R. P., S. Cardoso, J., & Lourenco, A. (2018, June ).

Evolution, Current challenges, and Future Possibilities

in ECG Biometrics. IEEE Access, 6, 34746-34776.

Li, H., & Jeremic, A. (2017). Semi-supervised Distributed

Clustering for Bioinformatics - Comparison Study., 4,

pp. 259-264.

Lin, S.-L., Chen, C.-K., Lin, C.-L., Yang, W.-C., & Chiang,

C.-T. (2014). Individual identification based on chaotic

electrocardiogram signals during muscular exercise.

The Institution of Engineering.

Liu, J., Yin, L., He, C., Wen, B., Hong, X., & Li, Y. (2018).

A Multiscale Autoregressive Model-Based Electro-

cardiogram Identification Method. IEEE Access,

18251-18263.

Odinaka, I., A. O’Sullivan, J., J. Sirevaag, E., & W.

Rohrbaugh, J. (2015, January). Cardiovascular

Biometrics: Combining Mechanical and Electrical

Signals. IEEE Transactions on Information on

Forensics and Security, 10, 16-27.

Odinaka, I., Lai, P.-H., D. Kaplan, A., A. O’Sullivan, J., J.

Sirevaag, E., & W. Rohrbaugh, J. (2012, December).

ECG Biometric Recognition: A Comparative Analysis.

IEEE Transactions on Information on Forensics and

Security, 7, 1812-1824.

Sidek, K., Khalil, I., & F. Jelinek, H. (2014, November).

ECG Biometric with Abnormal Cardiac Conditions in

Remote Monitoring System. ECG Biometric with

Abnormal Cardiac Conditions, 44, 1498-1509.

V. Oppenheim, A., & W. Schafer, R. (1989). Discrete-Time

Signal Processing. New Jersey: Prentie-Hall, Inc.

Zhang , Q., Zhou, D., & Zeng, X. (2017). HeartID: A

Multiresolution Convolutional Neural Network for

ECG-Based Biometric Human Identification in Smart

Health Applications. IEEE Access, 5, 11805-11816.

Segmented ECG Bio Identiﬁcation using Fréchet Mean Distance and Feature Matrices of Fiducial QRS Features

227