Classiﬁcation of Myoelectric Surface Signals of Hand Movements using

Supervised Learning Techniques

Marisol Cristel Galarza Flores

, Juan Felipe Miranda Medina

and Cristian L

opez del

Alamo

Universidad Nacional de San Agust

ın de Arequipa (UNSA), Arequipa, Peru

Keywords:

Electromyography, Support Vector Machines, Neural Networks, Wavelets, Principal Component Analysis.

Abstract:

This work presents a comparative study of techniques to classify four hand movements (ﬂexion, extension,

opening and closure) using myoelectric signals measured at the forearm in two separate channels: the bra-

chioradialis and the ﬂexor carpi ulnaris (FCU) muscle. The process of signal acquisition is described, as well

as signal normalization, hybrid feature extraction and classiﬁcation using two supervised learning techniques;

i.e., backpropagation and support vector machines. The classiﬁers were trained using the raw data from the

input signal. It was veriﬁed that the accuracy of the classiﬁcation is improved by feature extraction up to

2.25%, yielding a successful average classiﬁcation rate of 91.00%.

1 INTRODUCTION

Experiments related to electromyography (EMG) are

linked to the discovery of electricity in the late 16th

century (Kazamel and Warren, 2017). The array of

possibilities arising from the measurement of EMG

signals, however, was better understood only in the

20th century with the development of electronics and

programming: myoelectric prosthesis for amputees,

bionic exoskeletons, and teleoperated robots for mi-

crosurgeries or explosive deactivation are all current

applications that continue to be researched (Cabrera

and Jaramillo, 2010). The analysis of EMG signals,

however, is not exempt from challenges, since the

measured potentials present low amplitude and are

strongly non-stationary and the initial data is poorly

structured. There is thus the need to “develop new ef-

fective methods” for the analysis of EMG signals and

for their application to the study of human motricity

(Kurkin et al., 2019).

Earlier studies about the classiﬁcation of myo-

electric signals deployed neural networks (Hudgins

et al., 1993; Haihua et al., 2005; Durgesh and Lekha,

2010), ARTMAP (Carre

no and Vuskovic, 2005) and

Euclidean distance (Ferguson and Dunlop, 2002) as

classiﬁcation methods. More recent research, such as

the survey by (Kehri et al., 2016) identiﬁes Wavelets,

https://orcid.org/0000-0001-6419-0761

https://orcid.org/0000-0002-5239-2718

https://orcid.org/0000-0002-2568-650X

Principal Component Analysis (PCA), Support Vec-

tor Machines (SVM) and Neural Networks (NN) as

key techniques for EMG signal analysis. Further-

more, the studies by (Gupta et al., 2017) and (Sat-

apathy et al., 2019) emphasize on SVM and neural

networks as particularly relevant classiﬁcation tech-

niques.

This work is aimed towards the classiﬁcation of

four different hand movements (i.e., ﬂexion, exten-

sion, hand opening and hand closure) utilizing mea-

surements of EMG signals in the forearm. In this

respect, the comparative study by (Wołczowski and

Zdunek, 2017) shows that in general, higher rates of

accuracy (approximately 95 %) with lower compu-

tational complexity can be achieved utilizing feature

extraction techniques, thus outperforming conven-

tional methods such as Principal Component Analy-

sis (PCA). This is a key motivation in the method-

ology of this work, since its chief contribution is a

comparison accross two different processes. The ﬁrst

one refers to feature extraction, where we resort to

a hybrid approach combining (1) univariate selection

with a Chi-square distribution (henceforth referred to

as χ2) with Principal Component Analysis (PCA), (2)

χ2 with Wavelets, and (3) χ2 with PCA and Wavelets.

The second process corresponds to classiﬁcation al-

gorithms; we present a comparison of classiﬁcation

accuracy of back-propagation neural networks against

Support Vector Machines (SVM) for each of the three

feature extraction methods. Although the methods

Flores, M., Medina, J. and Álamo, C.

Classiﬁcation of Myoelectric Surface Signals of Hand Movements using Supervised Learning Techniques.

DOI: 10.5220/0010281802430251

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 243-251

ISBN: 978-989-758-490-9

243

deployed in this research have already been used by

other research groups for EMG signal classiﬁcation,

the novelty of this work is the comparative study that

can be helpful to plan similar experiments in the fu-

ture.

2 PREVIOUS WORK

ucel and Mehmet, 2001) and (Ferguson and Dun-

lop, 2002) proposed the extraction of signal features

prior to classiﬁcation. For their study they deployed

the Wavelet transform with principal components as

a feature extractor. In 2004, hybrid feature vec-

tors were proposed. In this regard, (Kilby and Hos-

seini, 2004) made a comparison of different Wavelet

families with DWT and WPT, concluding that the

Wavelets that yielded the best results for EMG sig-

nals where Daubechies, Summlet and Coiﬂet. On

the other hand, (Hargrove et al., 2007) classiﬁed 6

patterns of movement based on surface EMG signals

and EMG intramuscular signals. Their hypothesis

was that crosstalk would be weaker in intramuscu-

lar signals, which would allow for a better classiﬁ-

cation. Nevertheless, they found that there was no

signiﬁcant difference in the accuracy of the classiﬁca-

tion. In 2015, (Quinay

as-Burgos and Gaviria-L

opez,

2015) developed a two-channel system to detect the

intention of movement, achieving an accuracy per-

centage of 85 and 92.5% in the classiﬁcation of four

different movements, utilizing a hybrid vector of sta-

tistical components as a feature extractor. In 2016

they developed a classiﬁer based on a backpropaga-

tion neural network utilizing wavelength as the fea-

ture in the time domain for the feature extractor, ex-

tracting EMG signals to classify ﬁve different move-

ments, obtaining an accuracy percentage of 75.54%

± 5.17 and 67.37% ± 8.75. It was thus shown that

accuracy in movement classiﬁcation is not dependent

on the number of electrodes deployed. A better classi-

ﬁcation rate can be achieved by placing the electrodes

on the main muscles relative to the movement being

performed, instead of utilizing a large amount of elec-

trodes (Irastorza-Landa et al., 2017).

3 METHODOLOGY

Upon reviewing the state of the art, we concluded that

the classiﬁer that was most deployed was the back-

propagation neural network. In order to have a ref-

erence of comparison for this classiﬁer, we decided

to use support vector machines (SVM) as well. Re-

garding feature extraction, we chose a hybrid vector

with Wavelet transform components, for it was the

most deployed method. We chose principal compo-

nent analysis as well because it had the best results

in the literature and we added the univariate selection

method to our list, utilizing the Chi-square (χ2) dis-

tribution. The methodology we suggest is represented

in Figure 1.

In the development of this work, the following

activities were carried out: signal acquisition (Sec-

tion 3.1), signal preprocessing (Section 3.2), extrac-

tion of signal features (Section 3.3), signal classiﬁca-

tion (Section 3.4), result comparison (Section 4) and

conclusions from test analysis and results (Section 5).

3.1 Signal Acquisition

3.1.1 Features of the EMG Signal

An EMG signal has a typical amplitude that varies

between 0 and 6mV, and its useful frequency lies in

the range of 0 to 500 Hz although most part of the

energy is concentrated between 50 and 150 Hz (Ger-

dle et al., 1999). According to the Nyquist-Shannon

theorem, if the highest frequency contained in an ana-

log signal x

(t) is F

max

= B and the signal is sampled

at a rate F

> 2F

max

≡ 2B, then x

(t) can be fully re-

covered. If this criterion is not satisﬁed, there will

be frequency overlapping, otherwise known as alias-

ing. For this project, the sampling frequency had to

be at least greater than 300 Hz, therefore we chose to

sample every 2 ms, which is equivalent to a 500 Hz

sampling frequency. On the other hand, according to

(Birkedal et al., 2002), the ﬁrst 400 ms of a muscu-

lar movement are enough for the identiﬁcation of the

movement, therefore the signals were recorded with a

window of 400 ms. With these considerations, sam-

ples of four movements were taken in 10 different

participants, 10 samples for each one of them. The

participants did not perform any signiﬁcant physical

effort 24 hours prior to the experiment.

3.1.2 Electrode Placement

One of the most controversial aspects of surface EMG

is the placement of the electrodes (Aaron, 2010).

That is why, the Surface Electromyography for Non-

invasive Assessment of Muscles (SENIAM) standard

was elaborated in Europe to provide speciﬁc rec-

ommendations regarding the location, the size and

the shape of the electrodes (Hermens and Freriks,

1997). According to the SENIAM standard, the rec-

ommended value for the diameter of the electrodes

is 10 mm, while the inter-electrode distance, deﬁned

as the center-to-center distance of the conductive area

of the electrodes, should be 2 cm. For the shape of

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

244

Figure 1: Suggested methodology for signal classiﬁcation. Source: prepared by the authors.

the electrode, deﬁned as the conductive area that is

in touch with the skin, most of the literature recom-

mends a circular shape (Merletti and Parker, 2004).

In this study, the following signal characteristics

and process for signal acquisition where selected:

1. Superﬁcial (non-invasive) Ag-Cl electrodes.

2. The participants’ skin was disinfected with alco-

hol. In addition, the electrodes carried the saline

solution for the transmission of the electric im-

pulse.

3. The participant’s initial posture for signal acquisi-

tion is shown in Figure 2.

Figure 2: Initial position for signal acquisition. Source: pre-

pared by the authors.

4. For this study we chose the motor points of the

brachioradialis and the ﬂexor carpi ulnaris muscle

(FCU) muscle as shown in Figures 3 and 4.

5. The inter-electrode distance is 2 cm, and the

grounded electrode will be placed in the area near-

est to the elbow.

6. After placing the electrodes, the signals will be

visually inspected on the oscilloscope.

3.2 Signal Preprocessing

3.2.1 Sensing of the EMG Signal

Myoelectric signals are characterized by low ampli-

tude levels (typically between 0 and 6 mV) and there-

fore the sensing mechanism must include a low noise

ampliﬁer. A passband ﬁlter is also required since the

Figure 3: Electrode position in the brachioradialis. Source:

prepared by the authors.

Figure 4: Electrode position in the FCU muscle. Source:

prepared by the authors.

signal’s energy is concentrated around a 50 to 150 Hz

bandwidth. Furthermore, the signal must be condi-

tioned according to the input of the microcontroller

carrying out the signal processing. A sensor was fab-

ricated that included the stages of ampliﬁcation, ﬁlter-

ing and conditioning following the method proposed

by (Gomero et al., 2009). Upon comparing its per-

formance to the MyoWare Muscle sensor (MyoWare.,

2015), however, the latter yielded better results and

was therefore chosen for this project.

The resulting architecture of the sensing interface

was compact: it consisted of two MyoWare muscle

sensors (each of which includes low-noise ampliﬁca-

tion, passband ﬁltering and signal conditioning), an

Arduino Mega microcontroller (that converts the ana-

log input into a digital binary stream), and an SD

memory that stores the digitized version of the elec-

Classiﬁcation of Myoelectric Surface Signals of Hand Movements using Supervised Learning Techniques

245

tromyographic signal into a CSV ﬁle. The reason for

using two sensors rather than one is that, according

to our medical consultant Dante Condori, at least two

different channels are needed in order to detect four

different hand movements.

3.2.2 Signal Normalization

Each channel was normalized separately subtracting

the average offset amplitude to each measured input

signal. This is because each participant had a different

average offset amplitude value which corresponds to

the average of the signal measurement when the arm

is at rest.

3.3 Feature Extraction

3.3.1 Wavelet Transform

The Wavelet transform provides simultaneous infor-

mation both in the time and the frequency domains.

One of its most important parameters is the resolution

of the transform, associated with the level of decom-

position to be deployed (Mallat, 1991). The Wavelet

transform is used to analyze time series that contain

non-stationary signals in a wide frequency range (Tor-

rence and Compo, 1998), and is given by:

(s, τ) =

f (t)ψ

∗

s,τ

(t)dt , (1)

where f (t) is the signal being analyzed, ψ

∗

s,τ

(t) is the

expansion function or basis, i.e., the Wavelet func-

tion, and W

(s, τ) is the resulting Wavelet transform.

Wavelets are generated from the translation and scale

variation of the same Wavelet function ψ(t), known

as the “mother Wavelet”. In this work, we deploy as

part of the characteristic vector of the EMG signal the

approximation coeﬁcients (cA) of the mother Wavelet

Daubechies 4 (db4).

3.3.2 Principal Component Analysis (PCA)

The PCA algorithm starts from a mutually correlated

data set, and returns a set of information without any

linear correlation. The extractor of PCA character-

istics is most effective when there is a high correla-

tion in the variables of the input data (Daniel, 2015).

In this work, the ﬁrst 100 principal components were

taken to form the characteristic vector.

The determination of the number of principal components

is also possible by means of statistical inference methods,

as the work of (Liu, 2017) illustrates.

3.3.3 Univariate Selection

This feature selection is based on picking the N char-

acteristics with greater correlation with the expected

output. The Chi-square function was chosen for this

test. It was used to compare the observed frequen-

cies with the expected frequencies. In our classiﬁca-

tion method each of the four hand movements cor-

responds to a class. The classiﬁer returns one of the

four classes as an output given the measured input sig-

nals for a given participant. To verify that the number

of observed results in each class corresponds approx-

imately to the expected number, we make use of hy-

pothesis contrast utilizing the Chi-square distribution:

∗

∑

i=1

− E

)

. (2)

From this equation we have that the lower the χ

∗

value is, the higher the correlation between the ob-

served and the expected frequencies.

3.4 Classiﬁers

3.4.1 SVM

Support vector machine (SVM) is a classiﬁcation

technique based on exact mathematical models. To

achieve optimal results, cross-validation (Durgesh

and Lekha, 2010) on ten different test groups was de-

ployed.

SVM maps an input vector (input data) in a higher

spacial dimension, in which a maximal separation hy-

perplane is constructed. Two parallel hyperplanes are

constructed on each side of the hyperplane separating

the data. The separation hyperplane (MMH) is the

hyperplane that maximizes the distance between two

parallel hyperplanes. It is assumed that the higher the

margin or distance between the parallel hyperplanes,

the better the class separation will be (Vapnik, 2013).

If we consider Figure 5, we can see that the hy-

perplane of maximal margin is the medium line of

the widest “block” that we can insert between the two

classes so that they are perfectly separated.

3.4.2 Non-linear SVM

Not every problem is linearly separable. Therefore,

different kernels are required depending on the sets of

classes that are separated. The use of other kernels

offers a greater ﬂexibility, allowing for a greater sep-

arability margin of non-linear and multidimensional

classes. SVM allows for non-linear kernels such as

the polynomial and radial kernels shown in Figure

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

246

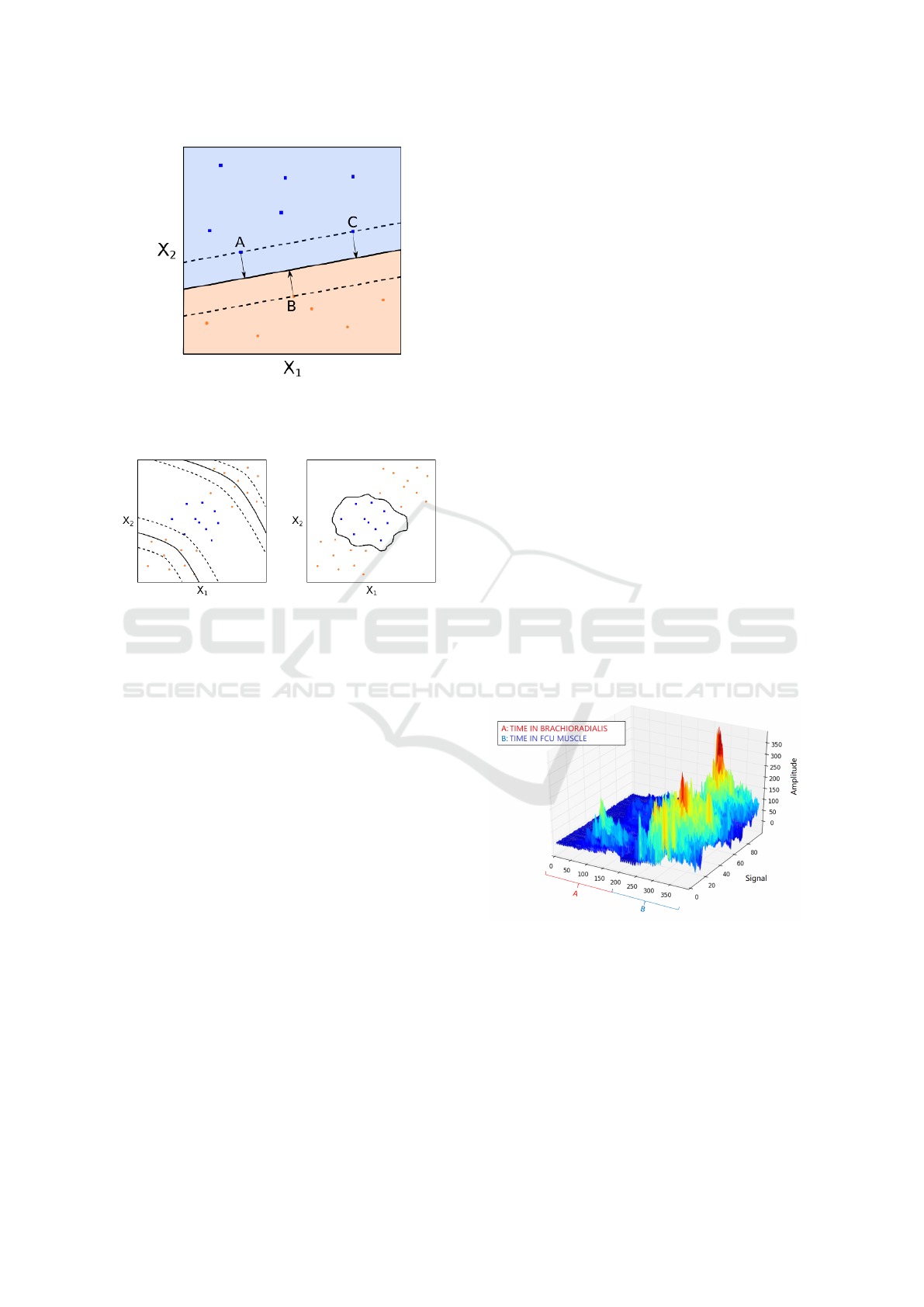
Figure 5: Maximal margin of the hyperplane with SVM for

points A, B and C. X

and X

represent each dimension of

a linearly separable two-dimensional hyperplane. Source:

(Quantstart., 2014).

Figure 6: SVM classiﬁcation with polynomial and radial

kernels, respectively. X

and X

represent each a dimen-

sion of a two-dimensional non-linearly separable hyper-

plane. Source: (Quantstart., 2014).

6. In this work, the radial kernel was deployed be-

cause the set of signals was not linearly separable, and

cross-validation was utilized for tests.

3.4.3 Neural Networks

Artiﬁcial neural networks are a computational repre-

sentation of complex biological systems formed by

numerous nervous cells that work in parallel and im-

plement learning functions in the form of iterative

adaptation of their parameters. They aim at charac-

teristics such as auto-organization, learning capacity,

generalization capacity and robustness against failure

(Anderson, 1995).

For this research we used a backpropagation neu-

ral network with a sigmoid activation function shaped

as a hyperbolic tangent that maps values in the range

(−1, 1). The network has two hidden layers, the ﬁrst

one with 100 neurons and the second one with 30 neu-

rons. This was the distribution that performed best in

a number of trials varying the number of neurons and

hidden layers.

4 TESTS AND RESULTS

Two classiﬁers were proposed: the support vector ma-

chine (SVM) and backpropagation neural networks.

Four different hand movements were studied (ﬂexion,

extension, hand opening and hand closure) and hun-

dred samples were extracted for each movement. This

data was gathered from ten test participants.

Figures 7, 8, 9 and 10, display the hundred regis-

tered signals for the movements of ﬂexion, extension,

hand opening and hand closure, respectively. In the X

axis an interval of 400 is observed which represents

the ﬁrst 200 movement takes of the corresponding

movement in the brachioradial muscle and the sec-

ond 200 takes represent the corresponding movement

in the FCU muscle. In the Y axis an interval of 100

is observed, where each number is a registered sig-

nal (from the 100 signals taken for each movement).

Low and high amplitudes of the input in the Z axis

correspond to blue and red colors, respectively.

The ﬁgures show that there are clear identiﬁca-

tion patterns for each movement, where the pattern

of the brachioradialis and FCU muscle is different in

amplitude and activation instant for each movement.

This is why a supervised learning method can clas-

sify these patterns in one of the four movements that

this work studies. All tests were conducted using

cross-validation as a technique for statistical analysis

to guarantee that the results are independent from the

partition between training data and test data.

Figure 7: Signals for the ﬂexion movement. The X axis rep-

resents the 200 takes in the brachioradialis and FCU muscle.

The Y axis represents each registered signal, and the Z axis

represents the signal amplitude. Source: prepared by the

authors.

4.1 Results

Three hybrid feature vectors were deployed in the

tests: (1) PCA and Chi-square, (2) Wavelet approx-

imation coefﬁcients and Chi-square, and (3) PCA

Classiﬁcation of Myoelectric Surface Signals of Hand Movements using Supervised Learning Techniques

247

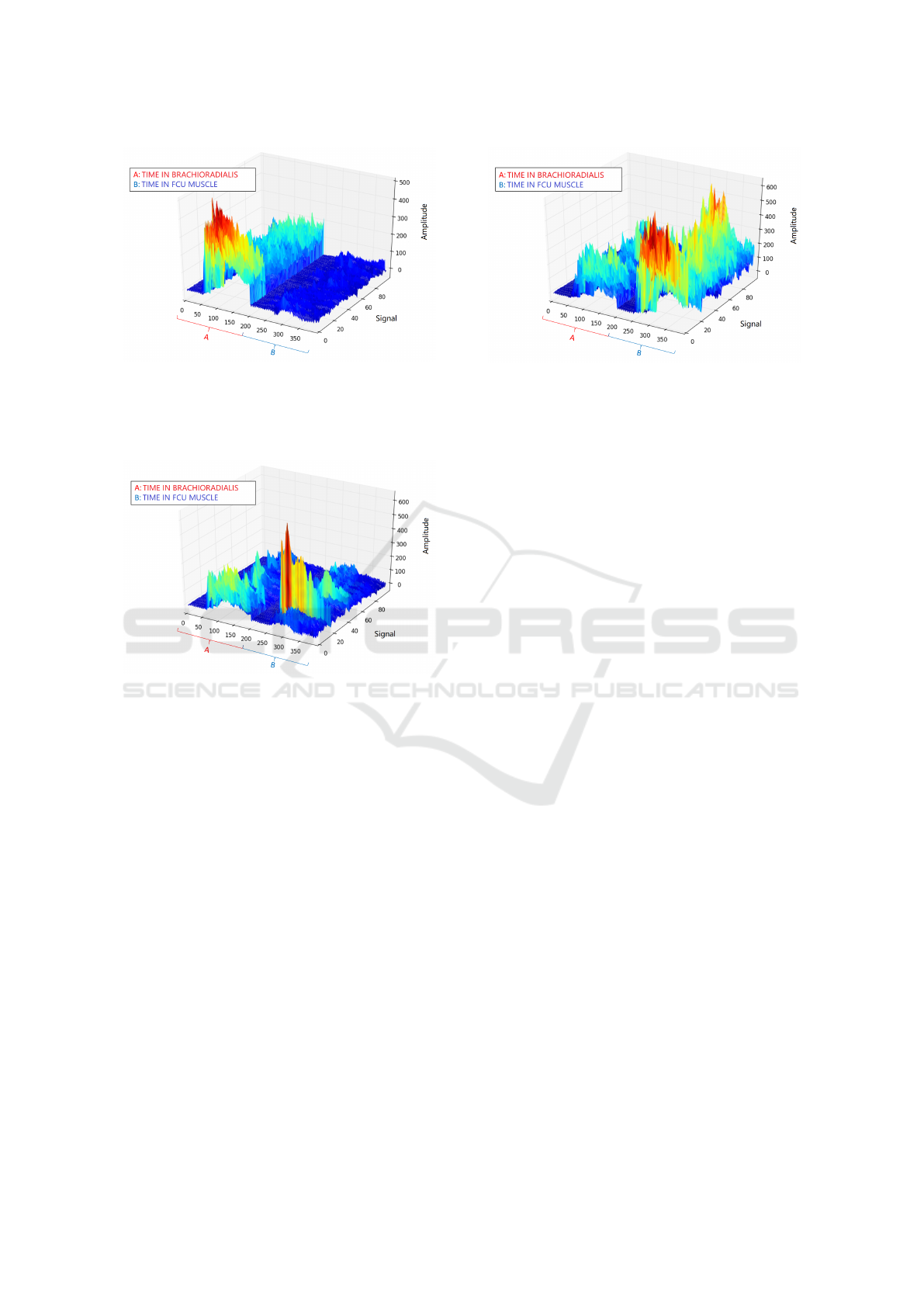
Figure 8: Signals for the extension movement. The X axis

represents the 200 takes in the brachioradialis and FCU

muscle. The Y axis represents each registered signal, and

the Z axis represents the signal amplitude. Source: prepared

by the authors.

Figure 9: Signals for the hand opening movement. The X

axis represents the 200 takes in the brachioradialis and FCU

muscle. The Y axis represents each registered signal, and

the Z axis represents the signal amplitude. Source: prepared

by the authors.

combined with Wavelet approximation coefﬁcients

and Chi-square. Each of these vectors was tested with

the two classiﬁers, namely SVM and backpropagation

neural networks. Some tests were also conducted with

the normalized original data, using the same classi-

ﬁers, to test if the feature extraction improved the de-

tection percentaje of the corresponding class.

4.1.1 Results with SVM

In this work we utilized the radial basis function ker-

nel. Tests were conducted with the four movements.

The results were estimated on the sample of 100 sig-

nals for each movement, deploying cross-validation

with 10 different groups of 90 signals of training and

10 test signals.

Different characteristic vectors were explored thus

obtaining a classiﬁcation accuracy of 88.75 % for the

original data without feature extraction, 91.00 % for

PCA and Chi-square, 91.00 % for Wavelet and Chi-

Figure 10: Signals for the hand closure movement. The

X axis represents the 200 takes in the brachioradialis and

ﬂexor cubital muscles. The Y axis represents each regis-

tered signal, and the Z axis represents the signal amplitude.

Source: prepared by the authors.

square, 89.00 % for PCA, Wavelets and Chi-square.

The details of the classiﬁcation for each movement

can be observed in Table 1.

From Table 1 we can see that the movement that

was hardest to detect with SVM was ﬂexion, while

the movement that is detected with highest accuracy

is extension. The best results were achieved with hy-

brid features vectors: Chi-square and PCA; and Chi-

square and wavelets, where an average detection ac-

curacy of 91.00 % in the classiﬁcation of the four

movements was achieved. These vectors improved in

2.25 % respect to classiﬁcation without feature extrac-

tion. The vector composed of Chi-square, PCA and

Wavelets did not improve the classiﬁcation accuracy

signiﬁcantly.

4.1.2 Results with Neural Networks

The results are estimated from the sampling of 100

signals for each movement, using cross-validation

with 10 different test groups of 90 training signals and

10 test signals.

Different feature vectors were tested yielding a

detection accuracy of 86.25 % for the original data,

82.00 % for PCA and Chi-square, 82.00 % for

Wavelet and Chi-square, and 89.00 % for PCA,

Wavelet and Chi-square. The details of the classiﬁ-

cation for each movement can be observed in Table 2.

From the Table 2 we can see that the movement

that was most difﬁcult to detect using backpropaga-

tion neural networks is hand opening, while the move-

ment that is detected with the highest accuracy is ex-

tension. This movement is the same as the highest

detection accuracy movement using SVM. The best

results were obtained with the hybrid feature vector:

PCA, χ

and Wavelets, where an average detection

accuracy of 89 % was achieved in the classiﬁcation of

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

248

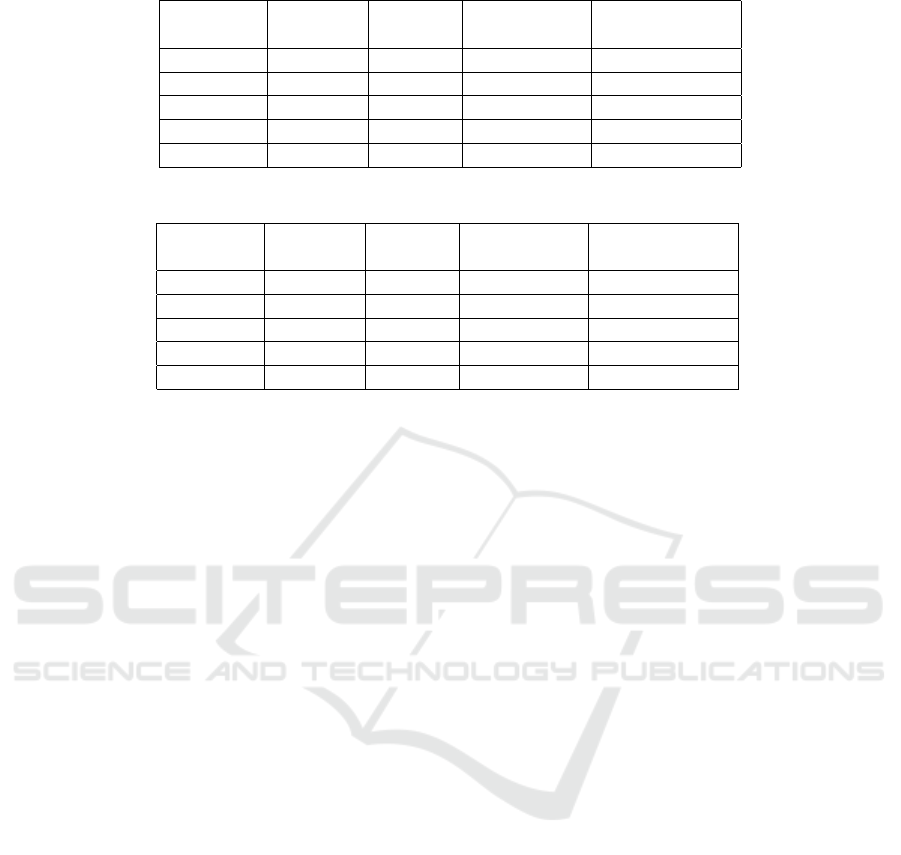
Table 1: Classiﬁcation accuracy with SVM.

Raw data χ

, PCA χ

, Wavelets

PCA, Wavelets

Flexion 86.00% 85.67% 85.67% 85.33%

Extension 94.67% 96.00% 96.00% 93.00%

Opening 86.00% 91.00% 91.00% 89.00%

Closure 88.33% 90.33% 90.33% 87.00%

Total 88.75% 91.00% 91.00% 89.00%

Table 2: Classiﬁcation accuracy with backpropagation neural networks.

Raw data χ

, PCA χ

, Wavelets

PCA, Wavelets

Flexion 83.00% 81.33% 81.33% 88.67%

Extension 92.67% 92.00% 92.00% 92.00%

Opening 81.33% 72.67% 72.67% 82.33%

Closure 88.00% 82.00% 82.00% 92.00%

Total 86.25% 82.00% 82.00% 89.00%

the four movements. This vector improved in 2.75 %

the result of the classiﬁcation. It is also observed that

the vectors formed by χ

and PCA; as well as χ

and

Wavelets, did not improve the accuracy of the classi-

ﬁcation without feature extraction.

In general, the highest average classiﬁcation ac-

curacy obtained in this work (over 90 %) is at the

level of the state of the art in the literature utilizing

soﬁsticated but more complex methods such as ma-

chine learning (Mora Rubio et al., 2020), ternary pat-

tern and discrete wavelet based iterative feature ex-

traction (Tuncer et al., 2020) and convolutional neural

networks with intrinsic feature extraction capabilities

(Zia ur Rehman et al., 2018).

5 CONCLUSIONS

This work has provided a comparison of different

methods for the classiﬁcation of four different hand

movements (extension, ﬂexion, hand opening, hand

closure) across two different lines. First, a compar-

ison of methods for feature extraction (χ

and PCA,

and Wavelets) and second, a comparison of meth-

ods for classiﬁcation (namely neural networks and

support vector machines). We have shown that the

SVM supervised classiﬁer has a better performance

than backpropagation neural networks for the classiﬁ-

cation of these four movements, and that these can be

recognized taking the ﬁrst 400 ms of the brachioradi-

alis and ﬂexor carpi ulnaris muscle (FCU) as an input.

With SVM, an accuracy of 91.00 % was achieved us-

ing a hybrid characteristic vector with components of

approximation coefﬁcients of Wavelet transform and

Chi-square. Likewise, an accuracy of 91.00 % was

also achieved deploying a hybrid characteristic vec-

tor constituted by the hundred principal components

(PCA) and Chi-square.

It was also observed that for the SVM classiﬁer,

ﬂexion was the most difﬁcult movement to detect,

while opening the hand was the most difﬁcult move-

ment for neural networks. On the other hand, in all

confusion matrices, the movement causing the most

classiﬁcation errors was closing the hand in the case

of SVM, while for backpropagation neural networks

both opening the hand and ﬂexing were problematic.

A greater number of distinct movements could be de-

tected if more channels were used. Nevertheless, the

high accuracy obtained with SVM, i.e., over 90 % is

comparable to other methods in the state of the art that

are computationally more expensive.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the Univer-

sidad Nacional de San Agust

ın de Arequipa (UNSA)

for ﬁnancing this research project with contract num-

ber N

◦

0091-2016-UNSA; to Imagine Labs team for

their valuable collaboration; to CiTeSoft UNSA, Al-

fredo Paz, Erasmo Sulla and Dante Condori for their

time and support; to Jorge Segura for his most gener-

ous technical contribution, and to all those who par-

took in this study, either as participants or motiva-

tional agents.

Classiﬁcation of Myoelectric Surface Signals of Hand Movements using Supervised Learning Techniques

249

REFERENCES

Aaron, C. G. I. (2010). Dise

no y construcci

on de un sistema

para la detecci

on de se

nales electromiogr

aﬁcas. PhD

thesis, Universidad Aut

onoma de Yucat

an, Mexico.

Anderson, J. A. (1995). An introduction to neural networks.

MIT press.

Birkedal, L., Collet, T., Dagilis, S., Delavernhe, G., and

Emborg (2002). Pattern recognition of upper-body

electromyography for control of lower limb prosthe-

ses. Institute of Electronic Systems, Aalborg Univer-

sity.

Cabrera, J. S. and Jaramillo, H. F. (2010). Mejora de pro-

cesos para el desarrollo de dispositivos prost

eticos de

mano. Ingenium, (21).

Carre

no, I. and Vuskovic, M. (2005). Wavelet-based fea-

ture extraction from prehensile emg signals. 13th

NordicBaltic on Biomedical Engineering and Medical

Physics (NBC’05 UMEA), pages 13–17.

Daniel, L. (2015). Un ejemplo sencillo sobre an

alisis de

componentes principales (pca, principal component

analysis). https://dlegorreta.wordpress.com.

Durgesh, K. S. and Lekha, B. (2010). Data classiﬁcation

using support vector machine. Journal of Theoretical

and Applied Information Technology, 12(1):1–7.

Ferguson, S. and Dunlop, G. R. (2002). Grasp recog-

nition from myoelectric signals. In Proceedings of

the Australasian Conference on Robotics and Automa-

tion, Auckland, New Zealand, volume 1.

Gerdle, B., Karlsson, S., Day, S., and Djupsj

obacka, M.

(1999). Acquisition, processing and analysis of the

surface electromyogram. In Modern techniques in

neuroscience research, pages 705–755. Springer.

Gomero, F. N. C., Campos, F. D. R., and Ch

avez,

S. J. Z. (2009). M

odulo de detecci

on, reg-

istro y presentaci

on de se

nales electrooculogr

aﬁcas.

Electr

onica-UNMSM, (24):3–12.

Gupta, T., Yadav, J., Chaudhary, S., and Agarwal, U.

(2017). Emg pattern classiﬁcation using neural net-

works. In The International Symposium on Intelligent

Systems Technologies and Applications, pages 232–

242. Springer.

Haihua, L., Xinhao, C., and Yaguang, C. (2005). Wavelet

transform analyzing and real-time learning method for

myoelectric signal in motion discrimination. In Neu-

ral Interface and Control, 2005. Proceedings. 2005

First International Conference on, pages 127–130.

IEEE.

Hargrove, L. J., Englehart, K., and Hudgins, B. (2007). A

comparison of surface and intramuscular myoelectric

signal classiﬁcation. IEEE transactions on biomedical

engineering, 54(5):847–853.

Hermens, H. and Freriks, B. (1997). The state of the art on

sensors and sensor placement procedures for surface

electromyography: a proposal for sensor placement

procedures. Deliverable of the SENIAM Project.

Hudgins, B., Parker, P., and Scott, R. N. (1993). A new

strategy for multifunction myoelectric control. IEEE

Transactions on Biomedical Engineering, 40(1):82–

94.

Irastorza-Landa, N., Sarasola-Sanz, A., Shiman, F., L

opez-

Larraz, E., Klein, J., Valencia, D., Belloso, A.,

Morin, F., Birbaumer, N., and Ramos-Murguialday,

A. (2017). Emg discrete classiﬁcation towards a my-

oelectric control of a robotic exoskeleton in motor re-

habilitation. In Converging Clinical and Engineering

Research on Neurorehabilitation II, pages 159–163.

Springer.

Kazamel, M. and Warren, P. P. (2017). History of elec-

tromyography and nerve conduction studies: A trib-

ute to the founding fathers. Journal of Clinical Neu-

roscience, 43:54–60.

Kehri, V., Ingle, R., Awale, R., and Oimbe, S. (2016). Tech-

niques of emg signal analysis and classiﬁcation of

neuromuscular diseases. In International Conference

on Communication and Signal Processing 2016 (IC-

CASP 2016). Atlantis Press.

Kilby, J. and Hosseini, H. G. (2004). Wavelet analysis of

surface electromyography signals. In Engineering in

Medicine and Biology Society, 2004. IEMBS’04. 26th

Annual International Conference of the IEEE, vol-

ume 1, pages 384–387. IEEE.

Kurkin, S. A., Khorev, V., Pitsik, E. N., Maksimenko, V. A.,

and Hramov, A. E. (2019). The approach to the detec-

tion of the movement precursor by electromyographic

signals. In ICINCO (1), pages 276–280.

Liu, Y. (2017). Statistical inference in principal component

analysis based on statistical theory. Italian Journal of

Pure and Applied Mathematics, (37):565–574.

Mallat, S. (1991). Zero-crossings of a wavelet trans-

form. IEEE Transactions on Information theory,

37(4):1019–1033.

Merletti, R. and Parker, P. A. (2004). Electromyography:

physiology, engineering, and non-invasive applica-

tions, volume 11. John Wiley & Sons.

Mora Rubio, A., Alzate Grisales, J. A., Tabares-Soto,

R., Orozco-Arias, S., Jim

enez Var

on, C. F., and

Padilla Buritic’a, J. I. (2020). Identiﬁcation

of hand movements from electromyographic sig-

nals using machine learning. Preprints. DOI:

10.20944/preprints202002.0443.v1.

MyoWare. (2015). Myoware

muscle sensor (at-04-001)

Datasheet. https://cdn.sparkfun.com/datasheets/

Sensors/Biometric/MyowareUserManualAT-04-001.

pdf.

Quantstart. (2014). Support vector machines: A guide

for beginners. https://www.quantstart.com/articles/

Support-Vector-Machines-A-Guide-for-Beginners/.

Quinay

as-Burgos, C. A. and Gaviria-L

opez, C. A. (2015).

Sistema de identiﬁcaci

on de intenci

on de movimiento

para el control mioel

ectrico de una pr

otesis de mano

rob

otica. Ingenier

ıa y Universidad, 19(1).

Satapathy, S. C., Raju, K. S., Shyamala, K., Krishna, D. R.,

and Favorskaya, M. N. (2019). Advances in Decision

Sciences, Image Processing, Security and Computer

Vision: International Conference on Emerging Trends

in Engineering (ICETE), Vol. 1, volume 3. Springer.

Torrence, C. and Compo, G. P. (1998). A practical guide to

wavelet analysis. Bulletin of the American Meteoro-

logical society, 79(1):61–78.

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

250

Tuncer, T., Dogan, S., and Subasi, A. (2020). Surface EMG

signal classiﬁcation using ternary pattern and discrete

wavelet transform based feature extraction for hand

movement recognition. Biomedical Signal Processing

and Control, 58:101872.

Vapnik, V. (2013). The nature of statistical learning theory.

Springer science & business media.

Wołczowski, A. and Zdunek, R. (2017). Electromyography

and mechanomyography signal recognition: Experi-

mental analysis using multi-way array decomposition

methods. Biocybernetics and Biomedical Engineer-

ing, 37(1):103–113.

ucel, K. and Mehmet, K. (2001). Emg signal classiﬁca-

tion using wavelet transform and fuzzy clustering al-

gorithms. Istanbul, Turkey: Ayazaga.

Zia ur Rehman, M., Waris, A., Gilani, S. O., Jochum-

sen, M., Niazi, I. K., Jamil, M., Farina, D., and Ka-

mavuako, E. N. (2018). Multiday emg-based classiﬁ-

cation of hand motions with deep learning techniques.

Sensors, 18(8):2497.

Classiﬁcation of Myoelectric Surface Signals of Hand Movements using Supervised Learning Techniques

251