
Unsupervised Gaze Prediction in Egocentric Videos by Energy-based
Surprise Modeling
Sathyanarayanan N. Aakur and Arunkumar Bagavathi
Department of Computer Science, Oklahoma State University, Stillwater, OK, 74078, U.S.A.
Keywords:
Unsupervised Gaze Prediction, Egocentric Vision, Temporal Event Segmentation, Pattern Theory.
Abstract:
Egocentric perception has grown rapidly with the advent of immersive computing devices. Human gaze pre-
diction is an important problem in analyzing egocentric videos and has primarily been tackled through either
saliency-based modeling or highly supervised learning. We quantitatively analyze the generalization capa-
bilities of supervised, deep learning models on the egocentric gaze prediction task on unseen, out-of-domain
data. We find that their performance is highly dependent on the training data and is restricted to the domains
specified in the training annotations. In this work, we tackle the problem of jointly predicting human gaze
points and temporal segmentation of egocentric videos without using any training data. We introduce an unsu-
pervised computational model that draws inspiration from cognitive psychology models of event perception.
We use Grenander’s pattern theory formalism to represent spatial-temporal features and model surprise as a
mechanism to predict gaze fixation points. Extensive evaluation on two publicly available datasets - GTEA
and GTEA+ datasets-shows that the proposed model can significantly outperform all unsupervised baselines
and some supervised gaze prediction baselines. Finally, we show that the model can also temporally segment
egocentric videos with a performance comparable to more complex, fully supervised deep learning baselines.
1 INTRODUCTION
The emergence of wearable and immersive comput-
ing devices for virtual and augmented reality has en-
abled the acquisition of images and videos from a
first-person perspective. Given the recent advances in
computer vision, egocentric analysis could be used to
infer the surrounding scene and enhance the quality of
living through immersive, user-centric applications.
At the core of such an application is the need to under-
stand the user’s actions and where they are looking.
More specifically, gaze prediction is an essential task
in egocentric perception. It refers to the process of
predicting human fixation points in the scene with re-
spect to the head-centered coordinate system. Beyond
enabling more efficient video analysis, studies from
psychology have shown that human gaze estimation
capture human intent to help collaboration (Huang
et al., 2015). While the tasks of activity recognition
and segmentation have been explored in recent liter-
ature (Lea et al., 2016), we aim to tackle the task of
unsupervised gaze prediction and temporal event seg-
mentation in a unified framework.
Drawing inspiration from psychology (Horstmann
and Herwig, 2015; Horstmann and Herwig, 2016; Za-
cks et al., 2001), we identify that the notion of pre-
dictability and surprise is a common mechanism to
jointly predict gaze and perform temporal segmenta-
tion. Defined broadly as the surprise-attention hy-
pothesis, studies have found that any deviations from
expectations have a strong effect on both attention
processing and event perception in humans. Specif-
ically, short-term spatial surprise, such as between
subsequent frames of a video, has a high probability
of human fixation and affects saccade patterns. Long-
term temporal surprise leads to the perception of new
events (Zacks et al., 2001). We leverage such findings
and formulate a framework that jointly models both
short-term and long-term surprise using Grenander’s
pattern theory (Grenander, 1996) representations.
A significant departure from recent pattern the-
ory formulations (Aakur et al., 2019), our framework
models bottom-up, feature-level spatial-temporal cor-
relations in egocentric videos. We represent the
spatial-temporal structure of egocentric videos us-
ing Grenander’s pattern theory formalism (Grenander,
1996). The spatial features are encoded in a local con-
figuration, whose energy represents the expectation of
the model with respect to the recent past. Configu-
rations are aggregated across time to provide a local
Aakur, S. and Bagavathi, A.
Unsupervised Gaze Prediction in Egocentric Videos by Energy-based Surprise Modeling.
DOI: 10.5220/0010288009350942
In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 5: VISAPP, pages
935-942
ISBN: 978-989-758-488-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
935
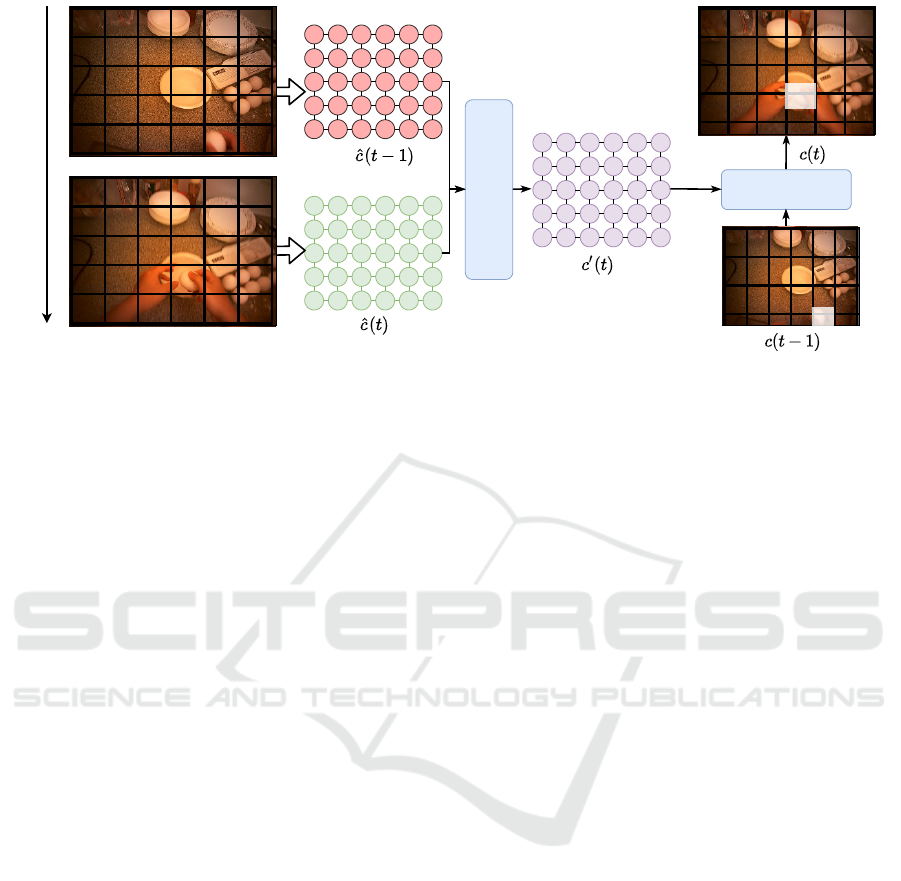
MxNgridoninput
Time
FeatureConfiguration
LocalTemporal
ConfigurationProposal
GazePrediction
LocalProposal
Figure 1: Overall Approach. The proposed approach consists of three essential stages: constructing the feature configuration,
a local temporal configuration proposal and the final gaze prediction. Note that the output of the gaze prediction module is
another configuration which is visualized as an attention map.
temporal proposal for capturing the spatial-temporal
correlation of video features. An acceptor function is
used to switch between saccade and fixation modes
to select the final configuration proposal. Localiz-
ing the source of maximum surprise provides atten-
tion points, and monitoring global surprise allows for
temporally segmenting videos.
Contributions. Our contributions are four-fold: (i)
We evaluate the ability of supervised gaze prediction
models to generalize to out of domain data, (ii) we in-
troduce an unsupervised gaze prediction framework
based on surprise modeling that enables gaze pre-
diction without training and outperforms all unsuper-
vised baselines and some supervised baselines, (iii)
we demonstrate that the pattern theory representation
can be used to tackle different tasks such as unsuper-
vised video event segmentation to achieve compara-
ble performance to state-of-the-art deep learning ap-
proaches, and (iv) we show that pattern theory repre-
sentations can be extended to beyond semantic, sym-
bolic reasoning mechanisms.
2 RELATED WORK
Saliency-based models treat the gaze prediction prob-
lem by modeling the visual saliency of a scene and
identifying areas that can attract the gaze of a per-
son. At the core of traditional saliency prediction
methods is the idea of feature integration (Treisman
and Gelade, 1980), which is based on the combi-
nation of multiple levels of features. Introduced by
Itti et al (Itti and Koch, 2000; Itti and Baldi, 2006),
there have been many approaches to saliency predic-
tion (Bruce and Tsotsos, 2006; Leboran et al., 2016;
Hou et al., 2011; Leboran et al., 2016), including
graph-based models (Harel et al., 2007), supervised
CNN-based saliency (Jiang et al., 2015) and video-
based saliency (Hossein Khatoonabadi et al., 2015;
Leboran et al., 2016).
Supervised Gaze Prediction has been an increas-
ingly popular way to tackle the problem of gaze pre-
diction in egocentric videos. Li et al. (Li et al.,
2013) proposed a graphical model to combine ego-
centric cues such as camera motion, hand positions,
and motion and modeled gaze prediction as a func-
tion of these latent variables. Deep learning-based
approaches have been the other primary modeling op-
tion. Zhang et al. (Zhang et al., 2017) used a Genera-
tive Adversarial Network (GAN) to handle the prob-
lem of gaze anticipation. The GAN was used to gen-
erate future frames, and a 3D CNN temporal saliency
model was used to predict gaze positions. Huang et
al. (Huang et al., 2018) used recurrent neural net-
works to predict gaze positions by combining task-
specific cues with bottom-up saliency. While very
useful, such deep learning models are increasingly
complex, and the amount of training data required by
such approaches is enormous.
3 MOTIVATION: WHY
UNSUPERVISED GAZE
PREDICTION?
In this section, we analyze the ability of current su-
pervised models to generalize beyond their training
domain. Most success in egocentric gaze prediction
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
936

Table 1: Evaluation of generalization capabilities of super-
vised models across scenes and domains.
Approach
Same Different
∆Domain Domain
(AAE) (AAE)
CNN-LSTM Predictor 9.82 16.49 6.67
2-Stream CNN 5.52 11.35 5.83
2-Stream CNN + LSTM 5.35 10.71 5.36
Ours (Unsupervised)* 11.6 9.2 -
*Does not use any training data.
has been through supervised learning. These mod-
els (Huang et al., 2018; Li et al., 2013; Zhang et al.,
2017), primarily based on deep learning approaches,
require large amounts of annotated training data in
the form of gaze locations and other auxiliary data
such as task label (Huang et al., 2018), camera mo-
tion, and hand location (Li et al., 2013), to name a
few. Such information requires manual human anno-
tation and can be expensive to obtain. Additionally,
it may not be possible to get annotated data for ev-
ery eventuality and domains for training supervised
models. The combination of these two issues means
that current systems are restricted to specific envi-
ronments. We evaluate cross-domain gaze prediction
by training supervised models on the GTEA Gaze+
dataset (Li et al., 2013) and evaluating on the GTEA
Gaze dataset (Fathi et al., 2012).
We use three supervised models as our baselines.
Namely, we evaluate a two-stream CNN architecture
to model spatial and temporal dynamics for saliency-
based attention prediction. We also add an LSTM-
based predictor to the two-stream model to add a sac-
cade model on top of the fixation points provided by
the CNN models. Finally, we train a simple CNN-
LSTM model to predict the gaze position from RGB
videos. Combined, these three baselines represent the
basic architectures used in the gaze prediction task us-
ing deep learning models. We quantify performance
using the Average Angular Error (AAE) and summa-
rize the results in Table 1. We denote GTEA Gaze+
as the same domain data and GTEA Gaze as the dif-
ferent domain data. We use the GTEA Gaze+ dataset
as the training domain since it has significantly more
annotated data than the GTEA Gaze dataset.
It can be seen that increasing the complexity of
the model provides exciting results on scenes from the
same domain (i.e., testing within the same dataset) but
also suffers a tremendous loss of performance when
testing on scenes from different domains. The 2-
Stream CNN models perform very well on the same
domain, achieving an average angular error as low as
5.52, but also sees a significant drop (5.83 and 5.36,
with and without an LSTM predictor, respectively).
The simple CNN-LSTM baseline performs reason-
ably well on the same domain data without any bells
and whistles but performs worse than saliency-based
models on out-of-domain data. In fact, all three mod-
els perform worse than Center Bias, which always
predicts the center point of the frame as the gaze po-
sition. We also show the performance of our unsu-
pervised model that does not use any training data.
Our model performs well across both domains with-
out significant loss in performance.
4 ENERGY-BASED SURPRISE
MODELING
In this section, we introduce our energy-based sur-
prise modeling approach for gaze prediction, as illus-
trated in Figure 1 and described in Algorithm 1. We
first introduce the necessary background on the pat-
tern theory representation and present the proposed
gaze prediction formulation.
4.1 Pattern Theory Representation
Representing Features. Following Grenander’s no-
tations ((Grenander, 1996)), the basic building blocks
of our representation are atomic components called
generators (g
i
). The collection of all possible gen-
erators in a given environment is termed the genera-
tor space (G
S
). While there can exist various types
of generators, as explored in prior pattern theory ap-
proaches (Aakur et al., 2019), we consider only one
type of generator, namely the feature generator. We
define feature generators as features extracted from
videos and are used to estimate the gaze at each time
step. Each generator represents both appearance- and
motion-based features at different spatial locations in
each frame of the video.
Capturing Local Regularities. We model tempo-
ral and spatial associations among generators through
bonds. Each generator g
i
has a fixed number of
bonds called the arity of a generator (w(g
i
)∀g
i
∈
G
S
). These bonds are symbolic representations of
the structural and contextual relationships shared be-
tween generators. Each bond is directed and are dif-
ferentiated through the direction of information flow
as either in-bonds or out-bonds. Each bond is iden-
tified by a unique coordinate and bond value such
that the j
th
bond of a generator g
i
∈ G
S
is denoted as
β
j
dir
(g
i
), where dir denotes the direction of the bond.
The energy of a bond is used to quantify the
strength of the relationship expressed between two
generators and is given by the function:
b
struct
(β
0
(g
i
), β
00
(g
j
)) = w
s
tanh(φ(g
i
, g
j
)). (1)
Unsupervised Gaze Prediction in Egocentric Videos by Energy-based Surprise Modeling
937
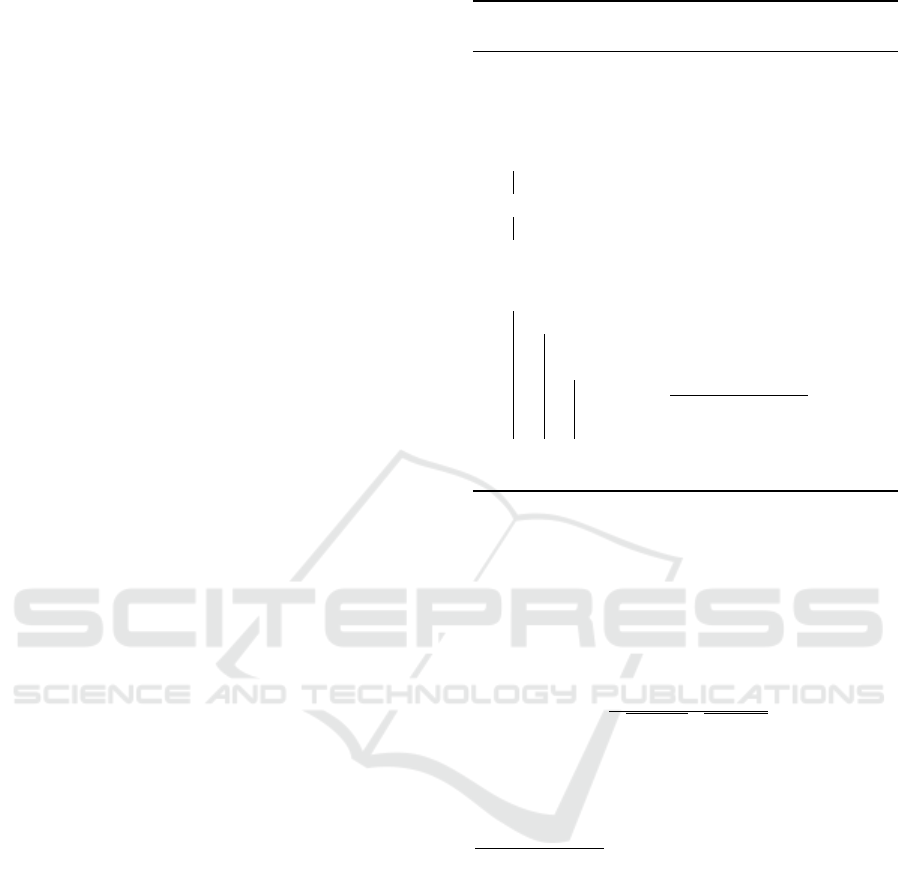
where β
0
and β
00
represent the bonds from the gen-
erators g
i
and g
j
, respectively; φ(·) is the strength
of the relationship expressed in the bond; and w
s
is
a constant used to scale the bond energies. In our
framework, φ(·) is a distance metric and provides a
measure of similarity between the features expressed
through their respective generators. Generators com-
bine through their corresponding bonds to form com-
plex structures called configurations. Each configura-
tion has an underlying graph topology, specified by a
connector graph σ ∈Σ, where Σ is the set of all avail-
able connector graphs. σ is also called the connection
type and is used to define the directed connections be-
tween the elements of the configuration. In our work,
we restrict Σ to a lattice configuration, as illustrated
in Figure 1, with bonds extending spatially and ag-
gregated temporally.
4.2 Local Configuration Proposal
The first step in the framework is the construction of
a lattice configuration called the feature configuration
( ˆc). The lattice configuration is a N ×N grid, with
each point (generator) in the configuration represent-
ing a possible region of fixation. We construct the
feature configuration at time t (defined as ˆc(t)) by di-
viding the input image into an N ×N grid. Each gen-
erator is populated by extracting features from each of
these grids. These features can be appearance-based
such as RGB values, motion features such as optical
flow (Brox and Malik, 2010), or deep learning fea-
tures (Redmon et al., 2016). We experiment with both
appearance and motion-based features and find that
motion-based features (Section 5) provide distract-
ing cues, especially with significant camera motion
associated with egocentric videos. Bonds are quanti-
fied across generators with the spatial locality, i.e., all
neighboring generators are connected through bonds.
The bond energy is set to 1 by default.
A local proposal for the time steps t is done
through a temporal aggregation of the previous k con-
figurations across time. The aggregation enforces
temporal consistency into the prediction and selec-
tively influences the current prediction. Bonds are
established across time by computing bonds between
generators with a spatial locality and are quantified
using the energy function defined in Equation 1. For
example, a bond can be established with generator
g
i
(t) in feature configuration at time t and the config-
uration at time t −1. We define φ(g
i
, g
j
) to be a met-
ric that combines both appearance-based and motion-
based features. We ensure that the function φ(g
i
, g
j
)
produces nonzero values proportional to the degree
of correlation between the features, both spatially and
Algorithm 1: Gaze Prediction using Pattern
Theory.
1 Gaze Prediction (I
t
, G
s
,C
t−1
, k, p, p
c
, c
b
);
2 ˆc(t) ← f eatureCon f ig(I
t
, G
s
)
3 c
0
(t) ←temporalAggregate(ˆc
t
,C
t−1
)
4 t ←Uni f ormSample(0, 1)
5 if t < p
c
then
6 c(t) ← c
0
(t)
7 else
8 c(t) ← c
b
9 G
i
(t) ← {g
1
, g
2
, . . . , g
n
∈ c(t)}
10 g
pred(t)
← selectGenerator(G
i
(t))
11 foreach g
i
∈ c(t) do
12 if E(g
pred
|c(t)) < E(g
i
|c(t)) then
13 t ←Uni f ormSample(0, 1)
14 if t < p then
15 E(g
i
) ←
E(g
i
)
d(g
pred
(t),g
pred
(t−1))
16 g
pred
(t) ← g
i
17 end
18 return g
pred
(t)
temporally and is formally defined as
φ(g
i
, g
j
) = min(α, φ
a
(g
i
, g
j
) + φ
m
(g
i
, g
j
)) (2)
where α is a modulating factor to ensure that the
energy does not explode to infinity, φ
a
(g
i
, g
j
) and
φ
m
(g
i
, g
j
) are appearance-based and motion-based
features, respectively; φ
a
(g
i
, g
j
) is used to quan-
tify the appearance-based affinity and is given by
φ
a
(g
i
, g
j
) = 1 −
∑
N
i=1
g
i
g
j
√
∑
N
i=1
(g
i
)
2
√
∑
N
i=1
(g
j
)
2
, and is used to
capture the spatial correlation between the visual fea-
tures at a given location in the current frame. On the
other hand, φ
m
(g
i
, g
j
) is used to quantify the motion-
based bond affinity and is given by φ
m
(g
i
, g
j
) =
∑
N
i=1
(g
i
−g
i
)(g
j
−g
j
)
N
. Both metrics produce nonzero val-
ues proportional to the degree of correlation. Hence,
their use in Equation 1 ensures that the bond energy is
reflective of the predictability of generators at various
time steps.
The temporal consistency is enforced through an
ordered weighted averaging aggregation operation of
configurations across time. Formally, the temporal
aggregation is a mapping function F : c
n
−→ c that
maps n configurations from previous time steps into
a single configuration as a local proposal for time
t. The function F has an associated set of weights
W = [w
1
, w
2
, . . . w
n
] lying in the unit interval and sum-
ming to one. W is used to aggregate configurations
across time using the function F given by
F(c
t−i
, . . . c
t
) =
k
∑
i=1
w
i
(c
t
c
t−i
) (3)
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
938

where refers to pairwise aggregation of bonds
across configurations c
t
and c
t−i
. W is a set of weights
used to scale the influence of each configuration from
the past on the current prediction. W is set to be an
exponential decay function given by a(1 −b)
k
, where
b is the decay factor and a is the initial value. We set
k to video fps, a and b are is set to 1 and 0.95. Hence,
the temporally local configuration has a more signif-
icant influence on the current configuration proposal
compared to temporally distant configurations.
4.3 Gaze Prediction
Intuitively, each generator in the configuration corre-
sponds to the predictability of each spatial segment
in the image. Hence, the predicted gaze position cor-
responds to the grid cell with most surprise, i.e., the
generator with maximum energy. We begin by con-
structing the initial feature configuration for time t
and temporally aggregating it to obtain the initial con-
figuration c0(t) as described in Section 4.2. Algo-
rithm 1 illustrates the process of finding the generator
with maximum energy. C
t−1
, I
t
, G
s
refer to the set of
past k configurations, the video frame at time t, and
the generator space, respectively.
In addition to na
¨
ıve surprise modeling, we intro-
duce additional constraints to more closely model hu-
man gaze, such as the choice between saccade and
fixation using two approaches. First, we do so by hav-
ing two acceptor functions (lines 5 −8 and 12 −15).
In the first function, the local temporal proposal is ac-
cepted with a probability of p
c
or rejected in favor
of a configuration with strong center bias (c
b
) as the
final prediction for time t. The role of this acceptor
function is to prevent the model from being distracted
due to spurious patterns in the input visual stream.
In the second acceptor function, we allow the model
to switch between saccade and fixation modes by not
forcing the model to always choose the generator with
the highest energy as the gaze position.
Every newly proposed generator is accepted if it
passes the test at line 12-14, which is either true for
new generators with energy lower than the current
generator’s or true with a certain probability (p) that
is proportional to the energy difference between the
recent and the old generators. Second, we scale each
generator’s energy with a distance function (d(·) in
line 15) that quantifies the distance between the pre-
vious predicted gaze point and the current generator.
This scaling ensures that the model can fixate on a
chosen target while allowing for the saccade function
to select a different target if required. Once the gener-
ator (g
pred
) is chosen, the final gaze point (x
pred
, y
pred
)
is computed as
(x
pred
, y
pred
) = (c
x
+ 0.5 ∗W
g
, c
y
+ 0.5 ∗H
g
) (4)
where (c
x
, c
y
) is the offset of the grid from the top
left corner of the image; (W
g
, H
g
) are grid width and
height respectively.
5 EXPERIMENTAL EVALUATION
In this section, we describe the experimental setup
used to evaluate our approach and present quantita-
tive and qualitative results on both gaze prediction and
event segmentation.
5.1 Data and Evaluation Setup
Data. We evaluate our approach on the GTEA (Fathi
et al., 2012) and GTEA+ (Li et al., 2013) datasets.
The two datasets consist of video sequences on meal
preparation tasks. GTEA contains 17 sequences of
tasks from 14 subjects, with each sequence lasting
about 4 minutes. GTEA+ contains longer sequences
of 5 subjects performing 7 activities. We use the of-
ficial splits for both GTEA and GTEA+ as defined in
prior works (Fathi et al., 2012; Li et al., 2013).
Evaluation Metrics. We use Average Angular Er-
ror (AAE) (Riche et al., 2013) as our primary eval-
uation metric, following prior efforts (Itti and Baldi,
2006; Fathi et al., 2012; Li et al., 2013). AAE is the
angular distance between the predicted gaze location
and the ground truth. Area Under the Curve (AUC)
measures the area under a curve for true positive ver-
sus false-positive rates under various threshold val-
ues on saliency maps. AUC is not directly applicable
since our prediction is not a saliency map.
5.2 Baseline Approaches and Ablation
Baselines. We compare with state-of-the-art unsuper-
vised and supervised approaches. We consider un-
supervised saliency models such as Graph-Based Vi-
sual Saliency (GBVS) (Harel et al., 2007), Attention-
based Information Maximization (AIM) (Bruce and
Tsotsos, 2006), Itti’s model (Itti and Koch, 2000),
Adaptive Whitening Saliency (AWS) (Leboran et al.,
2016), Image Signature Saliency (ImSig) (Hou et al.,
2011), OBDL (Hossein Khatoonabadi et al., 2015)
and AWS-D (Leboran et al., 2016). We also com-
pare against supervised models (DFG (Zhang et al.,
2017), Yin (Li et al., 2013) and SALICON (Jiang
et al., 2015), LDTAT (Huang et al., 2018)) that lever-
age annotations and representation learning capabili-
ties of deep neural networks.
Unsupervised Gaze Prediction in Egocentric Videos by Energy-based Surprise Modeling
939

Table 2: Evaluation on GTEA and GTEA+ datasets. We
outperform all unsupervised and some supervised baselines.
Supervision
Approach GTEA GTEA+
(AAE) (AAE)
None
Ours 9.2 11.6
Ours (Optical Flow) 10.1 13.8
Ours (Saccade) 12.5 14.6
AIM 14.2 15.0
GBVS 15.3 14.7
OBDL 15.6 19.9
AWS 17.5 14.8
AWS-D 18.2 16.0
Itti’s model 18.4 19.9
ImSig 19.0 16.5
Full
LDTAT 7.6 4.0
Yin 8.4 7.9
DFG 10.5 6.6
SALICON 16.5 15.6
Ablation. We perform ablations of our approach to
test the effectiveness of each component. We evalu-
ate the effect of different features by including optical
flow (Brox and Malik, 2010) as input to the model.
We remove the prior spatial constraint and term the
model “Ours (Saccade)”, highlighting its tendency to
saccade through the video without fixating.
5.3 Quantitative Evaluation
We present the results of our experimental evaluation
in Table 2. We present the Average Angular Error
(AAE) for both the GTEA and GTEA+ datasets and
group the baseline approaches into two categories - no
supervision and full supervision. Our approach out-
performs all unsupervised methods on both datasets.
The overall performance on GTEA Gaze is lower than
that on GTEA Gaze Plus, which could arguably be at-
tributed to the fact that 25% of ground truth gaze mea-
surements are missing. Note that the gap between the
performance of fully supervised models between the
two datasets is high and shows that they suffer from
the lack of a large number of training examples, which
is significantly lower in GTEA.
It is interesting to note that our model outperforms
saliency based methods, including the closely related
graph based visual saliency model and Itti’s model.
We attribute it to the use of multiple acceptor func-
tions (Section 4.3), which allows us to switch between
fixation and saccade modes and hence is not hin-
dered by saliency-based features that do not capture
task-dependent attention. Note that we significantly
outperform SALICON (Jiang et al., 2015), a fully
supervised convolutional neural network trained on
ground-truth saliency maps on both datasets. We also
outperform the GAN-based gaze prediction model
DFG (Zhang et al., 2017) on the GTEA dataset, where
Table 3: Evaluation on the temporal video segmentation
task on the GTEA Gaze datasets.
Supervision Approach Accuracy
Full
Spatial-CNN (S-CNN) 54.1
Bi-LSTM (Lea et al., 2016) 55.5
EgoNet (Singh et al., 2016) 57.6
Dilated TCN (Lea et al., 2016) 58.3
TCN (Lea et al., 2016) 64.1
None
Ours w/ 3D-CNN features 35.17
Ours (Streaming Eval.) 57.92
the amount of training data is limited. We also offer
competitive performance to Yin et al. (Li et al., 2013),
who use auxiliary information in the form of visual
cues such as hands, objects of interest, and faces.
This gap is particularly narrowed when considering
domains with lower data (GTEA Gaze) and the lack
of generalization (Section 3) shown by common deep
learning approaches to domains outside their training
environment. It should be noted that our approach
runs at 45 fps in a single threaded application, run on
an AMD ThreadRipper CPU, a significantly acceler-
ated method compared to deep learning approaches
and offers a way forward for resource-constrained
prediction.
5.4 Video Event Segmentation
To highlight our model’s ability to understand video
semantics and its subsequent ability to predict gaze
locations, we adapt the framework to perform event
segmentation in streaming videos. Instead of local-
izing specific generators, we monitor the global sur-
prise by considering the energy of the entire configu-
ration c(t). The energy of a configuration c is the sum
of the bond energies (Equation 1) in a configuration
and is given by
E(c) = −
∑
(β
0
,β
00
)∈c
b
struct
(β
0
(g
i
), β
00
(g
j
)) (5)
where a lower energy indicates that the generators are
closely associated with each other. Hence, a higher
energy suggests that the surprise faced by the frame-
work is higher. The configuration (frame) with the
highest energy is considered to hold the highest sur-
prise and is selected as an event boundary. We use the
error gating-based segmentation used in (Aakur and
Sarkar, 2019). We set the error threshold to be 2.5 as
opposed to 1.5, and the energy of the configuration
as the perceptual quality metric for event segmenta-
tion. We evaluate the performance of the approach on
the GTEA dataset and quantify its performance us-
ing accuracy. We use a 3D-CNN (Ji et al., 2012) net-
work pre-trained on UCF-101 (Soomro et al., 2012)
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
940

(a)
(b)
(c)
Figure 2: qualitative Examples: We present the predictions made by our model for three different sequences across different
tasks and domains. The predictions are shown as a gaussian map and the ground truth is highlighted in red.
to extract features. We use k-means clustering to as-
sign each segment to a cluster label. We then align
the prediction and ground-truth using the Hungarian
method before computing accuracy, following prior
works (Lea et al., 2016). As can be seen from Ta-
ble 3, our unsupervised approach achieves a tempo-
ral segmentation accuracy of 35.17%. We compare
against several state-of-the-art supervised deep learn-
ing approaches such as Spatial-CNN, Bi-LSTM, and
Temporal Convolutional Networks (TCN) (Lea et al.,
2016), which achieve accuracy of 54.1%, 55.5% and
64.1, respectively. Note that the class-agnostic accu-
racy, i.e., when evaluated in a streaming manner per
video, we obtain a segmentation accuracy of 57.92%,
which suggests that the actual segmentation is robust.
5.5 Qualitative Evaluation
We present some qualitative visualizations in Fig-
ure 2. We illustrate three cases from our model’s pre-
dictions. The ground-truth gaze position is shown in
red, and our predictions are shown as a heatmap. It
is interesting to note (particularly highlighted in Fig-
ure 2(b)) is the tendency of our model to fixate on
highly relevant regions and subsequent objects, even
though the ground-truth gaze positions vary. The pre-
dicted gaze then quickly adapts to the newer position
and starts fixating on the relevant object. This charac-
teristic suggests that despite purely bottom-up visual
processing, the notion of “surprise” has an underlying
task-bound nature. We attribute this to the two accep-
tor functions (lines 5−8 and 12−15) defined in Algo-
rithm 1). The former allows us to enforce some spatial
bias into the model and force the gaze prediction back
to the center of the image (the effect is highlighted in
Figure 2(a)). The latter helps fixate on certain objects
for a longer duration and help handle clutter and oc-
clusion for deriving task-specific object affordances,
without any specific training objectives and data.
6 CONCLUSION
In this work, we analyze the generalization ability
of supervised deep learning models to different do-
mains and scenes for the egocentric gaze prediction
task and find that their performance suffers when pre-
sented with out-of-domain data. To break the increas-
ing dependence on training data, we present one of the
first approaches to a unified framework for tackling
unsupervised gaze prediction and temporal segmenta-
tion, based on energy-based surprise modeling. Using
a novel formulation, we demonstrate that pattern the-
ory can be used to predict gaze locations in egocentric
Unsupervised Gaze Prediction in Egocentric Videos by Energy-based Surprise Modeling
941

videos. Our pattern theory representation also forms
the basis for unsupervised temporal video segmenta-
tion. Through extensive experiments, we demonstrate
that we obtain state-of-the-art performance on the un-
supervised gaze prediction task and provide compet-
itive performance on the unsupervised temporal seg-
mentation task on egocentric videos.
ACKNOWLEDGEMENT
This research was supported in part by the US Na-
tional Science Foundation grant IIS 1955230.
REFERENCES
Aakur, S., de Souza, F., and Sarkar, S. (2019). Generating
open world descriptions of video using common sense
knowledge in a pattern theory framework. Quarterly
of Applied Mathematics, 77(2):323–356.
Aakur, S. N. and Sarkar, S. (2019). A perceptual prediction
framework for self supervised event segmentation. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition, pages 1197–1206.
Brox, T. and Malik, J. (2010). Large displacement optical
flow: descriptor matching in variational motion esti-
mation. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 33(3):500–513.
Bruce, N. and Tsotsos, J. (2006). Saliency based on infor-
mation maximization. In Advances in Neural Infor-
mation Processing Systems, pages 155–162.
Fathi, A., Li, Y., and Rehg, J. M. (2012). Learning to recog-
nize daily actions using gaze. In European Conference
on Computer Vision, pages 314–327. Springer.
Grenander, U. (1996). Elements of pattern theory. JHU
Press.
Harel, J., Koch, C., and Perona, P. (2007). Graph-based
visual saliency. In Advances in Neural Information
Processing Systems, pages 545–552.
Horstmann, G. and Herwig, A. (2015). Surprise attracts
the eyes and binds the gaze. Psychonomic Bulletin &
Review, 22(3):743–749.
Horstmann, G. and Herwig, A. (2016). Novelty biases at-
tention and gaze in a surprise trial. Attention, Percep-
tion, & Psychophysics, 78(1):69–77.
Hossein Khatoonabadi, S., Vasconcelos, N., Bajic, I. V., and
Shan, Y. (2015). How many bits does it take for a stim-
ulus to be salient? In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 5501–5510.
Hou, X., Harel, J., and Koch, C. (2011). Image signature:
Highlighting sparse salient regions. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
34(1):194–201.
Huang, C.-M., Andrist, S., Saupp
´
e, A., and Mutlu, B.
(2015). Using gaze patterns to predict task intent in
collaboration. Frontiers in Psychology, 6:1049.
Huang, Y., Cai, M., Li, Z., and Sato, Y. (2018). Predicting
gaze in egocentric video by learning task-dependent
attention transition. In Proceedings of the European
Conference on Computer Vision (ECCV), pages 754–
769.
Itti, L. and Baldi, P. F. (2006). Bayesian surprise attracts
human attention. In Advances in Neural Information
Processing Systems, pages 547–554.
Itti, L. and Koch, C. (2000). A saliency-based search mech-
anism for overt and covert shifts of visual attention.
Vision Research, 40(10-12):1489–1506.
Ji, S., Xu, W., Yang, M., and Yu, K. (2012). 3d convolu-
tional neural networks for human action recognition.
IEEE transactions on pattern analysis and machine
intelligence, 35(1):221–231.
Jiang, M., Huang, S., Duan, J., and Zhao, Q. (2015). Sali-
con: Saliency in context. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 1072–1080.
Lea, C., Vidal, R., Reiter, A., and Hager, G. D. (2016).
Temporal convolutional networks: A unified approach
to action segmentation. In European Conference on
Computer Vision, pages 47–54. Springer.
Leboran, V., Garcia-Diaz, A., Fdez-Vidal, X. R., and Pardo,
X. M. (2016). Dynamic whitening saliency. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 39(5):893–907.
Li, Y., Fathi, A., and Rehg, J. M. (2013). Learning to predict
gaze in egocentric video. In Proceedings of the IEEE
International Conference on Computer Vision, pages
3216–3223.
Redmon, J., Divvala, S., Girshick, R., and Farhadi, A.
(2016). You only look once: Unified, real-time object
detection. In Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition, pages 779–
788.
Riche, N., Duvinage, M., Mancas, M., Gosselin, B., and
Dutoit, T. (2013). Saliency and human fixations:
State-of-the-art and study of comparison metrics. In
Proceedings of the IEEE International Conference on
Computer Vision, pages 1153–1160.
Singh, S., Arora, C., and Jawahar, C. (2016). First person
action recognition using deep learned descriptors. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition, pages 2620–2628.
Soomro, K., Zamir, A. R., and Shah, M. (2012). Ucf101:
A dataset of 101 human actions classes from videos in
the wild. arXiv preprint arXiv:1212.0402.
Treisman, A. M. and Gelade, G. (1980). A feature-
integration theory of attention. Cognitive Psychology,
12(1):97–136.
Zacks, J. M., Tversky, B., and Iyer, G. (2001). Perceiv-
ing, remembering, and communicating structure in
events. Journal of Experimental Psychology: Gen-
eral, 130(1):29.
Zhang, M., Teck Ma, K., Hwee Lim, J., Zhao, Q., and Feng,
J. (2017). Deep future gaze: Gaze anticipation on ego-
centric videos using adversarial networks. In Proceed-
ings of the IEEE Conference on Computer Vision and
Pattern Recognition, pages 4372–4381.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
942
