Multi-Task Architecture with Attention for Imaging Atmospheric

Cherenkov Telescope Data Analysis

Mika

el Jacquemont

1,2 a

, Thomas Vuillaume

1 b

, Alexandre Benoit

2 c

, Gilles Maurin

1 d

and Patrick Lambert

2 e

CNRS, LAPP, Univ. Grenoble Alpes, Universit

e Savoie Mont Blanc, Annecy, France

LISTIC, Univ. Savoie Mont Blanc, Annecy, France

Keywords:

Multitasking, Artiﬁcial Neural Networks, Gamma Rays, Attention.

Abstract:

Gamma-ray reconstruction from Cherenkov telescope data is multi-task by nature in astrophysics. The image

recorded in the Cherenkov camera pixels relates to the type, energy, incoming direction and distance of a parti-

cle from a telescope observation. We propose γ-PhysNet, a physically inspired multi-task deep neural network

for gamma/proton particle classiﬁcation, and gamma energy and direction reconstruction. We compare its

performance with single task networks on Monte Carlo simulated data and demonstrate the interest of recon-

structing the impact point as an auxiliary task. We also show that γ-PhysNet outperforms a widespread analysis

method for gamma-ray reconstruction. Finally, we study attention methods to solve relevant use cases. All the

experiments are conducted in the context of single telescope analysis for the Cherenkov Telescope Array data

analysis.

1 INTRODUCTION

Gamma-ray astronomy is the astronomical observa-

tion of the most energetic photons (above 100 keV)

produced by violent astrophysical phenomena (super-

nova remnants, gamma-ray bursts, active galactic nu-

clei, etc.) and potentially by dark matter annihilation.

When these high-energy particles enter the atmo-

sphere, they interact with its dense matter producing

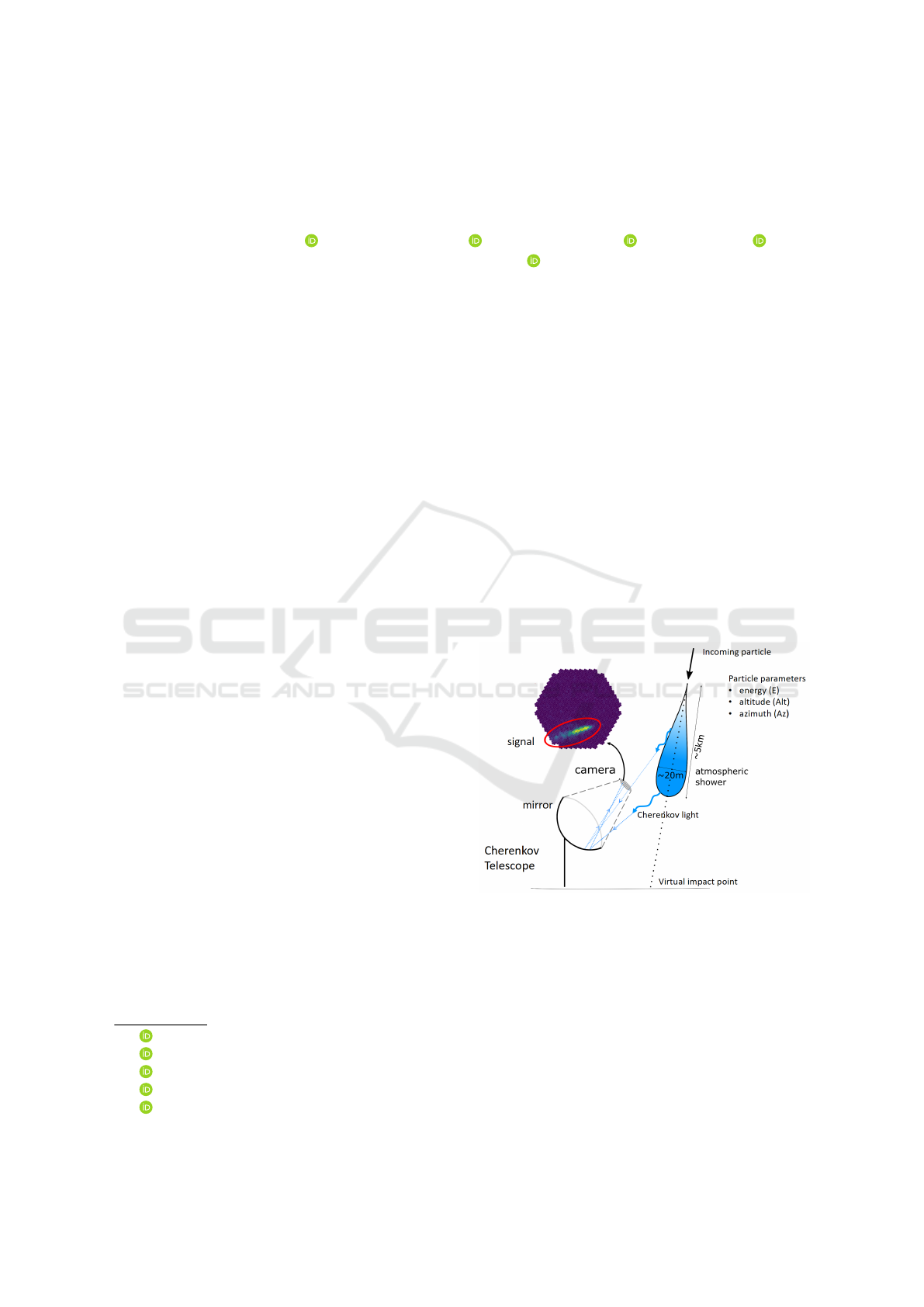
a particle shower. As illustrated in Figure 1, Imaging

Atmospheric Cherenkov Telescopes (IACTs) observe

the Cherenkov radiation (Hillas, 1985) emitted by this

shower. Their large mirrors collect the light to form

an image recorded by a high sensitivity camera usu-

ally made of photomultipliers. The gamma shower

then appears as an ellipsoid.

Since the ﬁrst IACT, the Whipple observatory

constructed in 1968, many others have been built

(e.g., H.E.S.S., MAGIC or VERITAS), mainly as ar-

rays of telescopes to make the most of the stereo-

scopic techniques. The Cherenkov Telescope Ar-

https://orcid.org/0000-0002-4012-6930

https://orcid.org/0000-0002-5686-2078

https://orcid.org/0000-0002-0627-4948

https://orcid.org/0000-0002-6970-0588

https://orcid.org/0000-0003-0478-9443

Figure 1: Imaging Atmospheric Cherenkov Telescope.

ray (CTA), the next generation of IACTs, will im-

prove sensitivity by a factor of 10 while also increas-

ing accuracy in gamma-ray detection. To achieve

these improvements, CTA will be composed of ∼ 100

telescopes of three different sizes with very high-

speed cameras (telescope readout event rate in kHz

range[0.6,10]). When in full operation, CTA will pro-

duce 210 PB of raw data per year to be analyzed in

real time and then reduced and compressed to 3 PB

before archiving. Moreover, thanks to an improving

534

Jacquemont, M., Vuillaume, T., Benoit, A., Maurin, G. and Lambert, P.

Multi-Task Architecture with Attention for Imaging Atmospheric Cherenkov Telescope Data Analysis.

DOI: 10.5220/0010297405340544

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 5: VISAPP, pages

534-544

ISBN: 978-989-758-488-6

knowledge of the telescopes and thus better analysis

algorithms, all the data already acquired will be re-

processed every year.

The Large Size Telescope 1 (LST1 (Ambrosi

et al., 2013)) is the ﬁrst prototype installed at the

Northern CTA site in La Palma. It has been de-

signed to detect gamma rays with an energy between

30 GeV and 3 TeV, which is especially interesting for

the study of transient phenomena such as gamma-ray

bursts recently observed for the ﬁrst time by IACTs

(Abdalla et al., 2019). During this preparation phase,

analysis methodologies are developed on simulated

data that make method comparison possible.

The purpose of the image analysis is to estimate

the energy and direction (as altitude and azimuth) of

the primary particle and to separate the gamma rays

from the cosmic ray background, mainly composed

of protons. This step is complex because cosmic rays

can generate very similar images and the signal-to-

noise ratio is typically lower than 1/1000. The anal-

ysis method is then driven by the gamma detection

in a high background noise and the regression of its

parameters in big data context. Moreover a sensitive

and real-time reconstruction will allow tracking and

discovering new astrophysical phenomena.

Several approaches have been considered in the

past to perform this analysis. The most common was

developed by A. M. Hillas (Hillas, 1985). It charac-

terizes the ellipsoid image by its moments up to sec-

ond order. To improve the sensitivity, these param-

eters have been combined with multivariate analysis

methods, relying on boosted decision trees or random

forests (Fiasson et al., 2010). Such approach will next

be referred to as Hillas + RF. However, this approach

doesn’t take into account the strong interdependence

between the energy, the arrival direction, the virtual

impact point on the ground of the particle and the im-

age produced (i.e., pixel intensity, shower shape and

position) that make the reconstruction multi-task by

nature. State-of-the-art methods (de Naurois and Rol-

land, 2009), named Template analysis, are based on

a pixel level comparison relying on a likelihood be-

tween a bank of image templates and the recorded

images. However, they are very slow (Parsons et al.,

2016) and each telescope of the array needs a huge

database of templates, which is not tractable for CTA

real-time analysis.

In this paper, we propose a deep multi-task ar-

chitecture, named γ-PhysNet, for single telescope

gamma event reconstruction (i.e., gamma/proton

classiﬁcation, energy and arrival direction recon-

struction) from IACT simulated data. Based on Con-

volutional Neural Networks (CNNs), the proposed

model has an inference rate close to the LST1 ac-

quisition rate, above 2.5kHz. We demonstrate the in-

terest of multi-task learning for IACT data analysis

and show that our architecture outperforms the wide-

spread Hillas + RF analysis method, in particular on

direction reconstruction and gamma/proton classiﬁca-

tion that are critical to improve the sensitivity of the

telescope. We then study several attention mecha-

nisms for the proposed architecture in two different

conﬁgurations to address relevant use cases.

2 RELATED WORK

2.1 Deep Learning for Imaging

Atmospheric Cherenkov Telescope

Data

Over the past decade, deep learning has emerged as

the leading approach in many computer vision tasks,

including image classiﬁcation (Touvron et al., 2019),

semantic segmentation (Yuan et al., 2020) and object

detection (Zhang et al., 2020). Recently, some effort

has been made to explore deep learning techniques

to solve astrophysical problems (Kim and Brunner,

2016; Brunel et al., 2019). IACT data analysis isn’t

out of step, from muon image analysis (Feng et al.,

2016) to gamma event reconstruction of CTA data or

other IACTs. Nieto et al. (Nieto et al., 2017) probe

very deep networks for gamma/proton classiﬁcation.

Reference (Mangano et al., 2018) presents a narrower

CNN to solve gamma/proton classiﬁcation, and en-

ergy and direction regression tasks. Shilon et al.

(Shilon et al., 2019) propose a combination of a CNN

and a Recurrent Neural Network, denoted CRNN, to

solve the same tasks in stereo-analysis (using several

telescopes). To solve the real data discrepancy issue,

Parsons et al. (Parsons and Ohm, 2019) propose to

combine IACT images and standard method param-

eters. These papers present promising results, espe-

cially for gamma/proton classiﬁcation. However, they

have handled the different reconstruction problems as

single tasks, without considering their strong interde-

pendence.

2.2 Multi-Task Learning

Multi-task learning (MTL) is a learning paradigm

which aims to improve the generalization (Caruana,

1997) of learned models. Former approaches (Thrun,

1996) have shown that transferring knowledge across

related tasks improves the generalization with fewer

data. MTL helps the model focus on features that

are relevant for all tasks. Recent methods based on

Multi-Task Architecture with Attention for Imaging Atmospheric Cherenkov Telescope Data Analysis

535

CNN have shown remarkable results on pose estima-

tion (Pavllo et al., 2019) or instance segmentation (He

et al., 2017).

In MTL, the tasks to address are trained simulta-

neously, using a partially shared representation. In

hard parameter sharing architectures, the most fre-

quently used, a whole part of the network is shared

between all tasks (Ruder, 2017). The shared part is

generally the encoder (Luvizon et al., 2018) or its ﬁrst

layers (Iizuka et al., 2016). In soft parameter sharing

architectures (Cao et al., 2018), each task is learned

with its own network. However, some additional lay-

ers are shared and constrained in order to encourage

their weights to be similar.

Balancing the tasks is critical. For most of the

MTL related papers (Luvizon et al., 2018; Ren and

Jae Lee, 2018), this is done, when speciﬁed, by hand.

This handcrafted weighting needs an extensive op-

timization process to ﬁnd optimal ones. However,

adaptive methods have been proposed in order to au-

tomatically balance task importance. Kendall et al.

(Kendall et al., 2018) model the homoscedastic un-

certainty for each task and use it as a proxy for task

balancing. Reference (Chen et al., 2018) proposes to

weight the tasks in order to balance their loss gradient

with regard to the last common layer. This leads to pe-

nalizing predominant tasks and encouraging weaker

tasks. Guo et al. (Guo et al., 2018) use learning

progress signals as key performance indicators to pri-

oritize difﬁcult cases at both task and example level.

Sener et al. (Sener and Koltun, 2018) consider MTL

as a multi-objective optimization to achieve Pareto

optimality for each task scale factor.

In this work, we propose a hard parameter sharing

architecture. Besides, to balance the tasks the Kendall

approach proved to be the most relevant.

2.3 Attention in Deep Learning

Attention is a mechanism that helps deep learning

model focus on relevant features based on a deﬁned

context through trainable weights. It originates from

the natural language processing (NLP) ﬁeld (Bah-

danau et al., 2015) and is the main component of

Transformer networks (Vaswani et al., 2017) that

achieve state-of-the-art performance on neural ma-

chine translation and image captioning. Parmar et

al. (Parmar et al., 2018) generalize the Transformer

architecture to image generation. Restricted self-

attention is considered to focus on local neighbor-

hoods. On the other hand, Wang et al. propose global

self-attention as a non-local operation for video clas-

siﬁcation, image segmentation, object detection and

pose estimation (Wang et al., 2018). Zhang et al.

(Zhang et al., 2019) adapt the global self-attention

for generative adversarial networks (GANs). They

use a stronger bottleneck controlled by a factor k,

denoted reduction ratio in the following. In addi-

tion, they introduce a learnable parameter to scale the

output of the attention module before summing back

with the input. While for computer vision tasks at-

tention modules are generally combined with convo-

lution blocks, Ramachandran et al. (Parmar et al.,

2019) propose stand-alone local self-attention models

for image classiﬁcation and object detection.

Global and local self-attention can be considered

as spatial attention mechanisms, as they capture long-

range dependencies in data, by weighting each pixel.

On the contrary, Hu et al. (Hu et al., 2018) introduce a

lightweight channel-wise attention denoted Squeeze-

and-Excitation. The squeeze operation produces a

channel descriptor of the input and is followed by an

adaptive recalibration, the excitation, and a scale op-

eration that weights the input channels. The excitation

acts as a bottleneck parametrized by a reduction ratio.

Reference (Sun et al., 2020) proposes dual attention

for U-Net to help improve model interpretability and

robustness. It combines Squeeze-and-Excitation with

a simple spatial attention path. The latter compresses

the number of input channels to one. It then applies

a sigmoid to the resulting pixel values to produce an

attention map that rescales the output of the Squeeze-

and-Excitation.

In this paper, we compare self-attention, Squeeze-

and-Excitation and Dual Attention.

3 γ-PhysNet FOR FULL EVENT

RECONSTRUCTION

3.1 Multi-Task Architecture

We propose a MTL architecture, γ-PhysNet, to

achieve full event reconstruction from IACT data. As

computation time is crucial, this is a hard parameter

sharing architecture composed of a backbone encoder

and a physically inspired multi-task block. The net-

work is fed with two-channel IACT data (see Section

4.1 for details) and, in a single pass, separates gamma

rays from background noise, and reconstructs the en-

ergy and the arrival direction of the primary particle.

It beneﬁts from the regression of the virtual impact

point of the particle as an auxiliary task. Even though

it is not needed by astronomers for higher-level analy-

sis, physics shows that this parameter provides mean-

ingful information to solve energy and direction re-

construction tasks.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

536

Relying on an extensive ablation study that we

cannot report in this paper, the backbone of γ-PhysNet

is the convolutional part of a ResNet-56 (He et al.,

2016b; He et al., 2016a), CIFAR-10 version, with

full pre-activation implemented with IndexedConv

(Jacquemont et al., 2019). IACT images can have

hexagonal pixels, as is the case for the LST cameras.

As there is no clear advantage so far (Nieto et al.,

2019) to transform them to square pixel images in

terms of performance, indexed convolutions provided

by IndexedConv package make it possible to process

directly hexagonal images.

The speciﬁcity of γ-PhysNet lies in its physically

inspired multi-task block. As illustrated in Figure 2,

it is composed of a global feature network and a local

feature network, both made of fully connected layers.

The global feature part, starting with a global average

pooling, is dedicated to energy regression as energy

can be considered as a global parameter with regard

to the input images: for a given arrival direction and

impact point, the amplitude of the acquired image is

roughly proportional to the primary gamma ray en-

ergy (V

olk and Bernl

ohr, 2009). The local feature

part is fed with ﬂattened feature maps provided by the

backbone encoder. It intends to exploit local and spa-

tial information to solve gamma/proton classiﬁcation,

and arrival direction and impact point regression tasks

as these reconstructed parameters are more deeply re-

lated to the shape, position and orientation of the sig-

nal in the camera.

Figure 2: Physically inspired Multi-task block.

3.2 Augmenting the Backbone with

Attention

The backbone of γ-PhysNet is composed of an initial

convolution and three stages of nine residual blocks

each. The ﬁrst layer of every stage is a subsampling

performed with a strided convolution. As illustrated

in Figure 3, we insert the attention modules after ev-

ery stage to beneﬁt from attention at each feature size

scale. Note that, in order to be compliant with our

case study, attention modules are not inserted into

backbone stages in order to limit the model complex-

ity and processing cost increase.

Figure 3: Adding attention to γ-PhysNet backbone. We in-

sert the attention modules after every stage of the ResNet-

56.

In this paper, we focus on Squeeze-and-Excitation

(SE), self-attention (SA) and dual attention (DA).

3.3 Computational Cost

The whole network, implemented with PyTorch, has

2.6 ×10

parameters (for LST images). Although it

has not yet been optimized for production, γ-PhysNet

inference rate on an NVIDIA V100 GPU is similar

to the telescope acquisition rate, from 2.5 to 4.5 kHz

depending on the attention method.

4 EXPERIMENTS

We ﬁrst demonstrate the interest of multi-task learn-

ing for IACT data analysis on simulated data for CTA.

We also show that the proposed architecture outper-

forms a widespread analysis method. Then we study

attention mechanisms for γ-PhysNet backbone with

two data ﬁltering conﬁgurations to address different

analysis use cases.

4.1 Dataset

For the following experiments, we use the dataset ref-

erenced as the LST4 mono-trigger Production (from

Multi-Task Architecture with Attention for Imaging Atmospheric Cherenkov Telescope Data Analysis

537

2019/04/15), the large-scale Monte Carlo production

generated by the LST collaboration for the LST1

commissioning. This dataset is not yet publicly avail-

able. The speciﬁcity of this production is that it only

contains the data of the four LSTs of the Northern

site of CTA. It is composed of events of different

types, including diffuse gammas, gammas from point

sources (dubbed as point-like) and protons. Diffuse

events correspond to extended sources while point-

like events correspond to sources situated at a par-

ticular direction. Gammas and protons have differ-

ent simulated energy distributions, both following a

power law with a spectral index of -2, leading to an

imbalanced dataset in terms of number of events per

energy.

The dataset has been calibrated and integrated

with DL1DataHandler (Kim et al., 2019). It is sep-

arated into a training set and a test set for each event

type. The images have two channels, one for pixel in-

tensity (unit being the number of photoelectrons) and

the other containing per-pixel temporal information

(time delays from the beginning of the event recorded

by the telescope). Data amplitude is not normalized

since it is related to the energy of the detected parti-

cles (V

olk and Bernl

ohr, 2009). Again, we rely on

simulated data as ground truth is impossible to obtain

from real data, and real CTA data are not yet avail-

able. Moreover, it allows for an in-depth comparison

of the models.

4.2 Training

For the following experiments, we train all the mod-

els using the data from the four telescopes of this

LST4 mono-trigger dataset to provide a more accu-

rate overview of the data variability. The models are

trained on gamma diffuse events, so as to reconstruct

events coming from any directions within the ﬁeld of

view, and on proton events.

For reproducibility, we repeat the experiments for

all the probed conﬁgurations with six different ran-

dom seeds for parameter initialization. We use the

standard cross-entropy loss for the classiﬁcation task

and the L1 loss for regression tasks. All the neu-

ral networks are trained with the same hyperparam-

eters. Indeed, a single experiment typically requires

between 4 and 40 hours (depending on the data se-

lection) on a V100 GPU hardware. Consequently, an

advanced optimization study of all the compared net-

works is not feasible at the step of the project. How-

ever, starting from the default optimized hyperparam-

eters of ResNet, extensive preliminary experiments

allowed deﬁning a common and well-performing hy-

perparameter set. We train the models for 25 epochs

with Adam (Kingma and Ba, 2015) as the optimizer.

The learning rate is set to 10

−3

and is decayed by a

factor of 10 every 10 epochs. We regularize the net-

works by applying a L2 penalty with a weight de-

cay of 10

−4

on their weights. We balance the dif-

ferent tasks with the uncertainty estimation method

presented in (Kendall et al., 2018). The task weights

are also learned with Adam as the optimizer with a

learning rate of 0.025 and a weight decay of 10

−4

. In

gamma-ray astronomy, proton events are considered

as background noise. To prevent them from disturbing

the learning of energy and direction task for gamma

events, we rely on a masked loss method. We set to

zero the loss of the regression parameters (energy, ar-

rival direction and impact point) when particles are

protons.

4.3 Evaluation Metrics

To comply with gamma-ray astronomy standardized

practice and most common scientiﬁc use cases, we

evaluate the different conﬁgurations on gamma point-

like and proton events. Their performance on en-

ergy and direction reconstruction tasks is measured

through resolution curves. The energy resolution rep-

resents, per energy bin, the half-width of the inter-

val around 0 which contains 68% of the distribution

of the relative prediction error. The angular resolu-

tion represents, per energy bin, the angle within which

68% of reconstructed gamma rays fall, relative to their

true direction. For both, lower is better. For the

gamma/proton classiﬁcation task, the overall perfor-

mance of the network is given by the area under the

ROC curve (AUC) and the F1 score.

As we repeat the experiment six times for all the

models, we illustrate the variability of these different

runs by drawing the resolution curves as surfaces, re-

ferred to as dispersion in this paper. The envelope of

the surface represents the min / max per bin and the

dots represent the average resolution per bin of the

six random seeds. This ”average” resolution is not

related to any physical reality as resolution is a statis-

tical measure of the error of a particular model. How-

ever, it gives a trend of the model performance and is

useful for readability.

4.4 Multi-Task Learning Performance

In this section we evaluate the interest of multi-task

learning for IACT data analysis, i.e., gamma/proton

classiﬁcation, energy and direction regression. We

compare the proposed architecture with single task

networks (ResNet-56). We probe the importance

of the impact point regression as an auxiliary task

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

538

by training γ-PhysNet without the impact point

task (γ-PhysNet w/o impact). We compare with a

widespread analysis method for IACTs event recon-

struction (Hillas + RF). The toolchain used, designed

relying on the open-source library cta-lstchain v0.1.0,

consists in extracting relevant image features fol-

lowed by inferring target particle parameters with ran-

dom forests using the library scikit-learn (Pedregosa

et al., 2011).

In this paper we cannot compare with (Shilon

et al., 2019) and (Mangano et al., 2018) as the ar-

chitectures presented are designed for stereo analysis

while our architecture is designed for single telescope

analysis. We neither compare with (Nieto et al., 2017)

as this work is related to a different telescope, is fo-

cused on classiﬁcation and does not take into account

the temporal information.

A series of selection cuts on image amplitude,

shower size and truncated showers is applied to the

data in order to keep good quality events. These cuts

are standard in the domain and necessary for the com-

parison with Hillas + RF method that discards the bad

quality events. The training set is composed of 388k

gamma diffuse events and 236k proton events.

4.4.1 Gamma/Proton Classiﬁcation

Table 1 clearly shows that our model outperforms

the Hillas + RF analysis method in both AUC and

F1 score. More speciﬁcally, the proposed architec-

ture improves the AUC by 6.9% and the F1 score by

30.7% compared to Hillas + RF. The contribution of

multitasking in γ-PhysNet architecture is also signiﬁ-

cant compared to the single task approach relying on

the ResNet architecture. However, the beneﬁt of the

impact point regression as an auxiliary task is not ob-

vious for gamma/proton classiﬁcation.

Table 1: AUC and F1 score of the gamma/proton classiﬁca-

tion task for the different models.

Model AUC F1 score

Hillas + RF 0.898 0.732

ResNet-56 0.954±0.001 0.949±0.001

γ-PhysNet 0.960±0.002 0.956±0.002

γ-PhysNet 0.961±0.002 0.955±0.001

w/o Impact

4.4.2 Energy Reconstruction

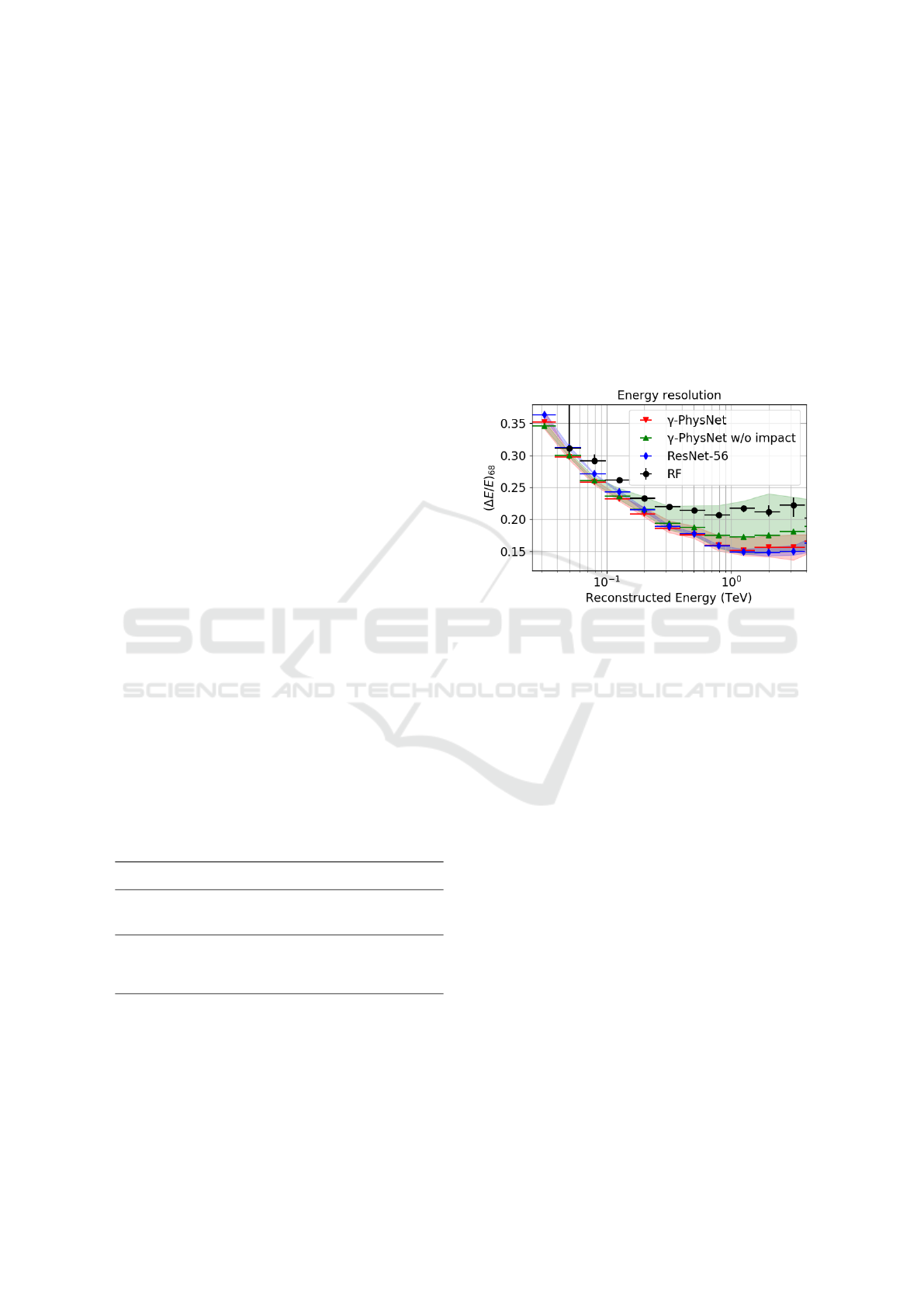
Figure 4 shows that all the evaluated deep neural net-

works (DNNs) outperform the Hillas + RF method

for the energy reconstruction task. γ-PhysNet de-

creases the relative error on the energy task by up to

0.08 at high energies and up to 1.1 at 31 GeV (the

point of the Hillas + RF curve is out of the plot).

The resolution curves of γ-PhysNet and the ResNet-

56 are very close almost everywhere. However γ-

PhysNet has slightly better results below 200 GeV.

At energies above 400 GeV, MTL seems to degrade

the performance, in particular without the regression

of the impact point. This can be explained physi-

cally as the particle energy is strongly correlated with

the observed intensity in the camera and the distance

from the telescope to the shower impact point. MTL

models have a higher dispersion than the single task

model.

Figure 4: Energy resolution as a function of the energy

in the LST energy range (lower is better). Comparison of

the performance on the energy regression task between the

probed models.

4.4.3 Direction Reconstruction

As for the gamma/proton classiﬁcation and the energy

regression tasks, Figure 5 shows that DNNs outper-

form the Hillas + RF analysis method for the direc-

tion reconstruction task. In particular, γ-PhysNet im-

proves the performance by 0.03° to 0.3° compared to

Hillas + RF. Moreover, for this task the contribution

of MTL is signiﬁcant, improving the results by up to

0.08° compared to the single task network. The pro-

posed architecture has also slightly better results with

the impact point reconstruction as an auxiliary task,

especially at higher energies (> 1 TeV). Both MTL

models have a lower variability.

4.5 Impact of the Attention Mechanisms

Our experiments presented in Section 4.4 show that

the proposed architecture outperforms the widespread

Hillas + RF analysis method and that MTL improves

the performance, especially for the direction recon-

struction task. In this section we focus on atten-

tion mechanisms for the backbone of γ-PhysNet. We

evaluate the different conﬁgurations (γ-PhysNet, γ-

Multi-Task Architecture with Attention for Imaging Atmospheric Cherenkov Telescope Data Analysis

539

Figure 5: Angular resolution as a function of the energy

in the LST energy range (lower is better). Comparison of

the performance on the arrival direction regression task be-

tween the probed models.

PhysNet SE, γ-PhysNet SA and γ-PhysNet DA) pre-

sented in Section 3.2 on the same data. To address

relevant use cases in gamma astronomy, we investi-

gate two series of selection cuts on image amplitude

and truncated showers, denoted high cuts (HC) and

low cuts (LC). These are different from Section 4.4 as

we don’t compare with Hillas + RF.

The HC consists in selecting images whose total

amplitude is higher than 1,000 photoelectrons while

higher than 50 photoelectrons for the LC. For both

we keep events whose shower is more than 80% con-

tained in the camera frame.

The HC is highly selective (training set: 121k

gammas and 75k protons), mainly at the lowest en-

ergies. The remaining events contain well deﬁned

and bright showers. In the context of single telescope

analysis, their parameters are easier to reconstruct, in

particular their arrival direction. Models trained with

the HC can address the use case of morphological

study of extended and bright sources.

The LC is far less selective (training set: 874k

gammas and 506k protons). It is worth noticing that it

is also less selective than the standard cuts applied in

Section 4.4. It allows processing more events of lower

energy albeit of less good quality. Models trained

with the LC can possibly address three use cases.

We can analyze sources emitting photons with en-

ergy lower than 100 GeV. This is particularly relevant

to the study of extragalactic objects and gamma-ray

bursts. As a second use case, we can observe the tem-

poral variability of the ﬂux of well-known sources.

Finally, we can also realize sky surveys to discover

new sources.

As detailed in Section 2.3, the probed attention

methods have a hyperparameter to control their bot-

tleneck, denoted reduction ratio. Relying on an ex-

tensive ablation study, we use the reduction ratio pre-

sented in Table 2 for the three attention mechanisms

and the two selection cuts. Noteworthy, depending on

the selection cuts we apply, the best reduction ratio

per attention mechanisms varies.

Table 2: Selected reduction ratio for the three attention

methods and the two selection cuts.

Attention HC LC

Squeeze-and-Excitation 2 4

Self-Attention 12 12

Dual Attention 8 16

4.5.1 High Cuts

Table 3 shows that all three attention methods and the

model without attention have similar results on the

classiﬁcation task. For the energy and direction re-

gression, Figure 6 and Figure 7 present the results

of the different methods in the range 100 GeV to

3 TeV as the selection ﬁlters discard most events be-

low 100 GeV. On the energy reconstruction task, all

the attention methods probed have a better average

performance than the model without attention. Their

results are also less spread. In particular, the dual at-

tention mechanisms performs clearly better on aver-

age, improving the resolution up to 0.055. Its dis-

persion is four times smaller than the one of self-

attention. The model without attention spreads ten

times more. On the direction reconstruction task,

γ-PhysNet with the Squeeze-and-Excitation and the

dual attention mechanisms outperform the other mod-

els, in average performance and in dispersion. In par-

ticular, they improve the resolution by 0.02° on most

of the energy range of interest, achieving a resolution

of 0.1° with a dispersion of 0.01°.

Table 3: High Cuts. AUC and F1 score of the gamma/proton

classiﬁcation task for the different models.

Model AUC F1 score

γ-PhysNet 0.990±0.001 0.981±0.001

γ-PhysNet 0.991±0.001 0.981±0.000

SE[2]

γ-PhysNet 0.989±0.001 0.980±0.001

SA[12]

γ-PhysNet 0.991±0.001 0.982±0.001

DA[8]

4.5.2 Low Cuts

With the low cuts, γ-PhysNet with the self-attention

method performs slightly worse on the classiﬁca-

tion task, as shown in Table 4. The other models

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

540

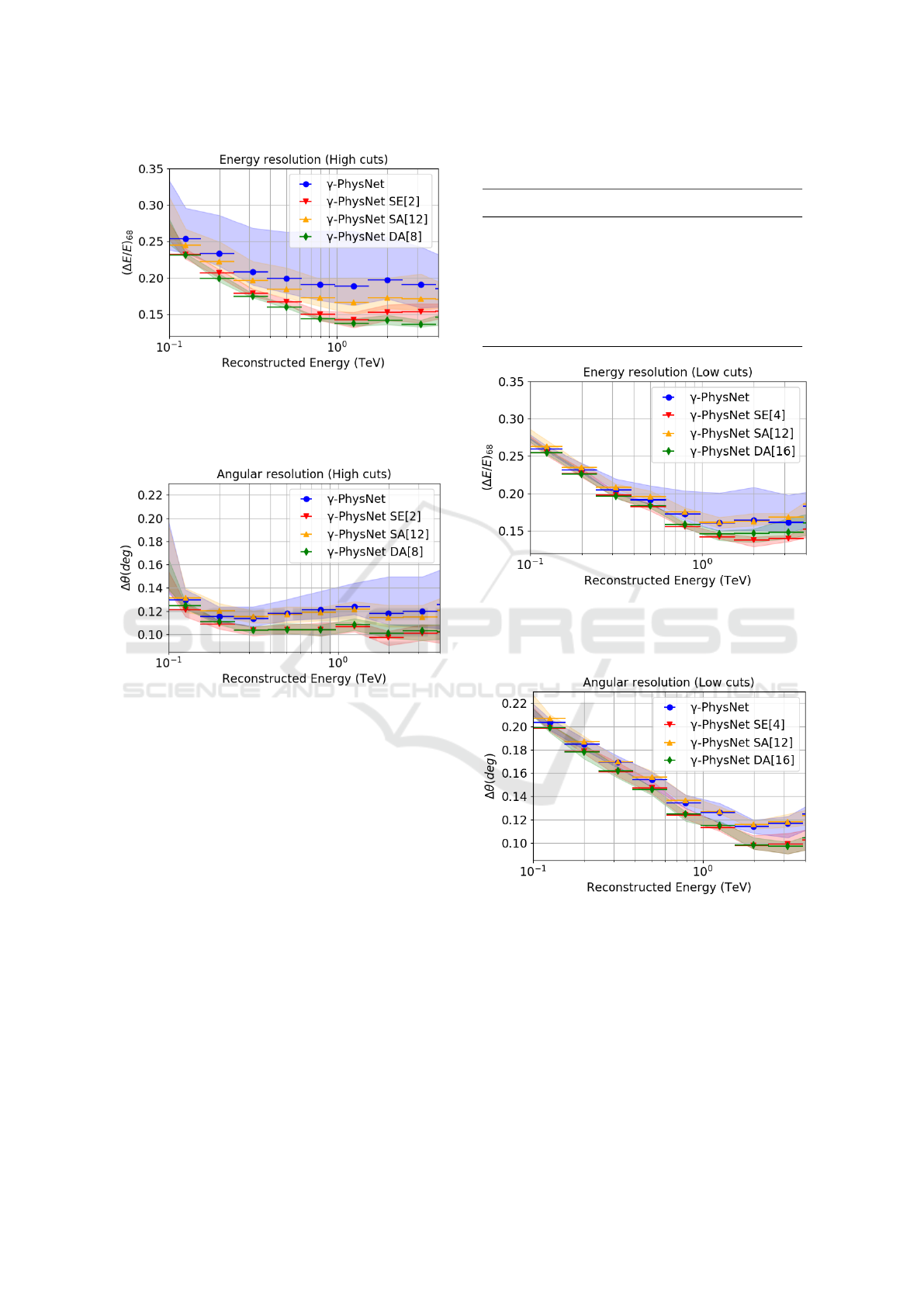
Figure 6: High cuts. Energy resolution as a function of

reconstructed energy. Comparison of the different attention

mechanisms for γ-PhysNet. The surface represents the min

/ max envelope per bin and the dots represent the average

resolution per bin of the six seeds.

Figure 7: High cuts. Angular resolution as a function of

reconstructed energy. Comparison of the different attention

mechanisms for γ-PhysNet. The surface represents the min

/ max envelope per bin and the dots represent the average

resolution per bin of the six seeds.

have comparable results within the standard deviation

range. For the energy and direction regression, Figure

8 and Figure 9 present the results in the same energy

range as for the high cuts for easy comparison. More-

over, below 100 GeV all models have similar perfor-

mance on both tasks. On the energy reconstruction

task, the models with Squeeze-and-Excitation and

dual attention perform better. They improve the re-

sults up to 0.03, in particular at high energies. All the

networks with attention have signiﬁcantly less spread

results. On the direction reconstruction task, again

the models with Squeeze-and-Excitation and dual at-

tention have better performance, improving the reso-

lution up to 0.02°. All the models have similar disper-

sion in their results.

Table 4: Low Cuts. AUC and F1 score of the gamma/proton

classiﬁcation task for the different models.

Model AUC F1 score

γ-PhysNet 0.882±0.001 0.932±0.003

γ-PhysNet 0.883±0.002 0.931±0.002

SE[4]

γ-PhysNet 0.879±0.003 0.930±0.001

SA[12]

γ-PhysNet 0.882±0.001 0.932±0.002

DA[16]

Figure 8: Low cuts. Energy resolution curves of the differ-

ent attention mechanisms for γ-PhysNet. The surface repre-

sents the min / max envelope per bin and the dots represent

the average resolution per bin of the six seeds.

Figure 9: Low cuts. Angular resolution curves of the differ-

ent attention mechanisms for γ-PhysNet. The surface repre-

sents the min / max envelope per bin and the dots represent

the average resolution per bin of the six seeds.

5 DISCUSSION

5.0.1 Contribution of Multi-Task Learning to

Gamma Astronomy

The comparison between γ-PhysNet and the

widespread Hillas + RF method presented in Section

Multi-Task Architecture with Attention for Imaging Atmospheric Cherenkov Telescope Data Analysis

541

4.4 shows that neural networks, in particular MTL,

dramatically improve the performance of IACT data

analysis. Improvements in energy resolution will

allow producing more detailed spectra, bringing

more constraints on sources modeling. Improving

the angular resolution and the classiﬁcation will

both improve the signal-to-noise ratio, thus allowing

the detection of fainter sources in a signiﬁcant way.

Studies of extended sources at very high energies are

quite recent. However, the studies made by H.E.S.S.

show extended emissions corresponding to angular

separation going from 0.05 degrees (corresponding to

H.E.S.S. angular resolution) (Aharonian et al., 2019)

to 0.3° (Hoppe et al., 2009). These values show

that the gains obtained in angular resolution, even

compared to the single task ResNet-56 (up to 0.08°),

could make the difference between observing a point

source and an extended source. This then allows for

morphological studies, bringing important insights

on the physics of these sources. Further, γ-PhysNet’s

results are consistent with ImPACT (Parsons et al.,

2016), a template-based method, and 500 times

faster.

5.0.2 Contribution of Attention

The principal lesson of the study on attention meth-

ods for γ-PhysNet presented in Section 4.5 is that

all attention methods help to reduce the variabil-

ity of the results and thus to improve the robust-

ness of the models. Another interesting insight is

that the self-attention mechanism, although the more

complex, constantly underperforms. On the other

hand, Squeeze-and-Excitation and dual attention sig-

niﬁcantly improve both energy and direction recon-

structions task performance compared to γ-PhysNet

without attention.

5.0.3 Real Data Discrepancy

Although we have high quality simulations to train

γ-PhysNet, real data will certainly differ from simu-

lated data. In (Shilon et al., 2019) Shilon et al. have

shown that for H.E.S.S., the angular resolution was

signiﬁcantly degraded when a CNN was applied to

real data, with a loss of about 0.04° compared to sim-

ulated data. In future work, we plan to use real data as

soon as they are available to improve the performance

of our architecture. Since ground truth is difﬁcult to

obtain from real data, GAN approaches could help to

build up relevant feature representations of the real

data. It has been successfully applied to light curve

analysis in (Pasquet et al., 2019). Moreover, a phase

of improvement of the simulation will be conducted

when real data are available. We expect our model to

beneﬁt from the updated simulation.

6 CONCLUSION

In this paper we have presented γ-PhysNet, a phys-

ically inspired deep multi-task architecture for sin-

gle telescope IACT full event reconstruction. Our

model exploits the multi-task nature of IACT events

to perform gamma / proton classiﬁcation, energy

and arrival direction reconstruction, outperforming

the widespread Hillas + Random Forest analysis on

Monte Carlo simulated data. Our extensive exper-

iments show that MTL in the context of CTA data

analysis achieves better performance than single task

networks. We have then realized a study on attention

mechanisms with two different selection cuts to ad-

dress relevant use cases. Our experiments show that

attention improves the performance and the robust-

ness on energy and direction regression tasks.

The contribution of our multi-task architecture

also lies in its speed as a substantial gain is expected

by using a single network instead of one for each of

the three tasks. Speed is actually a strong requirement

to enable real-time source and transient event detec-

tion as well as alert broadcasting to other observato-

ries.

ACKNOWLEDGEMENTS

We gratefully acknowledge ﬁnancial support from

the agencies and organizations listed here: www.cta-

observatory.org/consortium acknowledgment. This

project has received funding from the European

Union’s Horizon 2020 research and innovation

programme under grant agreement No 653477,

and from the Fondation Universit

e Savoie Mont

Blanc. This work has been done thanks to

the facilities offered by the Univ. Savoie Mont

Blanc - CNRS/IN2P3 MUST computing center and

HPC resources from GENCI-IDRIS (Grant 2020-

AD011011577) and computing and data processing

ressources from the CNRS/IN2P3 Computing Center

(Lyon - France). We gratefully acknowledge the sup-

port of the NVIDIA Corporation with the donation of

one NVIDIA P6000 GPU for this research.

REFERENCES

Abdalla, H., Adam, R., Aharonian, F., et al. (2019). A very-

high-energy component deep in the γ-ray burst after-

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

542

glow. Nature, 575(7783):464–467.

Aharonian, F., Ait, B. F., Bernl

ohr, K., Bordas, P.,

Casanova, S., Chakraborty, N., Deil, C., Donath, A.,

Hahn, J., Hermann, G., et al. (2019). Resolving the

crab pulsar wind nebula at teraelectronvolt energies.

Nature Astronomy.

Ambrosi, G., Awane, Y., Baba, H., et al. (2013). The

Cherenkov Telescope Array Large Size Telescope.

Proceedings of the 33rd International Cosmic Ray

Conference, pages 8–11.

Bahdanau, D., Cho, K., and Bengio, Y. (2015). Neural ma-

chine translation by jointly learning to align and trans-

late. In Bengio, Y. and LeCun, Y., editors, 3rd Interna-

tional Conference on Learning Representations, ICLR

2015, San Diego, CA, USA, May 7-9, 2015, Confer-

ence Track Proceedings.

Brunel, A., Pasquet, J., PASQUET, J., Rodriguez, N.,

Comby, F., Fouchez, D., and Chaumont, M. (2019).

A cnn adapted to time series for the classiﬁcation of

supernovae. Electronic Imaging, 2019(14):90–1.

Cao, J., Li, Y., and Zhang, Z. (2018). Partially shared

multi-task convolutional neural network with local

constraint for face attribute learning. In Proceedings

of the IEEE Conference on Computer Vision and Pat-

tern Recognition, pages 4290–4299.

Caruana, R. (1997). Multitask learning. Machine learning,

28(1):41–75.

Chen, Z., Badrinarayanan, V., Lee, C.-Y., and Rabinovich,

A. (2018). GradNorm: Gradient normalization for

adaptive loss balancing in deep multitask networks.

In Dy, J. and Krause, A., editors, Proceedings of the

35th International Conference on Machine Learning,

volume 80 of Proceedings of Machine Learning Re-

search, pages 794–803. PMLR.

de Naurois, M. and Rolland, L. (2009). A high performance

likelihood reconstruction of γ-rays for imaging atmo-

spheric Cherenkov telescopes. Astroparticle Physics,

32(5):231–252.

Feng, Q., Lin, T. T., Collaboration, V., et al. (2016). The

analysis of veritas muon images using convolutional

neural networks. Proceedings of the International As-

tronomical Union, 12(S325):173–179.

Fiasson, A., Dubois, F., Lamanna, G., Masbou, J., and

Rosier-Lees, S. (2010). Optimization of multivariate

analysis for IACT stereoscopic systems. Astroparticle

Physics, 34.

Guo, M., Haque, A., Huang, D.-A., Yeung, S., and Fei-Fei,

L. (2018). Dynamic task prioritization for multitask

learning. In Proceedings of the European Conference

on Computer Vision (ECCV), pages 270–287.

He, K., Gkioxari, G., Dollar, P., and Girshick, R. (2017).

Mask R-CNN. In Proceedings of the IEEE Interna-

tional Conference on Computer Vision (2017).

He, K., Zhang, J., Ren, S., and Sun, J. (2016a). Iden-

tity mappings in deep residual networks. In Euro-

pean conference on computer vision, pages 630–645.

Springer.

He, K., Zhang, X., Ren, S., and Sun, J. (2016b). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Hillas, A. (1985). Cerenkov light images of eas produced

by primary gamma. In International Cosmic Ray Con-

ference, volume 3.

Hoppe, S. et al. (2009). Detection of very-high-

energy gamma-ray emission from the vicinity of

PSR B1706-44 with H.E.S.S. arXiv e-prints, page

arXiv:0906.5574.

Hu, J., Shen, L., and Sun, G. (2018). Squeeze-and-

excitation networks. In Proceedings of the IEEE con-

ference on computer vision and pattern recognition,

pages 7132–7141.

Iizuka, S., Simo-Serra, E., and Ishikawa, H. (2016). Let

there be color! joint end-to-end learning of global and

local image priors for automatic image colorization

with simultaneous classiﬁcation. ACM Transactions

on Graphics (ToG), 35(4):1–11.

Jacquemont, M., Antiga, L., Vuillaume, T., Silvestri, G.,

Benoit, A., Lambert, P., and Maurin, G. (2019). In-

dexed operations for non-rectangular lattices applied

to convolutional neural networks. In Proceedings of

the 14th International Joint Conference on Computer

Vision, Imaging and Computer Graphics Theory and

Applications - Volume 5: VISAPP,, pages 362–371.

INSTICC, SciTePress.

Kendall, A., Gal, Y., and Cipolla, R. (2018). Multi-task

learning using uncertainty to weigh losses for scene

geometry and semantics. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion, pages 7482–7491.

Kim, B., Brill, A., Miener, T., Nieto, D., and Feng,

Q. (2019). DL1-Data-Handler: DL1 HDF5 writer,

reader, and processor for IACT data. https://doi.org/

10.5281/zenodo.3336561. v0.8.1-legacy.

Kim, E. J. and Brunner, R. J. (2016). Star-galaxy clas-

siﬁcation using deep convolutional neural networks.

Monthly Notices of the Royal Astronomical Society,

page stw2672.

Kingma, D. P. and Ba, J. (2015). Adam: A method for

stochastic optimization. In Bengio, Y. and LeCun,

Y., editors, 3rd International Conference on Learn-

ing Representations, ICLR 2015, San Diego, CA, USA,

May 7-9, 2015, Conference Track Proceedings.

Luvizon, D. C., Picard, D., and Tabia, H. (2018). 2d/3d

pose estimation and action recognition using multitask

deep learning. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition.

Mangano, S., Delgado, C., Bernardos, M. I., et al. (2018).

Extracting gamma-ray information from images with

convolutional neural network methods on simulated

cherenkov telescope array data. In IAPR Workshop

on Artiﬁcial Neural Networks in Pattern Recognition,

pages 243–254. Springer.

Nieto, D., Brill, A., Feng, Q., Jacquemont, M., Kim, B.,

Miener, T., and Vuillaume, T. (2019). Studying deep

convolutional neural networks with hexagonal lattices

for imaging atmospheric cherenkov telescope event

reconstruction. In ICRC 2019 - 36th International

Cosmic Ray Conference.

Multi-Task Architecture with Attention for Imaging Atmospheric Cherenkov Telescope Data Analysis

543

Nieto, D., Brill, A., Kim, B., et al. (2017). Explor-

ing deep learning as an event classiﬁcation method

for the Cherenkov Telescope Array. arXiv preprint

arXiv:1709.05889, pages 1–8.

Parmar, N., Ramachandran, P., Vaswani, A., Bello, I., Lev-

skaya, A., and Shlens, J. (2019). Stand-alone self-

attention in vision models. In Advances in Neural In-

formation Processing Systems, pages 68–80.

Parmar, N., Vaswani, A., Uszkoreit, J., Kaiser, L., Shazeer,

N., Ku, A., and Tran, D. (2018). Image transformer.

In Dy, J. and Krause, A., editors, Proceedings of the

35th International Conference on Machine Learning,

volume 80 of Proceedings of Machine Learning Re-

search, pages 4055–4064. PMLR.

Parsons, R., Murach, T., and Gajdus, M. (2016). Hess ii data

analysis with impact. In The 34th International Cos-

mic Ray Conference, volume 236, page 826. SISSA

Medialab.

Parsons, R. and Ohm, S. (2019). Background rejec-

tion in atmospheric cherenkov telescopes using recur-

rent convolutional neural networks. arXiv preprint

arXiv:1910.09435.

Pasquet, J., Pasquet, J., Chaumont, M., and Fouchez, D.

(2019). Pelican: deep architecture for the light curve

analysis. Astronomy & Astrophysics, 627:A21.

Pavllo, D., Feichtenhofer, C., Grangier, D., and Auli, M.

(2019). 3d human pose estimation in video with tem-

poral convolutions and semi-supervised training. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition, pages 7753–7762.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., Vanderplas, J., Passos, A.,

Cournapeau, D., Brucher, M., Perrot, M., and Duch-

esnay, E. (2011). Scikit-learn: Machine learning in

Python. Journal of Machine Learning Research, 12.

Ren, Z. and Jae Lee, Y. (2018). Cross-domain self-

supervised multi-task feature learning using synthetic

imagery. In Proceedings of the IEEE Conference on

Computer Vision and Pattern Recognition, pages 762–

771.

Ruder, S. (2017). An overview of multi-task learn-

ing in deep neural networks. arXiv preprint

arXiv:1706.05098.

Sener, O. and Koltun, V. (2018). Multi-task learning as

multi-objective optimization. In Advances in Neural

Information Processing Systems.

Shilon, I., Kraus, M., B

uchele, M., Egberts, K., Fischer, T.,

Holch, T. L., Lohse, T., Schwanke, U., Steppa, C., and

Funk, S. (2019). Application of deep learning meth-

ods to analysis of imaging atmospheric cherenkov

telescopes data. Astroparticle Physics, 105:44–53.

Sun, J., Darbeha, F., Zaidi, M., and Wang, B.

(2020). Saunet: Shape attentive u-net for inter-

pretable medical image segmentation. arXiv preprint

arXiv:2001.07645.

Thrun, S. (1996). Is learning the n-th thing any easier than

learning the ﬁrst? In Advances in neural information

processing systems, pages 640–646.

Touvron, H., Vedaldi, A., Douze, M., and J

egou, H. (2019).

Fixing the train-test resolution discrepancy. In Ad-

vances in Neural Information Processing Systems,

pages 8252–8262.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. In Advances in

neural information processing systems, pages 5998–

6008.

olk, H. J. and Bernl

ohr, K. (2009). Imaging very high en-

ergy gamma-ray telescopes. Experimental Astronomy,

25(1-3).

Wang, X., Girshick, R., Gupta, A., and He, K. (2018). Non-

local neural networks. In Proceedings of the IEEE

conference on computer vision and pattern recogni-

tion, pages 7794–7803.

Yuan, Y., Chen, X., and Wang, J. (2020). Object-contextual

representations for semantic segmentation. In Com-

puter Vision – ECCV 2020.

Zhang, H., Goodfellow, I., Metaxas, D., and Odena, A.

(2019). Self-attention generative adversarial net-

works. In International Conference on Machine

Learning, pages 7354–7363.

Zhang, H., Wu, C., Zhang, Z., et al. (2020). Resnest: Split-

attention networks. arXiv preprint arXiv:2004.08955.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

544