
Using Anatomical Priors for Deep 3D One-shot Segmentation
Duc Duy Pham, Gurbandurdy Dovletov and Josef Pauli
Intelligent Systems, Faculty of Engineering, University of Duisburg-Essen, Germany
Keywords:
Shape Priors, Anatomical Priors, One-shot Segmentation.
Abstract:
With the success of deep convolutional neural networks for semantic segmentation in the medical imaging
domain, there is a high demand for labeled training data, that is often not available or expensive to acquire.
Training with little data usually leads to overfitting, which prohibits the model to generalize to unseen prob-
lems. However, in the medical imaging setting, image perspectives and anatomical topology do not vary as
much as in natural images, as the patient is often instructed to hold a specific posture to follow a standardized
protocol. In this work we therefore investigate the one-shot segmentation capabilities of a standard 3D U-Net
architecture in such setting and propose incorporating anatomical priors to increase the segmentation perfor-
mance. We evaluate our proposed method on the example of liver segmentation in abdominal CT volumes.
1 INTRODUCTION
In medical image computing, semantic segmentation
of anatomical structures from various imaging modal-
ities is a crucial task to aid in image based diagnostics.
Therefore, research on automated segmentation meth-
ods is a major topic in the medical computing domain,
since manual segmentation is expensive and time con-
suming. Especially deep learning strategies have be-
come popular approaches to achieve state of the art re-
sults. Ronneberger et al.’s U-Net (Ronneberger et al.,
2015) has achieved a lot of attention, yielding impres-
sive results in many medical applications. While its
general architecture has been modified in numerous
ways, (Isensee et al., 2018) demonstrate the effec-
tiveness of a well trained U-Net without substantial
architectural modifications in the BraTS 2018 chal-
lenge. Therefore, the U-Net architecture has become
a competitive baseline for state of the art segmenta-
tion performance. However, it does not take into con-
sideration the low variation in shape for most anatom-
ical structures. Consequently, recent research aims at
incorporating shape priors into the segmentation pro-
cess. (Ravishankar et al., 2017) propose augmenting
the U-Net by means of a pre-trained autoencoder that
is used for shape regularization. The U-Net’s output
is corrected by the autoencoder to result in a feasible
shape. (Oktay et al., 2018) also utilize a pre-trained
autoencoder for shape preservation. However, the au-
toencoder’s encoding component is used to regularize
the weight adaptation process of a generic segmenta-
tion network during training, instead of merely cor-
recting the initial segmentation output. This is moti-
vated by (Girdhar et al., 2016)’s work on establish-
ing 3D representations of objects from 2D images.
(Dalca et al., 2018) take into consideration shape pri-
ors by means of pre-trained variational autoencoders
for an unsupervised learning scheme. (Pham et al.,
2019) present a 2D end-to-end architecture, in which
an autoencoder, trained for shape representation, is
imitated in latent space by a separate encoder, to di-
rectly leverage the autoencoder’s decoder for shape
consistent segmentation.
A limiting factor for most deep learning strategies is
the amount of data needed to sufficiently train deep
learning models. Especially in the medical domain,
labeled training data is scarce and expensive to ac-
quire. As a result, one-shot and few-shot learning ap-
proaches have been developed for classification tasks
in natural image settings (Koch et al., 2015; Santoro
et al., 2016; Snell et al., 2017; Vinyals et al., 2016).
There is, however, little research towards one-shot
and few-shot learning for segmentation tasks, e.g. by
(Dong and Xing, 2018; Michaelis et al., 2018), par-
ticularly for medical images, e.g. (Roy et al., 2020).
While distinguishing between tissue classes can be
more challenging than in natural images, medical im-
ages are usually more constrained regarding perspec-
tive and shapes. Our contributions are the following:
• We examine to which extend a 3D U-Net archi-
tecture is capable of segmenting unseen volumes
in a one-shot segmentation setting.
• We compare its results to architectures that make
174
Pham, D., Dovletov, G. and Pauli, J.
Using Anatomical Priors for Deep 3D One-shot Segmentation.
DOI: 10.5220/0010303101740181
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 2: BIOIMAGING, pages 174-181
ISBN: 978-989-758-490-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

use of additional anatomical priors.
• We present and investigate an architecture of our
own, which can be regarded as a combination of
(Pham et al., 2019)’s and (Oktay et al., 2018)’s
work.
2 METHODS
Motivated by(Oktay et al., 2018)’s contribution and
based on (Pham et al., 2019)’s work regarding
anatomical priors, we investigate a combined 3D seg-
mentation approach in a one-shot setting. We propose
a 3D end-to-end Imitating and Regularizing Encoders
and Enhanced Decoder Network (IRE
3
D-Net) that is
derived from the IE
2
D-Net, leveraging Oktay et al.’s
enforcement of stronger shape regularization. The
architecture consists of two convolutional encoders
f
enc
p
, f
enc
i
, one decoder g
dec
and one U-Net compo-
nent h
unet
as depicted in Fig. 1. While f
enc
p
and
g
dec
form a convolutional autoencoder (CAE), f
enc
i
and g
dec
constitute a segmentation hourglass network.
The standard U-Net module h
unet
is used to enhance
g
dec
for an image guided decoding process to increase
the decoder’s localization capabilities. Additionally,
f
enc
p
serves as a regularization module, that measures
the output’s shape consistency in latent space during
training.
2.1 Enforcing Shape Preservation
Convolutional autoencoders are able to both compress
their input into a meaningful representation in latent
space, and reconstruct the original input from this rep-
resentation with only little to none information loss.
We leverage this property to inject prior information
into the learning process of a deep learning network.
In our architecture we use the mapping from input to
latent feature space for two strategies of shape preser-
vation. On the one hand, we employ (Girdhar et al.,
2016)’s approach of imitating the autoencoder’s prior
encoder f
enc
p
in latent space by an additional imitat-
ing encoder f
enc
i
, that infers the actual medical vol-
ume instead of the ground truth volume. We denote
the input volume as x and the segmentation ground
truth as y, and Θ represents the trainable weights of
the architecture. Then the mapping of y into latent
space is
ˆz = f
enc
p
(y, Θ
enc
p
), (1)
whereas the imitation in latent space from x is
˜z = f
enc
i
(x, Θ
enc
i
). (2)
The formulation of an imitation loss
L
imit
(Θ
enc
i
|Θ
enc
p
) := ||ˆz − ˜z||
1
, (3)
where Θ
enc
i
is adaptable and Θ
enc
p
is fixed, enforces
f
enc
i
to encode the input volume in a similar fashion
to f
enc
p
during training. The idea is to utilize the au-
toencoder’s decoder g
dec
to achieve a segmentation
˜y = g
dec
( f
enc
i
(x, Θ
enc
i
), Θ
dec
) (4)
from x that is close to the ground truth y. Further-
more, the decoder receives skip connections from the
U-Net’s contracting path, enhancing the decoder’s lo-
calization capabilities.
On the other hand, we additionally leverage f
enc
p
to
restrain the output segmentation’s shape by compar-
ing its latent representation to the ground truth’s, em-
ploying a shape consistency loss
L
sc
(Θ
enc
i
, Θ
dec
, Θ
unet
|Θ
enc
p
) :=
f
enc
p
˜y + h
unet
(x)
2
− f
enc
p
(y)
1
, (5)
which is used to adapt Θ
enc
i
, Θ
dec
and Θ
unet
, whereas
Θ
enc
p
is kept fixed. Like (Oktay et al., 2018) we add
this loss as a regularizing term to the segmentation
losses of the segmentation networks. Inclined by the
success of ensemble methods, the output of the U-Net
module is finally added to the segmentation output
from the imitating hourglass network in a component-
wise manner.
2.2 Differences in Training and
Inference
As can be seen in Fig.1, our architecture consists
of two segmentation networks, i.e. the U-Net mod-
ule and the hourglass network module. Even though
the hourglass network’s decoder receives skip con-
nections from the U-Net’s contracting path, both ar-
chitectures are optimized separately using the Dice
Loss and regularized by L
sc
, weighted by a factor λ.
The autoencoder is also trained separately from the
segmentation networks by means of the Dice Loss.
The imitating encoder is optimized by the aforemen-
tioned imitation loss L
imit
. During training, the prior
encoder’s main purpose is to deliver a reference for
the imitation encoder to compare against. Since f
enc
p
needs a ground truth segmentation as input, it is es-
sentially replaced by f
enc
i
that is trained to map med-
ical images to a similar feature in latent space. Also,
shape consistency regularization is only possible dur-
ing training, therefore f
enc
p
is omitted during infer-
ence.
Using Anatomical Priors for Deep 3D One-shot Segmentation
175

Figure 1: Network Architecture. The architecture consists of four modules: the U-Net module (brown), the imitating encoder
(purple), the prior encoder (yellow), and the joint decoder (blue). The prior encoder is additionally used for shape consistency
of the output segmentation and the ground truth. For inference the prior encoder is omitted.
3 EXPERIMENTS
3.1 Data
We evaluated on the example of liver segmentation
from abdominal CT volumes, using both the Cancer
Imaging Archive Pancreas-CT data set (Clark et al.,
2013; Roth et al., 2016; Roth et al., 2015) (TCIA)
and the Beyond the Cranial Vault (BTCV) segmenta-
tion challenge (Landman et al., 2015; Xu et al., 2016)
with supplementary ground truth segmentations pro-
vided by (Gibson et al., 2018), resulting in ninety
abdominal CT volumes with corresponding ground
truths in total. Since we examine the one-shot ca-
pability of a standard U-Net implementation and the
effect of incorporating anatomical priors into a deep
learning architecture, the U-Net model, (Oktay et al.,
2018)’s ACNN , (Pham et al., 2019)’s IE
2
D and our
newly proposed IRE
3
D are all trained with only one
patient data set for each test scenario. In an exhaustive
leave-one-out cross validation manner, we trained ev-
ery architecture 90 times, using each patient data set
as one-shot training set once, and tested on the re-
maining patient data sets, that have not been involved
in training or validation. We arbitrarily used patients
40 and 90 as validation data sets. When training with
patient 40 we used patients 39 and 90 for validation
and when training with patient 90, we used patients 40
and 89 for validation. We considered the commonly
used Dice Similarity Coefficient (DSC) and the Haus-
dorff Distance (HD) as evaluation metrics. While the
DSC is a similarity measure between ground truth and
prediction, the HD measures the distance to the fur-
thest falsely classified voxel. As a reference (Ref)
we calculated the DSC for each test data set, which
is achieved by just regarding the ground truth of the
training data set as final segmentation for the test sets.
We additionally simulate a Situs Inversus case, in
which the organs are flipped. This is motivated by
our intention to investigate how the trained networks
react to cases that slightly differ from physiological
images obtained in the usual standard scanning pro-
cedure. We do so by inverting the stack ordering in
longitudinal axis for validation and all test data sets,
while keeping the ordering for the training set.
3.2 Implementation Details
We resized the CT volumes to an input size of 128 ×
128 × 96 and used Tensorflow 1.12.0 for our network
implementations. For all models, and for all the sep-
arately trainable modules, the optimization was per-
formed with an Adam Optimizer with an initial learn-
ing rate of 0.001. The training volume was aug-
mented by means of random translation and rotation.
With a batch size of 1, we trained each model for
2400 iterations and chose the model with best valida-
tion loss for evaluation. Starting with 32 kernels for
each convolutional layer in the first resolution level of
each encoder/contracting path, we doubled the num-
BIOIMAGING 2021 - 8th International Conference on Bioimaging
176
ber of kernels for each resolution level on the encod-
ing/contracting side and halved the number of kernels
on the expansive/decoding side for each architecture.
We used a kernel size of 3 × 3 × 3 for every convolu-
tional layer and 2 × 2 × 2 max-pooling in each archi-
tecture. The weight of the regularization term in both
the ACNN and the IRE
3
D was set to λ = 0.001, as
suggested by (Oktay et al., 2018). The experiments
were conducted on a GTX 1080 TI GPU.
4 RESULTS
Since the complete data set origins from two different
sources, we differentiate between 4 cases regarding
evaluation results:
• Q
11
: Trained on TCIA and tested on TCIA
• Q
12
: Trained on TCIA and tested on BTCV
• Q
21
: Trained on BTCV and tested on TCIA
• Q
22
: Trained on BTCV and tested on BTCV
These four cases are especially noticeable for the ref-
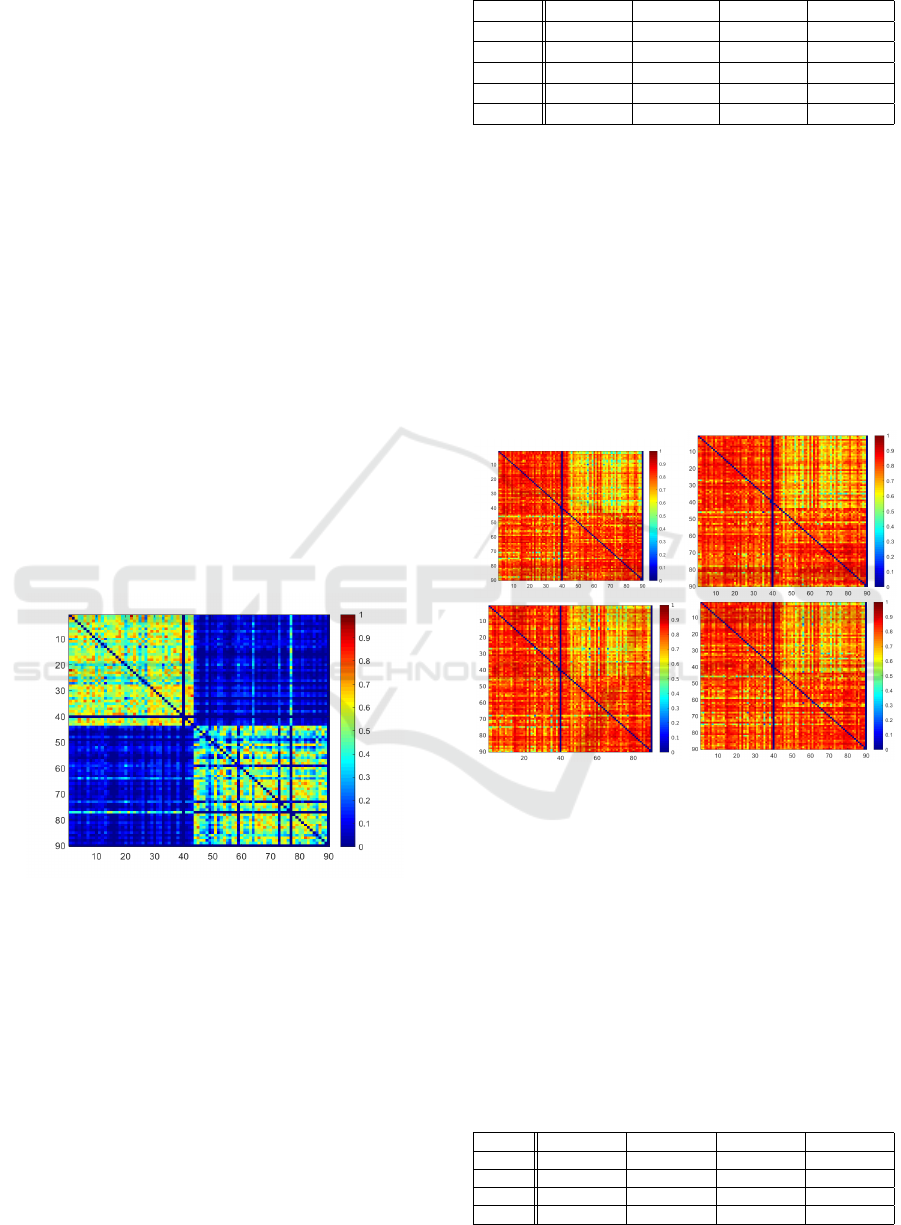
erence DSC measures in Fig.2, where the achieved
DSCs for each train/test patient combination is de-
picted as a heat map. Rows indicate the patient data
Figure 2: DSC Heatmap of Reference for ordinary setting.
Rows indicate patient used for training, columns represent
test data set.
set used for training, whereas columns represent the
patient test data set. While the columns for patient
40 and 90 are empty, as they serve as validation data
sets, a strong DSC change is visible from column
43 to 44 and row 43 to 44. In particular, the DSCs
get worse, when ground truths come from different
data sources. This indicates that there already is a
strong overlap between ground truths within each data
source. The segmentation problem might therefore be
easier when train and test patients are within the same
data source. This becomes quantitatively visible in
Table 1, in which the resulting mean DSCs for each
Table 1: Achieved DSCs in each case.
DSC Q
11
Q
12
Q
21
Q
22
Ref 53.7 ± 12 31.7 ± 13 31.7 ± 13 40.7 ± 20
U-Net 82.9±6 67.3 ± 11 78.4 ± 9 80.3±7
ACNN 82.5 ± 6 69.6 ± 10 79.0±8 79.7 ± 8
IE
2
D 82.1 ± 7 70.2 ± 11 78.4 ± 10 80.3 ± 7
IRE
3
D 81.8 ± 7 70.5 ±11 77.6 ± 10 80.1 ± 8
architecture in each case are shown.
For the reference and all tested architectures, the
best DSCs are achieved in Q
11
and Q
22
. Table 1 also
shows, that the standard U-Net yields the best results
regarding DSC in Q
11
and Q
22
, while architectures
with anatomical priors show slightly better results in
Q
12
and Q
21
, i.e. when data sources for training and
testing are different. Our proposed IRE
3
D architec-
ture achieves the best DSC result for the Q
12
case,
whereas for Q
21
Oktay et al.’s ACNN surpassed the
remaining models. Fig.3 depicts the DSC heatmaps
of all trained models.
Figure 3: DSC Heatmaps for each train/test combination of
U-Net, ACNN, IE
2
D, IRE
3
D (from top left to bottom right)
for ordinary setting. Rows indicate patient used for training,
columns represent test data set.
It becomes visually apparent, that the Q
12
case
seems to be especially difficult for all models. The ob-
servation that models with shape priors perform bet-
ter when source and target domain are different is,
however, only partly reflected by the Hausdorff Dis-
tances in Table 2. Surprisingly, the regularization in
the ACNN results in higher Hausdorff distances than
for the standard U-Net in all cases. Our proposed
IRE
3
D Network shows best results regarding HD in
Table 2: Achieved HDs in each case.
HD Q
11
Q
12
Q
21
Q
22
U-Net 50.8 ± 12.9 40.4±11.1 48.6 ± 14.2 48.2±12.7
ACNN 60.1 ± 19.1 45.6 ± 13.3 55.7 ± 23.5 54.8 ± 14.1
IE
2
D 48.1 ± 13.4 40.5 ± 10.5 45.9 ± 13.1 51.7 ± 12.4
IRE
3
D 47.8±12.8 40.4 ± 10.7 45.1±12.8 51.1 ± 12.8
Using Anatomical Priors for Deep 3D One-shot Segmentation
177
Q
11
and Q
21
, whereas in the challenging Q
12
case it
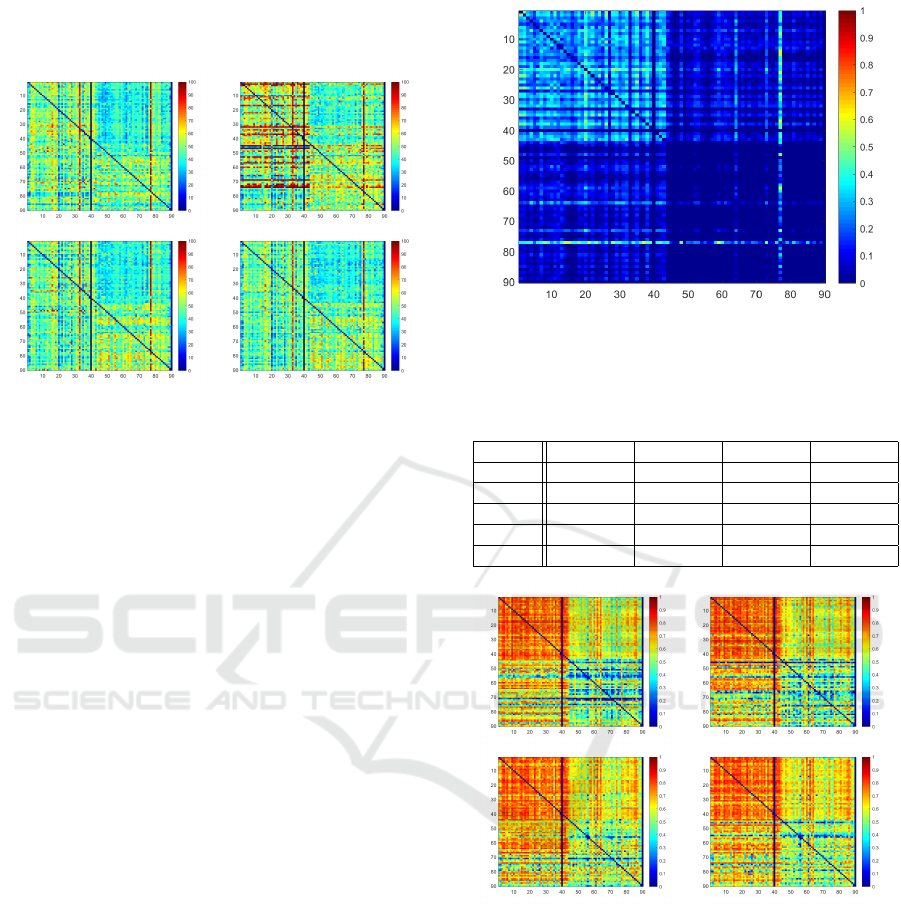
preforms equally well as the U-Net. Fig. 4 shows
Figure 4: Hausdorff Distance Heatmaps for each train/test
combination of U-Net, ACNN, IE
2
D, IRE
3
D (from top left
to bottom right) for ordinary setting. Rows indicate patient
used for training, columns represent test data set.
the maps of measured Hausdorff distances for each
train/test scenario in each model. Red indicates high
distances wheras blue represents low values. The sur-
prising observation is here visualized, as it can be seen
that the ACNN architecture seems to have difficulties
especially in Q
11
and Q
21
. While the tested models
with shape prior information and our proposed IRE
3
D
model show promising results for one-shot settings in
which source and target domain are different, it is still
surprising that a standard U-Net is also capable of
achieving that good DSC and HD scores when only
training with one data set. Therefore, we would like
to investigate if this observation still holds, when train
and test data show a stronger deviation, such as the Si-
tus Inversus setting.
4.1 Situs Inversus Simulation
In the Situs Inversus setting, it becomes imminent in
the Reference heat map in Fig. 5, that Q
22
yields the
most challenging case, whereas Q
11
seems to be the
easiest scenario.
This may be due to the fact, that in BTCV the
liver is not centered along the longitudinal axis. Thus,
when inverting the stack order, the overlap of liver re-
gions between training and testing data set is smaller
than in the other cases. In TCIA, particularly, the liver
is more centered, such that even when inverting the
order, the overlap of liver regions is still rather large.
Table 3 reveals, that the IE
2
D architecture and our
proposed model outperform the standard U-Net in all
cases except for Q
11
, where the standard U-Net yields
best DSC results.
Figure 5: DSC Heatmap of Reference for Situs Inversus
setting . Rows indicate patient used for training, columns
represent test data set.
Table 3: Achieved DSCs in each case for a situs inversus
setting.
Q
11
Q
12
Q
21
Q
22
Ref 26.0 ± 10 8.3 ± 8 8.3 ± 8 1.4 ± 5
U-Net 76.2±7 59.3 ± 11 60.4 ± 17 45.0 ± 18
ACNN 76.0 ± 7 61.1 ± 11 59.7 ± 19 45.9 ± 18
IE
2
D 75.4 ± 8 61.8 ± 11 63.7±16 52.4±16
IRE
3
D 75.8 ± 8 63.0±10 61.9 ± 16 51.2 ± 16
Figure 6: DSC Heatmaps for each train/test combination of
U-Net, ACNN, IE
2
D, IRE
3
D (from top left to bottom right)
for situs inversus setting. Rows indicate patient used for
training, columns represent test data set.
Figure 6 shows the DSC heatmaps of the trained
models for each train/test combination. It is di-
rectly noticable that for Q
11
all models perform very
well, wheras the most problematic case is Q
22
, i.e.
when there is only little segmentation overlap be-
tween training and testing image. To explore the im-
provements by incorporating shape priors compared
to U-Net we visualize the signed difference maps of
the DSC heatmaps in Fig.7. The first column of the
figure highlights the train/test cases in which U-Net
BIOIMAGING 2021 - 8th International Conference on Bioimaging
178

Figure 7: First column: DSC improvement for each
train/test combination, in which U-Net performs better than
ACNN, IE
2
D, IRE
3
D for situs inversus setting. Second
column: DSC improvement for each tra(from top to bot-
tom)in/test combinations, in which ACNN, IE
2
D, IRE
3
D
(from top to bottom) perform better than U-Net for situs
inversus setting. Rows indicate patient used for training,
columns represent test data set.
Table 4: Achieved HDs in each case for a situs inversus
setting.
HD Q
11
Q
12
Q
21
Q
22
U-Net 55.7±12.1 42.0±11.3 60.5±17.8 42.0±11.2
ACNN 64.4±18.0 46.9±14.0 71.9±24.4 51.6±18.0
IE
2
D 52.3±12.8 40.1±10.6 54.2±15.5 39.6±10.6
IRE
3
D 51.4±12.3 39.8±10.4 55.2±16.6 39.2±10.3
performs better, whereas the second column shows
the cases in which U-Net preforms worse. We can see
that for IE
2
D and IRE
3
D there are many cases, espe-
cially in Q
21
and Q
22
, in which U-Net yields inferior
DSC scores. Considering the Hausdorff distances in
Table 4, IE
2
D and IRE
3
D also show better results than
the U-Net in all cases. It is, however, surprising that
the shape regularization in ACNN, again, results in
considerably worse Hausdorff distances in all cases.
These observations are visualized in Fig.8, in which
the worse Hausdorff distances of ACNN become im-
mediately apparent in comparison to the other archi-
tectures. As before we would like to compare the
shape prior based models with the standard U-Net
by computing the signed difference in Hausdorff dis-
tances in Fig.9. The left column of the figure high-
lights in which train/test cases U-Net achieves worse
Hausdorff distances, whereas the right column shows
Figure 8: Hausdorff Distance Heatmaps for each train/test
combination of U-Net, ACNN, IE
2
D, IRE
3
D (from top left
to bottom right) for situs inversus setting. Rows indicate
patient used for training, columns represent test data set.
the scenarios, in which U-Net results in better dis-
tances. For ACNN it is surprisingly noticeable that
regarding Hausdorff distance U-Net seems to be su-
perior in most case. For IE
2
D and IRE
3
D, however,
in most cases U-net achievs inferior distances.
Figure 10 depicts exemplary segmentation results
in the situs inversus setting. It particularly shows,
Figure 9: First column: Hausdorff Distance worsening for
each train/test combination, in which U-Net performs worse
than ACNN, IE
2
D, IRE
3
D (from top to bottom) for situs in-
versus setting. Second column: Hausdorff Distance wors-
ening for each train/test combinations, in which ACNN,
IE
2
D, IRE
3
D (from top to bottom) perform worse than U-
Net for situs inversus setting. Rows indicate patient used
for training, columns represent test data set.
Using Anatomical Priors for Deep 3D One-shot Segmentation
179

Figure 10: Exemplary segmentation results from each architecture on the situs inversus setting. Left to right: U-Net, ACNN,
IE
2
D, IRE
3
D.
that the incorporation of Oktay et al.’s regularization
scheme yields smoother results and fewer outliers for
both the ACNN and our proposed IRE
3
D architecture,
which is reflected by the resulting DSC scores. How-
ever, shape regularization does not seem to reduce the
maximal outlier distance.
5 CONCLUSION
In this work we investigated the one-shot segmen-
tation capability of a standard U-Net and examined
how incorporating anatomical priors may change the
outcome on the example of liver segmentation from
CT. The U-Net delivers promising results in settings,
where the position of the liver shows low variation,
which is often the case when training and testing data
sets that come from the same source. We also ob-
served, that in cases of different data sources, where
the liver position may change drastically, the U-Net
shows strong weaknesses due to overfitting of the po-
sition, and that incorporating anatomical priors may
improve the segmentation results. We proposed a new
architecture, that incorporates anatomical information
in 2 ways and achieved promising and competitive re-
sults, particularly in settings of different data sources.
We demonstrated this on the example of the situs in-
versus setting, in which we achieved best results for
most cases regarding DSC and Hausdorff distance.
This was specifically notable in the more challenging
cases. In the future, we intend to further examine how
little data may be feasible for the U-Net to reach good
segmentation results in a constrained setting. We also
aim to extend our architecture for multi-organ one-
/few-shot segmentation tasks.
REFERENCES
Clark, K., Vendt, B., et al. (2013). The cancer imag-
ing archive (tcia): maintaining and operating a pub-
lic information repository. Journal of digital imaging,
26(6):1045–1057.
Dalca, A. V., Guttag, J., and Sabuncu, M. R. (2018).
Anatomical Priors in Convolutional Networks for Un-
supervised Biomedical Segmentation. In Proceedings
of the IEEE Conference on Computer Vision and Pat-
tern Recognition, pages 9290–9299.
Dong, N. and Xing, E. P. (2018). Few-shot semantic seg-
mentation with prototype learning. In BMVC, vol-
ume 3, page 4.
Gibson, E., Giganti, F., et al. (2018). Automatic multi-organ
segmentation on abdominal ct with dense v-networks.
IEEE transactions on medical imaging, 37(8):1822–
1834.
Girdhar, R., Fouhey, D. F., et al. (2016). Learning a Pre-
dictable and Generative Vector Representation for Ob-
jects. In European Conference on Computer Vision,
pages 484–499. Springer.
Isensee, F., Kickingereder, P., et al. (2018). No new-net. In
International MICCAI Brainlesion Workshop, pages
234–244. Springer.
Koch, G., Zemel, R., and Salakhutdinov, R. (2015).
Siamese neural networks for one-shot image recogni-
tion. In ICML Deep Learning Workshop, volume 2.
Landman, B., Xu, Z., et al. (2015). MICCAI multi-atlas la-
beling beyond the cranial vault - workshop and chal-
lenge. https://doi.org/10.7303/syn3193805.
Michaelis, C., Bethge, M., and Ecker, A. (2018). One-shot
segmentation in clutter. In International Conference
on Machine Learning, pages 3546–3555.
Oktay, O., Ferrante, E., et al. (2018). Anatomically Con-
strained Neural Networks (ACNNs): Application to
Cardiac Image Enhancement and Segmentation. IEEE
Transactions on Medical Imaging, 37(2):384–395.
Pham, D. D., Dovletov, G., Warwas, S., Landgraeber, S.,
J
¨
ager, M., and Pauli, J. (2019). Deep learning with
anatomical priors: imitating enhanced autoencoders in
latent space for improved pelvic bone segmentation in
mri. In 2019 IEEE 16th International Symposium on
Biomedical Imaging (ISBI 2019), pages 1166–1169.
IEEE.
Ravishankar, H., Venkataramani, R., et al. (2017). Learning
and Incorporating Shape Models for Semantic Seg-
mentation. In International Conference on Medical
Image Computing and Computer-Assisted Interven-
tion, pages 203–211. Springer.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:
Convolutional Networks for Biomedical Image Seg-
mentation. In International Conference on Medical
Image Computing and Computer-Assisted Interven-
tion, pages 234–241. Springer.
Roth, H. R., Farag, A., et al. (2016). Data From Pancreas-
CT. The Cancer Imaging Archive. http://doi.org/10.
7937/K9/TCIA.2016.tNB1kqBU.
BIOIMAGING 2021 - 8th International Conference on Bioimaging
180

Roth, H. R., Lu, L., et al. (2015). Deeporgan: Multi-level
deep convolutional networks for automated pancreas
segmentation. In International conference on medical
image computing and computer-assisted intervention,
pages 556–564. Springer.
Roy, A. G., Siddiqui, S., P
¨
olsterl, S., Navab, N., and
Wachinger, C. (2020). ‘squeeze & excite’guided few-
shot segmentation of volumetric images. Medical im-
age analysis, 59:101587.
Santoro, A., Bartunov, S., et al. (2016). One-shot learn-
ing with memory-augmented neural networks. arXiv
preprint arXiv:1605.06065.
Snell, J., Swersky, K., and Zemel, R. (2017). Prototypical
networks for few-shot learning. In Advances in Neural
Information Processing Systems, pages 4077–4087.
Vinyals, O., Blundell, C., et al. (2016). Matching networks
for one shot learning. In Advances in neural informa-
tion processing systems, pages 3630–3638.
Xu, Z., Lee, C. P., et al. (2016). Evaluation of six regis-
tration methods for the human abdomen on clinically
acquired ct. IEEE Transactions on Biomedical Engi-
neering, 63(8):1563–1572.
Using Anatomical Priors for Deep 3D One-shot Segmentation
181
