Non-linear Distortion Recognition in UAVs’ Images using Deep Learning

Leandro H. F. P. Silva

, Jocival D. Dias Jr

, Jean F. B. Santos

, Jo

ao F. Mari

Maur

ıcio C. Escarpinati

and Andr

e R. Backes

School of Computer Science, Federal University of Uberl

andia, Brazil

Federal University of Vic¸osa, Brazil

Keywords:

Unmanned Aerial Vehicles, Precision Agriculture, Non-linear Distortion, Deep Learning.

Abstract:

Unmanned Aerial Vehicles (UAV) have increasingly been used as tools in many tasks present in Precision

Agriculture (PA). Due to the particular characteristics of the ﬂight and the UAV equipment, several challenges

need to be addressed, such as the presence of non-linear deformations in the captured images. These deforma-

tions impair the image registration process so they must be identiﬁed to be properly corrected. In this paper,

we propose a Convolutional Neural Network (CNN) architecture to classify whether or not a given image has

non-linear deformation. We compared our approach with 4 traditional CNNs and the results show that our

model achieves has an accuracy similar to the compared CNNs, but with an extremely lower computational

cost, which could enable its use in ﬂight time, in a system embedded in the UAV.

1 INTRODUCTION

At the end of the 19th century, many studies addressed

the problem of the world population growth and the

relationship with the planet’s food production capac-

ity. However, since the 1960s, a series of technolog-

ical innovations has helped to increase food produc-

tion in the world, thus preventing food shortages from

becoming a problem for humanity. Among the devel-

oped technologies we can mention the use of irriga-

tion systems, mechanization of crops, chemical fertil-

izers, genetically modiﬁed foods, as well as the use

of satellite images. The latter allows to improve the

management of the area to be planted, allowing to an-

alyze the quantity of necessary inputs as well as the

area affected by pests, among other factors (Malthus,

1872; Hazell, 2009; Farmer, 1986).

More recently, the use of Unmanned Aerial Ve-

hicles (UAVs) has facilitated access to images of the

area to be cultivated with greater resolution and more

often, thus allowing a constant analysis of the region

and a better decision-making regarding the use of in-

puts and pest control. Unlike other aerial image ac-

quisition devices, such as satellites and large aircraft,

UAVs make it possible to capture images at low and

medium altitudes (50 to 400 m), providing a more de-

tailed view of the region under analysis. These UAVs

allow the use of a wide range of sensors that produce

the most diverse types of data on the studied area:

RGB cameras, heat capture sensors, multi and hyper-

spectral cameras, among others. In addition, recent

technological advances and their popularization have

reduced their costs (Jenkins and Vasigh, 2013), caus-

ing even small farmers to have adopted this technol-

ogy for many applications, such as growth estimation

or to identify other important agronomic characteris-

tics, such as nitrogen stress (McBratney et al., 2005;

Milella et al., 2019; Blackmer and Schepers, 1996;

Sankaran et al., 2015; Kataoka et al., 2003).

The remainder of this paper is organized as fol-

lows. Section 2 shows some recent papers published

in the area. In Section 3 we detail the problem and

their implications. In Section 4 we detail the non-

linear model. In Section 5, we present an overview

of the CNN and how it was used to deal with our

problem. Section 6 presents the image dataset used

in the experiments. Sections 7 and 8 present the ex-

periments and a discussion of the results. Section 9

presents the conclusions and future work.

2 RELATED WORK

In (Yasir et al., 2018), the authors presented a data-

driven framework for multispectral registration. The

proposed framework assumes that the greater the

number of control points, the better is the image align-

ment. Their work veriﬁes all spectra taken two by two

Silva, L., Dias Jr, J., Santos, J., Mari, J., Escarpinati, M. and Backes, A.

Non-linear Distortion Recognition in UAVs’ Images using Deep Learning.

DOI: 10.5220/0010309504470454

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages

447-454

ISBN: 978-989-758-488-6

447

in order to identify order of spectra that maximizes the

number of control points during the alignment pro-

cess.

In (Junior et al., 2020) the authors proposed to

modify the structure proposed by (Yasir et al., 2018)

for the process of registering multispectral images.

The modiﬁcation consists of the generalization orig-

inally proposed to work with methods based on key

points so that the spectral domain methods can be

used in the registration process with greater precision

and less execution time.

The authors in (Eppenhof and Pluim, 2019) pro-

posed the use of deep learning methods for image

registration with non-linear distortions as an alterna-

tive to traditional registration methods. The study in

question is motivated by the fact that traditional meth-

ods fail to estimate larger displacements and complex

deformation ﬁelds. For this complex scenario, a mul-

tiple resolution task is required. Therefore, (Eppen-

hof and Pluim, 2019) proposed the progressive train-

ing of neural networks to solve the problem. Thus,

instead of training a large Convolutional Neural Net-

work (CNN) in the one-time registration task, smaller

versions of the network were initially trained with

low resolution images and deformation ﬁelds. Dur-

ing the training, the network was progressively ex-

panded with additional layers, which were trained

with high-resolution data. Results showed that this

training mode allows a network to learn greater dis-

placements ﬁelds without sacriﬁcing registration ac-

curacy and that the resulting network is less prone

to registration errors compared to training the entire

network at once. The authors also agreed that a pro-

gressive training procedure leads to greater accuracy

of the record when learning large and complex non-

linear deformations.

The work of (Zhu et al., 2019) developed a cor-

respondence method based on learning multispectral

images (RGB and infrared) captured by satellite sen-

sors. The method in question involves a Convolu-

tional Neural Network (CNN) that compares a pair of

multispectral images in question and a search strategy

model that will check the corresponding point within

a search window in the target image for a given point

in the reference image. In this way, a densely con-

nected CNN was developed to extract the common

characteristics of the different spectral bands. The ex-

periments showed a high-performance power, in addi-

tion to the ability to generalize the proposed method,

being applicable in multitemporal remote sensing im-

ages and short-range images.

3 PROBLEM DEFINITION

Due its low altitude of ﬂight and the diversity of sen-

sors, many methods have been developed to process

the images obtained using UAVs. Some methods deal

with the fact that these images and the different bands

of frequencies must be organized in a mosaic that rep-

resents the entire area (Junior et al., 2019). However,

the registration process may be impaired by the pres-

ence of deformation on the images.

The cameras used in Precision Agriculture already

produce the most varied distortions in the images due

to the most diverse factors. Thus, when these cam-

eras are coupled to a UAV, this problem is heightened.

During a ﬂight, the UAV has three basic control axes:

yaw, pitch, and roll.

Thus, the success in identifying such distortions

in ﬂight time, with a system embedded in the UAV of

low computational cost, for example, would greatly

enhance the subsequent processes, whose objective is

to promote PA. This gain in PA activities would be

fundamentally because once an image was detected

with the presence of deformation, the mosaic process

would be facilitated. Such a facility would be, for

example, avoiding the need for new ﬂights to cover a

certain region or even discarding the captured images

that would not be of value for the process in question.

In short, in this paper, we address the problem

of identifying whether or not a given image has non-

linear deformation. To accomplish that we proposed

a Convolutional Neural Network model and compare

its performance with traditional CNNs from literature.

4 NON-LINEAR MODEL

A mapping function can be deﬁned mathematically

as a 2D function, which maps the (x, y) coordinates

of a given A image to the (x, y) coordinates of a B im-

age. Two main types of functions of mapping, Linear

and Non-Linear (or Non-Rigid), are characterized by

the type of deformation in the image (Gonzalez et al.,

2002).

Figure 1 shows the delimitation between linear

distortions, as well as non-linear distortions, which

are objects of this work.

Literature presents many works addressing the

problem of non-linear deformations, in the most var-

ied contexts in which these deformations can be

present (Walimbe and Shekhar, 2006; Shekhar and

Zagrodsky, 2002; Wang and Staib, 1998). According

to (Wang and Staib, 1998), there is no mathematical

model for this type of deformation because a given

anatomical structure does not result in the deforma-

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

448

Figure 1: Example of linear and non-linear transformations

(Uchida, 2013).

tion of another structure. Thus, an analogous model

is used to represent these deformations. A Eulerian

Reference can be used in the formulation of the non-

linear model. For this scenario, a component of the

image is tracked in relation to its ﬁnal coordinates.

For that, we will deﬁne the transformation in question

through a homeomorphic mapping of the coordinate

system in two dimensions, according to Equation 1:

w = (z, y) → (x − u

(w), y − u

(w)) (1)

where u(w) = [u = (w),u

(w)]

is the displacement

at each pixel w whose coordinate is denoted as (x,y).

This mapping allows for the detailed local transfor-

mation into the speciﬁc anatomy of the component of

the image.

The formulation of the non-linear model is also

deﬁned in (Christensen et al., 1996), where com-

ponents are considered to be displaced with a pro-

portional force. This spatial transformation satisﬁes

the Partial Differential Equation (PDE), as shown in

Equation 2:

µ∇

u + (µ + β)∇(∇ · u) = F(u) (2)

where µ(w) = 0 for w on the image boundary. In Equa-

tion 2, µ and β are Lam

e constants. The body force,

F(u), is the driving function that deforms the images.

5 CONVOLUTIONAL NEURAL

NETWORK

Recent advances in the use of GPUs and in the the-

ory of neural networks have allowed the development

of new machine learning techniques, including deep

learning. This is a category of neural networks algo-

rithms whose main characteristics is the presence of

a large number of neurons arranged in layers, which

are grouped into processing blocks.

Among the many deep learning algorithms Con-

volutional Neural Network (CNN) plays a important

role in many task ain areas as computer vision, speech

recognition and audio recognition. CNN is a network

which is based on the concept of receptive present in

the human visual system. In these networks, learning

process takes place through the use of different ﬁl-

ters that emphasizes characteristics present in the im-

age, thus imitating the human learning process. These

networks are able to analyze the spatial correlations

among pixels of an image to extract relevant attributes

for classiﬁcation, regression, and segmentation tasks

(LeCun et al., 1998; Guo et al., 2016; Ponti et al.,

2017). Literature shows that the vast majority of CNN

models are deﬁned using three types of layers: con-

volutional, pooling, and fully connected layers. These

layers can be combined in different ways to improve

CNN’s learning process. Next, we present a brief de-

scription of the mentioned layers.

In a convolutional layer, the main goal is to ex-

tract signiﬁcant attributes from an image. To achieve

this goal, several convolution operations are applied

to the input data and these operations act as receptive

ﬁlters that will highlight different attributes of a local

region of the image. In general, the aforementioned

ﬁlters are deﬁned as 3 × 3 or 5 × 5 kernels. Also, to

speed up the training of the network and consequent

improvement in results, the activation function REc-

tiﬁed Linear Unit (ReLU) and a batch normalization

operation are applied to the result of the convolutional

layer (LeCun et al., 2015).

The convolutional layer is usually followed by a

pooling layer. The main objective of this layer is to re-

duce the feature maps that were calculated by the pre-

vious layers. This way, network sensitivities to image

distortions and data changes are reduced. In general,

a 2 × 2 pooling mask is used according to established

criteria (e.g., maximum or the average of the pixels of

the region), which will reduce a region of 4 pixels to

a single value (Scherer et al., 2010).

Finally, we ﬁnd the fully connected (also known as

dense) layer. This layer receives as input the 2D fea-

ture maps obtained from previous layers and its main

objective is to learn a vector of 1D features capable

of discriminating the input image. The feature vector

is then used as input to a softmax classiﬁer that will

return the most likely equivalence class for the image.

Non-linear Distortion Recognition in UAVs’ Images using Deep Learning

449

6 IMAGE DATASET

6.1 Selected Images

For our experiments, we considered two mosaics cre-

ated from images captured by UAVs. These mosaics

have 18543 × 2635 and 8449 × 11180 pixels size.

These mosaics refer to two different areas planted

with sugar cane. It is worth mentioning that the mo-

saics were not captured with the same equipment and

under the same climatic conditions, which reﬂects dif-

ferent resolutions for each case.

From each mosaic, we selected grayscale patches

of 128 × 128 pixels size. Subsequently, we discard

patches that have little (or any) signiﬁcant visual in-

formation. This was determined by the number of

pixels (n) with a value of 0 in the patch. Thus, if

n < 10, the patch is considered for the composition of

the dataset; otherwise, the patch is discarded. There-

fore, we built two datasets, which we will call DS1

and DS2 and which have, respectively, 3353 and 2365

images. Figure 2 illustrates two examples of images

of patches generated for each dataset (Silva et al.,

2020).

Figure 2: Example of images that make up both datasets:

(a) DS1; (b) DS2.

6.2 Dataset Image Distortions

For the experiments we used the work (Eppenhof and

Pluim, 2019) to create non-linear deformations in the

images, where deformable transformations are im-

plemented just like B-spline transformations and dis-

placements are deﬁned in a grid. In (Eppenhof and

Pluim, 2019), as we deal with two-dimensional im-

ages, we used two grids, one for the displacements in

the y-directions, and one for the displacements in the

x-directions. Figure 3 shows the relationship of an

image in our dataset with its respective grid and the

distortion generated in that image through the grid.

Still according to (Eppenhof and Pluim, 2019), we

can concatenate other transformations through an in-

terpolator method. These transformations are applied

Figure 3: Distortion example: (a) Original image; (b) Orig-

inal image (a) with their respective grids; (c) Image after

applying the deformation.

in reverse order since they are applied to the sampling

grid and not to the images. Figure 4 shows an ex-

ample of a 10% translation followed by a 45 degrees

rotation around the point (0.5, 0.5), and then the B-

spline transformation.

Figure 4: Combination of transformations for the image in

Figure 3 (c).

To avoid black areas, we cropped a 64× 64 pixels size

region aligned with the center of the image, thus re-

moving any artifact added to the image by the selected

transformation method, as illustrated by Figure 5.

Figure 5: (a) Deformation-free image; (b) Deformed im-

age, according to (Eppenhof and Pluim, 2019); (c) Cropped

image.

Finally, when applying the transformations pre-

sented in all the patches of DS1 and DS2, we will have

the corresponding elastic distorted images in both

datasets. Thus, we have two equivalence classes: (1)

distortion-free images and (2) distorted images. Both

datasets will be available for replication and other ex-

periments as request.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

450

7 EXPERIMENTS

To classify the equivalence classes mentioned in the

previous section, we evaluated 4 traditional CNN

architectures: InceptionV3 (Szegedy et al., 2016),

ResNet (He et al., 2016), SqueezeNet (Iandola et al.,

2016) and VGG-16 (Simonyan and Zisserman, 2014).

We used these networks pre-trained in the 2012

dataset Imagenet (Krizhevsky et al., 2012) and made

the pertinent adjustments to our classiﬁcation prob-

lem. We also carried out a data augmentation to re-

duce the possibility of overﬁtting in our experiments.

In addition to the traditional CNNs, we proposed an

alternative architecture that will be presented as fol-

lows. Our architecture is motivated by (Marcos et al.,

2019b; Marcos et al., 2019a), where simpler CNNs

and sets of ﬁlters were used to solve less complex

classiﬁcation problems.

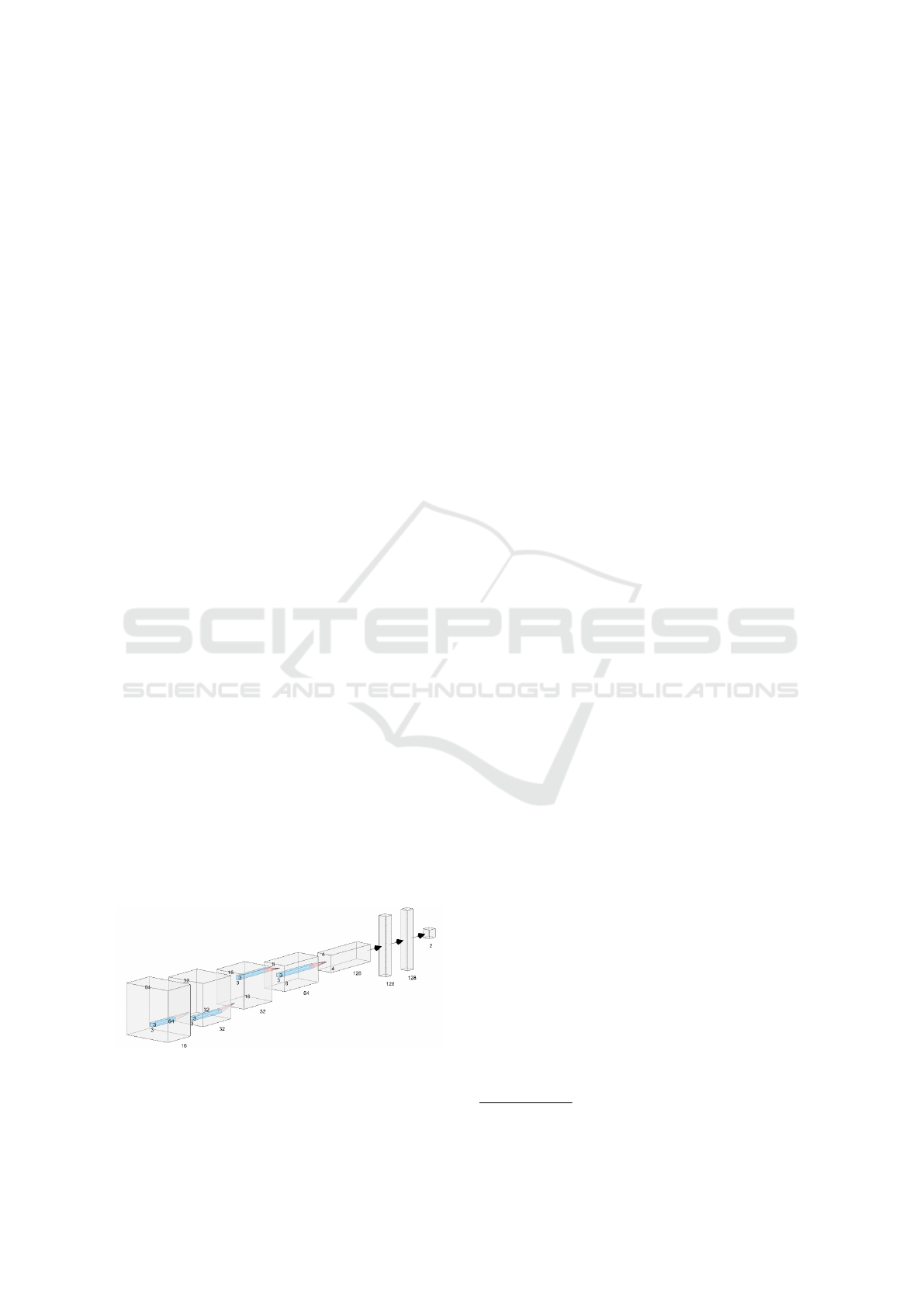
For our CNN, we took inspiration from the

AlexNet architecture. In its traditional architecture,

AlexNet has eight layers, the ﬁrst ﬁve of which are

convolutional, with a ReLU activation function, fol-

lowed by max-pooling layers, and the others consist

of dense layers (Krizhevsky et al., 2012). Due to the

reduced size of our images (64 × 64 pixels size), our

architecture has fewer layers when compared to tra-

ditional CNNs. We used 5 convolutional layers to

process the images and each layer has, respectively,

16, 32, 32, 64, and 128 ﬁlters, where, in all con-

volutional layers, the respective ﬁlters always have

the size 3 × 3. To improve its learning ability and

to enhance its training, we applied the ReLU non-

linearity activation function after each convolutional

layer. There is also a batch normalization after each

ReLU function, which is followed by a 2 × 2 max-

pooling layer. In the sequence, we used the result-

ing volume as an input for the dense layers. The ﬁrst

two dense layers have 128 neurons each and they use

ReLU as activation function. We also apply a 20%

dropout in each dense layer. Finally, the output layer

has 2 neurons that determine the equivalence class.

Figure 6 shows the structure of our CNN.

Figure 6: Illustration of the architecture of our CNN.

All CNNs were implemented using the Python

version of Tensorﬂow

, an open-source framework

for efﬁcient building, training, and use of deep neu-

ral network models. TensorFlow was developed by

Google (Abadi et al., 2016b) and it is based on

tensors and dataﬂow graphs. Tensors are numer-

ical multidimensional arrays to represent the data.

Dataﬂow graphs nodes represent operations and edges

describe the ﬂow of data throughout the processing

steps (G

eron, 2019; Abadi et al., 2016a; Hope et al.,

2017).

For the experiments we used 75% of the sam-

ples for training, while the remaning images were

used for validation. Experiments were conducted

on a Personal Computer with Intel(R) Core(TM) i7-

7700 CPU @ 3.60GHz, 32GB RAM, 64-bit Windows

OS and GPU NVIDIA GeForce GTX 1050 Ti, 4GB

GDDR5. We also used Python 3.6 and Keras 2.1.6-

tf with TensorFlow 1.10.0 and CUDA Toolkit 9.0 to

implement and test the experiments.

8 RESULTS

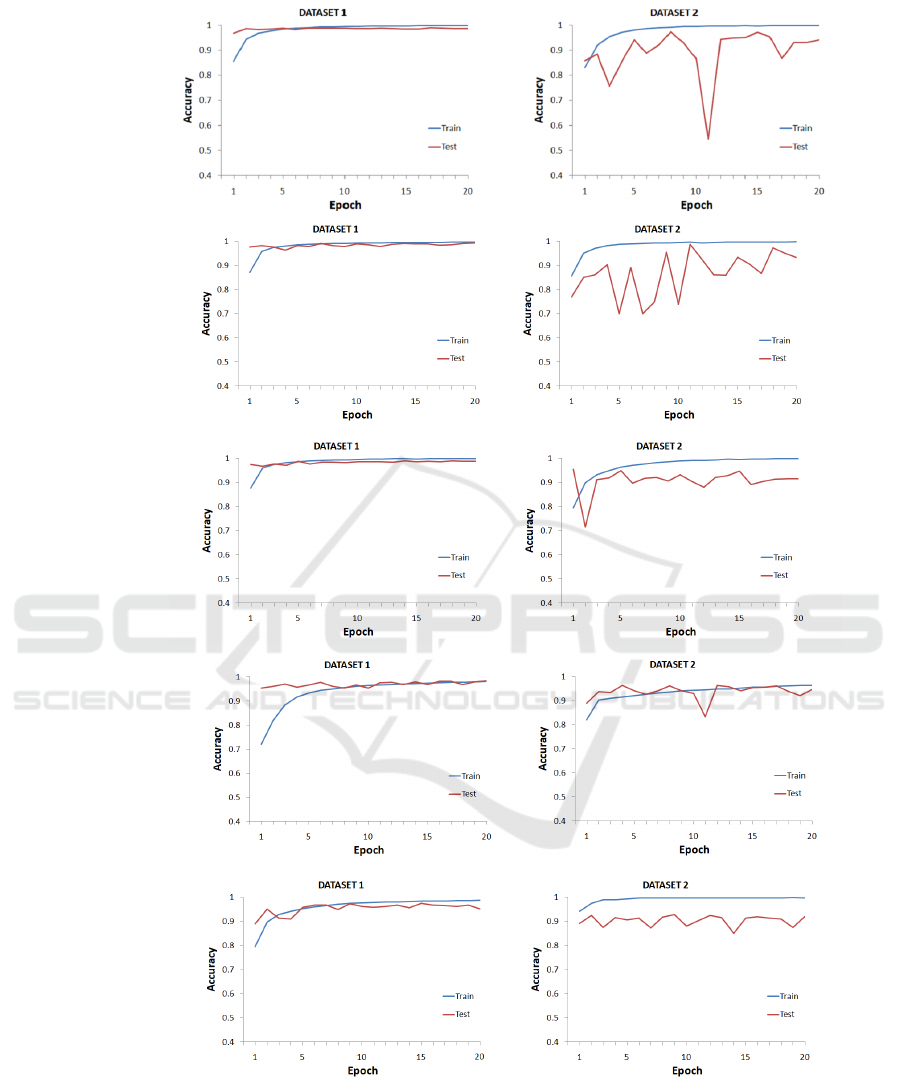
Figure 7 shows the evolution of the accuracy in both

test and training sets for all evaluated CNNs, i.e.,

ResNet, Inception-V3, VGG-16, SqueezeNet, as well

as our proposed model. Table 1 summarizes the ac-

curacy rates obtained by each CNN in each datasets

DS1 and DS2 after 20 epochs training. As we can see,

results demonstrate that all CNNs model are capable

of discriminate images according to the presence (or

not) of an elastic distortion. All models, including

ours, were able to achieve accuracy rates above 92%.

Even though all CNNs present high accuracies,

we noticed that dataset DS2 represents a greater chal-

lenge for all CNNs. While for dataset DS1 all CNNs

are able to achieve a stable accuracy over the epochs

in the test set, the same is to true for dataset DS2.

All evaluated CNNs exhibit a larger variation among

different epochs and their results increase or decrease

despite the good accuracy obtained in the training set.

Such behavior indicates that the feature learned in the

training set are not as robust in dataset DS2 as in

dataset DS1. This is corroborated by the results pre-

sented in Table 1, where we can see that all CNNs

present lower accuracies for dataset DS2 than DS1.

Another important point to be analyzed is the

computational cost of each CNN. Table 2 shows the

number of trainable parameters present in each CNN

in the context of the addressed problem. As one

can see, even though our proposed model presents

http://tensorﬂow.org

Non-linear Distortion Recognition in UAVs’ Images using Deep Learning

451

(a)

(b)

(c)

(d)

(e)

Figure 7: Accuracy of each evaluated CNN in both datasets: (a) ResNet; (b) InceptionV3; (c) VGG-16; (d) SqueezeNet; (e)

Proposed model.

the smaller success rate, it also presents the smallest

number of parameters and, as a consequence, a con-

siderably lower computational cost than traditional

CNNs. When compared with InceptionV3, our CNN

model obtained a accuracy 1.72% and 5.92% lower in

dataset DS1 and DS2, respectively. However, its com-

putational cost is smaller as it has only 0.64% of the

number of parameter of the InceptionV3 model. Ad-

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

452

ditionaly, we must emphasize that compared CNNs

were previously trained in the 2012 Imagenet dataset

while our proposed model was trained from scratch.

In this sense, given that the results of our architecture

are close to the traditional CNNs, this approach may

enable a great advance for the use of this resource in

a system embedded in the UAV. The UAV ﬂight time

detection can support subsequent processes (e.g., cor-

rection of detected distortion and image registration),

in addition to reducing the ﬁnancial costs inherent in

the process.

Table 1: Results obtained for each CNN model.

CNN model DS1 DS2

ResNet 98.95% 94.36%

InceptionV3 99.25% 98.84%

VGG-16 98.88% 95.35%

SqueezeNet 98.43% 96.41%

Proposed CNN 97.53% 92.92%

Table 2: Number of parameters of each CNN model.

CNN model # of parameters

ResNet 22,591,810

InceptionV3 22,081,826

VGG-16 14,797,122

SqueezeNet 723,522

Proposed 141,058

9 CONCLUSION

Convolutional Neural Networks demonstrated a high

power in the identiﬁcation of non-linear deformations

(and variants) in UAVs’ images. While most tradi-

tional architectures have a high computational cost,

a fact that could hinder such processing during ﬂight

time, our proposed CNN represents an attractive al-

ternative as it presents the lowest computational cost

with only a small decrease in the accuracy when com-

pared with traditional architectures. Also, as exposed

in the papers of (Eppenhof and Pluim, 2018; Eppen-

hof and Pluim, 2019), the process of detecting the de-

formation vector ﬁeld and the consequent image cor-

rection process has an enormous computational cost.

Thus, the identiﬁcation of the presence (or not) of

non-linear deformations between the images would

represent considerable gain.

In future work, we intend to propose a method to

correct the detected non-linear distortions, thus po-

tentializing the mosaic process of the images. Also,

given the possibility of UAVs having in many cases

multi and hyperspectral cameras, we intend to repli-

cate this work in multichannel images.

ACKNOWLEDGMENT

Andr

e R. Backes gratefully acknowledges the ﬁnan-

cial support of CNPq (National Council for Scien-

tiﬁc and Technological Development, Brazil) (Grant

#301715/2018-1). This study was ﬁnanced in part by

the Coordenac¸

ao de Aperfeic¸oamento de Pessoal de

ıvel Superior - Brazil (CAPES) - Finance Code 001.

The authors would like to thank the company Sensix

Inovac¸

oes em Drones Ltda (http://sensix.com.br) for

providing the images used in the tests.

REFERENCES

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z.,

Citro, C., Corrado, G. S., Davis, A., Dean, J., Devin,

M., et al. (2016a). Tensorﬂow: Large-scale machine

learning on heterogeneous distributed systems. arXiv

preprint arXiv:1603.04467.

Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean,

J., Devin, M., Ghemawat, S., Irving, G., Isard, M.,

Kudlur, M., Levenberg, J., Monga, R., Moore, S.,

Murray, D. G., Steiner, B., Tucker, P., Vasudevan, V.,

Warden, P., Wicke, M., Yu, Y., and Zheng, X. (2016b).

Tensorﬂow: A system for large-scale machine learn-

ing.

Blackmer, T. M. and Schepers, J. S. (1996). Aerial pho-

tography to detect nitrogen stress in corn. Journal of

Plant Physiology, 148(3-4):440–444.

Christensen, G. E., Miller, M. I., Vannier, M. W.,

and Grenander, U. (1996). Individualizing neuro-

anatomical atlases using a massively parallel com-

puter. Computer, 29(1):32–38.

Eppenhof, K. A. and Pluim, J. P. (2018). Pulmonary ct

registration through supervised learning with convolu-

tional neural networks. IEEE transactions on medical

imaging, 38(5):1097–1105.

Eppenhof, K. A. J. and Pluim, J. P. W. (2019). Pulmonary ct

registration through supervised learning with convolu-

tional neural networks. IEEE Transactions on Medical

Imaging, 38(5):1097–1105.

Farmer, B. (1986). Perspectives on the ‘green revolution’in

south asia. Modern Asian Studies, 20(1):175–199.

eron, A. (2019). Hands-On Machine Learning with Scikit-

Learn, Keras, and TensorFlow: Concepts, Tools, and

Techniques to Build Intelligent Systems. O’Reilly Me-

dia.

Gonzalez, R. C., Woods, R. E., et al. (2002). Digital image

processing.

Guo, Y., Liu, Y., Oerlemans, A., Lao, S., Wu, S., and Lew,

M. S. (2016). Deep learning for visual understanding:

A review. Neurocomputing, 187:27–48.

Hazell, P. B. (2009). The Asian green revolution, volume

911. Intl Food Policy Res Inst.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In 2016 IEEE Con-

Non-linear Distortion Recognition in UAVs’ Images using Deep Learning

453

ference on Computer Vision and Pattern Recognition

(CVPR), pages 770–778.

Hope, T., Resheff, Y. S., and Lieder, I. (2017). Learning

tensorﬂow: A guide to building deep learning systems.

” O’Reilly Media, Inc.”.

Iandola, F. N., Han, S., Moskewicz, M. W., Ashraf, K.,

Dally, W. J., and Keutzer, K. (2016). Squeezenet:

Alexnet-level accuracy with 50x fewer parameters and

<0.5mb model size. arXiv:1602.07360.

Jenkins, D. and Vasigh, B. (2013). The economic impact of

unmanned aircraft systems integration in the United

States. Association for Unmanned Vehicle Systems

International (AUVSI).

Junior, J. D. D., Backes, A. R., and Escarpinati, M. C.

(2019). Detection of control points for uav-

multispectral sensed data registration through the

combining of feature descriptors.

Junior, J. D. D., Backes, A. R., Escarpinati, M. C., Silva, L.

H. F. P., Costa, B. C. S., and Avelar, M. H. F. (2020).

Assessing the adequability of fft-based methods on

registration of uav-multispectral images.

Kataoka, T., Kaneko, T., Okamoto, H., and Hata, S. (2003).

Crop growth estimation system using machine vision.

In Proceedings 2003 IEEE/ASME International Con-

ference on Advanced Intelligent Mechatronics (AIM

2003), volume 2, pages b1079–b1083. IEEE.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Proceedings of the 25th International

Conference on Neural Information Processing Sys-

tems - Volume 1, NIPS’12, pages 1097–1105, USA.

Curran Associates Inc.

LeCun, Y., Bengio, Y., and Hinton, G. E. (2015). Deep

learning. Nature, 521(7553):436–444.

LeCun, Y. L., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of IEEE, 86(11):2278–2324.

Malthus, T. R. (1872). An Essay on the Principle of Popu-

lation..

Marcos, A. P., Rodovalho, N. L. S., and Backes, A. R.

(2019a). Coffee leaf rust detection using convolu-

tional neural network. In 2019 XV Workshop de Vis

Computacional (WVC), pages 38–42. IEEE.

Marcos, A. P., Rodovalho, N. L. S., and Backes, A. R.

(2019b). Coffee leaf rust detection using genetic algo-

rithm. In 2019 XV Workshop de Vis

ao Computacional

(WVC), pages 16–20. IEEE.

McBratney, A., Whelan, B., Ancev, T., and Bouma, J.

(2005). Future directions of precision agriculture.

Precision agriculture, 6(1):7–23.

Milella, A., Reina, G., and Nielsen, M. (2019). A multi-

sensor robotic platform for ground mapping and esti-

mation beyond the visible spectrum. Precision agri-

culture, 20(2):423–444.

Ponti, M. A., Ribeiro, L. S. F., Nazar

e, T. S., Bui, T.,

and Collomosse, J. (2017). Everything you wanted

to know about deep learning for computer vision but

were afraid to ask. In SIBGRAPI Tutorials, pages 17–

41. IEEE Computer Society.

Sankaran, S., Khot, L. R., Espinoza, C. Z., Jarolmasjed,

S., Sathuvalli, V. R., Vandemark, G. J., Miklas, P. N.,

Carter, A. H., Pumphrey, M. O., Knowles, N. R., et al.

(2015). Low-altitude, high-resolution aerial imaging

systems for row and ﬁeld crop phenotyping: A review.

European Journal of Agronomy, 70:112–123.

Scherer, D., M

uller, A. C., and Behnke, S. (2010). Eval-

uation of pooling operations in convolutional archi-

tectures for object recognition. In Artiﬁcial Neural

Networks - ICANN 2010 - 20th International Confer-

ence, Thessaloniki, Greece, September 15-18, 2010,

Proceedings, Part III, volume 6354 of Lecture Notes

in Computer Science, pages 92–101. Springer.

Shekhar, R. and Zagrodsky, V. (2002). Mutual information-

based rigid and nonrigid registration of ultrasound

volumes. IEEE transactions on medical imaging,

21(1):9–22.

Silva, L. H. F. P., Dias J

unior, J. D., Santos, J. F. B., Mari,

J. F., Escarpinati, M. C., and Backes, A. R. (2020).

Classiﬁcation of uavs’ distorted images using convo-

lutional neural networks. In Workshop de Vis

ao Com-

putacional, pages 98–108, Uberl

andia, Brazil.

Simonyan, K. and Zisserman, A. (2014). Very deep con-

volutional networks for large-scale image recognition.

arXiv preprint arXiv:1409.1556.

Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna,

Z. (2016). Rethinking the inception architecture for

computer vision. In 2016 IEEE Conference on Com-

puter Vision and Pattern Recognition (CVPR), pages

2818–2826.

Uchida, S. (2013). Image processing and recognition for

biological images. In Development, growth & differ-

entiation.

Walimbe, V. and Shekhar, R. (2006). Automatic elastic im-

age registration by interpolation of 3d rotations and

translations from discrete rigid-body transformations.

Medical Image Analysis, 10(6):899–914.

Wang, Y. and Staib, L. H. (1998). Elastic model based non-

rigid registration incorporating statistical shape infor-

mation. In International Conference on Medical Im-

age Computing and Computer-Assisted Intervention,

pages 1162–1173. Springer.

Yasir, R., Eramian, M., Stavness, I., Shirtliffe, S., and

Duddu, H. (2018). Data-driven multispectral image

registration. In 2018 15th Conference on Computer

and Robot Vision (CRV), pages 230–237. IEEE.

Zhu, R., Yu, D., Ji, S., and Lu, M. (2019). Matching

rgb and infrared remote sensing images with densely-

connected convolutional neural networks. Remote

Sensing, 11(23):2836.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

454