
Analysing Adversarial Examples for Deep Learning
Jason Jung, Naveed Akhtar and Ghulam Mubashar Hassan
Department of Computer Science & Software Engineering, The University of Western Australia, Australia
Keywords: Adversarial Examples, Adversarial Attacks, Imagenet, Neural Networks, Image Classifiers.
Abstract: The aim of this work is to investigate adversarial examples and look for commonalities and disparities
between different adversarial attacks and attacked classifier model behaviours. The research focuses on
untargeted, gradient-based attacks. The experiment uses 16 attacks on 4 models and 1000 images. This
resulted in 64,000 adversarial examples. The resulting classification predictions of the adversarial examples
(adversarial labels) are analysed. It is found that light-weight neural network classifiers are more suspectable
to attacks compared to the models with a larger or more complex architecture. It is also observed that similar
adversarial attacks against a light-weight model often result in the same adversarial label. Moreover, the
attacked models have more influence over the resulting adversarial label as compared to the adversarial attack
algorithm itself. These finding are helpful in understanding the intriguing vulnerability of deep learning to
adversarial examples.
1 INTRODUCTION
Image classification with deep neural networks
performs remarkably well. A model can be trained by
feeding it thousands of images, resulting in the ability
to accurately classify even the breeds of a dog.
However, these trained models can easily be deceived
by adversarial attacks (Akhtar & Mian, 2018). A well
calculated imperceptible perturbation can cause these
models to completely misclassify an image. The
image plus perturbation is known as an ‘adversarial
example’. An adversarial example which may appear
as a cat to the human eye may be classified as a dog
or even something entirely different, such as a tree by
the network. Since the discovery of these adversarial
attacks, there has been continued research into
finding ways to make the models more robust against
these attacks. A kind of arms race has taken place to
find stronger attacks and stronger defences (Akhtar &
Mian, 2018).
There has been a focus on developing stronger
attacks, however there is a lack of ‘analysis’ for these
attacks and for deep neural network classifier models.
The aim of this work is to address this, and gain
insights into the behaviour of models under different
attacks and analysing their mutual relations. The
focus is on gradient-based untargeted attacks.
2 RELATED WORKS & ATTACKS
A comprehensive survey of adversarial attacks for
deep learning in computer vision was written in early
2018 (Akhtar & Mian, 2018). The survey serves as a
comprehensive introduction into adversarial attacks
for interested readers.
Adversarial examples were first discovered by
Szegedy, et al., 2014. The following problem was
defined: find the smallest perturbation such that,
1. The resulting adversarial example (input image +
perturbation) is misclassified as a specific
targeted label.
2. The adversarial example’s pixel values remain
within the pixel bounds of the original input
image.
Because of the non-trivial task of solving the above,
a box-constrained Limited memory Broyden-
Fletcher-Goldfarb-Shanno (L-BFGS) algorithm was
used to find an approximate solution (Szegedy, et al.,
2014). The resulting attack is referred to as the L-
BFGS attack and was the first adversarial attack.
In 2015, Goodfellow et al. proposed the idea that
the underlying cause of adversarial examples was the
linearity of neural networks. This idea led to the Fast
Gradient Sign Method (FGSM). To calculate the
perturbation for this attack, take the sign of the
Jung, J., Akhtar, N. and Hassan, G.
Analysing Adversarial Examples for Deep Learning.
DOI: 10.5220/0010313705850592
In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 5: VISAPP, pages
585-592
ISBN: 978-989-758-488-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
585

gradient of the cost function with respect to the input
image (Goodfellow, Shlens, & Szegedy, 2015).
The Basic Iterative Method (BIM) is an extension
of the FGSM. For this attack, the FGSM is repeated
multiple times using a small step-size. After each
iteration, the result is clipped to ensure the
perturbation is within the 𝜖 -neighbourhood of the
original image. These improvements allowed the
BIM to be a stronger attack with smaller perturbations
(Kurakin, Goodfellow, & Bengio, 2017).
Madry et al. proposed the strongest attack
utilizing the local first order information about the
network, the Projected Gradient Attack (PGD). The
attack works similarly to BIM however the PGD is
restarted from many random points in the l-inf ball to
better understand the loss landscape. (Madry,
Makelov, Schmidt, Tsipras, & Vladu, 2019).
The PGD was found to be inefficient in the l-1
case, so the Sparse l-1 Descent attack (SLIDE) was
proposed. For the l-1 norm, the PGD updates a single
index of the perturbation at a time. The SLIDE uses a
pre-set percentile, then updates multiple indices with
the steepest descent directions in this percentile. The
result is then normalised to the unit l-1 norm (Tramèr
& Boneh, 2019).
DeepFool is another iterative gradient based
attack (Moosavi-Dezfooli, Fawzi, & Frossard, 2016).
This attack algorithm tries to approximate
classification regions (the regions corresponding to
different labels) and hyperplanes at the boundaries of
these regions. From the current image, it takes the
projection to the closest hyperplane. This projection
is used as the perturbation. These steps are repeated
until the classification changes (i.e. an adversarial
example is found).
The Decoupled Direction and Norm Attack
(DDN) was proposed as an improvement over the
very popular Carlini & Wagner (C&W) attack and
DeepFool (Rony, et al., 2019). The iterative portion
of the algorithm starts with clean image 𝒙
and steps
in the direction of the gradient of the loss function (g).
Depending on whether the result 𝒙
𝑔 is
adversarial or not, a separate 𝜖
sphere around 𝒙 will
have its radius decreased or increased. The 𝒙
𝑔
will then be projected onto the new sphere and the
resulting projected point will be 𝒙
, to be used for
the next iteration.
The Brendel & Bethge Attack is a combination of
a boundary attack and gradient attack (Brendel,
Rauber, Kümmerer, Ustyuzhaninov, & Bethge,
2019). The attack works by starting from an
adversarial sample point far away from the clean
input. Then it estimates the local geometry of the
boundary between the adversarial and non-
adversarial regions and follows the adversarial
boundary towards the clean input. It attempts to
minimize the distance to the clean input while staying
on the adversarial boundary.
Although there has been much research into
various areas surrounding adversarial attacks, the
main focus has been on creating stronger attacks and
more robust models. The most common dataset used
has been MNIST and CIFAR10. These contain
smaller images (10x10, 32x32) which require simpler
models and only include a small number of classes.
This project explores adversarial attacks with the
much larger Imagenet dataset which involves larger
images and 1000 classes.
Attack Success Rates (ASR) and perturbation size
are common metrics used to compare attacks. Aside
from this, there is little research on how these attack
algorithms and models may be related. By
investigating the resulting labels of many adversarial
examples for various attacks and models, this
research project aims to identify some possible
relations, commonalities and disparities between the
attacks and models.
3 EXPERIMENTAL DESIGN
For clarity, the setup of the main experiment is kept
simple. Run 16 adversarial attacks against 4 deep
neural network models with 1000 images. This
resulted in 64,000 adversarial examples. The top
classification predictions (or labels) of the resulting
adversarial examples were recorded. In addition, the
confidences of these predictions, as well as the
perturbations, were recorded. This data was then
analyzed to gain insight into these attacks and models.
The following analysis was performed:
- Calculate the Attack Success Rates (ASRs) of the
different attack + model combinations. The ASR
is a fraction of adversarial attacks which
successfully cause misclassification. The aim is
to look for patterns for attacks and/or models.
- Evaluate how frequent the most commonly
appearing label occurred. The aim is to analyze
the major influencer on the resulting adversarial
labels.
- See how the labels/predictions of the clean image
may transform to become the top prediction of
the adversarial example.
- Compare the adversarial labels of the attacks.
Attacks which resulted in similar adversarial
labels could be considered as being similar and
vice versa.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
586

3.1 Attacks
Gradient-based, untargeted attacks were chosen as the
adversarial attacks for this experiment. Gradient-
based attacks were used because of their simplicity
and variety. These attacks use the gradient of the cost
function w.r.t. the input to calculate the perturbation.
Targeted attacks aim to create an adversarial example
which is incorrectly classified as a specified class or
label (the target). Untargeted attacks do not care about
the resulting label of the adversarial example. They
simply minimize the chance of the correct label being
predicted. This work looks to analyze the resulting
labels of these untargeted attacks. The attacks shown
in Table 1 were used.
Table 1: Attack acronyms.
Acron
y
m Attac
k
PGD Pro
j
ected Gradient Descent
FGM
Fast Gradient Method – a generalized
version of FGM
BIM Basic Iterative Metho
d
SLIDE S
p
arse l-1 Descent
DF DeepFool
DDN Decou
p
led Direction and Nor
m
BBA Brendel and Beth
g
e Attac
k
These attacks can also be divided into Fixed
Epsilon Attacks (PGD, FGM, BIM, SLIDE) and
Minimization Attacks (DF, DDN, BBA). For Fixed
Epsilon Attacks, the epsilon or maximum
perturbation allowance is set before running the
attack. Minimization Attacks aim to minimize size
over the preset number of iterations.
Different perturbation l
p
norm versions of these
attacks were used. All 16 attacks can be seen in Table
2. The l
inf
norm is the maximum value of any element
of the perturbation. The l
1
norm is the sum of the
absolute values. The l
2
norm is the Euclidean norm
(square root of the sum of squares of the elements).
The perturbations for the attacks are restricted by
these norms.
Table 2: All adversarial attacks used in the main
experiment.
l-inf l-1 l-2
PGD PGD PGD
FGM FGM FGM
BIM BIM BIM
SLIDE
DF
DF
DDN
BBA BBA BBA
3.2 Models
Four deep neural network classifier models were
used: vgg16, resnet50, inception_v3 and mobilenet.
These models were chosen for their popularity,
availability and differences to one another. Vgg16 is
a deep network with its main feature being the many
convolutional layers. Resnet50 similarly consists of
many convolutional layers, however it is a residual
network, meaning it utilizes skip connections to
connect layers using shortcuts. Inception_v3 is a
complex network, using techniques such as
factorizing layers into smaller convolutions to reduce
the number of parameters and thus increase the
efficiency of the network. Mobilenet is an efficient,
light-weight network designed for mobile and
embedded vision applications.
3.3 Images
1000 images were used for this experiment. These
images were taken from the Imagenet database.
Specifically, from the ILSVRC2012 validation set.
From a set of images which were classified correctly
by all 4 experiment models, 1000 images were
randomly chosen.
3.4 Foolbox
The python library Foolbox was used to run the attack
algorithms and generate perturbations. Foolbox is a
popular library used for adversarial attacks against
machine learning models and benchmarking the
robustness of models against adversarial attacks
(Rauber, Zimmermann, Bethge, & Brendel, 2020).
The popularity, variety of attacks and fast
performance of the library made it a suitable choice
for this project.
3.5 Parameters
The parameters in Table 3 were used for this
experiment. The parameters were chosen mainly
based on previous works. The number of steps was
chosen based on experiment 2 results and with
consideration of the amount of time required to run
all the attacks. It was found that a very high number
of iterations/steps was not required for the adversarial
example to cause a misclassification.
For the Fixed Epsilon Attacks, the epsilon values
shown in Table 4 were used. These are based on
epsilon values commonly used in literature, then
scaling these values based on the image size.
Analysing Adversarial Examples for Deep Learning
587
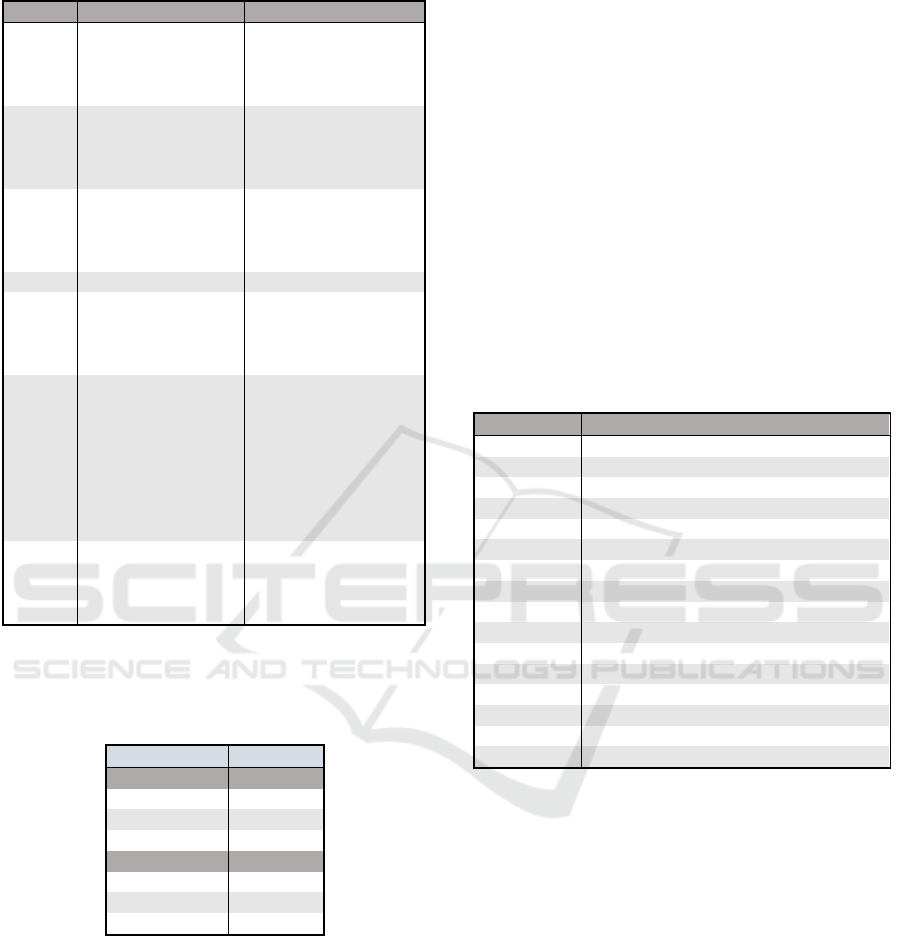
Table 3: Main experiment, adversarial attack parameters.
Attack Parameter Value
DNN init_epsilon 1 or 255 (depending
on ima
g
e bound
)
steps 200
g
amma 0.05
PGD rel_stepsize 0.025
abs
_
ste
p
size None
steps 50
random
_
start True
BIM rel_stepsize 0.2
abs
_
ste
p
size None
ste
p
s 10
random_start False
FGM random
_
start False
SLIDE quantile 0.99
rel
_
ste
p
size 0.2
abs_stepsize None
ste
p
s 50
BBA init_attac
k
None
overshoot 1.1
steps 100
l
r
0.001
lr_deca
y
0.5
lr
_
num
_
deca
y
20
momentu
m
0.8
b
inar
y_
search
_
ste
p
s 10
DF steps 100
candidates 10
overshoot 0.02
loss lo
g
its
Table 4: Epsilon values (perturbation sizes) used in the
experiment. The inception_v3 models requires the input
size to be 299x299x3 as opposed to 224x224x3 and has
been scaled appropriately.
pert. type value
not inception
l-inf 8
l-1 98,000
l-2 560
inception
l-inf 8
l-1 175,000
l-2 750
4 RESULTS AND DISCUSSION
16 attacks, 4 models and 1000 images were used to
generate 64,000 adversarial examples.
4.1 Attack Success Rates (ASR)
The attack success rates of each of the attacks was
obtained. From Table 5, it can be seen that adversarial
attacks are very effective on mobilenet, have similar
effectiveness against vgg16 and resnet50, and are less
effectiveness against inception_v3. This may be due
to the relative complexities of each of the neural
network architectures. Mobilenet’s lightweight
architecture appears to increase its vulnerability to
these adversarial attacks. On the other hand,
inception_v3’s more complex architecture appears to
increase its robustness against these attacks.
The FGM is a quick and basic attack involving
only a single step; as expected it has a lower ASR
compared to other attacks. The average ASR for each
model was:
Vgg16: 0.9679
Resnet50: 0.957625
Inception_v3: 0.8925
Mobilenet: 0.9907
Table 5: Attack Success Rates (ASR) of each adversarial
attack for each model (from 1000 images).
vgg16 rnet50 incep_v3 mnet
PGD_l1 0.968 0.991 0.946 0.999
PGD
_
l2 0.992 0.995 0.975 1.0
PGD
_
linf 1.0 0.999 0.999 0.999
BIM_l1 0.985 0.993 0.971 1.0
BIM
_
l2 0.998 0.994 0.988 1.0
BIM_linf 1.0 0.998 0.999 1.0
FGM
_
l1 0.875 0.837 0.588 0.959
FGM_l2 0.925 0.871 0.621 0.971
FGM
_
linf 0.977 0.924 0.663 0.983
SLIDE 1.0 0.998 1.0 1.0
DDN 0.948 0.93 0.999 0.998
DF_l2 0.909 0.876 0.805 0.969
DF
_
linf 0.982 0.939 0.943 0.989
BBA_l1 0.946 0.989 0.793 0.991
BBA
_
l2 0.985 0.989 0.996 0.994
BBA_linf 0.996 0.999 0.994 0.999
4.2 Label Influence Analysis
Figure 1 shows an image of a pair of jeans and the
adversarial example generated from a PGD_l1
adversarial attack. The perturbation can be seen as
being quite sparse. It has only been scaled by 16
times. Small pockets in the perturbation image which
have a relatively high value can be seen, with the rest
of the image having no/minimal change. This is
expected from the l1 norm perturbation restriction
(sum of absolute values of all elements) and indicates
that these small pockets encourage the
misclassification the greatest.
For this image (and the other 999 images), 64
adversarial examples were created (4 models x 16
attacks). For the adversarial example shown in Figure
1, the adversarial label (top prediction of the resulting
adversarial example) was miniskirt. In fact, 63 of the
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
588
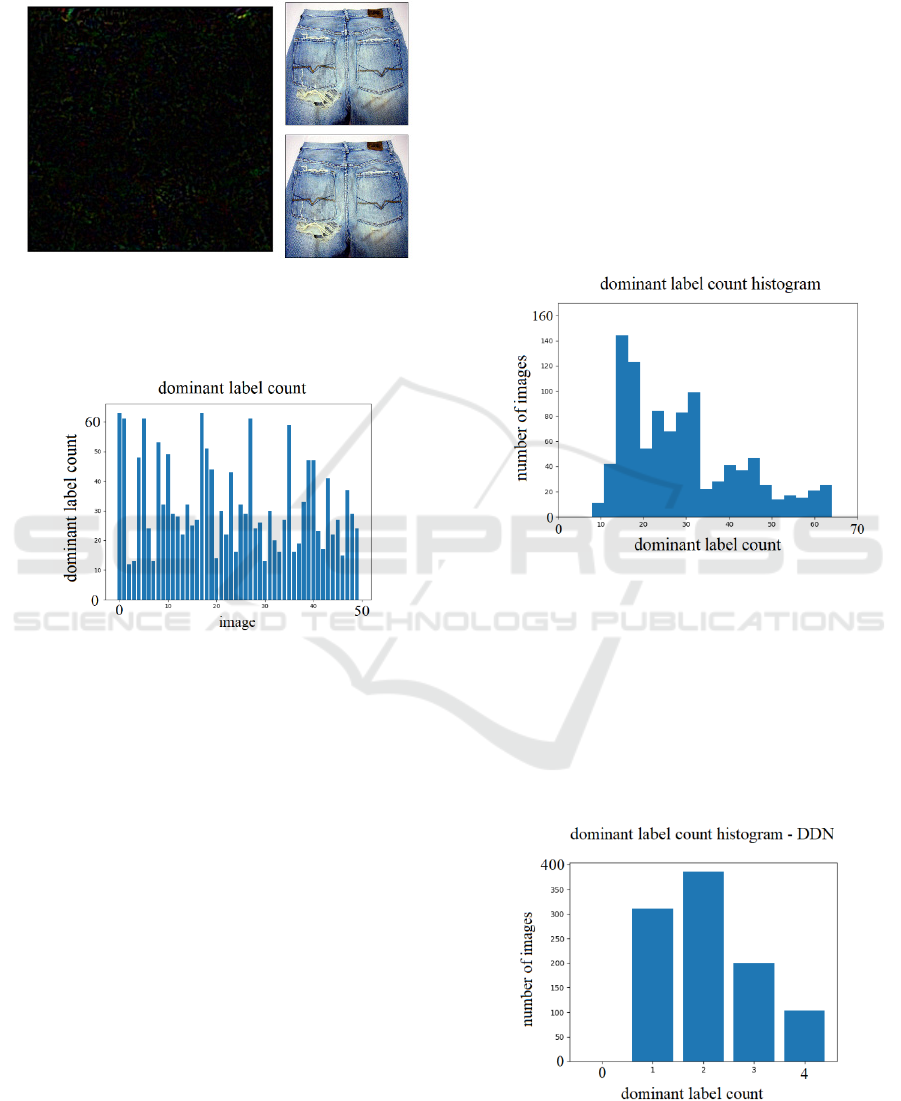
64 adversarial attacks for this image resulted in an
adversarial label of miniskirt. The remaining
adversarial label was hoopskirt.
Figure 1: Left: perturbation (x16) created using PGD_l1.
Top right: Clean, original image of a pair of jeans.
Bottom right: Adversarial example – misclassified as
miniskirt.
Figure 2: Plot of the number of times the most frequently
occurring label (dominant label) appears. For images 0 to
49.
From a set of adversarial examples (64 in this case)
of a single image, the ‘dominant label’ will be defined
as ‘the most frequently appearing adversarial label’.
The number of times the dominant label appears for
images 0 to 49 can be seen in Figure 2. For example,
the previous pair of jeans is image 0, the dominant
label is miniskirt and the number of times miniskirt
appears, or miniskirt count, is 63. This is represented
by the very first bar on the left.
From this plot, it can be seen that not all images
necessarily have a single dominant label. Images 2
and 3 have their dominant label only appearing 12 and
13 times. These images may have multiple
adversarial labels appearing as often, or almost as
often, as the dominant label.
The dominant label count of an image gives some
information about what influences the label. A high
count (e.g. image 0) means that regardless of the
attack and model, the resulting label is almost always
the same. In other words, the label is independent of
the attack and model, and only influenced by the
original image. On the other hand, a low count (e.g.
images 2 and 3), suggests that the adversarial label
isn’t greatly dependent on the original image.
The plot shown in Figure 2 can be extended for all
images from 0 to 999. A histogram of this extended
plot can be taken to visualize the dominant label count
of all 1000 images (Figure 3). The right-skewed
nature of the plot shows that most images have a low
dominant label count; the adversarial labels for these
images are not dependent just on the original image.
From this, it can be concluded that the image itself is
generally not a major influencer of the resulting
adversarial label.
Figure 3: Histogram of the number of images with each
dominant label count.
A similar histogram can be made with a focus on each
attack. Given a single adversarial attack, each image
now has 4 adversarial examples (from each model).
This can be seen in Figure 4 and Figure 5. The shape
of the histograms for all attacks are fairly similar. The
right skewed nature of all the plots once again
suggests that adversarial attacks do not have a large
influence over the resulting adversarial label.
Figure 4: Dominant label count histogram for the DDN
attack. 1000 images total, 4 attacks.
Analysing Adversarial Examples for Deep Learning
589
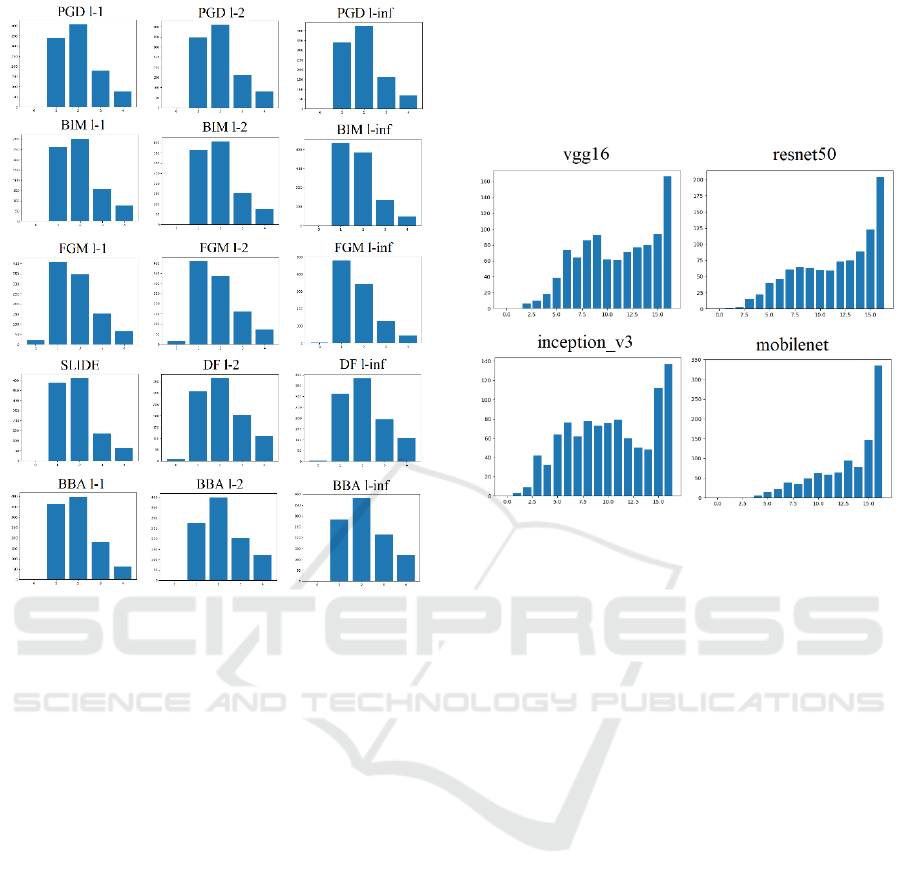
Figure 5: Dominant label count histograms for each
adversarial attack. Axes of each plot match Figure 4.
The same can be done with a focus on each model.
Given a single model, each image now has 16
adversarial examples (from each adversarial attack).
From Figure 6, it can be seen that these histograms
are left skewed. The images at the right end of the
histograms have a single adversarial label appear 15
or 16 times. For these images, regardless of the
adversarial attack, the resulting adversarial label is
the same.
From all these histograms it can be concluded that
the models, rather than the attacks, is the main
influencer of the resulting adversarial label, for a
given image. One potential explanation for this result
is that the attacks used were all gradient-based
attacks, which means the underlying algorithm for all
of these attacks are the similar; thus, all attacks cause
similar behaviors.
Comparing the models in Figure 6, mobilenet has
the ‘cleanest’ left skew, and inception_v3 appears to
be a normal distribution mixed with a left skewed
plot. The shapes of the other 2 models lie between
these 2 examples. The differences are likely due to the
differing network architectures. A light-weight
architecture seems to result in more consistent
adversarial label results.
By gaining insight into what influences the label,
i.e. the models, and the relationship between the
neural network architecture and the resulting
adversarial label, future defense techniques may be
able to use this information to better defend against
these untargeted attacks.
Figure 6: Dominant label count histograms for each model.
y-axis - number of images. x-axis - number of times most
freq. label appears (ranges from 0 to 16).
4.3 Label Movement Analysis
The movement of labels was also investigated. The
movement of labels refers to how the top label
predictions of the clean image may transfer to the top
predictions of the adversarial example. An example
diagram can be seen in Figure 7. The 2nd label or 2nd
highest prediction of the original image 0 is miniskirt
with a confidence of 1.02%, this becomes the
adversarial label or top prediction of the
corresponding adversarial image with a confidence of
99.34%.
Out of all 64,000 adversarial examples, it was
found that 52.2% of the 2nd label of the clean image
became the top prediction of the adversarial example.
12.2%, 5.8%, 3.4% of the 3rd, 4th and 5th labels of
the clean image become the top adversarial label.
4.7% of the time resulted in no label change (i.e.
adversarial attack failed), and 21.62% of the time
labels 6th – 1000th became the top prediction. Given
1000 possible classes, having the adversarial
examples’ top labels coming from the 2nd label of the
original images about half the time is a significant
result. Since the top predictions of the clean, original
image is only dependent on the image and model (and
not on the adversarial attack), the model and image
have a major influence on the resulting top
adversarial prediction/label.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
590
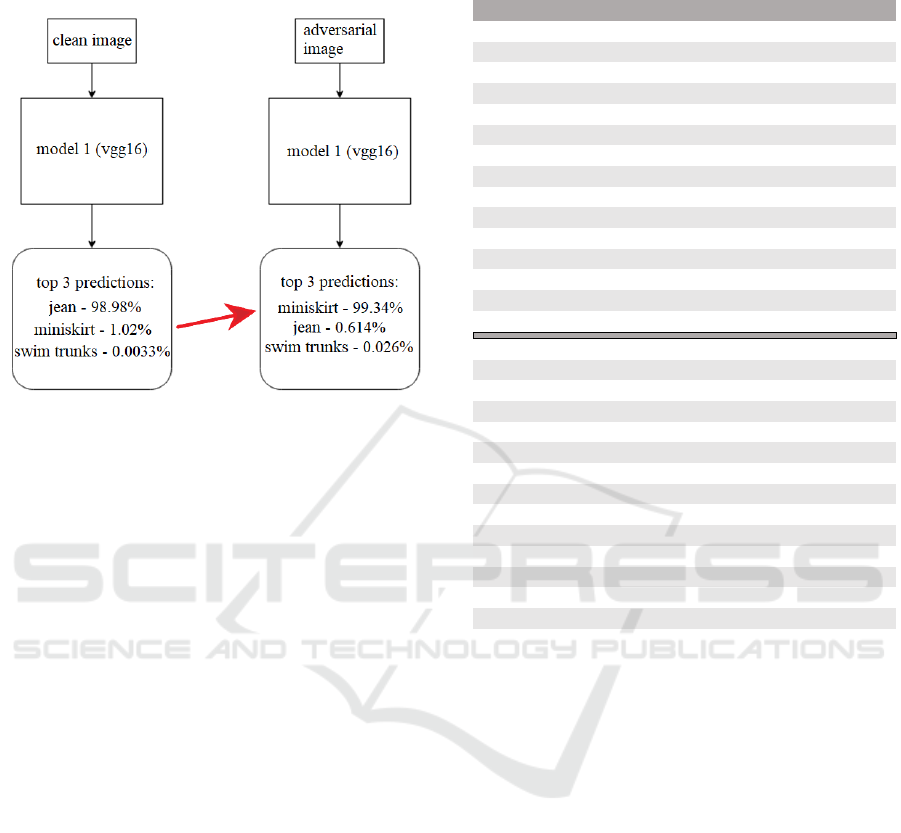
This result supplements the previous result
showing that models influence the resulting label.
Figure 7: Label movement example for image 0. Top 3
predictions for the clean image (left) and adversarial
example (PGD_l1) (right).
4.4 Compare Attack Labels
The adversarial labels for each attack was compared
with each other attack, for each model. For each pair
of attacks, the number of adversarial labels which
match (out of 1000 images) was recorded. The top
and bottom 15 matches can be seen in Table 6.
The top pairs of attacks in Table 6 are very similar
attacks. The algorithms of the BIM, PGD and FGM
attacks are extensions of one another. It would be
expected that the resulting labels for these attacks
would often match. On the other hand, the bottom half
shows pairs of very different attacks, resulting in few
matching labels. Also, worth noting is that
inception_v3 appears often as the model with these
low matching pairs of attacks. It may be due to its
higher complexity which may encourage more
variety in the adversarial labels. Mobilenet appears
often at the top of Table 6 also suggesting once again
that the light-weight network results in the same
adversarial labels.
Table 6: Number of matching labels between pairs of
attacks. List of top 15 and bottom 15.
model attack 1 attack 2 No. matches
mobilenet BIM
_
l1 BIM
_
l2 973
resnet50 BIM_l1 BIM_l2 947
mobilenet PGD
_
l1 BIM
_
l1 933
mobilenet PGD_l1 PGD_l2 931
v
gg
16 BIM
_
l1 BIM
_
l2 924
resnet50 FGM_l1 FGM_l2 919
mobilenet PGD
_
l1 BIM
_
l2 917
mobilenet BIM_l1 PGD_l2 916
mobilenet FGM
_
l1 FGM
_
l2 915
ince
p
tion
_
v3 FGM
_
l1 FGM
_
l2 913
resnet50 PGD_l1 PGD_l2 904
mobilenet PGD
_
l2 BIM
_
l2 903
mobilenet DDN BIM_l2 901
mobilenet BIM
_
l1 DDN 899
vgg16 PGD_l1 PGD_l2 890
ince
p
tion
_
v3 BIM
_
l1 BBA
_
l1 364
inception_v3 PGD_linf FGM_linf 363
ince
p
tion
_
v3 SLIDE FGM
_
linf 357
inception_v3 FGM_linf BBA_linf 355
ince
p
tion
_
v3 BBA
_
l1 BIM
_
l2 352
ince
p
tion
_
v3 BBA
_
l2 FGM
_
linf 348
inception_v3 DDN FGM_linf 345
v
gg
16 BBA
_
l1 BIM
_
linf 343
vgg16 BBA_l2 FGM_linf 343
ince
p
tion
_
v3 SLIDE BBA
_
l1 343
vgg16 FGM_linf BBA_linf 336
ince
p
tion
_
v3 BBA
_
l1 PGD
_
linf 330
inception_v3 BBA_l1 FGM_linf 316
ince
p
tion
_
v3 BBA
_
l1 BIM
_
linf 280
vgg16 BBA_l1 FGM_linf 274
5 DISCUSSION
The results from the experiment have shown that the
neural network models have more influence over the
resulting adversarial label as opposed to the
adversarial attack. In addition, a simpler, more light-
weight network architecture can be seen as being
more susceptible to attacks and results in the same
labels for many different attacks. This may be
explained by considering the classification space of
the models.
The classification space is a high dimensional
space where each position in this space maps to a
label. An image in this space would be classified by
placing it into this space and checking the mapping.
By adding perturbations, the goal of adversarial
attacks is to adjust the position of the image just
enough to change the region (or label) in this
classification space. To explain the differences found
in this experiment, a light-weight network may have
relatively large regions of distinct labels in this
Analysing Adversarial Examples for Deep Learning
591

classification space which are spaced apart as
opposed to interwoven classification regions. This is
illustrated in Figure 8. For the light-weight network,
once the perturbation has caused the image to reach a
new classification region, it has a large margin of
error before accidently switching labels to another or
even back to the original label. However, the more
complex network requires much more finesse, as a
slight change may cause the image to move into
another classification region. Assuming the initial
epsilon specified was enough to reach a new
classification region, this would explain the high ASR
against the light-weight mobilenet model and the
lower ASR against the more complex inception_v3
model. This would also explain why using different
attacks against the light-weight model often resulted
in the same label; given the attacks are similar (all
gradient-based), even with slight differences there is
a high chance they all end up in the same large
classification region.
Figure 8: 2D illustration of classification space for a light-
weight (left) and complex (right) network. Each colour
represents a different label or classification region.
These insights found in this work may assist future
researchers to develop more robust models against
untargeted gradient-based attacks. Since the analyzed
attacks were all gradient-based, future work would be
to consider other attack types as well. Additional
research into the classification space of the models for
the ImageNet models should also be considered. For
example, comparing the classification space of
simpler and more complex neural network models.
ACKNOWLEDGEMENT
This work was supported in part by Defence
Advanced Research Projects Agency (DARPA)
under the grant UTrap: University Transferrable
Perturbations for Machine Vision Disruption. The
U.S. Government is authorized to reproduce and
distribute reprints for Government purposes
notwithstanding any copyright annotation thereon.
The views and conclusions contained herein are those
of the authors and should not be interpreted as
necessarily representing the official policies or
endorsements, either expressed or implied, of
DARPA, or the U.S. Government.
REFERENCES
Akhtar, N., & Mian, A. (2018, Mar 28). Threat of
Adversarial Attacks on Deep Learning in Computer
Vision: A Survey. Retrieved from
https://arxiv.org/abs/1801.00553
Brendel, W., Rauber, J., Kümmerer, M., Ustyuzhaninov, I.,
& Bethge, M. (2019, Dec 12). Accurate, reliable and
fast robustness evaluation. Retrieved from
https://arxiv.org/abs/1907.01003
Eykholt, K., Evtimov, I., Fernandes, E., Li, B., Rahmati, A.,
Xiao, C., . . . Song, D. (2018, Apr 10). Robust Physical-
World Attacks on Deep Learning Models. Retrieved
from https://arxiv.org/abs/1707.08945
Goodfellow, I. J., Shlens, J., & Szegedy, C. (2015, Mar 20).
Explaining and Harnessing Adversarial Examples.
Retrieved from https://arxiv.org/abs/1412.6572
Kurakin, A., Goodfellow, I. J., & Bengio, S. (2017, Feb 11).
Adversarial Examples in the Physical World. Retrieved
from https://arxiv.org/abs/1607.02533
Madry, A., Makelov, A., Schmidt, L., Tsipras, D., & Vladu,
A. (2019, Sep 4). Towards Deep Learning Models
Resistant to Adversarial. Retrieved from
https://arxiv.org/abs/1706.06083
Moosavi-Dezfooli, S.-M., Fawzi, A., & Frossard, P. (2016,
Jul 4). DeepFool: a simple and accurate method to fool
deep neural networks. Retrieved from
https://arxiv.org/abs/1511.04599
Rauber, J., Zimmermann, R., Bethge, M., & Brendel, W.
(2020). Foolbox Native: Fast adversarial attacks to
benchmark the robustness of machine learning models
in PyTorch, Tensorflow and JAX. Retrieved from
https://joss.theoj.org/papers/10.21105/joss.02607
Rony, J., Hafemann, L. G., Oliveira, L. S., Ayed, I. B.,
Sabourin, R., & Granger, E. (2019, Apr 3). Decoupling
Direction and Norm for Efficient Gradient-Based L2
Adversarial Attacks and Defenses. Retrieved from
https://arxiv.org/abs/1811.09600
Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan,
D., Goodfellow, I., & Fergus, R. (2014, Feb 19).
Intruiging properties of neural networks. Retrieved
from https://arxiv.org/abs/1312.6199
Tramèr, F., & Boneh, D. (2019, Oct 18). Adversarial
Training and Robustness for Multiple Perturbations.
Retrieved from https://arxiv.org/abs/1904.13000.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
592
