A Wavelet Scattering Convolutional Network for Magnetic

Resonance Spectroscopy Signal Quantitation

Amirmohammad Shamaei

1,2 a

, Jana Starčuková

1 b

and Zenon Starčuk Jr.

1 c

Institute of Scientific Instruments of the CAS, Královopolská 147, 612 64 Brno, Czech Republic

Department of Biomedical Engineering, Faculty of Electrical Engineering and Communication,

Brno University of Technology, Technická 3058/10, 616 00 Brno, Czech Republic

Keywords: Magnetic Resonance Spectroscopy, Quantification, Deep Learning, Machine Learning.

Abstract: Magnetic resonance spectroscopy (MRS) can provide quantitative information about local metabolite

concentrations in living tissues, but in practice the quantification can be difficult. Recently deep learning (DL)

has been used for quantification of MRS signals in the frequency domain, and DL combined with time-

frequency analysis for artefact detection in MRS. The networks most widely used in previous studies were

Convolutional Neural Networks (CNN). Nonetheless, the optimal architecture and hyper-parameters of the

CNN for MRS are not well understood; CNN has no knowledge about the nature of the MRS signal and its

training is computationally expensive. On the other hand, Wavelet Scattering Convolutional Network

(WSCN) is well-understood and computationally cheap. In this study, we found that a wavelet scattering

network could hopefully be also used for metabolite quantification. We showed that a WSCN could yield

results more robust than QUEST (one of quantitation methods based on model fitting) and the same as a CNN

while being faster. We used wavelet scattering transform to extract features from the MRS signal, and a

superficial neural network implementation to predict metabolite concentrations. Effects of phase, noise, and

macromolecules variation on the WSCN estimation accuracy were also investigated.

1 INTRODUCTION

Magnetic Resonance Spectroscopy (MRS) has

attracted the MR community over the past seven

decades (Van Der Graaf, 2010). A significant part of

the interest in biomedical MRS stems from the

possibility of noninvasive measurements of

metabolites. Information about tissue metabolites can

help in clinical diagnostics. For instance, detection of

metabolic pathway changes may facilitate diagnosing

disease in earlier stages before anatomy changes can

be observed, and thus enable more efficient treatment.

E.g., in glioma, a decrease of N-acetylaspartate

(NAA) and creatine concentrations and an increase of

choline, lipids, and lactate predicts an increase of the

glioma grade (Robin A. de Graaf, 2019; Van Der

Graaf, 2010). To detect such changes, quantification

of MRS signals is required for obtaining the

metabolite concentrations in the tissue. However,

https://orcid.org/0000-0001-8342-3284

https://orcid.org/0000-0003-0337-7893

https://orcid.org/0000-0002-1218-0585

reliable quantification of MRS is difficult. The

existing MRS quantitation methods are based on

model fitting of the signal in either the time or the

frequency domain (Poullet et al., 2008). In recent

years, new novel machine learning solutions have

been proposed for quantification, one of which is

deep learning (DL). Even though the first usage of

machine learning dates back to the 1970s, it was

unpractical until the past decade due to lack of high-

performance hardware and novel algorithms (Chen et

al., 2020). DL has achieved many accomplishments

in a wide range of tasks, including the MRI field

(Alaskar, 2019). Due to the poor SNR, chemical shift

displacement, and overlapping signal components in

MRS signals, only recently has DL been used for

metabolite quantification of MRS signals in the

frequency domain (Hatami et al., 2018; Lee & Kim,

2019)

268

Shamaei, A., Star

cuková, J. and Star

cuk Jr., Z.

A Wavelet Scattering Convolutional Network for Magnetic Resonance Spectroscopy Signal Quantitation.

DOI: 10.5220/0010318502680275

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 268-275

ISBN: 978-989-758-490-9

Hatami et al. showed the first step in this area by

using the Convolutional Neural Network (CNN)

approach for simulated MRS signal quantification

(Hatami et al., 2018). Kim et al. conducted a

comprehensive study on brain metabolite

quantification using DL (Lee and Kim, 2019).

Nonetheless, the practical application of DL in MRS

has not been limited to quantifications only.

Kyathanahally et al. taught a CNN with time-

frequency data to detect and remove ghosting artifacts

in clinical magnetic resonance spectra of the human

brain (Kreis & Kyathanahally, 2018).

However, the optimal architecture and hyper-

parameters of CNN for MRS are not well understood.

Besides, training a CNN is a computationally

expensive and time-consuming task, and it usually

needs a big dataset (Bruna & Mallat, 2013).

Moreover, in the case of MRS signals, CNN has no

understanding of the nature of the signal, and

therefore, any shape difference of the signal under

investigation from signals in the training data set can

lead to CNN failure. If we look at a CNN as a

transformation from the time domain to a features

domain, due to the nature of MRS signals, the

transformation should be invariant to time shift,

deformation in the time domain, and frequency shift.

To satisfy such requirements, CNN could be designed

- an optimized and simple deep architecture

which pools the features using a nonlinear averaging

measure.

- a network with a fast computational

algorithm which is stable to time-shifting,

deformation in the time domain, and frequency shift.

Wavelet Scattering Convolutional Network

(WSCN) can be a method of choice. WSCNs are

well-understood, computationally cheap, and fast for

a deep learning task (Andén & Mallat, 2014; Bruna &

Mallat, 2013). Wavelet-based methods have

previously been used for MRS quantification and

water removal (Poullet et al., 2008; Suvichakorn et

al., 2008); but as far as we are aware, wavelet

transform has not been implemented by a deep

convolutional neural network to quantify MRS

signals.

Given the mentioned accomplishments of

machine learning in MRS for signal quantification,

this paper describes to our knowledge the first attempt

to use this state-of-the-art technique to quantify MRS

signals by WSCNs. We used wavelet scattering

transform to extract features from the free induction

decay (FID, i.e. the MRS signal in the time domain)

and a superficial neural network implementation to

predict metabolite concentrations.

In this study, we used two different basis sets. The

first basis set was the ISMRM challenge 2016

simulated basis set for comparing results of our

method with the results published for a CNN and

another conventional quantification method, QUEST

(Graveron-Demilly, 2014). For the second basis set,

we simulated our own metabolite signals and

generated different synthetic datasets from them for

evaluating our method against phase changing, noise,

and presence of macromolecule signals.

2 METHODS

All steps were run on a laptop with a 4-core Intel i7

processor running at 2.6 GHz and an NVIDIA GTX

1050Ti graphics processing units using Matlab

(R2019a, Mathworks Inc., Natick, MA, USA)

software.

2.1 Simulation of Metabolites

To build a basis-set signals, fifteen metabolites –

Alanine (Ala), Aspartate (Asp), Creatine (Cr),

Choline (Cho), Gamma Aminobutyric Acid (GABA),

Glutathione (GSH), Glutamine (Gln), Glutamate

(Glu), Lactate (Lac), N-Acetylaspartate (NAA), N-

acetyl-aspartyl-glutamate (NAAG), Phosphatidyl-

choline (PC), Phosphocreatine (PCr), Taurine (Tau)

and myo-Inositol (mIns) – were simulated at 9.4 T

magnetic field with the PRESS sequence (TE = 20

ms; TR = 2500 ms; acquisition points: 2048;

acquisition bandwidth: 4401.41 Hz; three PRESS

pulses with Hermite shapes and flip angles: P1 = 90°,

P2 = 180°, P3 = 180°). The simulation was performed

in NMRScopeB (Starčuk & Starčuková, 2017; Stefan

et al., 2009). The parameters selected in the sequence

were taken from an in-vivo experiment, which allows

reusing the simulated basis set.

2.2 Baseline and Macromolecule

Simulation

The baseline signals were simulated as a linear

combination of several Gaussian lines identified by

Osorio-Garcia (Opstad et al., 2008; Osorio-Garcia et

al., 2011). The number and parameters of Gaussian

lines were extracted from in-vivo signals using

inversion recovery (Osorio-Garcia et al., 2011).

2.3 Signal Generation Framework

The MRS signal was defined as a linear combination

A Wavelet Scattering Convolutional Network for Magnetic Resonance Spectroscopy Signal Quantitation

269

of amplitude-scaled frequency- and phase-shifted

metabolite signals, the baseline, and noise.

The model describing a time-domain MRS signal

s[n] as a combination of several metabolite profiles is

(Poullet et al., 2007):

   

 

nMMA

nXAns

MMMMMM

mmm

itnfi





+



)2(

(1)

where 









is the n-th sample of the m-th simulated

metabolite,  is the sampling period, A

is the

scaling factor of the metabolite, 

is the damping

factor, Δf

is the frequency shift of the m-th

metabolite affected by the static magnetic field

inhomogeneity, pH, temperature and chemical

composition of the tissue, 



is the phase of the m-

th metabolite, Δt is the time step, and M is the number

of metabolites.

Table 1 specifies the range of parameter values

used for generating different datasets according to

equation (1). For a comparison of our results with the

previous study (Hatami et al., 2018), the basis set

provided for the ISMRM challenge 2016 (ISMRM,

2016) was used to generate dataset DSS1 (20

metabolite and one macromolecule components). All

other datasets were generated using the basis set

simulated with NMRScopeB (15 metabolites). The

same parameter ranges that were used in the previous

study (Hatami et al., 2018) were also used in this

study for DSS1, but we decided to choose ranges of

parameters for other datasets (DSS2-DSS7) in the

same manner as we would do if we evaluated real

acquired spectra.

Instead of generating 500 000 signal samples per

dataset, in our study only 10 000 signal samples were

generated for validating the hypothesis that our

network is as robust as Hatami et al.'s approach

(Hatami et al., 2018) even with a smaller number of

samples but faster. Parameters were chosen randomly

from defined ranges with a uniform distribution. In

DSS1, random complex Gaussian noise was added to

signal samples based on the previous study (Hatami

et al., 2018). In the rest of the datasets, the SNR of the

signal samples was adjusted by adding random noise

such that the SNR was in the range of ~5 to ~15. In

this study, we used MATLAB built-in snr function

which calculates the signal-to-noise ratio (SNR) of an

MRS signal by computing the ratio of its summed

squared magnitude to that of the noise. In Table 1, the

presence of a parameter is marked by a tick and the

absence of a parameter by a cross.

2.4 Deep Learning

2.4.1 Invariant Wavelet Scattering Network

Invariant wavelet scattering network is a transform

from the time domain to the features domain, which

has three stages, namely, Convolution (wavelet),

Non-linearity, and Averaging (scaling factor).

In contrast to the classical wavelet transform, the

Complex wavelet transform is translation invariant.

In this study, we chose Morlet (Gabor) wavelets, a

type of complex wavelet transform, because they

have a simple mathematical representation.

Figure 1 illustrates the wavelet scattering

transform processes (see (Andén & Mallat, 2014;

Bruna & Mallat, 2013) for more details). In practice,

a scattering decomposition framework was created

with a signal input length of 1024 samples.

Table 1: Specification of datasets.

Name

Amplitude

)

Frequency

shift(Δf

)

Damping

range(

)

Noise

()

Phase ( 



)

MM (



)

Common

Separated

Constant

Changing

DSS1

(Hatami et

al., 2018)

[0, 1]

[-10, 10]







DSS2

[0.5 1]

[-10, 10]

[-5, 2.5]



DSS3

[0.5 1]

[-10, 10]

[-5, 2.5]



[











]



DSS4

[0.5 1]

[-10, 10]

[-5, 2.5]



[











]



DSS5

[0.5 1]

[-10, 10]

[-5, 2.5]



[











]



DSS6

[0.5 1]

[-10, 10]

[-5, 2.5]









DSS7

[0.5 1]

[-10, 10]

[-5, 2.5]





Within ±10 percent

of initial values

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

270

The framework had two filter banks; in other words,

the depth of the framework was 3. The quality factor

(the number of wavelet filters per octave) of the first

and second filter banks were 8 and 1, respectively.

For the given signal length and quality factors, the

output of the framework was a matrix with a size of

154 by 8 by 2. There were 154 scattering paths and 8

scattering windows for each of the real and imaginary

parts of the signal.

2.4.2 Regression

Figure 1: The process of wavelet scattering network;

averaging and convolution of a signal with wavelet filters

are showed by an arrow (green) and a circled star,

respectively.

Flattening and fully-connected layers were what we

had at the last stage of our network. The first step, so-

called flattening, was converting a feature matrix into

a 1-dimensional array. The matrices from the output

of WSCN were flattened to create a single long

feature vector. The flattening layer was connected to

a fully-connected layer, which was a feedforward

artificial neural network for the regression task.

Neural networks with the different number of neurons

in hidden layers were investigated. The best fully-

connected layer structure was obtained by trial and

error on the basis of the lowest error on the training

and validation dataset. The results showed that one

hidden-layer network with 20 neurons in the hidden

layer yielded better results than other network types.

The modeling performance and training were

evaluated by the mean square error (MSE) and scaled

conjugate gradient, respectively.

Figure 2 demonstrates the process of

transformation, flattening, and regression. The input

and output of a fully-connected layer were the

features vector and the relative amplitudes of various

metabolite basis spectra, respectively.

Figure 2: A schematic of feature extraction and flattening

and the training of an artificial neural network.

2.4.3 Quantification

80% of each dataset was allocated to the training set,

10% for validation and the rest 10% for the test set. It

applied to all datasets, DSS1 to DSS7, and then they

were fed to the network. First, the network was

trained with the training dataset; then, it was used to

predict the test dataset. The output of the network was

a vector in which each element represents the relative

amplitude of each metabolite.

2.5 Accuracy Evaluation

The Symmetric mean absolute percentage error

(SMAPE) is used to measure the accuracy of the

model. SMAPE is defined as below for each

metabolite:

 







 



′













 



′







(2)

Where m, N, A, and 

′

are the metabolite index, the

number of test datasets, the ground truth, and the

estimated amplitude, respectively.

3 RESULTS

3.1 Comparison between the

Quantification Result of QUEST,

CNN, and WSCN for ISMRM

Challenge Dataset

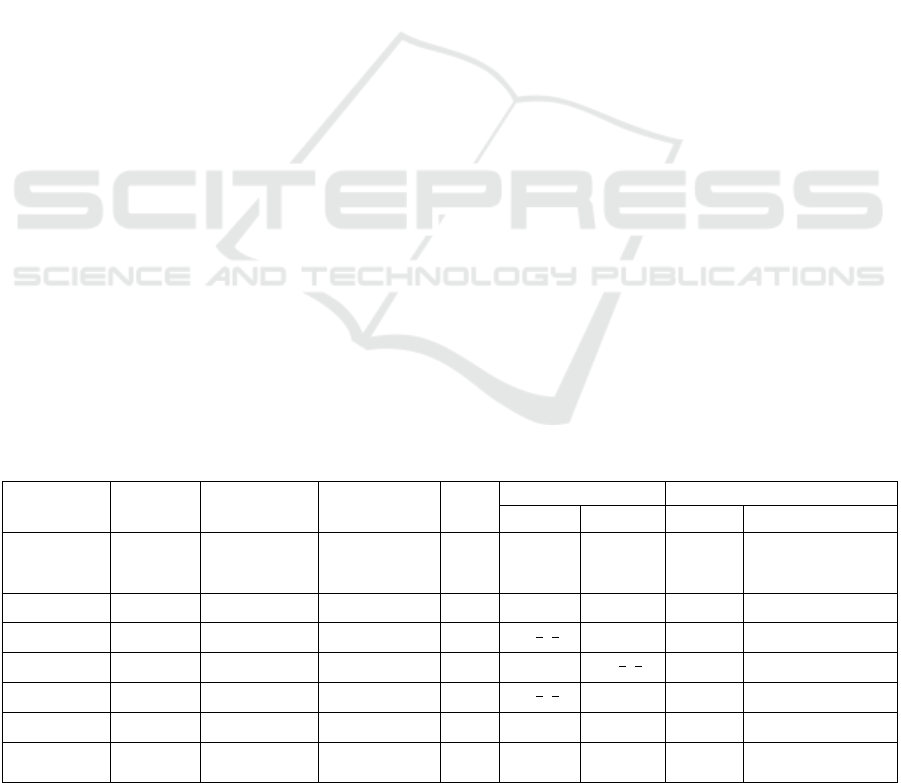
Figure 3 shows the comparison between different

methods, namely Quest, CNN, and WSCN, for

dataset DSS1, where the SNR of signals was set to 10.

The result for CNN and QUEST were extracted from

(Hatami et al., 2018).

Flattening

Feature

Extraction

Signal(s[n])

A Wavelet Scattering Convolutional Network for Magnetic Resonance Spectroscopy Signal Quantitation

271

Figure 3: Comparison between SMAPEs of each metabolite for the WSCN (red), the CNN (yellow), and Quest (green).

Figure 4: Comparison between SMAPEs of the concentration of all metabolites with fixed phases (DSS2), common phase

varied (DSS3) and independently varied phases (DSS4) (different phase changes for different metabolites). (Test datasets,

N=1000). The error bars represent the standard deviation.

3.2 Effect of Phase Variation and Noise

on WSCN Estimation Accuracy

The performance of WSCN was evaluated on

different datasets (DSS2 to DSS7) in table 1. Figure

4 shows the effect of metabolite phase variation in the

signals under test. We compared the result of signals

with a fixed phase, a common varied phase, and

independently varied phases. The average of

SMAPEs for DSS2, DSS3, and DSS4 were 1.13%,

1.38%, and 1.7%, respectively.

The results of the metabolite quantification for

DSS5 (DSS3 with added noise) is shown in Figure 5.

For all 15 metabolites, the average of SMAPE was

3.46% ± 2.81%. Asp with SMAPE of 6.00 ± 4.48 and

NAAG with SMAPE of 13.20% ± 10.12% were

quantified as highest and lowest SMAPE,

respectively. The average SMAPE of DSS5 was

increased by 151% compared to DSS3 (without

noise).

3.3 Effect of Macromolecules Variation

on WSCN Estimation Accuracy

Figure 6 shows a comparison between DSS6 and

DSS7. In dataset DSS6, the parameters of baseline

signals (11 Gaussian lines) are constant, while in

DSS7, amplitudes of Gaussian lines were randomly

varied in the range of ±10% of their initial values. For

all metabolites of DSS6 and DSS7, the average

SMAPEs were 5.92% ± 4.40% and 6.12% + 4.55%,

respectively. The average SMAPE of DSS6 and

DSS7 was increased by 73% compared to DSS5

(without Macromolecules inclusion).

Symmetric mean absolute

percentage error (SMAPE, %)

WSCN CNN Quest

Ala Asp Cr Cho GABA GSH Gln Glu Lac NAA NAAG PC PCr Tau mIns

Symmetric mean absolute

percentage error (SMAPE, %)

DSS2 DSS3 DSS4

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

272

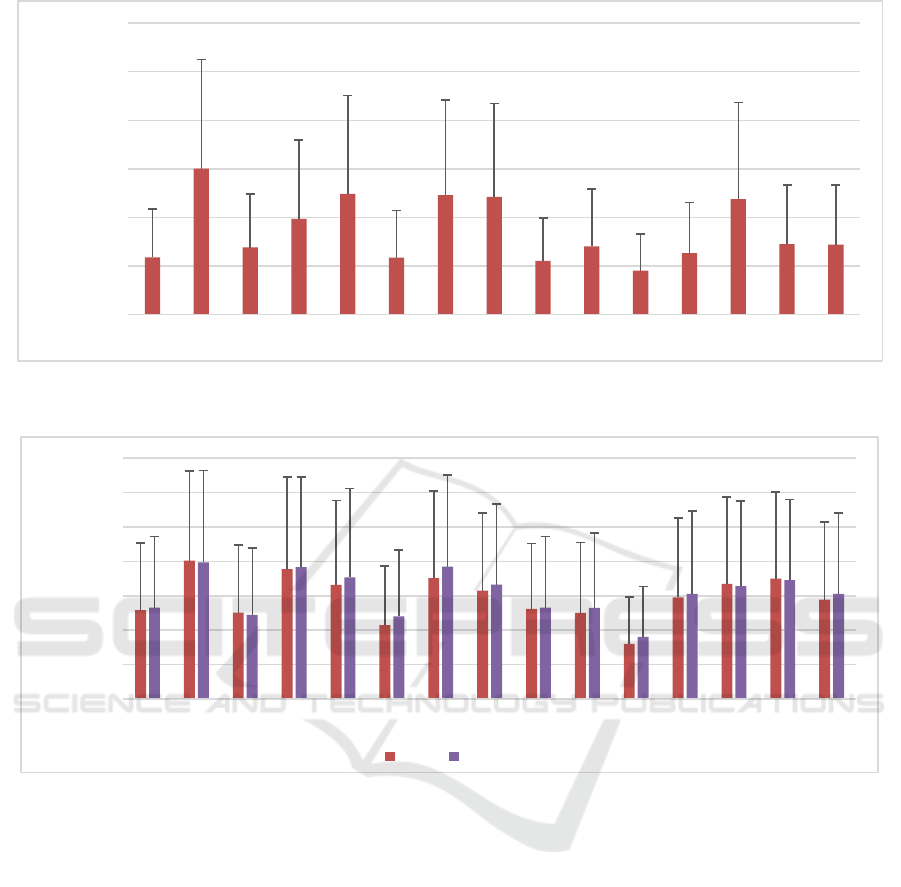
Figure 5: Symmetric mean absolute percent error (SMAPE) of the concentrations of all metabolites in dataset DSS5, which

contains noisy signal (N = 5000). The error bars represent the standard deviation.

Figure 6: Comparison between SMAPEs of the concentration of all metabolites in dataset DSS6, and DSS7 (Test datasets,

N=1000). In DSS6, the amplitudes of macromolecules lines were constant. In contrary, the amplitudes were varying within

±10% of initial range in DSS7. Both datasets are noisy and with common phase changing.

4 CONCLUSIONS

The aim of MRS signal quantification is to estimate

the amplitudes/areas (in time/frequency domain) of

different metabolites in the signal. The estimated

amplitudes/areas then can be converted to meaningful

numbers as the concentration of metabolites. The

conventional and widely used approach is to estimate

amplitudes of single sinusoids (areas of single peaks)

in MRS signal or to estimate the amplitudes (areas) of

whole metabolite signals (spectra). In the former

approach, the model is fitted to data using non-linear

least-squares analysis; the latter approach uses a basis

set of metabolite profiles in the model function and

uses a semi-parametric fitting technique. The oldest

method, so-called peak integration, is calculating

peaks area in a selected frequency interval.

Nonetheless, using these approaches for

quantification is challenging (Stagg & Rothman,

2014).

On the other hand, the quantification of the MRS

signal using deep learning has attracted huge interest

in recent years (Chen et al., 2020). DL can detect

important features in the MRS signal and

subsequently determine a non-linear mapping

between these features and the outputs, which can be

the concentrations of the metabolites. The most

widely used DL approach for quantification is CNN.

Nevertheless, this approach has drawbacks, for

example, poor understanding of the CNN architecture

and hyper-parameters for MRS, expensive and time-

Ala Asp Cr Cho GABA GSH Gln Glu Lac NAA NAAG PC PCr Tau mIns

Symmetric Mean absolute

percentage error (SMAPE, %)

Ala Asp Cr Cho GABA GSH Gln Glu Lac NAA NAAG PC PCr Tau mIns

Symmetric mean absolute

percentage error (SMAPE, %)

DSS6 DSS7

A Wavelet Scattering Convolutional Network for Magnetic Resonance Spectroscopy Signal Quantitation

273

consuming computation, and the need of a big dataset

for CNN training (Bruna and Mallat, 2013).

These shortages motivated us to develop a deep

network for MRS signal quantification, which can be

fast, well-understood, and works with a small dataset

of training samples. For this purpose, we used a

WSCN.

In every DL task, determining the proper input

and output of the network is an important step. In our

study, the input is an FID, i.e., time-domain signal,

and the network estimates amplitudes of the first

points of metabolite signals (what corresponds to

areas under metabolite signals in metabolite spectra).

In this work, we demonstrated that the use of the

wavelet scattering network could achieve better

results than the semi-parametric fitting technique

QUEST and similar results as the computationally

more demanding CNN (Figure 3).

It is known that the accuracy of estimation in the

peak integration approaches is influenced by phases

of peaks (Stagg & Rothman, 2014), and that phase

should be included in the model as one of the

unknown parameters. Therefore, we also investigated

whether WSCN is capable of estimating amplitudes

of metabolites in case that metabolite phases change.

It resulted in an increase in the complexity of the

model, but WSCN proved to have the capability of

handling this task. Figure 4 shows the WSCN can

quantify signals with common varied phases (with

SMAPE of 1.38%) as well as signals without fixed

phases (with SMAPE of 1.13%). The average of

MAPEs for DSS4 is increased by 36% and 17%

compared to DSS2 and DSS3, respectively. It

indicates that quantification can be moderately harder

for a dataset with independently varied phases.

Another source of error in quantification are

macromolecular signals, which stem in macro-

molecules present in the tissue under investigation. In

conventional quantification approaches, macro-

molecule signals can either be removed in the

preprocessing step or modeled in the quantitation

step. However, the risk of errors will be increased and

accumulated in fitting error in the former approach,

and therefore the latter approach is recommended.

However, macromolecule signals often overlap with

metabolite components, for which DL can be a

method of choice for disentangling. As we showed in

Figure 3, the WSCN could estimate macromolecules

better than other approaches. Later in this study, we

modeled the macromolecules signal as a set of

Gaussian lines using parameters (like linewidth,

frequency) measured using the inversion-recovery

recovery (Osorio-Garcia et al., 2011). Figure 6

demonstrates that the WSCN showed nearly the same

error for signals with randomly varied macro-

molecule lines and signals with fixed macromolecule

lines. This could indicate that despite the changing of

background signals parameters, the WSCN is stable

against nuisance components in MRS, such as

macromolecules. Additional research should be done

however with simulated signals that will imitate in-

vivo data.

To compare the learning times of both networks,

i.e., Hatami et al.'s CNN and our WSCN, we rebuilt

their CNN and fed both networks with the DSS5

dataset, and ran both networks in the earlier

mentioned system. Our proposed approach is

estimated to be 45 times faster than Hatami et al.'s

approach (the WSCN’s learning time was 5 min 40

sec precisely and the CNN’s learning time was 268

min). The WSCN showed that it could be faster than

the CNN due to using fixed-size filters and less

parameter optimization.

It should be noted that even though deep learning

showed promising results in areas like speech

recognition and image processing (Chen et al., 2020),

this study is one of the very initial steps in the

application of DL in MRS and more studies are

needed for proving DL suitability for in-vivo

spectroscopy. Below some of the limitations and open

issues are addressed:

1. In this study, we only quantified simulated

data. The amplitudes of metabolites in our

simulated data did not imitate the metabolite

concentrations in in-vivo data. Quantification of

simulated data with concentrations close to in-

vivo data should be investigated as the next step

together with data acquired from a phantom.

2. Real MRS data is influenced by numerous

factors such as voxel size, voxel placement,

radiofrequency (RF) coil sensitivity, receiver

gain, and other experimental factors. Further

research must take all factors into account.

3. A potential application of our proposed

approach is the quantification of MRSI data,

where a fast method is needed for quantification

of a set of MRS signal. Learning a network and

using it for only a single voxel may not be

efficient as using it for a set of signals.

ACKNOWLEDGEMENTS

This research was supported by European Union's

Horizon 2020 research and innovation program under

the Marie Skłodowska-Curie grant agreement No

813120 (INSPiRE-MED) and by European Regional

Development Funds under project "National

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

274

infrastructure for biological and medical imaging" of

the Ministry of Education, Youth and Sports of the

CR (No. CZ.02.1.01/0.0/0.0/16_013/0001775).

REFERENCES

Alaskar, H. (2019). Deep Learning-based Model Architec-

ture for Time-Frequency Images Analysis. January

2018.

Andén, J., & Mallat, S. (2014). Deep scattering spectrum.

IEEE Transactions on Signal Processing, 62(16),

4114–4128.

Bruna, J., & Mallat, S. (2013). Invariant scattering

convolution networks. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 35(8), 1872–1886.

Chen, D., Wang, Z., Guo, D., Orekhov, V., & Qu, X.

(2020). Review and Prospect: Deep Learning in

Nuclear Magnetic Resonance Spectroscopy. Chemistry

- A European Journal, 26(46), 10391–10401.

Graveron-Demilly, D. (2014). Quantification in magnetic

resonance spectroscopy based on semi-parametric

approaches. In Magnetic Resonance Materials in

Physics, Biology and Medicine (Vol. 27, Issue 2, pp.

113–130). Springer Verlag.

Hatami, N., Lyon, B., & Etienne, U. (2018). Magnetic

Resonance Spectroscopy Quantification using Deep

Learning.

ISMRM. (2016). MRS Fitting Challenge (ismrm.org

/workshops/Spectroscopy16/mrs_fitting_challenge/).

Kreis, R., & Kyathanahally, S. P. (2018). Deep Learning

Approaches for Detection and Removal of Ghosting

Artifacts in MR Spectroscopy. 863, 851–863.

Lee, H. H., & Kim, H. (2019). Intact metabolite spectrum

mining by deep learning in proton magnetic resonance

spectroscopy of the brain. Magnetic Resonance in

Medicine, 82(1), 33–48.

Opstad, K. S., Bell, B. A., Griffiths, J. R., & Howe, F. A.

(2008). Toward accurate quantification of metabolites,

lipids, and macromolecules in HRMAS spectra of

human brain tumor biopsies using LCModel. Magnetic

Resonance in Medicine, 60(5).

Osorio-Garcia, M. I., Sima, D. M., Nielsen, F. U.,

Dresselaers, T., Van Leuven, F., Himmelreich, U., &

Van Huffel, S. (2011). Quantification of in vivo 1H

magnetic resonance spectroscopy signals with baseline

and lineshape estimation. Measurement Science and

Technology, 22(11), 1–17.

Poullet, J. B., Sima, D. M., Simonetti, A. W., De Neuter,

B., Vanhamme, L., Lemmerling, P., & Van Huffel, S.

(2007). An automated quantification of short echo time

MRS spectra in an open source software environment:

AQSES. NMR in Biomedicine, 20(5), 493–504.

Poullet, J. B., Sima, D. M., & Van Huffel, S. (2008). MRS

signal quantitation: A review of time- and frequency-

domain methods. Journal of Magnetic Resonance,

195(2), 134–144.

Robin A. de Graaf. (2019). In Vivo NMR Spectroscopy. In

In Vivo NMR Spectroscopy (pp. 1–42).

Stagg, C., & Rothman, D. (2014). Magnetic Resonance

Spectroscopy: Tools for Neuroscience Research.

Starčuk, Z., & Starčuková, J. (2017). Quantum-mechanical

simulations for in vivo MR spectroscopy: Principles

and possibilities demonstrated with the program

NMRScopeB. Analytical Biochemistry, 529.

Stefan, D., Cesare, F. Di, Andrasescu, A., Popa, E.,

Lazariev, A., Vescovo, E., Strbak, O., Williams, S.,

Starcuk, Z., Cabanas, M., Van Ormondt, D., &

Graveron-Demilly, D. (2009). Quantitation of magnetic

resonance spectroscopy signals: The jMRUI software

package. Measurement Science and Technology, 20(10).

Suvichakorn, A., Ratiney, H., Bucur, A., Cavassila, S., &

Antoine, J. P. (2008). Quantification method using the

Morlet wavelet for Magnetic Resonance Spectroscopic

signals with macromolecular contamination.

Proceedings of the 30th Annual International Conf. of

the IEEE Engineering in Medicine and Biology Society,

EMBS’08 - “Personalized Healthcare through

Technology,” 2681–2684.

Van Der Graaf, M. (2010). In vivo magnetic resonance

spectroscopy: Basic methodology and clinical

applications. European Biophysics Journal, 39(4),

527–540.

A Wavelet Scattering Convolutional Network for Magnetic Resonance Spectroscopy Signal Quantitation

275