Visualization of Joint Spatio-temporal Models via Feature Recognition

with an Application to Wildland Fires

Devan G. Becker

1 a

, Douglas G. Woolford

and Charmaine B. Dean

Statistical and Actuarial Sciences, University of Western Ontario, London, Ontario, Canada

Statistics and Actuarial Science, Waterloo University, Waterloo, Ontario, Canada

Keywords:

Image Recognition, Non-negative Matrix Factorization, Log-Gaussian Cox Processes, Dimension Reduction.

Abstract:

Many spatial statistics applications result in a collection of spatial estimates, especially if a different (but

possibly correlated) estimate is produced for a sequence of time epochs. For a small collection of epochs, the

connections or trends between estimates and the prominent or common features can be found via inspection

of the spatial estimates. As the number of spatial estimates grows, this task becomes much more difﬁcult. We

present a method of summarizing a sequence of estimates using an image recognition technique called Non-

Negative Matrix Factorization which results in a meaningful decomposition of the source images into basis

functions and coefﬁcients. This visualization technique allows for investigation of trends over time as well as

common spatial features of the estimates without needing to ﬁt a temporal model or use pre-speciﬁed spatial

regions. We apply this technique to a sequence of models that jointly model the spatial location of wildland

ﬁres with the total burn area of each of the ﬁres. We discuss the extensions of the visualization technique to

the joint modelling framework and are able to draw new insights about the connection between the location

and size of the ﬁres.

1 INTRODUCTION

Sequences of continuous spatial ﬁelds are becoming

more common with more data collection. These can

come in the form of spatial ﬁelds measured or esti-

mated at discrete time points (e.g. sea surface temper-

ature measured daily, yearly estimates of ﬂood risk,

etc.), multiple variables measured or estimated over

the same spatial regions (e.g. distribution of differ-

ent species across the same habitat), or some combi-

nation of the two (e.g. species distribution measured

monthly). Much work has been done to estimate mul-

tivariate spatio-temporal models, but these models are

easy to misspecify and difﬁcult to estimate. This is

especially true in the presence of a large number of

spatial ﬁelds.

Some recent examples of analyses that resulted in

a collection of joint spatial and spatio-temporal mod-

els are as follows. A joint spatial model for predator-

prey relationships of marine species was ﬁt for each

year in Sadykova et al. (2017). They found that most

of the covariates which were signiﬁcant for habitat us-

age were likely to change with the changing climate.

https://orcid.org/0000-0003-3796-3946

Jones-Todd et al. (2018) ﬁt a joint spatio-temporal

model to determine predator-prey relationships in

avian species. Their model accounted for spatio-

temporal variation, but the results of the analysis still

included a large number of spatial plots to be inter-

preted. Finally, Python et al. (2016) ﬁt a joint spatial

model to yearly terrorist attacks around the globe.

In previous work, we performed a spatial analysis

of wildland ﬁres (Becker et al. 2020). This involved

jointly modelling the location of ﬁres along with the

size of those ﬁres. Locations of ﬁres were modelled

using a Log-Gaussian Cox Process (LGCP) frame-

work and sizes were modelled using a Log-Normal

survival model with assumed interval censoring; a

shared random effect was used to jointly model these

two outcomes. Due to computational complexity as

well as the winter creating a discontinuity between

ﬁre seasons, we restricted our data to one year at a

time. This model setup resulted in two spatial esti-

mates per year for 47 years worth of data. While not

excessive, it was still difﬁcult to see broad trends with

so many spatial estimates.

Here, we employ feature recognition algorithms to

summarise the joint spatial ﬁelds into basis functions.

Such techniques have been used for analysis of shot

Becker, D., Woolford, D. and Dean, C.

Visualization of Joint Spatio-temporal Models via Feature Recognition with an Application to Wildland Fires.

DOI: 10.5220/0010319602330239

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 3: IVAPP, pages

233-239

ISBN: 978-989-758-488-6

233

location in both basketball (Miller et al. 2014; Franks

et al. 2015) and hockey (Becker, Woolford, and Dean

2020). Those papers estimated a spatial point process

estimate for each player, then treated these estimates

as images to determine how players utilized regions of

the basketball court or hockey rink. The results illu-

minated similarities and differences between players

that would have been very difﬁcult to discern with the

naked eye. The authors all used this analysis to create

some measure for shot optimality. In what follows we

describe an image recognition technique and demon-

strate that applying it to estimates of a sequence of

spatial models is a useful visualization technique.

2 PRELIMINARIES

2.1 Non-negative Matrix Factorization

(NMF)

Non-negative Matrix Factorization (NMF) is a dimen-

sion reduction technique that decomposes a data ma-

trix into a matrix of basis functions and a matrix of

coefﬁcients for those basis functions. The This was

popularized as an image recognition technique by Lee

and Seung (1999), and has been used in a wide variety

of applications since (see, e.g., Gillis 2014).

For our purposes, NMF has the attractive feature

of being purely additive. That is, the estimated basis

functions as well as their coefﬁcients are both non-

negative, so a linear combination of the bases can only

add to the estimate. In PCA, the bases and coefﬁcients

and bases are allowed to be negative, so one basis may

be allowed to counteract the effect of another. With

purely additive bases, the basis functions all represent

a single feature. This restriction makes the estimated

basis functions directly interpretable.

The NMF algorithm works by factorizing an n×m

matrix V with non-negative entries into an n × r ma-

trix W and an r×m matrix H, where r is the number of

basis functions and must be speciﬁed prior to estima-

tion. The columns of W represent the basis functions.

Each row in the matrix H represents the coefﬁcients

for the corresponding basis in W . With these matri-

ces, we can approximate the ith column of V , which

we will denote V

·i

, as the matrix product W H

i·

Under certain constraints, NMF is particularly

useful for feature recognition in images (Gillis

(2014)). Assuming all images have the same pixel

dimensions and the colour of each pixel is a single,

non-negative number (e.g., grey scale), a matrix of

images can be constructed such that each column rep-

resents a single image. For instance, suppose we have

a collection of grey scale images of faces, all of which

have the same pixel dimensions and the faces are all

aligned in the same way (e.g. all eyes and mouths are

at the same location of the image). Each image can

be represented by a vector of non-negative numbers.

The NMF algorithm will estimate basis functions that

correspond to facial features. The coefﬁcient matrix

will determine how much of each basis function is re-

quired to construct a face.

To make this process more clear, consider

the following example. Suppose we have a ma-

trix V with n = 7 rows and m = 2 columns,

resulting in 14 entries total. The ﬁrst column

is [1, 2, 3, 4, 3, 2, 1]

and the second column is

[2, 3, 5, 7, 5, 3, 2]

. Clearly, both columns have a

similar pattern (or feature). If we want to characterize

this feature, we could use an NMF decompo-

sition, where we choose r = 1 since we know

there is a single feature. Doing so results in W =

[1.259, 2.099, 3.359, 4.618, 3.359, 2.099, 1.259]

which is a matrix with seven rows (n) and

one column (r). The coefﬁcient matrix is

H = [0.886, 1.496]. From this, the approxima-

tion for the ﬁrst column of V is W × 0.886 =

[1.116, 1.86, 2.977, 4.093, 2.977, 1.86, 1.116]

, which

is quite close to the original ﬁrst column (but with

some approximation error). Note that W and H

together have 9 entries compared to the original 14

and that inspection of W tells us about both columns

of the original matrix simultaneously.

The choice of r, the number of bases, also known

as the rank, is non-trivial. Too many basis functions

and the algorithm will simply be modelling the noise.

Too few and the approximations will not be accurate.

In some contexts, prior knowledge will be sufﬁcient

for choosing the number of bases. In other contexts

there are numerous heuristic approaches. Techniques

have been proposed by Brunet et al. (2004), Hutchins

et al. (2008), and Frigyesi and H

oglund (2008). A

properly motivated choice of r is imperative whenever

NMF is being used for analysis. As a visualization

technique, however, the choice of rank is dependent

on the usefulness of the visualizations.

Estimation of NMF models has been shown to be

NP-hard (Vavasis 2007). There have been many al-

gorithms developed to estimate the matrices (Wang

and Zhang 2013), and these methods have been im-

plemented in multiple software packages. We use the

NMF package in the R Statistical Software language,

and details can be found in Gaujoux and Seoighe

(2010).

IVAPP 2021 - 12th International Conference on Information Visualization Theory and Applications

234

2.2 NMF for Spatial Fields

To apply the NMF algorithm to estimates of a spa-

tial ﬁeld, we will follow the algorithm of Miller et al.

(2014) in their analysis of shots in professional bas-

ketball. Their algorithm broadly follows four steps:

1. Set up a matrix to represent the pixel locations,

then convert this matrix to a vector. For an q × s

pixel resolution, the ﬁrst row of this matrix can

be labelled p

= p

, p

, ... p

and the kth row

can be labelled p

= p

, p

, ... p

. The vector of

pixels will then have the form p = (p

, p

, ... p

2. Estimate each of the N models at the locations p.

The jth model is labelled λ

(p), which we will

shorten to λ

for convenience. Note that these es-

timates must be non-negative.

3. Combine the vectors of spatial models as col-

umn vectors in a matrix, = [λ

, λ

, ..., λ

], where

each λ

is a column.

4. Use an NMF algorithm to approximate matrices

W and H such that ≈ W H.

Due to the setup of this algorithm, the columns

of W will be spatial basis functions at pixels p and

the jth column of H will be a vector with r elements

which represent the contribution of each basis to the

approximation of λ

2.3 Shared Spatial Effects Models

The methods developed in this paper are applicable to

any joint modelling framework where a spatial ﬁeld is

estimated, but are especially useful for models with a

spatial effect that is split into two.

Suppose we have a joint model of the form

X,Y

(x(s), y(s)|Z(s), Λ(s), φ), where x(s) and y(s) are

our spatially referenced response variables, Z(s) and

Λ(s) are two estimated spatial ﬁelds, and φ = (φ

, φ

)

where φ

and φ

are the vectors of remaining model

parameters for X and Y , respectively, which may or

may not include further spatial terms and may have

some identical elements. Suppose further that our

model can be factored as:

X,Y

x(s), y(s)|Z(s), Λ(s), φ)

= f

(x(s)|Z(s), Λ(s), φ

) f

(y(s)|Z(s), φ

)

(1)

That is, conditional on the random ﬁeld Z(s), X(s)

and Y (s) are independent. In this formulation, it is

entirely possible that one of the elements of φ

is an-

other spatial ﬁeld. In fact, the visualization technique

that we will develop later is immediately extensible

to such a situation. For now, we are primarily inter-

ested in a model that contains a model-speciﬁc spatial

component as well as a shared spatial component.

For the purposes of this study, we do not need to

specify an estimation procedure. It is imperative that

the estimates from this technique are reasonable for

the visualization technique to be useful, but the visu-

alizations that we will present are agnostic to the par-

ticulars of the estimation procedure. In fact, the gen-

eral framework of the visualization techniques does

not require an estimate at all; it will sufﬁce to have

any combination of estimates and/or spatially and/or

temporally referenced data.

3 NMF FOR JOINT SPATIAL

MODELS

Suppose we have a sequence of N non-negative

estimates of spatial ﬁelds Z(s) and Λ(s) esti-

mated at pixel locations p. We will deﬁne

Z =

[

(p),

(p), ...,

(p)] as the matrix of spatial esti-

mates deﬁned in Section 2.2, with

deﬁned similarly.

There are several potential ways to apply the NMF

algorithm to these joint spatial models. The naive ap-

proach would be to approximate

Z ≈ W

(Z)

and

≈ W

(Λ)

. This would result in a set of basis

functions for

Z denoted W

(Z)

, and a set of basis func-

tions for

, W

(Λ)

. These basis functions would be en-

tirely separate and would miss pertinent shared fea-

tures.

Given the joint spatial modelling approach, we de-

sire a method for summarising the two ﬁelds that re-

tains any joint features. For instance, if large values

in Z(s) tend to correspond to large values in Λ(s), we

would like our visualizations to reﬂect this.

To achieve this goal, we can stack the

Z and

matrices as follows:

V =



(p)

(p) ...

(p)

(p) ...

(p)



(2)

In this construction, each column represents both

spatial ﬁelds present in the joint modelling approach.

From this construction, any given basis function con-

tains information about both spatial ﬁelds. It is trivial

to extend this to any number of spatial ﬁelds (assum-

ing the ﬁelds are well estimated).

Alternatively, one could combine the spatial ﬁelds

side-by side:

(alt)



(p)

(p) ...

(p)

(p) ...

(p)



(3)

Visualization of Joint Spatio-temporal Models via Feature Recognition with an Application to Wildland Fires

235

In this construction,

Z and

are still estimated

separately but will rely on the same basis functions.

To visualize the relationship between these two ﬁelds,

one could inspect the coefﬁcients.

To visualize common similarities between spatial

ﬁeld, we believe that the “stacked” approach in Equa-

tion (2) is more useful than the side-by-side approach

in Equation (3). The approximation to the estimates

will incorporate both spatial ﬁelds rather than drawing

from each ﬁeld separately. The interpretation of the

basis functions will make it immediately clear how

the spatial ﬁelds are related.

4 APPLICATION TO WILDLAND

FIRES

Our data consist of the locations and total burn area

of ﬁres from 1953 to 2000 in the province of British

Columbia, Canada. The model that we will be sum-

marising is given in full detail in Becker et al. (2020).

A brief description follows below.

The total burn area (in hectares) of a ﬁre is mod-

elled as a log-normal random variable such that the

mean depends on an intercept, ﬁre weather covariates,

and a spatial component. We assume that the spatial

component of this distribution can be modelled by a

Gaussian ﬁeld Λ(s).

The location of lightning-caused wildland ﬁres

is modelled by a log-Gaussian Cox process. This

model assumes that there is an underlying Gaussian

ﬁeld S(s), and conditional on this ﬁeld the number of

points in a region B is Poisson with rate parameter

exp(β

+ S(s) +C(s))ds, where β

is an intercept

and C(s) is the collection of spatial covariates (includ-

ing distance to the nearest highway or roadway and

elevation).

To link these two models, we separate S(s) into

two independent Gaussian ﬁelds S

(s) and S

(s) such

that exp(S(s)) = exp(S

(s) + γS

(s)) = Z(s)Λ(s)

We chose this notation to make it explicit that Z(s)

and Λ(s) are both non-negative. The linking parame-

ter γ exists so that the estimation procedure can cause

the joint component to vanish from the LGCP model

while retaining a spatial ﬁeld in the size model.

To demonstrate the results of this model, a com-

parison of the model output versus separate non-

parametric estimates is shown in Figure 1. The LGCP

random effect is clearly estimating the spatial distri-

bution of ﬁres, and the joint component is estimat-

ing the spatial variation in size. Note that the colours

are normalized such that the maximum value is the

brightest spot and should not be used for comparison.

The plot on the left (including both the LGCP and

LGCP

Joint

A. Model−based estimates

KDE (Location)

GAM (Size)

B. Non−parametric estimates

Figure 1: A. Spatial ﬁeld estimates from the joint spatial

model for wildland ﬁres in 1990. B. Spatial non-parametric

estimates of the locations and sizes for the same data. The

colour scale is chosen for so that the largest values of the

given ﬁeld are the brightest colour and are not meaningful

for comparison.

the Joint components) was converted into a vector of

pixels and combined with all of the other estimates

from this model. The NMF algorithm was run 100

times with different initial values at r = 3 to r = 20.

Based on the peaks in the cophenetic, dispersion, and

silhouette plots, and the “elbow” in the residual sum

of squares plot (as described in Chalise and Fridley

2017), we chose 8 basis functions (either 6 or 9 would

have also been supported by the diagnostic plots; they

were not as deﬁnitive as this makes it sound). Upon

visual inspection, this appears to retain interpretabil-

ity while avoiding “modelling noise”.

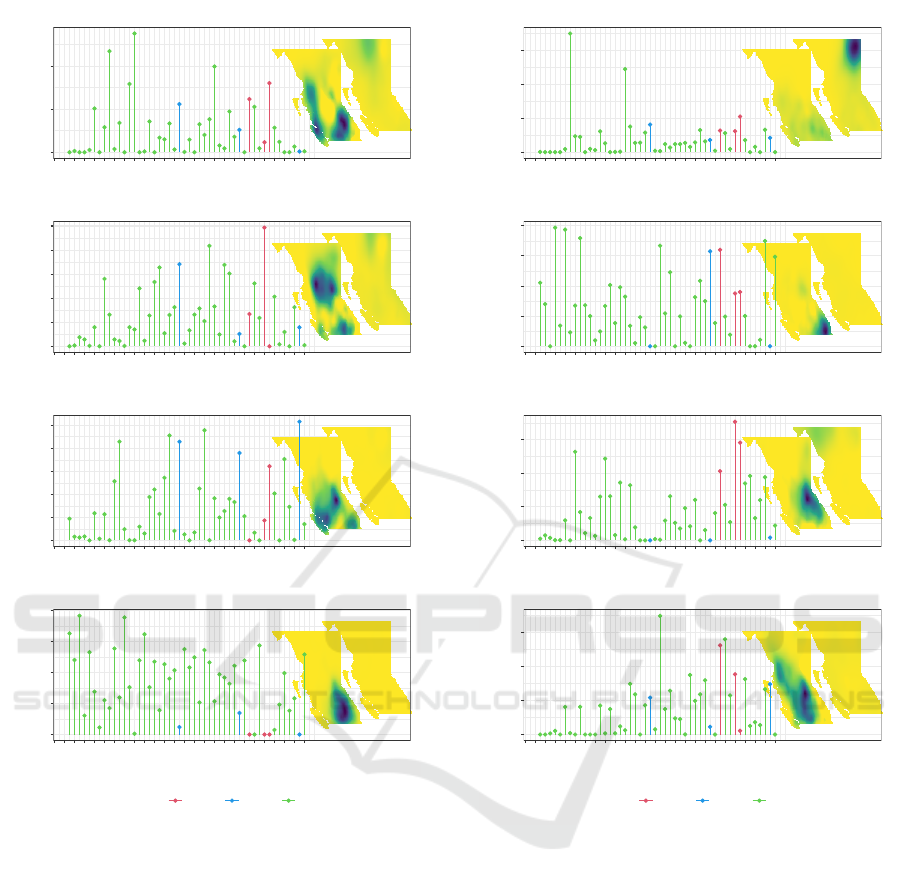
The resultant basis functions and coefﬁcients are

shown in Figure 2. The colours will be described in

the next section. Recall that the bases are additive, so

all of the original estimates can be approximated by

adding together the non-negative bases.

The NMF algorithm allows the basis functions to

overlap, so there are multiple bases the cover the same

regions. In particular, the mountainous area near the

south east of British Columbia is partially covered by

bases 1, 2, 5, and part of 8. In contrast, it appears that

the diagonal line down the south east of BC in basis

1 is cut out of basis 6, which has a conspicuously low

value in the same area.

IVAPP 2021 - 12th International Conference on Information Visualization Theory and Applications

236

0.0

0.2

0.4

1950

1952

1954

1956

1958

1960

1962

1964

1966

1968

1970

1972

1974

1976

1978

1980

1982

1984

1986

1988

1990

1992

1994

1996

1998

2000

Year

Coefficient

Coef. for Basis 1

0.0

0.1

0.2

0.3

0.4

0.5

1950

1952

1954

1956

1958

1960

1962

1964

1966

1968

1970

1972

1974

1976

1978

1980

1982

1984

1986

1988

1990

1992

1994

1996

1998

2000

Year

Coefficient

Coef. for Basis 2

0.0

0.1

0.2

0.3

0.4

0.5

1950

1952

1954

1956

1958

1960

1962

1964

1966

1968

1970

1972

1974

1976

1978

1980

1982

1984

1986

1988

1990

1992

1994

1996

1998

2000

Year

Coefficient

Coef. for Basis 3

0.00

0.25

0.50

0.75

1.00

1950

1952

1954

1956

1958

1960

1962

1964

1966

1968

1970

1972

1974

1976

1978

1980

1982

1984

1986

1988

1990

1992

1994

1996

1998

2000

Year

Coefficient

Coef. for Basis 4

"Cluster"

Comp.1 Comp.3 No Cluster

Figure 2: Bases and Coefﬁcients for bases 1 to 4. Within

each basis plot (the maps), the lower-left maps are the

LGCP-only effect and the upper-right maps are the shared

effects.

Basis 7 demonstrates that the estimated basis

functions are not required to be contiguous. The mul-

tiple regions in basis 7 represent places where ﬁres

tend to ignite (or not ignite) in the same year. Much

like how bases 1 and 6 ﬁt together, basis 7 also ap-

pears to be ﬁt with basis 8 like a puzzle piece.

There appears to be a stark contrast between years

where ﬁres occur in the mountainous region in the

east-by-south-east region, as described by basis 1, and

years where there are no ﬁres in this region. The co-

efﬁcients indicate that basis 1 is either a large com-

ponent of the LGCP estimate or it is not part of it at

all.

0.0

0.2

0.4

0.6

1950

1952

1954

1956

1958

1960

1962

1964

1966

1968

1970

1972

1974

1976

1978

1980

1982

1984

1986

1988

1990

1992

1994

1996

1998

2000

Year

Coefficient

Coef. for Basis 5

0.0

0.2

0.4

0.6

0.8

1950

1952

1954

1956

1958

1960

1962

1964

1966

1968

1970

1972

1974

1976

1978

1980

1982

1984

1986

1988

1990

1992

1994

1996

1998

2000

Year

Coefficient

Coef. for Basis 6

0.00

0.25

0.50

0.75

1950

1952

1954

1956

1958

1960

1962

1964

1966

1968

1970

1972

1974

1976

1978

1980

1982

1984

1986

1988

1990

1992

1994

1996

1998

2000

Year

Coefficient

Coef. for Basis 7

0.0

0.2

0.4

0.6

1950

1952

1954

1956

1958

1960

1962

1964

1966

1968

1970

1972

1974

1976

1978

1980

1982

1984

1986

1988

1990

1992

1994

1996

1998

2000

Year

Coefficient

Coef. for Basis 8

"Cluster"

Comp.1 Comp.3 No Cluster

Figure 3: Bases and Coefﬁcients for bases 5 to 8.

The difference in coefﬁcients for different years

reveals some potential patterns over time. This is

most evident in the increase in the coefﬁcient for ba-

sis 2 over time. This increase is mirrored by the de-

crease in the coefﬁcient for basis 5 over time. In par-

ticular, the coefﬁcient for basis 2 is much higher after

1985 than before, whereas the coefﬁcient for basis 5

is lower after 1985. Jdging by the basis functions,

this corresponds with more ﬁres in the middle of the

province rather than the south east.

For the joint component, we see that the algorithm

has split the northern area into west (basis 1), cen-

tre (basis 7), and east (basis 3). No other bases have

positive values, indicating that the joint effect only

appears to exist in the northern regions of BC. It is

also noteworthy that the joint effects are associated

strongly with the LGCP-only effects.

Visualization of Joint Spatio-temporal Models via Feature Recognition with an Application to Wildland Fires

237

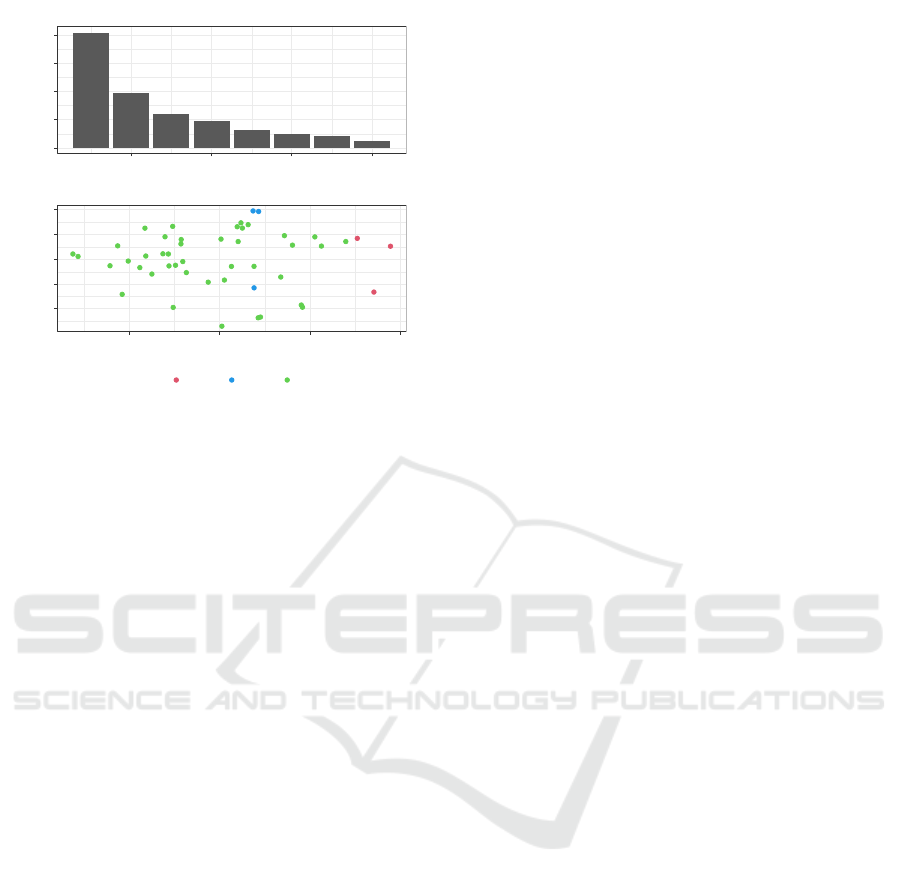
0.0

0.1

0.2

0.3

0.4

2 4 6 8

Principle Component

Percent of Variance Explained

Scree Plot for PCA

−0.4

−0.2

0.0

0.2

0.4

−0.4 0.0 0.4 0.8

PC1

PC2

"Cluster"

Comp.1 Comp.3 No Cluster

Principle Component Biplot

Figure 4: Scree plot and biplot, showing the colours that

were used in Figure 2. The points are coloured based on

how “abnormal” they are in comparison to the other points.

“Abnormality” was determined by visual inspection. The

green points are abnormal in terms of principle component

3, which is not shown.

The colours in Figure 2 are based on a princi-

ple components analysis of the estimated coefﬁcients.

The scree plot and the biplot are shown in Figure 4.

The “clusters” are based on simply checking whether

a given point has a principle component larger than

a speciﬁed value, where the speciﬁed value was cho-

sen by hand. This is not a rigorous outlier detection

method, but rather another visualization technique.

The green points, labelled “Comp.3”, are from the

same sort of heuristic in the direction of the third prin-

ciple component.

5 CONCLUSION

We have shown that stacking multiple spatial esti-

mates in Non-negative Matrix Factorization is an ef-

fective technique for summarising a sequence of joint

spatial estimates. The algorithm setup that we have

described can easily be extended to numerous ap-

plications where a large number of spatial estimates

must be interpreted by eye.

For our particular application, the NMF technique

quickly revealed that the shared random ﬁeld pri-

marily acts in the northern regions of BC. This pro-

vides insight into the relationship between ﬁre igni-

tion, spread, weather, and suppression efforts. Intu-

itively, weather that is conducive to large ﬁres would

also be conducive to multiple ignitions. This rela-

tionship is characterized by the joint modelling ap-

proach. However, ﬁres are only allowed to grow un-

abated in the northern regions of BC. The ﬁres in the

more populated southern regions are more likely to

be suppressed, which confounds the relationship be-

tween count and size.

The analysis also revealed years where the ﬁre be-

haviour was different from other years. The increase

in the value of the coefﬁcient for basis 2 is especially

interesting. In Becker et al. (2020), we found a sig-

niﬁcant effect for distance to highway or railway, with

this effect approaching 0 over time. We believe that

this may be due to imperfect detection of ﬁres that

are far from human populations. The increase in co-

efﬁcient for basis 2 appears to support this conclu-

sion; the region of British Columbia covered by the

basis saw an increase in population over time. The

increased importance of this basis may indicate bet-

ter detection of lightning-caused ﬁres, rather than a

change in ﬁre behaviour.

The technique that we described is not exclusive

to joint models in the framework of our research. The

techniques would be valid if one or both of the spa-

tial ﬁelds were observed perfectly. The technique

also works for spatial models that are estimated sep-

arately, in which case the basis functions and coefﬁ-

cients would help deduce spatial correlation between

the variables of interest. There is no theoretical con-

straint on N, the number of observations of spatial

ﬁelds, nor is there a constraint on the number of types

of spatial ﬁelds that are stacked on top of each other.

As with any other application of NMF without

pre-deﬁned bases, this technique is limited by the

need to investigate the rank. As a visualization tech-

nique it is worthwhile to investigate multiple values

of r, but this may be tedious and/or time consuming

depending on the size of the data.

NMF is frequently used as a clustering technique,

which is often interpreted as meaning that there is

the intention of prediction of new observations or in-

ference for population parameters. As described in

this paper, neither of these interpretations are valid.

We are applying NMF to point estimates from an-

other model while ignoring the rest of the variance.

The conclusions from this paper are broad trends, and

further investigation into individual model outputs is

required before and predictions or inferences can be

made. This visualization technique is not intended to

replace careful inspection of model output and inter-

pretation of model parameters. Instead, it is a sin-

gle, useful step in the long process of spatio-temporal

model estimation.

IVAPP 2021 - 12th International Conference on Information Visualization Theory and Applications

238

ACKNOWLEDGEMENTS

We acknowledge the support of the Natural Sci-

ences and Engineering Research Council of Canada

(NSERC), [funding reference numbers RGPIN-2015-

04221 and RGPIN-2014-06187]. Additional support

was provided by a CANSSI Collaborative Re- search

Team grant and the Institute for Catastrophic Loss Re-

duction. We would also like to thank Michael Schuck-

ers and Nathan Sandholtz for conversations regarding

the work on NMF for hockey data and Steve Taylor

for his insight into the work on wildland ﬁre mod-

elling.

REFERENCES

Becker, Devan G., Douglas G. Woolford, and Charmaine

B. Dean. 2020. “Algorithmically Deconstructing Shot

Locations as a Method for Shot Quality in Hockey.”

Journal of Quantitative Analysis in Sports Ahead of

Print.

Becker, Devan G., Douglas G. Woolford, Charmaine B.

Dean, and W. John Braun. 2020. “Visualization

and Joint Analysis of Monitored Multivariate Spatio-

Temporal Data with Applications to Forest Fire Mod-

elling and Sports Analytics.” Western University Elec-

tronic Thesis and Dissertation Repository, March.

Brunet, J. P., P. Tamayo, T. R. Golub, and J. P. Mesirov.

2004. “Metagenes and Molecular Pattern Discovery

Using Matrix Factorization.” Proceedings of the Na-

tional Academy of Sciences 101 (12): 4164–9. https:

//doi.org/10.1073/pnas.0308531101.

Chalise, Prabhakar, and Brooke L. Fridley. 2017. “Inte-

grative Clustering of Multi-Level ‘Omic Data Based

on Non-Negative Matrix Factorization Algorithm.”

Edited by Shyamal D Peddada. PLOS ONE 12

(5): e0176278. https://doi.org/10.1371/journal.pone.

0176278.

Franks, Alexander, Andrew Miller, Luke Bornn, and Kirk

Goldsberry. 2015. “Characterizing the Spatial Struc-

ture of Defensive Skill in Professional Basketball.”

The Annals of Applied Statistics 9 (1): 94–121. https:

//doi.org/10.1214/14-AOAS799.

Frigyesi, Attila, and Mattias H

oglund. 2008. “Non-

Negative Matrix Factorization for the Analysis of

Complex Gene Expression Data: Identiﬁcation of

Clinically Relevant Tumor Subtypes.” Cancer In-

formatics 6 (January): CIN.S606. https://doi.org/10.

4137/CIN.S606.

Gaujoux, Renaud, and Cathal Seoighe. 2010. “A Flexible

Software Package for Nonnegative Matrix Factoriza-

tion,” 9.

, Nicolas. 2014. “The Why and How of Nonnegative Ma-

trix Factorization.” arXiv:1401.5226 [Cs, Math, Stat],

March. http://arxiv.org/abs/1401.5226.

Hutchins, Lucie N., Sean M. Murphy, Priyam Singh, and

Joel H. Graber. 2008. “Position-Dependent Motif

Characterization Using Non-Negative Matrix Factor-

ization.” Bioinformatics 24 (23): 2684–90. https://doi.

org/10.1093/bioinformatics/btn526.

Jones-Todd, Charlotte M., Ben Swallow, Janine B. Illian,

and Mike Toms. 2018. “A Spatiotemporal Multi-

species Model of a Semicontinuous Response.” Jour-

nal of the Royal Statistical Society: Series C (Ap-

plied Statistics) 67 (3): 705–22. https://doi.org/10.

1111/rssc.12250.

Lee, Daniel D., and H. Sebastian Seung. 1999. “Learning

the Parts of Objects by Non-Negative Matrix Factor-

ization.” Nature 401 (6755): 788–91. https://doi.org/

10.1038/44565.

Miller, Andrew, Luke Bornn, Ryan Adams, and Kirk

Goldsberry. 2014. “Factorized Point Process Inten-

sities: A Spatial Analysis of Professional Basketball.”

arXiv:1401.0942 [Stat], January. http://arxiv.org/abs/

1401.0942.

Python, Andr

e, Janine Illian, Charlotte Jones-Todd,

and Marta Blangiardo. 2016. “A Bayesian Ap-

proach to Modelling Fine-Scale Spatial Dynamics

of Non-State Terrorism: World Study, 2002-2013.”

arXiv:1610.01215 [Stat], October. http://arxiv.org/

abs/1610.01215.

Sadykova, Dinara, Beth E. Scott, Michela De Dominicis,

Sarah L. Wakelin, Alexander Sadykov, and Judith

Wolf. 2017. “Bayesian Joint Models with INLA Ex-

ploring Marine Mobile PredatorPrey and Competitor

Species Habitat Overlap.” Ecology and Evolution 7

(14): 5212–26. https://doi.org/10.1002/ece3.3081.

Vavasis, Stephen A. 2007. “On the Complexity of Nonneg-

ative Matrix Factorization.” arXiv:0708.4149 [Cs],

September. http://arxiv.org/abs/0708.4149.

Wang, Yu-Xiong, and Yu-Jin Zhang. 2013. “Nonnega-

tive Matrix Factorization: A Comprehensive Review.”

IEEE Transactions on Knowledge and Data Engineer-

ing 25 (6): 1336–53. https://doi.org/10.1109/TKDE.

2012.51.

Visualization of Joint Spatio-temporal Models via Feature Recognition with an Application to Wildland Fires

239