Video Action Classiﬁcation through Graph Convolutional Networks

Felipe F. Costa

, Priscila T. M. Saito

and Pedro H. Bugatti

Department of Computing, Federal Unversity of Technology - Parana,

1640 Alberto Carazzai Ave., Cornelio Procopio, Brazil

Keywords:

Deep Learning, Graph Convolutional Network, Computer Vision, Action Classiﬁcation.

Abstract:

Video classiﬁcation methods have been evolving through proposals based on end-to-end deep learning archi-

tectures. Several works have testiﬁed that end-to-end models are effective for the learning of intrinsic video

features, especially when compared to the handcrafted ones. In general, convolutional neural networks are

used for deep learning in videos. Usually, when applied to such contexts, these vanilla deep learning networks

cannot identify variations based on temporal information. To do so, memory-based cells (e.g. long-short term

memory), or even optical ﬂow techniques are used in conjunction with the convolutional process. However,

despite their effectiveness, those methods neglect global analysis, processing only a small quantity of frames

in each batch during the learning and inference process. Moreover, they also completely ignore the semantic

relationship between different videos that belong to the same context. Thus, the present work aims to ﬁll these

gaps by using information grouping concepts and contextual detection through graph-based convolutional neu-

ral networks. The experiments show that our method achieves up to 87% of accuracy in a well-known public

video dataset.

1 INTRODUCTION

Nowadays, there is a high availability of complex data

like images and videos. To cope with this huge vol-

ume of complex data, new methods needs to be de-

veloped to automatically retrieve and/or classify these

data. Moreover, due to the evolution of hardware re-

sources (e.g., GPUs), it was possible to use proposed

algorithms that were previously costly like convolu-

tional neural networks (CNNs) for CPU architectures

(Krizhevsky et al., 2012).

The greatest advances in deep learning for pat-

tern recognition in images was the use of convolutive

cores of the CNNs. It occurs because they are capable

of learning deep features robust to noise, distortions

and translations in images. The CNN, in terms of ro-

bustness and precision, was a new level reached in the

state-of-the-art and have been widely used in machine

learning for computer vision (LeCun et al., 1998).

A CNN applies convolution layers to extract fea-

tures from the image (or video frame), generating

maps that can consider color channels and also reduce

the spatial dimensions of the image, and ﬁnally reach

https://orcid.org/0000-0002-7289-6032

https://orcid.org/0000-0002-4870-4766

https://orcid.org/0000-0001-9421-9254

a dense (fully connected) layer to perform the classi-

ﬁcation (end-to-end). This way of learning to extract

feature through convolutional kernels is clearly differ-

ent from obtain (handcrafted) features using a speciﬁc

image descriptor.

In recent years, as occurred in images, video clas-

siﬁcation techniques have been proposed using deep

learning (e.g., CNNs). However, the greatest difﬁ-

culty in working with videos is the time variable that

should be considered. This factor leads to several

problems such as changes in camera position, light-

ing, information variance due to the evolution of im-

age frames, among other complexities that the inclu-

sion of time adds to the relations of these sequential

static images.

Currently, the semantic characteristics of the

change in the temporal variable of videos are treated

by different ways in deep learning. There are so-

lutions that depend on CNNs to extract spatial fea-

tures from images, which are used as input to mod-

els that have temporal learning characteristics. Other

techniques apply long-short term memory structures

(Hochreiter and Schmidhuber, 1997), or even use in-

dependent CNNs for static images in conjunction with

optical ﬂow (Simonyan and Zisserman, 2014). How-

ever, all current methods do not capture and gather in

a well-suited fashion the context and interconnection

490

Costa, F., Saito, P. and Bugatti, P.

Video Action Classiﬁcation through Graph Convolutional Networks.

DOI: 10.5220/0010321304900497

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages

490-497

ISBN: 978-989-758-488-6

of videos (or frames) that relate to each other to as-

sist the learning process. Thus, to mitigate this prob-

lem, we proposed a method based on graph neural

networks (GNNs and variants) capable of connecting,

through different policies, the frames and/or videos

from a given context. These connections are seam-

lessly integrated into the learning process enhancing

the model in a great extent. Therefore, the present

work aims to propose approaches to perform such ag-

gregation of information and achieve improvements

regarding video classiﬁcation problems.

2 BACKGROUND

CNNs have been extremely successful in machine

learning problems in which the data representation

have a tensor structure (multidimensional) and need

robustness w.r.t. geometric transformations (invari-

ance and/or equivariance regarding translation, rota-

tion, among others).

There are two implications for equivariance, the

ﬁrst is the equivariance measurement (symmetry for

functions from one space with symmetry to another)

and the second is the invariance. For instance, a

given image I can be translated to I

(for the new

coordinates of (x

, y

)) with the original coordinates

, y

) through (x

− u, y

− v). Therefore, m

= m

is equivalent to the ﬁnal measurements of convolu-

tions (through geometric coefﬁcients from the convo-

lutional kernels). In other words, it means that the

location of a given object in the image should not be

static to be detected.

Although the CNNs present translational equivari-

ance and invariance they are not capable to establish

contextual connections between different objects or

images (e.g., frames from a video). As a matter of

fact, a core assumption of CNNs is that instances are

independent of each other. However, these connec-

tions are the cornerstones to reach a suitable context

recognition. Then, to aggregate such information to

the state-of-the-art CNNs we can use the Graph Neu-

ral Networks (GNNs).

GNNs (and their variants) are categorized in deep

learning as geometric models. The idea of these mod-

els is to work with multidimensional metrics consid-

ering the equivariance proposed by the CNNs. Just

as a convolution kernel consists of working with a

ﬁxed coefﬁcient of a geometric aspect in the image

(i.e., matrix of pixels), the GNN tries to general-

ize these ﬁlters by normalizing the distance between

points (e.g., pixels) in the non-euclidean space.

A variant of GNN is the so-called graph convolu-

tional network (GCN). The idea of a GCN architec-

ture is to use the automatic learning potential based

on convolution kernels to tackle problems with arbi-

trarily structured graph approaches. The proposal of

GCN was to bridge the gap between spectral-based

approaches and spatial-based approaches. Some

works proposed to generalize CNN models through

adaptations (Duvenaud et al., 2015; Li et al., 2016)

to allow non-euclidean spaces. Other works, using

the spectral graph theory (Bruna et al., 2014; Henaff

et al., 2015), deﬁned ﬁlters based on classic CNN.

However, we considered GCNs because the ﬁlters are

shared for the entire graph.

The goal of graph-based neural networks is to

learn a set of input signals from a graph G = (ν, ε)

with an adjacency matrix A and input matrix X

N×D

where N is the number of nodes and D is the number

of features (dimensionality). Each layer produces an

output Z

N×F

where F represents the number of fea-

tures per node. Thus, the linear Equation 1 can be

formally deﬁned:

(l+1)

= f (H

(l)

, A) (1)

where H

(0)

= X, Z = H

(l)

and l refers to the lth-layer.

It is possible to note that the deﬁnition is linear. How-

ever, to solve non-convex problems we need to con-

sider non-linearity. Then, a formalization to this is

given by Equation 2.

f (H

(l)

, A) = σ(AH

(l)

) (2)

where σ is a non-linear function (e.g., rectiﬁed linear

unit, sigmoid, among others), and W a weight matrix

per layer l that will be learned.

However, there is a problem in multiplying with

an adjacency matrix A. For each graph’s node the fea-

ture vectors of all its neighbors are aggregated, ex-

cept the node itself. To solve this issue, an identity

matrix I to the adjacency matrix A is considered, re-

sulting in

A. Another problem is that multiplying by

matrix A it will change the scale of the feature vec-

tors. To cope with this problem it is used the degree

matrix D where all the lines add up multiplying

by D

−1

. Then, Equation 3 formalizes the propagation

f (H

(l)

, A) in a normalized way.

f (H

(l)

, A) = σ(

−

(l)

) (3)

Regarding video classiﬁcation, several deep learn-

ing approaches are not only computationally expen-

sive, but also present problems w.r.t. the temporal

dimension. CNN models are well established to de-

scribe static images and applied in many video clas-

siﬁcation problems. However, they present several

problems related to the temporal reasoning. For in-

stance, vanilla CNNs does not consider global fea-

tures of the video. According to the literature, similar

Video Action Classiﬁcation through Graph Convolutional Networks

491

to images, there are two main approaches to perform

video classiﬁcation. The ﬁrst one is to obtain hand-

crafted features and the other to reasoning through a

deep learning model (deep features).

The handcrafted approaches consist of creating

descriptors, based on an a priori knowledge about

the problem, so that the learning model provides cor-

rect classiﬁcations. Generally, these works are based

on proposing new description methods (feature ex-

traction) in videos with compact dimensions, for in-

stance using Harris 3D outlines (Laptev, 2005), Hes-

sian measures (Dollar et al., 2005), cuboid model-

ing or even techniques that use optical ﬂow to extract

dense trajectories (Wang et al., 2011). These captured

features are normally passed to a histogram.

Generally, video classiﬁcation using deep learning

approaches considers end-to-end architectures (i.e.,

comprises the learning of deep features and the clas-

siﬁcation task at the same pipeline). There are sev-

eral techniques that can be used in video classiﬁcation

to create temporal semantics. However, several mod-

els present restrictions w.r.t. the number of frames

analyzed. For instance, 3D conversion networks (Ji

et al., 2013; Karpathy et al., 2014) can only apply

partial clips with frames to learn features from a sin-

gle tensor. In (Karpathy et al., 2014) the authors

demonstrated that their model is only a fraction better

than CNN when trained with individual frames from

a video. It is important to note that convolutions are

employed locally and limited to a few frames, due to

restrictions of huge tensors to be allocated in memory

at once.

Some other approaches made an effort to trans-

mit temporal information to the networks. For in-

stance, in (Simonyan and Zisserman, 2014) the au-

thors passes the optical ﬂow as an input parameter for

inference, limited to 10 frames only. However, this

model suffers from the same restriction problems of

local video information, since important information

from any frame may be lost. Moreover, it was not

so superior to a naive approach where single frames

passed to a 2D CNN.

Instead of trying to learn the spatio-temporal re-

sources limited to short-time periods, some works

aggregates CNNs with long-short term architectures

(LSTMs). It is consistent to use CNN architectures

to extract the features, and then apply them to LSTM

units. This allows to understand the patterns accord-

ing to the temporal variable (Baccouche et al., 2010).

However, LSTMs present high computational cost

and limited accuracies.

Other works (Yue-Hei Ng et al., 2015; Jain et al.,

2013) attempted to not use additional information, as

those provided by LSTM. They proposed variations

regarding the pooling layers at the video level to di-

minish the computational cost. Despite that, their ac-

curacies were similar to the LSTM approaches.

3 PROPOSED APPROACH

The motivation to our work is that, usually, the lit-

erature proposals neglect global analysis, processing

only short-time sequences due to computational costs.

Besides, they also ignore the semantic relationship

between different videos that belong to the same con-

text.

Thus, in this work we propose a new approach ca-

pable to create and explore the relationship between

different videos and/or frames of a given context, im-

proving the state-of-the-art results. To do so, we use

information grouping concepts and contextual detec-

tion through graph-based convolutional neural net-

works, and create a relationship between feature maps

from the videos.

Figure 1 shows the pipeline of our proposed ap-

proach. In step 1 we extracted deep features using a

given CNN architecture. Any CNN from the literature

can be used in this step. Moreover, to reduce the com-

putational cost, transfer learning (e.g., through Ima-

geNet) is also used, and frame sampling methods too.

To simplicity purpose we omitted these conditional

steps from Figure 1. Considering the step 2 each deep

feature vector is mapped into a graph node. In step

3 a relationship/connection policy is used to link the

graph nodes. Then, with the set of nodes and their

connections we generate an adjacency matrix to rep-

resent the global structure of the graph. It is important

to highlight that currently our approach consider only

undirected graphs. Finally, in step 4 we pass the adja-

cency matrix to a graph convolutional neural network

that consider the relationship between different nodes

to learn a model. Clearly, this pipeline describes the

training phase of our approach.

These are the general steps of our approach. How-

ever, different policies can be applied to each step.

Our ﬁrst policy is to extract features from a sample

of frames to diminish the computational cost. Frame

samplings are performed to consider regular exclu-

sion and frame selection intervals. For instance, if

there are F frames for a video and the intention to

get M frames (where F > M), then the ratio of F

to M is the increment value that will be used to se-

lect the frames (naive policy). After the selection of

frames per video, each one of them is given as input

to a CNN architecture, generating deep features. It

is important to note that in this step, several sampling

and/or clustering techniques from the literature can be

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

492

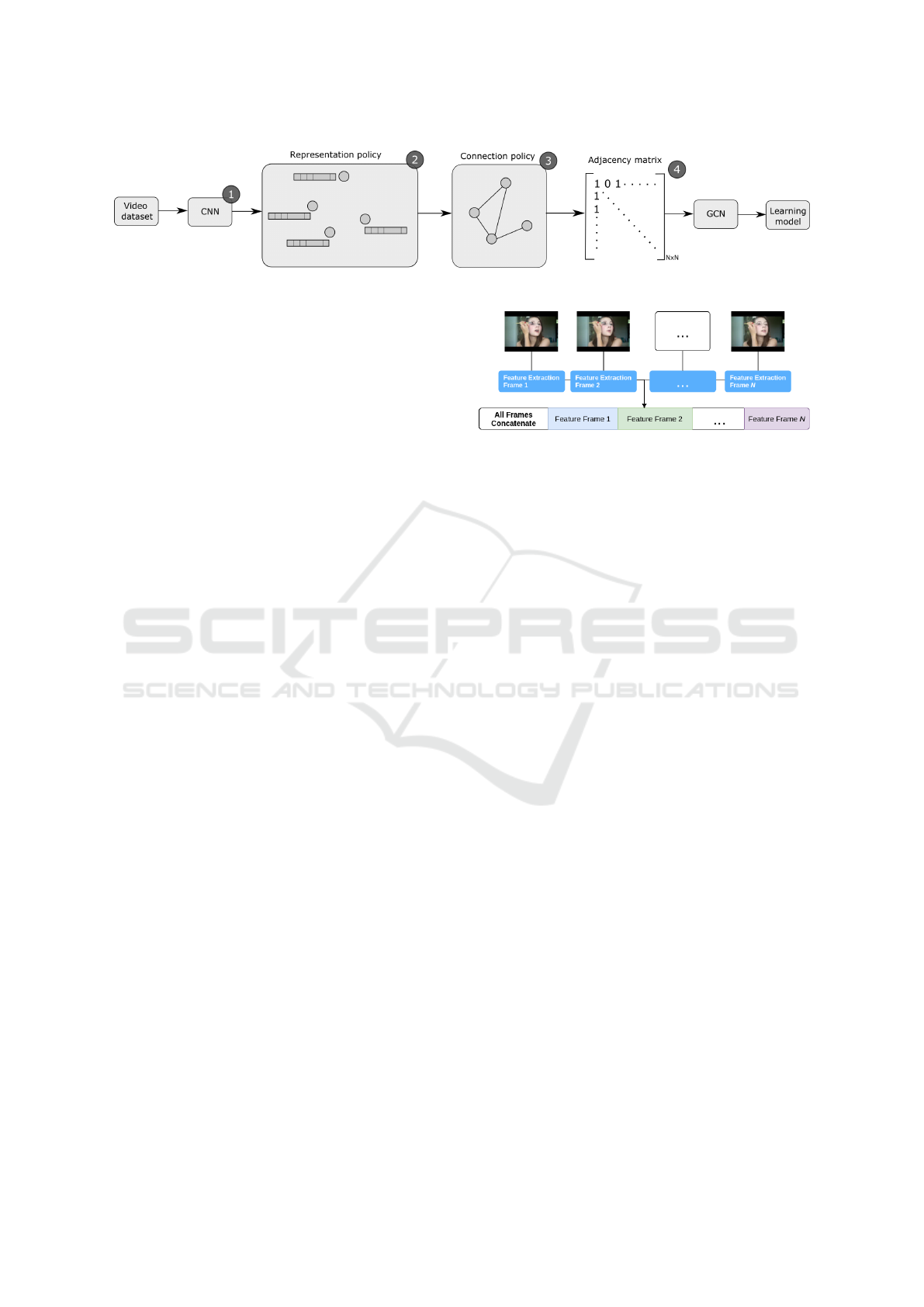
Figure 1: Pipeline of the proposed proposed aprroach.

used. To corroborate the efﬁcacy of our approach we

create baseline (naive policies) instances of it. We fol-

low this plan because several literature papers (Zhang

et al., 2019; Luo et al., 2018; Lu

ıs Estevam Junior

et al., 2019), when analyzing the trade-off between

computational cost and accuracy, indicated that the

simpler the method, the better the trade-off.

In the construction stage of the graph, our ap-

proach also allows different policies. We can use

different node representations, edges’ weighting and

connection/pruning strategies. Considering as input

to the construction stage the selected frames (e.g.,

sampling), and their respective features, we proposed

different node representations. The ﬁrst one is to con-

catenate each feature vector and then assign it to a

node (see Figure 2). In this policy each node has the

global representation of a video, and obviously, it will

impact in the nodes’ connection policies. It is easy to

see that many policies can be derived from our ap-

proach. For instance, instead of consider each node

as the entire video, we can represent each node by

a given frame from a video. It is interesting to note

that we can also join both policies, building an hierar-

chical representation of the videos as an hyper-graph.

Although this hierarchical policy is relevant, the fo-

cus of this work was in the proposal of the general

approach, since several policies can be derived and

exploited from it.

Regarding the nodes’ connections several policies

can also be applied. The most naive that we can

consider are self-connections of the nodes, that is,

connected only to themselves. The second one is to

consider a complete graph (i.e., connections between

all nodes). Another one is to build the connections

through a distance between the nodes (in our case the

dissimilarity between videos or frames depending of

the node representation policy).

Once we can use weighted connections between

the nodes this opens ways to pruning strategies. In

the present paper we consider naive dissimilarity mea-

sures (i.e., Euclidean distance) and pruning strategies

(i.e., threshold-based pruning) to testify the efﬁcacy

of our approach even with baseline policies against

the four literature methods. Clearly, the policies are

not mutually exclusive - e.g., we can aggregate two or

more policies to generate a new one.

Figure 2: Connection of Frames.

4 EXPERIMENTS

The experiments were performed considering four

comparison models, the LRCN (Donahue et al., 2014)

and C3D (Tran et al., 2014), which are based on three-

dimensional convolutions. They are robust models

and describe relevant tests and results in their respec-

tive works. In addition, experiments were carried out

with other two models known from the literature, one

using CNNs aggretated to LSTMs (Hochreiter and

Schmidhuber, 1997) and another one using a multi-

layer perceptron (MLP) (Murtagh, 1991).

The execution conditions were taken based on the

complexity of the CNN architectures. Then, we cho-

sen the ResNet50 architecture (He et al., 2015) pre-

trained on ImageNet (i.e., transfer learning) to extract

the deep features. The same features were used as

input to the models based on LSTM and MLP.

4.1 Video Dataset Description

To perform the experiments we used the UCF101

dataset (Soomro et al., 2012). It is public, widely-

known and used in several literature works to achieve

video action recognition. Another reason to chose

UCF101 is that it undergoes a small change in volume

of samples per class (balancing) and presents a real

scenario with 13320 video clips. Basically, it consists

of web videos that are recorded in unrestricted envi-

ronments and, generally, considering: camera move-

ment, various lighting conditions, partial occlusion

and low quality frames. The name UCF101 makes

reference to the number of classes that comprises in

a collection divided into 5 general action categories

(human-object, human-human interaction, only body

Video Action Classiﬁcation through Graph Convolutional Networks

493

Table 1: Experiment Settings.

Model Batch Size Frames Learning Rate Early Stopping

C3D 2 16 0.05 50

LCRN 76 10 0.05 50

MLP 128 3 0.05 50

LSTM 128 3 0.05 50

GCN (Ours) 39960 3 0.05 50

in motion, playing musical instruments and sports)

(Soomro et al., 2012).

The UCF101 dataset presents 180 frames on av-

erage, according to the duration and the frame rate

(25fps) of its videos. To perform the experiments, the

video memory of the GPU was limited to loading only

39,960 images as a total subset, both for testing and

training. It means that 3 frames were used to represent

a video (F = 3). This is a considerable restriction,

since each video from the dataset has 180 frames on

average. To obtain suitable results the approach needs

to capture effectively the contextual domain.

4.2 Scenarios

To accomplish fair comparisons we tune the same hy-

perparameters for all methods. Table 1 shows the hy-

perparameters considered for each method. Indeed,

just the batch size and the number of frames were

modiﬁed. This was needed because of the speciﬁca-

tions of some literature methods to be executed. For

instance, C3D and LRCN requires 16 and 10 frames,

respectively. Considering the LSTM-based method

and MLP we used 3 frames. It is important to note

that C3D and LRCN are not so ﬂexible as the others.

Both literature methods represent the entire videos as

one sample. Hence, for experiments we also consid-

ered that each graphs’ node is represented by the con-

catenation of the deep features from its videos’ frames

(node representation policy, see Section 3)

The batch size was deﬁned considering the mem-

ory restrictions. It is clearly to note that, as we are

using a vanilla GCN in our experiments, the entire

graph need to be into memory, then our batch size was

deﬁned as the number of graphs’ nodes (e.g., 39960

because we employ the node representation that con-

sider each node as video from the dataset).

The test and training proportions were made in or-

der to separate 60% of the dataset for training and

40% for testing. The same samples were used for all

methods.

4.2.1 Threshold-based Policy

Considering the threshold-based pruning policy (see

Section 3) we focused on manipulating the connec-

tion threshold of the adjacency matrix. First, we cal-

culated the Euclidean distance among nodes (repre-

sented by the feature vectors of the videos). Then, a

given connection is created when two videos have a

greater similarity than the average distance consider-

ing a complete graph (see Equation 4).

d =

∑

j=1

− v

)

(4)

where the adjacency matrix entry A(v

, v

) = 1 if d <

threshold, otherwise A(i, j) = 0.

We also considered dummy connections to sup-

port the proposed approach hypothesis. To do so, we

considered a complete graph construction policy and

a self-connection policy. Clearly, other dummy poli-

cies could be analyzed, such as a random construction

policy. However, this exhaustive analysis was not the

focus of the present paper.

4.3 Results and Discussion

According to the obtained results we can note that

our proposed approach not only provides a ﬂexible

way to apply different strategies and policies, but

also reached competitive accuracies when compared

with literature methods. Table 2 shows the accuracies

achieved by the literature methods against our pro-

posed approach considering different instantiations

of it. We considered 3 different instances of our

proposed w.r.t. the connection policies, that were:

complete graph, self-loop connections and threshold-

based (more details about these policies see Sections

3 and 4.2.1).

From Table 2 we can see that our approach with

the complete graph policy obtained better accuracy

than C3D and LRCN, reaching an accuracy gain of up

to 1.9 and 3.1 times higher, respectively. Analyzing

our approach with the threshold-based we achieved

87% of accuracy. Therefore, it was better than us-

ing the complete graph policy (65% of accuracy) and

MLP, presenting an accuracy gain of up to 34% and

19%, respectively. Finally, our approach considering

the self-loop connections policy obtained an accuracy

of 92%, that was the best one regarding all the other

methods. It is also possible to note that LSTM almost

ties with our approach.

Surprisingly, the dummy connection considering

self-loops presents the best accuracy. Analyzing this

result we can argue that the complete graph and

threshold-based policies still introduce some kind of

contextual noise to the learning process. This is also

the reason that a simple MLP also obtained a good

accuracy, because it just consider the input video w/o

connections. We believe that, as mentioned in (Wu

et al., 2019) by the authors, adding self-loops to the

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

494

Table 2: Models’ Accuracies.

Model Accuracy

C3D 33%

LRCN 21%

MLP 73%

LSTM 89%

Our approach - Complete Graph 65%

Our approach - Self-loop 92%

Our approach - Threshold-based 87%

graph shrinks the spectrum (eigenvalues) of the nor-

malized graph. In other words, the largest eigenvalue

of the graph becomes smaller. Hence, it is possible

to build more robust ﬁlters that does not degrade the

performance. However, we believe that deeper analy-

sis must be performed in the future to corroborate this

hypothesis considered in the present paper.

It is important to mention some results regarding

the early stopping variable and the number of epochs.

C3D, LRCN, LSTM and MLP, from a total of 1000

epochs, presented a saturation at the 691st, 431st,

250th and 300th epochs. Regarding GCN, since the

entire graph is allocated at memory, there is only one

batch per epoch. Then, we considered more epochs

because the weights are updated just when the en-

tire dataset is evaluated. It was deﬁned a limit of

4000 epochs. Considering the threshold-based pol-

icy approach the experiments were interrupted at the

3213rd epoch. On the other hand, when we applied

the complete graph and self-loop connections poli-

cies, an early stopping occurred 2500 times.

In order to provide a deeper analysis regarding

the accuracy results, we also generated the confu-

sion matrix of each method under analysis. To bet-

ter visualize the results, since UCF101 presents 101

classes, we applied a mapping function into the con-

fusion matrices considering a heatmap, i.e., the hotter

the color, the higher the accuracy (white is the hottest

color and black is the coldest). Figures 3 to 9 illus-

trate these heatmaps obtained from the confusion ma-

trices according to C3D, LRCN, MLP, LSTM, our ap-

proach w/ complete graph, self-loop connections and

threshold-based policy, respectively.

Analyzing the heatmaps is clear to note that

C3D and LRCN presented several errors in different

classes, these methods obtained the worst results in

classes with actions like “Playing”. It is also inter-

esting to see that all methods failed in classify im-

ages from the “Jump Rope” class. Maybe, it occurs

because of the subtlety of the “rope” object into the

images.

Figure 3: Heatmap obtained by C3D.

Figure 4: Heatmap obtained by LRCN.

Figure 5: Heatmap obtained by MLP.

Video Action Classiﬁcation through Graph Convolutional Networks

495

Figure 6: Heatmap obtained by LSTM.

Figure 7: Heatmap obtained by Our Approach w/ Complete

Graph.

Figure 8: Heatmap obtained by Our Approach w/

Threshold-based.

Figure 9: Heatmap GCN obtained Our Approach w/ Self-

loop

5 CONCLUSIONS

Video action recognition is a complex task. It also

presents high computational cost, because it requires

to deal with huge volume of data. Thus, it is im-

portant to reach the best trade-off between efﬁciency

and effectiveness. Therefore, this paper proposes a

new approach to create and explore the relationship

between different videos of a given context, improv-

ing the state-of-the-art regarding video action recog-

nition.

The proposed approach showed good results in the

classiﬁcation of actions in videos using GCNs. To do

so, graph connections were generated in a simple way

and with low computational cost, considering that the

model is fully loaded into memory. When compared

to models based on three-dimensional convolutional

ﬁlters, such as C3D and its variations, the proposed

approach provided better ﬂexibility w.r.t. representa-

tion mechanisms of the samples and higher accura-

cies.

The best results were reached using our approach

with one of the simplest policies (i.e., self-loop con-

nections), in which the computational cost to generate

the graph is extremely low. It is also important to con-

sider that models with more parameters tends to lead

to a higher time complexity. Moreover, they present

results that are often inferior and with a relatively bad

trade-off compared with our proposed approach (even

when comparing the amount of batches in memory

and the number of frames needed).

Despite the aforementioned factors, our approach

still presents some drawbacks. One of them concerns

the time to generate the graphs, since it is an expen-

sive task. However, this is an ofﬂine process, which is

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

496

generated only once. Of course, if there is an incre-

ment in the video dataset, the graph must be generated

again, but this factor affects any other classiﬁcation

method from the literature.

Thus, in general, the proposed approach proved

to be promising when compared with competing lit-

erature methods. In addition, it opens up many pos-

sibilities for future modiﬁcations, improvements and

analyzes. It is relevant to consider that it is possible

to try methods working in batch with models based

on geometric deep learning, providing other ways to

gain even more ﬂexibility.

ACKNOWLEDGEMENTS

This work was supported by Coordination for the Im-

provement of Higher Education Personnel (CAPES),

National Council of Scientiﬁc and Technological De-

velopment (CNPq), Fundac¸

ao Arauc

aria, SETI and

UTFPR.

REFERENCES

Baccouche, M., Mamalet, F., Wolf, C., Garcia, C., and

Baskurt, A. (2010). Action classiﬁcation in soccer

videos with long short-term memory recurrent neural

networks. In ICANN, pages 154–159. Springer Berlin

Heidelberg.

Bruna, J., Zaremba, W., Szlam, A., and Lecun, Y. (2014).

Spectral networks and locally connected networks on

graphs. In ICLR, pages 1–14.

Dollar, P., Rabaud, V., Cottrell, G., and Belongie, S. (2005).

Behavior recognition via sparse spatio-temporal fea-

tures. In PICCN, pages 65–72. IEEE Computer Soci-

ety.

Donahue, J., Hendricks, L. A., Rohrbach, M., Venugopalan,

S., Guadarrama, S., Saenko, K., and Darrell, T.

(2014). Long-term Recurrent Convolutional Networks

for Visual Recognition and Description. arXiv e-

prints, page arXiv:1411.4389.

Duvenaud, D. K., Maclaurin, D., Iparraguirre, J., Bom-

barell, R., Hirzel, T., Aspuru-Guzik, A., and Adams,

R. P. (2015). Convolutional networks on graphs for

learning molecular ﬁngerprints. In NIPS, pages 2224–

2232. Curran Associates, Inc.

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep Resid-

ual Learning for Image Recognition. arXiv e-prints,

page arXiv:1512.03385.

Henaff, M., Bruna, J., and LeCun, Y. (2015). Deep con-

volutional networks on graph-structured data. CoRR,

abs/1506.05163.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural Computing, 9(8):1735–1780.

Jain, M., J

egou, H., and Bouthemy, P. (2013). Better

exploiting motion for better action recognition. In

CVPR, pages 2555–2562.

Ji, S., Xu, W., Yang, M., and Yu, K. (2013). 3d convolu-

tional neural networks for human action recognition.

IEEE TPAMI, 35(1):221–231.

Karpathy, A., Toderici, G., Shetty, S., Leung, T., Suk-

thankar, R., and Fei-Fei, L. (2014). Large-scale video

classiﬁcation with convolutional neural networks. In

CVPR, pages 1725–1732.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In NIPS, pages 1097–1105. Curran Asso-

ciates, Inc.

Laptev, I. (2005). On space-time interest points. Interna-

tional Journal of Computer Vision, 64(2):107–123.

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. In Proceedings of the IEEE, pages 2278–2324.

Li, Y., Tarlow, D., Brockschmidt, M., and Zemel, R. S.

(2016). Gated graph sequence neural networks.

CoRR, abs/1511.05493.

ıs Estevam Junior, V., Pedrini, H., and Menotti, D.

(2019). Zero-Shot Action Recognition in Videos: A

Survey. arXiv e-prints, page arXiv:1909.06423.

Luo, Z., Jiang, L., Hsieh, J.-T., Niebles, J. C., and Li,

F. F. (2018). Graph distillation for action detection

with privileged information. In Proceedings of ECCV,

pages 1–18.

Murtagh, F. (1991). Multilayer perceptrons for classiﬁca-

tion and regression. Neurocomputing, 2(5):183 – 197.

Simonyan, K. and Zisserman, A. (2014). Two-stream con-

volutional networks for action recognition in videos.

In NIPS, pages 568–576. Curran Associates, Inc.

Soomro, K., Zamir, A. R., and Shah, M. (2012). Ucf101:

A dataset of 101 human actions classes from videos in

the wild. CoRR, abs/1212.0402.

Tran, D., Bourdev, L., Fergus, R., Torresani, L., and Paluri,

M. (2014). Learning Spatiotemporal Features with

3D Convolutional Networks. arXiv e-prints, page

arXiv:1412.0767.

Wang, H., Kl

aser, A., Schmid, C., and Liu, C. (2011). Ac-

tion recognition by dense trajectories. In CVPR, pages

3169–3176.

Wu, F., Souza, A., Zhang, T., Fifty, C., Yu, T., and Wein-

berger, K. (2019). Simplifying graph convolutional

networks. In ICML, pages 6861–6871. PMLR.

Yue-Hei Ng, J., Hausknecht, M., Vijayanarasimhan, S.,

Vinyals, O., Monga, R., and Toderici, G. (2015). Be-

yond Short Snippets: Deep Networks for Video Clas-

siﬁcation. arXiv e-prints, page arXiv:1503.08909.

Zhang, H.-B., Zhang, Y.-X., Zhong, B., Lei, Q., Yang, L.,

Du, J.-X., and Chen, D.-S. (2019). A comprehen-

sive survey of vision-based human action recognition

methods. Sensors, 19:1005.

Video Action Classiﬁcation through Graph Convolutional Networks

497