Grocery Recognition in the Wild:
A New Mining Strategy for Metric Learning
Marco Filax, Tim Gonschorek and Frank Ortmeier
Chair of Software Engineering, Otto-von-Guericke-University, Magdeburg, Germany
Keywords:
Grocery Recognition, Few-Shot Learning, Assistive Computer Vision, Features Extraction.
Abstract:
Recognizing grocery products at scale is an open issue for computer-vision systems due to their subtle visual
differences. Typically the problem is addressed as a classification problem, e.g., by learning a CNN, for
which all classes that are to be distinguished need to be known at training time. We instead observe that the
products within stores change over time. Sometimes new products are put on shelves, or existing appearances
of products are changed. In this work, we demonstrate the use of deep metric learning for grocery recognition,
whereby classes during inference are unknown while training. We also propose a new triplet mining strategy
that uses all known classes during training while preserving the ability to perform cross-folded validation. We
demonstrate the applicability of the proposed mining strategy using different, publicly available real-world
grocery datasets. The proposed approach preserves the ability to distinguish previously unseen groceries
while increasing the precision by up to 5 percent.
1 INTRODUCTION
Product recognition is subject to many researchers’
works (Merler et al., 2007; George and Floerkemeier,
2014; Baz et al., 2016; Mittal et al., 2018; Tonioni and
Di Stefano, 2017; Varadarajan and Srivastava, 2018).
It was used in different settings, e.g., to track the
user’s attention (Rallapalli et al., 2014) or guide vi-
sually impaired people (Winlock et al., 2010; Franco
et al., 2017). Typically, the goal is to predict a gro-
cery product’s fine-grained class from a single image.
All classes that shall be predicted need to be known
at training time if the problem is addressed in a clas-
sification manner. That means all grocery products
need to be known at training time, i.e., all stock keep-
ing units (SKUs) that are to be recognized. Grocery
recognition, however, embodies three major aspects
differentiating the problem from standard classifica-
tion tasks.
First, layouts of grocery items change over time.
The appearance of products is an active area of
research (Mumani and Stone, 2018). (Rettie and
Brewer, 2000) pointed out that 73 percent of the pur-
chase decisions are made at the point of sale. This fact
indicates that visual elements of packaging are an im-
portant aspect to increase sales. This justifies the em-
pirical observation that the visual layouts of grocery
items change over time. A learned classifier would
need to be fine-tuned continuously to distinguish gro-
cery products in the wild.
Second, the number of different classes in the
wild is potentially larger than in academic datasets.
Grocery product datasets contain currently up to
50.000 different classes (Cheng et al., 2020). How-
ever, widely used broad datasets, e.g., the Ima-
geNet database, comprise 21.841 different non-empty
classes, but typically only 1000 classes are used to
train modern deep neuronal networks. A grocery
recognition system, however, must be able to distin-
guish potentially millions of products.
Third, the number of classes grows continuously.
This makes it impossible to recognize new products
in the classification setting because the classes are not
available during training time. Grocery recognition
renders to be an open-set (Bendale and Boult, 2016)
problem. A well-known example of an open-set prob-
lem is face matching (Schroff et al., 2015) in which
images of unseen individuals during operation need
to be matched. Standard classifiers cannot be used for
open-set problems.
These three properties motivate us to revisit the
grocery recognition problem. In contrast to existing
approaches, we address the problem as an open-set
problem (Bendale and Boult, 2016), in which training
and test sets have disjoint classes, e.g., completely dif-
ferent products, that, however, sometimes share large
498
Filax, M., Gonschorek, T. and Ortmeier, F.
Grocery Recognition in the Wild: A New Mining Strategy for Metric Learning.
DOI: 10.5220/0010322304980505
In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages
498-505
ISBN: 978-989-758-488-6
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Barnes-Hut-SNE visualization of R
D
. Samples are drawn from T
t
of the Magdeburg Groceries dataset. These SKUs
were unknown at training time. We observe that similar grocery products are mapped to clusters in the embedding space,
indicating separability. They form relatively dense regions, although there are some mislabeled patches. Further, products
that share large amounts of visual elements, e.g., similar cereals of different weights, are mapped to close overlapping regions.
visual similarities due to the fine-grained nature of
groceries. We tackle the problem from a metric learn-
ing perspective in which we ultimately evaluate the
similarity of image patches, e.g., the similarity of a
reference image, which was taken under studio con-
ditions, and images taken in the sales area.
An exemplary application of the learned image
patch embeddings is depicted in Figure 1. It depicts
a Barnes-Hut-SNE (van der Maaten, 2013) visualiza-
tion of the Magdeburg Groceries (Filax et al., 2019)
test set. All SKUs are unknown during training time.
The embeddings produce dense clusters if the prod-
ucts do not share visual similarities. The clusters are
scattered if subtle visual differences can only distin-
guish the products
The contribution is two-folded: On the one hand,
we use metric learning for distinguishing the fine-
grained visual differences of grocery products to miti-
gate the problems described above. We employ an on-
line triplet matching learning, in which a model shall
produce an embedding for an SKU image, which is
similar to embeddings generated from other images
of that SKU.
On the other hand, we propose a new mining
strategy that yields better results on multiple datasets
while being compatible with cross-folded validation.
We compare the proposed strategy with the de facto
standard mining strategy. We argue that the proposed
strategy can be used with different metric learning ap-
proaches that use other loss functions.
The remainder of this work is structured as fol-
lows. In the following section, we summarize existing
approaches and argue that these tackle the problem in
a standard classification manner. We describe our pro-
posed approach in Section 3 and propose a new triplet
sampling strategy. We present findings from our ex-
periments with three grocery datasets in Section 4 and
evaluate the best model under real-world constraints.
We conclude our work in Section 5.
2 RELATED WORK
Fine-grained product recognition came to the atten-
tion of the scientific community in 2007. (Merler
et al., 2007) published a dataset consisting of different
synthetic items and real-world videos of one particu-
lar grocery store. The authors were the first to eval-
uate the performance of SIFT (Lowe, 1999) in this
recognition setting. (Mittal et al., 2018) proposed a
hierarchical approach. Their idea is to classify lo-
gos using SIFT first before refining this information
to identify the particular item. In (Baz et al., 2016;
Tonioni and Di Stefano, 2017), the authors proposed
a similar system that includes the spatial relation be-
tween the products on the shelves.
Man-Made features seemed insufficient for fine-
grained recognition because datasets were rather lim-
ited, and the overall accuracy was not saturated.
Learned classification systems gained more attention.
(George and Floerkemeier, 2014) proposed a hybrid
system based on a learned classifier. The idea is to di-
vide an image into different equally sized grids. These
Grocery Recognition in the Wild: A New Mining Strategy for Metric Learning
499

regions are fed into a CNN to predict a class. The
authors use SIFT features to localize individual in-
stances within the classified cells.
Another hybrid system elevates the observa-
tion that grocery products consist of colorful re-
gions (Karlinsky et al., 2017). The authors use Dens-
eSIFT (Wang et al., 2010) features to generate possi-
ble item hypotheses and classify them with a VGG-
like (Simonyan and Zisserman, 2015) model.
In (Franco et al., 2017), the authors proposed to
exploit another observation: many products have cor-
ners. The authors generate item hypothesizes based
on corner detections. These hypotheses were used to
predict a class using a CNN.
Other authors use specific properties of gro-
cery products, such as scene text (George et al.,
2015; Xiong and Grauman, 2016), multiple views
for training (Bastan and Yilmaz, 2016) or try to
tackle the problem in an end-to-end learning proce-
dure (Varadarajan and Srivastava, 2018). These re-
lated works classify groceries. Tackling the problem
as a classification problem holds the inevitable as-
sumption that all SKUs are known at training time.
These works neither address unknown classes during
test time nor rapidly changing products’ visual ap-
pearances.
An exception to this gap is (Tonioni et al., 2018)
and (Tonioni and Di Stefano, 2019). We consider
these works to share the most similarities with our ap-
proach because the authors also propose to learn an
embedding function similar to ours. In both works,
the authors use triplets to learn an embedding func-
tion, but on closed datasets. The actual triplet min-
ing strategy is not elaborated. It is to assume that
the default sampling methodology was used (cf. Sec-
tion 3.3.1). As suggested in (Wu et al., 2017), triplet
mining has an immense impact on the accuracy of the
system. We believe that the impact of the actual strat-
egy needs to be evaluated on publicly available large-
scale datasets.
3 DISTINGUISHING GROCERIES
We tackle finding corresponding items within gro-
cery stores as an open set recognition (Scheirer et al.,
2013) problem, in which a fixed, finite set of known
classes does not exist. Recognizing groceries means
to encounter unknown SKUs at some time. The pro-
posed recognition system purely relies on patches’
similarities, namely a single example acquired from
the web and multiple examples from the sales floor.
Examples are shown in Figure 1.
The major steps to solve this problem are the over-
all design of an embedding function, which is learned
with the training goal definition, the loss function.
The approaches’ overall performance is dependent on
the triplet mining strategy (Wu et al., 2017).
3.1 Embedding Function
Face recognition (Schroff et al., 2015) renders to be
similar to fine-grained grocery recognition with the
goal to learn an embedding function f
θ
(x) : R
n×n
→
R
D
. f
θ
(x) is parameterized by θ and transforms dif-
ferent images from R
n×n
of the same grocery product
to metrically close points on the manifold R
D
. Sim-
ilarly, f
θ
(x) transforms images of different SKUs to
metrically distant points on R
D
.
Images of SKUs in the wild contain various
noises, e.g., rotational and affine transformations or
color shifts. f
θ
(x) needs to be invariant to these trans-
formations. Therefore, it is composed of a CNN.
We adopt (Deng et al., 2018) used for face recog-
nition and choose a ResNet-50 (He et al., 2016) as
the base network, remove the final layer, and replace
the average pooling layer with a maximum pooling
layer. Directly after this, we employ a batch normal-
ization layer (Ioffe and Szegedy, 2015), followed by
a dropout layer (Srivastava et al., 2014), and a fully
connected embedding layer, which is followed by an-
other batch normalization layer (Ioffe and Szegedy,
2015).
3.2 Loss Function
We deploy a triplet loss function and learn an em-
bedding between the input space and the embedding
space directly. The vanilla triplet loss (Schroff et al.,
2015) is described as
L(θ) =
∑
a,p,n
y
a
=y
p
6=y
n
[m + D
a,p
− D
a,n
]
+
(1)
where D
f
θ
(x
i
, x
j
) = || f
θ
(x
i
) − f
θ
(x
j
)||
2
2
and [m + •]
+
is the rectifying hinge function with a margin param-
eter m that determines the desired distance between
positive and negative image pairs in N-dimensional
Euclidean space. x
a
, x
p
, x
n
represent an anchor x
a
,
a positive sample x
p
and a negative sample x
n
from
R
n×n
. x
a
and x
p
depict the same SKU and shall pro-
duce close points on R
D
. x
a
and x
n
are different items
and shall produce more distant points than x
a
and x
p
.
(Hermans et al., 2017) pointed out, that the num-
ber of possible triplets, which are sampled using an
offline triplet mining strategy, e.g., as deployed in the
vanilla triplet loss (Schroff et al., 2015), grows cu-
bically. This prevents training from converging fast
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
500

because many triplets are uninformative during later
epochs. The authors proposed to sample triplets in an
online manner and approximate the training goal from
small batches of data. These batches need to be care-
fully designed to maximize the information f
θ
(x) can
learn from. The maximal information can be acquired
from hard triplets, that might result in sublime false
predictions. Selecting only hard triplets oversamples
possible outliers and prevents f
θ
from converging.
Thus, it is vital to sample hard and easy triplets, so-
called moderate triplets, that are the hardest among a
small subset of data (Hermans et al., 2017; Wu et al.,
2017).
We follow the idea of online triplet sampling and
adopt the loss function initially described in (Hermans
et al., 2017). Our loss shall pull positive samples as
close as possible together. We eliminate the margin
parameter and have to rely on a different hinge func-
tion: the softplus. The loss is described as
L(θ, B ) =
Y
∑
i=1
K
∑
a=1
[log(1 + exp( max
p=1..K
(D
f
θ
(x
i
a
, x
i
p
))−
min
j=1..C
n=1..K
i6= j
(D
f
θ
(x
i
a
, x
j
n
))))]
(2)
with B being a batch of images, Y is the set of classes.
K is the number of samples drawn for every class.
3.3 Triplet Mining
Mining moderate triplets is important for good con-
vergence (Hermans et al., 2017; Wu et al., 2017). In
the following, we describe two strategies to select im-
ages to form mini-batches. We sample images into
a mini-batch b ∈ B based purely on their class. The
very basic idea is based on two different types of slic-
ing the dataset. The state-of-the-art method is to slice
a given dataset into two disjoint sets by splitting all
classes Y into two sets. We propose to split the dataset
by X except for the test set. This dataset split pre-
serves cross-validation ability as it consists of three
subsets - train, validation, and test - while allowing
the embedding function to be trained on substantially
more classes. This is because the number of classes
in the train and validation set are identical. The test
set is completely disjoint from the train and validation
set. In this work, the set of classes in the test sets, as
well as the individual samples per class, are identical
for both mining strategies. Let the dataset be given by
T = {(x, y) | x ∈ X ∧y ∈ Y } (3)
where X ⊂ R
n×n
is the set of images, and Y the set of
all classes.
We preserve a set of classes for evaluation to sup-
port the fact that grocery products’ visual appearances
change over time, and new products are created. We
split the set of classes Y in two disjoint classes Y
t
and
Y
l
such that Y = Y
t
∪Y
l
and Y
t
∩Y
l
=
/
0. We want to
point out that X is also split into two disjoint classes
X
t
and X
l
because every image has exactly one class.
Our test set is defined as
T
t
= {(x, y) | x ∈ X
t
∧ y ∈ Y
t
}. (4)
T
l
is the remaining data for training and validation. T
l
is defined as
T
l
= {(x, y) | x ∈ X
l
∧ y ∈ Y
l
}. (5)
T
t
is used for testing and fixed for every dataset to
ensure comparability in this work’s experiments.
3.3.1 Triplet Mining over Y
The default approach to sample triplets is to generate
disjoint sets of classes and use them to train and test
a model. Using the same set to tune the hyperparam-
eters and evaluate the model can be flawed.
We use separate training, validation and test sets
and split Y
l
into Y
train
and Y
val
. Y
train
is used to train
the embedding function. Y
val
is used to tune the hy-
perparameters such that the embedding function gen-
eralizes to unseen classes. T
train
and T
val
are defined
as
T
train
= {(x, y) | x ∈ X
l
∧ y ∈ Y
train
} (6)
and
T
val
= {(x, y) | x ∈ X
l
∧ y ∈ Y
val
}. (7)
Both are constructed such that Y
l
= Y
train
∪ Y
val
and
Y
train
∩Y
val
=
/
0. These disjoint sets w.r.t. their image
classes shall be used to sample batches for training
and validation tasks.
For online triplet mining, it is important to sam-
ple images from s different classes. We sample k
instances for every class to mitigate the influence of
outliers, whereas k ≥ 2. A training batch B
train
is con-
structed as
B
train
=
s
[
j=1

(x
i
, y
j
) | x
i
∈ X
l
∧y
j
∈ Y
train
∧0 < i < k

(8)
and a validation batch B
val
as
B
val
=
s
[
j=1

(x
i
, y
j
) | x
i
∈ X
l
∧ y
j
∈ Y
val
∧ 0 < i < k

.
(9)
Every class’s first sample is used as the anchor
and the other k − 1 as positive and negative exam-
ples. Using this sampling strategy, we train the em-
bedding function such that it is capable of distinguish-
ing images in T
l
. Further, we tune the hyperparame-
ters based on T
val
.
Grocery Recognition in the Wild: A New Mining Strategy for Metric Learning
501

3.3.2 Triplet Mining over X
We propose splitting the dataset T
l
into disjoint sets
based on the number of samples across all classes. As
shown in Equation 3, we assume that the given dataset
consists of Y , and each class Y
i
comprises multiple
x ∈ X
i
with X
i
∈ X
l
and Class(X
i
) = Y
i
. We exploit
this property to sample from X
l
. We split all images
that belong to Y
l
into two disjoint sets, such that
T
train
= {(x, y) | x ∈ X
train
∧ y ∈ Y
l
} (10)
and
T
val
= {(x, y) | x ∈ X
val
∧ y ∈ Y
l
} (11)
whereas X
l
= X
train
∪ X
val
and X
train
∩ X
val
=
/
0 .
We sample batches by drawing s different classes
and selecting k ≥ 2 samples per class. The first sample
of every class serves as an anchor, and the others form
positive and negative samples. We construct training
batches B
train
and validation batches B
val
such that
B
train
=
s
[
j=1

(x
i
, y
j
) | x
i
∈ X
train
∧y
j
∈ Y
l
∧0 < i < k

(12)
and
B
val
=
s
[
j=1

(x
i
, y
j
) | x
i
∈ X
val
∧ y
j
∈ Y
l
∧ 0 < i < k

(13)
These two sampling strategies are used to train an
embedding function using the loss function described
in Equation 2.
4 EXPERIMENTS
We validate the feasibility of the proposed triplet min-
ing strategy with three databases from the given use
case of product recognition. All experiments are ex-
ecuted following a strict test protocol with disjoint
classes for test and training purposes. According to
the two different mining strategies, we train the em-
bedding functions, i.e., mining over Y and mining
over X, as described in the previous section. We con-
sider the strategy mining over Y as the default min-
ing strategy described in related works and compare
it with the proposed mining over X strategy. In our
experiments, we preserve a specific set of classes for
testing T
t
. T
t
is disjoint with T
l
. T
t
is fixed across
all experiments with a dataset, i.e., we use the same
classes to test differently trained embedding func-
tions.
We conduct the experiments with the three differ-
ent databases: Stanford Online Products (Song et al.,
2016), Magdeburg Groceries (Filax et al., 2019), and
AliProducts (Cheng et al., 2020). We report the mean
Recall@k for k = [1, 2, 4, 8] for a standard retrieval
task using the Euclidean distance. All experiments
are executed in a three cross-fold manner to preserve
comparability. We resize all images to a fixed size
of 128x128 pixels for the sake of computational effi-
ciency.
The Stanford Online Products database (Song
et al., 2016) consists of 120.053 images of 22.634 dif-
ferent fine-grained classes. We preserve 3671 classes
for testing and treat the fine-grained products - and not
the broader categories - as individual classes for all
experiments. The remaining 18.963 product classes
are used to train different embedding functions.
Further, we use another real-world grocery prod-
uct dataset (Filax et al., 2019). The Magdeburg Gro-
ceries dataset consists of 23.360 different grocery
product classes. The dataset is two-folded: it holds
product images taken under controlled conditions and
41.955 images taken in the wild. The reference prod-
uct images were collected from the web and typically
contain only the product and white background. The
other images are taken in an unrestricted manner: they
depict 871 different product classes on shelves with
fine-grained bounding box annotations. In this work,
we are using both types of images. 871 web images
serve as anchors, and over 524.500 crops of individ-
ual grocery products from various angles will provide
positive and negative samples. 171 classes are used as
T
t
.
The AliProducts (Cheng et al., 2020) dataset holds
2.700.772 images with 50.030 different SKUs. This
dataset is considered to be noisy because it was
mainly crawled from the web. The authors released
dedicated training, validation, and test splits, how-
ever, with overlapping SKUs. The latter two were
manually annotated. This particular type of dataset
split suffers from the defects described previously:
other products, such as new ones, cannot be distin-
guished if a classifier is used. We rearrange these
splits by randomly choosing 3671 SKUs that will be
used for testing. The remaining set of images T
l
was
split as described in Section 3.
4.1 Mining Strategies
We use both triplet mining strategies, presented in
Section 3, to train embedding functions and evaluate
their performance. We split every dataset just as de-
scribed: We split T in T
t
and T
l
and randomly select
SKUs with their images as T
t
. T
t
is fixed for every
dataset and identical for the different mining strate-
gies. T
t
and T
l
are disjoint. T
l
is split into three
disjoint folds to conduct our experiments in a cross-
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
502

Figure 2: Three examples from the Magdeburg Groceries
dataset. The first column depicts the query image, whereas
the remaining four columns depict the top-4 nearest neigh-
bors from T
t
. All SKUs were unknown during training.
validation manner whereby we combine two folds as
T
train
and use the remaining fold as T
val
w.r.t. the min-
ing strategy.
The majority of hyperparameters remain fixed
throughout all experiments and are derived from re-
lated works. The base network is derived from a
ResNet-50 (He et al., 2016). After the last convolu-
tional layer, we add a global max pooling layer. We
follow (Deng et al., 2018) and employ a BN-Dropout-
FC-BN structure for the embedding network. We
set the dropout rate to 0.6 for all of our experiments
and train the models with an embedding dimension of
256. All models are trained with Adam (Kingma and
Ba, 2019), a batch size of 170, k = 3, and a learn-
ing rate of 5 × 10
−4
without decay. We train the em-
beddings functions for 200, 800, 1000 epochs for the
Stanford Online Products, AliProducts and Magde-
burg Groceries dataset, respectively. The base net-
work is initialized with ImageNet weights and tuned
after a small initialization phase. We use the same hy-
perparameters for the experiments with the proposed
mining over X strategy.
Figure 2 depicts three different qualitative exam-
ples from the Magdeburg Groceries database. We de-
pict different, randomly sampled query images in the
first column drawn from the test set T
t
. All queries are
taken from real shelves and the retrievals are drawn
from the set of reference images to represent a real-
world use case. Exactly one positive retrieval is pos-
sible per query because we have precisely one true
positive per class. The top-4 retrievals are shown in
the remaining four columns per row. The dataset was
collected in a semi-automatic approach and suffers
from some labeling artifacts. This can be why it is
not always possible to retrieve the true, correct sam-
ple from the dataset. The embedding function was
able to retrieve a sufficiently large number of correct
samples. We see from the different top-k retrievals
that they typically can only be distinguished through
fine-grained graphical elements. This is especially of
interest as products were completely unknown dur-
ing training. An example of this is shown in the
first row: these different products can only be dis-
tinguished through the actual dog breed, which only
occupies a small portion of the product.
In total, we trained 18 embedding functions on
three different datasets to acquire a quantitative grasp
of the solution. We report the mean Recall@k for
the individual datasets. Table 1 depicts the average
Recall@k for standard retrieval tasks on the three dif-
ferent datasets. X and Y stand for the respective min-
ing strategy - mining over X and mining over Y . In all
three datasets, we observe that the standard approach
could be outperformed by at least 1% Recall@1. For
the Magdeburg Groceries datasets, we see a dramatic
increase of almost 5%. We conclude that the proposed
mining strategy, mining over X, can produce better re-
sults than the standard approach what is surprising es-
pecially because of the simplicity of the approach. We
see that the embedding functions trained with the min-
ing over X strategy are superior to functions trained
with mining over Y from our experiments. Note that
the underlying data structure does not change, except
for the total amount of classes available to train each
embedding function. We assume that this fact justi-
fies the performance gain w.r.t. Recall@k. With the
proposed mining strategy, we can train the embedding
functions from more classes than with traditional ap-
proaches because a subset of Y is preserved for val-
idation in the latter case. One could of course omit
the validation set to increase the overall amount of
Table 1: Recall@k in % from the test set T
t
with three
different datasets. We report the average recall over k =
[1, 2, 4, 8] of three models trained in a three-fold cross-
validation procedure per dataset and mining strategy. We
conclude that the triplet mining over X performs slightly
better than the standard sampling technique to mine over Y.
Recall@
1 2 4 8
Stanford Online Products
X 58.05% 64.36% 69.31% 73.88%
Y 57.45% 63.51% 68.63% 73.52%
Magdeburg Groceries
X 70.72% 82.56% 87.50% 90.97%
Y 65.08% 77.35% 84.29% 88.64%
AliProducts
X 78.04% 85.22% 88.07% 89.38%
Y 76.50% 84.39% 87.61% 89.35%
Grocery Recognition in the Wild: A New Mining Strategy for Metric Learning
503

classes in Y . This, however, is prone to overfit as
the learned embedding functions might perform sig-
nificantly worse in the wild. Omitting the validation
set completely, say to increase the number of SKUs
in T
train
, is prone to overfitting and might prevent
the embedding function from performing reasonable
good in the wild.
The results demonstrate that the usage of triplets
to distinguish products and groceries works suffi-
ciently well. This is because we distinguish com-
pletely unknown products that share large visual sim-
ilarities. We believe that this is possible due to
the nature of the data structure in these fine-grained
datasets. We observe that there are fine-grained
classes in the T
train
as well as fine-grained classes in
T
t
. It is to assume that the given model generalizes
to the overall use case of distinguishing grocery prod-
ucts in the wild, i.e., to unseen classes beyond T
t
.
4.2 Groceries in the Wild
Distinguishing groceries means to encounter un-
known SKUs that share large visual similarities with
already known products. It is inevitable to design a
recognition system such that it can correlate unseen
SKUs. But that also means not to purely distinguish-
ing unknown products. A strict evaluation protocol,
such as deployed above, underestimates the actual
performance in the wild if T
t
has probes that were
not used to train the models but belong to previously
available SKUs. In this setting, we perform an ad-
ditional experiment to evaluate the best embedding
function under real-world constraints.
In the real world, we assume that there is an om-
nipresent set of SKUs. That means that some of the
SKUs, known at training time, are also known at in-
ference time. In the following, we evaluate the per-
formance of the best embedding function under this
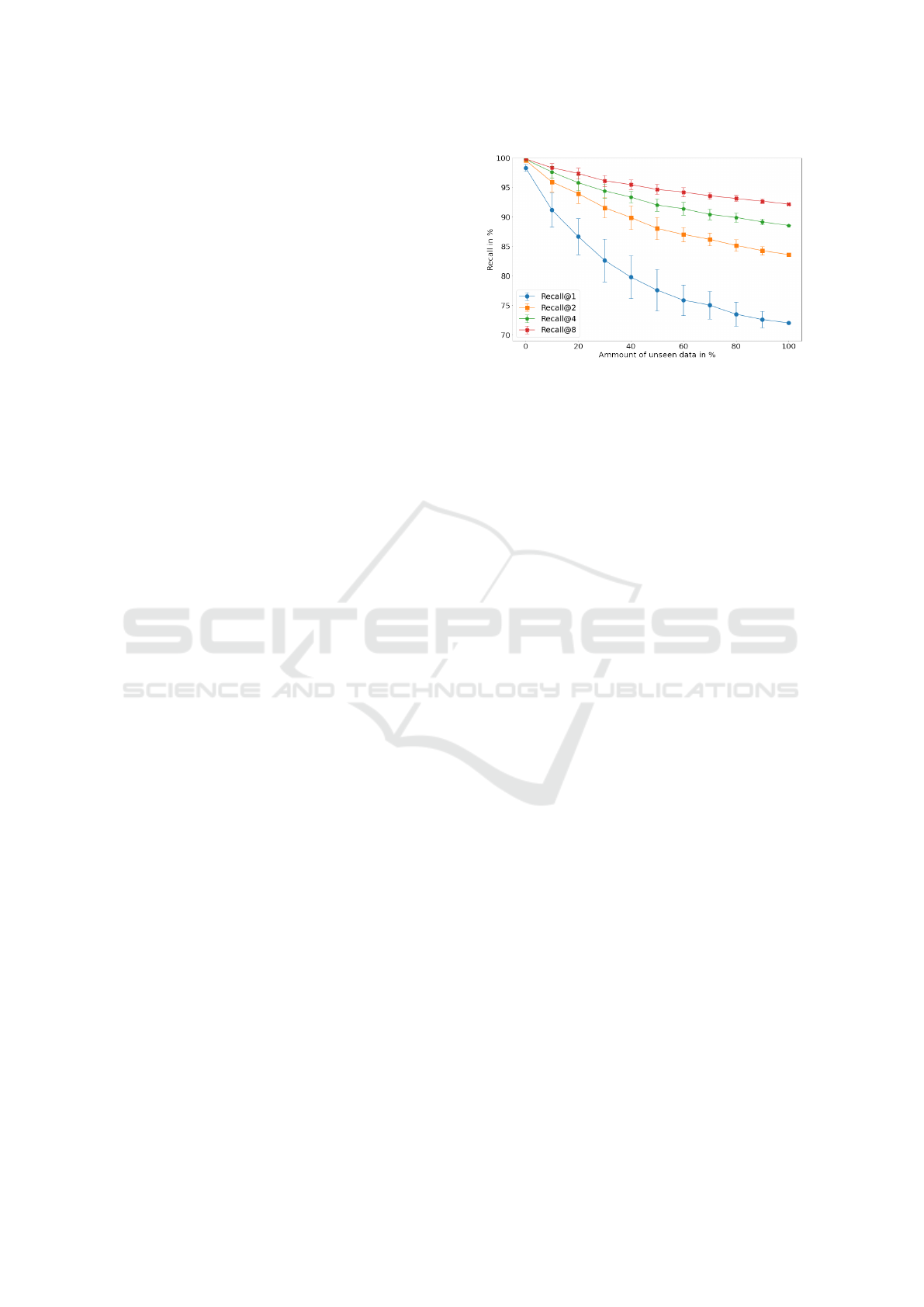
assumption. The results are depicted in Figure 3.
We exemplary select the Magdeburg Groceries
dataset and evaluate the best embedding function
trained with the proposed mining over X . We sample
unknown SKUs from T
t
and known SKUs from T
val
in 10% percent steps, such that the mixtures consist of
various percentages of unknown objects. The remain-
ing known classes are drawn from T
val
. As the con-
crete performance is subject to the fine-grained nature
of SKUs, and dependents on the SKUs that share sim-
ilarities, we sample 100 different mixtures per step.
Figure 3 depicts the Recall@k for k = [1, 2, 4, 8]
for this experiment. We observe that Recall@k is
superior to the results reported with the strict pro-
tocol if we use known SKUs during inference. The
performance of an embedding function in the wild is
Figure 3: We evaluate the generalization capabilities of the
best f
θ
(x) trained with triplet mining over X on the Magde-
burg Groceries dataset. We compute the Recall@k for dif-
ferent mixtures of known and unknown SKUs drawn from
T
val
and T
t
. We observe that the Recall@k decreases as the
amount of known SKUs decreases.
strongly related to the mixture of known and unknown
SKUs during inference. If the products in the wild
are mostly known at training time, the results increase
such that the Recall@1 is larger than 95%. Using em-
beddings to distinguish grocery products works suffi-
ciently well in general, but even better the more SKUs
are already known at training time.
We conclude that using embeddings can produce
comparable results to standard classification solutions
but can also be used to distinguish unseen SKUs.
If the amount of unknown products is substantially
large, we await comparable results to traditional clas-
sifiers. However, using embeddings should perform
better as traditional classifiers if the amount of un-
known SKUs is large enough, as traditional classifiers
are condemned to predict invalid results for unknown
SKUs.
5 CONCLUSION
In this work, we distinguish fine-grained grocery
products in the wild. We use metric learning, for
which we use triplets to learn an embedding function
and ultimately estimate the visual similarities of im-
age patches. The chosen approach allows us to deter-
mine the subtle visual differences of previously un-
known SKUs. Standard approaches, such as tradi-
tional classifiers, would need to be retrained to per-
form similar tasks. Metric learning for grocery recog-
nition overcomes this issue.
We propose a new sampling metaphor that uses
multiple samples per class to increase the total num-
ber of classes useable for training. We demon-
strate that the proposed mining strategy increases the
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
504

Recall@1 compared to the standard approach by up
to 5%. We evaluate the performance of a trained em-
bedding function in the wild, e.g., in different mix-
tures of known and unknown SKUs. We conclude that
the proposed approach, combined with the proposed
mining strategy, can distinguish grocery products in
the wild - even if they are unknown at training time.
REFERENCES
Bastan, M. and Yilmaz, O. (2016). Multi-View Product
Image Search Using Deep ConvNets Representations.
arXiv:1608.03462.
Baz, I., Yoruk, E., and Cetin, M. (2016). Context-aware hy-
brid classification system for fine-grained retail prod-
uct recognition. In IVMSP, pages 1–5. IEEE.
Bendale, A. and Boult, T. E. (2016). Towards Open Set
Deep Networks. In CVPR, pages 1563–1572. IEEE.
Cheng, L., Zhou, X., Zhao, L., Li, D., Shang, H., Zheng, Y.,
Pan, P., and Xu, Y. (2020). Weakly Supervised Learn-
ing with Side Information for Noisy Labeled Images.
In ECCV, pages 306–321. Springer.
Deng, J., Guo, J., Xue, N., and Zafeiriou, S. (2018). Ar-
cFace: Additive Angular Margin Loss for Deep Face
Recognition. arXiv:1801.07698.
Filax, M., Gonschorek, T., and Ortmeier, F. (2019). Data
for Image Recognition Tasks: An Efficient Tool for
Fine-Grained Annotations. In ICPRAM, pages 900–
907. SciTePress.
Franco, A., Maltoni, D., and Papi, S. (2017). Grocery
product detection and recognition. Expert Syst. Appl.,
81:163–176.
George, M. and Floerkemeier, C. (2014). Recognizing
Products: A Per-exemplar Multi-label Image Classifi-
cation Approach. In ECCV, pages 440–455. Springer.
George, M., Mircic, D., Soros, G., Floerkemeier, C.,
and Mattern, F. (2015). Fine-Grained Product Class
Recognition for Assisted Shopping. In ICCVW, pages
546–554. IEEE.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep Resid-
ual Learning for Image Recognition. In CVPR, pages
770–778. IEEE.
Hermans, A., Beyer, L., and Leibe, B. (2017). In De-
fense of the Triplet Loss for Person Re-Identification.
arXiv:1703.07737.
Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-
celerating deep network training by reducing internal
covariate shift. arXiv:1502.03167.
Karlinsky, L., Shtok, J., Tzur, Y., and Tzadok, A. (2017).
Fine-Grained Recognition of Thousands of Object
Categories with Single-Example Training. In CVPR,
pages 965–974. IEEE.
Kingma, D. P. and Ba, J. L. (2019). Adam: A method for
stochastic optimization. arXiv:1412.6980.
Lowe, D. (1999). Object recognition from local scale-
invariant features. In ICCV, pages 1150–1157. IEEE.
Merler, M., Galleguillos, C., and Belongie, S. (2007). Rec-
ognizing Groceries in situ Using in vitro Training
Data. In CVPR, pages 1–8. IEEE.
Mittal, T., Laasya, B., and Dinesh Babu, J. (2018). A Logo-
Based Approach for Recognising Multiple Products
on a Shelf. In IntelliSys, pages 15–22. Springer.
Mumani, A. and Stone, R. (2018). State of the art of user
packaging interaction (UPI). Packag. Technol. Sci.,
31(6):401–419.
Rallapalli, S., Ganesan, A., Chintalapudi, K., Padmanab-
han, V. N., and Qiu, L. (2014). Enabling physical ana-
lytics in retail stores using smart glasses. In MobiCom,
pages 115–126. ACM Press.
Rettie, R. and Brewer, C. (2000). The verbal and vi-
sual components of package design. J. Prod. Brand
Manag., 9(1):56–70.
Scheirer, W. J., de Rezende Rocha, A., Sapkota, A., and
Boult, T. E. (2013). Toward Open Set Recognition.
TPAMI, 35(7):1757–1772.
Schroff, F., Kalenichenko, D., and Philbin, J. (2015).
FaceNet: A unified embedding for face recognition
and clustering. In CVPR, pages 815–823. IEEE.
Simonyan, K. and Zisserman, A. (2015). Very Deep Con-
volutional Networks for Large-Scale Image Recogni-
tion. arXiv:1409.1556.
Song, H. O., Xiang, Y., Jegelka, S., and Savarese, S. (2016).
Deep Metric Learning via Lifted Structured Feature
Embedding. In CVPR, pages 4004–4012. IEEE.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: A simple way
to prevent neural networks from overfitting. JMLR,
15:1929–1958.
Tonioni, A. and Di Stefano, L. (2017). Product Recognition
in Store Shelves as a Sub-Graph Isomorphism Prob-
lem. In ICIAP, pages 682–693. Springer.
Tonioni, A. and Di Stefano, L. (2019). Domain invariant
hierarchical embedding for grocery products recogni-
tion. Comput. Vis. Image Underst., 182:81–92.
Tonioni, A., Serra, E., and Di Stefano, L. (2018). A
deep learning pipeline for product recognition on store
shelves. In IPAS, pages 25–31. IEEE.
van der Maaten, L. (2013). Barnes-Hut-SNE.
arXiv:1301.3342.
Varadarajan, S. and Srivastava, M. M. (2018). Weakly
Supervised Object Localization on grocery
shelves using simple FCN and Synthetic Dataset.
arXiv:1803.06813.
Wang, J.-G., Li, J., Yau, W.-Y., and Sung, E. (2010). Boost-
ing dense SIFT descriptors and shape contexts of face
images for gender recognition. In CVPRW, pages 96–
102. IEEE.
Winlock, T., Christiansen, E., and Belongie, S. (2010). To-
ward real-time grocery detection for the visually im-
paired. In CVPRW, pages 49–56. IEEE.
Wu, C.-Y., Manmatha, R., Smola, A. J., and Krahenbuhl, P.
(2017). Sampling Matters in Deep Embedding Learn-
ing. In ICCV, pages 2859–2867. IEEE.
Xiong, B. and Grauman, K. (2016). Text detection in stores
using a repetition prior. In WACV, pages 1–9. IEEE.
Grocery Recognition in the Wild: A New Mining Strategy for Metric Learning
505