Roughness Index and Roughness Distance for Benchmarking Medical

Segmentation

Vidhiwar Singh Rathour, Kashu Yamakazi and T. Hoang Ngan Le

Department of Computer Science and Computer Engineering, University of Arkansas, Fayetteville, Arkansas 72701, U.S.A.

Keywords:

Surface Analysis, Roughness Distance, Irregular Spikes/Holes, Medical Imaging, Medical Segmentation,

Volumetric Segmentation.

Abstract:

Medical image segmentation is one of the most challenging tasks in medical image analysis and has been

widely developed for many clinical applications. Most of the existing metrics have been ﬁrst designed for

natural images and then extended to medical images. While object surface plays an important role in medical

segmentation and quantitative analysis i.e. analyze brain tumor surface, measure gray matter volume, most

of the existing metrics are limited when it comes to analyzing the object surface, especially to tell about

surface smoothness or roughness of a given volumetric object or to analyze the topological errors. In this

paper, we ﬁrst analysis both pros and cons of all existing medical image segmentation metrics, specially

on volumetric data. We then propose an appropriate roughness index and roughness distance for medical

image segmentation analysis and evaluation. Our proposed method addresses two kinds of segmentation

errors, i.e. (i) topological errors on boundary/surface and (ii) irregularities on the boundary/surface. The

contribution of this work is four-fold: (i) detect irregular spikes/holes on a surface, (ii) propose roughness index

to measure surface roughness of a given object, (iii) propose a roughness distance to measure the distance of

two boundaries/surfaces by utilizing the proposed roughness index and (iv) suggest an algorithm which helps

to remove the irregular spikes/holes to smooth the surface. Our proposed roughness index and roughness

distance are built upon the solid surface roughness parameter which has been successfully developed in the

civil engineering.

1 INTRODUCTION

In this paper we ﬁrst discuss the pros and cons of vari-

ous metrics that have been commonly used for bench-

marking the medical image segmentation task. We

emphasize on the limitations of existing metrics, such

as Hausdorff distance when evaluating the volumetric

segmentation. Our study shows that the existing vol-

umetric metrics are unable to measure the topologi-

cal errors specially when irregular spikes/holes are on

the surface. We then propose (i) an algorithm that

helps to detect irregular spikes/holes that exist on a

given object surface; (ii) a roughness index that de-

scribes how rough an object is given an object’s sur-

face; (iii) a roughness distance that aims at compar-

ing the surfaces between two given objects; (iv) an al-

gorithm that aims at removing the small outliers and

the irregular spikes/holes to smooth the surface. As

compared to other volumetric segmentation metrics

i.e. Hausdorff distance, our proposed roughness dis-

tance is able to measure the topological error whereas

roughness index evaluates the surface roughness. Fur-

thermore, we conduct the experiment to show that our

proposed irregular spikes/holes detection and surface

smoothing can be applied as a post-processing step

in any image segmentation algorithm to improve the

accuracy.

2 DESCRIPTION OF PURPOSE

Medical image segmentation is an important research

topic in medical analysis and has attracted attention in

past couple of years. With the abundance of medical

data available it has become easier to perform seg-

mentation task. However, evaluation and validation

of medical segmentation, specially volumetric data is

still a major concern because majority evaluation met-

rics have been developed as piece-wise setting for 2D

natural images and then extended to medical images

including volumetric data. As categorized in (Shi

et al., 2013), there are four types of segmentation er-

rors i.e. quantitative or the number of objects, area of

Rathour, V., Yamakazi, K. and Le, T.

Roughness Index and Roughness Distance for Benchmarking Medical Segmentation.

DOI: 10.5220/0010335500820093

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 2: BIOIMAGING, pages 82-93

ISBN: 978-989-758-490-9

segmentation, contour or the object boundary, and the

presence of holes, or irregularities in the boundary of

segmentation. The ﬁrst type of error, which regards

the number of objects, can be mitigated by increas-

ing the training data. Most of the common evaluation

metrics (i.e. Dice score , Sensitivity, Speciﬁcity, etc)

have focused to solve the second type of error, i.e.

area of segmentation which is a well-known problem

in any segmentation task in both computer vision and

medical analysis. For the third type of error, i.e. ob-

ject contour/boundary error, there are a limited num-

ber of metrics that have been developed. Hausdorff

distance (HDD) and Average Symmetric Surface Dif-

ference (ASSD) (Gerig et al., 2001) are the ones that

have been used for calculating errors on object sur-

face. The last error, which is related to topological

errors such as holes and spikes, still remains as a chal-

lenging problem in medical analysis. Several attempts

such as (Joshi et al., 2007) (Li et al., 2006) (Wu and

Chen, 2002) has focused on the last error category by

considering the smoothness and roughness criteria. In

this work, we address the last two kinds of errors,

i.e. (i) topological error on boundary/surface and

(ii) irregularities on boundary/surface as demon-

strated in Fig:1.

Different from 2D objects, volumetric objects

need the consistency and continuous between slides.

A comparison between consistency-inconsistency and

regularity-irregularity in volumetric data is given in

Fig:1 where each slide is presented in a cuboid (one

volumetric is considered as a set of slices) and ζ is

the distance between the surface and center of grav-

ity. The inconsistency or irregularity is deﬁned as

an abrupt or a sudden spike/hole. In Fig:1, the reg-

ular spike/hole is given in the top (Fig:1.a) where

spike or hole is gradually formed from slice to slice

whereas the irregular spike/hole is given in the bot-

tom (Fig:1.b) where spike or hole suddenly appeared.

Different from the previous works (Joshi et al.,

2007) (Li et al., 2006) (Wu and Chen, 2002) which

use geometric graph i.e., minimum s-t cut, we make

use of solid surface roughness parameter in civil

engineering to propose roughness metric (Chang

et al., 2006) (Tonietto et al., 2019) (Gadelmawla et al.,

2002). Our contribution can be summarized as fol-

lows:

• Revise and analyze the existing segmentation

metrics that have been used in medical analysis

(Sec:3).

• Propose an algorithm which helps to detect

all irregular spikes/holes on the object surface

(Sec:4.1).

• Introduce a roughness index that measures the

surface roughness given an object in (Sec:4.2).

Figure 1: An illustration of a regular spike/hole (a) v.s an

irregular spike/hole (b).

Our proposed roughness index is based on the

solid surface roughness parameter that has been

successfully developed in the civil engineering

(Chang et al., 2006) (Tonietto et al., 2019) (Gadel-

mawla et al., 2002).

• Propose a roughness distance metrics which

computes the surface distance between two sur-

faces (Sec:4.3).

• Propose an algorithm which helps to remove the

irregular spikes/holes and to smooth the contour

(Sec:4.4).

3 RELATED WORK

In this section, we will revise all existing segmenta-

tion metrics that have been commonly used in medi-

cal analysis. We ﬁrst categorize the existing segmen-

tation metrics into two groups, namely, region-based

metrics and boundary-based metrics. We then anal-

yse the pros and cons of each metric in the following

subsections.

3.1 Region-based Metrics

By deﬁnition, region-based metrics are used to

evaluate the area occupied by the segmentation. The

region-based metrics, which are based on pixel-wise,

have been ﬁrst developed for spatial images (2D)

segmentation in computer vision in general and then

extended to volumetric (3D) segmentation in medical

Roughness Index and Roughness Distance for Benchmarking Medical Segmentation

imaging. These types of metrics tend to work well

when there is clear demarcation with respect to data

and when the contour is smooth. However they tend

to fail when the the data has holes or boundary is

irregular. These metrics tend to evaluate the second

type of segmentation error, i.e. area of segmentation.

The following is some common region based metrics

that are popularly used volumetric segmentation.

Segmentation Problem Setting: In the image seg-

mentation problem, evaluation process is performed

between the ground-truth G created by the human and

segmentation predicted P by some algorithmic model.

Dice Similarity Coefﬁcient (DSC): Initially intro-

duced as Dice (Dice, 1945) also known as the F1

score is one of the most commonly used metrics

in validating medical image segmentation (Linguraru

et al., 2012) (Linguraru et al., 2009) in both spa-

tial images and volumetric data. Lets consider P as

the predicted volumetric segmentation vector and G

as the ground-truth, then DSC can be calculated as

shown in Eq:1.

DSC =

2|P ∩ G|

|P| + |G|

(1)

Symmetric Volume Difference (SVD): introduced

by (Campadelli et al., 2009) and Jaccard Similarity

Coefﬁcient (JSC) introduced by (Liu et al., 2012) are

similar to DSC and can be mathematically computed

from DSC as shown in Eq:2 and Eq:3.

SVD = 1 − DSC (2)

JSC =

|P ∩ G|

|P ∪ G|

DSC

2 − DSC

(3)

DSC although works well with data that is clearly de-

marcated, yet it tends to produce unwanted results if

the segmentation boundary is ambiguous. Also DSC

cannot tell anything about the boundary information,

roughness and smoothness of a volumetric surface or

the topological error on the boundary surface. JSC

and SVD have the same inherent problems as DSC.

Precision (Pre), Recall (Rec) and Sensitivity

(Sens): Precision is deﬁned as the volume of correctly

segmented volume to the total volume that has been

segmented. Recall (also referred to as Sensitivity) is

the the ratio of correctly segmented volume over the

ground-truth.

Pre =

|P ∩ G|

|P|

(4)

Rec/Sens =

|P ∩ G|

|G|

(5)

Precision takes into account only the volume that

has been segmented correctly but does not consider

the under-segmented volume. Recall on the other

hand does not consider the over-segmented volume.

However these two metrics are extensively being

used in computer vision for segregation tasks (Wolz

et al., 2012) (Campadelli et al., 2010).

Speciﬁcity (Spec): Speciﬁcity also referred to as

Selectivity is the ratio of portion of total volume

that is not common to the ground-truth (G) and pre-

dicted segmentation (P) by the portion not included

in ground-truth (G). True Negative (TN) is the por-

tion of volume that is not common to the ground-truth

(G) and predicted segmentation (P) and False Positive

(FP) is the potion of volume belonging to predicted

segmentation (P) that is not common to ground-truth

(G):

Speciﬁcity(Spec) =

|(P ∪ G)

(6)

Here C denotes the compliment component which is

illustrated in Fig:2. The segmented volumetric S con-

tains two parts corresponding to foreground F and

background G, where G = F

𝒮

∪

ℱ

𝒢 = ℱ

Figure 2: An Illustration of compliment using in Eq:6.

Green cuboid F represents the set for which compliment

is being calculated, and Black cuboid S represents the uni-

versal set of which F is a part.

Relative Volume Difference (RVD): RVD is de-

ﬁned as the ratio of absolute difference in volume

between the predicted volumetric segmentation vec-

tor (P) and the ground-truth (G) to the ground-truth

(G). It is commonly used as a reference to other met-

rics(Heimann et al., 2009) (Linguraru et al., 2012).

RVD = |

|P| − |G|

|G|

| (7)

RVD computed the relative difference in volume be-

tween predicted volumetric segmentation vector (P)

and the ground-truth (G) and hence it does not take

into consideration the overlap between them.

3.2 Boundary-based Metrics

Different from region-based metrics, which are de-

signed to work on entire area, boundary-based metrics

focus on boundary or surface only. In this section, we

BIOIMAGING 2021 - 8th International Conference on Bioimaging

revise two common boundary-based metrics, namely,

Average Symmetric Surface Difference (ASSD) and

Hausdorff Distance (HDD) as follows:

Hausdorff Distance (HDD): Hausdorff distance

(HDD) is deﬁned as the maximum possible distance

from a point/voxel on one boundary/surface to the

corresponding closest point/voxel on another bound-

ary/surface (Gerig et al., 2001) (Chen et al., 2012b)

(Liu et al., 2012) (Chen et al., 2012a). The HDD be-

tween the ground-truth boundary/surface ∂G and the

predicted segmentation boundary/surface ∂P is de-

ﬁned as follows:

HDD = max

x∈∂G

((|x,∂P|

)) (8)

where |x,∂P|

is the shortest L

distance between

a point/voxel x on the ground-truth boundary/surface

∂G and the predicted segmentation boundary/surface

∂P, namely, |x,∂P|

= min

y∈∂P

||(x − y)||

. Thus,

Eq.9 is rewritten as:

HDD = max

x∈∂G

((|x,∂P|

)) = max

x∈∂G

((min

y∈∂P

||x − y||

))

(9)

Because both P and G are symmetric, the bidi-

rectional Hausdorff distance between ground-truth

boundary/surface ∂G and the predicted segmentation

boundary/surface ∂P is computed as:

HDD = max (max

x∈∂G

((|x,∂P|

)),(max

x∈∂P

((|y,∂G|

))

(10)

Hausdorff distance, which is computed as the max-

imum distance between two surface, has been com-

monly used in practice. HDD only tells about the

maximum possible distance. However, it is unable to

describe the surface roughness as well as detect topo-

logical errors which are critical problems in medical

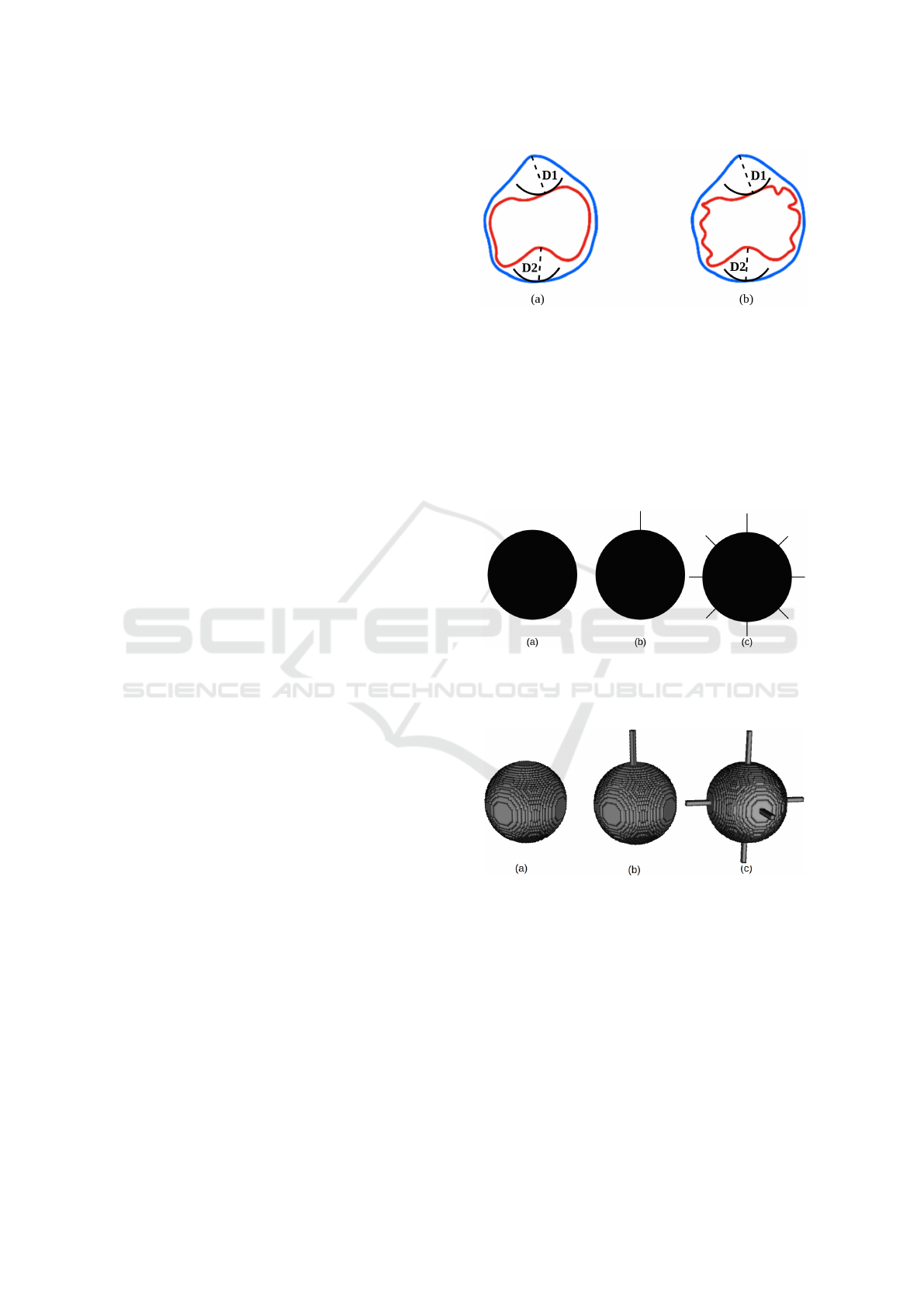
imaging. Fig:3 illustrates some limitations of HDD.

In this ﬁgure, suppose the ground-truth boundary G

is presented in blue curve whereas the predicted seg-

mentation P is shown in red curve. Two cases are

considered in this example, namely, smooth predicted

segmentation (Fig:3(a)) and rough predicted segmen-

tation (Fig:3(b)) with some topological errors on the

predicted segmentation boundary. Let denote D

and

as the distance between G and P, i.e. D

max

x∈∂G

((|x,∂P|

) and the distance between P and

G, i.e. D

= max

x∈∂P

((|y,∂G|

). As shown in Fig:3,

the distance D

and D

are the same in two cases,

thus the HDD is unchanged, i.e. HDD = max(D

)

even the predicted boundary in Fig:3(b) is different

from the one in Fig:3(a). Compared to the predicted

boundary in Fig:3(a), the one in Fig:3(b) is rougher

and with more topological changes.

Fig:4, 5 further explains the limitations of HDD.

In this example, the ground-truth is given in Fig:4, 5

Figure 3: Illustration of HDD in two cases: smooth pre-

dicted boundary (a) and rough predicted boundary with

topological changes (b). Blue curve is ground-truth bound-

ary G and red curve is predicted segmentation boundary P.

is distance from G to P and D

is distance from P to G.

(a) and Fig:4, 5 (b) and (c) are two different predicted

segmenting results. As shown in Fig:4, 5, there are

little irregular spikes on (b) and many irregular spikes

on (c), however, the HDD between the ground-truth

and the predicted segmenting results are the same.

Figure 4: From left to right 2D (a): ground-truth; (b) pre-

dicted segmentation with little irregular spikes; (c) pre-

dicted segmentation with many irregular spikes.

Figure 5: From left to right 3D (a): ground-truth; (b) pre-

dicted segmentation with little irregular spikes; (c) pre-

dicted segmentation with many irregular spikes.

Average Symmetric Surface Difference (ASSD):

ASSD (Chen et al., 2012b) (Chen et al., 2012a)

(Yokota et al., 2013) is the average of all the distances

from points/voxels on the boundary/surface of the

ground-truth mask to the boundary/surface of the

predicted segmentation mask, and vice versa. Denote

P and G as the predicted segmentation mask and the

ground-truth mask. The boundary/surface of P and

G are then deﬁned as ∂P and ∂G. Mathematically,

ASSD is computed as follows:

Roughness Index and Roughness Distance for Benchmarking Medical Segmentation

Table 1: Summary of existing metrics on volumetric segmentation:- Red : Predicted Segmentation(P), Blue: ground-truth(G),

Purple: True Positive(TP), ’C’ in the subscript suggests the compliment of the vector the image description is shown in Fig 6.

Type Metrics Equation Visualization

Region-Based

DSC

2|P∩G|

|P|+|G|

PREC

|P∩G|

|P|

JSC

|P∩G|

|P∪G|

DSC

2−DSC

REC, SES

|P∩G|

|G|

SET

|P∪G|

|G|

RVD |

|P|−|G|

|G|

Contour Based HDD max(max

x∈∂G

((|x,∂P|

)),(max

x∈∂P

((|y,∂G|

))

ASSD

∑

x∈∂G

(|x,∂P|

∑

x∈∂P

(|x,∂G|

)

|∂G|+|∂P|

ASSD =

∑

x∈∂G

(|x,∂P|

) +

∑

x∈∂P

(|x,∂G|

)

|∂G| + |∂P|

(11)

ASSD is a good metrics for cross distance compu-

tation between boundaries of two surfaces however

ASSD has the same limitations as HDD that it cannot

compute the roughness or smoothness on one partic-

ular surface.

The existing metrics can be summarized in Table

I where the visualization is further explain in Fig.6.

4 PROPOSED METRICS

In this section, our proposed metrics for surface

roughness analysis in medical segmentation will be

Figure 6: Explanation of annotations & visualization that

are used in table 1.

detailed. Our proposed roughness index and rough-

ness distance is based on the real world average

roughness parameter(Tonietto et al., 2019) as de-

BIOIMAGING 2021 - 8th International Conference on Bioimaging

scribed in Sec:4.1. In civil engineering domain,

roughness parameter of a particular surface is calcu-

lated using a laser to map the irregularities on the sur-

face (Tonietto et al., 2019). All the symbols and nota-

tions used to describe the proposed metrics have been

summarized in Table:2.

4.1 Irregular Spike/Hole Detection

Roughness is a very important parameter that is fre-

quently used in civil engineering domain (Chang

et al., 2006) (Tonietto et al., 2019) (Gadelmawla et al.,

2002). Civil engineers use the roughness parameter

to measure the inconsistencies on a particular sur-

face such as a slab of concrete or metal. A surface

proﬁle gauge or a Digital Holographic Microscope is

used to map the ﬂuctuations on the surface (Tonietto

et al., 2019). The roughness parameter(Tonietto et al.,

2019) in civil engineering domain is deﬁned in Eq:12

and illustrated in Fig:9a , where ζ

is the perpendicular

distance of a point from the laser plane also referred

to as the height coordinate (Tonietto et al., 2019) is

calculated using a laser moving on a ﬁxed plane par-

allel to the object surface and N is the total number of

points where height coordinate is calculated.

RoughnessParameter =

∑

|ζ

| (12)

We extended the term height coordinate to use it

in 2D and 3D domain by calculating the distance of

the surface point from the center of gravity C

instead

of a plain, as illustrated in Fig: 9c for a closed con-

tour laser plain can be approximated as the center of

gravity. We have deﬁned ζ (Zeta) as the distance of

a surface point for a contour P

Sur f ace

from center of

gravity C

as shown in Eq:13. Here P

Sur f ace

is the ma-

trix that has value 1 or 0 based on whether the location

in the segmentation mask P belongs to the surface or

not respectively.

ijk

(

|(i, j,k),C

Sur f ace

(i, j,k) = 1

0 Otherwise

(13)

For roughness in 2D and 3D we use a Distance

Matrix ζ

that contains the distance of each corre-

sponding surface point from the center of gravity C

as shown in Eq:14. This matrix can be used to detect

and correct surface roughness. The main purpose of

calculating ζ is to track the variations in surface. As

illustrated in Fig:1 an irregular hole/spike is marked

by an abrupt change in ζ while for a regular hole/spike

change in ζ takes place gradually.

(i,j,k) = ζ

i jk

(14)

Figure 7: Illustration of how neighbors of a reference point

D0 are considered for 2D (a) and 3D (b) Distance matrix

. In the given ﬁgure D0 is a position in distance matrix

, that belongs to the contour and for which roughness ∆ζ

needs to be calculated.

To detect roughness we deﬁne Roughness Matrix

∆ζ

containing roughness value ∆ζ (Delta zeta) for

each surface location as shown in Eq:17. Roughness

∆ζ of a location on surface can be deﬁned as the sum

of differences between ζ and its contour neighbors

Neighbors

, belonging to the set of neighbors S

Neighbors

illustrated in Fig:7 and described in Eq:15 and Eq:16.

∆ζ

ijk

∑

(ζ

i jk

− ζ

Neighbors

) (15)

Neighbors

∈ S

Neighbors

(16)

∆ζ

(i,j,k) = ∆ζ

i jk

(17)

lets consider a 2D example for various cases of

roughness as shown in Fig:8.

• Case 1: shows the condition of a plain where the

neighbors are at the same distance from C

as the

point for which ∆ζ needs to be calculated, so ∆ζ

will be ((D − D) + (D − D)) = 0

• Case 2: shows a slope where ∆ζ will be ((D −

D)+ (D −D) + (D −(D + 1))+ (D −(D − 1))) =

• Case 3: is an example of hole where ∆ζ will be

((D − D) + (D − D) + (D − (D + 1)) + (D − (D +

1))) = 2

• Case 4: which is a spike where ∆ζ will be ((D −

D) + (D − D) + (D − (D + 1))) = 1

Hence it can be easily concluded that |∆ζ| for a

location close to zero will denote a smooth surface

and greater then zero will refer to rough surface.

4.2 Roughness Metrics

Roughness parameter is a term usually used to deter-

mine the roughness of a solid surfaces(Chang et al.,

2006) (Tonietto et al., 2019) (Gadelmawla et al.,

2002). We extended this term to use in 2D and 3D sur-

face vector domain. As shown in Eq:18 The Rough-

ness Index (RI) in 3D can be calculated by dividing

Roughness Index and Roughness Distance for Benchmarking Medical Segmentation

Table 2: Symbols along with their descriptions.

Symbol Description Symbol Description

P Predicted segmentation mask G ground-truth segmentation mask

Center of gravity of a contour ∂S

Segment of an array S with a ﬁxed window size w

ζ ζ

i j

i jk

Distance of a contour position (i,j,k) from C

Distance matrix, ζ

(i, j,k) = ζ

i jk

Neighbor

Distance ζ of neighbor S

Neighbor

set of neighboring ζ

Neighbor

of ζ

∆ζ ∆ζ

∆ζ

i j

∆ζ

i jk

Roughness at a matrix position (i,j,k)

ζ Difference between ζ for P and G

∆ζ

matrix of ∆ζ ∆ζ

Rough Boolean matrix, where ∆ζ

∈ (0,1)

Figure 8: Different cases of roughness when dealing with

2D segmentation mask, In the ﬁgure ζ is the corresponding

distance of contour point from center of gravity C

the segmentation surface S into small surface element

∂S

of a ﬁxed window size w, and then calculating

the average deviation of ζ from the mean ζ

Mean

for

all surface voxels in the surface element ∂S

as illus-

trated in Fig:9b. In Eq:18 ∂S

denotes a point on the

surface element ∂S

, M is the total no of surface ele-

ments ∂S

that the contour surface is divided into and

N is the total no of points i inside each surface element

that belong to the contour surface, Here |∂S

equal to ζ that we calculated in previous section.

RI =

∑

∂S

∈S

∑

|(|∂S

) − Mean(|∂S

(18)

Roughness is a relative quantity. An object that is

rough as compared to one surface may be smooth as

compared to other. Hence it can be difﬁcult to tell

about the roughness of a surface unless we have a

baseline to compare the roughness index. Hence we

introduce Roughness Ratio (RR) that tells about the

relative difference between roughness of two objects.

The roughness ratio has been deﬁned in Eq: 19 where

R I

and R I

are the roughness index of predicted

segmentation and ground-truth respectively.

RR =

|RI

− RI

(19)

(a) In civil engineering domain Roughness is calculated by

moving a laser parallel to the surface to ﬁnd height coordi-

nate ζ and then using it to ﬁnd the roughness parameter of

the surface using Eq:12.

Surface Element

Center of gravity C0

(b) In medical domain the segmentation mask is a closed

object as opposed to a ﬂat surface in civil engineering,

hence we calculate the distance of object surface ζ from

center of gravity instead of a plane. This ζ is used to calcu-

late roughness index and surface/roughness distance.

the surface is rolled into a closed contour.

Figure 9: Illustration of how to compute roughness (a):

Roughness parameter is calculated by moving laser on

ﬁxed plane paralleled to the surface, (b): Roughness index

and surface/roughness distance is calculate from an origin

which is deﬁned as the center of medical image and (c):

How the method of calculating roughness can be extended

to medical imaging domain.

BIOIMAGING 2021 - 8th International Conference on Bioimaging

4.3 Roughness Distance

In this section, we propose Roughness Distance

which is considered as surface distance between two

surfaces. Let denote

ζ as the difference between the

ζ for predicted segmentation (ζ

) and ground-truth

segmentation (ζ

) as shown in Eq:20 and Roughness

Distance Matrix

as the matrix containing

ζ values

as shown in equation Eq:21

ijk

= ζ

i jk

− ζ

i jk

(20)

(i,j,k) =

i jk

(21)

Simply speaking roughness distance matrix

can be calculated by subtracting distance matrix for

ground-truth segmentation ζ

from distance matrix

for predicted segmentation ζ

as shown in equation

Eq:22. Roughness distance can be used to calculate

the roughness change between two object, ground-

truth and predicted segmentation in our case.

= ζ

− ζ

(22)

We also propose Average Roughness Distance

(ARD) which as the name suggest is the average

surface/roughness distance between two objects as

shown in Eq:23. ARD is a metric that tells us about

the average difference between the surface of two ob-

jects. ARD can be used as a substitute of HDD to

compare roughness.

ARD = Mean(|

|) (23)

4.4 Surface Smoothing

In this section we will propose a method for smooth-

ing a contour that has roughness on its surface.

Smooth contour can be obtained by using either

of the two methods which include using roughness

matrix ∆ζ

or roughness distance matrix

that

were calculated in previous sections.

For contour smoothing rough boolean matrix

∆ζ

is used where the value can be one or zero

based on whether the position is considered as rough

or smooth respectively as shown in Eq:24 where

κ is the threshold roughness value in range of (0 ,

max(∆ζ

)).

∆ζ

Bm(i,j,k)

(

1, |∆ζ

i jk

| > κ

0, Otherwise

(24)

Similarly ∆ζ

can also be computed using the

roughness distance matrix

as shown in Eq:25

where κ

is the threshold distance in range of (0 ,

max(

)).

∆ζ

Bm(i,j,k)

(

1, |

i jk

| > κ

0, Otherwise

(25)

This rough boolean matrix ∆ζ

can be used for

contour smoothing as shown in Eq: 26 where P

Rough

is the segmentation mask before contour smoothing

and P

Smooth

is the one after smoothing. It is important

to note here that both methods return a smooth con-

tour, However while ∆ζ

requires only the rough seg-

mentation contour,

also required the correspond-

ing ground-truth segmentation contour.

Smooth

= |P

Rough

− ∆ζ

| (26)

Algorithm 1: Calculate Roughness index(RI) of a 3D con-

tour.

Require: S ∈ {0,1} ∨ S[x, y, z]

) ← 0

N ← 0

RI ← 0

for (X,Y,Z) ∈ S do

) ← (X

) + (X,Y,Z)

N ← N + 1

end for

) ← (X

)/N

M ← 0

for ∂S

∈ S do

C ← 0

for (X,Y,Z) ∈ ∂S

← D

+ |(X,Y, Z),(X

C ← C + 1

end for

← D

N ← 0

← 0

for (X,Y,Z) ∈ ∂S

← R

+ |(|(X,Y, Z),(X

) − D

N ← N + 1

end for

← R

M ← M + 1

RI ← RI + R

end for

RI ← RI/M

5 DISCUSSION &

EXPERIMENTATION

5.1 Results and Comparison

The Table 1 summarizes all the metrics that are cur-

rently being used for evaluation of 3D medical im-

Roughness Index and Roughness Distance for Benchmarking Medical Segmentation

ages. As stated earlier the region based metrics can-

not calculate the roughness and smoothness of a 3D

contour. Also Hausdorff distance is capable of ﬁnd-

ing the maximum distance between the ground-truth

and predicted but it fails to capture the small rough-

ness on the surface.

In our experiments we used 2D and 3D segmen-

tation images of size (100 × 100) and (100 × 100 ×

100) as shown in Fig:4 and Fig:5 respectively. In both

cases (a) is a smooth segmentation treated as ground-

truth, (b) is a segmentation with small spike of 20

pixel length and (c) has many spikes, where the top

spike has the same length of 20 as (b) and all other

spikes are of smaller length for both 2D and 3D ex-

ample.

Mathematically the roughness index (RI) for a cir-

cle and sphere should be 0, but because for images the

coordinate system is integral not continuous, even a

smooth circle has a small RI greater then 0. Hence,

we treat it as Residual Roughness Index RI

Residual

. In

our experiments we have treated the RI for ground-

truth segmentation as residual. The absolute rough-

ness index RI

Absolute

can be calculated by subtracting

Residual

from RI as shown in Eq:27 .

Absolute

= RI − RI

Residual

(27)

In our experiments we varied the window size and

calculated roughness index for various window sizes.

For 2D image we ﬁrst performed 2D convolution on

the image using a kernel and dilation operator to con-

vert the 2D image into a contour. We then used a 2D

window and moved it on the image and calculated the

variation of distance from each boundary location to

the center of gravity of the contour using mean dis-

tance for all boundary locations present in the win-

dow. We used the strides equal to the window size

so that each location is used to calculate roughness

index exactly once. The plot of RI and RR vs win-

dow size for images in Fig:4 is shown in Fig:10 and

Fig:11 respectively. Similarly for 3D images we ﬁrst

performed 3D convolution on the image using a ker-

nel and dilation operator to convert the 3D image into

a contour. We then used a 3D window to calculate the

RI of each image in Fig:5. The RI and RR vs win-

dow size graph has been shown in Fig:12 and Fig:13

respectively.

It can be inferred from Fig:10 and Fig:11 that win-

dow size plays a very important role in RI calculation.

In our experimentation we found that the optimal win-

dow size must be between 3% to 10% of the image

smallest dimension. It is also important to note that

Roughness index is a standalone metrics but it can be

used to compare the roughness of two image through

roughness ratio that we have used in our experiments.

Figure 10: Graph of Roughness index Vs Window size for

2D images in Fig:4(a), (b) and (c).

Figure 11: Plot of Roughness ratio Vs window size

for Fig:4(a)(ground-truth), Fig:4(b)(little roughness pre-

dicted segmentation) and Fig:4(a)(ground-truth segmenta-

tion), Fig:4(c)(high roughness predicted segmentation).

Figure 12: Graph of Roughness index Vs Window size for

3D images in Fig:5(a), (b) and (c).

A tabular comparison between roughness ratio

(RR), average roughness distance (ARD) and Haus-

dorff distance (HDD) has been shown in Table 3. It

can be easily inferred from the table that RR and ARD

were capable of ﬁnding the difference in roughness

for the two image pairs that HDD failed to do.

For contour smoothing we used the algorithms

discussed in Sec:4.1 and Sec:4.3 to smooth the con-

BIOIMAGING 2021 - 8th International Conference on Bioimaging

Table 3: Comparison of Roughness Index RI, Roughness Ratio RR and Average Roughness Distance ARD with respect to

Hausdorff Distance, The window size considered for RI calculation is 7% of image size i.e. 7. From top to bottom Fig:4(a)(2D

ground-truth segmentation) and Fig:4(b)(2D little roughness predicted segmentation), Fig:4(a)(2D ground-truth segmenta-

tion) and Fig:4(c)(2D high roughness predicted segmentation), Fig:5(a)(3D ground-truth segmentation) and Fig:5(b)(3D little

roughness predicted segmentation), Fig:5(a)(3D ground-truth segmentation) and Fig:5(c)(3D high roughness predicted seg-

mentation).

Images

Absolute

Roughness

Index

Roughness

Ratio

Average

Roughness

Distance

Hausdorff

Distance

0 and 0.0120 0.0235 0.3178 20

0 and 0.0703 0.1377 0.7736 20

0 and 0.0015 0.0070 0.0592 20

0 and 0.0068 0.0317 0.0692 20

Figure 13: Plot of Roughness ratio Vs window size

for Fig:5(a)(ground-truth), Fig:5(b)(little roughness pre-

dicted segmentation) and Fig:5(a)(ground-truth segmenta-

tion), Fig:5(c)(high roughness predicted segmentation).

tours as shown in Fig:14. It is clear from Fig:14

that roughness distance method produces a more

satisfying result as compared to roughness matrix

method, The reason being that roughness distance

uses ground-truth segmentation as reference. How-

ever this is also a drawback because roughness dis-

tance method is constraint by the need of a refer-

ence distance matrix. Furthermore roughness dis-

tance method will produce unsatisfactory results if the

center of gravity for P and G are not same, i.e. the seg-

mentation masks are not aligned. However this prob-

lem can be overcome by using the center of gravity of

segmentation mask G for both P and G.

Roughness matrix method is a robust method

for detecting and removing surface roughness. For

roughness calculation we considered a window size of

three which includes a total of eight neighbors for 2D

and twenty six neighbors for 3D as shown in Fig:7.

Roughness Index and Roughness Distance for Benchmarking Medical Segmentation

Figure 14: Contour smoothing for two type of segmenta-

tion, Circle (top) and star (bottom). Smoothing has been

performed using the methods discussed in sections Sec:4.1

and Sec:4.3 and the Absolute roughness index RI

Absolute

speciﬁed below each image. The window size for RI calcu-

lation is 7% of image size i.e. 7 and roughness threshold κ

, κ

for the given experiments was taken as 0.

this method is capable for detecting irregular spikes of

width 1 pixel, However this method can be extended

to detect spikes of multiple pixels by increasing the

window size and the number of neighbors in neigh-

bors set S

Neighbors

. The method for smoothing holes is

same but in that case we will add a surface point to

the surface instead of removing it in case of a spike.

6 CONCLUSION

In this paper we ﬁrst discussed the pros and cons of

various metrics that have been commonly used for

the medical image segmentation task. We emphasize

more on the limitations of existing metrics for vol-

umetric segmentation. We then proposed (i) an al-

gorithm that helps to detect all irregular spikes/holes

that exist in the object surface; (ii) a roughness met-

ric that describes how rough of a given object; (iii)

a roughness distance that aims at comparing the sur-

faces between two given objects; (iv) an algorithm

that aims at removing irregular spikes/holes to smooth

the surface. Compare to other volumetric segmen-

tation metrics i.e. Hausdorff distance, our proposed

roughness distance is able to measure the topologi-

cal error whereas roughness metric present the sur-

face roughness. Furthermore, our proposed irregular

spikes/holes detection and surface smoothing can be

applied as a post-processing step in any image seg-

mentation algorithm to improve the accuracy.

ACKNOWLEDGEMENT

This research was supported in part by the Depart-

ment of Radiology, University of Arkansas of Medi-

cal Science UAMS.

REFERENCES

Campadelli, P., Casiraghi, E., and Esposito, A. (2009).

Liver segmentation from computed tomography

scans: a survey and a new algorithm. Artiﬁcial in-

telligence in medicine, 45(2-3):185–196.

Campadelli, P., Casiraghi, E., and Pratissoli, S. (2010). A

segmentation framework for abdominal organs from

ct scans. Artiﬁcial Intelligence in Medicine, 50(1):3–

11.

Chang, J.-R., Chang, K.-T., and Chen, D.-H. (2006). Ap-

plication of 3d laser scanning on measuring pave-

ment roughness. Journal of Testing and Evaluation,

34(2):83–91.

Chen, X., Udupa, J. K., Bagci, U., Zhuge, Y., and Yao,

J. (2012a). Medical image segmentation by combin-

ing graph cuts and oriented active appearance models.

IEEE TIP, 21(4):2035–2046.

Chen, Y., Wang, Z., Hu, J., Zhao, W., and Wu, Q. (2012b).

The domain knowledge based graph-cut model for

liver ct segmentation. Biomedical Signal Processing

and Control, 7(6):591–598.

Dice, L. R. (1945). Measures of the amount of ecologic

association between species. Ecology, 26(3):297–302.

Gadelmawla, E., Koura, M., Maksoud, T., Elewa, I., and

Soliman, H. (2002). Roughness parameters. Journal

of materials processing Technology, 123(1):133–145.

Gerig, G., Jomier, M., and Chakos, M. (2001). Valmet:

A new validation tool for assessing and improving

3d object segmentation. In MICCAI, pages 516–523.

Springer.

Heimann, T., Van Ginneken, B., Styner, M. A., Arzhaeva,

Y., Aurich, V., et al. (2009). Comparison and eval-

uation of methods for liver segmentation from ct

datasets. TIP, 28(8):1251–1265.

Joshi, A. A., Shattuck, D. W., Thompson, P. M., and Leahy,

R. M. (2007). Surface-constrained volumetric brain

registration using harmonic mappings. IEEE Trans

Med Imaging, 26(12):1657–1669.

Li, K., Wu, X., Chen, D. Z., and Sonka, M. (2006). Optimal

surface segmentation in volumetric images-a graph-

theoretic approach. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 28(1):119–134.

Linguraru, M. G., Pura, J. A., Pamulapati, V., and Summers,

R. M. (2012). Statistical 4d graphs for multi-organ

abdominal segmentation from multiphase ct. Medical

image analysis, 16(4):904–914.

Linguraru, M. G., Yao, J., Gautam, R., Peterson, J., Li, Z.,

Linehan, W. M., and Summers, R. M. (2009). Re-

nal tumor quantiﬁcation and classiﬁcation in contrast-

enhanced abdominal ct. PR, 42(6):1149–1161.

BIOIMAGING 2021 - 8th International Conference on Bioimaging

Liu, Y., Cheng, H.-D., Huang, J., Zhang, Y., and Tang, X.

(2012). An effective approach of lesion segmentation

within the breast ultrasound image based on the cel-

lular automata principle. Journal of digital imaging,

25(5):580–590.

Shi, R., Ngan, K. N., and Li, S. (2013). The objective

evaluation of image object segmentation quality. In

International Conference on Advanced Concepts for

Intelligent Vision Systems, number 3, pages 470–479.

Springer.

Tonietto, L., Gonzaga, L., Veronez, M. R.,

de Souza Kazmierczak, C., Arnold, D. C. M.,

and da Costa, C. A. (2019). New method for evalu-

ating surface roughness parameters acquired by laser

scanning. Scientiﬁc reports, 9(1):1–16.

Wolz, R., Chu, C., Misawa, K., Mori, K., and Rueckert, D.

(2012). Multi-organ abdominal ct segmentation us-

ing hierarchically weighted subject-speciﬁc atlases. In

MICCAI, pages 10–17. Springer.

Wu, X. and Chen, D. Z. (2002). Optimal net surface prob-

lems with applications. In Automata, Languages and

Programming, pages 1029–1042.

Yokota, F., Okada, T., Takao, M., Sugano, N., Tada, Y.,

Tomiyama, N., and Sato, Y. (2013). Automated ct seg-

mentation of diseased hip using hierarchical and con-

ditional statistical shape models. In MICCAI, pages

190–197. Springer.

Roughness Index and Roughness Distance for Benchmarking Medical Segmentation