Front-end Design Optimization for Ionoacoustic 200 MeV Protons

Beam Monitoring with Sub-millimeter Precision for Hadron Therapy

Applications

Elia Arturo Vallicelli

1,2 a

, Mattia Oliver Cosmi

, Andrea Baschirotto

1,2 b

and

Marcello De Matteis

1,2 c

Department of Physics, University of Milano, Bicocca, Milan, Italy

Italian Institute for Nuclear Physics (INFN), Section of Milano, Bicocca, Milan, Italy

Keywords: Nuclear Imaging, Particle Accelerator, Particle Beam Measurements, Acoustic Waves, Analog Circuits,

Digital Circuits.

Abstract: This paper presents the design of a multichannel acoustic detector optimized for sensing proton induced

thermo-acoustic signals (ionoacoustic signals) in clinical scenarios experiments. Ionoacoustics is a promising

technique for real-time monitoring of proton beams with interesting possible applications in oncological

hadron therapy. However, clinical scenarios are characterized by very low signal amplitudes (few tens

millipascals). State-of-the-art experiments use general purpose acoustic sensors and heavily rely on averaging

(up to thousands beam shots) to detect a clear signal, at the cost of a significant extra-dose above clinical

limits. To overcome this limit, this paper presents the design of a dedicated acoustic sensor that exploits spatial

correlation (multichannel sensor) to increase the SNR with no extra-dose and localize the maximum energy

deposition of a 200 MeV proton beam in clinical scenarios (35 mGy/shot dose, 25 mPa signal amplitude).

The results are validated by a complete cross-domain simulation of the physical (proton beam), acoustic (wave

propagation) and electrical (sensor and electronics frequency response and noise) environments. The

presented detector achieves a clear 20.5 dB single-shot SNR (35 mGy total dose) and can localize the

maximum energy deposition with 0.5 mm precision (<1% w.r.t. the particle range) with ~1/100 dose reduction

compared to state-of-the-art.

1 INTRODUCTION

Charged particles interact with matter by depositing

energy along their path until they fully stop at the end

of their range (Knoll, 2000). However, the energy

deposition is not homogeneous, but it follows the so-

called Bragg curve (shown in Fig. 1), with the highest

dose deposition (defined as deposited energy per unit

mass of the absorber) occurring at a certain depth

within the target material corresponding to the Bragg

Peak (BP). Moreover, very limited doses are

deposited in the pre-Bragg and post-Bragg region.

This particular feature is exploited in hadron therapy,

an oncological treatment that uses beams of charged

particles (mainly protons and carbon ions) to deliver

high radiation doses in very specific volumes inside a

https://orcid.org/0000-0003-0905-151X

https://orcid.org/0000-0002-8844-5754

https://orcid.org/0000-0003-1061-1262

patient, corresponding to the tumor location (Parodi,

2018; Min, 2006; Hueso-González, 2018; Mirandola,

2015). This allows to damage the tumor cells while

preserving the surrounding healthy tissue, with a

much-localized dose deposition compared to

traditional X-ray based radiation therapy. Given the

high selectivity of the dose deposition, measurement

techniques are required to verify during or just after

the treatment that the dose has been deposited within

the target volume and thus all the tumor tissue has

been treated. This is usually done by means of nuclear

imaging techniques (Position Emission Tomography

or prompt gamma ray imaging) that however require

bulky and expensive detectors and have intrinsically

limited precision of new millimeters.

Vallicelli, E., Cosmi, M., Baschirotto, A. and De Matteis, M.

Front-end Design Optimization for Ionoacoustic 200 MeV Protons Beam Monitoring with Sub-millimeter Precision for Hadron Therapy Applications.

DOI: 10.5220/0010346600770087

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 1: BIODEVICES, pages 77-87

ISBN: 978-989-758-490-9

Figure 1: Bragg curve for 200 MeV Protons and ionoacoustic signal source at the Bragg Peak.

An interesting alternative Bragg Peak localization

technique based on the ionoacoustic effect has been

proposed by Sulak in 1979 (Sulak, 1979). The

ionoacoustic effect is the generation of an acoustic

wave from the fast and localized energy deposition

occurring at the BP. Such acoustic wave can be

acquired by a set of acoustic sensors (AS) to precisely

localize the BP in space. The Time of Flight (ToF) of

the acoustic wave travelling from the BP to the AS

can be measured and thus the distance between the

BP and the AS can be calculated, localizing the BP in

space. Such technique requires a simpler detector and

has proved sub-mm precision at pre-clinical and

clinical energies. Hayakawa acquired a clear acoustic

signal during an hepatic cancer treatment in 1995,

whereas more recently sub-mm precision has been

achieved using water phantoms by various

experiments at clinical energies (Hayakawa, 1995;

Assmann, 2015; Lehrack, 2020; Patch, 2016; Jones,

2016).

However, state of the art experiments use off-the-

shelf general purpose detectors (acoustic sensors and

electronics) that limit the measurement performance,

as shown in (Riva, 2018; Vallicelli, 2019; Vallicelli,

2020; Samir, 1979). To improve the Signal-to-Noise

Ratio (SNR), state of the art heavily relies on post-

processing (in the form of averaging up to 1000

different beam shots). However, this SNR

improvement comes at the cost of an extra-dose (that

would be delivered to the patient in clinical

applications) that exceed clinical limits, effectively

preventing this technique to be applied in clinical

scenarios (Vallicelli, 2020).

To overcome this limitation, this work proposes a

different approach to improve the SNR without

introducing extra-dose. Instead of temporal averaging

(i.e. averaging of multiple beam shots), the concept of

spatial averaging is presented, in the form of

averaging the signals acquired by different acoustic

sensors. Multichannel acoustic sensors (MAS) are

composed by N

independent acoustic sensors

(channels), whose outputs are sensed simultaneously

by N

different acoustic sensors. Effectively, for each

beam shots, N

different signals are acquired and can

be averaged to improve the SNR without any extra

dose compared to a single-channel AS approach, that

would require Nch different beam shots (and thus N

times the dose) to achieve the same SNR increase.

Nevertheless, this multichannel approach requires

a dedicated sensor and analog front-end design and

cannot rely on off-the-shelf components. For this

reason, this paper presents the design and

characterization of a detector (called High-Energy

Proton Sound Detector, HE-ProSD) that can localize

the BP in space with sub-mm precision in a clinical

scenario characterized by a 200 MeV proton beam

delivering 10 mGy/shot dose at the BP and generating

a 1 Pa acoustic signal at the BP and 23 mPa amplitude

at the sensor surface, located 7.5 cm away from the

BP. Such characteristics are typical of ionoacoustic

experiments at clinical energies such as (Assmann,

2015) and (Jones, 2016).

This work is organized as follows. Section II presents

the main characteristics of the 200 MeV experimental

scenario. Section III presents the AS and AFE design

that will be characterized by extensive cross-domain

simulations whose results are presented in Section IV.

Finally, in Section V these results will be discussed,

and conclusions will be drawn.

BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices

Figure 2: Ionoacoustic signal propagation and sensing.

Table 1: Characteristics of pre-clinical and clinical

scenarios.

Proton

Energy

20 MeV 65 MeV 200 MeV

Protons per

shot

Beam range

in water

4.1 mm 38 mm 259 mm

FWHM

0.3 mm 2.9 mm 19.2 mm

Dose/shot at

800

mGy/sho

100

mGy/sho

35 mGy/shot

Pressure at

80 Pa 10 Pa 3.5 Pa

Pressure at

5 Pa 300 mPa 25 Pa

2 200 MeV PROTONS

EXPERIMENTAL SCENARIO

Ionoacoustic experiments become more critical when

the beam energy increases because the dose deposited

at the BP will be increasingly lower and this results in

a weaker pressure signal.

Whereas sub-clinical experiments at 20 MeV

energy are characterized by tens or hundreds of Pa at

the BP, this value decreases to around 5 Pa at 65 MeV

(lowest energy for clinical applications) and around 1

Pa for 200 MeV (highest energy for clinical

applications). A brief comparison between pre-

clinical and clinical scenarios is presented in Table 1.

In this work a 200 MeV proton beam scenario has

been chosen because it represents the most critical

scenario for ionoacoustic signal sensing and is

therefore the most interesting to show the capability

of the spatial averaging approach. 200 MeV protons

are characterized by a high penetration and a low

dose, which gives rise to a weak and low frequency

acoustic signal, two characteristics that make it

difficult to use them for localization of the Bragg

peak. More precisely, the BP is at 25.9 cm depth in a

water phantom and the ionoacoustic signal (at 7.5 cm

from the BP in the axial direction) has an amplitude

of 25 mPa and a frequency spectrum that peaks at 40

kHz, as reported in (Assmann, 2015) and (Jones,

2016). Fig. 2 shows the typical ionoacoustic

experimental setup. The proton beam enters in the

water tank passing through a Kapton entrance

window and deposits energy following the Bragg

curve, that generates a correspondingly increase in

pressure (acoustic source) highlighted in yellow-red

in Fig. 2.A, where red indicates a higher dose and

pressure, whereas yellow indicates a lower dose and

pressure variation.

Figure 3: 200 MeV protons ionoacoustic signal spectrum.

The pressure wave propagates in water (Fig. 2.B

and C shown 20 μs and 40 μs after the beam shot

respectively) and reaches the detector surface after

around 60 μs, as shown in Fig. 2.D, where it is

transduced in voltage domain, as represented in Fig.

2.E. With reference to Fig. 2.C, two different acoustic

signals can be observed, one originated in the BP that

propagates spherically and can be used for BP

localization and one other in the pre-Bragg region,

that propagates as a cylindrical wave mostly

perpendicular to the beam axis.

This scenario has been completely modelled using

Geant4 to estimate the energy deposition profile, k-

Wave to simulate the pressure wave propagation in

space (Fig. 2) and Matlab to model the AS and AFE

in terms of frequency response and noise power.

The acoustic signal spectrum is shown in Fig. 3

and peaks below 40 kHz, as shown in (Assmann,

2015) and (Jones, 2016).

Front-end Design Optimization for Ionoacoustic 200 MeV Protons Beam Monitoring with Sub-millimeter Precision for Hadron Therapy

Applications

Figure 4: Precision vs SNR.

Table 2: HE-ProSD Performance Requirements.

Parameter Value

Beam Energy 200 MeV protons

Dose/shot @ Bragg peak 35 mGy

Acoustic Signal Bandwidth 40 kHz

Signal amplitude 25 mPa

Desired Precision 0.5 mm

Required HE-ProSD SNR

(SNR

HE-ProSD

) for 0.5 mm

precision

20 dB

AFE Noise Figure (NF

AFE

) 1 dB

Directivity Noise Figure

(NF

DIR

)

1 dB

Acoustic Sensor SNR

(SNR

)

22 dB

Finally, the BP-AS distance (d

BP-AS

) can be

calculated by measuring the acoustic wave time of

flight (ToF) and applying equation (1), where c

the sound speed in water, equal to 1498 m/s at 23°C.

𝑑



=𝑇𝑜𝐹∙𝑐



(1)

To determine the localization precision, the

distance d

BP-AS

has been repeatedly measured 1000

times with different noise realizations. Random noise

fluctuations shift the measured position in space, thus

introducing a random error with a standard deviation

equal to the localization precision. Repeating the

measurements 1000 times (with the same SNR but

different noise realization) guarantees a good statistic

and an accurate measurement precision evaluation.

3 HIGH-ENERGY PROTON

SOUND DETECTOR DESIGN

3.1 HE-ProSD Design Requirements

The first step in the HE-ProSD design is to define the

specifications to be met. The desired localization

precision has been set to 0.5 mm.

The relationship between SNR and measurement

precision was obtained by measuring the precision as

described in Section II, obtaining the d

BP-AS

precision

at different SNR values. The results are shown in Fig.

4. To achieve sub-mm precision a minimum 14 dB

SNR is required, whereas to obtain the desired 0.5 mm

precision the detector SNR needs to be as high as 20

dB. However, this SNR value has to be achieved at the

detector output, including AS and AFE noise power

and acoustic sensor non-idealities that will be

described in the next section. For this reason, the

acoustic sensor SNR (SNR

) must be larger than the

final required detector SNR (SNR

HE-ProSD

, 22 dB)

because it degrades due to the analog front-end noise

power and acoustic sensor BP-AS misalignments

(caused by non-ideal AS directivity). These factors

cause an SNR loss that require the the SNR

to be

higher than the final SNR

HE-ProSD

by an amount equal

to the AFE Noise Figure (NF

AFE

) and the AS directivity

Noise Figure (NF

DIR

), following equation (2).

𝑆𝑁𝑅



=𝑆𝑁𝑅



−𝑁𝐹



−𝑁𝐹



(2)

At this point, a NF

AFE

and NF

DIR

budget can be

assigned to the AFE, equal to 1 dB each, thus bringing

the final SNR

requirement to 22 dB. Considering a

25 mPa signal amplitude, such SNR

value

corresponds to an input referred sensor noise power

of 1.4 mPa

RMS

Effectively, this first design step determines the

performance requirements for the AS, which are

listed in Table 2.

Each channel of the MAS needs to fulfill different

requirements:

 The AS resonance frequency needs to match the

40 kHz signal bandwidth;

 The single-channel Output-Referred Noise Power

(ORN) must be high enough so that the AFE noise

requirements imposed by the 1 dB NFAFE can be

met;

 The single channel sensor must be able to acquire

signals coming from different directions limiting

their attenuation to that imposed by the NF.

The design of a single channel that meets the

requirements of bandwidth, noise and directivity will

be presented first. Then the number of channels

necessary to obtain the required SNR

value (22 dB)

through spatial averaging will be determined.

BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices

Figure 5: Acoustic Sensor frequency response.

Figure 6: Single element acoustic sensor scheme.

Table 3: PIC255 PZT piezoelectric parameters.

Parameter Symbol Value

Frequency Coefficient Nf 40 kHz

Relative permittivity ε

1750

Piezoelectric voltage

coefficient

25·10

-3

V/(Pa·m)

Piezoelectric thickness Th 51 mm

PIC255 Acoustic

Impedance

33 MRayl

Matching Layer

acoustic impedance

7 MRayl

3.2 Frequency Response and

Sensitivity

Ionoacoustic signals are typically sensed by

piezoelectric sensors that transduce pressure

variations into voltage variations. Piezoelectric

sensors have a frequency response characterized by a

passband and a resonance frequency, as shown in Fig.

5. The sensor has its maximum sensitivity at the

resonant frequency, and it decreases by about 10 dB

in the linear part of the frequency response. Lead-

Zirconate-Titanate are among the most performing

materials commercially available for such

applications.

Figure 7: Acoustic impedance mismatch effects.

This section will refer to the PIC255 PZT

produced by PiCeramics, whose characteristic

parameters are listed in Table 3. The resonance

frequency depends on the frequency coefficient N

(2000 Hz·m) and on the thickness TH of the

piezoelectric according to equation (n) and as shown

in Figure 6.

𝑓



𝑁

𝑇ℎ

(3)

A resonant frequency of 40 kHz has been chosen in

this case to match the signal frequency. This sets the

piezoelectric thickness to 51 mm and allows to

calculate the sensitivity at resonance frequency using

equation (n), where g

is the piezoelectric voltage

coefficient, equal to 25 mV/(Pa·m):

𝑆



=𝑔



∙𝑇𝐻

(4)

Considering the 51 mm piezoelectric thickness,

the PZT sensitivity is 1.3 mV/Pa. However, this

sensitivity value is usually reduced to about 60-80%

due to the impedance mismatch between the water

(acoustic signal propagation medium) and the

piezoelectric material itself (Vallicelli, 2020; Samir,

1979). In fact, whenever an acoustic wave traveling

in one medium encounters another medium with

different mechanical properties, it is partly

transmitted and partly reflected, as shown

qualitatively in Figure 7. The transmission coefficient

ηT depends on the acoustic impedances of the

materials (defined as the product between density and

speed of sound in the medium) and is equal to:

𝜂





2𝑍



𝑍



𝑍



(5)

Water has an acoustic impedance of 1.5 MRayl,

very different from the 33 MRayl of the PZT, and

therefore in a direct interface between the two

materials only 40% is transmitted, causing a

corresponding loss of sensitivity.

Front-end Design Optimization for Ionoacoustic 200 MeV Protons Beam Monitoring with Sub-millimeter Precision for Hadron Therapy

Applications

Figure 8: Sensitivity loss due to sensor directivity.

For this reason, an intermediate layer (called

matching layer) is placed between the water and the

piezoelectric to act as an impedance matching and

increase the amplitude of the transmitted wave. A

60% transmission coefficient can be achieved with a

matching material that have an acoustic impedance

equal to 7 MRayl. Typical materials with 7 MRayl are

silicone rubbers or araldite. Using multiple matching

layers of different materials, even higher transmission

coefficients can be obtained (Samir, 1979; Vallicelli,

2020). The overall sensitivity S (including

piezoelectric sensitivity S

PZT

and matching layer

effects) is therefore equal to:

𝑆=𝜂



∙𝑔



∙𝑇𝐻 (6)

The matching layer usually has a thickness equal

to a quarter-wavelength to further minimize the

reflected component of the acoustic wave. This leads

to a final AS sensitivity of 770 μV/Pa.

3.3 Sensor Capacitance and Noise

Power

Piezoelectrics are capacitive sensors and thus their

output referred noise power can be estimated equal to

kT/C. Their capacitance, and thus output referred

noise power, can be estimated from the formula for a

parallel-faced capacitor, where A is the piezoelectric

area, ε

and ε

are respectively the dielectric constants

of the vacuum (value) and relative dielectric constant

of the piezoelectric material (value):

𝐶=𝜀



𝜀



𝐴

𝑇ℎ

(7)

Thus, the output-referred noise power of the

sensor channel is:

𝑂𝑅𝑁=



𝑘𝑇

𝐶



𝑘 𝑇 𝑇ℎ

𝜀



𝜀



𝐴

(8)

Effectively, all parameters of this equation are

determined except the sensor area, that can be sized

to fulfill the NF

AFE

requirement. In fact, the larger the

sensor area, the smaller its ORN will be and this will

force the AFE to have increasingly stringent noise

specifications to meet the NF

AFE

requirement. Ultra-

low noise AFE performances (<1 nV/√Hz Power

Spectral Density, PSD) can be reached using

monolithic transistors in JFET technology (Vallicelli,

2020), which however cannot be integrated into

standard CMOS technologies and therefore do not

meet the miniaturization requirements needed for

multi-channel sensors. On the other hand, standard

CMOS processes allow high miniaturization

(opening the possibility of multichannel sensor and

spatial averaging) while still achieving good noise

performances. An input-referred noise power spectral

density of 10 nV/Hz was assigned to the AFE,

corresponding to an integrated noise power in the

signal bandwidth equal to 2.5 uV

RMS

. Such AFE IRN

PSD is well within the possibilities of standard

CMOS processes.

Finally, to comply with the 1 dB NF

AFE

requirements, the ORN of the MAS single channel

must be equal to 5 μV

RMS

, corresponding to a 5.4 cm2

single channel area, or a square sensor with a side

length L of 2.3 cm. This sets the maximum area that

fulfills the NF

AFE

requirements.

3.4 Single Channel Directivity

Ideal acoustic sensors are omnidirectional, i.e. they

can acquire a signal regardless of its direction of

arrival. However, real acoustic sensors are

characterized by a certain amount of directivity, that

is, they attenuate signals arriving from directions

other than their axis, as shown in Figure 8. This

characteristic, for a given frequency of the acoustic

signal, depends on the difference between the width

of the acoustic sensor (L) and the wavelength. In

particular, if the acoustic sensor is small compared to

the wavelength it will behave almost ideally

(omnidirectional), while as its size increases it will

become more and more directive. Since the position

of the Bragg peak is not known a priori, each channel

cannot be previously oriented towards the BP.

BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices

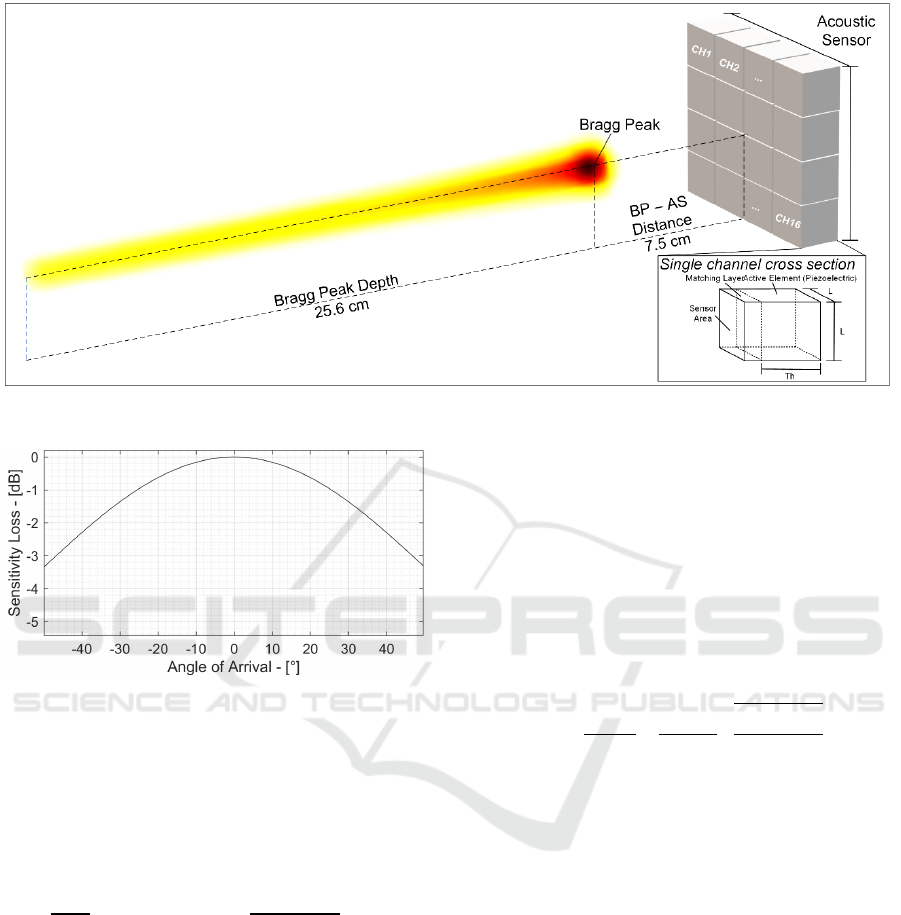
Figure 10: High-Energy Proton Sound Detector Scheme.

Figure 9: Single channel sensitivity loss due to its

directivity.

If the single channel element is very directive, it

will attenuate off-axis signals a lot, effectively

lowering the AS sensitivity and final SNR. The

directivity of a single channel element can be

determined using the Fraunhofer laws of diffraction.

𝑆



𝜃



𝑆

=𝑑𝑖𝑟



𝜃



=𝑠𝑖𝑛𝑐

𝜋𝑓𝐿𝑠𝑖𝑛



𝜃



𝑐



 (9)

Considering a sensor with L = 2.3 cm, the overall

sensitivity loss due to directivity is shown in Figure

9. In particular, considering the 7.5 cm AS-BP

distance, the maximum angle to fulfil the 1 dB NF

DIR

specification is 25°, corresponding to a 3.5 cm off-

axis shift of the BP location w.r.t. the channel

element. This directivity loss is particularly relevant

in the case of multichannel sensors, because the

presence of different channels implies that some

channels are not perfectly aligned with the BP, thus

experiencing some loss due to their directivity. In this

case the 2.3 cm single channel size meets the

directivity requirement.

3.5 Multichannel Acoustic Sensor

Design

The single channel equivalent input referred noise

power can be calculated dividing the ORN by the AS

sensitivity:

𝐼𝑅𝑁



𝑂𝑅𝑁



𝑆

𝜂



∙𝑔





𝑘𝑇

𝜀



𝜀



∙𝐴∙𝑇ℎ

(10)

Substituting the parameters found in the previous

sections, the single channel capacitance is 167 pF and

its input-referred noise power IRN

is equal to 6.6

mPa

RMS

. Thus, the single channel SNR

1Ch

is 8.5 dB.

To achieve the desired 20 dB SNR, the spatial

averaging technique exploits signals sensed by N

channels to improve the final SNR

Nch

as in Equation

11.

𝑆𝑁𝑅

ℎ

=𝑆𝑁𝑅



+10log



𝑁



(11)

Thus, 16 channels are necessary to meet the 20 dB

SNR

requirement, achieving a total 12 dB increase

and a final 20.5 dB SNR

Nch

. These channels are

arranged in a 4x4 matrix to compose the HE-ProSD

as shown in Figure 10.

Front-end Design Optimization for Ionoacoustic 200 MeV Protons Beam Monitoring with Sub-millimeter Precision for Hadron Therapy

Applications

Figure 11: Top: Single channel signal including sensor and AFE noise power. Bottom: 16-channels spatial average signal

including sensors and AFE noise power.

4 HE-PROSD VALIDATION AND

SIMULATION RESULTS

To validate the design procedure presented in Section

III and to show how a dedicated sensor can improve

the localization performances, a sensor has been

designed for a specific experimental scenario present

in literature, represented by a 200 MeV proton beam

with a 35 mGy dose deposition per shot and 7.5 cm

sensor-BP distance, in a scenario equivalent to what

is found in literature.

The physical environment has been simulated

using Geant4 to extract the 3D dose deposition profile

and thus calculate the pressure increase spatial

distribution. k-Wave has then been used to simulate

the pressure wave propagation in space and to

determine the signal sensed by each channel of the

sensor. The pressure domain signals have been

transformed into voltage domain by multiplying for

the sensor sensitivity of 770 uV/Pa. Then the signal

has been band-passed to represent the sensor

frequency response (60 kHz -3dB frequency) and a

band-shaped thermal noise has been added. The

single channel SNR ranges from 0.4 dB (central

channels, closer to the BP) and 0.4 dB (external

channels, further away from the BP).

Two different HE-ProSD results are presented:

 Single channel ToF measurement

 16-channels ToF measurement

4.1 Single Channel Time of Flight

Measurement

Fig. 11 shows the single-channel signal including

sensor and AFE noise power, overlapped with the

same signal not including noise (dotted line). The

measured SNR is 8.7 dB, including sensor and AFE

noise power. Although the SNR is relatively low, the

ionoacoustic signal is recognizable and can be used to

calculate a ToF and thus localize the BP in space. By

repeating the ToF measurement with different noise

realization (with the same SNR value), a 1.5 mm

precision has been found.

BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices

Figure 12: 16 Channels signals of HE-ProSD (without

noise).

Figure 13: Measured BP position (10k repetitions) obtained

by the 16-channels spatial average of the HE-ProSD.

Table 4: Comparison with state of the art.

This work Assmann,

2015

Jones, 2016

Proton

energy

200 MeV 200 MeV 200 MeV

Acoustic

Sensor

16-

channels

array

1 channel

hydrophone

1 channel

hydrophone

Acoustic

Sensor

Bandwidth

40 kHz 200 kHz 200 kHz

Analog

Front-End

Dedicated

Analog

Front-End

General

purpose

LNA and

oscilloscope

General

purpose LNA

and

oscilloscope

Detector

distance

7.5 cm 7.5 cm 5 cm

Detector

noise floor

1.8

mPa

RMS

n.a. 27 mPa

RMS

Signal

amplitude

25 mPa

2 mPa

0-peak

30 mPa

0-peak

SNR – single

shot

20.5 dB n.a. -2 dB

Precision –

single shot

0.5 mm n.a. n.a.

Dose - single

shot

35 mGy n.a. 35 mGy

Final

Precision

0.5 mm 0.34 mm 2.2 mm

Total Shots 1 1000 ~60

Total Dose 35 mGy 10 Gy 2 Gy

4.2 HE-ProSD Time of Flight

Measurement

Fig. 12 shows the 16 different signals acquired by the

16 channels of the HE-ProSD. A different offset has

been applied to each channel and noise has been

removed for ease of representation. Each channel

signal has a slightly different phase because the

distance between the acoustic source (BP) and the

channels are different, and consequently the ToF. To

apply the space-domain average, the 16 channels

have to be re-phased. A Delay and Sum (DAS)

algorithm has been applied and the output is shown in

Fig. 12. Compared to Fig. 11, the SNR has improved

thanks to spatial averaging, and is equal to 20.7 dB. It

is important to highlight that such SNR improvement

has been achieved with the same dose deposition as

the single-channel SNR.

To determine the localization precision, ToF

measurements have been performed with different

noise realization and the resulting BP position has

been shown in Fig. 14. The corresponding

localization precision is 0.5 mm, obtained with a total

35 mGy dose.

4.3 HE-ProSD Performance

Comparison with State of the Art

Table 4 shows a comparison between HE-ProSD

performance and state of the art experiments at 200

MeV protons. Although the HE-ProSD results are

obtained by simulations, all the most relevant noise

and non-idealities are included and the results show a

clear trend, that is that a dedicated detector design is

fundamental to significantly reduce the dose

necessary to achieve a given precision.

In fact, state of the art uses commercial single-

channel hydrophones, general-purpose amplifiers and

oscilloscopes, with the result of not optimizing SNR

performance (eg integrating noise on a much higher

band than that of the signal) in the digital domain and

of having to compensate by resorting to averages in

the digital domain. However, averaging is not an

efficient tool in increasing SNR as it reduces the noise

power according to sqrt (N

), thus requiring a large

number of averages (and therefore extra-dose) to

significantly improve SNR. Indeed, while the noise

power decreases as sqrt (N

), the dose increases

linearly with Nsh, resulting in a large extra-dose. In

comparison, using the spatial mean results in an

increase in SNR equal to sqrt (N

) but without using

extra-dose. If the single channel of HE-ProSD were

used to obtain 0.5 mm of precision using the time

domain average, 16 shots of the beam would be

Front-end Design Optimization for Ionoacoustic 200 MeV Protons Beam Monitoring with Sub-millimeter Precision for Hadron Therapy

Applications

needed (instead of 16 channels), for a total dose of

about 0.5 Gy, of the same order of magnitude. of

(Assmann, 2015) and (Jones, 2016). Thanks to the

dedicated design, HE-ProSD allows to obtain 0.5 mm

of precision using a dose of 35 mGy, using

respectively 0.35% and 1.75% dose compared to

(Assmann, 2015) and (Jones, 2016).

5 DISCUSSION AND

CONCLUSIONS

This paper presents the design of a multi-channel

acoustic sensor that allows to locate with sub-

millimeter precision a beam of protons at 200 MeV at

doses compatible with those of clinical treatments.

Compared to the state of the art, this detector uses a

different approach, that is, it moves the SNR increase

from the digital domain (post-processing) to the

analog domain (detector improvement). This

approach exploits a dedicated design of a

multichannel acoustic sensor that allows to use the

average in the space domain instead of the time

domain, obtaining an increase of SNR without any

extra-dose. This detector, called High-Energy Proton

Sound Detector (HE-ProSD), has been validated with

cross domain simulations that include 3D deposition

of energy in space (Geant4), generation and

propagation of the acoustic signal up to the sensor.

Then, the sensor was fully modelled in mechanical

(resonant frequency, physical size), acoustic

(acoustic impedance and diffraction / directivity

matching) and electrical (sensor capacity, input and

output noise power) terms. Finally, an analog front-

end was modeled in terms of frequency response and

noise power and used to process the signal generated

by the multi-channel acoustic sensor. To evaluate the

performance of the HE-ProSD, the Bragg peak of a

proton beam at 200 MeV was localized and the

measurement was repeated with different noise

realizations (including both acoustic sensor and

electronics noise) and is An accuracy of 0.5 mm was

found for an acoustic signal of 25 mPa amplitude and

35 mGy of dose deposited at the Bragg peak. By

comparing these results with what has been obtained

from the state of the art (Assmann, 2015; Jones,

2016), a significant dose reduction was obtained with

the same localization precision. Although this work

includes only simulation results and an experimental

validation of the performance obtained is necessary,

it is clear that for a possible application of the

ionacoustic technique in clinical scenarios it is

necessary to move from off-the-shelf and general

purpose detectors to a dedicated design that exploits

the potential of multichannel sensors through the

development of integrated circuits front-ends to

achieve high SNR in the particularly critical clinical

scenarios (Baschirotto, 2009; De Matteis, 2006).

ACKNOWLEDGMENT

This work has been supported by the Proton Sound

Detector (ProSD) project funded by the Italian

Institute for Nuclear Physics (INFN).

REFERENCES

Glenn F. Knoll, “Radiation Sources,” in Radiation

detection and measurement, John Wiley & Sons, 2000,

ch. 1, pp. 1–28.

Parodi, Katia, and Jerimy C. Polf. "In vivo range

verification in particle therapy." Medical physics 45.11

(2018): e1036-e1050.

C. H. Min, C. H. Kim, M. Y. Youn, and J. W. Kim, “Prompt

gamma measurements for locating the dose falloff

region in the proton therapy,” Applied Physics Letters,

Vol. 89, no. 18, pp: 1-3, November 2006.

Hueso-González, F., Rabe, M., Ruggieri, T. A., Bortfeld,

T., & Verburg, J. M. (2018). A full-scale clinical

prototype for proton range verification using prompt

gamma-ray spectroscopy. Physics in Medicine &

Biology, 63(18), 185019.

A. Mirandola, S. Molinelli, G. Vilches Freixas, et al.,

“Dosimetric commissioning and quality assurance of

scanned ion beams at the Italian National Center for

Oncological Hadrontherapy,” Radiation measurement

physics, vol. 42, no. 9, pp. 5287-5300, September.

2015.

L. Sulak, T. Armstrong, H. Baranger, at al., "Experimental

studies of the acoustic signature of proton beams

traversing fluid media," Nuclear Instruments and

Methods Vol. 161, no. 2, Pages 203-217, May 1979.

Y. Hayakawa, J. Tada, N. Arai, et al. "Acoustic pulse

generated in a patient during treatment by pulsed proton

radiation beam." Radiation Oncology Investigations

Vol. 3, no.1, pp. 42-45, Jan. 1995.

W. Assmann, S. Kellnberger, S. Reinhardt, et al.,

“Ionoacoustic characterization of the proton Bragg

peak with sub-millimeter accuracy,” Medical Physics,

Vol. 42, no. 2, pp. 567-574, Feb 2015.

Lehrack, Sebastian, et al. "Ionoacoustic detection of swift

heavy ions." Nuclear Instruments and Methods in

Physics Research Section A: Accelerators,

Spectrometers, Detectors and Associated Equipment

950 (2020): 162935.

Patch, S. K., et al. "Thermoacoustic range verification using

a clinical ultrasound array provides perfectly co-

registered overlay of the Bragg peak onto an ultrasound

BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices

image." Physics in Medicine & Biology 61.15 (2016):

5621.

Jones, K. C., Vander Stappen, F., Sehgal, C. M., & Avery,

S. (2016). Acoustic time‐of‐flight for proton range

verification in water. Medical physics, 43(9), 5213-

5224.

M. Riva, E. A. Vallicelli, A. Baschirotto, and M. De

Matteis, “Acoustic Analog Front End for Proton Range

Detection in Hadron Therapy,” IEEE Transactions on

Biomedical Circuits and Systems, Vol. 12, no. 4, pp.

954-962, April 2018.

Vallicelli, Elia A., et al. "Mixed-Signal Ionoacoustic

Analog Front-End for Proton Range Verification with

24 μm Precision at 0.8 Gy Bragg Peak Dose." 2019 26th

IEEE International Conference on Electronics, Circuits

and Systems (ICECS). IEEE, 2019.

Vallicelli, E. A., Turossi, D., Gelmi, L., Baù, A., Bertoni,

R., Fulgione, W., ... & De Matteis, M. (2020). A 0.3

nV/√ Hz input-referred-noise analog front-end for

radiation-induced thermo-acoustic pulses. Integration.

M.A. Samir, E. Dardiry, A Theory for Optimization in the

Use of Acoustic Emission Transducers, vol. 1, Roger

Hill, 1979

Vallicelli, Elia Arturo, et al. "22 dB Signal-to-Noise Ratio

Real-Time Proton Sound Detector for Experimental

Beam Range Verification." IEEE Transactions on

Circuits and Systems I: Regular Papers (2020).

Baschirotto, A., Delizia, P., D’Amico, S., Chironi, V.,

Cocciolo, G., & De Matteis, M. (2009). “Low power

analog design in scaled technologies”. Proceedings of

the Topical Workshop on Electronics for Particle

Physics, TWEPP 2009, Pages 103-109. Paris; France;

21 September 2009

De Matteis, M., D'Amico, S., & Baschirotto, A. (2006,

June). Power-minimization design procedure for Rauch

biquadratic cells. In 2006 Ph. D. Research in

Microelectronics and Electronics (pp. 141-144). IEEE.

Front-end Design Optimization for Ionoacoustic 200 MeV Protons Beam Monitoring with Sub-millimeter Precision for Hadron Therapy

Applications