3D Reconstruction of Deformable Objects from RGB-D Cameras: An

Omnidirectional Inward-facing Multi-camera System

Eva Curto

and Helder Araujo

Institute for Systems and Robotics, University of Coimbra, R. Silvio Lima, Coimbra, Portugal

Keywords:

Reconstruction, RGB-D, Omnidirectional, Multi-camera, Deformations.

Abstract:

This is a paper describing a system made up of several inward-facing cameras able to perform reconstruction of

deformable objects through synchronous acquisition of RGBD data. The conﬁguration of the camera system

allows the acquisition of 3D omnidirectional images of the objects. The paper describes the structure of the

system as well as an approach for the extrinsic calibration, which allows the estimation of the coordinate

transformations between the cameras. Reconstruction results are also presented.

1 INTRODUCTION

In this paper a system for the 3D reconstruction of de-

formable objects is described. The system is made up

of several inward-facing cameras to allow for the ac-

quisition of the whole surface of the object. The sys-

tem performs the synchronous and time-stamped ac-

quisition of RGB-D images enabling the synchronous

acquisition of 3D images of deformations. Therefore,

the main contribution of this work is the assembly of

the system itself, putting together and setting up the

appropriate hardware and software.

The ﬁrst algorithms for RGB-D-based dense 3D

geometry reconstruction were developed only for

static scenes. (Curless and Levoy, 1996) introduced

the fundamental work of volumetric fusion and in-

spired the most modern approaches. The ability to

provide real-time RGB-D reconstruction appears in

2002 with a system based on a 60 Hz structured-

light rangeﬁnder (Rusinkiewicz et al., 2002). Al-

though it is no longer a recent algorithm, KinectFu-

sion (Newcombe et al., 2011) had a signiﬁcant impact

on the computer graphics and vision communities.

This work was the basis for many new methods of

3D reconstruction of static and dynamic scenes. They

proposed the fusion of all data streamed from a Kinect

sensor into a single global implicit surface model of

the observed (static) scene in real-time. The current

sensor pose is simultaneously obtained by tracking

the live depth frame relative to the global model us-

https://orcid.org/0000-0002-0477-0091

https://orcid.org/0000-0002-9544-424X

ing a coarse-to-ﬁne Iterative Closest Point (ICP) al-

gorithm, which uses all the observed depth data avail-

able. The real-time system of (Whelan et al., 2016)

is capable of capturing comprehensive dense globally

consistent surfel-based maps of room scale environ-

ments. The online BundleFusion approach of (Dai

et al., 2017) allows a robust pose estimation, optimiz-

ing per frame for a global set of camera poses by con-

sidering the complete history of RGB-D input with an

efﬁcient hierarchical method.

The ﬁrst approach to handle online deformable

tracking of arbitrary general deforming objects was

the template-based method presented by (Zollh

ofer

et al., 2014). In VolumeDeform (Innmann et al.,

2016), they propose using sparse RGB feature match-

ing to improve tracking robustness and handle scenes

with a little geometric variation. Besides, they pro-

pose an alternative representation for the deforma-

tion warp ﬁeld. Unlike DynamicFusion (Newcombe

et al., 2015), VolumeDeform uses the same volumet-

ric model to represent the reconstructed space. The

previous methods, (Newcombe et al., 2015), (Inn-

mann et al., 2016), achieved excellent results. How-

ever, they have a few limitations. The intermittent

conversion from Signed Distance Field (SDF) to mesh

for correspondence estimation leads to loss of accu-

racy, computational speed, and the capability to cap-

ture topological changes conveniently. Additionally,

both require 6D motion to be estimated per grid point,

while a 3D ﬂow ﬁeld is sufﬁcient in Miroslava et al.

(Slavcheva et al., 2017) method - KillingFusion - due

to the dense smooth nature of the SDF representation

and the use of alignment constraints directly over the

544

Curto, E. and Araujo, H.

3D Reconstruction of Deformable Objects from RGB-D Cameras: An Omnidirectional Inward-facing Multi-camera System.

DOI: 10.5220/0010347305440551

In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages

544-551

ISBN: 978-989-758-488-6

ﬁeld. Therefore, KillingFusion provides a non-rigid

reconstruction pipeline, based on a single data repre-

sentation – SDF, which does not require explicit cor-

respondences and can handle topological changes.

The previous method employs a combination of

two regularizers, which are challenging to balance

and thus result in over-smoothing and loss of high-

frequency details. SobolevFusion (Slavcheva et al.,

2018) proposes to deﬁne the gradient ﬂow in Sobolev

space H

−1

instead of a gradient ﬂow based on an L

inner product, which is known to be susceptible to lo-

cal minima.

This section introduced the work discussed in this

paper as well as referred some state-of-art techniques

in 3D reconstruction. This paper has the follow-

ing structure: Section 2 describes the camera’s sys-

tem and the surrounding setup and explains how the

cameras were synchronized by hardware. The third

section explains the method of extrinsic calibration

used to obtain the relative position and orientation.

Then, in Section 4, we have the reconstruction phase

described and illustrated with reconstructed objects.

The ﬁnal considerations of this paper are stated in sec-

tion 5.

2 SYSTEM DESCRIPTION

2.1 Cameras

Our camera system is composed of four Intel Re-

alsense D415 cameras. The choice of these cameras

took into account several factors:

• Low cost;

• The D415 come with Intel’s RealSense SDK 2.0,

which is an open-source, cross-platform SDK;

• Their ﬁeld of view is well suited for high accuracy

applications such as 3D scanning;

• The rolling shutter on the depth sensor allows us

to have highest depth quality per degree.

• Theses cameras can all be hardware synchronized

to capture at identical times and frame rates.

Considering that this work proposes the omnidirec-

tional reconstruction of objects, these speciﬁcations

are satisfactory for the applications envisaged.

The D415, showed in Figure 1, has two main com-

ponents, the vision processor and the depth module.

The vision processor D4 is either on the host proces-

sor motherboard or on a discrete board with either

USB3.0 Gen1 or MIPI connection to the host proces-

sor. The depth module includes left and right imagers

Figure 1: Image of a RealSense D415 camera.

for stereo vision with the optional IR projector

and RGB color sensor.

The essential speciﬁcations of the D415 camera are

indicated in Table 1.

Table 1: Speciﬁcations of Intel RealSense D415.

Features

Use Environment:

Indoor/Outdoor

Image Sensor Technology:

Rolling Shutter,

1.4µm × 1.4µm pixel size

Maximum Range:

Approx. 10 meters.

Depth

Depth Technology:

Active IR Stereo

Minimum Depth Distance (Min-Z):

0.16m

Depth Field of View (FOV):

◦

±2

◦

× 40

◦

±1

◦

× 72

◦

±2

◦

Depth Output Resolution:

Up to 1280 × 720

Depth Frame Rate:

Up to 90 fps

RGB

RGB Sensor Resolution:

1920 × 1080

RGB Sensor FOV (H x V x D):

69.4

◦

× 42.5

◦

× 77

◦

(±3

◦

)

RGB Frame Rate:

30 fps

2.2 Experimental Setup

Each camera is mounted on a C clamp camera sup-

port, which is ﬁxed to the table. The cameras are

equally distant between neighboring cameras since

we intend to maximize the horizontal ﬁelds of view.

The objects that will be reconstructed are illuminated

by led light in addition to natural light. In order to

avoid problems with specular reﬂections that could

induce more noise in RGBD acquisition and conse-

quently conduce to poor reconstruction results, we

opted to use a metallic table painted with a matte

black color. Matte allows avoiding specular reﬂec-

3D Reconstruction of Deformable Objects from RGB-D Cameras: An Omnidirectional Inward-facing Multi-camera System

545

tions while metallic allows for the absorption of the

IR energy.

The synchronous acquisition of RGB-D images

from multiple cameras (four in the case) requires a

host system with enough processing power to read

from the USB ports streaming the high-bandwidth

data, and doing some amount of the real-time post-

processing, rendering, and analysis. All the work

from the data acquisition, calibration to the recon-

struction was made on a PC. This was a processor

with a Intel Core i9-9900k CPU @ 3.60GHz x 16,

a GeForce RTX 2070/PCle/SSE2, running Ubuntu

16.06 LTS.

The setup described in this section is shown in

Figure 2.

Figure 2: Picture of the omnidirectional camera system.

2.3 Hardware Synchronization

One of the requirements for our setup is the synchro-

nization between cameras, since it should also per-

form the estimation of 3D deformations.

Hardware synchronization is described in

(Grunnet-Jepsen et al., 2018), from Intel. Following

this reference, we connected the cameras via synchro-

nization cables, considering three of the cameras as

slaves and the fourth one as master. For each camera,

depth and color frames are saved as well as the

metadata. For each frame the following information

is saved: the serial number of the camera, the type

of stream (color or depth), the frame timestamp,

the sensor timestamp, the actual exposure, the gain

level, the boolean value of auto-exposure, the time of

arrival, the backend timestamp and the actual fps.

Using a hub to connect the four cameras to the

PC, the higher resolution that we achieve with the

hardware synchronization and all the color and depth

streams activated was 640 × 360. Thus, all the acqui-

sitions were made with this resolution setting.

3 EXTRINSIC CAMERA

CALIBRATION

This section begins with a brief description of the

extrinsic calibration. Then the multi-camera method

used is described.

3.1 Theory

Considering m cameras and n object points

, Y

, Z

, 1]

, j = 1, ..., n. We assume the pinhole-

camera model. The 3D points

are projected to 2D

image points ˜x

˜x









= λ

˜x

= P

, λ

∈ R

(1)

where u, v are pixel coordinates, λ

the scale factors

and P

is the projection matrix of a given camera. This

3 x 4 matrix has 11 degrees of freedom. This projec-

tion matrix can be further decomposed as:

= K

], (2)

where K

is the matrix of the intrinsic parameters, R

is the rotation matrix relative to the world coordinate

system and t

is the translation vector relative to the

world coordinate system.

We aim at estimating the relative positions and ori-

entations between the reference coordinate systems of

the depth cameras. The relative positions and ori-

entations are described by 6 parameters, being 3 for

rotation and 3 for translation. These are the exter-

nal/extrinsic parameters. In the case of this setup the

intrinsic parameters as well as the extrinsic parame-

ters between the cameras of each stereo pair and the

rgb camera and depth cameras are obtained from the

RealSense SDK. Then, the goal of the calibration is

to estimate the relative rotations and translations be-

tween the four different depth cameras (each of which

uses a coordinate system attached to the left camera of

each pair).

Figure 3 shows a schematic diagram of a four-

camera setup.

3.2 Overview of the Multi-camera

Method

The point clouds obtained by each depth camera are

expressed in their coordinate system. To obtain the

relative transformation we based our approach on the

method described in (Matsumoto and Aguilar-Rivera,

2018). This multi-camera calibration method is, on

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

546

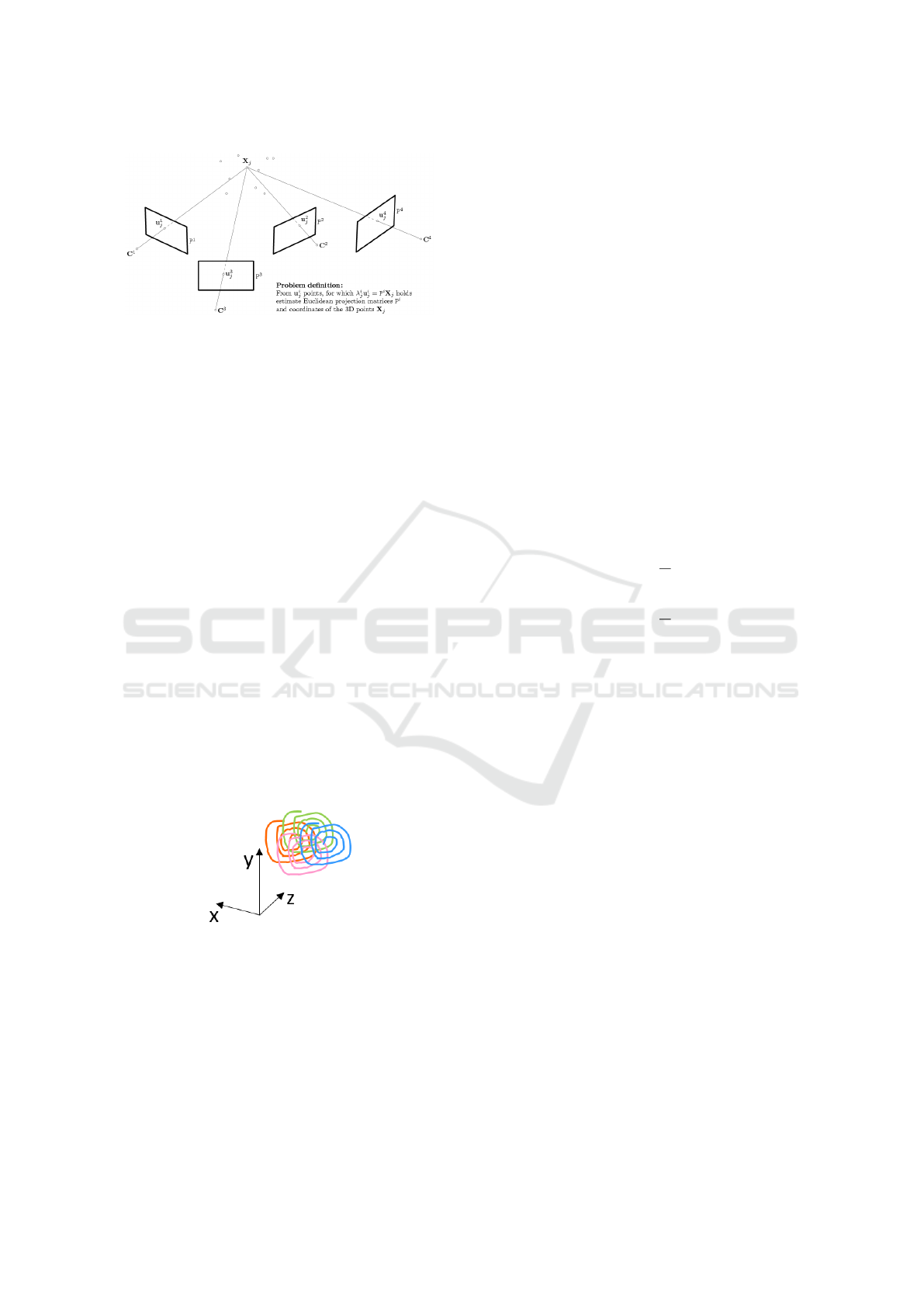
Figure 3: Multi-Camera calibration problem (Svoboda

et al., 2005).

the other hand, based on the approach described in

(Svoboda et al., 2005), where a small and easily de-

tectable bright spot is used to create a virtual calibra-

tion object. This bright spot is simultaneously visible

in all cameras avoiding the occurrence of occlusion.

Since the cameras are synchronized, the user has only

to wave the light through the working volume, there-

fore generating the required data. The remaining cal-

ibration procedure is fully automatic. The bright spot

projections are detected independently in each RGB

camera, so the correspondences are established by the

time stamps. Each detected point is also mapped into

the depth image. Before starting to generate the 3D

trajectory for calibration, the environment illumina-

tion is dimmed and the user can adjust the brightness

threshold for pointer detection and tracking. As a re-

sult, the detection of the light spot both in the RGB

image and in the infrared images (depth) is facilitated

and robust. The pointer location in the RGB image is

converted to the corresponding location in the depth

image. From the depth image, the 3D position of the

pointer (relative to the camera) was estimated. Figure

4 illustrates the four 3D trajectories, each one of them

regarding one speciﬁc camera.

Figure 4: Illustration of 3D trajectories for extrinsic calibra-

tion.

These trajectories are then ﬁltered to remove out-

liers. The resulting ﬁltered 3D points of each trajec-

tory are then used to estimate the relative orientations

and translations between cameras.

3.3 Finding Optimal Rotation and

Translation between Corresponding

3D Points

The optimal rigid 3D registration problem can be

characterized, according to (Arun et al., 1987) with:

RA +t = B, (3)

for noise-free data. Since the data is noisy, the least-

squares error is minimized by:

err =

∑

i=1

||RA

+t −B

, (4)

where A and B are sets of 3D points with known cor-

respondences. R is a 3 × 3 rotation matrix and t is the

3 × 1 translation vector.

To estimate the optimal rigid transformation, both

point clouds are centered at the origins of their co-

ordinate systems. Therefore, the centroids of both

datasets are ﬁrst estimated:

centroid

∑

, (5)

centroid

∑

, (6)

where A

and B

are 3 × 1 vectors, corresponding to

the point pair i, with the coordinates of the 3D points,

i.e., [X, Y, Z]

To ﬁnd the optimal rotation, we ﬁrst re-center both

datasets so that both centroids are at origin. This re-

moves the translation component, leaving only the

rotation to estimate. The rotation is estimated using

the SVD method by Arun, performed on the point-set

cross-covariance matrix given by (Kanatani, 1994):

H = (A − centroid

)(B − centroid

)

, (7)

[U, S, V ] = SV D(H), (8)

R = VU

, (9)

where H is the point-set cross-covariance matrix and

A − centroid

is an operation that subtracts each col-

umn in A by centroid

. When ﬁnding the rotation

matrix, we have to take into account the case of the re-

ﬂection matrix. That is, sometimes, the SVD method

returns this reﬂection matrix, which is numerically

correct but is nonsense. This is addressed by check-

ing the determinant of R and checking if it is negative

(-1). If it is, then the 3rd column of V is multiplied by

-1.

3D Reconstruction of Deformable Objects from RGB-D Cameras: An Omnidirectional Inward-facing Multi-camera System

547

After the rotation matrix is found, we estimate t

using the initial equation (3) RA + t = B but using the

centroids:

R × centroid

+t = centroid

, (10)

t = centroid

− R × centroid

. (11)

3.4 Evaluation of the Calibration

Using the data acquired as previously described, the

estimation of the relative rotation matrices and rel-

ative translation vectors can be performed. Since

we are dealing with an omnidirectional system (Fig-

ure 5), a relative simple criterion can be applied to

estimate the overall estimation error. Assume that



1×3



represents the coordinate transfor-

mation from coordinate system i to coordinate system

j. Then, in the speciﬁc case of four coordinate sys-

tems the following condition holds:

= I

4×4

(12)

This condition can be used to obtain an estimation

of the overall error in the four coordinate transforma-

tions. In general the errors obtained are small, with

the overall translation error smaller than 5% of the

distance between consecutive images. Errors in each

coordinate transformation can be minimized by using

the above error criterion in a global optimization pro-

cedure.

Figure 5: Schematic diagram representing the transforma-

tions between cameras.

4 RECONSTRUCTION

The reconstruction of a deformable object is possi-

ble since we have a synchronous acquisition system

of RGBD data and the relative positions and orienta-

tions of the cameras are known. These transforma-

tions allow us to combine the four point clouds. The

coordinate system of one of the cameras is used as a

reference coordinate system.

Since the visual ﬁelds of adjacent cameras over-

lap, duplicated points occur in the omnidirectional

point cloud. This can lead to a non-homogeneous re-

construction. To overcome this issue, the omnidirec-

tional merged point cloud is ﬁltered using the Vox-

elGrid ﬁlter from PCL library. The VoxelGrid ﬁlter

downsamples the point cloud by taking a spatial aver-

age of the points in the cloud conﬁned by each voxel.

The set of points which lie within the bounds of a

voxel are assigned to that voxel and are statistically

combined into one output point.

In this paper, diverse examples of object recon-

struction are presented. Firstly, we analyze the re-

constructions of a small wooden box and of a shoe

with a mold—two different objects in terms of shape,

material and color. Then, we reconstruct two white

polystyrene spheres with different radius. For the re-

construction of the spheres, in an attempt to mitigate

the noise involving the object, three acquisitions of

each camera were used to generate a mean point cloud

for the respective camera. The four mean point clouds

(corresponding to the four cameras) are then trans-

formed and ﬁltered in one merged point cloud, simi-

lar to the previous reconstructions. Finally, the recon-

struction of a deformable object is presented, a hippo

balloon, in different stages of emptying.

4.1 Reconstruction of a Wooden Box

and a Shoe

The omnidirectional system synchronously acquired

RGB-D data viewed by each camera pointed at the

box. The different views taken at the same timestamp

of the wooden box are shown in Figure 6.

Figure 6: The four different views of the wooden box.

Figures 7 and 8 show the reconstruction of the

wooden box in different perspectives. We can notice

some noise around the corners of the box and also the

lack of sharpness of the upper face.

The shoe, unlike the box, is very curved and made

of a much brighter material. The different views of

the shoe taken at the same timestamp are in Figure 9.

In the shoe reconstructions, presented in Figures

10 and 11, it is possible to observe that, since it has

no corners, there is not as much noise as in the case

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

548

Figure 7: Real box on the left and reconstructed box on the

right: ﬁrst perspective view.

Figure 8: Real box on the left and reconstructed box on the

right: second perspective view.

Figure 9: The four different views of the shoe.

Figure 10: Real shoe on the left and reconstructed shoe on

the right: ﬁrst perspective view.

Figure 11: Real shoe on the left and reconstructed shoe on

the right: second perspective view.

of the box. On the other hand, we have some holes,

well visible in Figure 11, resulting from specular re-

ﬂections.

4.2 Reconstruction of Two White

Polystyrene Spheres

The two spheres used for reconstruction are made

of white polystyrene and have a very soft surface.

The smaller sphere has approximately 3cm of radius,

while the bigger has approximately 7.5cm. The two

spheres can be seen in Figure 12.

Figure 12: Picture of the two spheres. The smaller sphere

(3cm radius) on the left and the bigger (7.5cm radius) on the

right side.

As mentioned before, for the reconstruction of the

spheres three point clouds from each camera were ac-

quired, with the aim of generating an average point

cloud. In Figure 13 the average point clouds for the

biggest sphere are presented.

Figure 13: The four different views of the sphere.

Similar to the other reconstructions, these views

are then used to build the omnidirectional point cloud.

In order to analyze the quality of the reconstructions,

for both, the 3cm radius and the 7,5cm radius sphere,

the approximated model of the spheres was estimated.

The parameters of the models were obtained using a

robust estimator, the M-estimator SAmple Consen-

sus (MSAC) algorithm (Torr and Zisserman, 2000).

This RANSAC variation is based on the following

steps: drawing randomly a minimal sample set; esti-

mating the model and then evaluating the model. This

process is repeated until the last iteration that corre-

sponds to the best model.

In Figures 14 and 15, we can view the estimated

model of the spheres ﬁtting the point clouds of the

real spheres.

To analyze the reconstruction of the spheres we

used the mean error, that is, the average of the dis-

tances from the inliers points (points belonging to the

point cloud that were used to estimate the paramet-

ric model of the sphere) to the surface of the sphere

generated by the parametric model. In table 2, the av-

erage errors for the two spheres are presented for four

cases namely: the reconstruction made with only one

acquisition per camera, 1

acquisition, 2

acquisi-

tion and 3

acquisition and the reconstruction made

3D Reconstruction of Deformable Objects from RGB-D Cameras: An Omnidirectional Inward-facing Multi-camera System

549

Figure 14: On the left side we have the point cloud of the

7,5cm radius sphere and on the right side, the point cloud

and the plot of the sphere model.

Figure 15: On the left side we have the point cloud of the

3cm radius sphere and on the right side, the point cloud and

the plot of the sphere model.

with the mean point clouds. The smallest average er-

ror is obtained for the reconstruction performed with

the mean point clouds.

Table 2: The mean errors obtained for the different esti-

mates of the parametric models.

Sphere of radius 7.5cm Sphere of radius 3cm

acq. 0.0034m 0.0020m

acq. 0.0029m 0.0020m

acq. 0.0033m 0.0021m

Mean of acq. 0.0021m 0.0017m

4.3 Reconstruction of a Hippo Balloon

Deforming

For the reconstruction of the balloon in Figure 16,

point clouds were acquired during its emptying.

The balloon was reconstructed in three different

stages/time instants, considering that in each stage,

the images from each camera are synchronized. The

reconstructions are shown in Figure 17, where a plot

with the three point clouds together is also presented.

Figure 16: Picture of the hippo-shaped balloon.

Figure 17: The ﬁrst three plots show the hippo balloon’s

reconstructions in three different sequential phases of the

emptying. The fourth image illustrates the three point

clouds, being notorious the deformation occurring with the

emptying.

5 CONCLUSION

This paper describes a system designed to acquire

synchronized 3D omnidirectional images of objects.

That allows for the 3D reconstruction of objects that

are articulated or deformable. The experimental re-

sults show that specular surfaces as well as sharp cor-

ners do not yield good quality reconstructions. Since

no controlled illumination is used in the system, we

plan to add an illumination system to improve the re-

construction quality. The reconstructions of spheres

allow us to conclude that the reconstructions that use

the mean of point clouds from each camera seem to

have a lower mean error relative to its sphere models,

which is an indicator that reconstruction itself is also

better. Finally, the balloon’s reconstruction shows that

this system is suitable for the reconstruction of objects

that deform.

ACKNOWLEDGEMENTS

This work was partially supported by Project COM-

MANDIA SOE2/P1/F0638, from the Interreg Sudoe

Programme, European Regional Development Fund

(ERDF), and by the Portuguese Government FCT,

project no. 006906, reference UID/EEA/00048/2013.

VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications

550

REFERENCES

Arun, K. S., Huang, T. S., and Blostein, S. D. (1987). Least-

squares ﬁtting of two 3-d point sets. IEEE Trans-

actions on pattern analysis and machine intelligence,

(5):698–700.

Curless, B. and Levoy, M. (1996). A volumetric method for

building complex models from range images. In Pro-

ceedings of the 23rd annual conference on Computer

graphics and interactive techniques, pages 303–312.

Dai, A., Nießner, M., Zollh

ofer, M., Izadi, S., and Theobalt,

C. (2017). Bundlefusion: Real-time globally consis-

tent 3d reconstruction using on-the-ﬂy surface rein-

tegration. ACM Transactions on Graphics (ToG),

36(4):1.

Grunnet-Jepsen, A., Winer, P., Takagi, A., Sweetser, J.,

Zhao, K., Khuong, T., Nie, D., and Woodﬁll, J. (2018).

Using the Intel

 RealSense TM Depth cameras

D4xx in Multi-Camera Conﬁgurations.

Innmann, M., Zollh

ofer, M., Nießner, M., Theobalt, C.,

and Stamminger, M. (2016). Volumedeform: Real-

time volumetric non-rigid reconstruction. In Euro-

pean Conference on Computer Vision, pages 362–379.

Springer.

Kanatani, K.-i. (1994). Analysis of 3-d rotation ﬁtting.

IEEE Transactions on pattern analysis and machine

intelligence, 16(5):543–549.

Matsumoto, J. and Aguilar-Rivera, M. (2018). 3DTracker-

FAB documentation.

Newcombe, R. A., Fox, D., and Seitz, S. M. (2015). Dy-

namicfusion: Reconstruction and tracking of non-

rigid scenes in real-time. In Proceedings of the IEEE

conference on computer vision and pattern recogni-

tion, pages 343–352.

Newcombe, R. A., Izadi, S., Hilliges, O., Molyneaux, D.,

Kim, D., Davison, A. J., Kohi, P., Shotton, J., Hodges,

S., and Fitzgibbon, A. (2011). Kinectfusion: Real-

time dense surface mapping and tracking. In 2011

10th IEEE International Symposium on Mixed and

Augmented Reality, pages 127–136. IEEE.

Rusinkiewicz, S., Hall-Holt, O., and Levoy, M. (2002).

Real-time 3d model acquisition. ACM Transactions

on Graphics (TOG), 21(3):438–446.

Slavcheva, M., Baust, M., Cremers, D., and Ilic, S. (2017).

Killingfusion: Non-rigid 3d reconstruction without

correspondences. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 1386–1395.

Slavcheva, M., Baust, M., and Ilic, S. (2018). Sobolev-

fusion: 3d reconstruction of scenes undergoing free

non-rigid motion. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 2646–2655.

Svoboda, T., Martinec, D., and Pajdla, T. (2005). A con-

venient multicamera self-calibration for virtual envi-

ronments. Presence Teleoperators Virtual Environ.,

14(4):407–422.

Torr, P. H. and Zisserman, A. (2000). Mlesac: A new ro-

bust estimator with application to estimating image

geometry. Computer vision and image understanding,

78(1):138–156.

Whelan, T., Salas-Moreno, R. F., Glocker, B., Davi-

son, A. J., and Leutenegger, S. (2016). Elasticfu-

sion: Real-time dense slam and light source estima-

tion. The International Journal of Robotics Research,

35(14):1697–1716.

Zollh

ofer, M., Nießner, M., Izadi, S., Rehmann, C., Zach,

C., Fisher, M., Wu, C., Fitzgibbon, A., Loop, C.,

Theobalt, C., et al. (2014). Real-time non-rigid recon-

struction using an rgb-d camera. ACM Transactions

on Graphics (ToG), 33(4):1–12.

3D Reconstruction of Deformable Objects from RGB-D Cameras: An Omnidirectional Inward-facing Multi-camera System

551