
A Random Walker Can Optimize the Exploration without the Large
Capacity Memory
Tomoko Sakiyama
a
Department of Information Systems Science, Faculty of Science and Engineering, Soka University, Tokyo 192-8577, Japan
Keywords: Random Walk, Super-diffusion, Memory, Resource Distribution.
Abstract: A random walker explores an unknown field and sometimes changes its movement property using new spatial
information obtained by it during its exploration. An important matter is the relation between the movement
property of a random walker and the use for acquired information. I recently developed a random walk model
in which a walker coordinated its directional rule based on its experiences and found that this model presented
an optimal random walk, which demonstrated a so-called Lévy walk with μ = 2.00. Here, I investigate the
foraging efficiency for that model and verify whether a large memory capacity is required or not in order to
maintain the foraging efficiency. My findings reveal that the proposed model can apply to biological processes
where a random walker does not have a high memory capacity.
1 INTRODUCTION
Animals demonstrate random search in the absence of
prior knowledge in order to get some information,
such like spatial information (Kareiva and Shigesada,
1983; Viswanathan et al. 2001; Bartumeus et al. 2005,
2008; Bartumeus and Levin, 2008). Many random
search models such like the Lévy walk or the
Brownian walk model are effective for random
exploration and have been very well studied
(Bartumeus et al. 2005, 2008; Bartumeus and Levin,
2008). A Lévy walk, which exhibits a scale-free
distribution, is defined as a process where an agent
takes steps of length l at each time and the probability
density function of those steps decays asymptotically
as a power law:
P(l) ~ l
−μ
, where 1 < μ ≦3
Several studies of animal foraging strategies
have reported that Lévy walks are efficient where
resource is sparse and randomly distributed
(Bartumeus et al. 2005; Humphries and Sims,2014).
On the contrary, the advantage of Lévy walks will
disappear in high-density environments where
resource is abundant (Bartumeus et al. 2005;
Humphries and Sims,2014). The Lévy and
Brownian walks show similar exploration
a
https://orcid.org/0000-0002-2687-7228
efficiencies if extremely abundant resources are
available for random walkers.
The search ability for food resources is a matter of
life and death for random walkers. To this end, the
search ability of random walk models has been
extensively investigated (Sakiyama and Gunji, 2013).
Recently, I developed a random walk model named
as the self-reference model (Sakiyama, 2020). A
walker in that model avoids a certain direction using
the past information. At the same time however, the
walker modulates its directional rule if it experiences
some directional inconsistencies in the recent series
of its movements. The self-reference model exhibited
a so-called power-law tailed movement with optimal
μ value (μ ≈ 2.0) (Bartumeus et al. 2005). In this
paper, I check the paramenter effects by examining
the performance of resource search ability of this
model. Here, a random walker obeying that model
explores a two-dimensional field where food
resources are distributed. I investigate the parameter
effects in respect with the exploration ability of the
walker and discuss the unnecessity of a large memory
capacity.
Sakiyama, T.
A Random Walker Can Optimize the Exploration without the Large Capacity Memory.
DOI: 10.5220/0010369902090212
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 3: BIOINFORMATICS, pages 209-212
ISBN: 978-989-758-490-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
209

2 MATERIALS & METHODS
2.1 The Self-reference Walks
Each trial is run for a maximum of 1,000 time steps.
Field size is set to 1,000 × 1,000. Periodic boundary
is assumed. I set the simulation stage for each trial and
set the agent at the origin; (x (0), y (0)) = (0, 0). In this
algorithm, the agent moves in two-dimensional
square lattices. On each time step, the agent selects
one direction among four discrete directions and
updates its position like follows;
(x (t+1), y (t+1)) = (x (t)+1, y (t)) with Prob (+x),
(x (t+1), y (t+1)) = (x (t)-1, y (t)) with Prob (-x),
(x (t+1), y (t+1)) = (x (t), y (t)+1) with Prob (+y),
(x (t+1), y (t+1)) = (x (t), y (t)-1) with Prob (-y),
Prob (+x) + Prob (-x) + Prob (+y) + Prob (-y) = 1.00.
At the beginning of each trial, the agent equally
selects each direction.
A directional move that consists of a series of the
different move, such as +y, -x or +x, +y and so on, is
counted as
if (x (t+1) - x (t)) = (x (t) - x (t-1)) = ±1
or (y (t+1) - y (t)) = (y (t) - y (t-1)) = ±1,
Exp (t+1) = Exp (t),
otherwise,
Exp (t+1) = Exp (t) + 1
For example, “Exp (t+1)” can be “Exp (t) + 1” when
the agent moves in +x direction at time t-1 and is
going to move in -x direction at time t.
If Exp (t) exceeds a threshold number, th, the four
directional probabilities are changed as follows and
the agent obeys these new rules from the next time
step;
if x (t+1) - x (t) = +1,
Prob (+x) = φ,
Prob (-x) = Prob (+y) = Prob (-y) = (1-φ)/3
if x (t+1) - x (t) = -1,
Prob (-x) = φ,
Prob (+x) = Prob (+y) = Prob (-y) = (1-φ)/3
if y (t+1) - y (t) = +1,
Prob (+y) = φ,
Prob (+x) = Prob (-x) = Prob (-y) = (1-φ)/3
if y (t+1) - y (t) = -1,
Prob (-
y) = φ,
Prob (+x) = Prob (-x) = Prob (+y) = (1-φ)/3
Here, φ indicates a random number that satisfies
ratio is the element of a set [0.25, 1.00]. Here, the
maximum random number was set to 1.00 in order to
produce a straight movement toward a certain
direction. Note that Exp (t) is reset to 0 at that time.
The agent obeys a biased directional rule in order
to avoid moving in a certain direction. By doing so,
the agent can avoid visited positions to some extent
and effectively explore. At the same time however,
the agent modifies its rule when the agent experiences
several series of the different directional move such
like +x, -x or -y, -x and so on.
Only at first, i.e., at time t=0, where the agent
calculates (x (1), y (1)) by obeying a Brownian-like
walk, the four directional probabilities are modified
as follows independently of Exp (t):
if x (1) - x (0) = +1,
Prob (+x) = φ,
Prob (-x) = Prob (+y) = Prob (-y) = (1-φ)/3
if x (1) - x (0) = -1,
Prob (-x) = φ,
Prob (+x) = Prob (+y) = Prob (-y) = (1-φ)/3
if y (1) - y (0) = +1,
Prob (+y) = φ,
Prob (+x) = Prob (-x) = Prob (-y) = (1-φ)/3
if y (1) - y (0) = -1,
Prob (-y) =
φ,
Prob (+x) = Prob (-x) = Prob (+y) = (1-φ)/3
In our simulations, th is set to 5 as a default value.
3 RESULTS
Here, food resources are randomly distributed on the
field and the resource density is set to 0.001. The
agent can consume food items if those items are
located within 5.0 radii. Food depletion, which means
that food items disappear once the agent consumes
those items, does not occur. Therefore, the agent can
consume each food item whenever it detects that item
within 5.00 radii. Later however, I will check the
effect of the resource density and the food depletion.
Food depletion is an important factor for the search
ability and the movement strategy of random walkers.
This is because the random walker with sub-diffusive
movements does not have a trouble with consuming
food resources if food depletion does not occur since
it can find and consume resources again and again.
On the contrary, the random walker may need to
change its strategy if food depletion occurs due to the
fact that no items can be found by the walker once it
consumes those items. Therefore, the effects of food
depletion will reveal the performance of my model.
Paradigms-Methods-Approaches 2021 - Workshop on Novel Computational Paradigms, Methods and Approaches in Bioinformatics
210
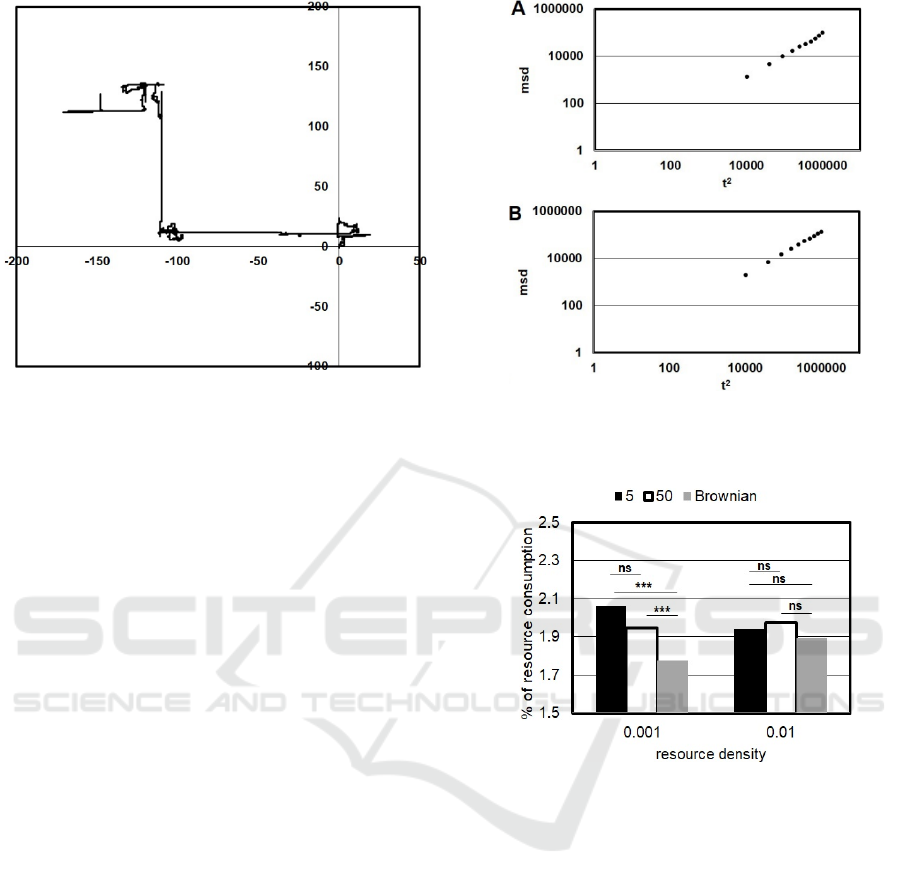
Figure 1: An example of the agent’s trajectories where the
resource depletion does not occur. The parameter th = 5.
First, I focus on movement properties of the
model. Figure 1 shows an example of an agent
trajectory obtained from 1 trial. According to this
figure, the agent seems to sometimes produce straight
movements. In fact, the mean squared displacement
(msd) between the start point and end points reveals
that the agent demonstrates a super diffusive
movement (Figure 2A). Here, each end point was
obtained every 100 time steps and each msd obtained
from 100 trials was plotted. In the random walk
analysis, the relation between the mean squared
displacement <R
2
> and the step is often calculated
since this property presents the diffusive property of
the walker. It is well known that his property follows
the following relation (Viswanathan et al. 1999):
<R
2
> ~ t
2H
Parameter H is determined depending on the
model (H>1/2 for a Lévy walk (super-diffusion),
H=1/2 for a Brownian walk (normal diffusion) and
H<1/2 for sub-diffusive movements). The fit for
parameter H according to Figure 2 was H ~ 0.91,
indicating that super-diffusion was achieved (R-
squared=0.99).
For the evaluation of the parameter effects, I
replaced the parameter th from 5 with 50. Figure 2B
represents the diffusive property in case of th = 50.
Results suggest that super-diffusive movements can
be maintained even after the parameter replacement
(Figure 2B: threshold = 50, H ~ 0.91, R-squared =
0.99).
Figure 2: Log-scale plot of mean squared displacement
(msd) and t
2
obtained from 100 trials for each threshold. A.
th = 5. B. th = 50.
Figure 3: % of resource consumption in respect with
resource density; 0.001 and 0.01 for each threshold value
and for the Brownian walker under the condition where the
resource depletion does not occur. *** indicates p < 1.0E-
03, ns indicates non-significant.
In fact, the resource search ability of this model
seems to be not dependent on the parameter threshold.
According to Figure 3, which showed the fraction of
the resource consumption, I found that there was no
significant difference between th =5 and 50 (Figure 3:
resource density = 0.001, th =5 (2.06) vs. th = 50
(1.95), Mann-Whitney U test, P = 0.58, NS).
Furthermore, this tendency is not changed even after
the resource density is replaced with 0.01(Figure 3:
resource density = 0.01, th =5 (1.94) vs. th = 50
(1.97), Welch Two Sample t-test, t = -0.69, df =
195.88, P = 0.49, NS) Here, I counted the number of
resources consumed by the agent on each trial and
converted it to the percentage against the total number
distributed on the field. Importantly, I found that the
A Random Walker Can Optimize the Exploration without the Large Capacity Memory
211

proposed model outperformed the Brownian walk
model when resource density was low (Figure 3:
resource density = 0.001, th =5 (2.06) vs. Brownian
(1.78), Mann-Whitney U test, P < 1.0E-04, th =50
(1.95) vs. Brownian (1.78), Mann-Whitney U test, P
< 1.0E-04, resource density = 0.01, th =5 (1.94) vs.
Brownian (1.90), Welch Two Sample t-test, t = 0.57,
df = 134.35, P = 0.57, NS, th =50 (1.97) vs. Brownian
(1.90), Welch Two Sample t-test, t = 0.96, df =
141.83, P = 0.34, NS). These results suggest that the
proposed model can search effectively in the low-
density environment and the performance is not
affected by the parameter threshold. In other words,
the agent is not necessarily to remember a large
number of “Exp”.
To investigate the influence of the food depletion
to the search ability, I also conducted the same
analysis under the condition where resource items
were depleted once the agent consumed items. Figure
4 indicates that the proposed model again
outperforms the Brownian walker model.
Interestingly, this tendency is found not only in the
low density environment but also in the (relative)
high density environment (Figure 4: resource density
= 0.001, th =5 (0.17) vs. th = 50 (0.16), Mann-
Whitney U test, P = 0.31, NS, resource density = 0.01,
th=5 (0.17) vs. th = 50 (0.17), Mann-Whitney U test,
P = 0.39, NS, resource density = 0.001, th =5 (0.17)
vs. Brownian (0.03), Mann-Whitney U test, P < 1.0E-
15, th =50 (0.16) vs. Brownian (0.03), Mann-Whitney
U test, P < 1.0E-15, resource density = 0.01, th =5
(0.17) vs. Brownian (0.03), Mann-Whitney U test, P
< 1.0E-15, th =50 (0.17) vs. Brownian (0.03), Mann-
Whitney U test, P < 1.0E-15). This is perhaps because
a Brownian walker presents normal-diffusive
movements, which may result in the inefficient search
of the food resources under the condition where
resource items are depleted.
Figure 4: % of resource consumption in respect with
resource density; 0.001 and 0.01 for each threshold value
and for the Brownian walker under the condition where the
resource depletion occurs. *** indicates p < 1.0E-03, ns
indicates non-significant.
4 CONCLUSIONS
In the developed random walker algorithm, the agent
modulates its directional rule and avoids a certain
direction. However, it modifies its directional rule
when the inconsistency of the recent series of the
directional move beyond a threshold value. As a
results, I found that the agent presented and
maintained super-diffusive movements in some
threshold values. Thanks to this, that model
outperforms the Brownian walk model when the
resource density is low or when resources are
depleted once the agent consumes those items.
Moreover, the performance of resource search ability
was not influenced by the threshold replacement.
These results suggest that the proposed model does
not require the large number of “Exp” to achieve an
effective search.
REFERENCES
Bartumeus, F., Catalan, J., Viswanathan, G.M., Raposo,
E.P., Luz, M.G.E., 2008. The influence of turning
angles on the success of non-oriented animal
searches. J. Theor. Biol. 252, 43-
55.doi:10.1016/j.jtbi.2008.01.009.
Bartumeus, F., Levin, S.A., 2008. Fractal reorientation
clocks: linking animal behavior to statistical patterns of
search. Proc. Natl Acad. Sci. USA 105, 19072–19
077.doi:10.1073/pnas.0801926105.
Bartumeus, F., Luz, M.G.E., Viswanathan, G.M., Catalan,
J., 2005. Animal search strategies: a quantitative
random-walk analysis. Ecology 86, 3078
3087.doi:10.1890/04-1806 (doi:10.1890/04-1806).
Kareiva, R.M., Shigesada, N., 1983. Analyzing insect
movement as a correlated random walk. Oecologia
(Berlin) 56, 234–238.doi:10.1007/BF00379695
(doi:10.1007/BF00379695).
Humphries, N. E., Sims, D.W., 2014. Optimal foraging
strategies: Lévy walks balance searching and patch
exploitation under a very broad range of conditions. J.
Theor. Biol. 358:179-193.
Sakiyama, T., 2020. A Recipe for an Optimal Power-Law
Tailed Walk. Submitted.
Sakiyama, T., Gunji, Y.P., 2013. Emergence of an optimal
search strategy from a simple random walk. J. R. Soc.
Interface.10 (20130486).
Viswanathan, G.M., Afanasyev, V., Buldyrev, S.V.,
Havlin, S., Luz, M.G.E., Raposo, E.P., Stanley, H.E.,
2001. Statistical physics of random searches.
Braz. J. Phys. 31, 102–108.doi:10.1590/S0103
97332001000100018.
Viswanathan, G.M., Buldyrev, S.V., Havlin, S., Da Luz,
M.G.E., Raposo, E.P., Stanley, H.E., 1999. Optimizing
the success of random searches. Nature 401, 911–914.
(doi:10.1038/44831).
Paradigms-Methods-Approaches 2021 - Workshop on Novel Computational Paradigms, Methods and Approaches in Bioinformatics
212
