
Contrast Ratio during Visualization of Subsurface Optical
Inhomogeneities in Turbid Tissues: Perturbation Analysis
Gennadi Saiko
a
and Alexandre Douplik
b
Department of Physics, Ryerson University, Toronto, Canada
Keywords: Biomedical Imaging, Diffuse Approximation, Turbid Tissues.
Abstract: Visualization and monitoring of the capillary loops and microvasculature patterns in dermis and mucosa are
of interest for various clinical applications, including early cancer and shock detection. We developed an
approach for the assessment of the contrast ratio during the visualization of subsurface optical heterogeneities.
Using the diffuse approximation and perturbation analysis, we considered light absorption heterogeneities as
negative light sources. We estimated the contrast ratio as a function of the surface layer's optical properties
for diffuse and collimated wide beam illumination. Based on findings, we formulated several practical
suggestions: a) proper selection of camera (with maximum dynamic range) is of paramount importance, b)
narrow-band illumination is more efficient than white light illumination, and c) use of collimated light
provides up to 60% improvement in contrast vs. diffuse illumination. Obtained results can be used for the
optimization of imaging techniques
1 INTRODUCTION
Visualization and monitoring of capillary loops in the
dermis and mucosa are of interest for various clinical
applications, including early cancer and shock
detection (Kanawade, 2010). Unusual capillary and
capillary loop shapes can be precursors of cancer
transformations (e.g., angiogenesis) or auto-immune
diseases (scleroderma). Rapid changes in their shape
and sizes can be one of the first signs of shock
development. This interest drives continuous
improvements in image quality in traditional optical
systems and rapidly emerging lensless (Schelkanova,
2016) optical systems.
Because of the low-contrast nature of images of
absorption patterns ("defects") in highly-light-
scattering biotissues, several techniques were
proposed to increase this contrast – (1) a narrow band
imaging providing a better contrast than white light
imaging (Saiko, 2020); (2) optical clearing to
improve the imaging quality; (3) transformation and
analysis of the image into a different colorspace (e.g.,
RGB->HSV) where subsurface inhomogeneity or
"defect" appears enhanced (Zhanwu, 2006). In
particular, Goffredo et al. (Goffredo, 2012)
a
https://orcid.org/0000-0002-5697-7609
b
https://orcid.org/0000-0001-9948-9472
considered various color channel transformations to
increase sensitivity and specificity for such defect
discovery.
Given the continuous efforts to increase the
superficial tissue image quality, it is essential to
estimate its potential limitations. In our previous
works, we have tried to evaluate the limits of defect
detectability; namely a defect detectability depth (a
maximum depth at which the defect can be detected)
using computer simulations and a simple lattice
model (Saiko, 2012). Initial assessment predicted
(Saiko, 2012) that the detectability depth is limited by
1/ '
s
, where
'
s
is the reduced scattering
coefficient of the surface layer. However, more
rigorous analysis is required, which needs to include
quantifiable parameters relevant, in particular, to
human perception. A contrast ratio defined according
to Weber's law as
/
bb
cx I Ix I
, where I
b
and I(x) is the intensity at the background and a point
x, respectively, can serve as such parameter (Saiko,
2014a; Saiko, 2020)). We define a threshold contrast
ratio, c
th,
as a minimum contrast ratio, which can be
resolved by a particular optical device. Our definition
implies that an optical system can not visualize the
94
Saiko, G. and Douplik, A.
Contrast Ratio during Visualization of Subsurface Optical Inhomogeneities in Turbid Tissues: Perturbation Analysis.
DOI: 10.5220/0010374100940102
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 2: BIOIMAGING, pages 94-102
ISBN: 978-989-758-490-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

defect if the measured contrast ratio is less than c
th
.
Respectively, a detectability depth Z can be defined
as a defect depth, where the measured contrast ratio
for the defect is equal to c
th
. Z is a function of a) the
threshold contrast ratio, b) the optical tissue
parameters (absorption coefficient, scattering
coefficient, index of refraction, anisotropy factor),
and c) defect parameters (volume, incremental
absorption coefficient, and depth). Even though for a
human eye, the threshold contrast ratio is around
0.1(Le, 2013), images with lower contrast ratio can be
digitally enhanced and still can be used for feature
examination or pattern recognition.
In automated processing scenarios, the threshold
contrast ratio is limited by the camera's dynamic
range, and we can estimate the threshold contrast
ratio, which can be obtained using commercially
available cameras. In the most typical scenario (e.g.,
with USB2 cameras), commercial cameras use 24bits
for each pixel (3 colors x 8bits). A standard camera
has 10-bit analog-to-digital converter (ADC), and due
to bandwidth restriction in USB2 format, just 8 bits
are employed. Thus, each channel's dynamic range is
2
8
=256, making the camera facilitate the contrast
ratio up to
_max
8
1
0.004
21
th
c
. A more realistic
dynamic range (40%-80% of maximum) gives
c
th
=0.005-0.01. Similarly, for more advanced
cameras (e.g., USB3 or GigE), each color channel is
represented by 10-12bits, and the real dynamic range
can be as high as 1600-3200, which consequently
translates into c
th
=0.0003-0.0006. In our assessments
below, we will use c
th
=0.01 and 0.001 as threshold
contrast ratios, representing cameras with 8 and 12
bits per channel.
An analytical dependence of the contrast ratio on
the depth of inhomogeneity location has been found
(Dolin, 1997) for refractive index-matched boundary.
In (Aksel, 2011), an absorber's depth was assessed
using spatially resolved diffuse reflectance
measurements. In the current work, we will evaluate
how the depth of inhomogeneity location and optical
parameters of the surrounding biotissue affect the
image contrast in realistic conditions: a) refractive
index mismatched boundary, and b) clinically
relevant illumination scenarios (collimated and
diffuse wide beam illumination). We will then use
this information to find the detectability depth for
such a defect for a particular optical system, which we
will characterize using the threshold contrast ratio.
In a nutshell, we will determine the contrast ratio
for a particular defect (defects), characterized by
volume V and absorption coefficient
a
, and located
at the depth Z inside the tissue. Finding an exact
solution to this problem in the general case is
problematic. We will be looking for an approximate
solution. For this purpose, we have developed a
perturbation approach focusing on two typical
illumination scenarios in biotissue imaging and
spectroscopy (Saiko, 2014b): diffuse illumination
(e.g., ambient light) and collimated wide beam
illumination. To quantify the relative impact of each
optical parameter on the detectability depth Z, we will
determine dimensionless sensitivities (the relative
change in the detectability depth Z for a given relative
change in a parameter p, (
Z/Z)/(
p/p)) for all
parameters (scattering or absorption coefficient,
index of refraction, etc.).
2 METHODS
2.1 Tissue Model
Human skin and mucosal tissues have a layered
structure (Meglinski, 2002). Based on our primary
task to visualize the capillary grid, we can group
covering tissues into (I) bloodless epithelium, (II)
blood-containing papillary layer of the dermis (skin),
or lamina propria (mucosa), and (III) underlying
tissues (see Fig 1A). Living cells in epithelium
receive oxygen and nutrients through the diffusion
from capillaries located in the papillary layer
underneath. Thus, the thickness of living cells
epithelium layers is limited by the oxygen diffusion
length and typically does not exceed 100m.
However, the stratum corneum, which includes "non-
supplied" cells, can be much thicker in some organs,
such as feet, soles, or palms.
2.2 Geometry
Based on our tissue model, the epithelium (including
stratum corneum) can be considered an optical filter
that covers absorption features and deteriorates the
image's quality. To evaluate how the measured
contrast ratio is affected by the presence of this
outermost layer, we can consider the following model
(see Fig 1B): the homogeneous top layer (Layer I)
covers Layer II, which consists of 2 areas: a)
homogeneous background, b) capillaries, which can
be considered as heterogeneous (either absorption or
scattering) features or "defects." Below this layer II,
there is another layer III, which represents all
underlying tissues. As we are interested in estimating
the effects of the outermost surface layer, in order to
simplify calculations, we can consider simplified
geometry (Fig 1C): the homogeneous semi-infinite
Contrast Ratio during Visualization of Subsurface Optical Inhomogeneities in Turbid Tissues: Perturbation Analysis
95

Figure 1: The logical transition from tissue microstructure (A) to heterogeneous dermis layer representation (B) to geometry
that allows evaluating upper bound on the contrast ratio (C). Areas (a) and (b) of the panel B are background tissue and
capillary (defect), respectively.
tissue characterized by an absorption coefficient
a
and "defects" described by the volume V and
absorption coefficient
a
+
a
and located at the
depth Z (here
a
is an incremental absorption
coefficient associated with the defect). In this case,
the contrast presented by the features will be
maximized, and we can estimate the upper bound (the
best-case scenario) for visualization of these
particular features.
2.3 Mathematical Model
The light propagation problem in homogeneous tissue
can be solved exactly for specific geometries (e.g.,
slab, semi-space, or spheroid in diffuse
approximation, slab and semi-space in Kubelka-
Munk model (see, e.g. (Saiko, 2014b)). The presence
of an arbitrary defect complicates things significantly,
and we have to look for an approximate solution. A
perturbation theory can be a useful approach to find
such an approximate solution: we start from the exact
solution for the semi-space geometry and add the
defect as a perturbation. Our perturbation approach
consists of the following steps:
1. We find a solution for light distribution in
homogeneous semi-infinite tissue (the radiant energy
fluence rate
()r
(W/m
2
)).
2. If we know the radiant energy fluence rate
()r
at some particular point
r
, then we can
calculate additional (or incremental) absorbed optical
power density
()
a
r
(W/m
3
) for some optical
heterogeneity with the absorption coefficient
a
+
a
located at this point. If the volume of the
heterogeneity is V, then the additional power
absorbed at this heterogeneity will be
()
a
rV
(W).
3. Alternatively, the heterogeneity can be
considered a negative (or inverse) point source with
power
()
a
rV
, located at the point
r
. The
radiant energy fluence rate induced by such a source
can be calculated exactly.
This problem can be analyzed using the diffuse
approximation (Star, 2011).
Step 1: For a semi-infinite medium with wide
beam diffuse illumination, the total radiant energy
fluence rate within the tissue far from the borders of
the beam depends only on the depth z (Eq. 6.88 in
(Star, 2012)):
21
exp( )
4
()
11
eff
d
eff
z
z
rh
(1)
Where
/
eff a
D
,
1/3
tr
D
,
(1 )
tr a s
g
, r
21
is the coefficient of
reflection of diffuse light on the border of tissue and
air (r
21
can be approximated using the relative index
of refraction n: r
21
≈1-n
-2
),
21
21
1
2
1
r
hD
r
. Here
without losing generality (we are looking for the
contrast ratio, which is dimensionless), we also
assumed that the incident light's surface density is 1
(W/m2).
Similarly, we can solve the semi-infinite problem
for wide beam collimated illumination. The
difference here is the presence of collimated term,
which dissipates proportionally to
exp( ( ) )
as
z
. For the biologically relevant
BIOIMAGING 2021 - 8th International Conference on Bioimaging
96

case,
sa
we have an expression (Eq. 6.83 in
(Star, 2012)):
21
21
exp( )
5
()
11
2exp( ( ) )
eff
c
eff
as
z
r
z
rh
z
(2)
The advantage of the wide beam diffuse
illumination scenario is that it allows obtaining
closed-form expressions. We omit collimated light
calculations for the sake of brevity and present only
results.
Step 2: The additional power absorbed at the
inhomogeneity can be found by multiplication of
Eq.1 or 2 on V
a
,
Step 3: The diffuse source with power P in
isotropic medium generates radiant energy fluence
rate on the distance R from the source
3
() exp( )
4
tr
seff
P
RR
R
(3)
Thus, we can represent our defect as the point
source described by Eq.3, where power P is the power
calculated on step 2 with a minus sign (negative
source). To take into account the boundary
conditions, we can use the diffusion dipole model
(Frerrerd, 1973; Kienle, 1994). In addition to the
initial source located at depth Z, we can consider the
second source (with opposite sign) located on the
distance 2h+Z above the surface. In this case, total
flux approximately satisfies realistic boundary
condition for all r (
22
rxy
) and z=0
(Haskell, 1994)
(, )
(, ) 0
rz
rz h
z
(4)
3 RESULTS
If the inhomogeneity is located at (0,0,Z), then the
fluence rate at any point on the surface of the tissue
surface (here we assume cylindrical coordinates) in
the presence of mismatched border will be:
221/2
221/2
221/2
221/2
3()
()
4
exp( ( ) )
()
exp( ((2 ) ) )
((2 ) )
atr
s
eff
eff
ZV
r
Zr
Zr
hZ r
hZ r
(5)
Where
(Z)=
d
(Z) for diffuse illumination (Eq.1)
and
(Z)=
c
(Z) for collimated illumination (Eq.2).
Another realistic clinical scenario is to resolve
two heterogeneities located under the surface using
imaging techniques. It can be the case for assessing
whether an imaging technique can visualize each
blood capillary separately. Thus, we will consider two
geometries: a single defect or heterogeneity (Fig. 2A)
and two identical defects on the same depth (Fig. 2B).
Figure 2: Geometry of heterogeneities: a single defect (A)
and two defects (B).
3.1 Contrast in Case of a Single
Heterogeneity
Let's consider a single inhomogeneity located at
(0,0,Z) (see Fig 2A). Far from the inhomogeneity, its
effect is negligible. Thus, we can take the unperturbed
flux rate on the surface at this point as a background
(
b
=
(0)). Near the inhomogeneity, we cannot ignore
the flux rate from the inhomogeneity,
s
(r). If we
compare the background flux with the fluence rate on
the surface in the presence of the inhomogeneity
(
(r)=
(0)+
s
(r)), we can calculate the contrast ratio
at any point on the surface of the tissue
() ()
()
(0)
bs
b
rr
cr
(6)
here again
(0)=
d
(0) for diffuse illumination (Eq.1)
and
(0)=
c
(0) for collimated illumination (Eq.2).
3.1.1 Diffuse Illumination
For diffuse illumination from Eq.5 with
(Z)=
d
(Z)
and Eq.6, we will get:
221/2
221/2
221/2
221/2
3exp()
()
4
exp( ( ) )
()
exp( ((2 ) ) )
((2 ) )
tr a eff
eff
eff
VZ
cr
Zr
Zr
hZ r
hZ r
(7)
Immediately above the heterogeneity (r=0) from
Eq.7, we can get a compact expression
Contrast Ratio during Visualization of Subsurface Optical Inhomogeneities in Turbid Tissues: Perturbation Analysis
97
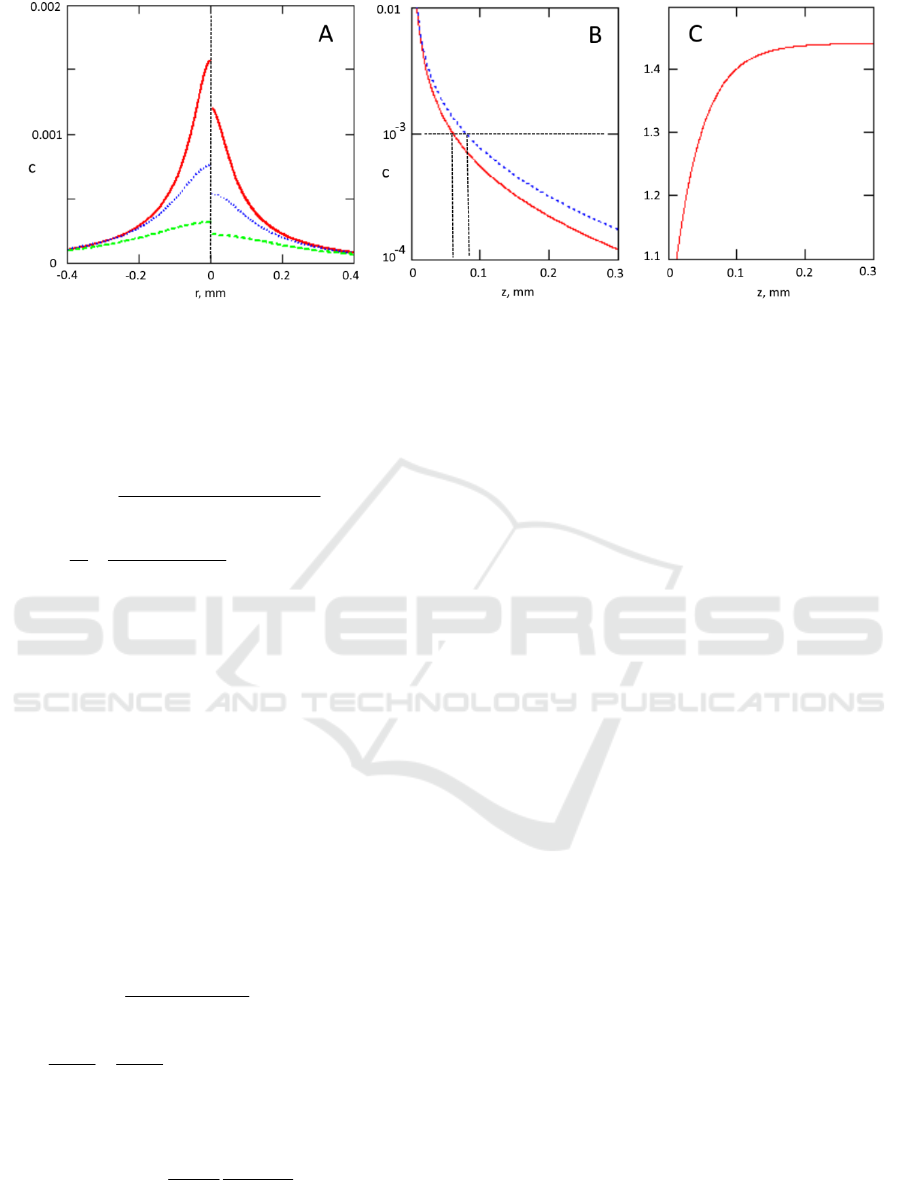
Figure 3: Panel A- radial dependence of the contrast ratio (collimated illumination- left side, diffuse illumination –right side)
on the surface above the defect located at depth 0.05mm (solid red line), 0.1mm (dotted blue line) and 0.2mm (dashed green
line). Panel B- the contrast in the point above the defect c(0) as a function of the defect depth (in mm) for wide beam diffuse
(solid red line) and collimated (dotted blue line) illumination. Panel C- the ratio of contrasts for collimated illumination and
diffuse illumination. Tissue parameters were:
a
=0.033mm
-1
and
'
s
=5mm
-1
(reticular dermis),
a
=28mm
-1
(the whole blood
with 70% oxygenation at 532nm), V=20x20x20m
3
, n=1.33.
3exp(2)
(0)
4
exp( 2 )
1
2
tr a eff
eff
VZ
c
h
ZhZ
(8)
3.1.2 Collimated Illumination
We can also analyze how the contrast will be different
for the same defect for diffuse and collimated
illumination. As we just discussed, the contrast at any
point on the surface of the tissue for the defect located
on the depth Z taking into account Eq.6 would be
() ()/ (0)
s
cr r
, here
(z)
is the
unperturbed flux distribution for either diffuse light
(Eq.1) or collimated light (Eq.2). Thus, taking into
account that for our negative source
s
(r)~-
a
V
Z)~
Z) after simple reducing, we can find
that the ratio of contrasts for collimated light and
diffuse light will be
()/ (0)
/
()/ (0)
2
exp( ( ) )
22
cc
cd
dd
aseff
Z
cc
Z
a
z
aa
(9)
here for the sake of brevity, we introduced
21
21
51
11
eff
r
a
rh
.
We have analyzed the problem in a realistic case
of the upper part of the capillary loop in the
dermis:
a
=0.033mm
-1
and
'
s
=5mm
-1
for reticular
dermis (Meglinski, 2002),
a
=28mm
-1
(the whole
blood with 70% oxygenation at 532nm),
V=20x20x20m
3
, n=1.33. Results are presented in
Fig 3.
Fig 3B shows that such defects can be visualized
(with c
th
=0.001) till approximately 0.07 mm for
diffuse illumination and 0.09 mm for collimated
illumination.
3.2 Contrast in Case of Double
Heterogeneity
To analyze this problem for diffuse illumination, let's
consider two heterogeneities located at (X,0,Z) and (-
X,0,Z) (see Fig 2B). If we compare fluence rate on the
surface far from the heterogeneities (background,
b
=
d
(0)) and the fluence rate on the surface in the
presence of the inhomogeneities (
(x,y)=
d
(0)
+
s
(x,y)) we can calculate contrast ratio at any point
(x,y,0) on the surface of the tissue. Using Eq. 5 for
each inhomogeneity, we can get Eq. 10.
To distinguish these two heterogeneities, there
should be some contrast between a point above any of
these heterogeneities (e.g. (X,0,0)) and the point
between two heterogeneities (0,0,0)- see Eq.11
So, if
c>c
th
, then we can distinguish two
heterogeneities. In the opposite case, we will see them
as a single heterogeneity with the length 2X.
BIOIMAGING 2021 - 8th International Conference on Bioimaging
98
(10)
221/2 221/2
221/2 221/2
221/2
221/2
3 exp( ) exp( )
(,0) (0,0)
4
exp( ( 4 ) ) exp( (2 )) exp( ((2 ) 4 ) )
(4) 2 ((2)4)
exp( ( ) ) exp( ((2
22
()
tr a eff eff
eff eff eff
eff eff
VZ Z
ccX c
Z
Z X hZ hZ X
Z X hZ hZ X
ZX h
ZX
221/2
221/2
)))
((2 ) )
ZX
hZ X
(11)
We have analyzed the problem in a realistic case
of upper part of capillary loop in dermis:
a
=0.033mm
-1
and
'
s
=5mm
-1
,
a
=28mm
-1
,
V=20x20x20m
3
, n=1.33, X=0.1mm. Results are
presented in Fig 4.
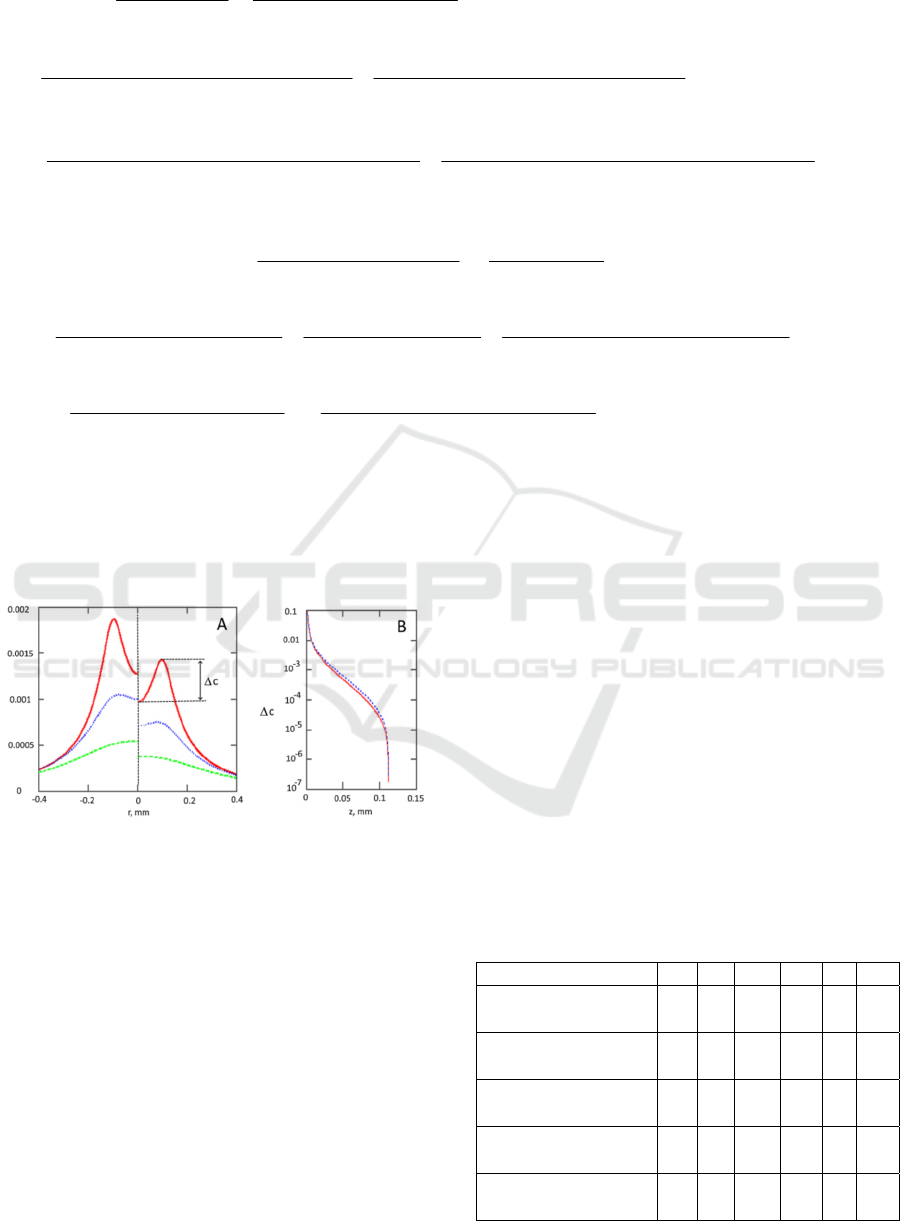
Figure 4: Panel A- Dependence of the contrast ratio
(collimated illumination – left side, diffuse illumination-
right side) on the surface above the defects located at depth
0.05mm (solid red line), 0.1mm (dotted blue line) and
0.2mm (dashed green line). Panel B- c(difference in
contrast in the point above the defect c(X,0) and between
defects c(0,0)) as a function of the defect depth Z (in mm)
for wide beam diffuse (solid red line) and collimated
(dotted blue line) illumination. Tissue parameters:
a
=0.033mm
-1
,
'
s
=5mm
-1
,
a
=28mm
-1
(the whole blood
with 70% oxygenation at 532nm), V=20x20x20m
3
,
n=1.33. Half distance between defects X=0.1mm.
Resolution depth for such scenario is
approximately 0.034mm (for c
th
=0.001).
In addition, we have calculated the sensitivity of
observables (detectability depth and contrast ratio) to
changes in any optical tissue parameters (z/z/p/p,
where p is an optical tissue parameter, e.g., absorption
coefficient) by varying each optical parameter (
a
,
a
,V, n) and half-distance between defects X by -
20%, -10%, 10%, and 20%. We also split
'
s
into
s
and g and studied each of these variables separately
(assuming g=0.8,
s
=25mm
-1
). Results for the normal
skin (Meglinski, 2002) are presented in Table 1.
For example, one can see that in the case of a
single defect imaged with an 8-bit camera (c
th
=0.01),
the largest relative impact has the anisotropy factor:
1% change in the anisotropy factor leads to a 3.6%
change in the detectability depth. In this case, the
effect can be ranked (from the highest to the lowest):
the anisotropy factor, defect parameters (
a
, V),
scattering coefficient, index of refraction. The impact
of the absorption coefficient of the tissue is relatively
minimal.
Table 1: Dimensionless sensitivities ((z/z)/(p/p)) of
observables (in rows) to changes in optical parameters of
the tissue (
a
,
s
, g, n) and defect (
a
,V, X).
Observables
a
s
g n X
a,
V
Detectability depth z for
c
th
=0.01 (single defect)
0.00 0.90 -3.60 0.10 n/a 0.90
Detectability depth z for
c
th
=0.001 (single defect)
-0.06 0.51 -2.15 0.41 n/a 0.72
Detectability depth z for
c
th
=0.01 (double defect)
0.00 0.79 -2.89 0.00 0.26 0.79
Detectability depth z for
c
th
=0.001 (double defect)
0.00 0.32 -1.43 0.00 0.67 2.59
Contrast ratio c for the
defect located at z=0.1mm
-0.06 0.76 -3.25 0.76 n/a 1.08
2 2 21/2 2 2 21/2
2 2 21/2 2 2 21/2
2221/2
2221/2
3 exp( )
(, )
(, )
4
exp( ( ( ) ) ) exp( ( ( ) ) )
(( ) ) (( ) )
exp( ((2 ) ( ) ) ) exp(
((2 ) ( ) )
tr a eff
b
b
eff eff
eff eff
VZ
xy
cxy
ZxXy ZxXy
ZxXy ZxXy
hZ xX y
hZ xX y
2221/2
2221/2
((2 ) ( ) ) )
((2 ) ( ) )
hZ xX y
hZ xX y
Contrast Ratio during Visualization of Subsurface Optical Inhomogeneities in Turbid Tissues: Perturbation Analysis
99

4 DISCUSSION AND
CONCLUSIONS
We have analyzed several scenarios that can be used
for image quality characterization in tissue imaging.
We found that various optical parameters contribute
differently to the contrast ratio. The absorption
coefficient of the tissue does have a very minimal
impact. The most substantial effect has the anisotropy
factor g (due to our initial value g=0.8, it is
approximately four times (g/(1-g)) stronger than
s
),
followed by properties of the defect and scattering
coefficient of the tissue. The refraction index and the
distance between defects have minimal impact. These
data provide the relative impact of various factors on
the experiment's accuracy and can be used to guide
experimental and Monte Carlo simulations.
While a few tissue optical parameters can be
varied in an experiment (e.g., tissue scattering
coefficient and refraction index through optical
clearing), the absorption coefficient for
inhomogeneity is the single factor that can be varied
in practice. Moreover, the contrast linearly depends
on this factor, and detection depth strongly depends
on it as well (high sensitivity, see Table 1). Thus,
proper wavelength selection (e.g., at the absorption
peak of hemoglobin) is of paramount importance for
visualization.
We considered two realistic illumination
scenarios: wide beam diffuse illumination (e.g.,
ambient light) and wide beam collimated illumination
(e.g., a medical light source, laser). Results are very
similar. However, it should be noted that collimated
illumination provides better image contrast (see Fig
3B and 4B for comparison). For our parameters, 40%
contrast improvement can be achieved using
collimated illumination (see Fig 3C). We can estimate
the maximum enhancement provided by the
collimated light. Taking into account that
,
s
aeff
and using Eq.9, we can find that for
deep defects (
1/
s
Z
)
21
21 21
5
/
25 2(1 )(1 )
cd
eff
ra
cc
arrh
(12)
In case of the matched boundary (
21
0r
):
/5/(34/3)
cd a tr
cc
(13)
Such as in most tissues
s
>>
a,
this ratio can be
estimated as 5/3. That means that for the matched
boundary, collimated light provides 66%
improvement over diffuse light. These results are in
agreement with previously reported models (Saiko,
2020).
If we know the contrast ratio associated with the
defect, we can assess whether a particular imaging
system can visualize it. Namely, if the camera's
threshold contrast ratio is above the defect contrast
ratio, the defect can be imaged. We assessed that the
realistic threshold contrast ratio for commercially
available cameras is in the 0.01-0.001 range for 8-12
bits cameras. Because the dynamic range of a camera
used in measurements is the primary factor limiting
the recognition of objects with low contrast, the
proper selection of a camera is vital for imaging
subsurface structures.
Out estimations of the defect detectability depth
are in a qualitative agreement with MC simulations
(Saiko, 2014a). In particular, MC simulations have
shown (Saiko, 2014a) that diffuse reflectance
spectroscopy can potentially identify absorption
inhomogeneities located at a depth of 0.5–1.0 of the
transport mean free path l
s
= 1/μ
s
'.
It should be noted that the proposed "detectability
depth" is different from a mean sampling (or
interrogation) depth (see, e.g. (Bevilacqua, 2004)).
The mean sampling depth can be viewed as the first
moment of the photon scattering density function (or
PSDF) for various photon trajectories (e.g., in a
Monte Carlo simulation). The mean sampling depth
depends on the tissue's optical properties (
a
and'
s
)
and source-detector separation (if any). The
detectability depth depends on
a
and
'
s
, the
properties of the defect (namely volume V and
absorption coefficient
a
), and the imaging system's
properties (namely the threshold contrast ratio c
th
).
Conceptually, our approach is a perturbation
expansion. The zeroth term is the light distribution in
a homogeneous semi-infinite issue, and the first-order
term is the linear contribution caused by the presence
of inhomogeneities (defects).
To keep the perturbation approach valid, we need
to satisfy several conditions. Firstly, the light field
change within the defect caused by its absorption
properties should be small. Given that the defect in
our case is illuminated from all sides, then the impact
will be negligible if
1/3
/2 1
a
V
, which is satisfied
for our defect parameters.
Secondly, the diffuse approximation provides
accurate light distribution far from sources and
borders: when the mean optical free path (1/
t
) is
much smaller than the size under consideration. For
our quasi-1D problem, the defect depth z is the only
characteristic size and
1
t
z
. However, the diffuse
approximation is still a useful approximation, even
BIOIMAGING 2021 - 8th International Conference on Bioimaging
100

close to boundaries (Chai, 2008). In particular,
(Lehtikangas, 2012) found that the relative error of
fluence rate near the surface is between 3.73% and
6.31% for the DA when μ
s
= 50 mm
−1
and μ
s
= 5
mm
−1
, respectively. Such as we intend to provide
rough estimations (e.g., feasibility assessment of
technology, estimate maximum detectability depth
for a particular wavelength, select appropriate bit
depth for the camera), we expect that its major
conclusions will hold.
In addition to general questions about the
applicability of the diffuse approximation, some
additional questions arise while using this
perturbation approach: a) what is the volume of the
heterogeneity to keep this approach valid, and b) if we
have multiple heterogeneities, what are the criteria to
make sure that they do not interact with each other,
namely that their impacts are additive.
To address the first question, we can consider that
we have a one-dimensional problem with constant
illumination in the horizontal plane in the zeroth
approximation. Thus, the defect will be small enough
if the light distribution within the defect will be
homogeneous:
z
l
z
, where l
z
is the vertical
size (the height on Fig 2A) of the defect. Taking into
account Eq.1, this condition can be rewritten as
1
eff z
l
.
The requirement (b) can be reformulated as
follows: the fluence rate induced by all other defects
is much smaller than the homogeneous field at this
point. Using Eq.1 and Eq.2, we can estimate the
required distance R between defects with volume V
as:
0
3
4
atr
V
RR
, which is less than 1m for
our parameters.
In light of requirement (b), we can take a look at
the applicability of our approach to vertical (e.g.,
capillaries) and horizontal (e.g., nail fold capillaries)
linear heterogeneities. One can easily find that due to
slow descendants of the fluence rate induced by a
single defect (Eq.3), the integral of the fluence rate
diverges at any point of the continuous curve of
sources. Thus, even though it is possible to calculate
the impact of inhomogeneity in these scenarios, such
solutions' validity will be doubtful. Consequently,
this approach can be applied only to sets of discrete
heterogeneities with distances between them
0
3
4
atr
V
RR
.
If the inhomogeneity's parameters are known
(e.g., in the case of a blood vessel), then the contrast
ratio can be used to extract the surface layer's
parameters, e.g., its thickness. Measuring contrast at
multiple wavelengths (e.g., multispectral or
hyperspectral imaging) may obtain further insights
into the epithelial layer's composition.
As a natural extension of previous works (Saiko,
2012, 2014a, 2014b), the current results explicitly
contain absorption coefficient, thus allowing a direct
MC verification.
In summary, we propose a simple perturbation
model, which links optical tissue parameters with the
contrast ratio in reflectance imaging geometry. Using
the proposed model, we derived explicit expressions
for the contrast ratio in the case of tissue imaging with
diffuse and collimated wide beam illumination. Using
the contrast ratio, the detectability depth can be
estimated for a particular imaging system. The
relative impact of optical tissue parameters on the
detectability depth can also be determined. The
proposed approach can be exploited for the
assessment and optimization of tissue imaging
techniques.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the support
for this study from NSERC Discovery grant
(Douplik), Ryerson Health Fund, NSERC Engage
support, and infrastructural support from Institute for
Biomedical Engineering, Science and Technology
(IBEST), a partnership between Ryerson University
and St. Michael's Hospital (Toronto).
REFERENCES
Kanawade, R. et al., 2010, Vessel density modulation
detection in skin model by using spatially resolved
diffuse reflectance techniques for application of early
sign of shock detection. Photodiagnosis and
Photodynamic Therapy; 7: P14
Schelkanova, I. et al., 2016, Spatially resolved, diffuse
reflectance imaging for subsurface pattern visualization
toward development of a lensless imaging platform:
phantom experiments. J. Biomed. Opt.21 (1): 015004.
Saiko, G., Betlen, A., 2020, Optimization of Band Selection
in Multispectral and Narrow-Band Imaging: an
Analytical Approach, Adv. Exp Med Biol 1232:361-367.
Zhanwu, X., Miaoliang, Z., 2006, Color-based skin
detection: survey and evaluation. In: Proceedings of the
12th International Conference on Multi-Media
Modelling, vol 10, Beijing.
Goffredo, M. et al., 2012, Quantitative color analysis for
capillaroscopy image segmentation, Med Biol Eng
Comput 50:567–574
Contrast Ratio during Visualization of Subsurface Optical Inhomogeneities in Turbid Tissues: Perturbation Analysis
101

Saiko, G. Douplik, A., 2012, Real-Time optical monitoring
of capillary grid spatial pattern in epithelium by
spatially resolved diffuse reflectance probe, J Innov.
Opt. Heal. Scie., 05(02): 1250005
Saiko G. et al., 2014 Optical Detection of a Capillary Grid
Spatial Pattern in Epithelium by Spatially Resolved
Diffuse Reflectance Probe: Monte Carlo Verification,
Sel. Top. Quantum Electron. IEEE J. 20(2): 7000609
Le D. et al., 2013, Monte Carlo modeling of light–tissue
interactions in narrow band imaging, J. Biomed. Opt.,
18 (1): 010504-1–010504-3.
Dolin, L.S., 1997 On the possibility of detecting an
absorbing object in a strongly scattering medium using
the method of continuous optical sounding,
Radiophysics and Quantum Electr, 40(10): 799-812.
Aksel, E.B., et al., 2011, Localization of an absorber in a
turbid semi-infinite medium by spatially resolved
continuous-wave diffuse reflectance measurements. J
Biomed Opt.; 16(8):086010.
Saiko, G. Douplik, A., 2014, Reflectance of Biological
Turbid Tissues under Wide Area Illumination: Single
Backward Scattering Approach, Int. J. of Photoenergy,
241364
Meglinski, I. V. Matcher, S. J., 2002, Quantitative
assessment of skin layers absorption and skin
reflectance spectra simulation in the visible and near-
infrared spectral regions, Physiol. Meas. 23:741753.
Star, W.M., 2011, Diffusion Theory of Light Transport, in
Optical-Thermal Response of Laser-Irradiated Tissue
(2nd Ed) Ed. by A.J. Welch, Dordrech, NLD: Springer,
Frerrerd, R.J. Longini, R.L. 1973, Diffusion dipole source,
J. Opt. Soc. Am. 63: 336-337
Kienle, A., Patterson, M.S, 1994, Improved solutions of the
steady-state and the time-resolved diffusion equations
for reflectance from a semi-infinite turbid medium, J.
Opt. Soc. Am. A 14: 246-254.
Haskell R.C., et al., 1994, Boundary conditions for the
diffuse equation in radiative transfer, J. Opt. Soc. Am.
A 11: 2727-2741.
Bevilacqua F. et al., 2004, Sampling tissue volumes using
frequency-domain photon migration. Phys. Rev. E;
69(5):51908.
Chai, C. et al. 2008, Analytical solution of P3
approximation to radiative transfer equation for an
infinite homogenous media and its validity, J. Modern
Opt, 55(21): 3611-3624.
Lehtikangas, O. et al., 2012, Modeling boundary
measurements of scattered light using the corrected
diffusion approximation. Bio Opt Exp. 3(3):552–571.
BIOIMAGING 2021 - 8th International Conference on Bioimaging
102
