Convolution-based Soma Counting Algorithm for Confocal Microscopy

Image Stacks

Shih-Ting Huang, Yue Jiang and Hao-Chiang Shao

Department of Statistics and Information Science, Fu Jen Catholic University, Taiwan, Republic of China

Keywords:

Neuroblast, Soma Detection, Drosophila Brain, Confocal Microscopy.

Abstract:

To facilitate brain research, scientists need to identify factors that can promote or suppress neural cell differ-

entiation mechanisms. Accordingly, the way to recognize, segment, and count developing neural cells within

a microscope image stack becomes a fundamental yet considerable issue. However, it is currently not feasible

to develop a DCNN (deep convolutional neural network) based segmentation algorithm for confocal ﬂuores-

cence image stacks because of the lack of manual-annotated segmentation ground truth. Also, such tasks

traditionally require meticulous manual preprocessing steps, and such manual steps make the results unstable

even with software support like ImageJ. To solve this problem, we propose in this paper a convolution-based

algorithm for cell recognizing and counting. The proposed method is computationally efﬁcient and nearly

parameter-free. For a 1024 × 1024 × 70 two-channel image volume containing about 100 developing neuron

cells, our method can ﬁnish the recognition and counting tasks within 250 seconds with a standard deviation

smaller than 4 comparing with manual cell-counting results.

1 INTRODUCTION

Biological labs need to identify factors, including

gene fragments, that can promote or suppress neural

cell differentiation mechanisms to facilitate brain re-

search. To understand the impact of the transplanted

gene fragment on neurodevelopment, the difference

of the number of neural cells between the wild type,

i.e., the phenotype of the typical form of a species

as it occurs in nature, and a mutant, i.e., the indi-

vidual with transplanted RNA interference fragments,

should be clariﬁed. Hence, the way to recognize,

segment, and count developing neural cells within

a microscope image volume becomes a fundamental

yet considerable issue. However, it is currently not

feasible to segment these kinds of confocal ﬂuores-

cence image volumes by using convolutional neural

networks (CNN), such as U-Net (Ronneberger et al.,

2015) or 3D U-Net (C¸ ic¸ek et al., 2016), because of

i) the lack of labeled segmentation ground truth and

ii) the oversized confocal image volumes. Also, such

tasks traditionally require meticulous manual steps,

so the results cannot be stable even with software sup-

port like ImageJ (Ima, 2020). To settle down this

problem, we propose in this paper an algorithm for

https://orcid.org/0000-0002-3749-234X

cell recognizing and counting based on convolutional

operators and conventional image processing skills.

The proposed method is computationally efﬁcient,

nearly parameter-free, and aims to extract trustworthy

segmentation ground truth for developing advanced

CNN-based algorithms. For a 1024 × 1024 × 70 fo-

cal stack, focused on the calyx of the mushroom body

in the Drosophila brain, containing about 100 devel-

oping neuron cells, our method can ﬁnish the recog-

nition and counting tasks within 240 seconds with a

standard deviation smaller than 4 comparing with the

manual cell-counting results. To process this kind of

confocal image volume, the current standard is still

a computer-aided manual procedure, for instance, us-

ing common software including ImageJ (Ima, 2020)

and Imaris (ima, 2020). However, these programs

require manual input, and therefore they cannot pro-

vide reliable results if the user does not have sufﬁcient

anatomical knowledge of the ﬂy brain and neurons.

In addition, because for confocal microscopy imag-

ing the sampling interval on the z-axis is usually three

times the sampling interval on the x- and the y- axes,

it is difﬁcult and time-consuming to clarify the rela-

tionship between soma candidates on adjacent slices.

Therefore, we proposed this method to segment and

count neuroblast cells.

Huang, S., Jiang, Y. and Shao, H.

Convolution-based Soma Counting Algorithm for Confocal Microscopy Image Stacks.

DOI: 10.5220/0010388403510356

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 351-356

ISBN: 978-989-758-490-9

351

Figure 1: Maximum intensity projection (MIP) of an exam-

ple confocal ﬂuorescence image volume. Red balls are neu-

ron cell bodies (soma), green channel records neural ﬁbres

and cell membranes, and dark red areas are background tis-

sues of ﬂy brain. Note that in order to avoid confusion in red

and green channels, we illustrate all MIP images by swap-

ping blue and red channels later in this paper. Note that in

this ﬁgure we render the RED channel in blue so that even

color-blind readers can distinguish soma from neural ﬁbers

and membranes.

2 RELATED WORK

To process 2D+Z confocal ﬂuorescence image vol-

umes, several methods were proposed. However,

most of them focus on image atlasing and surface reg-

istration (Chen et al., 2012; Shao et al., 2013; Shao

et al., 2014), a few of them describe segmentation

strategies on neuron ﬁbers and neuropils (Shao et al.,

; Shao et al., 2019), but none of them depicts soma

(cell body) identiﬁcation methods. Although in (Shao

et al., ) Shao et al. trace neural ﬁbers within a brain-

bow/ﬂybow (Livet et al., 2007; Hadjieconomou et al.,

2011) image volume by identifying soma candidates

ﬁrst (Shao et al., ), their method lacks a mechanism

to rule out false somas so that it is hard for their

method to separate independent neurons. In addition,

Shao and his co-authors also stated in (Shao et al.,

2011) and (Shao et al., ) that the effectiveness of im-

age processing routines designed for confocal ﬂuores-

cence images may be degraded due to ﬂuorescence

halation. The pin-hole of the confocal microscope

still cannot ﬁlter out ﬂuorescence emitted from out-

of-focus planes. Hence, some anti-halation methods

are still necessary for confocal imagery. To remove

halation, Shao et al. adopted morphological top-hat

transfrom in (Shao et al., ). However, this strategy re-

quires a pre-deﬁned marker and a suitable structural

element, so it cannot be robust. Therefore, we ﬁ-

nally decided to utilize the common most deconvo-

lution method, i.e., Lucy-Richardson deconvolution

(Fish et al., 1995), to remove all possible ﬂuerescence

halation due to the imaging point spread function. In

next section, we will describe our method in detail.

3 METHOD

3.1 Overview

A common strategy to detect neuron cell bodies is to

use morphological operations, i.e., erosion and dila-

tion with handcrafted structural elements, as reported

in (Shao et al., ). However, such a strategy is not ro-

bust against noises and therefore needs several post-

processing steps to rule out unqualiﬁed candidates of

neuron cell bodies.

The proposed method was designed for two pur-

poses. First, this method was developed to provide

a cell-body identiﬁcation result that is more stable

than those obtained by manual procedures. Second,

this method was developed to mass-produce cell body

segmentation results for a further study like training

and specializing in a U-net for this application. There-

fore, the proposed method was designed and imple-

mented by using primarily convolutional operations.

3.2 Soma Identiﬁer

To systematically extract neuron cell bodies (soma),

we ﬁrst derive several W × H × Z feature maps by

convoluting source image volume with several 2D+Z

Gaussian kernels of different σ

and window size w

Practically, each Gaussian kernel is a 3D array with

its entries speciﬁed by following equations.

= I ∗ G

(σ

), (1)

where ∗ denotes 3D convolution, and G

is a w

× w

convolution kernel with entries deﬁned by

= αe

−X

X/σ

with X

= (x, y,3z). (2)

Here, I is the source image volume, F

is the fea-

ture map corresponding to the i

Gaussian convolu-

tion kernel G(σ

), and α denotes a constant gain

factor used to normalize G

. Note that the factor 3 in

Eq. (2) reﬂects the sampling interval in the z axis, as

we will describe in Section 4.1.

The aforementioned convolution step can be re-

garded as a template matching process. Consequently,

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

352

we can ﬁnd candidates of neuron cell bodies by iden-

tifying local maximums on all feature map F

. By let-

ting δ

( j) denote the list recording the j

local maxi-

mum of feature map F

, this second step aims to ﬁnd

the intersection set of local maximums of all feature

maps. We use ∆

main

to denote the resulting intersec-

tion set, that is,

∆

main

= ∩

. (3)

3.3 Halation Suppression

However, neurons cell bodies may be locally-

concentrated near speciﬁc neuropils; in this situation,

for example, two close neuron cell bodies would be

entangled on microscopy images and thus usually re-

sult in one ridge, rather than two local maximums, on

the feature map. To overcome this difﬁculty, we apply

Richardson–Lucy deconvolution (Richardson, 1972)

method to remove the effect of halation in the ﬂuores-

cence image volume so that neuron cell bodies, which

cluster within a small region, becomes distinguish-

able. Then, we repeat the Soma identiﬁer procedure

described in previous subsection by utilizing smaller

convolution kernels, denoted as G

ps f

(σ

ps f

), and

then detect the local maximums to ﬁnd cell bodies

candidates again. We use ∆

aux

to denote Cell bod-

ies detected in this stage. Note that Richardson–Lucy

deconvolution method requires a user-speciﬁed blur

kernel, i.e., the point spread function (PSF); in our

implementation, the blur kernel used in this step is

also the convolution kernel G

ps f

(σ

ps f

Because Richardson–Lucy deconvolution may en-

hance/highlight imaging noise, fake cell body candi-

dates would be produced after the second convolu-

tional detection procedure. To settle this issue, we

collect experiment results of more than 80 confocal

image volumes, each acquired with different sam-

ple preparation condition and imaging conﬁgurations,

and then induce following judgement rules.

• For any two cell body candidates, if the distance

between them is no larger than 10 voxels, we rule

out the one with lower average brightness.

• If a new cell body candidate (derived in the sec-

ond step) does not locate within the bounding box

of any soma candidate obtained in the ﬁrst step,

we will disregard it unless its average brightness

reaches level of top 1%.

Finally, because we now have only about 80 image

volumes of different geno-types and different imag-

ing parameter settings, all above rules are developed

empirically. We will show our experiment result in

next section.

(a) (b)

Figure 2: Visualized graph of different soma candidates. (a)

a typical graph showing only one soma; (b) a graph show-

ing two concatenated soma; (c) one another example of two

concatenated soma; and, (d) a local graph showing there are

three soma within this area.

3.4 Graph Reconstruction for Manual

Validation

This step is optional in our design; and, it will be ap-

plied if the number of neural cell bodies in the left

brain and that in the right brain are too different. In

this step, we reconstruct and visualize a graph model

for pixels of each extracted soma, and this visualiza-

tion can at least assist users to verify if there are mul-

tiple neural cell bodies within an “extracted soma”.

Demonstrated in Figure 2 are examples of visualized

graphs. Note that these are K-nearest-neighbor (kNN)

graphs derived by taking each pixel’s (x, y, z, inten-

sity) information into account. Through this represen-

tation, we can validate the effective number of somas

within “one soma candidate”, predicted by our algo-

rithm, efﬁciently.

4 EXPERIMENT RESULT

4.1 Dataset

All source image volumes used in this paper were ac-

quired by an LSM-700 confocal microscope. Each

image volume contains two channels. The red chan-

nel records ﬂuorescence emitted by neuron cell bodies

by using the excitation laser at 555nm, and the green

channel records neuron cell membrane and neuron

ﬁbers by using the excitation laser at 488 nm. The spa-

tial dimension of all image volumes is 1,024× 1,024,

and an image volume may contain about 50 ∼ 100

Convolution-based Soma Counting Algorithm for Confocal Microscopy Image Stacks

353

(a)

(b)

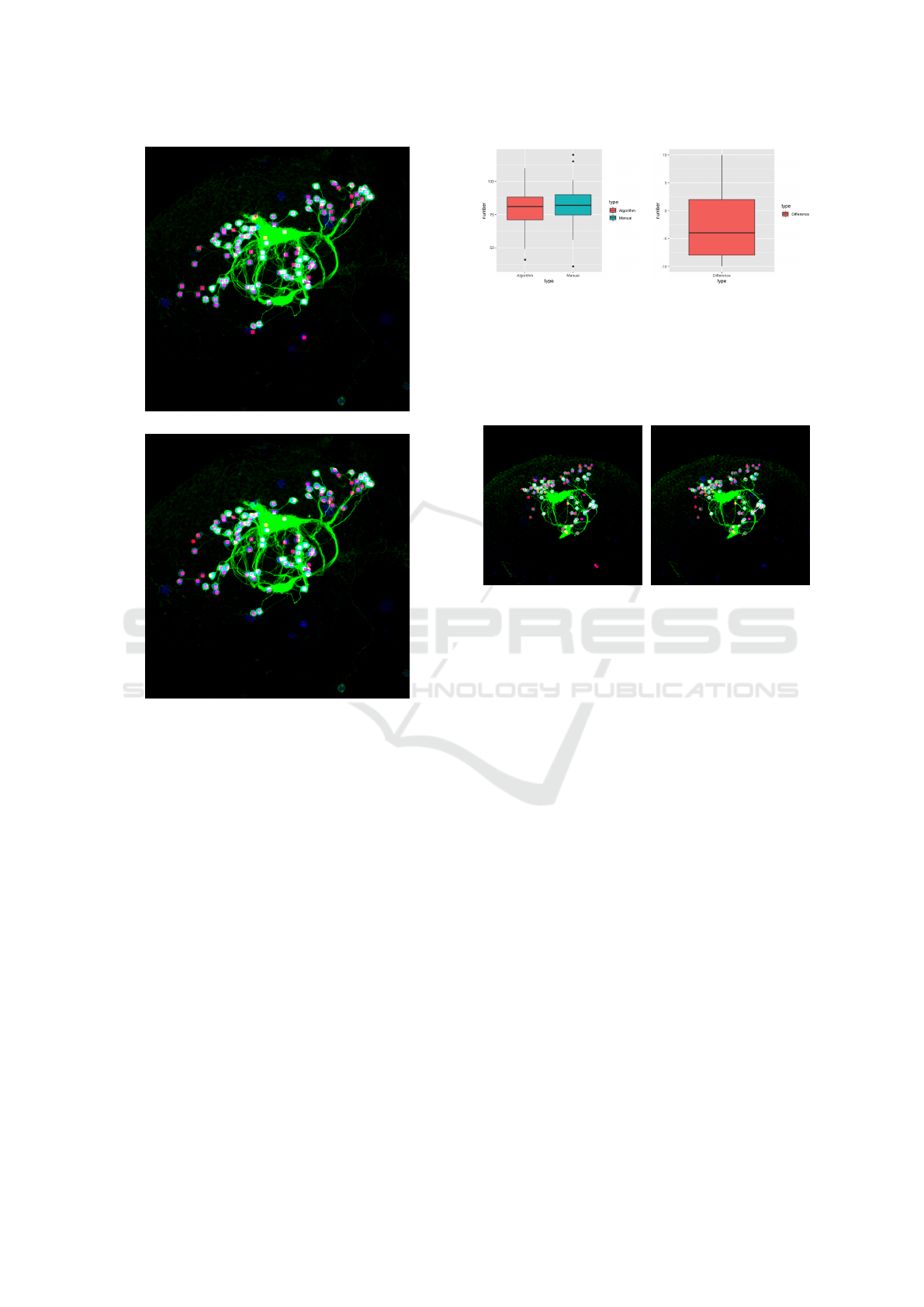
Figure 3: Comparison between MIP images of (a) our re-

sult and (b) the manual labeling result of the image volume

shown in Figure 1. The source image volume contains 100

slices.

slices. Note that the actual size of each voxel is about

0.16 × 0.16 × 0.50µm

4.2 Discussion

Because there is not state-of-the-art or benchmark

method in this ﬁeld, we compare our segmentation

results with manual counting/labeling results. Figure

3 shows the comparison among the MIP image of one

source volume, the MIP image of our soma identiﬁ-

cation result, and the MIP image of manual labeling

result. Here, red balls are neural cells, green channel

records neural ﬁbres and cell membranes, and dark

red areas are background tissues of ﬂy brain. Note

that we changed the source red-channel that records

neuron cell bodies to the blue-channel so that even

readers with color-vision-deﬁciency can read our il-

lustrations. Also, summarized in Figure 4 is the sta-

(a) (b)

Figure 4: Statistical comparison. (a) This plot shows that

the average number of extracted soma of the proposed

method is almost the same with that of manual counting

result. (b) This plot shows that the difference between our

segmentation result and manual ground truth mostly rang-

ing from -7.5 to 2.5.

(a) (b)

Figure 5: Comparison between MIP images of the manual

labeling result and our result. This source image volume

contains 82 slices. (a) Result derived by our method. (b)

Manual labelling result.

tistical information of our experiment soma counting

results. Finally, shown in Figures 5 ∼ 9 are results of

other ﬁve image volumes.

These experiment results prove that the proposed

method can provide much more stable and reliable

soma counting results than manual process. How-

ever, the proposed method now has two obvious draw-

backs. First, it may misrecognizes other cells as neu-

roblasts once they were labeled by the antibody dur-

ing the stain process. Second, for image volumes with

low brightness, several neuron cell bodies may be dis-

regarded because their voxel intensities are too weak

to hold their contour shape.

5 CONCLUDING REMARKS

In this paper, we proposed a cell-counting proto-

type algorithm for confocal ﬂuorescence image vol-

umes. Compared with time-consuming manual and

software-assisted cell-counting strategies, the pro-

posed method can ﬁnish the calculation of a 1024 ×

1024 × 80 image volume within 5 minutes and pro-

vide a better and more stable segmentation and count-

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

354

(a) (b)

Figure 6: Comparison between MIP images of the manual

labeling result and our result. This source image volume

contains 83 slices. (a) Result derived by our method. (b)

Manual labelling result.

(a) (b)

Figure 7: Comparison between MIP images of the manual

labeling result and our result. This source image volume

contains 89 slices. (a) Result derived by our method. (b)

Manual labelling result.

ing result. The proposed method has one primary lim-

itation. That is, for ﬂat, disc-shaped neuron cell bod-

ies, especially those with extra-low brightness and ex-

isting on less than three slices, the proposed algorithm

may fail to recognize them.

The proposed algorithm currently may also fail to

recognize ﬂat and disc-shaped cells, especially those

that only exist on less than three slices. We are cur-

rently working on this issue. Also, as for the neurob-

(a) (b)

Figure 8: Comparison between MIP images of the manual

labeling result and our result. This source image volume of

a wide-type contains 76 slices. (a) Result derived by our

method. (b) Manual labelling result.

(a) (b)

Figure 9: Comparison between MIP images of the manual

labeling result and our result. This source image volume

of a wild-type contains 67 slices. (a) Result derived by our

method. (b) Manual labelling result.

last in Drosophila brain, there is still one another sam-

ple preparation method, which is designed for imag-

ing tissue in a very large ﬁeld of view but labeling

neuron cell membrane only. Hence, one of our future

extensions is to modify our prototype algorithm for

this kind of image.

ACKNOWLEDGEMENT

This work supported by MOST 107-2320-B-030-012-

MY3. The authors want to thank Prof. Hung-Hsiang

Yu from the Institute of Cellular and Organismic Bi-

ology, Academia Sinica, Taiwan for providing the

source confocal microscopy image volumes.

REFERENCES

(2020). Imagej. https://imagej.nih.gov/ij/.

(2020). Imaris. https://imaris.oxinst.com/.

Chen, G.-Y., Wu, C.-C., Shao, H.-C., Chang, H.-M., Chi-

ang, A.-S., and Chen, Y.-C. (2012). Retention of

features on a mapped drosophila brain surface us-

ing a bezier-tube-based surface model averaging tech-

nique. IEEE transactions on biomedical engineering,

59(12):3314–3326.

C¸ ic¸ek,

O., Abdulkadir, A., Lienkamp, S. S., Brox, T.,

and Ronneberger, O. (2016). 3d u-net: learning

dense volumetric segmentation from sparse annota-

tion. In International conf. on medical image comput-

ing and computer-assisted intervention, pages 424–

432. Springer.

Fish, D., Brinicombe, A., Pike, E., and Walker, J. (1995).

Blind deconvolution by means of the richardson–lucy

algorithm. JOSA A, 12(1):58–65.

Hadjieconomou, D., Rotkopf, S., Alexandre, C., Bell,

D. M., Dickson, B. J., and Salecker, I. (2011). Fly-

bow: genetic multicolor cell labeling for neural circuit

analysis in drosophila melanogaster. Nature methods,

8(3):260–266.

Convolution-based Soma Counting Algorithm for Confocal Microscopy Image Stacks

355

Livet, J., Weissman, T. A., Kang, H., Draft, R. W., Lu,

J., Bennis, R. A., Sanes, J. R., and Lichtman, J. W.

(2007). Transgenic strategies for combinatorial ex-

pression of ﬂuorescent proteins in the nervous system.

Nature, 450(7166):56–62.

Richardson, W. H. (1972). Bayesian-based iterative method

of image restoration. JoSA, 62(1):55–59.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. In International Conference on Medical

image computing and computer-assisted intervention,

pages 234–241. Springer.

Shao, H.-C., Cheng, W.-Y., Chen, Y.-C., and Hwang, W.-L.

Colored multi-neuron image processing for segment-

ing and tracing neural circuits. In 2012 19th IEEE

International Conference on Image Processing, pages

2025–2028. IEEE.

Shao, H.-C., Hwang, W.-L., and Chen, Y.-C. (2011). Opti-

mal multiresolution blending of confocal microscope

images. IEEE transactions on biomedical engineer-

ing, 59(2):531–541.

Shao, H.-C., Wang, Y.-M., and Chen, Y.-C. (2019). A two-

phase segmentation method for drosophila olfactory

glomeruli. In 2019 IEEE International Conf. on Image

Processing (ICIP), pages 265–269. IEEE.

Shao, H.-C., Wu, C.-C., Chen, G.-Y., Chang, H.-M., Chi-

ang, A.-S., and Chen, Y.-C. (2014). Developing a

stereotypical drosophila brain atlas. IEEE Transac-

tions on Biomedical Engineering, 61(12):2848–2858.

Shao, H.-C., Wu, C.-C., Hsu, L.-H., Hwang, W.-L., and

Chen, Y.-C. (2013). 3d thin-plate spline registration

for drosophila brain surface model. In 2013 IEEE In-

ternational Conf. on Image Processing, pages 1438–

1442. IEEE.

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

356