FPGA Implementation of Filters in Medical Imaging

Arban Uka

1 a

, Gerald Topalli

, Julian Hoxha

and Nihal Engin Vrana

Department of Computer Engineering, Epoka University, Tirane, Albania

Department of Electronics and Communication Engineering, Istanbul Technical University, Istanbul, Turkey

Spartha Medical, Strasbourg, France

Keywords:

FPGA, Real-time Systems, Medical Image Analysis.

Abstract:

Real time analysis of images is an inherent expectation of the medical imaging research area. Monitoring

of important medical data requires the acquisition of high-quality images at a high rate. Nowadays many

experiments are conducted on multiwell culture plates to determine the inﬂuence of different physical and

chemical conditions on a speciﬁc biological sample. Often the medical practitioners need to supervise the

complete data acquisition process in order to ensure the collection of reliable data. For this reason, some

pre-processing steps including noise removal, contrast enhancement and preliminary edge detection needs to

be implemented in real time. Here in this work we review important contribution on the implementation of

ﬁlters on FPGAs and report runtime of 8 ms for images sized 1000x1000 pixels when two or more ﬁlters are

applied subsequently.

1 INTRODUCTION

The implementation of signal processing tasks on

FPGA-s has gained a momentum as the amount of

data to be analysed has increased. One of the ma-

jor ﬁelds that requires a real-time implementation and

high throughput at the same time is medical ﬁeld. Bi-

ological systems can sense or produce low level sig-

nals and these signals can reveal important physiolog-

ical parameters for the cells or tissues (Simon et al.,

2016). The successful signal acquisition, ampliﬁca-

tion and manipulation has closed an important gap

between biology and electronics. The development

of experimental instrumentation has brought forth the

challenge of analysing large data input. The use of

microﬂuidic chambers facilitates the monitoring of

the cellular material by gathering a series of different

signals that develop in time (Curto et al., 2017). One

important source of input data is the optical imag-

ing. Images acquired at a speciﬁc rate reveal the cell

mobility, cell shape and other important parameters

such as circularity, perimeter, area, eccentricity etc.

Cell imaging is one of the most challenging prob-

lems and biologists need real time implementation for

cell detection, counting and classiﬁcation (Chen et al.,

2006). Even when an experienced medical practi-

tioner uses a medical imaging device, the side help

https://orcid.org/0000-0003-0037-0207

of computationally assisted image processing proce-

dures such as auto-focus metrics evaluation, contrast

adjustment and noise removal greatly improve the

data acquisition quality. All these steps constitute a

high throughput of data and it comes with a certain

computational complexity that may compete with the

computing system speciﬁcation. This challenge can

be overcome with the use of FPGA as they provide

a fast, robust system with a high throughput. Here

in this work we review major contribution of FPGA-s

in medical imaging and then we propose an improve-

ment in the architecture that leads to a shorter run-

time.

2 RELATED WORK

The implementation of complex algorithms on FP-

GAs is reported in the literature all for the same rea-

sons and the major aspects are optimization of the

run-time and physical resources, which in this case

is the number of used LUT and registers. Hauck

and Borrielo developed automatic mapping tools from

high level speciﬁcation to FPGA programming ﬁles

(Hauck and Borriello, 1995). They harness several

FPGA boards at the same time and in the constructed

system they view the pins connecting different FPGA

as the ﬁxed routes whereas the FPGA are viewed as

Uka, A., Topalli, G., Hoxha, J. and Vrana, N.

FPGA Implementation of Filters in Medical Imaging.

DOI: 10.5220/0010392601950200

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 1: BIODEVICES, pages 195-200

ISBN: 978-989-758-490-9

195

dynamic units as they can be routed and rerouted.

They have also worked on how to ﬁnd partition order-

ings (Hauck and Borriello, 1997). An automatic map-

ping approach goes through ﬁve phases, in the follow-

ing order: Synthesis, Partitioning/Global Placement,

Global Routing, FPGA Place, FPGA Route. Anguita

et al., (2003) have provided a detailed description of

the hardware design and implemented support vec-

tor machine learning algorithms on FPGA (Anguita

et al., 2003).This initial fundamental work paved the

way for the implementation of large scale problems

on more complex systems (Cadambi et al., 2009).

Wang and Ni (2004) implemented encryption and de-

cryption algorithms on FPGA as they are more secure

and consume less power (Wang and Ni, 2004). They

optimized all the components and achieved a better

accuracy than all the previous models while using a

minimum number of LUT, registers and slices. Chou

et al., (1993) discussed the implementation of digital

ﬁlters on FPGA (Chou et al., 1993). Through many

examples, they illustrated the superior capabilities of

FPGA over other computing units. At the same time,

researchers have developed frameworks to implement

Verilog designs on FPGA devices (Shah et al., 2019).

3 FILTERS AND THE USED

ARCHITECTURE

Important parameters of the ﬁlters used in image pro-

cessing are: the type (linear vs nonlinear), size and

sparsity measure. In a common CPU the ﬁlter size af-

fects the computational time, whereas in FPGA-s the

clock frequency would not be affected. The only fac-

tor that would be affected would be the latency num-

ber. The same type of ﬁlter (for example Laplacian ﬁl-

ter) can be formulated in different ways with different

sparsity levels. In case one constructs the design as a

function of the ﬁlter, as in the case of FPGA-s, then a

higher sparsity measure would require a smaller num-

ber of resources.

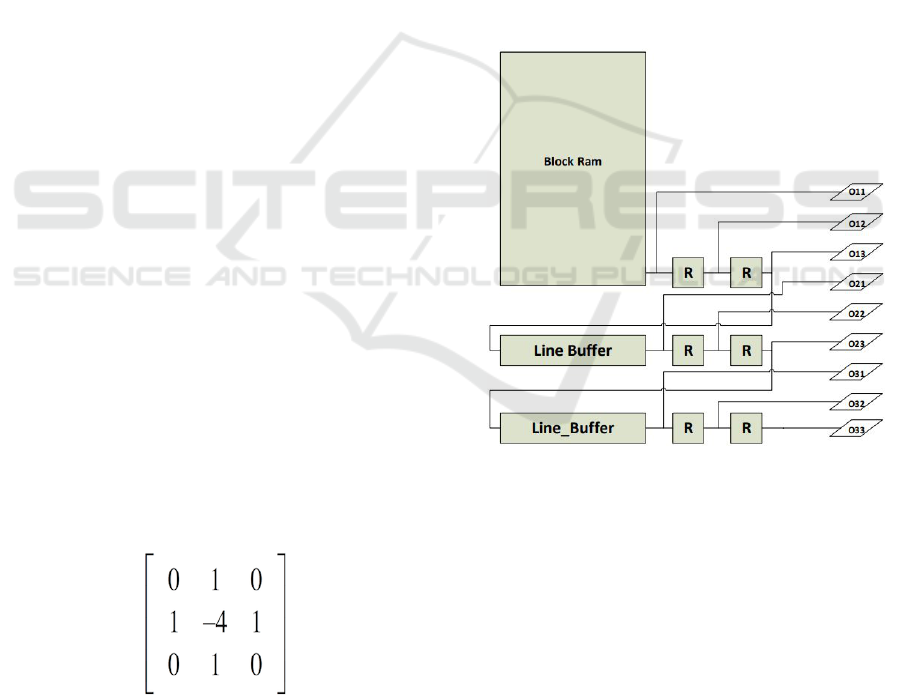
Figure 1: Second derivative Laplacian ﬁlter.

3.1 Laplacian Filter

A Laplacian ﬁlter is the second derivative of the pixel

intensity in two dimensions and serves as an edge de-

tector. One of the variations of this kernel for this

type of ﬁlter with sparsity measure of 44% is shown

in Figure 1. This kernel slides on the pixels of the

image computing the second derivative. The second

derivative of a function shows the behaviour of the

ﬁrst derivative. At edges, the ﬁrst derivative of the

image changes, thus the value of the second derivative

will not be zero. The faster the change on the edge in-

formation, the bigger the second derivative will be.

For the implementation of Laplacian ﬁlter, two stages

are needed. The ﬁrst stage should be able to generate

a sliding window which perfectly imitates the sliding

Kernel in convolution systems. The sliding window

will be generated by means of a Block Ram, a set of

8-bit registers and line-buffers connected as shown in

Figure 2.

Figure 2: Sliding window generator.

The second stage should be able to do the mathe-

matical operation that the Laplacian kernel performs.

For the Kernel shown in Figure 1, there are four ad-

ditions and one multiplication which are to be per-

formed in the second stage of the Laplacian ﬁlter. The

addition and multiplication operation is performed in

purely combinational circuits that are known in prac-

tice to have a high critical path which contributes neg-

atively to the maximum operating frequency of the

system. In order to reduce the critical path, the sec-

ond stage is pipelined as shown in Figure 3.

BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices

196

Figure 3: Pipeline adder tree.

3.2 Two Input Sorter

Two Input Sorter is a digital device, which gets two

unsigned 8-bit numbers and produces two unsigned 8-

bit outputs. The two outputs of the device are called

High (the larger of the two 8-bit numbers) and Low

(the smaller of the 8-bit numbers) that are abbreviated

as H and L, respectively. Two Input Sorter utilizes an

unsigned comparator which compares the two inputs

and produces a signal high or low, depending on the

relative size. This signal is then processed by means

of 8-bit 2x1 MUX-s which yield the proper output dis-

tribution. The schematic of the Two input sorter cell

is shown in Figure 4.

Figure 4: Two input sorter.

3.3 Pipeline Shear Sorting

Shear Sorting is a famous algorithm, which can sort

three numbers. In order to reduce the critical path, the

shear sorting can be designed in a pipelined version.

The pipeline registers are clock synchronized and re-

duce the critical path. The pipelined version of the

three-input shear sorter employing the circuit in Fig-

ure 4 (denoted as the LH unit) is shown in Figure 5.

The triple input sorter, shown in Figure 5, is built from

three dual input sorters, along with pipeline buffers

between each dual input sorter. This allows the small-

est possible critical path.

Figure 5: Pipelined three input sorter.

3.4 Median Finder

Median ﬁnder shown in Figure 6 will utilize the slid-

ing window generator design (see Figure 2) along

with the pipelined three input sorter. The data from

the window generator output O13, O23, O33 will be

sent to the ﬁrst ordering comparator for data ordering,

and the results will be sent to the second consecutive

pipeline stage. Before the second comparison is done,

the present data needs to stay in the second stage of

Figure 6 for two clock cycles more. In order to make

this possible, two registers need to be cascaded. The

second comparing results will be sent to the ﬁnal me-

dian comparator to obtain the ﬁnal result.

FPGA Implementation of Filters in Medical Imaging

197

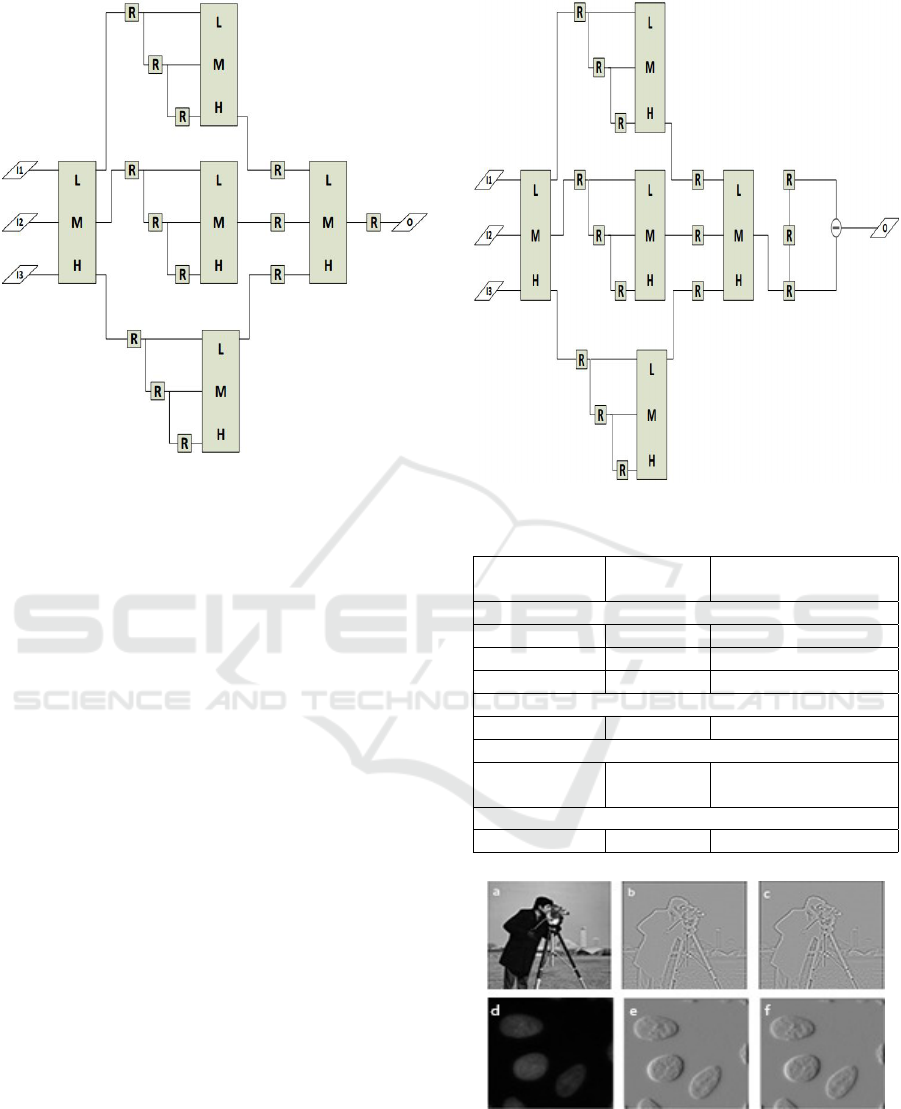
Figure 6: Median Finder.

3.5 Median Finder with First Derivative

We then implemented the ﬁrst derivative subsequently

to the median ﬁlter without changing the frequency

of the system (still operating at one clock-cycle). The

derivative operator commonly used for edge detection

is severely affected by the noise and the implemen-

tation right after the median ﬁlter would maintain a

good performance overall.

4 SIMULATIONS

The systems were implemented on a ZCU104 FPGA.

In Table 1, the architecture speciﬁcations after the

place and route step are shown. The simulation and

implementation of the ﬁlters was carried out on Vi-

vado 2020.2 available in Xilinx packet. The ﬁlters

are intended for Zynq Ultrascale+ family of prod-

ucts. The large number of transistors that are avail-

able in the FPGA always brings in the discussion of

the power consumption. In the table below we report

also the power consumption for both combination of

the ﬁlters.

The FPGA was operating at 125 MHz and after

each clock-cycle of 8 ns the computed value of a pixel

is recorded after the median ﬁlter and the derivative.

Results after applying these two kernels are shown in

Figure 8. For an image of 1000 by 1000 the estimated

run-time on FPGA was 8 ms, whereas on MATLAB

the run-time was 100 ms.

Figure 7: Median ﬁnder and derivative for edge detection.

Table 1: Table to test captions and labels.

Laplacian

Filter

Median + Derivative

Filter

CLB Logic

LUT 121 371

Registers 103 585

Carry8 2 2

I/O

IOB 12 9

Frequency

Maximum

Frequency

125M Hz 125M Hz

Power

Power 7.8 W 8.5 W

Figure 8: A: the original image, b: image ﬁltered in MAT-

LAB and c: FPGA generated image with Laplacian ﬁlter; d:

original nucleus image, e: MATLAB generated image and

f: the FPGA generated image with median and ﬁrst deriva-

tive ﬁlter.

BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices

198

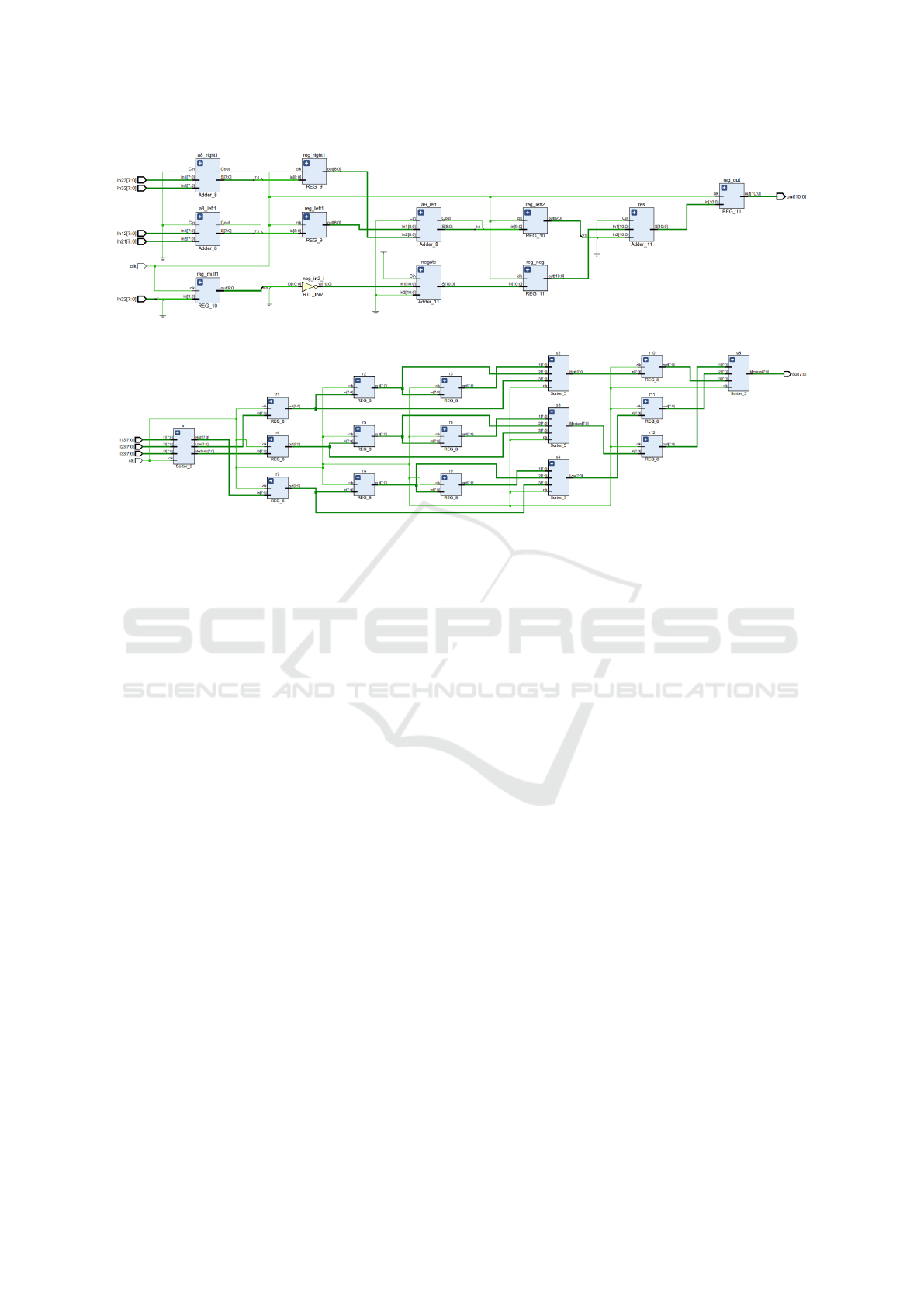
Figure 9: Laplace Filter.

Figure 10: Median Filter.

The RTL schematics of Laplace Filter and Median

Filter are shown in Figure 9 and Figure 10 respec-

tively.

5 CONCLUSION

In this work we reported the designs of the two in-

put sorter, pipelined three-input sorter and median ﬁl-

ter. We implemented Laplacian and Median ﬁlters

achieving a shorter run-time than previous reports in

the literature. Then we implemented median ﬁlter and

derivative ﬁlters for noise removal and edge detection

where the clock period was 8 ns thus maintaining out-

put after each clock cycle. The subsequent application

of derivative ﬁlter following the median ﬁlters aims at

reducing the common error that is inherent in noisy

data. Also there is a 12.5 fold improvement in run-

time compared to MATLAB run in a i7-8700 3.2 GHz

dual core workstation. Implementation of these pre-

processing steps on portable units would greatly im-

prove the quality and the efﬁciency of the work of

medical practitioners especially in cases when they

are combined with microscopic image acquisition.

ACKNOWLEDGEMENTS

This project has received funding from the Euro-

pean Union’s Horizon 2020 research and innovation

program under grant agreement No 760921 (PAN-

BioRA).

REFERENCES

Anguita, D., Boni, A., and Ridella, S. (2003). A digital ar-

chitecture for support vector machines: theory, algo-

rithm, and fpga implementation. IEEE Transactions

on neural networks, 14(5):993–1009.

Cadambi, S., Durdanovic, I., Jakkula, V., Sankaradass, M.,

Cosatto, E., Chakradhar, S., and Graf, H. P. (2009). A

massively parallel fpga-based coprocessor for support

vector machines. In 2009 17th IEEE Symposium on

Field Programmable Custom Computing Machines,

pages 115–122. IEEE.

Chen, X., Zhou, X., and Wong, S. T. (2006). Automated

segmentation, classiﬁcation, and tracking of cancer

cell nuclei in time-lapse microscopy. IEEE Transac-

tions on Biomedical Engineering, 53(4):762–766.

Chou, C.-J., Mohanakrishnan, S., and Evans, J. B. (1993).

Fpga implementation of digital ﬁlters. In Proc. Icspat,

volume 93, page 1. Citeseer.

Curto, V. F., Marchiori, B., Hama, A., Pappa, A.-M.,

Ferro, M. P., Braendlein, M., Rivnay, J., Fiocchi, M.,

Malliaras, G. G., Ramuz, M., et al. (2017). Organic

transistor platform with integrated microﬂuidics for

in-line multi-parametric in vitro cell monitoring. Mi-

crosystems & nanoengineering, 3(1):1–12.

Hauck, S. and Borriello, G. (1995). Logic partition order-

ings for multi-fpga systems. In Proceedings of the

1995 ACM third international symposium on Field-

programmable gate arrays, pages 32–38.

Hauck, S. and Borriello, G. (1997). Pin assignment for

multi-fpga systems. IEEE transactions on computer-

FPGA Implementation of Filters in Medical Imaging

199

aided design of integrated circuits and systems,

16(9):956–964.

Shah, D., Hung, E., Wolf, C., Bazanski, S., Gisselquist,

D., and Milanovic, M. (2019). Yosys+ nextpnr: an

open source framework from verilog to bitstream for

commercial fpgas. In 2019 IEEE 27th Annual Inter-

national Symposium on Field-Programmable Custom

Computing Machines (FCCM), pages 1–4. IEEE.

Simon, D. T., Gabrielsson, E. O., Tybrandt, K., and

Berggren, M. (2016). Organic bioelectronics: bridg-

ing the signaling gap between biology and technology.

Chemical Reviews, 116(21):13009–13041.

Wang, S.-S. and Ni, W.-S. (2004). An efﬁcient fpga imple-

mentation of advanced encryption standard algorithm.

In 2004 IEEE International Symposium on Circuits

and Systems (IEEE Cat. No. 04CH37512), volume 2,

pages II–597. IEEE.

BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices

200