Simple Matrix Factorization Collaborative Filtering for Drug

Repositioning on Cell Lines

an Carrera

1,3 a

, Eduardo Tejera

2 b

and In

es Dutra

3 c

Departamento de Inform

atica y Ciencias de la Computaci

on, Escuela Polit

ecnica Nacional, Quito, Ecuador

Grupo de Quimio-Bioinform

atica, Universidad de Las Am

ericas, Quito, Ecuador

Departamento de Ci

encia de Computadores, Universidade do Porto, Porto, Portugal

Keywords:

Drug Repositioning, Recommender Systems, Collaborative Filtering.

Abstract:

The discovery of new biological interactions, such as interactions between drugs and cell lines, can improve

the way drugs are developed. Recently, there has been important interest for predicting interactions between

drugs and targets using recommender systems; and more speciﬁcally, using recommender systems to predict

drug activity on cellular lines. In this work, we present a simple and straightforward approach for the discovery

of interactions between drugs and cellular lines using collaborative ﬁltering. We represent cellular lines by

their drug afﬁnity proﬁle, and correspondingly, represent drugs by their cell line afﬁnity proﬁle in a single

interaction matrix. Using simple matrix factorization, we predicted previously unknown values, minimizing

the regularized squared error. We build a comprehensive dataset with information from the ChEMBL database.

Our dataset comprises 300,000+ molecules, 1,200+ cellular lines, and 3,000,000+ reported activities. We have

been able to successfully predict drug activity, and evaluate the performance of our model via utility, achieving

an Area Under ROC Curve (AUROC) of near 0.9.

1 INTRODUCTION

Drug repositioning is the process of ﬁnding new uses

outside the scope of the original medical indication

for existing drugs. Drug repositioning offers a bet-

ter risk-versus-reward trade-off compared with other

drug development strategies because repositioning

candidates have often been through several stages of

clinical development, and therefore have well-known

safety and pharmacokinetic proﬁles. Phases like in

vitro and in vivo screening, chemical optimization,

toxicology, bulk manufacturing, formulation devel-

opment and even early clinical development have, in

many cases, already been completed and can there-

fore be bypassed, when testing already developed

drugs (Ashburn and Thor, 2004).

De novo drug development process can take 13 to

15 years and cost between US$2 and $3 billion. De-

velopment costs are increasing, though the number of

drugs yearly approved per dollar spent on develop-

ment has remained ﬂat or decreased (Nosengo, 2016).

https://orcid.org/0000-0003-4337-7433

https://orcid.org/0000-0002-1377-0413

https://orcid.org/0000-0002-3578-7769

Paul Ehrlich, winner of 1908 Nobel Prize for

Physiology or Medicine, postulated the ‘magic bullet’

concept: drugs that go straight to their intended cell-

structural targets. Targeted medicine should in theory

efﬁcaciously attack pathogens yet remain harmless in

healthy tissues (Strebhardt and Ullrich, 2008).

One of the problems with Ehrlich’s postulate is

that once the drug reaches the body, it has no way

to prevent affecting other targets besides its main pur-

pose, causing the undesired effects of drugs. This is

the essence of the proven inefﬁciency of drug discov-

ery approaches based on the magic bullet paradigm

(Cruz-Monteagudo et al., 2017).

Drug repositioning works by testing biological in-

teractions or effects of drugs on genes, protein bind-

ing and molecular pathways affecting the genotype

and phenotype of humans. It identiﬁes new thera-

peutic indications for known drugs that have different

targets (Dovrolis et al., 2017). The fundamental as-

sumption is that agents with similar properties have

similar therapeutic effects. Fig. 1 illustrates how drug

repositioning can work.

Drug repositioning is part of computer-aided drug

design (CADD), classiﬁed in structure-based and

ligand-based. Ligand-based CADD is grounded on

768

Carrera, I., Tejera, E. and Dutra, I.

Simple Matrix Factorization Collaborative Filtering for Drug Repositioning on Cell Lines.

DOI: 10.5220/0010394007680775

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 5: HEALTHINF, pages 768-775

ISBN: 978-989-758-490-9

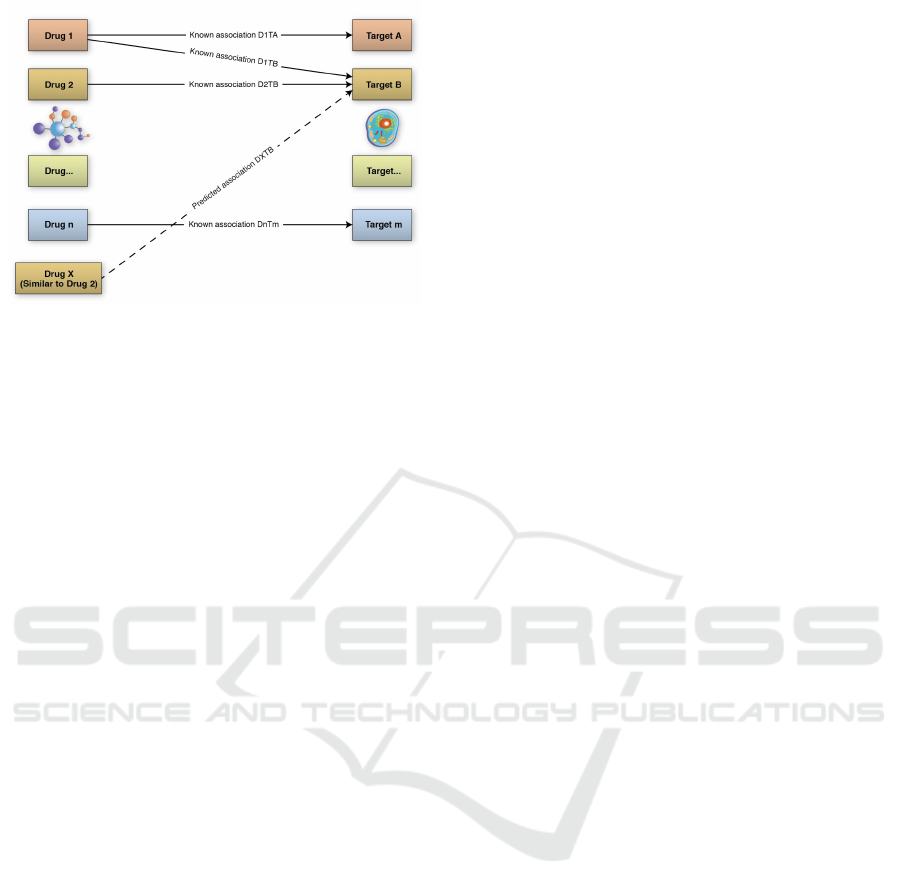
Figure 1: An example of how drug repositioning works.

molecular activity databases, tagging small molecules

as active and inactive, and through chemical similar-

ity searches (Sliwoski et al., 2014). Ligand-based

CADD is generally preferred when no or little struc-

tural information about the drug targets is available.

In every method for drug repositioning, each drug,

target, and disease has to be represented by a feature

vector. These vectors can be based on different prop-

erties: chemical structures, side effects, ﬁngerprints,

genomic characters of targets, and phenotype infor-

mation of diseases. These models can get very com-

plex and require a large set of data, combining ge-

nomic information about cellular lines, and chemical

information about drugs.

In this work we aim to predict drug activities on

cell lines while providing a minimum amount of in-

formation, i.e., drug-cell line afﬁnity proﬁles. We

present a simple and straightforward model for drug

repositioning for cellular lines using a recommender

system. The performance shown by the model is

strong, considering the simplicity of the model.

The remainder of this work is organized as fol-

lows: Section 2 describes the motivation and rele-

vance of this work, and Section 3 presents a sum-

mary of relevant related work. Section 4 describes

the dataset and methodology, and Section 5 shows the

obtained results and model evaluation. Section 6 dis-

cusses the contribution of this work, and the limita-

tions of our proposed model. Finally, Section 6 refers

to links to the database and software ﬁles for repro-

ducibility.

2 MOTIVATION

The goal of recommender systems is to infer customer

interests. The entity to which the recommendation is

provided is referred to as the user, and the product be-

ing recommended is referred to as an item. Therefore,

recommendation analysis is often based on the previ-

ous interaction between users and items, because past

interests and proclivities are often good indicators of

future choices (Aggarwal, 2016).

In recommender systems, a m × n ranking matrix,

called R, is formed, where m is the number of users,

and n is the number of items. The elements of the

matrix are denoted r, where r

i j

is the ranking given by

the user i to the item j. This matrix is very sparse, as

it only contains observed data. Collaborative ﬁltering

recommender systems aim to predict missing ratings,

and ﬁll matrix R. Predicted ratings are denoted ˆr

for

the previously unknown ranking given by the user u

to the item v.

Collaborative ﬁltering recommender systems

work with user-item interactions, and use the collabo-

rative power of the ratings provided by multiple users

to make recommendations. The main challenge is the

sparsity of ratings matrices (Aggarwal, 2016).

As described by (Wang et al., 2019), drug reposi-

tioning is analogous to recommendation systems. We

can understand the drug repositioning concept as rec-

ommending previously unknown drug-target interac-

tions. In this case, the ranking matrix R is an inter-

action matrix, where r

i j

represents the drug i reported

activity, or inactivity, on target j. Predicted values ˆr

represent a possible activity of drug u on target v.

In this work, our goal is to recommend potential

drugs for targets. In our case, targets will be cellular

lines.

A cellular line is a population of cells, that, given

appropriate surroundings, can live, multiply, and even

express differentiated properties in a tissue-culture

dish. This cell culture is used to perform experiments

in vitro (Alberts et al., 2002). Cell lines are a very

important tool for research into the biochemistry and

cell biology of multicellular organisms.

Large drug screening projects are carried out us-

ing cancer cell lines. Cell lines help in choosing the

most effective chemotherapeutic regimen for a pa-

tient, given that an ineffective chemotherapy may in-

crease mortality and decrease quality of life in cancer

patients (Chen et al., 2013).

Drug repositioning for cellular lines is thus of

great concern, as it can help make faster and less ex-

pensive development of cancer therapies. However,

related work usually focuses developing models on

speciﬁc sets of cellular lines, using as well a small set

of candidate drugs. There aren’t many research pa-

pers aiming at a more comprehensive model with a

large set of drugs and cell lines. There is an opportu-

nity of achieving this goal using collaborative ﬁltering

recommender systems.

Simple Matrix Factorization Collaborative Filtering for Drug Repositioning on Cell Lines

769

3 RELATED WORK

For the past years, there has been interest on re-

search about recommender systems for drug reposi-

tioning for cellular lines, as several research papers

have approached the subject. Following, we present

a brief summary of the most relevant work in the

subject. Table 1 synthesizes ﬁndings of such work.

(Gao et al., 2012) presents a collaborative ﬁltering

model for predicting inhibitors of the Hedgehog Sig-

naling Pathway. Authors use a collaborative ﬁltering

model for QSAR modeling, based on collective ma-

trix factorization (Singh and Gordon, 2008). They

build a matrix X, with data about the interactions of

chemical compounds on cell lines, and matrix Y , with

the descriptions of compounds, using two different

molecule descriptors: a general descriptor and a drug-

like index (DLI) for compound representation. Work

focuses on predicting interactions for 4 cellular lines:

BxPC-3, NCI-H446, SW1990, and NCI-H157.

Performance is evaluated measuring squared cor-

relation coefﬁcient (R-square) and Root mean squared

error (RMSE). Authors achieve values of R-square

ranging from 0.4 to 0.7, and RMSE from 0.4 to 0.8.

(Cheng et al., 2012) develops three inference

methods to predict new drug-target interactions:

drug-based similarity inference (DBSI), target-based

similarity inference (TBSI) and network-based infer-

ence (NBI). These three methods are based on com-

plex network theory. Authors construct 4 benchmark

datasets comprising: 445, 210, 223, and 54 com-

pounds against 664 enzymes, 204 ion channels, 95

GPCRs and 26 nuclear receptors, respectively.

Results of 10-fold cross validation perfor-

mance evaluation for AUC were 0.9756±0.006,

0.9766±0.007, 0.9466±0.019 and 0.8386±0.087 for

enzymes, ion channels, GPCRs and nuclear receptors,

respectively. Authors validate the predictions experi-

mentally as well, in wet lab, for enzyme DPP-IV, and

receptors ERα and ERβ.

(Wang et al., 2019) constructs and decomposes

three-dimensional tensors, consisting on associations

among drugs, targets and diseases, to derive latent

factors reﬂecting the functional patterns of the three

entities. Authors apply Topological Data Analysis

(TDA) to cluster drugs, targets and diseases into func-

tional groups.

Authors construct a dataset comprising 549 drugs

from Drug-Bank, 424 targets from Human Protein

Reference Database (HPRD) and 340 diseases from

the Comparative Toxicogenomics Database (CTD).

They model the problem of triplet association (drug-

target-disease) prediction as tensor completion. A 3D

association tensor χ is factorized into three matrices,

called factor matrices. By multiplying factor matri-

ces, another tensor

χ is generalized, which contains

the approximation of the observations in χ and new

predictions recovered from the functional patterns.

This is a 3D version of singular value decomposition

(SVD). Authors assess their performance with area

under the ROC curve (AUC), ranging from 0.9673 to

0.999, and area under precision-recall curve (AUPR),

ranging from 0.861 to 0.9967.

(Suphavilai et al., 2018) proposes a method

CaDRReS that predicts cancer drug responses for un-

seen cell-lines/patients based on learning projections

into a latent pharmacogenomic space. Authors con-

struct datasets from two large-scale studies: CCLE

and GDSC (Suphavilai et al., 2018). Datasets contain

information on 491 cell-lines, 19 drugs and 9096 ex-

periments from CCLE, and 983 cell-lines, 223 drugs

and 179,633 experiments from GDSC.

Authors calculate cell-line features based on gene

expression information, and use matrix factoriza-

tion to learn a latent space to project drug and cell

line data. They evaluate their models for each cell

line, using the normalized discounted cumulative gain

(NDCG). Results show that values of NDCG range

between 0.6 and 0.9.

(Zhang et al., 2018) presents a hybrid interpola-

tion weighted collaborative ﬁltering method to ap-

proximate the sensitivity of a given cell line to a drug

predicting anti-cancer drug response. Authors nor-

malize genomic expression proﬁles of cell lines to

draw their similarity matrix, and use chemical struc-

tures of drug compounds to draw their similarity ma-

trix.

Authors construct two datasets: the ﬁrst with in-

formation from GDSC project, consisting of 652 cell

lines, 135 drugs, and 70,676 activity data points (ma-

trix 80.3% complete); the second dataset with infor-

mation from CCLE project, with 491 cell lines, 23

drugs, and 10,870 activity data points (matrix 96.25%

complete). Results are assessed with measures

including average Pearson Correlation Coefﬁcient

(PCC), and RMSE between predicted and observed

drug responses. Performance results show drug-

averaged PCC of 0.58±0.15 and RMSE 1.51±0.39

for the GDSC dataset, and drug-averaged PCC of

0.74±0.08 and RMSE 0.53±0.15 for the CCLE

dataset.

(Wang et al., 2018) develops a multi-rank, multi-

layered recommender system, called ANTENNA.

Authors obtain a dataset of 199,338 chemical com-

pounds, 6,277 genes, with 233,378 unique chemical-

gene active pairs, from the combination of ZINC,

ChEMBL, and DrugBank databases, as well as the

Comparative Toxicology Database (CTD). Authors

aim at predicting novel drug-gene-disease associa-

HEALTHINF 2021 - 14th International Conference on Health Informatics

770

Table 1: Summary on the most relevant work about recommender systems for drug repositioning for cellular lines.

Work Predicting Goal Dataset size

Method Results

(Gao et al.,

2012)

Inhibitors of Hedgehog Sig-

naling Pathway

93 compounds, 4

cell lines

Collaborative ﬁlter-

ing + Content-based

R-square: [0.4-

0.7] RMSE:

[0.4-0.8]

(Cheng

et al., 2012)

Drug-target interactions via

network-based inference

445 compounds,

664 enzymes

(largest)

Content-based AUC:

0.9756±0.006

(Wang et al.,

2019)

Drug, target and disease as-

sociations by tensor decom-

position

549 drugs, 424 tar-

gets, 340 diseases

3D tensor decompo-

sition

AUC [0.97-

0.99] AUPR

[0.86-0.99]

(Suphavilai

et al., 2018)

Cancer drug responses for

unseen cell-lines/ patients

based on latent pharma-

cogenomic space.

983 cell lines, 223

drugs, 179,633 ex-

periments (largest)

Matrix decomposi-

tion

NDGC [0.6-

0.9]

(Zhang

et al., 2018)

Anti-cancer drug responses

of cell lines, incorporating

cell line and drug similari-

ties

652 cell lines, 135

drugs, 70,676 ac-

tivities (largest)

Weighted interpola-

tion collaborative ﬁl-

tering

PCC:0.58±0.15

RMSE:

1.51±0.39

(Wang et al.,

2018)

Novel chemical - gene - dis-

ease associations

6,277 genes,

199,338 com-

pounds, 233,378

activities

Multi-rank, multi-

layered

FDR<0.02

(Liu et al.,

2018)

Anti-cancer Drug Response N/A Neighborhood-based

collaborative ﬁl-

tering with Global

Effect Removal

PCC S/R: 0.89

RMSE S/R:

0.47

(Emdadi and

Eslahchi,

2020)

Effective cell-line and drug

features for computing drug

sensitivity

555 cell lines, 98

drugs (largest)

Logistic matrix fac-

torization

AUC: 0.76

tions, modeling the prediction of drug-disease associ-

ation problem as a One Class Collaborative Filtering

(OCCF) problem, as they understand negative data

as not needed for training the model. ANTENNA

predicted that 21,921 novel drug-disease associations

with Benjamini-Hochberg adjusted false discovery

rate (FDR) less than 0.02. Authors perform predic-

tions on a set of two cell lines, MCF-7 and MDA-

MB 468. Experimental assessment of predictions was

done in wet lab by detecting the binding of selected

drugs to a set of 438 kinases.

(Liu et al., 2018) proposes a neighborhood-based

collaborative ﬁltering, with global effects removal

recommender system, for drug-response prediction.

Model incorporates similarities of drugs and of cell

lines in additional to the known drug response. Re-

sults are evaluated using PCC and RMSE as perfor-

mance metrics. Authors evaluated their model using

the GDSC, and CCLE datasets. They did not include

the size of their datasets. Model shows as perfor-

mance metrics a drug-averaged PCC S/R of 0.89, and

a drug-averaged RMSE S/R of 0.47.

(Emdadi and Eslahchi, 2020) presents a Drug Sen-

sitivity Prediction using Logistic Matrix Factorization

approach. Authors focus on the discovery of effec-

tive features of cell lines and drugs for computing the

probability of interaction of cell lines and drugs by

logistic matrix factorization approach. Authors built

two benchmark datasets, the ﬁrst, based on GSDC,

contains 555 cell lines and 98 drugs, and the second,

based on CCLE, 363 cell lines and 24 drugs.

Authors ﬁnd the t-most nearest neighbors for a

new cell line and estimate its latent vector, based on

average of its neighbors latent vectors. After obtain-

ing the latent vector, authors can predict IC

values

across all drugs for the cell line. Results show an AUC

of 0.760 for the GDSC dataset, and an AUC of 0.776

for the CCLE dataset.

In general, interesting work has been made on this

subject. Several papers include information from dif-

ferent datasets, each one develops its own method,

and different performance metrics are used. Nev-

ertheless, we can identify a lack of a general com-

prehensive model. Most work is done for speciﬁc

datasets, or speciﬁc diseases. Thus, we could bene-

ﬁt from a more general approach.

Simple Matrix Factorization Collaborative Filtering for Drug Repositioning on Cell Lines

771

Moreover, we noted that all methods construct

their interaction matrices with positive interaction

values, i.e., they include information of targets that

are interact with a drug, but not include information

about targets that do not interact with a drug. We hy-

pothesize that negative interaction values could pro-

vide an interesting improvement on drug reposition-

ing recommender systems.

4 MATERIALS AND METHODS

In this work we aim at predicting drug-cell line in-

teractions using collaborative ﬁltering of an interac-

tion matrix. The ﬁrst step is to prepare the data

for the interaction matrix. We selected ChEMBL

database, an open large-scale bioactivity database ac-

cessible at https:ebi.ac.uk/chembl. ChEMBL hosts

extracted data from the medicinal chemistry litera-

ture, and bioactivity data from new sources, includ-

ing: datasets from neglected disease screening, drug

metabolism and disposition data and bioactivity data

from patents (Gaulton et al., 2012).

We follow the data preparation methodology from

(Tejera et al., 2019). Tejera et al. presents a method-

ology for discovering associations between drugs and

cell lines based on drug similarity and k-nearest

neighbors using a dataset derived from ChEMBL

database.

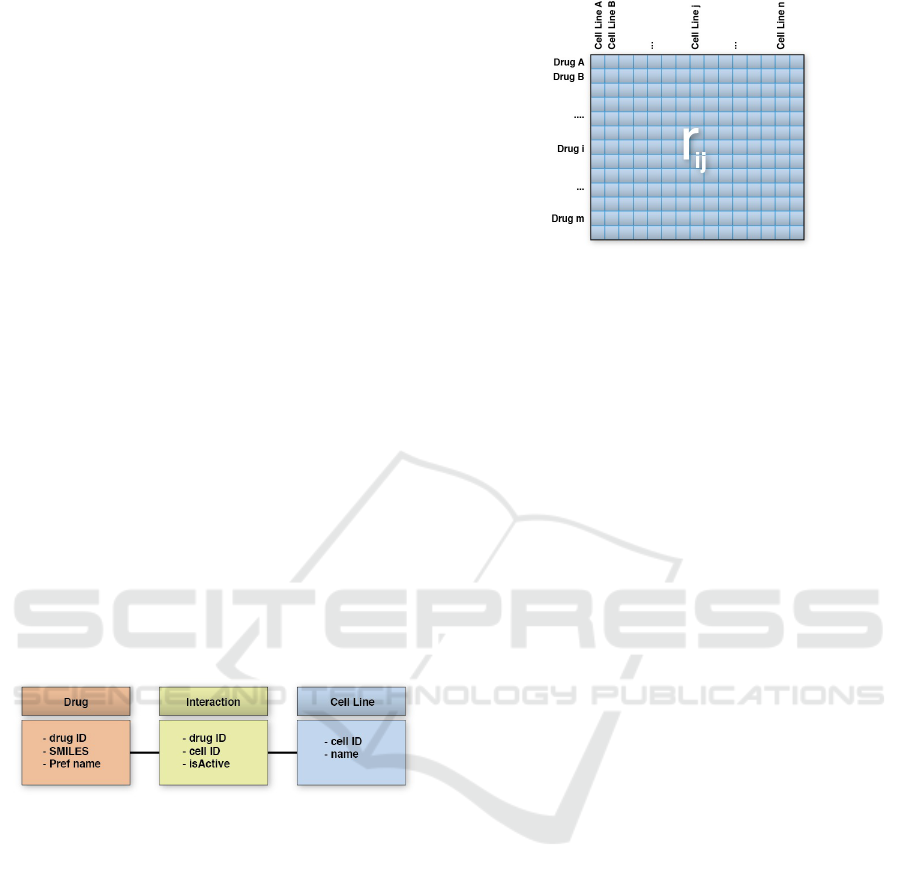
Figure 2: Simpliﬁed ChEMBL Data Model.

We simpliﬁed the data model from ChEMBL for

constructing the interaction matrix. Figure 2 shows

our data model: table Drug presents the information

about chemical compounds, table Cell Line about

the cellular lines, and table Interaction summarizes

the information about the reported assays and activi-

ties for a given drug-cell line pair.

Then, we select experimental data of cellular lines

from ChEMBL to populate Interaction table, and

ranking matrix R (Fig. 3). We select activities report-

ing IC50, GI50 and EC50. These values correspond to

drug concentration: IC50 is drug concentration caus-

ing 50% inhibition of the desired activity. GI50 is

concentration for 50% of maximal inhibition of cell

proliferation, and EC50 is the concentration causing

50% of maximum effect for any measured biological

effect of interest.

Figure 3: Interaction Matrix R.

We classify activities into sensitive and resistant.

An activity is sensitive when concentration is less than

or equal to 10µM, and resistant when otherwise. In

the Interaction table of the data model (Fig. 2 ), the

isActive property is boolean, having a True value

for sensitive, and False for resistant.

Most drug-cell line pairs report several assay

records, with different concentration values. We dis-

card pairs with less than 10 records, as we need con-

ﬁrmed information for our model. If there are ambi-

guities, i.e., some records report concentrations over

10µM, and other records report concentrations under

10µM, isActive property is not set.

Interaction matrix R contains all possible drug-cell

line combinations. A given r

i j

element represents the

drug i activity on cell line j. For populating matrix R,

we assigned a value of 1 for sensitive, −1 for resis-

tant, and 0 for the unknown values.

Then, process is performed over different versions

of ChEMBL. We worked with versions 24, 25, 26,

and 27 (latest).

After data tables are set, we can deploy our Col-

laborative Filtering Recommender System, as shown

in Fig. 4. We use package scikit-surprise

Python implementation for Recommender Systems

(Hug, 2020), following documentation from: sur-

prise.readthedocs.io.

For computing unkown values, we use singular

value decomposition (SVD), which requires factoring

R matrix (Koren et al., 2009). Estimated rankings ˆr

i.e., the drug u activity on cell line v, are computed

using the formula described in equation 1.

ˆr

= µ + b

+ b

+ q

(1)

To infer the unkown interaction values, we minimize

the regularized squared error, as shown in equation 2:

∑

∈R

train

− ˆr

)

+ λ



+ b

+ ||q

+ ||p



(2)

Minimization is performed in several epochs by

stochastic gradient descent SGD, as shown in equa-

HEALTHINF 2021 - 14th International Conference on Health Informatics

772

Figure 4: Collaborative Filtering for computed estimated values ˆr

i j

tion 3. Error e

is the difference between reported

and predicted values. Baselines b

and b

correspond

to drugs, and cell lines, respectively, and are initial-

ized to 0.

← b

+ γ(e

− λb

)

← b

+ γ(e

− λb

)

← p

+ γ(e

· q

− λp

)

← q

+ γ(e

· p

− λq

)

(3)

We perform a 10-fold cross-validated GridSearch

to ﬁnd the best conﬁguration for the algorithm. For

our problem, the best conﬁguration is: 300 epochs,

learning rate γ = 0.002, and regularization term λ =

0.1.

5 RESULTS

For assessing predictions, we compared predicted val-

ues to actual values; which is deﬁned by (Aggarwal,

2016) as performance evaluation via utility.

We trained our model with data from ChEMBL

version 24. Then, obtained the difference between a

newer version (25, 26, and 27) and 24 as ground-truth.

This difference contains only the records in the newer

version that do not appear in base version 24. Finally,

we compared predictions for unknown values to the

reported values in the difference dataset.

We mapped results as shown in Fig. 5. Ground-

truth values are discrete: −1 for inactivities, and 1 for

activities. Predicted values are continuous, and range

between −1 and 1. Mapping shows that we can iden-

tify predicted values for inactivities. Predictions have

a large error rate which can be caused by model spar-

sity.

We computed two metrics to assess our results:

Root mean squared error (RMSE), and Area Under

Receiver Operating Characteristic curve (AUROC).

RMSE computes the overall error over set

R (equation

4). ROC curve is drawn by plotting the false-positive

rate on the X-axis and the true-positive rate the Y-axis

for varying values of a threshold t. AUROC provides

Figure 5: Results mapping (Predicted value vs Actual

value) for versions 24 and 25.

a concrete quantitative evaluation of the effectiveness

of the method (Aggarwal, 2016).

RMSE =

∑

ˆr

∈

− ˆr

)

. (4)

Table 2 shows values of RMSE and AUC for

model trained with ChEMBL version 24, and tested

against versions 25, 26, and 27. Best values are ob-

tained when training with v24, and testing v25.

Fig. 6 shows ROC curves for model trained with

ChEMBL version 24, and tested against versions 25,

26, and 27. When versions are more apart, i.e., v24

for training, and v27 for testing, performance de-

creases.

Finally, when working with the two most recent

versions of ChEMBL, training with v26, and testing

with v27, we achieve a RMSE of 0.684, and an Area

Under ROC curve of 0.830. Fig. 7 shows the ROC

curve for versions 26 and 27.

Table 2: RMSE and AUC for different testing datasets.

Train Test RMSE AUC

v24 v25 0.7398 0.8961

v24 v26 0.7751 0.8747

v24 v27 0.7838 0.8694

Simple Matrix Factorization Collaborative Filtering for Drug Repositioning on Cell Lines

773

(a) Versions 24 and 25.

(b) Versions 24 and 26.

Figure 6: ROC curve for versions (former is for training,

latter is for testing).

6 DISCUSSION

This work achieves its goal of developing a sim-

ple, straightforward, and comprehensive model for

the discovery of new drug-cell line interactions using

a collaborative ﬁltering recommender system. The

strong points of our model are its simplicity and its

performance. In our recommender system, an inter-

action matrix is formed, where the reported activities

Largest dataset if more than one is deﬁned

Corresponding to largest dataset if more than one is de-

ﬁned

Figure 7: ROC curve for versions 26 and 27.

(or inactivities) of drugs over cellular lines are stored.

Unknown values are then computed using simple ma-

trix factorization, minimizing the regularized squared

error.

Our model evaluates predicted rankings via util-

ity (Aggarwal, 2016), comparing two versions of the

same database. We use four versions of ChEMBL

database: 24 to 27. Predictions are assessed by com-

paring newer with older versions, e.g., train our model

with version 24, obtain the difference between version

25 and 24 as our ground-truth, and then assess if the

new values of version 25 can be predicted from the

information of version 24.

Compared with other recommender system mod-

els for drug repositioning, as described in Section 3,

our model is more comprehensive, i.e., it works for

a larger set of cellular lines and drugs. In our case,

our model comprehends a set of 314,392 molecules,

1,254 cellular lines, and 3,057,368 reported activities.

Our model performs well when dealing with spar-

sity, as Interaction Matrix R was only 0.77% com-

plete. Also, this model includes negative examples

of drug-cell line interactions.

We present a model that does not integrate chem-

ical data for drugs, nor genomic data for cell lines.

Nevertheless, we have been able to obtain a strong

performance for our predictions.

This work has the limitation of the cold-start prob-

lem, which is deﬁned as what items would the system

recommend to a new user, for certain characteristics

of items and users. Given that our model does not

incorporate drug or cell lines characterization data,

there is no way of answering the cold-start problem.

In further work, methodology can be extended to

incorporate chemical data for drugs, or genomic data

for cell lines, thus leveraging this model, achieving

better performance, and approaching the cold-start

problem.

HEALTHINF 2021 - 14th International Conference on Health Informatics

774

REPRODUCIBILITY

Experiments were performed on a server at the De-

partment of Computer Science at the University of

Porto. Server is a GNU/Linux server with 503GiB

of RAM, 96-core Intel(R) Xeon(R) Gold 6252 CPU

@ 2.10GHz processor.

Datasets and Python code for these experiments

are stored in Github repository: (https://github.com/

ivan-carrera/biostec2021).

REFERENCES

Aggarwal, C. C. (2016). Recommender Systems: The Text-

book. Communications of the ACM. Springer Inter-

national Publishing, NY, USA.

Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K.,

and Walter, P. (2002). Isolating cells and growing

them in culture. In Molecular Biology of the Cell. 4th

edition. Garland Science.

Ashburn, T. T. and Thor, K. B. (2004). Drug reposition-

ing: identifying and developing new uses for exist-

ing drugs. Nature Reviews Drug Discovery, 3(8):673–

683.

Chen, J., Cheng, G.-H., Chen, L.-P., Pang, T.-Y., and Wang,

X.-L. (2013). Prediction of Chemotherapeutic Re-

sponse in Unresectable Non-small-cell Lung Cancer

(NSCLC) Patients by 3-(4,5-Dimethylthiazol-2-yl)-

5-(3-carboxymethoxyphenyl)-2-(4-sulfophenyl)-2H-

tetrazolium (MTS) Assay. Asian Paciﬁc Journal of

Cancer Prevention, 14(5):3057–3062.

Cheng, F., Liu, C., Jiang, J., Lu, W., Li, W., Liu, G., Zhou,

W., Huang, J., and Tang, Y. (2012). Prediction of

Drug-Target Interactions and Drug Repositioning via

Network-Based Inference. PLoS Computational Biol-

ogy, 8(5):e1002503.

Cruz-Monteagudo, M., Sch

urer, S., Tejera, E., P

erez-

Castillo, Y., Medina-Franco, J. L., S

anchez-

Rodr

ıguez, A., and Borges, F. (2017). Systemic

QSAR and phenotypic virtual screening: chasing

butterﬂies in drug discovery. Drug Discovery Today,

22(7):994–1007.

Dovrolis, N., Kolios, G., Spyrou, G., and Maroulakou, I.

(2017). Laying in silico pipelines for drug reposition-

ing: a paradigm in ensemble analysis for neurodegen-

erative diseases. Drug Discovery Today, 22(5):805–

813.

Emdadi, A. and Eslahchi, C. (2020). DSPLMF: A Method

for Cancer Drug Sensitivity Prediction Using a Novel

Regularization Approach in Logistic Matrix Factor-

ization. Frontiers in Genetics, 11.

Gao, J., Che, D., Zheng, V. W., Zhu, R., and Liu, Q. (2012).

Integrated QSAR study for inhibitors of hedgehog sig-

nal pathway against multiple cell lines:a collaborative

ﬁltering method. BMC Bioinformatics, 13(1):186.

Gaulton, A., Bellis, L. J., Bento, A. P., Chambers, J.,

Davies, M., Hersey, A., Light, Y., McGlinchey, S.,

Michalovich, D., Al-Lazikani, B., and Overington,

J. P. (2012). ChEMBL: a large-scale bioactivity

database for drug discovery. Nucleic Acids Research,

40(D1):D1100–D1107.

Hug, N. (2020). Surprise: A python library for recom-

mender systems. Journal of Open Source Software,

5(52):2174.

Koren, Y., Bell, R., and Volinsky, C. (2009). Matrix Factor-

ization Techniques for Recommender Systems. Com-

puter, 42(8):30–37.

Liu, H., Zhao, Y., Zhang, L., and Chen, X. (2018). Anti-

cancer Drug Response Prediction Using Neighbor-

Based Collaborative Filtering with Global Effect Re-

moval. Molecular Therapy - Nucleic Acids, 13:303–

311.

Nosengo, N. (2016). Can you teach old drugs new tricks?

Nature, 534(7607):314–316.

Singh, A. P. and Gordon, G. J. (2008). Relational Learning

via Collective Matrix Factorization. In Proceedings

of the 14th ACM SIGKDD International Conference

on Knowledge Discovery and Data Mining, KDD ’08,

page 650–658, New York, NY, USA. Association for

Computing Machinery.

Sliwoski, G., Kothiwale, S., Meiler, J., and Lowe, E. W.

(2014). Computational methods in drug discovery.

Pharmacological Reviews, 66(1):334–395.

Strebhardt, K. and Ullrich, A. (2008). Paul Ehrlich’s magic

bullet concept: 100 years of progress. Nature Reviews

Cancer, 8(6):473–480.

Suphavilai, C., Bertrand, D., and Nagarajan, N. (2018). Pre-

dicting Cancer Drug Response using a Recommender

System. Bioinformatics, 34(22):3907–3914.

Tejera, E., Carrera, I., Jimenes-Vargas, K., Armijos-

Jaramillo, V., S

anchez-Rodr

ıguez, A., Cruz-

Monteagudo, M., and Perez-Castillo, Y. (2019). Cell

ﬁshing: A similarity based approach and machine

learning strategy for multiple cell lines-compound

sensitivity prediction. PLoS ONE, 14(10):1–11.

Wang, A., Lim, H., Cheng, S.-Y., and Xie, L. (2018).

ANTENNA, a Multi-Rank, Multi-Layered Recom-

mender System for Inferring Reliable Drug-Gene-

Disease Associations: Repurposing Diazoxide as a

Targeted Anti-Cancer Therapy. IEEE/ACM Transac-

tions on Computational Biology and Bioinformatics,

15(6):1960–1967.

Wang, R., Li, S., Cheng, L., Wong, M. H., and Leung, K. S.

(2019). Predicting associations among drugs, targets

and diseases by tensor decomposition for drug reposi-

tioning. BMC Bioinformatics, 20(S26):628.

Zhang, L., Chen, X., Guan, N.-N., Liu, H., and Li, J.-Q.

(2018). A Hybrid Interpolation Weighted Collabora-

tive Filtering Method for Anti-cancer Drug Response

Prediction. Frontiers in Pharmacology, 9(SEP).

Simple Matrix Factorization Collaborative Filtering for Drug Repositioning on Cell Lines

775