Link Prediction for Wikipedia Articles based on Temporal Article

Embedding

Jiaji Ma and Mizuho Iwaihara

Graduate School of Information, Production and Systems, Waseda University, Japan

Keywords:

Graph Embedding, Link Prediction, Temporal Random Walk.

Abstract:

Wikipedia articles contain a vast number of hyperlinks (internal links) connecting subjects to other Wikipedia

articles. It is useful to predict future links for newly created articles. Suggesting new links from/to existing

articles can reduce editors’ burdens, by prompting editors about necessary or missing links in their updates.

In this paper, we discuss link prediction on linked and versioned articles. We propose new graph embeddings

utilizing temporal random walk, which is biased by timestamp difference and semantic difference between

linked and versioned articles. We generate article sequences by concatenating the article titles and category

names on each random walk path. A pretrained language model is further trained to learn contextualized

embeddings of article sequences. We design our link prediction experiments by predicting future links between

new nodes and existing nodes. For evaluation, we compare our model’s prediction results with three random

walk-based graph embedding models DeepWalk, Node2vec, and CTDNE, through ROC AUC score, PRC

AUC score, Precision@k, Recall@k, and F1@k as evaluation metrics. Our experimental results show that our

proposed TLPRB outperforms these models in all the evaluation metrics.

1 INTRODUCTION

Wikipedia is now one of the most popular multilin-

gual online encyclopedias all over the world (Zesch

et al., 2007). A large number of volunteers actively

create and edit articles to expand shared knowledge.

Wikipedia editors keep modifying articles reﬂecting

signiﬁcant topics and improving quality through var-

ious maintenance tasks. Updating an article creates a

timestamped version of the article. Wikipedia article

links are essential for readers to ﬁnd relevant articles

via navigation. Also, the link structure of Wikipedia

is a prime source of knowledge graphs. Since arti-

cles are newly created and updated, system-support

for suggesting new links from/to existing articles is

necessary to reduce editors’ burdens.

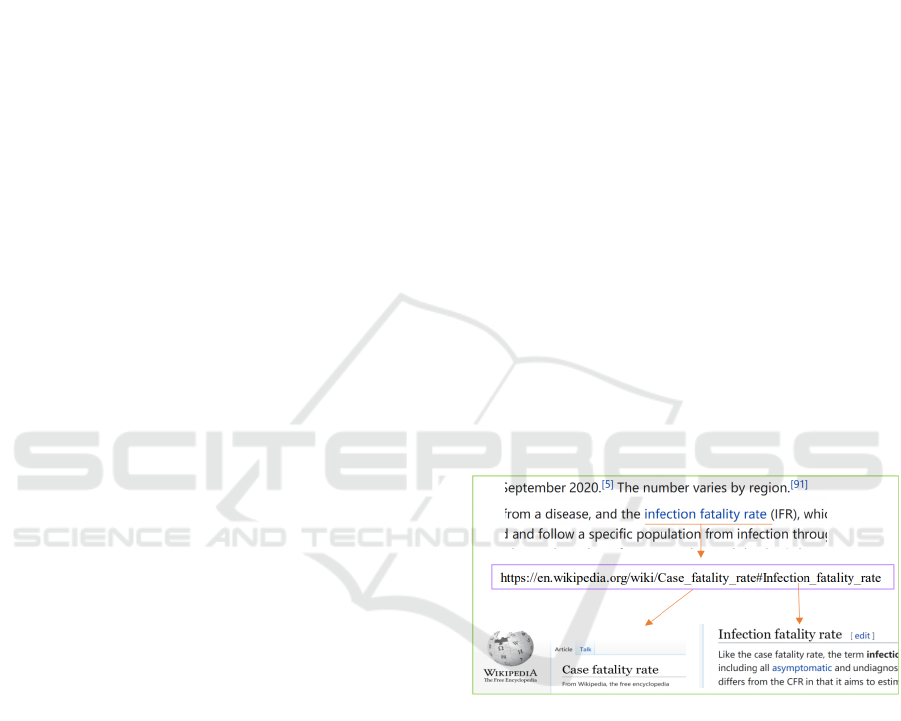
Figure 1 shows an example of an internal link. The

article “COVID-19 pandemic”contains the phrase

“infection fatality rate,” which is linked to one section

of another Wikipedia article “Case fatality rate.”

Categories in Wikipedia play an important role in

classifying articles into multiple hierarchies of diverse

topics. Properly assigning categories to newly created

articles is also an important but costly task for human

editors.

The evolutional aspect of internal links of

Wikipedia can be modeled as a temporal link graph,

Figure 1: Example of Wikipedia internal link.

which is a series of graphs where nodes represent ar-

ticles, and edges represent links, and each graph is

indexed by a timestamp. In this paper, we discuss a

new method for predicting links between newly added

articles and existing articles. The temporal link graph

of Wikipedia shows the following characteristics: 1)

The number of articles of hot topics is mostly con-

tinuously growing. 2) New articles are likely to be

linked to other articles under a common category. 3)

New links are more likely to be created between two

articles having a high semantic similarity.

We dicuss link prediction based on temporal graph

embeddings which can extract temporal, structural

and semantical similarities of linked articles, which

have not been considered in existing temporal/non-

Ma, J. and Iwaihara, M.

Link Prediction for Wikipedia Articles based on Temporal Article Embedding.

DOI: 10.5220/0010639900003064

In Proceedings of the 13th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2021) - Volume 1: KDIR, pages 87-94

ISBN: 978-989-758-533-3; ISSN: 2184-3228

temporal link predictions. Major contributions of this

paper are summarized below:

• We propose temporal link prediction methods

based on new node embeddings that consist of two

temporal random walk strategies: Random walk

biased by similarity on common categories and

random walk biased by semantic similarity.

• For temporal random walk biased by semantic

similarity, we propose generating node embed-

dings from token sequences of article texts along

walk paths. We utilize two document embed-

ding methods: FastText (Bojanowski et al., 2017)

with character n-gram and further pre-training of

RoBERTa (Liu et al., 2019).

• Our proposed algorithms are evaluated on real

temporal link graphs extracted from Wikipedia

dump, consisting of article sets on three topics

from January 1st to July 20th, 2020. Our rig-

orous evaluations on prediction accuracy show

that our proposed RoBERTa-based method out-

performs major link prediction algorithms.

The rest of this paper is organized as follows. Sec-

tion 2 covers related work. Section 3 deﬁnes our tem-

poral link prediction task. Section 4 shows the pro-

posed methods. Section 5 explains experimental de-

signs and evaluation results. Section 6 concludes this

paper.

2 RELATED WORK

The survey (Yue et al., 2020) covers link prediction

methods based on graph embeddings. Graph embed-

ding methods can be grouped into three categories:

Matrix factorization-based, random walk-based, and

neural network-based methods. After obtaining node

embeddings, the downstream prediction tasks in these

categories are basically the same.

DeepWalk (Perozzi et al., 2014) learns latent rep-

resentations of nodes in a network. Given a current

start node, DeepWalk randomly samples a node from

its neighbors as the next visit node and repeats this

process until the visit sequence length meets a preset

condition. After obtaining a sufﬁcient number of node

walking sequences, SkipGram is applied to generate

node embeddings.

Node2vec (Grover and Leskovec, 2016) learns a

mapping of nodes to a low-dimensional space of fea-

tures that maximizes the likelihood of preserving net-

work neighborhoods of nodes. Node2vec uses a bi-

ased random walk, which sets two hyperparameters p

and q to control the strategy of the random walk. Af-

ter sampling node sequences, the remaining steps are

the same with DeepWalk.

The in-depth survey (Divakaran and Mohan,

2019) of temporal link prediction shows comparisons

of the following embedding-based temporal link pre-

diction algorithms. CTDNE (Nguyen et al., 2018) uti-

lizes continuous-time dynamic network embedding to

address the problem of learning an appropriate net-

work representation for improving the accuracy of

predictive models. They extend the deﬁnition of static

graph random walk to temporal graph random walk

and propose several effective biased random walk

strategies.

DynamicTriad (Zhou et al., 2018) preserves struc-

tural information and evolution patterns of a given

network. The general idea of the model is to impose a

triad to model the dynamic changes of network struc-

tures. They model how a closed triad develops from

an open triad, which is called a triad closure process

and is a fundamental mechanism in the formation and

evolution of dynamic networks.

DynGEM (Goyal et al., 2018) employs a deep au-

toencoder as its core and leverages the advances in

deep learning to generate highly non-linear embed-

dings. The major advantages of DynGEM include:

The embeddings are stable over time, can handle

newly added nodes in dynamic graphs, and has bet-

ter running time than using static embedding methods

on each snapshot of a series of dynamic graphs.

A crucial problem of the above methods is that

their embeddings are intended to preserve link neigh-

borhoods, but deep features nodes are representing,

such as semantic similarities, are not considered. If a

node represents an article, link neighbors as well as

semantic neighbors can be useful for the link predic-

tion task. Since Wikipedia articles are texts, we ar-

gue that semantic similarity measured on representa-

tive parts of article texts, such as titles and categories,

can be exploited for this task. Thus, we discuss graph

embeddings that can reﬂect both link structures and

textual similarities between nodes.

3 OBJECTIVES AND

PRELIMINARIES

Given a series of graph snapshots [G

, G

, ..., G

T −1

where sufﬁx obeys timestamp order, our goal is to pre-

dict links between new nodes in the next graph G

and nodes existing before T. Each node in each graph

snapshot has two attributes; one is a word sequence

called article text, and the other is a set of word se-

quences called category. The article texts and cate-

gories of nodes may also change between snapshots.

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

Figure 2 left (Snapshots) illustrates our objectives.

Since new articles are constantly created, we aim to

predict new links between newly added articles (the

orange node at t = 2) and existing articles in the last

graph G

For convenience, we unify the series of graph

snapshots [G

, G

, ..., G

] into one temporal (multi-)

graph G = (V, E), where N is a set of nodes corre-

sponding to a subset of Wikipedia articles. Let E be

the set of edges, representing Wikipedia article links,

where each link e

= (u, v,t

) ∈ E means that there is

a link from node u to node v at time t

Figure 2 right shows an example of a uniﬁed tem-

poral graph G = (V, E). The light blue node has an

edge to the purple node at timestamps t = 1 and t = 2.

After unifying the snapshots, the light blue node will

have two edges directed to the purple node, where the

edges are labeled with timestamps 1 and 2.

Figure 2: Example of generating the temporal graph.

The set of temporal neighbors of a node v at

time t

is deﬁned as Γ

(v) = {(w, t

) | ∃e = (v, w, t

) ∈

E such that T (e) > t

}, where t

= T (e) is the times-

tamp of edge e.

4 METHODOLOGIES

Our method consists of three main parts: Temporal

random walk, learning node (article) embeddings, and

link prediction. After article embeddings are gener-

ated, a conventional link prediction method is applied.

4.1 Article Sequences

The random walk part has two steps. Step 1 is select-

ing an initial random walk edge, and Step 2 is exe-

cuting temporal random walks. For Step 1, we pro-

pose a biased strategy for edge selection. For Step

2, we propose two strategies, which are random walk

by common categories and random walk by semantic

similarity.

After one random walk is executed, the walk path

shows a node sequence, from which we can gener-

ate an article sequence, which is the concatenation

of the article texts along the walk path. The article

sequences are utilized as sentences for training node

embeddings.

Since typical Wikipedia articles are quite long and

complex, we should extract important article compo-

nents that are useful for link prediction. The follow-

ing article components are well summarizing topics

of one article or one link, thus suitable as article texts:

(1) article title, (2) leading k tokens of the article, (3)

category names, (4) the title of a link, and (5) the

text around the target of a link. Considering random

walk length and the length limit of 512 tokens of the

BERT/RoBERTa encoder, for article texts we choose

(1) article title and (3) category names, which are rep-

resenting the topics of one article than the other article

components.

4.2 Random Walk Strategies

4.2.1 Initial Edge Selection

Given a temporal graph G = (V, E), we ﬁrst need to

select an edge as the initial edge of a random walk.

To deal with this problem, we utilize temporal bias in

sedge election (Nguyen et al., 2018), such that each

edge is given a weight according to freshness of its

timestamp. Speciﬁcally, each weight is given by a

softmax function on the exponential distribution of

timestamp decay. Each edge e

= (u, v, t

) ∈ E is as-

signed with the following probability:

Pr(e

) =

(T (e

)−t

min

)

∑

∈E

(T (e

)−t

min

)

(1)

where t

min

is the minimum edge timestamp in graph

G, and T (e

) denotes the timestamp of edge e

. The

above deﬁnes a distribution that heavily favors edges

appearing later in time.

4.2.2 Temporal Random Walk

After selecting an initial edge e

= (u, v,t

) at time t

for initiating a temporal random walk, we need to se-

lect the next node to visit by the random walk. The

main principle of our temporal random walk is that

the timestamp of the next edge must not be less than

the current time.

We design two techniques to bias temporal ran-

dom walks by sampling the next node via calculat-

ing each neighbor probability based on common cat-

egories (Section 4.2.3) and semantic similarity (Sec-

tion 4.2.4).

We generate an article sequence along each ran-

dom walk path. For example, when walking to node

v at timestamp t

, we append the article text (Sec-

tion 4.1) of v into the article sequence of the ran-

Link Prediction for Wikipedia Articles based on Temporal Article Embedding

dom walk until the walk length reaches the max walk

length.

4.2.3 Random Walk by Common Categories

Figure 3 shows a partial list of categories in

Wikipedia

2020 United States presidential election, Donald

Trump 2020 presidential campaign, Donald Trump,

Mike Pence, Joe Biden 2020 presidential campaign,

Joe Biden, Kamala Harris

Figure 3: Categories of article 2020 United States Presiden-

tial Election (partial).

The degree of common categories can be mea-

sured by the Jaccard coefﬁcient of the current node’s

categories and the next neighbor node’s categories:

Jaccard(v, w, t

, T (w)) =

cat

) ∩ n

cat

(T (w))|

cat

) ∪ n

cat

(T (w))|

(2)

where n

cat

) represents the categories of article v at

timestamp t

, and n

cat

(T (w)) represents the categories

of a candidate article w at timestamp T (w). Symbols

“∩” and “∪,” respectively, denote the intersection and

union of two article categories, respectively, where

the exact category names are used as identiﬁers. Sym-

bol | · | is the number of categories in this set.

We deﬁne the probability of selecting node v’s

temporal neighbor w ∈ Γ

(v) as:

Pr(w) =

T (w)−t

+λ×Jaccard(v,w,t

,T (w))

∑

∈Γ

(v)

T (w

)−t

+λ×Jaccard(v,w

,T (w

))

(3)

The difference T (w) −t

is the time span between

the current timestamp t

and the next link’s timestamp

T (w). λ is a hyperparameter to control the inﬂuence

of time span bias and common categories bias.

4.2.4 Random Walk by Semantic Similarity

Another bias strategy for the temporal random walk

is to consider semantic similarity between two nodes,

which can be measured by cosine similarity on docu-

ment embeddings of two nodes. We generate the em-

bedding vector of node v from its article sequence,

by utilizing the pretrained language model RoBERTa

(Liu et al., 2019), which is an improved version of

the pretrained language model BERT. Compared with

BERT (Devlin et al., 2019), RoBERTa uses dynamic

masking and byte-level BPE (Byte-Pair Encoding),

where BPE can cope with out-of-vocabulary words

by subword decomposition.

https://en.wikipedia.org/wiki/2020 United States

presidential election

To generate node embeddings Emb(v) by

RoBERTa, we enter the article sequence of v into

RoBERTa, where the article sequence is truncated

to ﬁt into the length limitation of 512 tokens of

RoBERTa. The output at < s > token is a 768-

dimensional vector, which can be used as the node

(article) embedding.

Now suppose our current node of a random walk

is v, and one candidate neighbor is node w. We in-

troduce the following probability function combining

time decay and semantic similarity, for the probability

of walking to this candidate node w.

Pr(w) =

T (w)−t

+α×cosine(Emb(v),Emb(w))

∑

∈Γ

(v)

T (w

)−t

+α×cosine(Emb(v),Emb(w

))

(4)

Here, t

is the current timestamp, and T (w) is the

timestamp of edge (v, w). T (w) − t

is the time dif-

ference of the current timestamp t

and the next link’s

timestamp T (w). α is a hyperparameter to control the

weight of timestamp difference and semantic similar-

ity of articles.

4.3 Learning Node Embeddings

In this paper, we propose training of node embed-

dings from article sequences collected along random

walk paths, so that semantic neighbors and link neigh-

bors are smoothly integrated into a single embedding

space.

In Section 4.2.4, document embedding Emb(v)

from the article text of a node v was introduced.

However, for temporal link prediction we introduce

different node embeddings, denoted as Emb

(v[t])

for the embedding of node v at timestamp t. Node

embeddings Emb

(v[t]) are trained from article se-

quences along temporal random walk paths, so that

temporal, structural, and semantic similarities are

smoothly integrated into a single node representa-

tion. We consider two embedding algorithms, Fast-

Text (Bojanowski et al., 2017) and further pre-training

of RoBERTa for training of Emb

(v[t]).

4.3.1 FastText with Character N-gram

The word embedding model word2vec does not dis-

tinguish the words “apple” and “apples.” To over-

come this problem, FastText (Bojanowski et al., 2017)

uses a bag of character-level n-grams to represent a

word. For the word “apple,” suppose the value of n

is 3, then its trigram decomposition is “<ap,” “app,”

“ppl,” “ple,” “le>.” Thus, we can represent the word

vector of “apple” by superimposing the vectors of the

ﬁve trigrams.

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

In temporal random walk, we generate article se-

quences by concatenating article texts along each

walk path. Then we apply FastText with character

n-gram to train embeddings from these article se-

quences.

4.3.2 Further Pretraining of RoBERTa by

Article Sequences

We can construct a corpus consisting of the sentences

where each sentence corresponds to the article se-

quence along each temporal random walk path. Then

on this corpus, we perform further pre-training of

RoBERTa by the Masked Langrage Model (MLM),

such that word tokens are generated by the RoBERTa

tokenizer with byte-pair encoding, and dynamically

mask randomly selected tokens in each input se-

quence with a special token [MASK]. The objective

of MLM is the cross-entropy loss on predicting the

masked tokens.

By the above further pretraining on the corpus,

the RoBERTa model will learn contextualized embed-

dings of article sequences. In our case, the RoBERTa

model will produce embeddings Emb

(v[t]) such

that texts appearing in link neighbors of v will have

higher similarities with Emb

(v[t]) than texts that

are remote from v in the temporal link graph.

4.4 Two Link Prediction Methods

Since our targets are directed graphs, following

(Crichton et al., 2018), we adopt the concatenation

method to construct the feature vector of each directed

edge. Given a link from u to v at time t, we obtain

Emb

(u[t]) and Emb

(v[t]), namely the embed-

dings of the article sequences of nodes u and v at time

t. Then the concatenation [Emb

(u[t]), Emb

(v[t])]

of these embeddings is used as the feature vector of

the link from u to v. Temporal link prediction is per-

formed by a logistic regression classiﬁer on the fea-

ture vectors regarding a target article node.

We summarize our proposed temporal link pre-

diction methods into TLPFT and TLPRB. TLPFT

(Temporal Link Prediction with FastText) is the

method with the biased initial edge selection strat-

egy (1), random walk with common categories (3),

and learning node embeddings through FastText with

character n-grams.

TLPRB (Temporal Link Prediction with

RoBERTa) is the method with the biased initial

edge selection strategy (1), random walk by semantic

similarity (4), and learning node embeddings through

further pre-training RoBERTa by article sequences

along walk paths. Then we apply these embeddings

for link prediction in the same way.

Figure 4 contrasts the differences between TLPFT

and TLPRB.

Figure 4: Pipelines of TLPFT and TLPRB.

5 EXPERIMENTS

5.1 Datasets

Now we describe the construction of our evaluation

datasets, which are sampled from Wikimedia dump.

The time span from 2020-01-01 to 2020-07-20 is ex-

tracted, consisting of thirteen snapshots in the English

Wikipedia server.

We select three topics: 2020 Protests, 2020

United States Presidential Election, COVID-19

Pandemic, and extract all the articles in these top-

ics from each snapshot in the Wikimedia dump. We

extracted three types of information for building our

temporal graph: The title of each article at each times-

tamp, the category lists of each article at each times-

tamp, and the hyperlinks between all the articles at

each timestamp.

The detailed descriptions of our three datasets are

summarized in Table 1. Each row of the table cor-

responds to a timestamp. The columns Nodes and

Edges, respectively, are the numbers of nodes and

edges, respectively, of the graph at each timestamp.

5.2 Baseline Models

As our baseline models, we choose the following

three graph embedding algorithms which are also

based on random walk:

• DeepWalk (Perozzi et al., 2014): This model is a

basic random walk graph embedding method that

can be applied for a directed or undirected un-

Link Prediction for Wikipedia Articles based on Temporal Article Embedding

Table 1: Statistics of the three datasets.

2020 Protests

2020 U.S.

Presidential

Election

COVID-19 Pandemic

Nodes Edges Nodes Edges Nodes Edges

Jan.1 676 19456 1220 90465 1778 17890

Jan.20 695 20786 1226 93924 1853 18982

Feb.1 704 21286 1229 95755 1911 19876

Feb.20 712 21896 1245 98824 2040 22456

Mar.1 715 22009 1250 99800 2120 25486

Apr.1 726 22523 1276 102608 2759 208020

Apr.20 731 22610 1296 105270 3006 276751

May.1 733 23140 1303 106657 3127 314667

May.20 739 24424 1311 108050 3278 367660

Jun.1 768 25604 1314 108421 3351 382105

Jun.20 925 43502 1322 108704 3431 405540

Jul.1 951 51982 1331 110250 3471 429762

Jul.20 976 55594 1342 112344 3554 456680

weighted graph. However, temporal information

is not utilized by DeepWalk.

• Node2vec (Grover and Leskovec, 2016): This

model introduces two hyperparameters p and q

for a biased random walk. Parameter p controls

the probability of repeating the node just visited,

and parameter q controls whether the walk is out-

ward or inward on edge direction. Node2vec also

does not consider temporal information.

• CTDNE (Nguyen et al., 2018): This model is de-

signed for temporal graph embedding. CTDNE

provides three temporal random walk strategies,

which are uniform, exponential, and linear.

We choose two versions of the original CTDNE

model, in terms of temporal random walk strategies

for bias on initial edge selection and bias on neighbor

edge selection, denoted as CTDNE (none-none) and

CTDNE (none-exponential).

CTDNE can deal with temporal graphs, but Deep-

Walk and Node2vec are applicable for static graphs.

To make the results more descriptive, we unify all

the graphs in the training set into one graph and ap-

ply DeepWalk and Node2vec on this uniﬁed graph for

static link prediction.

For comparison, we set the random walk parame-

ters of all models to be the same. Table 2 shows the

parameter values used in the experiments. To show

the effectiveness of further pre-training RoBERTa by

article sequences, we added a new comparative model

RoBERTa Embedding that just uses the pre-trained

RoBERTa for obtaining node embeddings from arti-

cle sequences, without further pretraining by MLM.

5.3 Design of Experiments

For evaluating prediction results, we adopt AUC

(Area Under the Curve) of ROC, which is one of

Table 2: Parameter values of radom walk.

Parameter Description Value

window size used for the SkipGram al-

gorithm

walk length max random walk path

length

num walks how many times random

walk start per node

embedding

size

graph embedding vector

dimension

768

p used for random walk bias

strategy in Node2vec

q used for random walk bias

strategy in Node2vec

0.5

the most important evaluation metrics for checking

any classiﬁcation model’s performance (Yang et al.,

2015), where a higher AUC score means better pre-

diction performance.

We also measure Precision@k, Recall@k, and

F1@k, which respectively mean precision, recall, and

F1-score on the top-k links predicted by a method.

The micro-averages of these metrics on the test nodes

are shown.

Figure 5 illustrates the split of the test and train-

ing sets in our experiments. The construction of the

training and test link sets is as follows. The newly

added links at the last timestamp (July 20th) are held

out as the test link set. The remaining links in the last

timestamp, and all the links in the preceeding times-

tamps, where the test link set is excluded, constitute

the training link sets. Biased temporal random walk

is carried out on the training link set, and article se-

quences along the walk paths are extracted for train-

ing node embeddings by our TLPFT or TLPRB.

We use the concatenation method to generate edge

features, and label them with 1 or 0 based by whether

there is a directed link.

Finally, we use logistic regression as a classiﬁer

for link prediction. The evaluation metrics are ROC

AUC score, PRC AUC score, and micro–averages of

Precision@K, Recall@K, and F1@K.

The number of node pairs in the training and test-

ing datasets are shown in Table 3.

Table 3: Number of node pairs in train and test datasets.

Dataset Node Pairs in

Training Set

Node Pairs in

Test Set

2020 Protests 107228 48231

2020 United Presi-

dential Election

222812 29383

COVID-19 Pan-

demic

877544 582975

The random walk of DeepWalk and Node2vec

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

Figure 5: Split of train and test link sets.

Table 4: Experimental results on three datasets.

Methods

2020 Protests

2020 United States

Presidential Election

COVID-19 Pandemic

ROC AUC PRC AUC ROC AUC PRC AUC ROC AUC PRC AUC

DeepWalk 0.712 0.111 0.661 0.046 0.921 0.378

Node2vec 0.719 0.118 0.69 0.058 0.938 0.461

CTDNE(None-None) 0.727 0.1 0.727 0.092 0.926 0.488

CTDNE(None-Exponential) 0.725 0.098 0.725 0.063 0.918 0.379

RoBERTa Embedding 0.759 0.095 0.756 0.089 0.977 0.574

TLPFT 0.773 0.115 0.773 0.088 0.976 0.594

TLPRB 0.791 0.12 0.79 0.105 0.981 0.678

Figure 6: Micro-averaged Precision@k, Recall@k, and F1@k on three datasets.

needs to reach newly created nodes, to learn structure

information of the new nodes. So 1% of randomly se-

lected edges in the training set are allocated to the new

nodes, and each non-isolated new node is assigned at

least one adjacent edge.

The parameters p and q of the walking strategy

in DeepWalk are ﬁxed to 1, while for Node2vec grid

search is used to ﬁnd the best combination of param-

eters p and q from 0.25, 0.5, 1, 2, 4.

5.4 Experimental Results and Analysis

Table 4 shows the ROC AUC and PRC AUC scores

of the models on the three datasets.

As shown in the above experimental results, we

can draw the following conclusions.

Node2vec is better than DeepWalk in all the cases,

but CTDNE is better than the static graph embed-

ding methods DeepWalk and Node2vec. One rea-

son is that CTDNE learns temporal evolution pat-

tern of link structure through temporal random walk.

The pre-trained RoBERTa model was trained by raw

English Wikipedia articles (Liu et al., 2019). So,

RoBERTa Embedding can appropriately produce em-

bedding vectors of articles. The results indicate that

temporal random walk coupled with semantic simi-

larity is showing an apparent improvement over the

three graph embedding models.

As for our proposed models, the results show that

both TLPFT and TLPRB outperform the baselines

Link Prediction for Wikipedia Articles based on Temporal Article Embedding

by a signiﬁcant margin. By comparing TLPRB and

RoBERTa Embedding, it can be seen that further pre-

training RoBERTa by MLM on article sequences is

signiﬁcantly improving the performance, indicating

that TLPRB is learning contexutality in sequences of

titles and category names, which beneﬁts prediction

of neighboring new nodes.

TLPFT is better than the baseline models, indi-

cating that semantic similarity captured by FastText,

which is capable of embedding out-of-vocabulary

words in article texts by k-gram decomposition, and

TLPFT is even surpassing RoBERTa Embedding.

However, TLPFT is not as effective as TLPRB, in-

dicating that embeddings of FastText do not capture

contexts in article sequences, while TLPRB is further

pretrained by a large number of article sequences, to

learn semantic similarity and contextual relationship

between neighboring articles.

Figure 6 shows micro-averaged Precision@k, Re-

call@k, and F1@k curves with k=5, 10, 50, 100

on the three datasets. Combining the results on the

aggregated performance by the AUC scores and the

ranking performance by the Top-K results, our overall

conclusion is that TLPRB performs best in both AUC

and Top-K evaluations, and TLPFT performs the next

in the AUC evaluation.

6 CONCLUSION AND FUTURE

WORK

In this paper, we proposed a new method for predict-

ing article links in Wikipedia, which utilizes tempo-

ral random walk to generate graph embeddings. Our

graph embedding model is based on temporal random

walk, biased by temporal feature and semantic rela-

tionships of article texts between node pairs. We eval-

uated on three temporal graph datasets extracted from

Wikipedia dump. Our experimental results show that

our proposed model TLPRB outperforms the base-

lines and simple RoBERTa-based model in this tem-

poral link prediction on versioned articles.

For future work, we consider that the current deﬁ-

nition of common categories is based on identical cat-

egory names. Semantic similarity and hierarchical re-

lationships between categories can be explored.

REFERENCES

Bojanowski, P., Grave, E., Joulin, A., and Mikolov, T.

(2017). Enriching word vectors with subword infor-

mation. Transactions of the Association for Computa-

tional Linguistics, 5:135–146.

Crichton, G., Guo, Y., Pyysalo, S., and Korhonen, A.

(2018). Neural networks for link prediction in realis-

tic biomedical graphs: a multi-dimensional evaluation

of graph embedding-based approaches. BMC bioin-

formatics, 19(1):1–11.

Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K.

(2019). BERT: Pre-training of deep bidirectional

transformers for language understanding. In Proceed-

ings of the 2019 Conference of the North American

Chapter of the Association for Computational Lin-

guistics: Human Language Technologies, Volume 1

(Long and Short Papers), pages 4171–4186.

Divakaran, A. and Mohan, A. (2019). Temporal link pre-

diction: a survey. New Generation Computing, pages

1–46.

Goyal, P., Kamra, N., He, X., and Liu, Y. (2018). Dyngem:

Deep embedding method for dynamic graphs. arXiv

preprint arXiv:1805.11273.

Grover, A. and Leskovec, J. (2016). node2vec: Scal-

able feature learning for networks. In Proceedings

of the 22nd ACM SIGKDD international conference

on Knowledge discovery and data mining, pages 855–

864.

Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D.,

Levy, O., Lewis, M., Zettlemoyer, L., and Stoyanov,

V. (2019). Roberta: A robustly optimized bert pre-

training approach. arXiv preprint arXiv:1907.11692.

Nguyen, G. H., Lee, J. B., Rossi, R. A., Ahmed, N. K., Koh,

E., and Kim, S. (2018). Continuous-time dynamic net-

work embeddings. In Companion Proceedings of the

The Web Conference 2018, pages 969–976.

Perozzi, B., Al-Rfou, R., and Skiena, S. (2014). Deepwalk:

Online learning of social representations. In Proceed-

ings of the 20th ACM SIGKDD international confer-

ence on Knowledge discovery and data mining, pages

701–710.

Yang, Y., Lichtenwalter, R. N., and Chawla, N. V. (2015).

Evaluating link prediction methods. Knowledge and

Information Systems, 45(3):751–782.

Yue, X., Wang, Z., Huang, J., Parthasarathy, S., Moosav-

inasab, S., Huang, Y., Lin, S. M., Zhang, W., Zhang,

P., and Sun, H. (2020). Graph embedding on biomed-

ical networks: methods, applications and evaluations.

Bioinformatics, 36(4):1241–1251.

Zesch, T., Gurevych, I., and M

uhlh

auser, M. (2007). An-

alyzing and accessing wikipedia as a lexical seman-

tic resource. Data Structures for Linguistic Resources

and Applications, 197205.

Zhou, L., Yang, Y., Ren, X., Wu, F., and Zhuang, Y. (2018).

Dynamic network embedding by modeling triadic clo-

sure process. In Proceedings of the AAAI Conference

on Artiﬁcial Intelligence, volume 32.

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval