Improving Image Filters with Cartesian Genetic Programming

Julien Biau

, Dennis Wilson

2 a

, Sylvain Cussat-Blanc

3 b

and Herv

e Luga

3 c

Kawantech, Toulouse, France

ISAE-SUPAERO, Toulouse, France

University of Toulouse, Toulouse, France

Keywords:

Genetic Programming, Cartesian Genetic Programming, Image Processing, Genetic Improvement.

Abstract:

The automatic construction of an image ﬁlter is a difﬁcult task for which many recent machine learning meth-

ods have been proposed. However, these approaches, such as deep learning, do not allow for the ﬁlter to be

understood, and they often replace existing ﬁlters designed by human engineers without building on this ex-

pertise. Genetic improvement offers an alternative approach to construct understandable image ﬁlter programs

and to build them by improving existing systems. In this paper, we propose a method for genetic improvement

of image ﬁlters using Cartesian Genetic Programming. We introduce two operators for genetic improvement

which allow insertion and deletion of a node in the graph in order to quickly improve a given ﬁlter. These

new operators are tested in three different datasets starting from published or engineered ﬁlters. We show that

insertion and deletion operators improve the performance of CGP to produce newly adapted ﬁlters.

1 INTRODUCTION

The automatic construction of image ﬁlters through

machine learning has led to a number of novel appli-

cations. A common algorithm for this problem type

is deep convolutional neural networks which learn a

sequence of parameterized ﬁlters and which can to-

tal millions of parameters (He et al., 2016). While

the performance of these methods on large datasets

is impressive, surpassing human performance on vi-

sual recognition tasks (He et al., 2015), an impor-

tant obstacle in the application of these models is

their lack of interpretability. Furthermore, these sys-

tems are often used to replace systems designed by

human experts and are unable to beneﬁt from com-

puter vision expertise. Previous work have been pub-

lished in which Genetic Algorithms are used to im-

prove the appearance and the visual quality of images

characterized by a bimodal gray level intensity his-

togram, by strengthening their two underlying sub-

distribution (Rundo et al., 2019). Additional work

have been done using genetic programming in the

ﬁeld of video change detection to automatically se-

lect the best algorithms, combine them in different

https://orcid.org/0000-0003-2414-0051

https://orcid.org/0000-0003-1360-1932

https://orcid.org/0000-0001-8675-197X

ways, and perform the most suitable post-processing

operations on the outputs of the algorithms (Bianco

et al., 2017). Finally, a system for the automatic gen-

eration of computer vision algorithms at interactive

frame rates using GPU accelerated image process-

ing has been developed using genetic programming

(Ebner, 2009) and work have been done to evolve ob-

ject detectors using GPU processing (Ebner, 2010).

Genetic programming offers an attractive alternative

for this machine learning task. By combining low-

level and high-level image processing functions, a ﬁl-

ter can be constructed which is fully understandable

and auditable. The set of functions can be chosen

by experts to meet computational or legibility require-

ments and can build on expert functions like those in

the OpenCV

library used in this work. Furthermore,

existing image ﬁlters can be formulated as starting

points for optimization; genetic improvement of soft-

ware has demonstrated that evolution can build upon

human-designed programs to improve their efﬁciency

and ﬁx bugs (Arcuri and Yao, 2008). This allows for

a ﬁnal program which is higher performing than the

original human-designed code, but which remains un-

derstandable and explainable by human experts.

In this work, we use Cartesian Genetic Program-

ming (CGP) (Miller, 1999), a popular form of graph

https://opencv.org/

Biau, J., Wilson, D., Cussat-Blanc, S. and Luga, H.

Improving Image Filters with Cartesian Genetic Programming.

DOI: 10.5220/0010640000003063

In Proceedings of the 13th International Joint Conference on Computational Intelligence (IJCCI 2021), pages 17-27

ISBN: 978-989-758-534-0; ISSN: 2184-2825

genetic programming, to improve on existing image

ﬁlters and to generate new ﬁlters. In CGP, programs

are represented as graphs of functions, which allows

for encoding existing ﬁlters through modifying the

program graph. We propose novel genetic operators

speciﬁcally for genetic improvement in CGP, demon-

strating that inserting nodes into the program graph

can improve evolution based on ﬁlter accuracy. We

study standard CGP, CGP with a starting population

of experts, and the proposed mutation operators on a

set of image masking benchmarks, two from previ-

ous work on CGP (Leitner et al., 2012) and one new

benchmark on urban trafﬁc. Our evolution allow to

quickly improve an image ﬁlter designed by a human

with basic knowledge.

This article is structured as follows. In Section 2,

we illustrate Cartesian Genetic Programming and its

application to image processing; we then review ge-

netic improvement. In Section 3, we describe the pro-

posed node insertion and node deletion operations for

genetic improvement with CGP. We present the image

processing tasks and experimental parameters in Sec-

tion 4, using tasks and image functions from existing

work in image processing using CGP. In Section 5,

we compare different evolutionary processes, starting

from random populations and from expert ﬁlters, and

using the proposed operators. We also study the re-

sulting image ﬁlters, demonstrating the transparency

of program graphs created by CGP. Finally, in Section

6, we discuss possible applications of this method and

deﬁne future directions for this research.

2 RELATED WORKS

This work builds on two extensive bodies of genetic

programming literature: Cartesian Genetic Program-

ming (Miller, 1999), speciﬁcally its application to im-

age processing and a study of possible genetic oper-

ators, and genetic improvement, the optimization of

expert-designed programs through evolution.

2.1 Cartesian Genetic Programming

Cartesian Genetic Programming (CGP) is a form of

Genetic Programming (GP) in which programs are

represented as directed, often acyclic graphs indexed

by Cartesian coordinates. CGP was invented by

Miller and Thomson (Miller et al., 1997; Miller, 1999;

Miller and Thomson, 2000) for use in evolving digi-

tal circuits, but has since been applied in a large num-

ber of domains (Miller, 2011). CGP is used in (Khan

et al., 2011) to evolve neural networks, in (Harding

et al., 2013) for object detection in image processing,

and in (Kalkreuth et al., 2016) for image noise reduc-

tion. Its beneﬁts include node neutrality, being the

encoded parts of the genome that do not contribute to

the interpreted program, node reuse, and a ﬁxed rep-

resentation that reduces program bloat (Miller, 2001).

A recent review of CGP is given in (Miller, 2019).

In CGP, functional nodes, deﬁned by a set of

evolved genes, connect to program inputs and to other

functional nodes via their Cartesian coordinates. The

outputs of the program are taken from any internal

node or program input based on evolved output co-

ordinates. CGP nodes are arranged in a rectangular

grid of R rows and C columns. Nodes are allowed to

connect to any node from previous columns based on

a connectivity parameter L which sets the number of

columns back a node can connect to. In this work,

as in many others (Miller, 2019), R = 1, meaning all

nodes are in a single row.

The CGP genotype consists of a list of node genes;

each node in the genome encodes the node function,

the coordinates of the function inputs (here referred

as Connection 0 and Connection 1), and optionally

parameters for the node function. Connection 0 and

Connection 1 can be outputs of previous nodes or pro-

gram inputs. Finally, the end of the genome encodes

the nodes which give the ﬁnal program output. By

tracing back from these output nodes, a single func-

tion can be derived for each program output, offering

a concise and legible program representation.

The genes in CGP are optimized through using

the 1+λ algorithm. A population of λ individuals

are randomly generated and evaluated on a test prob-

lem. Evaluation is performed by decoding the pro-

gram graph from the individual genotype and apply-

ing the program to a speciﬁc problem such as image

masking, as in this work. The best individual based on

this evaluation is retained for the next generation. A

mutation operator is applied to this individual to cre-

ate λ new individuals; in CGP, the mutation operator

randomly samples a subset of new genes from a uni-

form distribution. This new population is evaluated

and the best individual is retained for the next genera-

tion; this iterative process continues until a conﬁgured

stopping criterion is satisﬁed.

2.2 Cartesian Genetic Programming for

Image Processing

An important choice in using CGP is the set of possi-

ble node functions. In the original circuit design ap-

plication, the node functions were logic gates such as

AND and NOR. Applications of CGP in game play-

ing and data analysis use a standard set of mathemat-

ical functions such as x + y, x ∗ y, and cos(x) for a

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

node with inputs x and y. Function sets must be de-

ﬁned such that outputs of any node will be valid for

another node; in mathematical functions, this is often

guaranteed by restraining the domain and range of the

functions between -1 and 1.

Cartesian Genetic Programming for Image Pro-

cessing (CGP-IP) is an adaption of CGP which uses

image processing functions and which applies pro-

grams directly to images (Harding et al., 2006). The

inputs and outputs of the evolved functions are images

which allows for consistency between node functions;

each node function is deﬁned to input an image of a

ﬁxed size and output an image of the same size. CGP-

IP has previously used a set of 60 functions (Hard-

ing et al., 2012b) from OpenCV, a standard and open-

source image processing library.

In previous work (Harding et al., 2006), CGP-IP

has used an island population distribution algorithm.

In this method, multiple populations compete inside

“islands” which are independent 1 + λ evolutionary

algorithms. A migration interval parameter dictates

the frequency of expert sharing between the islands,

allowing for synchronization of the best individual

across islands. Island models have been demonstrated

as an alternative to the Genetic Algorithm and aid

in preserving genetic diversity (Whitley et al., 1998).

Their use in CGP-IP has shown improvement com-

pared to the 1 + λ algorithm.

CGP-IP individuals are evaluated by applying the

evolved ﬁlter to a set of images, comparing them to

target images, and computing a difference metric be-

tween the output image from the evolved ﬁlter and

the target, such as the mean error or Matthews Cor-

relation Coefﬁcient (MCC) (Matthews, 1975). In this

paper, we use MCC, which measures the quality of bi-

nary classiﬁcation and has been showed particularly

adapted to classiﬁcation tasks using CGP (Harding

et al., 2012a). Calculations are based on the confusion

matrix, which is the count of the true positives (TP),

false positives (FP), true negatives (TN) and false neg-

atives (FN):

mcc =

T P ∗ T N − FP ∗ FN

(T P + FP)(T P + FN)(T N +FP)(T N + FN)

(1)

A MCC with a score of 1 corresponds to a per-

fect classiﬁcation, 0 to a random classiﬁer, and -1 to

a fully inverted classiﬁcation. Our ﬁtness function for

evolution is deﬁned as follows:

f itness = 1 − mcc. (2)

In this work, evolution is therefore used to min-

imize the objective function, searching for programs

with a higher MCC.

2.3 Genetic Improvement

Genetic Improvement (GI) is a relatively recent ﬁeld

of software engineering research that uses search to

improve existing software. Using handwritten code

as a starting point, GI searches the space of program

variants created by applying mutation operators. The

richness of this space depends on the power and ex-

pressivity of the mutation operators, which can mod-

ify existing code by changing functions or parame-

ters, add new code, and, in some cases, remove parts

of a program. Over the past decade, the GI ﬁeld

has greatly expanded and current research on GI has

demonstrated many potential applications. Genetic

improvement has been used to ﬁx software bugs (Ar-

curi and Yao, 2008; Langdon and Harman, 2015),

to drastically speed up software systems (Langdon

and Harman, 2015; White et al., 2011), to port a

software system between different platforms (Lang-

don and Harman, 2010), to transplant code features

between multiple versions of a system (Petke et al.,

2014), to grow new functionalities (Harman et al.,

2014) and more recently to improve memory (Wu

et al., 2015) and energy usage (Bruce et al., 2015).

The majority of Genetic Improvement work uses

Genetic Programming to improve the programs un-

der optimisation (Arcuri and Yao, 2008; Langdon and

Harman, 2010; Langdon and Harman, 2015; Petke

et al., 2014; White et al., 2011). In most methods, ap-

plying GI to an existing program is done by encoding

the existing program within a GP tree and then com-

puting the corresponding genome. GP mutation op-

erators are applied to the encoded program to gener-

ate adjacent programs. For this purpose, the program

encoding and operators must be deﬁned both to be

suited to the initial program to be improved and with

additional functions to allow evolution to improve the

functional graph. The ﬁtness used during the evolu-

tionary optimization of the program can be based on

various metrics, such as program length, efﬁciency,

relevance to given test cases, or others (Arcuri and

Yao, 2008; Langdon and Harman, 2010; White et al.,

2011).

In this work, we propose operators for genetic im-

provement in CGP. To our knowledge, this is the ﬁrst

use of CGP for GI, as the majority of GI literature uses

tree representations of programs instead of graphs.

The proposed node insertion and deletion mutation

operators are similar to existing mutation operators

for tree-based GI but are studied here in the context

of graph evolution.

Improving Image Filters with Cartesian Genetic Programming

3 GENETIC IMPROVEMENT IN

CGP-IP

In this section, we deal with insertion and deletion

operators speciﬁcally designed for GI with CGP. In

the standard CGP,the evolution is only based on the

injection of random mutation to node genes which

is equivalent to connections or functions. Genomes

are of constant sizes and adding and/or removing

functional nodes inside the graph can be difﬁcult for

the evolution to ﬁnish. To this end, previous work

has proposed self-modifying genomes (Harding et al.,

2011) which use functions which can add or remove

nodes but only while the graph is executing. In our

proposal we do insertion and deletion of node using

mutation operators in order to change the size of the

graph during it’s evolution. These operators are de-

signed to maintain the active subgraph of a program,

i.e. they are not destructive. Source code of the im-

plementation in Python for our CGP-IP can be found

here

A mutation consists of applying one of the three

following operators: node insertion, node deletion or

standard parameter modiﬁcation using a uniform dis-

tribution. The node operators have conﬁgurable mu-

tation rates r

ins

and r

del

corresponding to the proba-

bility of the application of these mutation operators.

If one of these structural operators is applied, it will

be the only mutation performed; otherwise, standard

parameter modiﬁcation mutation occurs. In this work,

ins

= 0.1 and r

del

= 0.1 for all experiments.

3.1 Node Insertion

The node insertion operator adds a new node between

two connected nodes in the active graph of a CGP in-

dividual. To allow for node insertion, we change the

total possible graph length of a CGP individual, R ∗ C

or the number of columns C in this case, and adapt this

value during evolution. In order to preserve the struc-

ture of the program, the connections of other nodes

in the genome are adjusted after a node insertion. As

described in Algorithm 1 and illustrated in Figure 1,

the connection genes of all nodes after the inserted

node are increased by 1. This preserves the exist-

ing connections in the graph and simply inserts the

new node between two previously connected random

nodes. We study two possible insertions: using an

identity (NOP) function, this action does not immedi-

ately change the program graph, and using a random

function, which can.

https://github.com/julienbiau/CGP-IP-GI

Algorithm 1: Insertion of a node with a random function.

Data: nodes is an array containing all nodes

NOP insertion is a boolean

Result: node inserted at position index

index = getRandomActiveNode();

nodes.insert(index,copyNode(nodes[index]));

// connection 0 of next node is linked to

// inserted node

nodes[index+1].conn0 = 1;

// connection 1 of next node is increasing by

// 1 to maintain his links after insertion

nodes[index+1].conn1 = nodes[index+1].conn1

+ 1;

if NOP insertion then

// set a NOP function

nodes[index].function = NOP;

else

// set a Random function

nodes[index].function =

getRandomFunction();

end

for i ← index to nodes.length do

if i − nodes[i].conn0 < index then

nodes[i].conn0 = nodes[i].conn0 + 1;

end

if i − nodes[i].conn1 < index then

nodes[i].conn1 = nodes[i].conn1 + 1;

end

for i ← 0 to out puts.length do

if nodes.length − out puts[i] < index then

outputs[i] = outputs[i]+1;

end

Figure 1: Graph with an random node N inserted at index 4.

3.2 Node Deletion

The node deletion operator removes a node from the

active graph of a CGP individual, as shown in Fig-

ure 2. After a node deletion we adjust the rest of the

genome to ensure that other parts of the graph are not

impacted. Speciﬁcally, as described in Algorithm 2,

all nodes which connected to the removed node are

in turn connected to the Connection 0 input of the

removed node, and all nodes after the selected node

have their connection genes decremented by 1.

These operators does induce a global beneﬁt to the

CGP evolution by growing a topology over the evolu-

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

Algorithm 2: Deletion of a node.

Data: nodes is an array containing all nodes

Result: node deleted at position index in the

graph

if active nodes.length > 1 then

index = getRandomActiveNode();

for i ← 0 to out puts.length do

if nodes.length − out puts[i] == index

then

outputs[i] =

outputs[i]+nodes[index].conn0;

end

for i ← 0 to active nodes.length do

if i − nodes[i].conn0 == index then

nodes[i].conn0 = nodes[i].conn0 +

nodes[index].conn0;

end

for i ← index to nodes.length do

if i − nodes[i].conn0 < index then

nodes[i].conn0 = nodes[i].conn0 -

end

if i − nodes[i].conn1 < index then

nodes[i].conn1 = nodes[i].conn1 -

end

nodes.remove(index);

end

Figure 2: Graph with a deletion of node 2.

tion instead of searching in a graph with a ﬁxed max-

imum size. However, we more speciﬁcally study this

in the case of Genetic Improvement, where existing

image ﬁlters can be improved through the node inser-

tion and deletion operators.

4 EXPERIMENTS

To evaluate the insertion and deletion operators in the

context of genetic improvement, we study the effect

of using ﬁlter made using human expert as the starting

point and using the proposed structural mutation op-

erators. Speciﬁcally, we compare the following con-

ﬁgurations:

Baseline: standard CGP-IP. Starting chromosome is

randomly deﬁned at the beginning. Insertion and

deletion mutations are disabled.

Fixed Size: standard CGP-IP, but active nodes in the

initial population are exclusively composed of func-

tion extracted from an expert ﬁlter and are positioned

at the beginning of the graph. Inactive node are ran-

domly decided after active nodes in the graph. Inser-

tion and deletion mutations are disabled.

Fixed Size with NOP: standard CGP-IP, but active

nodes in the starting population are composed of

functions extracted from an expert ﬁlter and are in-

tertwined with NOP function between each Connec-

tion 0 input. For example, if the ﬁlter contains 10

functions, the initial genome will be composed of 20

actives nodes (10 nodes with functions and 10 NOP

nodes). Inactive nodes are randomly added after the

active nodes. Insertion and deletion operators are dis-

abled.

Adapting with NOP: The initial genome is built as

in the ﬁxed size method, ie with an expert individ-

ual. Insertion and deletion operators are enabled. If

an insertion occurs, only NOP function are inserted.

Adapting with Random: The initial genome is built,

as can be seen in the ﬁxed size method. Insertion and

deletion operators are enabled. If an insertion occurs,

the function of the inserted node is randomly selected

from the function library.

Adapting, No Expert: Starting chromosome is ran-

domly deﬁned at the beginning. Insertion and dele-

tion mutations are enabled. If an insertion occurs,

the function of the inserted node is randomly selected

from the function library.

These conﬁgurations allow for detailed and inde-

pendent study of the two proposed CGP-IP improve-

ments in this work: genetic improvement of exist-

ing image ﬁlters and structural mutation operators of

node insertion and deletion. The ﬁxed size conﬁgu-

rations isolate the possible beneﬁt of building atop al-

ready designed image ﬁlter individuals, with the dif-

ference that the expert experience is encoded in the

starting genome. The three adapting conﬁgurations

allow for study of the node insertion and deletion

operators, in particular for their use for genetic im-

provement. Once again, the distinction between addi-

tional random genetic information and NOP is made;

for the node insertion operator, this difference deter-

mines if the functional phenotype of the CGP-IP indi-

vidual is modiﬁed by node insertion (adapting with

random) or if the insertion mutation is only struc-

tural (adapting with NOP). Finally, the adapting, no

expert conﬁguration allows for independent study of

the beneﬁts of the node insertion and deletion opera-

Improving Image Filters with Cartesian Genetic Programming

tors when starting from random genes, as in baseline

CGP-IP.

4.1 CGP-IP Parameters

In this work, we have used the following parameters

for CGP-IP:

• R: the number of rows in CGP is 1

• C: the number of columns in CGP is set to 50

for all experiments, but can change with the node

addition and deletion operators

• r

mut

: mutation rate for each gene is 0.25

• r

ins

: node insertion mutation operator rate is 0.1

• r

del

: node deletion mutation operator rate is 0.1

• Number of islands: the number of parallel 1 + λ

evolutions is 4

• λ: the population size on each island is 4

• Synchronisation interval between islands: number

of generations before islands compare their ﬁtness

to update them with the best chromosome is 20

• Number of generations: 1000 for the Mars task

and 2000 for the Lunar and Urban Trafﬁc tasks

Each node of the graph is encoded with 8 param-

eters (see table 1). The function allele represents an

index in the list of image processing functions. The

second allele, Connection 0, is a connection with a

previous node where output will be taken as input for

the function. The third allele, Connection 1, is a con-

nection with a previous node where output will be

taken as input for the function (not all functions used

connection 1). The fourth, ﬁfth and sixth alleles, Pa-

rameters 0, 1 and 2, are real numbers that are the ﬁrst,

second and third parameters of the function. These al-

leles are not necessarily used as not all functions have

three parameters. For example, Gabor Filter parame-

ters are only used with Gabor ﬁlter functions. During

the evolution process, mutation can occur either on

function index, on connection or on parameters.

Table 1: Parameters of a node.

Parameter Type Range

Function INT # of function

Connection 0 INT # of node/input

Connection 1 INT # of node/input

Parameter 0 REAL [−∞, ∞]

Parameter 1 INT [-16, 16]

Parameter 2 INT [-16, 16]

Gabor Filter Freq. INT [0, 16]

Gabor Filter Orien. INT [-8, 8]

4.2 Image Processing Functions

The function we designed herewith is based on the

CGP-IP function set (Harding et al., 2006). How-

ever, new functions have been added to the OpenCV

library since this previous work. In addition to the

existing list of image processing function (Harding

et al., 2012b) already in CGP-IP, we have added the

OpenCV functions watershed and distance transform.

4.3 Datasets

In this work, we aim to construct an image ﬁlter which

provides a binary classiﬁcation of an input image, al-

lowing for the recognition of a desired object type.

We use three different datasets for this task: images

from Mars rovers, which was used in (Leitner et al.,

2012), a similar Lunar dataset, and an Urban Trafﬁc

dataset, which is a new application for CGP-IP.

4.3.1 Mars Dataset

The Mars dataset is based on 5 images extracted from

1449 images that compose the McMurdo Panorama

(Figure 3) taken by the rover Spirit on Mars

Figure 3: Full image from the Spirit rover.

The purpose of applying our algorithm on this

dataset is to extract rocks from the images. Input im-

ages (Figure 4.A) have a resolution of 347x871 pix-

els and show rocks on the martian terrain. The target

output is a binary mask (Figure 4.B), which identiﬁes

pixels with rocks as 1 and other pixels as 0. Figure

4.C display the overlay result.

For this dataset, we use an expert ﬁlter proposed

by (Leitner et al., 2012), described in Listing 1 and

displayed in Figure 5. This ﬁlter was generated us-

ing CGP-IP on the same dataset and has already a

high accuracy, this allows us to study if further im-

provement using node addition and deletion is possi-

ble. For this dataset, we use 1000 generations for evo-

lution and run 6 independent trials; given the starting

point, 1000 generations was determined to be enough

for establishing a convergence.

http://pancam.sese.asu.edu/mcmurdo v2.html

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

A : Input B : Output C : Overlay

Figure 4: An example from the Mars image dataset. The

objective is to identify the rocks in the image.

def b a s e _ chr o m o s ome ( in pu t ):

# in pu t is co m po s ed of R [0] , G [1] ,

B [2] , H [3] , S [4] , V [ 5]

no de 0 = cv2 . G a us s i a nBl u r ( inp ut

[5] ,(3 ,3) )

no de 1 = np . sqrt ( n ode0 )

no de 2 = i np ut [4]

no de 3 = cv2 . u ns h a rp e n ( no de2 ,13 )

no de 4 = n od e1 *7. 00 1

no de 5 = cv2 . b i l ate r a l fil t e r ( n ode4

,9)

no de 6 = n o rma l ize ( node 5 )

no de 7 = n od e3 *4 .0 3

no de 8 = n od e7 + no de 6

no de 9 = cv2 . b i l ate r a l fil t e r ( n ode8

,11)

no de 1 0 = cv2 . t hr e s ho l d ( node9

,1 77 . 24 ,25 5)

re tu r n nod e10

Listing 1: Python encoding of the Mars gene base.

4.3.2 Lunar Dataset

The Lunar dataset

is based on 5 images extracted

from 9,766 realistic renders of rocky lunar land-

scapes, and their segmented equivalents (the 3 classes

are the sky, smaller rocks, and larger rocks). This

dataset was created by Romain Pessia and Genya

Ishigami of the Space Robotics Group

, Keio Univer-

sity, Japan. As with the Mars dataset, the new pur-

pose of using this dataset here is to extract rocks from

the images. The input images have a resolution of

720x480 pixels (Figure 6.A) and the target output im-

ages (Figure 6.B) classify the large rocks in the image.

https://www.kaggle.com/romainpessia/artiﬁcial-lunar-

rocky-landscape-dataset

http://www.srg.mech.keio.ac.jp/index en.html

Figure 5: Graph of the Mars gene evolved with CGP-IP

(Leitner et al., 2012).

A : Input B : Output

Figure 6: An example from the Lunar image dataset.

We use the same ﬁlter proposed by (Leitner et al.,

2012) and used on the Mars dataset for this dataset

(5). This allows us to study the adaptation of a ﬁlter

from one dataset to another, where the size and color

of the image changes, and where the target landscape

is very different. For this dataset, evolution is run for

2000 generations on 6 independent trials.

4.3.3 Urban Trafﬁc

To achieve this new purpose, we apply CGP-IP to

identifying moving objects in a city landscape. Using

this dataset allows to build a ﬁlter that extracts and

follows the speciﬁc objects in the video. To do so, the

ﬁlter needs to ﬁnd each objects that exhibit a move-

ment between individual frame in a frame to frame

comparison. The dataset was made using video from

urban trafﬁc livestream cameras

and output masks

were generated using Mask-RCNN (He et al., 2018)

to keep only relevant objects. We use videos of 5 min-

https://camstreamer.com/live/streams/14-trafﬁc

Improving Image Filters with Cartesian Genetic Programming

A : Input B : Output

Figure 7: Example from the Urban Trafﬁc image dataset.

utes in length, with 16 bit RGB color and a resolution

of 1024x576 pixels. The images are then converted

into grayscale for input and a sequence of 5 images

are processed together by the evolved ﬁlter (Figure

7.A). The target classiﬁcation (Figure 7.B) identiﬁes

large objects such as pedestrians and vehicles.

The expert ﬁlter used in this dataset was designed

by engineers. It works by ﬁrst subtracting the pre-

vious image from the current one, then by applying

erode and dilate function to remove noise. The ﬁlter

is detailed in Listing 2 and shown in Figure 8. For this

dataset, evolution was run for 2000 generations over

6 independent trials.

def b a s e _ chr o m o s ome ( inpu t1 , inp ut 2 ):

# in p ut 1 is co m pos ed of R [0] , G [1] ,

B [ 2]

# in p ut 2 is co m pos ed of R [0] , G [1] ,

B [ 2]

no de 0 = i np u t1 [0] + i n pu t1 [1]

no de 1 = n od e0 + in p ut 1 [2]

no de 2 = n od e1 / 3

no de 3 = i np u t2 [0] + i n pu t2 [1]

no de 4 = n od e3 + in p ut 2 [2]

no de 5 = n od e4 / 3

no de 6 = n od e5 - no de 2

no de 7 = cv2 . t hr e s ho l d ( no de6 ,50 ,255)

no de 8 = cv2 . di l at e ( no de7 )

no de 9 = cv2 . di l at e ( no de8 )

re tu r n node9

Listing 2: Python encoding of the Urban Trafﬁc gene base.

5 RESULTS

The results over the three datasets is dealt with here-

after. CGP-IP is able to construct image ﬁlters which

accurately classify the desired objects in all cases,

but the adaptive structure conﬁgurations show a clear

beneﬁt when compared with baseline CGP-IP.

Figure 9 shows evolution over 2000 iterations on

the Mars dataset. Adapting with random converges

more rapidly and towards better classiﬁcation than the

Figure 8: Graph of the Urban Trafﬁc gene, human designed.

Figure 9: Average and standard deviation of ﬁtness accu-

racy for Mars over 40 runs.

other methods. The other conﬁgurations show little

difference. Adapting with NOP ends with the worst

ﬁtness, with an accuracy inferior to both adapting

with random and ﬁxed size with NOP. This demon-

strates that adding nodes alone is not advantageous;

rather, the addition of nodes which change the pheno-

type program should be preferred.

The similarity of the results with the Mars dataset

is not a surprise given that the expert individual was

the result of a previous CGP-IP experiment. However,

it is notable that both baseline and adapting, no ex-

pert, which do not use this starting point, converge to

match the other individuals.

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

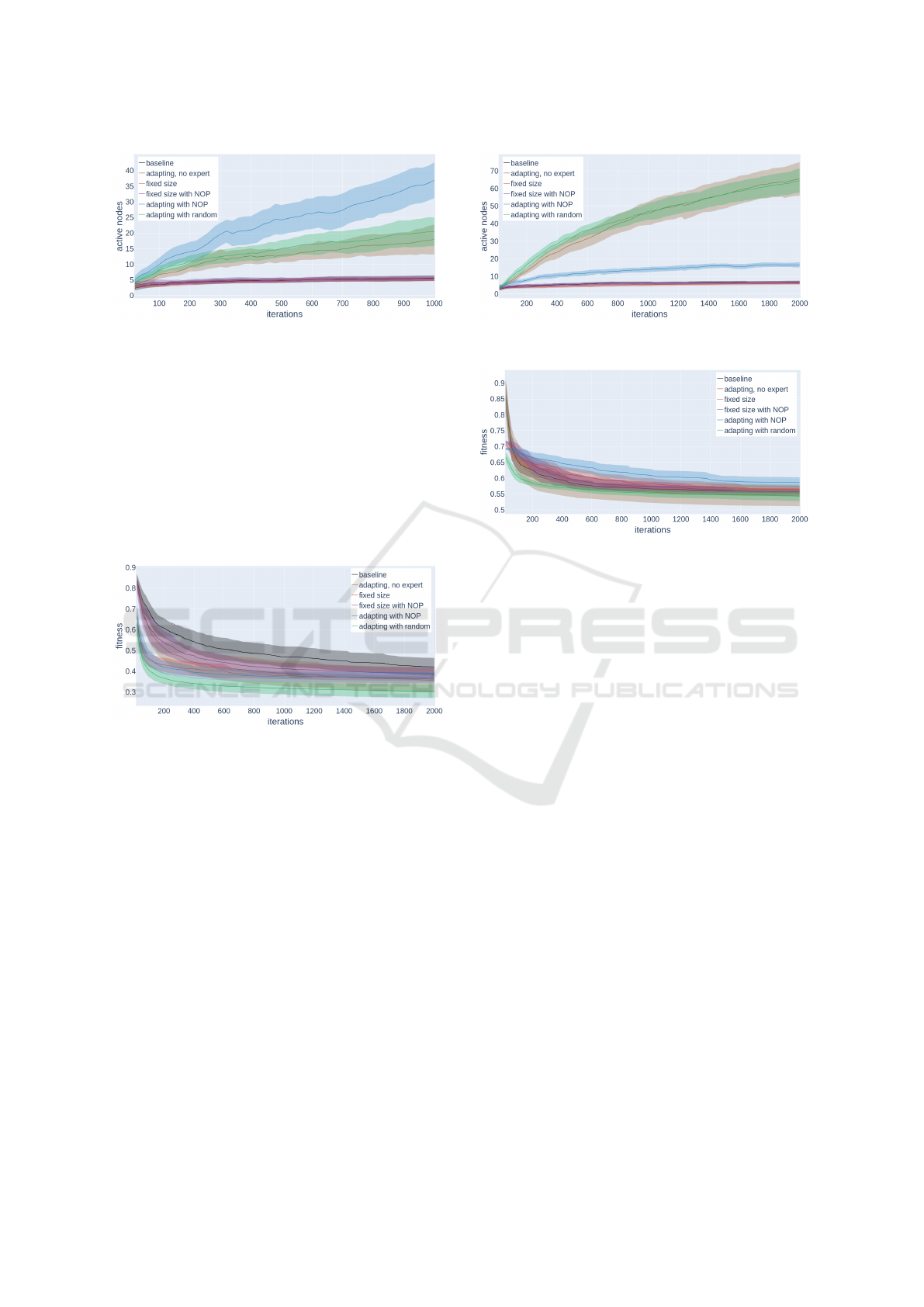
Figure 10: Average and standard deviation of actives nodes

for Mars overs 40 runs.

Figure 10 displays the active graph size for the

Mars dataset. baseline, ﬁxed size and ﬁxed size with

NOP slowly increase to 5/6 actives nodes. For adapt-

ing with NOP, the actives nodes constantly increase

throughout evolution. Adapting with random and

adapting, no expert converge to similar size due to

using the same addition operation. It is clear that the

insertion operation results in a larger graph than uni-

form random mutation, even though there is a deletion

operator also present.

Figure 11: Average and standard deviation of ﬁtness accu-

racy for Lunar overs 40 runs.

Figure 11 displays evolution over 2000 genera-

tions on the Lunar dataset. Adapting with random

performs better and quicker than ﬁve others with a

better variance and ttest p-value of less than 1e

−5

Baseline starts slower than the ﬁve other experiments

with a higher variance and worse ﬁnal performance.

While adapting, no expert does eventually converge

to similar accuracy as other conﬁgurations which start

with an expert, the beneﬁt of starting with an expert

is demonstrated through the suboptimal performance

of baseline. It should also be noted that the expert

used on this dataset was initially trained on the Mars

dataset,this does show that a ﬁlter is efﬁciently appli-

cable from one task to another.

Figure 12 shows that baseline, ﬁxed size and

ﬁxed size with NOP increase slowly to 7 actives

nodes. For this dataset, the adaptive conﬁgurations

with random function insertion grow larger than when

adding NOP, which is the opposite of the node size

Figure 12: Average and standard deviation of actives nodes

for Lunar overs 40 runs.

Figure 13: Average and standard deviation of ﬁtness accu-

racy for Urban Trafﬁc over 40 runs.

behavior for the Mars dataset. The adapting graphs

reach enormous sizes after 2000 generations, oversiz-

ing the initial maximum graph size settled to 50.

Figure 13 shows that the evolution of the ﬁtness

function over 2000 iterations on the Urban Trafﬁc

dataset. Adapting with random outperforms and

converges faster than baseline, ﬁxed size, ﬁxed size

with NOP and adapting with NOP (p-value of Stu-

dent t-test <1e

−5

both at iteration 300 as well as at

iteration 2000). It is important to note that the stan-

dard deviation over the 40 runs is somewhere small

with this method in comparison to other methods.

This should be interpreted as proof that the adapting

with random not only does perform better than other

but also that to solution of similar quality indepen-

dently of the randomness of the evolutionary process.

Adapting, no expert performs slower than adapting

with random but achieve a better ﬁtness after 700 it-

erations and continue to decrease. This demonstrates

a potential disadvantage of starting with an expert in-

dividual, which is early convergence based on this in-

dividual and lack of exploration when compared to a

random initialization.

Figure 14 shows that ﬁxed size and ﬁxed size with

NOP reduces the graph cardinal down to 7 active

nodes. Here, as in the Lunar dataset, the random node

insertion conﬁgurations continue to grow throughout

evolution although their is a clear compression step

visible after nearly 500 generations for adapting, no

expert this in turn does demonstrate the beneﬁt of the

Improving Image Filters with Cartesian Genetic Programming

Table 2: Average ﬁtness and standard deviation of each experiment on each dataset.

Lunar Mars Urban trafﬁc

Baseline 0.42 (0.09) 0.23 (0.05) 0.56 (0.02)

Adapting, no expert 0.36 (0.12) 0.21 (0.08) 0.55 (0.07)

Fixed sized 0.36 (0.02) 0.21 (0.04) 0.56 (0.02)

Fixed size with NOP 0.39 (0.05) 0.23 (0.04) 0.56 (0.01)

Adapting with NOP 0.37 (0.05) 0.26 (0.1) 0.59 (0.03)

Adapting with random 0.3 (0.07) 0.2 (0.03) 0.54 (0.03)

Figure 14: Average and standard deviation of actives nodes

for Urban Trafﬁc over 40 runs.

deletion operator.

To summarize: each experiment (Table 2), adapt-

ing with random performs better and quicker than

standard CGP-IP with a lower variance and a ttest

p value less than 1e-5. Our evolution with random

function outperform the standard CGP-IP (baseline)

and ﬁxed size with NOP in each case. Adapting

with NOP converges a bit faster but ends with an in-

ferior accuracy. As expected, the baseline chromo-

some converge slower with a higher variance than the

others. The proposed mutation operators (insertion of

NOP and random function) greatly increase the num-

ber of active nodes in the graph unlike standard CGP-

IP, where the number of active nodes is relatively sta-

ble. With Urban trafﬁc dataset, adapting, no expert

performs better than adapting with random after 700

iterations this emphases that it is important to start

from an efﬁcient base chromosome, otherwise genetic

improvement will be outperformed by the classic evo-

lution done with a random chromosome.

6 CONCLUSION

In this paper, we propose mutation operators for CGP-

IP for use in the context of genetic improvement. To

this end, our algorithm adds new functions in a graph

and keeps existing connections intact. We have tested

CGP-IP with these operators on 3 datasets and have

shown that it consistently outperforms standard CGP-

IP, increasing the convergence speed and ﬁnal accu-

racy on all datasets.

Our method has the additional interest to slowly

but constantly increase the number of active nodes.

This allows evolution to access new research space

leading to better accuracy. This conclusion is in line

with previous work on incremental growth of neural

networks (Stanley and Miikkulainen, 2002) or gene

regulatory networks (Cussat-Blanc et al., 2015). For

example, the NeuroEvolution of Augmenting Topolo-

gies (NEAT) (Stanley and Miikkulainen, 2002) al-

gorithm demonstrates that increasing program com-

plexity throughout search can improve the optimiza-

tion. That is consistent with the results in this work,

both when starting with an expert-designed image ﬁl-

ter and when using a random initial population.

An avenue for exploration with this method is

the reduction of graph complexity over time. While

the node insertion operators are clearly beneﬁcial for

evolution, they reintroduce the problem of bloat into

CGP. We aim to study the different mutation rates to

see if large graphs can be automatically avoided in

evolution.

In practice, this method can be used to converge

quickly to a better solution using a efﬁcient human de-

signed ﬁlter than when starting from a random chro-

mosome. This allows for application of this method

which builds on existing image processing pipelines,

especially those which use CGP-IP.

REFERENCES

Arcuri, A. and Yao, X. (2008). A novel co-evolutionary

approach to automatic software bug ﬁxin. CEC, pages

162–168.

Bianco, S., Ciocca, G., and Schettini, R. (2017). Combina-

tion of video change detection algorithms by genetic

programming. IEEE Transactions on Evolutionary

Computation, 21(6):914–928.

Bruce, B. R., Petke, J., and Harman, M. (2015). Reduc-

ing energy consumption using genetic improvement.

GECCO.

Cussat-Blanc, S., Harrington, K., and Pollack, J. (2015).

Gene regulatory network evolution through augment-

ing topologies. IEEE Transactions on Evolutionary

Computation, 19(6):823–837.

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

Ebner, M. (2009). Engineering of computer vision algo-

rithms using evolutionary algorithms. In Blanc-Talon,

J., Philips, W., Popescu, D., and Scheunders, P., ed-

itors, Advanced Concepts for Intelligent Vision Sys-

tems, pages 367–378, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Ebner, M. (2010). Evolving object detectors with a gpu

accelerated vision system. In Tempesti, G., Tyrrell,

A. M., and Miller, J. F., editors, Evolvable Systems:

From Biology to Hardware, pages 109–120, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Harding, S., Graziano, V., Leitner, J., and Schmidhuber, J.

(2012a). Mt-cgp: Mixed type cartesian genetic pro-

gramming. Genetic and Evolutionary Computation

Conference.

Harding, S., Leitner, J., and Schmidhuber, J. (2006). Ge-

netic programming theory and practice. Journal of

Intelligent and Robotic Systems.

Harding, S., Leitner, J., and Schmidhuber, J. (2012b).

Cartesian genetic programming for image processing.

Genetic Programming Theory and Practice X.

Harding, S., Leitner, J., and Schmidhuber, J. (2013). Carte-

sian Genetic Programming for Image Processing. Ge-

netic Programming Theory and Practice X, pages 31–

44.

Harding, S., Miller, J., and Banzhaf, W. (2011). Self-

modifying cartesian genetic programming. Natural

Computing Series.

Harman, M., Jia, Y., and Langdon, W. (2014). Babel pid-

gin: Sbse can grow and graft entirely new functional-

ity into a real world system. SSBSE Challenge, pages

247–252.

He, K., Gkioxari, G., Doll

ar, P., and Girshick, R. (2018).

Mask r-cnn.

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Delving deep

into rectiﬁers: Surpassing human-level performance

on imagenet classiﬁcation.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Kalkreuth, R., Rudolph, G., and Krone, J. (2016). More ef-

ﬁcient evolution of small genetic programs in Carte-

sian Genetic Programming by using genotypie age.

In 2016 IEEE Congress on Evolutionary Computation

(CEC), pages 5052–5059. IEEE.

Khan, G. M., Miller, J. F., and Halliday, D. M. (2011). Evo-

lution of cartesian genetic programs for development

of learning neural architecture. Evolutionary compu-

tation, 19(3):469–523.

Langdon, W. and Harman, M. (2010). Evolving a cuda ker-

nel from an nvidia template. CEC, pages 1–8.

Langdon, W. B. and Harman, M. (2015). Optimising

existing software with genetic programming. TEC,

19(1):118–135.

Leitner, J., Harding, S., F

orster, A., and Schmidhuber, J.

(2012). Mars terrain image classiﬁcation using carte-

sian genetic programming. 11th International Sympo-

sium on Artiﬁcial Intelligence, Robotics and Automa-

tion in Space (i-SAIRAS).

Matthews, B. W. (1975). Comparison of the predicted and

observed secondary structure of t4 phage lysozyme.

Biochimica et Biophysica Acta, 405(2):442–451.

Miller, J., Thomson, P., Fogarty, T., and Ntroduction, I.

(1997). Designing electronic circuits using evolu-

tionary algorithms. arithmetic circuits: A case study.

Genetic Algorithms and Evolution Strategies in Engi-

neering and Computer Science, pages 105–131.

Miller, J. F. (1999). An empirical study of the efﬁciency of

learning boolean functions using a cartesian ge- netic

programming approach. Proceedings of the Genetic

and Evolutionary Computation Conference, volume 2,

pages 1135–1142.

Miller, J. F. (2001). What Bloat? Cartesian Genetic Pro-

gramming on Boolean Problems. 2001 Genetic and

Evolutionary Computation Conference Late Breaking

Papers, pages 295–302.

Miller, J. F. (2011). Cartesian genetic programming.

Springer.

Miller, J. F. (2019). Cartesian genetic programming: its sta-

tus and future. Genetic Programming and Evolvable

Machines, pages 1–40.

Miller, J. F. and Thomson, P. (2000). Cartesian Genetic

Programming. In Lecture Notes in Computer Science

(including subseries Lecture Notes in Artiﬁcial Intel-

ligence and Lecture Notes in Bioinformatics), volume

1802, pages 121–132. Springer.

Petke, J., Harman, M., Langdon, W., and Weimer, W.

(2014). Using genetic improvement and code trans-

plants to specialise a c++ program to a problem class.

EuroGP, 137–149.

Rundo, L., Tangherloni, A., Nobile, M. S., Militello, C.,

Besozzi, D., Mauri, G., and Cazzaniga, P. (2019).

Medga: A novel evolutionary method for image en-

hancement in medical imaging systems. Expert Sys-

tems with Applications, 119:387–399.

Stanley, K. O. and Miikkulainen, R. (2002). Efﬁcient evo-

lution of neural network topologies. Journal of Com-

puting and Information Technology, 7:33–47.

White, D. R., Arcuri, A., and Clark, J. A. (2011). Evolution-

ary improvement of programs. TEC, 15(4):515–538.

Whitley, D., Rana, S., and Heckendorn, R. B. (1998). The

island model genetic algorithm: On separability, pop-

ulation size and convergence. Journal of Computing

and Information Technology, 7:33–47.

Wu, F., Weimer, W., Harman, M., Jia, Y., and Krinke, J.

(2015). Deep parameter optimisation. GECCO.

Improving Image Filters with Cartesian Genetic Programming