Reward Prediction for Representation Learning

and Reward Shaping

Hlynur Davíð Hlynsson and Laurenz Wiskott

Institut für Neuroinformatik, Ruhr-Universität Bochum, Universitätsstraße 150, Bochum, Germany

Keywords:

Reinforcement Learning, Representation Learning, Deep Learning, Machine Learning.

Abstract:

One of the fundamental challenges in reinforcement learning (RL) is the one of data efﬁciency: modern

algorithms require a very large number of training samples, especially compared to humans, for solving en-

vironments with high-dimensional observations. The severity of this problem is increased when the reward

signal is sparse. In this work, we propose learning a state representation in a self-supervised manner for re-

ward prediction. The reward predictor learns to estimate either a raw or a smoothed version of the true reward

signal in an environment with a single terminating goal state. We augment the training of out-of-the-box RL

agents in single-goal environments with visual inputs by shaping the reward using our reward predictor during

policy learning. Using our representation for preprocessing high-dimensional observations, as well as using

the predictor for reward shaping, is shown to facilitate faster learning of Actor Critic using Kronecker-factored

Trust Region and Proximal Policy Optimization.

1 INTRODUCTION

Deep learning has enjoyed great success in recent

years with a fortunate combination of larger data sets,

increasing computational capabilities and advances in

algorithm design in addition to an ample offering of

ﬂexible software ecosystems. In particular, reinforce-

ment learning (RL), which is the discipline of ma-

chine learning concerned with general goal-directed

behavior. RL has shown great promise since Deep-

Mind combined the principles of RL with deep learn-

ing to achieve human-like skill on Atari video games

(Mnih et al., 2013). Since then, the list of games

where machine triumphs over man grows longer with

the addition of algorithms surpassing human capabil-

ities in games such as Go, (Silver et al., 2016), Poker

(Brown and Sandholm, 2019) and a restricted version

of DOTA 2 (Berner et al., 2019).

Even though the dominance of humans is being

tested by RL agents on numerous fronts, there are

still great difﬁculties for the ﬁeld to overcome. For in-

stance, the data that is required for algorithms to reach

human performance is on a far larger scale than that

needed by humans. Furthermore, the general intelli-

gence of humans remains unchallenged. Even though

an RL agent has reached superhuman performance in

one ﬁeld, its performance is usually poor when it is

tested in new areas.

The study of methods to overcome the problem of

data efﬁciency (Hlynsson et al., 2019) and transfer-

ability of RL agents in environments where the agent

must reach a single goal is the focal point of this work.

We consider a simple way of learning a state represen-

tation by predicting either a raw or a smoothed ver-

sion of a sparse reward yielded by an environment.

The two objectives, learning a representation and pre-

dicting the reward, are directly connected as we train

a deep neural network for the prediction and the hid-

den layers of this network learn a reward-predictive

representation of the input data.

The reward signal is created by collecting data

from a relatively low number of initial episodes using

a controller that acts randomly. The representation is

then extracted from an intermediate layer of the pre-

diction model and re-used as general preprocessing

for RL agents, to reduce the dimensionality of visual

inputs. The agent processes inputs corresponding to

its current state as well as the desired end state, which

is analogous to mentally visualizing a goal before at-

tempting to reach it. This general approach of relying

on state representations, that are learned to predict the

reward rather than maximizing it, has been motivated

in the literature (Lehnert et al., 2020) and we show

that our representation is well-suited for single-goal

environments. Our work adds to the growing body

of knowledge related to deep unsupervised (Hlynsson

Hlynsson, H. and Wiskott, L.

Reward Prediction for Representation Learning and Reward Shaping.

DOI: 10.5220/0010640200003063

In Proceedings of the 13th International Joint Conference on Computational Intelligence (IJCCI 2021), pages 267-276

ISBN: 978-989-758-534-0; ISSN: 2184-3236

267

and Wiskott, 2019) and self-supervised (Schüler et al.,

2018) representation learning .

We also investigate the effectiveness of augment-

ing the reward for RL agents, when the reward is

sparse, with a novel problem-agnostic reward shap-

ing technique. The reward predictor, which is used

to train our representation, is not only used as a part

of an auxiliary loss function to learn a representation,

but it is also used during training the RL system to

encourage the agent to move closer to a goal loca-

tion. Similar to advantage functions in the RL litera-

ture, given the trained reward predictor, the agent re-

ceives an additional reward signal if it moves from

states with a low predicted reward to states with a

higher predicted reward. We ﬁnd this reward augmen-

tation to be beneﬁcial for our test environment with

the largest state-space.

2 BACKGROUND

2.1 Markov Decision Processes

A partially-observable Markov decision process

(POMDP) is a tuple

(S ,A,P ,R ,P(s

),Ω,O,γ) (1)

which we also refer to as the environment.

The environment starts in a state s ∈ S drawn from

P(s

), from which the agent interacts sequentially

with the environment by choosing action a

from ac-

tion space A at time steps t.

Given the agent’s state s

and action a

, the transi-

tion function P governs the next state s

t+1

. The agent

receives an observation o

∈ Ω, determined by the ob-

servation function O, and a reward r

, determined by

the reward function R .

A discount factor γ ∈ (0,1) is usually included in

the deﬁnition of POMDPs and it comes into play in

the optimization function of the agent. Namely, the

objective of an RL agent is to learn a policy π that

determines the behavior of the agent in the environ-

ment by mapping states to a probability distribution

over A, written π(a, s) = P(a

= a|s

= s). The policy

should maximize the expected discounted future sum

of rewards, or the expected return:

∞

∑

t=0

(2)

2.2 Reward Shaping

Sparse rewards in environments is a common problem

for RL agents. The agent’s goal is to associate its in-

puts with actions that lead to high rewards, which can

be a lengthy process if the agent only rarely experi-

ences positive or negative rewards.

Reward shaping (Mataric, 1994) is a popular

method of modifying the reward function of an MDP

to speed up learning. It is useful for environments

with sparse rewards to augment the training of the

agent but skillful applications of reward shaping can

in principle aid the optimization for any environ-

ment – although the efﬁcacy of the reward shaping

is highly dependent on the details of the implemen-

tation (Amodei and Clark, 2016). In the last few

years, reward shaping has been shown to be use-

ful for complex video game environments, such as

real-time strategy games (Efthymiadis and Kudenko,

2013) and platformers (Brys et al., 2014) and it has

also been combined with deep neural networks to im-

prove agents in ﬁrst person shooter games (Lample

and Chaplot, 2017).

As an illustration, consider learning a policy for

car racing. If the goal is to train an agent to drive op-

timally, then supplying it with a positive reward for

reaching the ﬁnish line ﬁrst is in theory sufﬁcient.

However, if it is punished for actions that are never

beneﬁcial, for instance crashing into walls, it priori-

tizes learning to avoid such situtations, allowing it to

explore more promising parts of the state space.

Furthermore, just reaching the goal is insufﬁcient

if there is competition. To make sure that we have a

winning racer, a small negative reward can be intro-

duced at every time step to urge the agent to reach the

ﬁnish line quickly. Note that the details of the reward

shaping in this example requires domain knowledge

from a designer who is familiar with the environment.

It would be more generally useful if the reward shap-

ing would be autonomously learned, just as the policy

of the agent, as we propose to do in this work.

2.3 Reward-predictive/Maximizing

Representations

(Lehnert et al., 2020) make the distinction be-

tween reward-maximizing representations are reward-

predictive representations. They argue how reward-

maximizing representations can transfer poorly to

new environments while reward-predictive represen-

tations generalize successfully. Take the simple grid

world navigation environments in Figure 1, for exam-

ple. The agent starts at a random tile in the grid and

gets a reward of +1 by reaching the rightmost column

in Environment A or by reaching the middle column

in Environment B. The state space in Environment A

can be compressed from the 3 × 3 grid to a vector of

length 3, [φ

,φ

] of reward-predictive representa-

NCTA 2021 - 13th International Conference on Neural Computation Theory and Applications

268

tions. To predict the discounted reward, it sufﬁces to

describe the agent’s state with φ

if it is in the jth row.

0 0 1

0 1 0

Environment A

Environment B

Available

actions:

State Representation

Optimal action

Figure 1: Reward-maximizing vs. reward-predictive

representations. In this grid world example, the agent

starts the episode at a random location and can move up,

down, left, or right. The episode ends with a reward of 1

and terminates when the agent reaches the rightmost col-

umn. Both the reward-predictive representation and reward-

maximizing representation φ

and φ

, respectively, are use-

ful for learning the optimal policy in Environment A. The

reward-predictive representation φ

collapses each column

into a single state to predict the discounted future reward.

The reward-maximizing representation φ

makes no such

distinction as moving right is the optimal action in any state.

It is a different story if the representations are transfered to

Environment B, where reaching the middle column is now

the goal. The representation φ

can be reused and the op-

timal policy is found if agent now takes a step left in φ

However, the representation φ

is unable to discriminate

between the different states and is useless for determining

the optimal policy.

The reward-maximizing representation for Envi-

ronment A is much simpler: the whole state space can

be collapsed to a single element φ

, with the optimal

policy of always moving to the right. If these rep-

resentations are kept, then the reward-predictive rep-

resentation φ

is informative enough for a RL agent

to learn how to solve Enviroment B. The reward-

maximizing representation φ

has discarded too many

details of the environment to be useful for solving this

new environment.

2.4 Successor Features

The successor representation algorithm learns two

functions: the expected reward R

received after

transitioning into a state s, as well as the matrix

of discounted expected future occupancy of each

state, assuming that the agent starts in a given state

and follows a particular policy π. Knowing the quan-

tities R

and M

allows us to rewrite the value func-

tion:

(s) = E



(s)M

(s,s

)



(3)

The motivation for this algorithm is that it com-

bines the speed of model-free methods, by enabling

fast computations of the value function, with the ﬂex-

ibility of model-based methods for environments with

changing reward contingencies.

This method is made for small, discrete envi-

ronments but it has been generalized for continuous

environments with so-called feature-based successor

representations, or successor features (SFs) (Barreto

et al., 2016). The SF algorithm similarly calcu-

lates the discounted expected representation of future

states, given the agent takes the action a in the state s

and follows a policy π:

(s,a) = E

∞

∑

t=0

t−1

t+1

= s,a

= a

(4)

where φ is some state representation. Both the SF ψ

and the representation φ can be deep neural networks.

3 RELATED WORK

3.1 Reward-predictive Representations

(Lehnert et al., 2020) compare successor features

(SFs) to a nonparametric Bayesian predictor that

is trained to learn transition and reward tables for

the environment, either with a reward-maximizing

or a reward-predictive loss function. (Lehnert and

Littman, 2020) prove under what conditions suc-

cessor features (SFs) are either reward-predictive or

reward-maximizing (see distinction in Section 2.3).

They also show that SFs work succesfully for transfer

learning between environments with changing reward

functions and unchanged transition functions, but

they generalize poorly between environments where

the transition function changes.

Our work is distinct from the reward-predictive

methods that they compare as our representation does

not need to calculate expected future state occupancy,

as is the case for SFs. Our method scales better

for more complicated state-spaces because we do not

tabulate the states, as they do with their Bayesian

model, but learn arbitrary continuous features of high-

dimensional input data. In addition to that, learning

our reward predictor is not only a "surrogate" objec-

tive function as we use it for reward shaping as well.

3.2 Reward Shaping

The advantages of reward shaping are well under-

stood in the literature (Mataric, 1994). A recent trend

in RL research is the study of methods that can learn

the reward shaping function in an automatic manner,

without the need of (often faulty) human intervention.

Reward Prediction for Representation Learning and Reward Shaping

269

(Marashi et al., 2012) assume that the environment

can be expressed as a graph and that this graph formu-

lation is known. Under these strong assumptions, they

perform graph analysis to extract a reward shaping

function. More recently, (Zou et al., 2019) propose

a meta-learning algorithm for potential-based auto-

matic reward shaping. Our approach is different from

previous work as we assume no knowledge about the

environment and train a predictor to approximate (po-

tentially smoothed) rewards, which is then used to

construct a potential-based reward shaping function.

3.3 Goal-conditioned RL

(Kaelbling, 1993) studied environments with multiple

goals and small state-spaces. In their problem setting,

the agent must reach a known but dynamically chang-

ing goal in the fewest number of moves. The observa-

tion space is of a low enough dimension for dynamic

programming to be satisfactory in their case. (Schaul

et al., 2015) introduce the Universal Value Function

Approximators and tackle environments of larger di-

mensions by learning a value function neural network

approximator that accepts both the current state and

a goal state as the inputs. In a similar vein, (Pathak

et al., 2018) learn a policy that is given a current state

and a goal state and outputs an action that bridges the

gap between them. (Hlynsson et al., 2020) learn a

predictable representation that is paired with a repre-

sentation predictor and combine it with graph search

to ﬁnd a given goal location. In contrast to these ap-

proaches, we learn a reward-predictive representation

in a self-supervised manner which is used to prepro-

cess raw inputs for RL policies.

4 APPROACH

In this section, we explain our approach mathemati-

cally. Intuitively, we train a deep neural network to

predict either a raw or a smoothed reward signal from

a single-goal environment. The output of an inter-

mediate layer in the network is then extracted as the

representation – for example, by simply removing the

top layers of the network. The full reward predictor

network is used for reward shaping by rewarding the

agent for moving from lower predicted values toward

higher predicted values of the network.

4.1 Learning the Representation

Suppose that f

: R

→ [0, 1] is a differentiable func-

tion parameterized by θ and c is a positive integer.

We use f

to approximate the discounted return in a

POMDP with a sparse reward: the agent receives a

reward of 0 for each time step except when it reaches

a goal location, at which point it receives a positive

reward and the episode terminates.

Given an experience buffer D =

{(s

t+1

)

}, we create a new data set

∗

= {(s

∗

t+1

)

}. The new rewards are

calculated according to the equation

∗

= γ

t+m

(5)

where γ ∈ [0,1] is a discount factor and M > m > 0

is the difference between t and the time step index

of the ﬁnal transition in that episode, for some max-

imum time horizon M. Throughout our experiments,

we keep the value of the discount factor equal to 0.99

and we train on D or D

∗

Assume that our differentiable representation

function φ : R

→ R

is parameterized by θ

and maps

the d-dimensional raw observation of the POMDP to

the c-dimensional feature vector. We train the rep-

resentation for the discounted-reward prediction by

minimizing the loss function

L( f

[φ

t+1

)],r

∗

) = (r

∗

− f

[φ

t+1

)])

(6)

with respect to the parameters θ of f and the parame-

ters θ

of φ over the whole data set D

∗

. See Figure 2

for a conceptual overview of our representation learn-

ing.

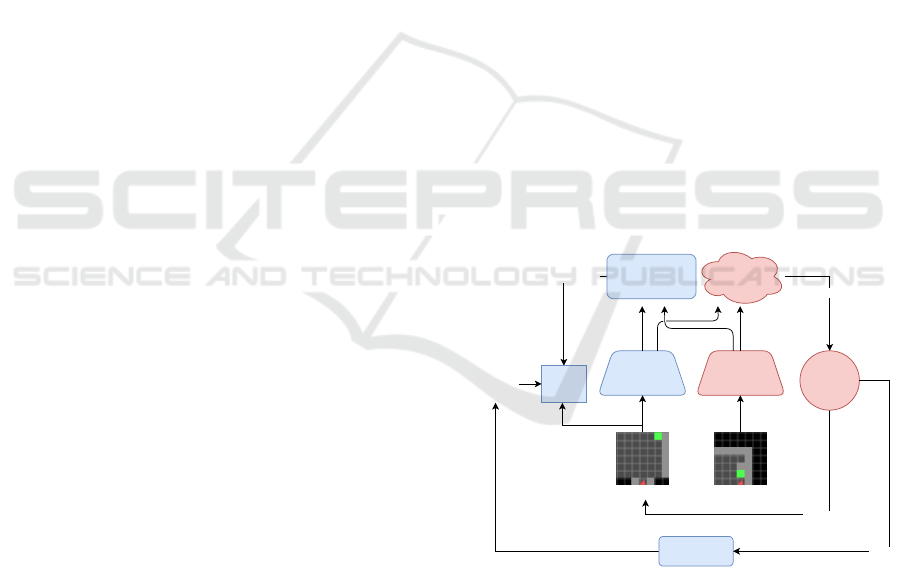
Representation Representation

Action

Policy

Prediction

Reward Predictor

Loss

fuction

Current state Goal state

Smoothed

Reward

New state

Environment

Reward

smoothing

Reward

Figure 2: Learning and Using the Representation. Our

representation and reward predictor is trained with the ele-

ments highlighted in blue. The trained representation is then

used for dimensionality reduction for an RL agent, that in-

teracts with the environment as indicated by the elements

highlighted in red.

4.2 Reward Shaping

(Ng et al., 1999) deﬁne a reward shaping function F

as potential-based if there exists a function f : S → R

such that for all states s,s

∈ S the equation holds:

NCTA 2021 - 13th International Conference on Neural Computation Theory and Applications

270

F(s, a, s

) = γ f (s

) − f (s) (7)

and γ is the MDP’s discount factor. They prove

for single-goal environments that every optimal pol-

icy for the MDP M = (S ,A, P ,R ,P(s

),γ) is also

optimal for its reward-shaped counterpart M

(S ,A, P ,R + F,P(s

),γ), and vice versa. They also

show, for a given state space S and action space A,

that if F is not potential-based, then there exist a tran-

sition function P and a reward function R such that

no optimal policy in M

is optimal in M.

We would like our reward shaping function to

be potential-based (Equation 7) to reap the theoreti-

cal advantages and propose a potential-based reward

shaping function based on the reward predictor

F(s, a, s

) =



γ f

(φ

]) − f

(φ

[s])



(H − I)/H

= γ f

∗

) − f

∗

(s)

(8)

where f

∗

= f

(φ

])(H −I)/H, f

is the reward pre-

dictor and φ

is our representation from the previous

section. Note that both f

and φ

are assumed to be

fully trained before the policy of the agent is trained,

for example using data gathered by a random policy,

but they can in principle also be updated as the policy

is being learned. The factor (H − I)/H scales down

the intensity of the reward shaping where I ∈ N

the number of episodes that the agent has experienced

and H ∈ N

is the maximum number of episodes

where the agent is trained using reward shaping. The

strength of the reward shaping is the highest in the be-

ginning to counteract potentially adverse effects of er-

rors in the reward predictor. It is also more important

to incentivize moving toward the general direction of

the goal in the early stages of learning, after which the

un-augmented reward signal of the environment is al-

lowed to "speak for itself" and guide the learning of

the agent toward the goal precisely.

5 METHODOLOGY AND

IMPLEMENTATION

5.1 Environment

The method is tested on 3 different gridworld envi-

ronments based on the Minimalistic Gridworld Envi-

ronment (MiniGrid) (Chevalier-Boisvert et al., 2018).

Tiles can be empty, occupied by a wall or occupied

by lava. The constituent states of S are determined by

the agent’s location and direction (facing north, west,

south or east), along with the goal’s location. The

steps taken since the episode’s initialization is also

(a) Full World States.

(b) Agent’s Point of View.

Figure 3: Two-Room Environment. The red agent must

reach the green goal in as few steps as possible. The agent

starts each episode between the two rooms, facing a random

direction (up, down, left or right). Each column corresponds

to a snapshot of 1 episode. The light tiles correspond to

what the agent sees while the dark tiles are unseen by the

agent. (a) Examples of the full state (b) The observation

from the agent’s current state (c) A goal observation. This

is the agent’s point of view from a state that separates the

agent from the goal by 1 action.

tracked for reward calculations. See Figure 3a for 3

different world states in one of our environments.

The action space A has 3 actions: (1) turn left,

(2) turn right and (3) move forward. The transition

function is deterministic. The agent relocates to the

tile it faces if it moves forward and the tile is empty

and nothing happens if the tile is occupied by a wall.

The episode terminates if the tile is occupied by lava

or the goal. The agent rotates in place if it turns left or

right. Reaching the green tile goal gives a reward of

1 − 0.9 ·

#steps taken

#max steps

, other actions give no reward. The

environment times out after #max step = 100 steps.

The discount factor is γ = 0.99.

We consider the following three environments:

5.1.1 Two-room Environment

The world is a 8 × 17 grid of tiles, split into two

rooms, where walls are placed at different locations

to facilitiate discrimination between the rooms from

the agent’s point of view. (Figure 3). The agent is

placed between the two rooms, facing a random di-

rection. The goal is at 1 of 3 possible locations. This

Reward Prediction for Representation Learning and Reward Shaping

271

is a modiﬁed version of the classical four-room envi-

ronment layout (Sutton et al., 1999).

5.1.2 Lava Gap Environment

In this environment, the agent is in a 4 × 4 room with

a column of lava either 1 or 2 spaces in front of the

agent (Figure 4) with a gap in a random row. The

agent always starts in the upper left corner and the

goal is always in the lower right corner.

Figure 4: The Lava Gap Environment. The red agent

must reach the green goal in as few steps as possible while

avoiding the orange lava tiles.

5.1.3 Four-room Environment

An expansion to the two-room environment with two

additional rooms (Figure 5) and both the agent and

the goal location are placed at random locations.

Figure 5: Four-Room Environment. The agent and goal

locations are randomized in each episode. The 7 × 7 grid of

highlighted tiles in front of the agent is the observation.

5.2 Baselines

We combine our representations with two RL al-

gorithms as implemented in Stable Baselines (Hill

et al., 2018) using the default hyperparameters: (1)

Actor Critic using Kronecker-Factored Trust Region

(ACKTR) (Wu et al., 2017) and a version of the Prox-

imal Policy Optimization (PPO2) algorithm (Schul-

man et al., 2017).

For both algorithms, 6 variations are compared:

(1) ACKTR / PPO2 with raw image inputs (Deep

RL), (2) inputs are preprocessed with successor fea-

tures (SF), (3) inputs are preprocessed using our rep-

resentation, trained on raw reward predictions (Ours

1r), (4) the input is preprocessed using our represen-

tation and the reward is shaped, trained on raw re-

ward predictions (Ours 1r + Shaping), (5) the input

is preprocessed using our representation, trained on

smoothed reward predictions (Ours 64r), (6) the in-

put is preprocessed using our representation and the

reward is shaped, trained on smoothed reward predic-

tions (Ours 64r + Shaping). Care has been taken to

ensure that each model has the same architecture and

number of parameters.

5.3 Model Architectures

Every model is realized as a neural network using

Keras (Chollet et al., 2015). Below, the representa-

tion and policy networks are used for our method and

the SF comparison, the reward prediction network is

used only for our method and the deep RL network is

used only for the deep RL comparison, where the RL

algorithm also learns the representation.

The Representation Networks: are two convolu-

tional networks with a 28 × 28 × 3 input. The ﬁrst

layer discards every other column and row. This is

followed by 8 ﬁlters of size 3 × 3 with a stride of 3.

This is followed with a ReLU activation and a 2 × 2

max pooling layer with a stride of 2. The pooling

layer’s output is passed to a layer with 16 convolu-

tional ﬁlters of size 3×3 and a stride of 2 and a ReLU

activation. The output is passed to a linear dense layer

with 16 units, deﬁning the dimension of the represen-

tation. No zero padding is applied in any layer.

The Policy Networks: are 3-layer fully-connected

networks accepting the concatenated output of the

representation network for the agent’s current point of

view and the goal observation as input. The ﬁrst two

layers have 64 units and a ReLU activation and the

last layer has 3 units and a linear activation function.

The three units represent the three actions left, right,

and forward in a one hot encoding. Winner takes all

is used to decide on the action.

Our Reward Prediction Network: is a 3-layer fully-

connected network with the same input as the pol-

icy network: the concatenated representation of the

agent’s current view and the goal observation. The

ﬁrst two layers have 256 units and a ReLU activation

but the last layer has 1 unit and a logistic activation.

The Deep RL Network: stacks the representation

network and the policy network on top of each other.

The representation network accepts the input and out-

puts the low-dimensional representation to the policy

network that outputs the action scores.

5.4 Training the Representation and

Predictor Networks

We collect a data set of 10 thousand transitions by

following a random policy in the two-room environ-

ment. For this data collection, each episode has a 50%

NCTA 2021 - 13th International Conference on Neural Computation Theory and Applications

272

chance to have the goal location in the bottom room

or on the left side of the top room (see the left and

middle pictures in Figure 3a). The reward predictor

and the representation are trained in this manner for

all experiments, including the lava gap and the four-

room environment. Thus, we use a representation and

reward predictor that have never seen lava. For the ex-

periments with smoothed rewards, the sparse reward

associated with the observations in the data set is aug-

mented by associating a new reward to the 64 states

leading to observations with a positive reward using

Equation 5 with a discount factor of 0.99. Ater the re-

ward has been (potentially) smoothed in this way, ob-

servations associated with a positive reward are over-

sampled 10 times to balance the data set, regardless

of whether the reward has been augmented or not.

6 RESULTS AND DISCUSSION

6.1 Two-room Environment

We start by visualizing the outputs of our reward pre-

dictor in the rooms, depending on the goal location, in

Figure 6. Each square indicates the average predicted

reward for transitioning to the corresponding tile.

The predicted reward spikes in a narrow region

around the two goal locations that were used to train

the raw reward predictor (Figure 6a), but the area of

states with high predicted rewards is wider around

the test goal. This difference is due to overﬁtting on

the speciﬁc training paths that were more frequently

taken toward the respective goals, but this does not

harm the generalization capabilities of the network.

The peakyness of the predictions disappears when the

predictor is trained on the smoothed rewards (Figure

6b). However, higher predicted rewards in the cor-

ner of the other room appear. Both scenarios, raw

and smoothed reward prediction, show promise for

the application of reward shaping under our training

scheme, as the agent beneﬁts from ﬁnding neighbor-

hoods with higher values of predicted reward until it

reaches the goal, instead of relying on a sparse reward

that is only given when the agent lands on the goal.

In Figure 7, we illustrate the variance of the mean

reward (left side) and the variance of the optimal per-

formance (right side) of the different methods, as a

function of the time steps taken for training. We aver-

age over 10 runs and in each run we perform 10 test

rollouts, so each point is the aggregate of 100 episodes

in total. The error bands indicate two standard devia-

tions. This methodology of generating the plots also

applies to Figure 9, Figure 10 and Figure 11.

(a) Raw reward prediction.

(b) Smoothed reward prediction.

Figure 6: Predicted Rewards, Two-room environment.

The predictor is trained on the setups shown on the left and

in the middle, and tested for the setup on the right.

The learning curves of ACKTR and PPO2 get

close to a mean reward of 1 the fastest using our rep-

resentations. There no signiﬁcant beneﬁt from us-

ing smoothed reward shaping for ACKTR, and the

raw reward shaping is in fact harmful in this case.

For PPO2, the agent using our representation that is

trained on raw reward predictions learns the fastest.

Regular deep RL is clearly outperformed by the vari-

ants that use reward-predictive representations. We

believe that this is because RL agents can generally

beneﬁt from the input being preprocessed, as the com-

putational overhead for learning the policy is reduced.

This effect is enhanced when the preprocessing is

good, which is the case for our representation: it ab-

stracts away unnecessary information as it trained to

output features that indicate the distance between the

agent and the goal, when the goal is in view.

The difference in the performance of a method on

the left hand side vs. the right hand side can be ex-

plained due to systematically different behaviors. For

example, an agent might be poor at searching for the

goal, giving it low average mean rewards, but it takes

the direct course to the goal when it sees it, giving it

a good average minimum episode length.

Reward Prediction for Representation Learning and Reward Shaping

273

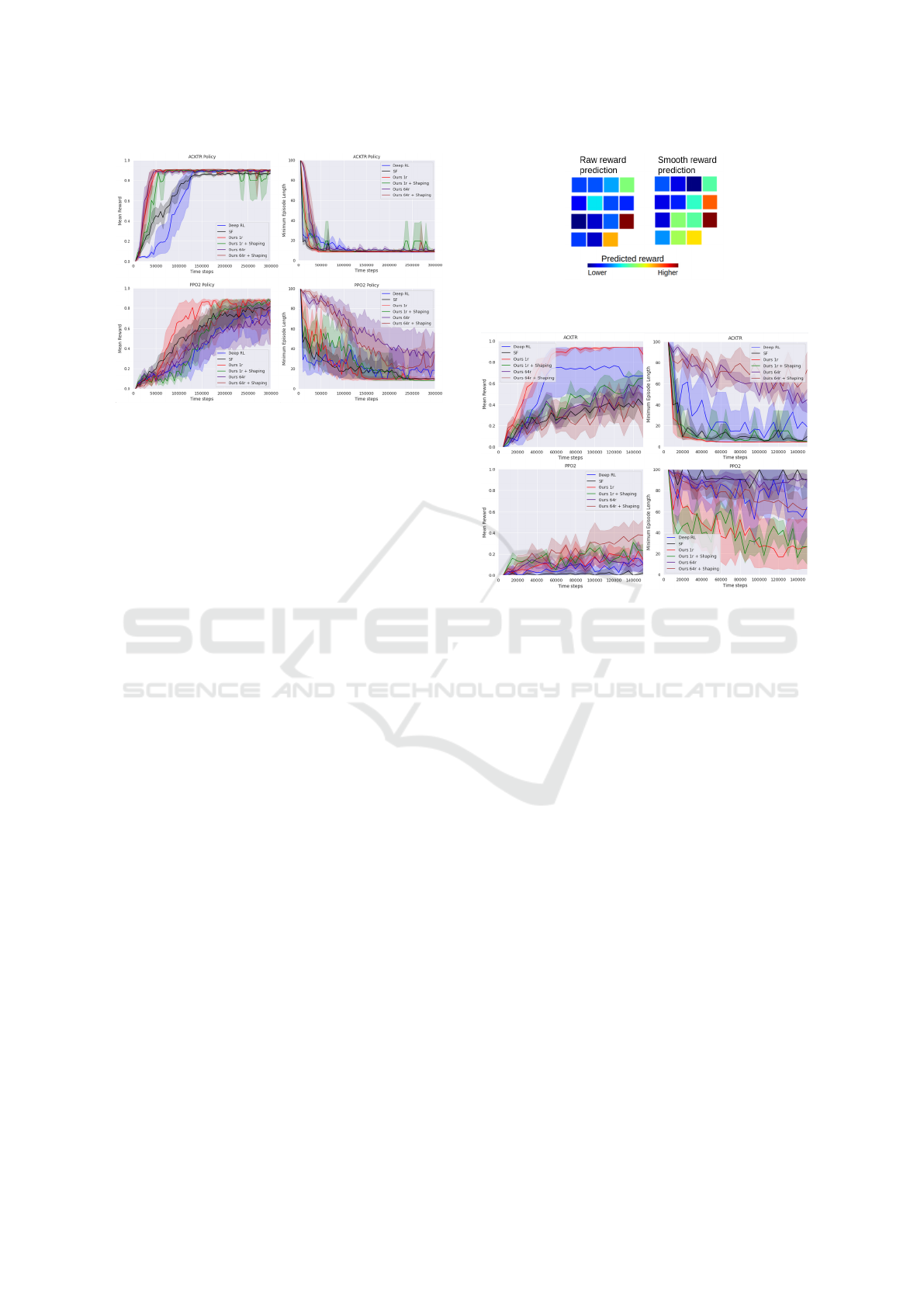
Figure 7: Two-room Environment. In these experiments,

there are only two rooms and the agent must reach a goal

that is always at the same location.

6.2 Lava Gap Environment

6.2.1 Learning from Scratch

The heatmaps of average predicted rewards are visu-

alized in Figure 8. The reward predictor was trained

on the two-room environment. The tiles closest to

the goal have the highest values, with a particularly

smooth gradient toward the goal for the smoothed-

reward predictor, which demonstrates that there is

potential gain from transfering the prediction-based

reward shaping between similar environments. The

learning performance of the different methods can be

seen in Figure 9. The decidedly fastest learning can

be observed when the actor-critic method is combined

with our representation, trained on raw reward predic-

tions and without reward shaping. Regular deep RL is

the second-best but with a very large variance on the

performance. Our reward shaping variations and the

SFs are very close in performance, albeit signiﬁcantly

worse than the other two. The poor performance of

reward shaping can be explained by the fact that there

are very few states, which makes the reward shap-

ing unnecessary in such a simple environment. All

the methods look more similar when PPO2 optimiza-

tion is applied, with respect to the mean rewards, but

our variant that is trained on smooth reward prediction

and uses reward shaping reaches the highest average

performance in the last iterations.

6.2.2 Transfer Learning

To investigate how the methods compare for adapting

to new environments, we trained the policies for 8000

steps on the two-room environment before learning

to solve the lava gap environment, see Figure 10. Our

Figure 8: Predicted Rewards, Lava Gap. Average pre-

dicted reward per state in the lava gap environment.

Figure 9: Lava Gap Experiment. All policies learn to

solve the lava gap environment from scratch.

method, without reward shaping, facilitates the fastest

learning for ACKTR in this case. Deep RL is the most

severely affected by this change, which is probably

due to the method learning a reward-maximizing rep-

resentation in one environment that does not transfer

well to another environment. Every PPO2 variation

looks bad for this scenario, but smooth-reward predic-

tion representation with reward shaping has the high-

est mean reward and our raw-reward prediction rep-

resentation has the lowest average minimum episode

length.

6.3 Four-room Environment

In our ﬁnal comparison, we add two additional rooms

to the two-room environment and randomize both the

goal location and the starting position of the agent,

with the results shown in Figure 11. Looking at the

minimum episode lengths, for the ACKTR learner,

our raw-reward prediction representation with reward

shaping performs best and the one without reward

shaping comes in second. There is little discernible

difference between the performance of SFs and Deep

RL, but they both perform signiﬁcantly worse than

our methods. The scale of the mean reward is a great

deal lower than in the previous experiments since the

NCTA 2021 - 13th International Conference on Neural Computation Theory and Applications

274

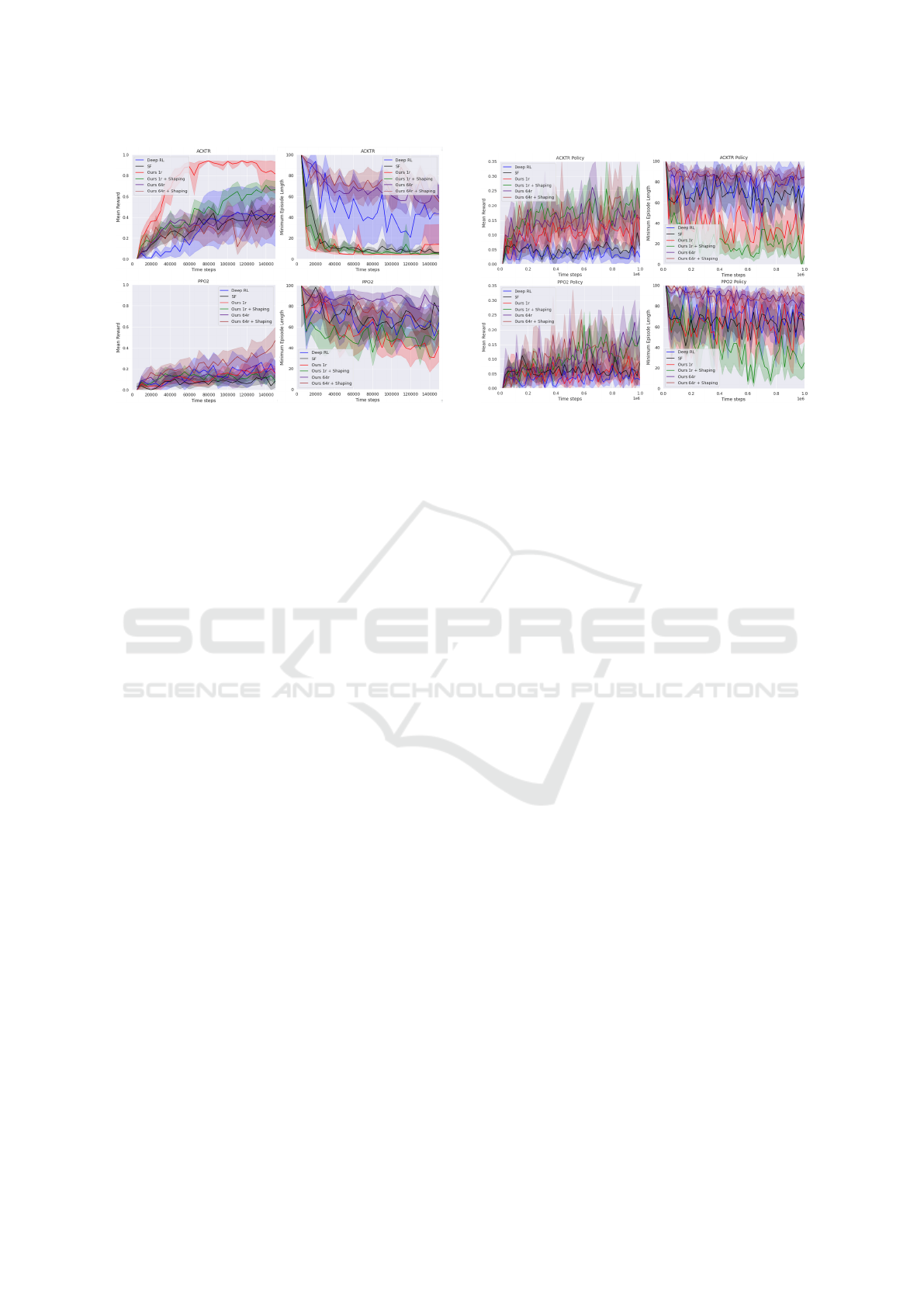
Figure 10: Re-learning Experiment The policies are

trained for 8 thousand training steps on the two-room envi-

ronment before being trained on the lava gap environment.

average distance between the starting tile of the agent

and the goal is much larger than in the previous two

environments.

For this scenario, all the methods look similarly

bad for the PPO2 policy, except for our raw-reward

representations, with reward shaping, which has the

lowest minimum episode length. The big advantage

of reward shaping in this environment compared to

the two-room environment can be explained by the in-

creased complexity, making the reward shaping more

helpful in guiding the agent’s search. In the previ-

ous experiments, the agent and goal locations start at

ﬁxed locations, allowing the agents to solve it by rote

memorization. The reward shaping function calcu-

lated by the raw-reward predictor fares signiﬁcantly

better in this situation. We hypothesize that this is

due to the smoothed-reward predictor distracting the

agent by pushing it to corners, as the visualization in

Figure 6b would suggest.

The reward shaping given by the raw-reward pre-

dictor is more discriminative, as we see in Figure 6a.

The agent receives a positive reward as soon as the

goal reaches its point of view, which is any location

up to 6 tiles in front of it and no further than 3 tiles

away from it to the left or to the right. This allows the

reward shaping function to guide the agent directly to

the goal, assuming that they are in the same room and

that there is no wall obstructing the agent’s ﬁeld of

vision.

7 CONCLUSION

Processing high-dimensional inputs for reinforcement

learning agents remains a difﬁcult problem, especially

if the agent must rely on a sparse reward signal to

Figure 11: Full Four-room Environment. The agent and

goal are placed at random locations at the start of each

episode.

guide its representation learning. In this work, we put

forward a method to help alleviate this problem with a

method of learning representations that preprocesses

visual input for reinforcement learning (RL) methods.

Our contributions are (i) a reward-predictive repre-

sentation that is trained simultaneously with a reward

predictor and (ii) a reward shaping technique using

this trained predictor. The predictor learns to approx-

imate either the raw reward signal or a smoothed ver-

sion of it and it is used for reward shaping by encour-

aging the agent to transition to states with higher pre-

dicted rewards.

We used a view of the goal as a second input for

the methods in our experiments, but this is in princi-

ple not necessary as moving toward the green tile as it

becomes visible is sufﬁcient. Removing the goal in-

put might encourage the agents to learn policies that

scan all the rooms faster until the goal reaches its ﬁeld

of vision.

We have shown the usefulness of our represen-

tation and our reward shaping scheme in a series of

gridworld experiments, where the agent receives a vi-

sual observation of its goal as input along with an

observation of its immediate surroundings. Prepro-

cessing the input using this representation speeds up

the training of two out-of-the-box RL methods, Ac-

tor Critic using Kronecker-Factored Trust Region and

Proximal Policy Optimization, compared to having

these methods learn the representations from scratch.

In our most complicated experiment, combining our

representation with our reward shaping technique is

shown to perform signiﬁcantly better than the vanilla

RL methods, which hints at its potential for success,

especially in more complex RL scenarios.

Reward Prediction for Representation Learning and Reward Shaping

275

ACKNOWLEDGEMENT

We would like to thank Moritz Lange for his valuable

contribution to the preparation of this paper.

REFERENCES

Amodei, D. and Clark, J. (2016). Faulty reward

functions in the wild. https://blog.openai.com/

faulty-reward-functions/,2016.

Barreto, A., Dabney, W., Munos, R., Hunt, J. J., Schaul,

T., Van Hasselt, H., and Silver, D. (2016). Successor

features for transfer in reinforcement learning. arXiv

preprint arXiv:1606.05312.

Berner, C., Brockman, G., Chan, B., Cheung, V., D˛ebiak,

P., Dennison, C., Farhi, D., Fischer, Q., Hashme,

S., Hesse, C., et al. (2019). Dota 2 with large

scale deep reinforcement learning. arXiv preprint

arXiv:1912.06680.

Brown, N. and Sandholm, T. (2019). Superhuman ai for

multiplayer poker. Science, 365(6456):885–890.

Brys, T., Harutyunyan, A., Vrancx, P., Taylor, M. E.,

Kudenko, D., and Nowé, A. (2014). Multi-

objectivization of reinforcement learning problems by

reward shaping. In 2014 international joint confer-

ence on neural networks (IJCNN), pages 2315–2322.

IEEE.

Chevalier-Boisvert, M., Willems, L., and Pal, S. (2018).

Minimalistic gridworld environment for openai gym.

https://github.com/maximecb/gym-minigrid.

Chollet, F. et al. (2015). Keras. https://keras.io.

Efthymiadis, K. and Kudenko, D. (2013). Using plan-based

reward shaping to learn strategies in starcraft: Brood-

war. In 2013 IEEE Conference on Computational In-

teligence in Games (CIG), pages 1–8. IEEE.

Hill, A., Rafﬁn, A., Ernestus, M., Gleave, A., Kanervisto,

A., Traore, R., Dhariwal, P., Hesse, C., Klimov, O.,

Nichol, A., Plappert, M., Radford, A., Schulman, J.,

Sidor, S., and Wu, Y. (2018). Stable baselines. https:

//github.com/hill-a/stable-baselines.

Hlynsson, H. D., Schüler, M., Schiewer, R., Glasmachers,

T., and Wiskott, L. (2020). Latent representation pre-

diction networks. arXiv preprint arXiv:2009.09439.

Hlynsson, H. D. and Wiskott, L. (2019). Learning gradient-

based ica by neurally estimating mutual information.

In Joint German/Austrian Conference on Artiﬁcial

Intelligence (Künstliche Intelligenz), pages 182–187.

Springer.

Hlynsson, H. D., Wiskott, L., et al. (2019). Measuring

the data efﬁciency of deep learning methods. arXiv

preprint arXiv:1907.02549.

Kaelbling, L. P. (1993). Learning to achieve goals. In IJCAI,

pages 1094–1099. Citeseer.

Lample, G. and Chaplot, D. S. (2017). Playing fps games

with deep reinforcement learning. Proceedings of the

AAAI Conference on Artiﬁcial Intelligence, 31(1).

Lehnert, L. and Littman, M. L. (2020). Successor features

combine elements of model-free and model-based re-

inforcement learning. Journal of Machine Learning

Research, 21(196):1–53.

Lehnert, L., Littman, M. L., and Frank, M. J. (2020).

Reward-predictive representations generalize across

tasks in reinforcement learning. PLoS computational

biology, 16(10):e1008317.

Marashi, M., Khalilian, A., and Shiri, M. E. (2012). Auto-

matic reward shaping in reinforcement learning using

graph analysis. In 2012 2nd International eConfer-

ence on Computer and Knowledge Engineering (IC-

CKE), pages 111–116. IEEE.

Mataric, M. J. (1994). Reward functions for accelerated

learning. In Machine learning proceedings 1994,

pages 181–189. Elsevier.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M.

(2013). Playing atari with deep reinforcement learn-

ing. arXiv preprint arXiv:1312.5602.

Ng, A. Y., Harada, D., and Russell, S. (1999). Policy invari-

ance under reward transformations: Theory and appli-

cation to reward shaping. In Icml, volume 99, pages

278–287.

Pathak, D., Mahmoudieh, P., Luo, G., Agrawal, P., Chen,

D., Shentu, Y., Shelhamer, E., Malik, J., Efros, A. A.,

and Darrell, T. (2018). Zero-shot visual imitation. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition Workshops, pages 2050–

2053.

Schaul, T., Horgan, D., Gregor, K., and Silver, D. (2015).

Universal value function approximators. In Interna-

tional conference on machine learning, pages 1312–

1320.

Schüler, M., Hlynsson, H. D., and Wiskott, L. (2018).

Gradient-based training of slow feature analysis by

differentiable approximate whitening. arXiv preprint

arXiv:1808.08833.

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and

Klimov, O. (2017). Proximal policy optimization al-

gorithms. arXiv preprint arXiv:1707.06347.

Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,

Van Den Driessche, G., Schrittwieser, J., Antonoglou,

I., Panneershelvam, V., Lanctot, M., et al. (2016).

Mastering the game of go with deep neural networks

and tree search. nature, 529(7587):484–489.

Sutton, R. S., Precup, D., and Singh, S. (1999). Between

mdps and semi-mdps: A framework for temporal ab-

straction in reinforcement learning. Artiﬁcial intelli-

gence, 112(1-2):181–211.

Wu, Y., Mansimov, E., Grosse, R. B., Liao, S., and Ba, J.

(2017). Scalable trust-region method for deep rein-

forcement learning using kronecker-factored approxi-

mation. In Advances in neural information processing

systems, pages 5279–5288.

Zou, H., Ren, T., Yan, D., Su, H., and Zhu, J. (2019).

Reward shaping via meta-learning. arXiv preprint

arXiv:1901.09330.

NCTA 2021 - 13th International Conference on Neural Computation Theory and Applications

276