Solving a Problem of the Lateral Dynamics Identification of a UAV
using a Hyper-heuristic for Non-stationary Optimization
Evgenii Sopov
a
Reshetnev Siberian State University of Science and Technology, Krasnoyarsk, Russia
Keywords: Hyper-heuristics, Evolutionary Algorithms, Non-stationary Optimization, Autoregressive Neural Networks,
Lateral Dynamics Identification.
Abstract: A control system of an Unmanned Aerial Vehicle (UAV) requires identification of the lateral and longitudinal
dynamics. While data on the longitudinal dynamics can be accessed via precise navigation devices, the lateral
dynamics is predicted using such control parameters as aileron, elevator, rudder, and throttle positions.
Autoregressive neural networks (ARNN) usually demonstrate high performance when modeling dynamic
systems. At the same time, the lateral dynamics identification problem is known as non-stationary because of
constantly changing operating conditions and errors in control equipment buses. Thus, an optimizer for ARNN
must be accurate enough and must adapt to the changes in the environment. In the study, we have proposed
an evolutionary hyper-heuristic for training ARNN in the non-stationary environment. The approach is based
on the combination of the algorithm portfolio and the population-level dynamic probabilities approach. The
hyper-heuristic selects and controls online the interaction of five evolutionary metaheuristics for dealing with
dynamic optimization problems. The experimental results have shown that the proposed approach
outperforms the standard back-propagation algorithm and all single metaheuristics.
1 INTRODUCTION
Fully automatic UAVs have many advantages, in
particular, reduced piloting costs, the ability to fly for
a longer time, faster response, and the ability to
control more external factors at the same time. When
developing autonomous UAVs, one must design a
control system, which would be sufficiently robust in
the changing operating conditions (changes in
direction and gusts of wind, changes in the density of
the air environment, etc.) and in errors in control
equipment buses (errors in measuring aerodynamic
parameters, errors of executive bodies, etc.). The
UAV control system must be able to identify the
parameters, which are used for the UAV control
(Handbook of Unmanned Aerial Vehicles, 2015).
Any UAV can be modeled as a non-linear
dynamic system. The system usually has 6 degrees of
freedom and can be decomposed into two
independent subsystems with 3 degrees of freedom
for representing the lateral and longitudinal dynamics
of the UAV (Chen & Billings, 1992). The
longitudinal dynamics is used for solving trajectory
a
https://orcid.org/0000-0003-4410-7996
motion and navigation problems. Nowadays, these
problems are efficiently solved by processing data
from precise navigation devices. The lateral dynamics
control is used for stabilizing the UAV on the flight
path. In this study, we will focus on the problem of
identifying the lateral dynamics parameters.
One of the efficient approaches for modeling
dynamic systems is autoregressive neural networks,
which have demonstrated high performance in
solving many real-world identification problems
(Bianchini et al., 2013. Billings, 2013). The problem
of training neural networks is an optimization
problem, which usually is solved by gradient
methods. At the same time, identification of the
lateral dynamics is performed in the changing
environment, thus, the optimization problem belongs
to the class of non-stationary optimization. An
optimization algorithm applied for training ARNN
must be able to adapt to the changes in the
environment.
In the field of evolutionary computation, there
exist approaches for dealing with non-stationary
problems. When solving real-world optimization
Sopov, E.
Solving a Problem of the Lateral Dynamics Identification of a UAV using a Hyper-heuristic for Non-stationary Optimization.
DOI: 10.5220/0010643100003063
In Proceedings of the 13th International Joint Conference on Computational Intelligence (IJCCI 2021), pages 107-114
ISBN: 978-989-758-534-0; ISSN: 2184-2825
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
107

problems, usually we have no a priori information on
types of changes and moments when changes appear.
Therefore, it is hard to select and tune an appropriate
evolutionary algorithm (EA) for solving a particular
problem.
In the study, we have proposed an evolutionary
hyper-heuristic for training ARNN in the non-
stationary environment. A hyper-heuristic is a
metaheuristic for constructing, selecting, and
operating low-level heuristics and metaheuristics.
The proposed approach is based on the combination
of the algorithm portfolio applied in the field of
machine learning and the population-level dynamic
probabilities approach applied in evolutionary
computation. The proposed hyper-heuristic selects
and controls online the interaction of five
evolutionary metaheuristics for dynamic optimization
problems. Every single metaheuristic has advantages
within a certain type of changes in the environment.
The proposed approach has been applied for
solving a real-world problem of identifying the lateral
dynamics of a fixed-wing UAV with remote control.
We have compared the performance of the proposed
approach with the standard back-propagation
algorithm and all single metaheuristics.
The rest of the paper is organized as follows.
Section 2 describes related work. Section 3 describes
the proposed approach and experimental setups. In
Section 4, the experimental results are presented and
discussed. In the conclusion, the results and further
research are discussed.
2 RELATED WORK
2.1 Artificial Neural Networks for
Identification of UAV Parameters
The target parameters for solving the identification of
the lateral dynamics problem are pitch, roll, and yaw
angles. The angles correspond to three Euler angles
and determine the UAV's orientation in the normal
coordinate system (Figure 1). Pitch angle (𝜃) is the
angle between the longitudinal axis of UAV and the
horizontal plane. Roll angle (𝛾) is the angle of
rotation of UAV around the longitudinal axis. And
yaw angle (𝜓) is the angle of rotation of UAV in the
horizontal plane relative to the vertical axis.
The target parameters depend on the following
values of control parameters: positions of aileron
(∆𝑎), elevator (∆𝑒), rudder (∆𝑟), and throttle control
lever (∆𝑡ℎ). Since UAV is a dynamic system, the
current values of the target parameters also depend on
the values in the past moments (Handbook of
Unmanned Aerial Vehicles, 2015. Puttige &
Anavatti, 2007).
Figure 1: Angles of pitch, roll, and yaw.
There exist various approaches for the
identification of UAV parameters. One of the popular
tools for identifying parameters is artificial neural
networks (NNs). The advantage of NNs is their
simple hardware implementation. NN training for the
identification of parameters can be done offline after
collecting data about the UAV operation or online
during the flight. Online training allows the model to
be adapted to changes in operating conditions during
the flight, but usually, the identification accuracy is
lower, because less training data is used for training
(Bianchini et al., 2013. Billings, 2013. Puttige &
Anavatti, 2007. Omkar et al., 2015).
In this study, we will use a recurrent NN, namely
nonlinear autoregressive with exogenous inputs
model (NARX), which has proved its effectiveness in
solving hard dynamic modeling and control problems
(Billings, 2013).
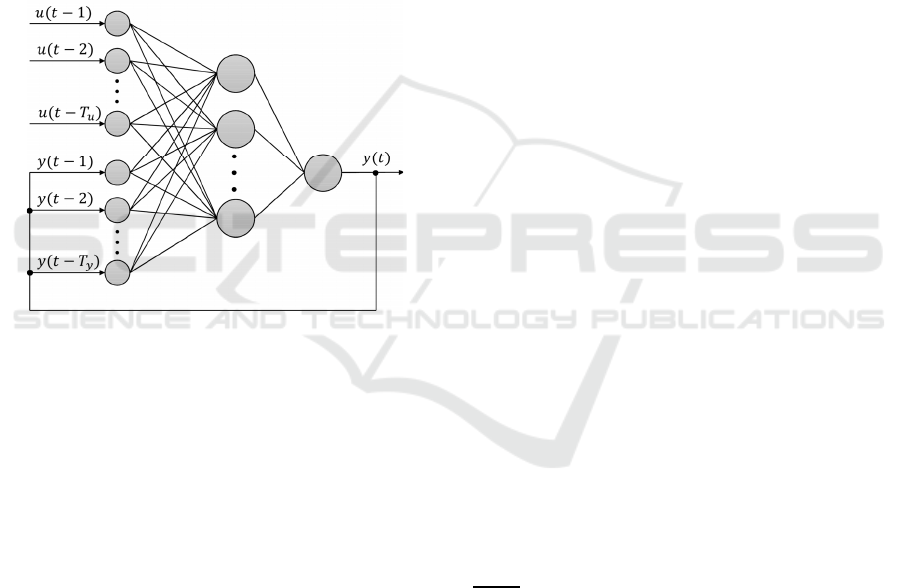
We denote the target parameters as (1) and the
controlled parameters as (2):
𝑦(𝑡) = (𝜃(𝑡),𝛾(𝑡),𝜓(𝑡)),
(1)
𝑢(𝑡) = (∆𝑎(𝑡),∆𝑒(𝑡),∆𝑟(𝑡),∆𝑡ℎ(𝑡)).
(2)
Then the autoregressive model can be represented in
the form of the dependence (3), which must be
identified using a NN (Figure 2):
𝑦
(
𝑡
)
=
𝑓

(
𝑢
(
𝑡−1
)
,…,𝑢
(
𝑡−𝑇

)
,
𝑦
(
𝑡−1
)
,…,𝑦(𝑡−𝑇

),
(3)
here 𝑇

and 𝑇

are the numbers of 𝑢 and 𝑦 values
from the previous time instances (the lag).
2.2 Evolutionary Non-stationary
Optimization and Hyper-heuristics
Optimization problems that change over time are
called dynamic optimization problems (DOP) or
ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications
108

time-dependent problems (also called non-stationary
optimization or optimization in changing (non-
stationary or dynamic) environment) (Yang, 2013.
Branke, 2002).
In non-stationary problems, the value and position
of the global optimum can change over time, thus an
optimization algorithm must be able to track changes
and adapt to a new environment. The performance
criteria of the algorithm are the accuracy and speed of
adaptation to changes. Traditional “blind-search”
approaches, including EA, do not have the necessary
properties for performing adaptation to changes in the
environment and they tend to converge to the best-
found solution, losing information about the search
space accumulated at the previous stages of the
search.
Figure 2: ARNN architecture.
Many heuristics for non-stationary optimization
have been proposed: restarting the search procedure,
local search to adapt to changes, memory
mechanisms, mechanisms for maintaining diversity,
multi-population approaches, adaptation and self-
adaptation, algorithms with overlapping generations,
etc. At the same time, there exist many different types
of changes in the environment, which can
demonstrate different features, speeds, and strength
of changes. Each of the heuristics mentioned above
performs well with some types of changes and fails
with others (Nguyen et al., 2012). Unfortunately,
many real-world DOPs have unpredictable changes
(Yang, 2013).
A hyper-heuristic is a meta-approach, which
creates, selects, or combines different basic
operations, basic heuristics, or combinations of
heuristics for solving a given problem or for
increasing the performance of solving the problem.
One of the applications of hyper-heuristic is the
automated design and self-adaptation of EAs (Burke
et al., 2013). A classification of hyper-heuristics is
proposed in (Burke et al., 2018). Based on the
classification, we need to design an online selective
hyper-heuristic for solving non-stationary
optimization problems using a predefined set of
heuristics.
3 PROPOSED APPROACH AND
EXPERIMENTAL SETUPS
3.1 Online Selective Hyper-heuristic
for Non-stationary Optimization
In the field of machine learning, there is a well-known
approach called the algorithm portfolio, which was
originally proposed for the selection of strategies in
financial markets, and now is used to select
algorithms for solving computationally complex
problems (Baudiš & Pošík, 2014). The main idea of
the portfolio of algorithms method is to assess the
performance of algorithms depending on the input
data of the problem being solved. The user of the
method must define the performance criterion and the
selection strategy. The choice of the algorithm can be
done once (offline) or using a schedule in the process
of solving the problem based on the current situation
(online). In this work, we will use a modified offline
error (Nguyen et al., 2012):
The strategy for choosing a heuristic must provide
an effective solution to the problem. For preventing
the greedy (local) behavior of the hyper-heuristic, we
will use a probabilistic choice. The probabilities of
choosing a specific heuristic should adapt when
changes in the environment appear. The probabilities
of less effective heuristics should be decreased in
favor of more efficient ones. A similar approach in
EAs is called the Population-Level Dynamic
Probabilities (PDP) adaptation method (Niehaus &
Banzhaf, 2001).
We denote the set of heuristics as 𝐻=

ℎ


(𝑖 =
1,
|
𝐻
|
. The set 𝐻 contains the following heuristics
used in the field of non-stationary optimization:
restarting, local adaptation to changes, implemented
as a variable local search (VLS) (Vavak et al., 1998),
an explicit memory mechanism (Branke, 1999), a
mechanism for maintaining diversity based on the
niche method (Ursem, 2000), and self-tuning EA with
controlled mutation (Grefenstette, 1999).
In the study, the probabilities of choosing
heuristics are not specified explicitly but are
presented by the distribution of the number of
evaluations of the fitness function by each of the
Solving a Problem of the Lateral Dynamics Identification of a UAV using a Hyper-heuristic for Non-stationary Optimization
109

heuristics. To do this, the whole population of size
𝑃𝑜𝑝𝑆𝑖𝑧𝑒 is divided into subpopulations of
size 𝑠𝑢𝑏𝑃𝑜𝑝

,𝑖=1,
|
𝐻
|
, where 𝑃𝑜𝑝𝑆𝑖𝑧𝑒 =
∑
𝑠𝑢𝑏𝑃𝑜𝑝

|

|

.
The size of a subpopulation is defined by
evaluating the vectors of the parameters of global and
local adaptation.
The vector of global adaptation parameters 𝑣

(9) is used to estimate the probability of occurrence
of changes of a particular type. The probabilities of
using heuristics that have shown higher performance
in the previous cycles should increase. The re-
evaluation of 𝑣

is based on the PDP model.
The vector of local adaptation parameters 𝑣

(10) ranks heuristics in the local adaptation cycle until
the next changes in the environment.
The pool of redistributed resources is formed by
subtracting random individuals from each
subpopulation ∆

. The value of ∆

is a
parameter of the hyper-heuristic. Condition (4) must
be satisfied for ensuring that even the least effective
heuristic is involved in finding a solution.
∆

:
𝑠𝑢𝑏𝑃𝑜𝑝

−∆


≥𝑠𝑢𝑏𝑃𝑜𝑝

,𝑖=1,|𝐻|







,
(4)
here ∆

is a parameter for the distribution of
sizes of subpopulations 𝑠𝑢𝑏𝑃𝑜𝑝

,𝑖=
1,|𝐻|







, 𝑠𝑢𝑏𝑃𝑜𝑝

is the minimal size of a
subpopulation.
The performance of heuristics in one local cycle
is estimated using a modified offline error (5), which
is minimized.
𝑚𝑂𝐸

(
ℎ

)
=
=



∑
𝑓
(𝑥

(ℎ

),𝑡)



,
(5)
here 𝑚𝑂𝐸

is the performance of ℎ

, 𝑇

is the
number of generations between two changes in the
environments, 𝑐 is the counter for local cycles
( 𝑐 = 1,2,… ), 𝑓 is the fitness function value for
the best-found individual 𝑥

(ℎ

) by ℎ

at the
moment 𝑡.
To calculate the parameters of global 𝑣

(𝑡,𝑐)
and local 𝑣

(𝑡) adaptations, heuristics are ranked
by the values 𝑚𝑂𝐸

and by 𝑓(𝑥

(ℎ

),𝑡),
respectively:
𝑟𝑎𝑛𝑘


≤𝑟𝑎𝑛𝑘


,
if 𝑚𝑂𝐸

(
ℎ

)
≤𝑚𝑂𝐸

ℎ

,
(6)
𝑟𝑎𝑛𝑘


≤𝑟𝑎𝑛𝑘


,
if
𝑓
(𝑥

(ℎ

),𝑡) ≤
𝑓
(𝑥

(ℎ

),𝑡),
(7)
here 𝑟𝑎𝑛𝑘


,𝑟𝑎𝑛𝑘


∈
[
1,
|
𝐻
|
]
,𝑖=1,
|
𝐻
|







.
At the initialization stage, the global adaptation
parameter and the distribution of the sizes of
subpopulations are filled with equal values (8) and
(11). At the next local adaptation cycle, the global
parameter is recalculated as a linear combination of
the previous and new values, where the new value is
calculated using the distribution proportional to the
global adaptation ranks (9).
𝑣


(
0,0
)
=

|

|
,𝑖=1,
|
𝐻
|







,
(8)
𝑣


(
𝑡,𝑐 +1
)
=
(
1−η
)
∙𝑣


(
𝑡,𝑐
)
+
+η ∙
∙

|

|





|

|
∙
(|

|

)
,
(9)
𝑣


(
𝑡
)
=𝑟𝑎𝑛𝑘


,
(10)
here η∈[0,1] is the global learning rate (default
value is η=0.5).
When calculating new values of the sizes of
subpopulations, ∆

of random individuals is
subtracted from each subpopulation. The whole pool
of individuals is distributed taking into account the
value of the local adaptation parameters for
encouraging effective heuristics within the current
state of the environment and taking into account the
value of the global parameters for encouraging
heuristics to predict new changes in the environment
(12).
𝑠𝑢𝑏𝑃𝑜𝑝

(
0
)
=

|

|
,
(11)
𝑠𝑢𝑏𝑃𝑜𝑝

(
𝑡+1
)
=
𝑠𝑢𝑏𝑃𝑜𝑝

(
𝑡
)
−∆

+
∆

∙
|

|

×
×
∙(
|

|



(

)
)
|

|
∙
(|

|

)
+𝑣


(
𝑡
)
 .
(12)
After determining the new sizes of subpopulations,
we redistribute individuals using random migrations.
The traditional “the best replaces the worst” approach
is less effective because leads to premature
convergence and the loss of population diversity.
Control of changes in the environment in the
proposed approach is performed by recalculating the
fitness of the current best-found solution.
The proposed hyper-heuristic is presented below
using a pseudo-code:
Input: a set of basic heuristics H, a
detector for changes in the environment,
the performance criterion for selecting
heuristics (5).
Initialization: the whole population is
divided into |H| subpopulations of equal
ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications
110

size, each heuristic is assigned to its
subpopulation.
Do while the problem is solving (a cycle
of global adaptation):
Re-evaluate the global adaptation
parameters vector (6)-(12).
Do while the changes in the
environment are not detected:
Re-distribute sizes of subpopulations
according to parameters of the global
and local adaptation vectors.
Do for the predefined number of
generations (a cycle of local
adaptation):
Solve the optimization problem
by evolving all subpopulations
using their assigned heuristics.
If the changes are detected,
then stop the local adaptation
cycle.
Re-evaluate the local adaptation
parameters vector ().
Output: a set of the best-found
solutions from all generations.
3.2 The Lateral Dynamics
Identification Problem
The problem of identifying the parameters of lateral
motion dynamics in real-time was solved for a UAV
developed at the University of New South Wales in
Australia (Puttige & Anavatti, 2007. Isaacs et al.,
2008). The UAV is a compact aircraft with a fixed
wing (high-wing). The UAV equipment includes
onboard equipment and a ground control station for
remote control. Parameter identification data
provided by the School of Engineering and
Information Technology (University of New South
Wales, Canberra, Australia).
Training data are represented by 6 datasets
obtained for different operating conditions of the
UAV. All values of the measured parameters were
recorded with a frequency of 0.02 sec. The datasets
volumes (the number of records) are 17981, 11532,
6774, 20112, 8681, and 15756.
Because of the limitations of the UAV onboard
equipment, the following settings of NN are used: the
number of neurons in the hidden layer is up to 10 (in
(Puttige & Anavatti, 2007) only 4 neurons are used),
the maximum number of training epochs is 15, the
size of the subsample (mini-batch) for training up to
25 examples. In this study, we will use similar
parameter requirements to compare the results with
the previously obtained results. We have defined the
following effective setting of NN hyper-parameters
using the grid search: the number of neurons in the
hidden layer is 5, the size of the subsample is 25,
𝑇

=𝑇

=7 . Settings for the hyper-heuristic
approach are presented in Table 1.
Table 1: Settings for hyper-heuristic.
Paramete
r
Value
Population size, 𝑃𝑜𝑝𝑆𝑖𝑧𝑒
100
The number of subpopulations,
|
𝐻
|
5
The minimum size of a subpopulation,
𝑠𝑢𝑏𝑃𝑜𝑝

5
The dimensionality of the optimization problem 93
Chromosome encoding accuracy in genetic
algorithm
1.0E-2
The number of independent runs 40
The archive size for the explicit memory
algorithm
5
The niche size for the diversity maintenance
mechanism
0.025
We use the root mean square error (RMSE) for
each target parameter as a performance measure. The
results obtained by the proposed approach are
compared with the results obtained by the
conventional backpropagation method, by EAs using
one of the basic heuristics of non-stationary
optimization, by an estimation of a random choice of
one of the basic heuristics, and with the results
obtained earlier by UAV developers.
4 EXPERIMENTAL RESULTS
AND DISCUSSION
The software implementation of algorithms for our
experiments was performed in Python 3.7 using the
Keras package for NNs.
The results of solving the problem averaged over
all datasets are shown in Table 2. The box-plot
diagrams obtained from independent runs are shown
in Figure 3.
An example of the NN operations on an interval
of 500 values (10 sec) is shown in Figure 4.
Figure 5 shows the results of ranking the
approaches averaged over all runs and target angles
(the lower the better). Table 3 shows the results of
testing the hypothesis about a statistically significant
difference in the results of the experiments (Mann-
Whitney-Wilcoxon test, MWW).
As can be seen from the results of experiments,
EAs for non-stationary optimization significantly
outperform the traditional method for training NN
using the backpropagation of the error. The heuristic
for restarting the search procedure has the largest
variance of results, which may indicate that changes
in the environment are not very intense and may be
cyclic.
Solving a Problem of the Lateral Dynamics Identification of a UAV using a Hyper-heuristic for Non-stationary Optimization
111

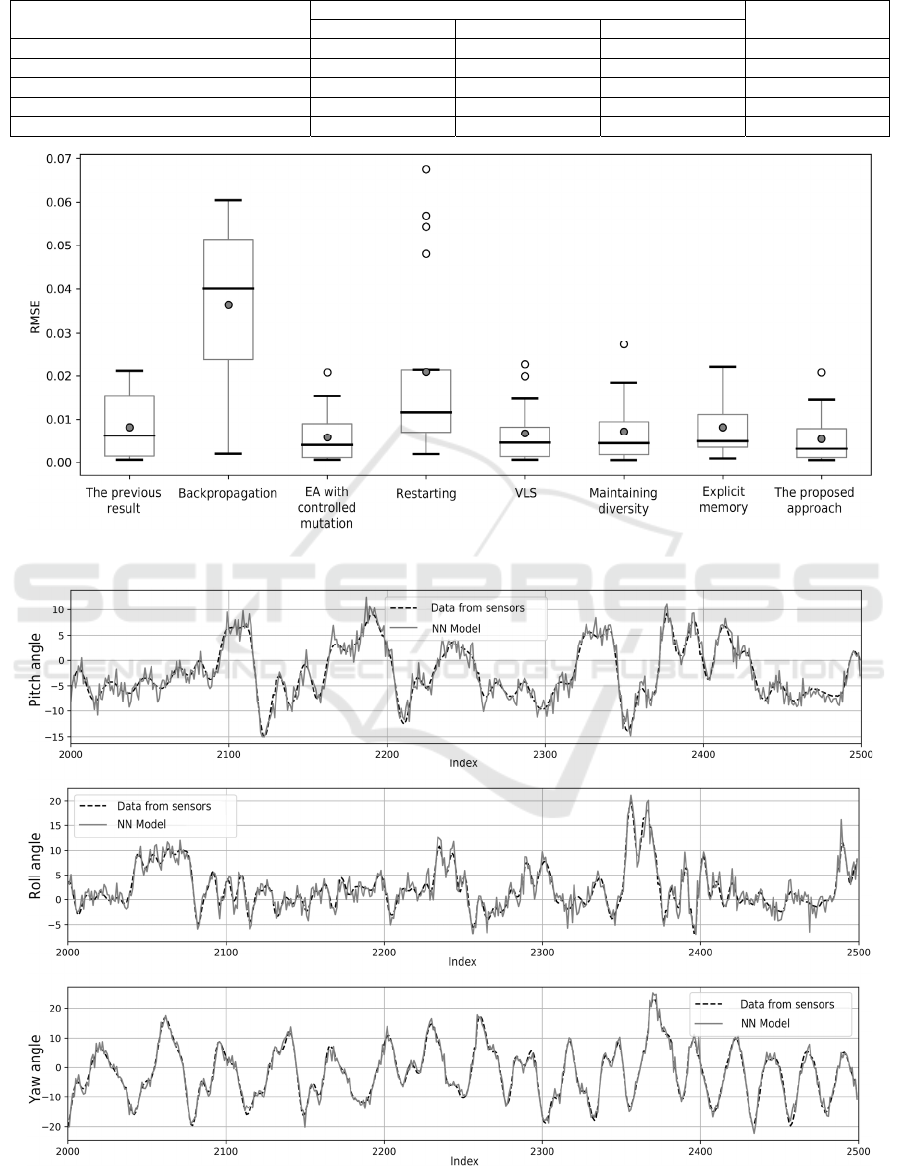
Table 2: The results of the UAV Lateral Dynamics Identification Problem Solving (RMSE).
Approach
Angles, degrees
Mean
Roll Pitch Yaw
The p
r
evious resul
t
0.0068 0.0167 0.0010 0.0082
Backpropagation 0.0102 0.0534 0.0316 0.0318
The best single heuristic 0.0041 0.0123 0.0009 0.0058
Average for basic heuristics 0.0084 0.0184 0.0022 0.0097
Hype
r
-heuristic 0.0048 0.0108 0.0008 0.0054
Figure 3: Box-plots for the results.
Figure 4: An example of the model-based prediction for 10 seconds using dataset 1.
ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications
112

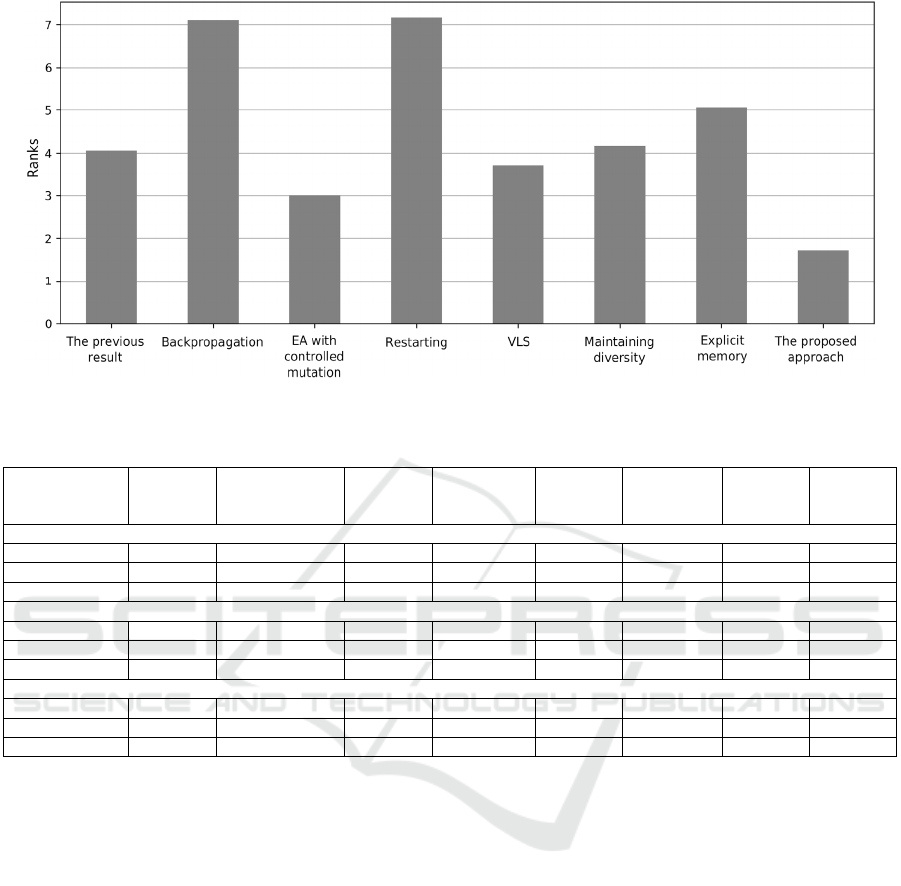
Figure 5: The ranking of the approaches.
Table 3: The results of the MWW test.
The proposed
approach is
The
previous
resul
t
NN with the
backpropagation
algorithm
EA with
controlled
mutation
Restarting
optimization
VLS
Maintaining
diversity
Explicit
memory
Sum
Roll angle
b
ette
r
4 3 36655 32
equal 1 0 2 0 0 1 1 5
worse 1 3 1 0 0 0 0 5
Pitch angle
b
ette
r
4 6 46354 32
equal 1 0 1 0 3 1 2 8
worse 1 0 1 0 0 0 0 2
Yaw angle
b
ette
r
4 6 36455 33
equal 0 0 3 0 2 1 1 7
worse 2 0 0 0 0 0 0 2
For the roll angle, the best results, averaged over
all data sets, were obtained by the EA with controlled
mutation. For pitch and yaw angles, the proposed
approach outperforms the best results obtained with a
single heuristic. The results obtained using the
proposed approach also outperform the results
previously obtained by UAV developers.
As we can see, the proposed approach
outperforms the performance of randomly selecting
one of the heuristics for all target parameters,
estimated as the performance averaged over all single
heuristics. That means if we have no a priori
information on the problem and cannot select an
appropriate heuristic, training NN using the proposed
hyper-heuristic is more preferable.
5 CONCLUSIONS
Non-stationary optimization is a challenging task for
many optimization techniques. EAs propose many
different heuristics for dealing with DOPs, but in real-
world problems, the choice of an appropriate
algorithm is not obvious and difficult. The hyper-
heuristic conception proposed to design a high-level
meta-approach for operating many low-level
heuristics or algorithms that make it possible to
automatically build the problem-specific approach
online.
In the study, we have proposed a new hyper-
heuristic for solving DOPs based on the combination
of the algorithm portfolio and the population-level
dynamic probabilities approach. The hyper-heuristic
has been applied for solving the hard non-stationary
real-world problem of identifying the lateral
dynamics of a UAV using ARNN. The experimental
results have shown that the proposed approach
outperforms the standard backpropagation algorithm,
which is not able to adapt to changes in the
environment. The proposed hyper-heuristic also
Solving a Problem of the Lateral Dynamics Identification of a UAV using a Hyper-heuristic for Non-stationary Optimization
113

outperforms single non-stationary heuristics, because
it can select an effective combination of heuristics for
an arbitrary situation in the environment.
In our further work, we will investigate the
proposed approach with different sets of heuristics
and will attempt to introduce better feedback in the
adaptation process.
ACKNOWLEDGEMENTS
The reported study was funded by RFBR and FWF
according to the research project №21-51-14003.
REFERENCES
Handbook of Unmanned Aerial Vehicles (2015). Editors K.
Valavanis, George J. Vachtsevanos. Springer
Science+Business Media Dordrecht. 3022 p.
Chen, S., Billings, S.A. (1992). Neural networks for
nonlinear dynamic system modeling and identification.
Int. J. Contr., vol. 56, no. 2. pp. 319–346.
Bianchini, M., Maggini, M., Jain, L.C. (2013). Handbook
on Neural Information Processing. Intelligent Systems
Reference Library, vol. 49. Springer-Verlag Berlin
Heidelberg. 538 p.
Billings, S.A. (2013). Nonlinear System Identification:
NARMAX Methods in the Time, Frequency, and Spatio-
Temporal Domains. John Wiley & Sons. 596 p.
Puttige, V.R., Anavatti, S.G. (2007). Comparison of Real-
time Online and Offline Neural Network Models for a
UAV. 2007 International Joint Conference on Neural
Networks, Orlando, FL. pp. 412-417.
Omkar, S.N., Mudigere, D., Senthilnath, J. Vijaya Kumar,
M. (2015). Identification of Helicopter Dynamics based
on Flight Data using Nature Inspired Techniques. Int. J.
Appl. Metaheuristic Comput. 6, 3. pp. 38-52.
Yang, Sh. (2013). Evolutionary Computation for Dynamic
Optimization Problems. The Genetic and Evolutionary
Computation Conference, GECCO 2013. 63 p.
Branke, J. (2002) Evolutionary Optimization in Dynamic
Environments. Genetic Algorithms and Evolutionary
Computation, vol. 3, Springer. 208 p.
Nguyen, T.T., Yang, S., Branke, J. (2012). Evolutionary
dynamic optimization: A survey of the state of the art.
Swarm and Evolutionary Computation. № 6. pp. 1–24.
Burke, E.K., et al. (2013) Hyper-heuristics: A Survey of the
State of the Art. Journal of the Operational Research
Society, Volume 64, Issue 12. pp. 1695–1724.
Burke, E.K., Hyde, M.R., Kendall, G., Ochoa, G., Özcan,
E., Woodward, J.R. (2018). A Classification of Hyper-
Heuristic Approaches: Revisited. International Series
in Operations Research & Management Science. pp.
453–477.
Baudiš, P., Pošík, P. (2014). Online Black-Box Algorithm
Portfolios for Continuous Optimization. In: Bartz-
Beielstein T., Branke J., Filipič B., Smith J. (eds)
Parallel Problem Solving from Nature – PPSN XIII.
PPSN 2014. Lecture Notes in Computer Science, vol
8672. pp. 40-49.
Niehaus, J., Banzhaf, W. (2001). Adaption of Operator
Probabilities in Genetic Programming. In: Miller J.,
Tomassini M., Lanzi P.L., Ryan C., Tettamanzi A.G.B.,
Langdon W.B. (eds) Genetic Programming. EuroGP
2001. Lecture Notes in Computer Science, vol 2038. pp.
325-336.
Vavak, F., Jukes, K. A., Fogarty, T. C. (1998). Performance
of a genetic algorithm with variable local search range
relative to frequency of the environmental changes. In
Proc. of the Third Int. Conf. on Genetic Programming.
San Mateo, CA: Morgan Kaufmann. pp. 602–608.
Branke, J. (1999). Memory enhanced evolutionary
algorithms for changing optimization problems. In
Proceedings of the IEEE Congress on evolutionary
computation, vol 3.
pp. 1875-1882.
Ursem, R.K. (2000). Multinational GAs: multimodal
optimization techniques in dynamic environments. In
Proceedings of the genetic and evolutionary
computation conference. Morgan Kaufmann,
Massachusetts.
Grefenstette, J. J. (1999). Evolvability in dynamic fitness
landscapes: A genetic algorithm approach. In IEEE
Congress on Evolutionary Computation.
Isaacs, Puttige, V., Ray, T., Smith, W., Anavatti, S. (2008).
Development of a memetic algorithm for Dynamic
Multi-Objective Optimization and its applications for
online neural network modeling of UAVs. 2008 IEEE
International Joint Conference on Neural Networks
(IEEE World Congress on Computational Intelligence),
Hong Kong. pp. 548-554.
ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications
114