Continuous Parameter Control in Genetic Algorithms using Policy

Gradient Reinforcement Learning

Alejandro de Miguel Gomez

1 a

and Farshad Ghassemi Toosi

2 b

Just Eat Takeaway.com, Madrid, Spain

Department of Computer Science, Munster Technological University, Cork, Ireland

Keywords:

Reinforcement Learning, Genetic Algorithms.

Abstract:

Genetic Algorithms are biological-inspired optimization techniques that are able to solve complex problems by

evolving candidate solutions in the search space. Their evolutionary features rely on parameterized stochastic

operators that are sensitive to changes and, ultimately, determine the performance of the algorithms. In recent

years, Reinforcement Learning has been proposed for online parameter control in contrast to traditional ﬁne-

tuning, which inevitably leads to suboptimal conﬁgurations found through extensive trial-and-error. In this

regard, the current literature has focused on value-based Reinforcement Learning controllers for Genetic Al-

gorithms without exploring the advantages of policy gradient methods in such environments. In this study, we

propose a novel approach to leverage the continuous nature of the latter with agents that learn a behavior pol-

icy and enhance the performance of Genetic Algorithms by tuning their operators dynamically at runtime. In

particular, we look at Deep Deterministic Policy Gradient (DDPG) and Proximal Policy Optimization (PPO).

The resulting hybrid algorithms are tested on benchmark combinatorial problems and performance metrics are

discussed in great detail considering the existing work based on Q-Learning and SARSA.

1 INTRODUCTION

Since the late 1990s, parameter calibration in Evo-

lutionary Algorithms has gained increasing attention

from researchers for a key reason (Eiben et al., 1999)

- the optimal performance of any metaheuristic opti-

mization technique is highly dependent on parameter

settings. Over the years, the literature has converged

to a concrete classiﬁcation of strategies (Karafotias

et al., 2014b) that can be pursued in order to accom-

plish this part of the development work: i) Parameter

tuning consist in setting parameters and operators be-

fore running an algorithm and keep them frozen dur-

ing the run. Alternatively, ii) parameter control is

aimed at updating the parameters and operators dy-

namically at runtime according to the current state of

the search.

Parameter tuning in Evolutionary Algorithms still

remains the typical approach for most applications.

However, it is time consuming and requires exten-

sive trial-and-error experimentation. Additionally,

the parameter performance landscape is not static,

https://orcid.org/0000-0002-5327-6436

https://orcid.org/0000-0002-1105-4819

thus a given set of parameters may not be appro-

priate for all the stages of the search process. This

has been empirically shown in several studies (Eiben

et al., 1999), (Karafotias et al., 2014b) and (Aleti and

Moser, 2016). On the other hand, parameter con-

trol methodologies use deterministic rules and adap-

tive feedback mechanisms for adjusting the param-

eters during the optimization. These techniques are

prone to take short-sighted decisions as they are built

on top of immediate estimations of the results ob-

tained (Sakurai et al., 2010). Moreover, they represent

very speciﬁc models applied to concrete parameters

that are hard to ﬁt into the broader ﬁeld.

Over the last decade, a number of surveys around

this area (Karafotias et al., 2014b) highlighted the

lack of effective general-purpose strategies for cali-

brating Evolutionary Algorithms. Nevertheless, it is

becoming clear that the answer could be found in

automated systems capable of understanding the op-

timization’s evolutionary dynamics and guiding the

search accordingly. In this regard, Reinforcement

Learning techniques have been proposed as an univer-

sal alternative to the existing parameter control mech-

anisms (Drugan, 2019). The design of these algo-

de Miguel Gomez, A. and Toosi, F.

Continuous Parameter Control in Genetic Algorithms using Policy Gradient Reinforcement Learning.

DOI: 10.5220/0010643500003063

In Proceedings of the 13th International Joint Conference on Computational Intelligence (IJCCI 2021), pages 115-122

ISBN: 978-989-758-534-0; ISSN: 2184-2825

115

rithms allow them to learn a decision policy by maxi-

mizing the expected value of a reward function in the

long-run. This makes them appropriate controllers for

overseeing the internals of Evolutionary Algorithms

and focus on the success of a dynamic optimization

process by taking optimal decisions at each time step.

In this paper, we are going to assess the per-

formance of a novel approach for continuous pa-

rameter control in Genetic Algorithms using two

widely-known policy gradient Reinforcement Learn-

ing methods in the context of combinatorial optimiza-

tion problems. In particular, we are going to answer

the following research questions:

• RQ1: Do DDPG and PPO policy gradient

methods outperform the existing Q-Learning and

SARSA value-based controllers?

• RQ2: How does the learning overhead of DDPG

and PPO policy gradient algorithms compare

to value-based methods with Q-Learning and

SARSA?

• RQ3: What is the performance gain from using

policy gradient continuous parameter control as

opposed to ofﬂine parameter tuning?

• RQ4: Can DDPG and PPO policy gradient con-

trollers generalize to larger instances of the same

optimization problem?

2 DESIGN AND

IMPLEMENTATION

The main components of Reinforcement Learning

problems with respect to the task of parameter con-

trol are:

• Agent: A Reinforcement Learning algorithm.

• Environment: A genetic algorithm for solving an

optimization problem.

• State: The set of features that describe the status

of the optimization at a particular time step.

• Action: The probability of crossover and muta-

tion applied in the environment at a particular time

step.

• Reward: A function that provides feedback to the

agent based on the effect of its actions on the en-

vironment.

In this study, the implementation of the agents fol-

lows the original design proposed by the authors of

DDPG (Lillicrap et al., 2015), PPO (Schulman et al.,

2017), Q-Learning (Dayan and Watkins, 1992) and

SARSA (Rummery and Niranjan, 1994).

2.1 Optimization Problems

Three benchmark problems are selected for running

experiments. Please note they all fall under the cat-

egory of NP and consequently their optimal solution

can be veriﬁed in polynomial time.

2.1.1 N-Queen

In the game of chess, the queen is one of the most ver-

satile pieces that can move horizontally, vertically and

diagonally all across the board. The N-Queen puzzle

is a classic constraint satisfaction problem in Com-

puter Science and Evolutionary Algorithms, in which

the goal is to place N queens on a NxN chessboard

so that no queens attack each other by being on the

same column, row or diagonal. Originally, it was in-

troduced by chess composer Bezzel (Olson, 1993) in

1848 as the 8-queen problem, and later extended to N

queens.

2.1.2 OneMax

OneMax (H

ohn and Reeves, 1996) is an extensively

studied test problem for Evolutionary Computation.

The goal is to maximize the number of ones in a

bit string or list of length N. The task is very well

suited for Genetic Algorithms as the binary encoding

of the candidate solutions matches the expected chro-

mosome representation directly.

2.1.3 Password Cracker

The Password Cracker is a combinatorial problem

inspired by the Inﬁnite Monkey Theorem, which

is a proposition that was ﬁrstly conceptualized by

Borel (E.Borel, 1913) and became a popular example

to illustrate simple concepts of probability.

Standard modern computers can produce 96

unique ASCII character codes that range from 32 to

127 - including uppercase and lowercase letters, dig-

its, punctuation marks and various symbols. There-

fore, a password can be represented as a list of inte-

gers of length equal to the number of characters in a

given string, and, consequently, it is possible to use

this encoding for chromosome representation in an

evolutionary optimizer. The goal is to maximize the

number of ASCII codes matching the target password

through evolution, paying attention to the order of the

characters in the text.

2.2 Genetic Operators

The design of the optimizer follows closely the de-

fault conﬁguration implemented in PyGAD (Pygad,

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

116

2021). The operators that are responsible for the dy-

namics of the environment regardless of the parame-

ter control strategy applied to the algorithm are: ran-

dom initialization, roulette-wheel selection, single-

point crossover and ﬂip-bit mutation.

2.3 State Space

The state representation of the environment encapsu-

lates enough information for an agent to learn a pol-

icy. The literature around parameter control for Ge-

netic Algorithms has largely adopted a set of three in-

dicators that seemingly matches this deﬁnition (Dru-

gan, 2019).

Firstly, average ﬁtness of the population

f is cal-

culated across the existing individuals in the most re-

cent generation. Secondly, the best population ﬁt-

ness score is simply the best candidate solution to

the problem max( f ) in the current generation. Lastly,

entropy-based population diversity H( f ) is a measure

of ﬁtness heterogeneity in the population using Shan-

non’s entropy from information theory. Ultimately,

the goal is to obtain a quantitative indicator of the

ﬁtness distribution, so that the entropy is minimized

when all the individuals in the population are equally

ﬁtted, and maximized when the ﬁtness scores are uni-

formly distributed.

H( f ) = −

∑

i=1

P( f

)logP( f

)

This environment has been designed to work with

both continuous and discrete state spaces. In the for-

mer, an agent receives a set of real-valued features.

For the latter, it requires a preprocessing step to cre-

ate a ﬁnite number of states. For this purpose, we

have simply followed the most common approach in

the literature and created equally sized bins for all the

features (Karafotias et al., 2014a).

2.4 Action Space

Reinforcement Learning agents are expected to learn

optimal values for two fundamental parameters in

Evolutionary Computation according to the state of

the optimization: the crossover and mutation prob-

ability. We have developed an environment that is

able to handle continuous and discrete actions so that

learning algorithms of different nature can be trained

on the same task. For the former, the action space con-

siders the full range of valid crossover and mutation

rates from 0 to 1. Alternatively, in the discrete action

space setup, the agent chooses among a ﬁnite num-

ber of actions that have been discretized in advance.

Following the literature’s design choice (Karafotias

et al., 2014a), we ﬁrstly create equally sized bins of

crossover and mutation probabilities, and these are

applied to the environment by uniformly sampling a

ﬂoat number from the interval of values the agent’s

selected bin or action belongs to.

2.5 Reward

One of the main challenges in Reinforcement Learn-

ing applications concerns the design of the reward

function. The agent adapts its behavior based on feed-

back provided by the environment and this is expected

to be informative enough to guide the learning algo-

rithm towards the goal. In the context of parameter

control in Genetic Algorithms, it is required to answer

the following question: “How do Genetic Algorithms

optimize the best?”.

The existing literature has widely focused on a

reward deﬁnition based on the relative improvement

from the best parent of the previous generation to

the best child in the current one. This deﬁnition

overcomes the credit assignment problem in Rein-

forcement Learning (Dulac-Arnold et al., 2015) but

it is prone to return misleading cumulative rewards

throughout the episode due to the nature of the calcu-

lation - that is the sum of immediate relative improve-

ments over time.

Nevertheless, a simpler reward function that takes

into account the impact on cumulative rewards, and

the one we implemented for this work, could be just

the average ﬁtness of the resulting population

af-

ter performing an action. Thus, the agent will try to

increase the average ﬁtness at each generation, which

eventually leads to the problem’s optimal solution. In

fact, this answers the question we stated earlier: Ge-

netic Algorithms optimize the best by maximizing the

average ﬁtness of the population.

2.6 Measuring Performance

We propose three tasks for each benchmark problem

that range from easily solvable to highly constrained

environments with respect to the search space.

Firstly, baseline conﬁgurations are set according

to the population size and number of generations that

a vanilla genetic algorithm with default parameters

has a probability of ﬁnding the optimal solution in the

90th percentile. We then create two extra conﬁgura-

tions of larger instances that have to be solved under

the same population and generations conditions. Con-

sequently, these are more challenging problems as the

search space has increased while the sample size, it-

erations and memory available is limited to the initial

scenario.

Continuous Parameter Control in Genetic Algorithms using Policy Gradient Reinforcement Learning

117

Table 1: Experimental conﬁgurations of environments

for measuring performance and runtime of Reinforcement

Learning controllers. Population size and number of gener-

ations are set to 100 and 1,000, respectively, for each exper-

iment.

Problem Size Search Space

N-Queen 8, 12, 15 n

OneMax 30, 35, 40 2

Password Cracker 8, 10, 12 96

We test the performance of two value-based meth-

ods, Q-Learning and SARSA, and two policy gra-

dient agents, DDPG and PPO. These algorithms are

benchmarked against the genetic algorithm with de-

fault crossover and mutation rate to measure the per-

formance gain from using intelligent systems for pa-

rameter control. The role of the default values is to

set the baseline results from an effort-less run without

ﬁne tuning. In this regard, we follow the approach of

popular software such as MATLAB and Simulink

which mutation and crossover rates default to 1% and

80%, respectively.

After training Reinforcement Learning algorithms

on each conﬁguration shown in Table 1, agents are

then evaluated on 100 runs to account for the stochas-

tic component in the population initialization step.

The training and testing environments are seeded dif-

ferently to make sure the behavior policy can be ap-

plied on unseen but similar conditions. The results

are aggregated in the form of performance metrics by

taking the average of the following indicators:

• Success Rate: Percentage of times the optimal

solution was found.

• Steps: Number of generations to ﬁnd the optimal

solution.

• Best Fitness: Fitness value of the best individual

found at the last generation.

• Trajectory: Total number of generations per run.

• Policy Processing Time: Percentage of system

and user CPU time the algorithm spent processing

a state and selecting an action for the environment.

This is also referred to as learning overhead.

• Runtime: Total amount of system and user CPU

time measured in seconds per run.

We measure CPU processing time instead of wall time

to exclude other non process-wide computations in

the background. Similarly, we differentiate between

steps and trajectory to evaluate the episodes where the

optimal solution was found in isolation from unsuc-

cessful runs.

https://es.mathworks.com/help/gads/genetic-

algorithm-options.html.

2.7 Evaluating Scalability

In the ﬁeld of Machine Learning, models are usually

evaluated based on their ability to generalize to new

data of which the underlying distribution is represen-

tative of the training distribution. Similarly, in Evo-

lutionary Computation, generalization can be under-

stood as the ability to behave optimally on different,

larger optimization landscapes - also known as scal-

ability. It is common sense that in this scenario the

distribution of the training data no longer matches the

task and it’s expected to see a drop in the performance

of Reinforcement Learning algorithms.

Table 2: Experimental conﬁgurations for evaluating scal-

ability in Reinforcement Learning controllers. Population

size and number of generations are set to 100 and 1,000,

respectively, for each experiment.

Problem Training Test

N-Queen 8 [8, 15]

OneMax 30 [30, 40]

Password Cracker 8 [8, 12]

We evaluate the rate of success of controllers

trained on the smallest instance of each task on larger

search spaces of the same problem - Table 2 shows

the problem sizes used for test and training. This is

benchmarked against a genetic algorithm with default

parameter values of 80% and 1% for crossover and

mutation rate, respectively, to measure the unﬁtness

of the policies as the size of the tasks increases. The

results are aggregated over a 100 tests runs to mitigate

the stochastic component in the algorithms.

3 EVALUATION AND RESULTS

This section is aimed at providing a clear overview

around the performance and scalability of policy gra-

dient and value-based algorithms for parameter con-

trol on the benchmark problems introduced earlier.

3.1 N-Queen

Reinforcement Learning controllers have outper-

formed the vanilla genetic algorithm on every con-

ﬁguration of the N-Queen problem overall, show-

ing higher success rate and faster convergence - see

Table 3. As the search space increases, there is a

clear degradation in performance in spite of the con-

troller applied. Regardless, DDPG has managed to

learn policies that reported signiﬁcantly better results

(RQ1).

Policy gradient agents spent 8% to 12% of the run-

time processing the state and selecting an action for

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

118

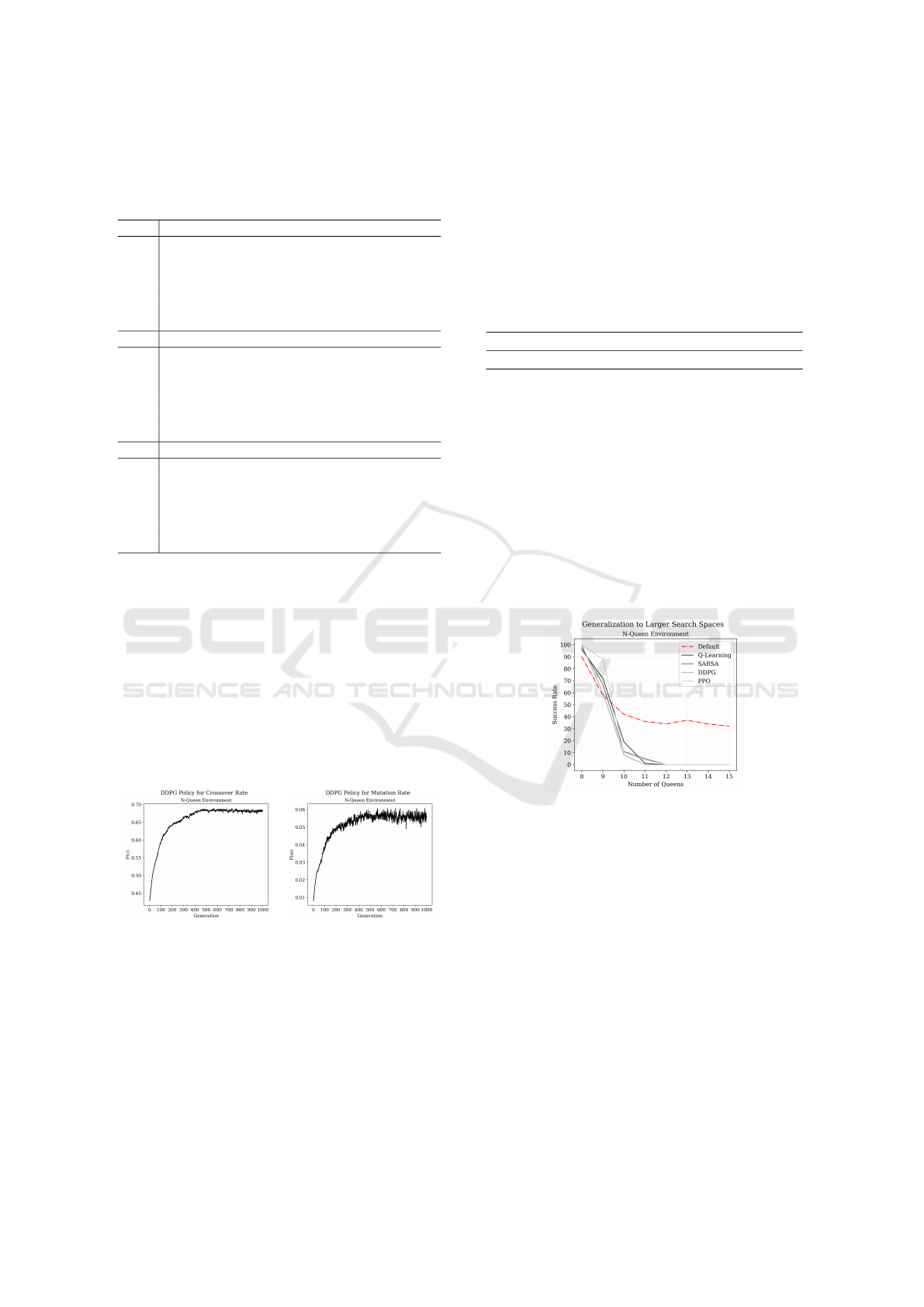
Table 3: Averaged performance results across 100 randomly

initialized test instances of the N-Queen problem for sizes

8, 12 and 15. SR: Success Rate, S: Steps, BF: Best Fitness,

PPT: Policy Processing Time, RT: Runtime.

S8 Default Q-L SARSA DDPG PPO

SR 90% 96% 98% 100% 100%

S 124.4 165.1 114.4 144.3 128.5

BF 85% 98% 99% 100% 100%

T 387.1 198.4 132.2 144 128.5

PPT 0.0% 0.2% 0.2% 10.1% 12.7%

RT 1.0s 1.3s 0.9s 1.0s 0.9s

S12 Default Q-L SARSA DDPG PPO

SR 34% 62% 68% 84% 66%

S 382.9 300.4 304.9 330.7 300.4

BF 67.0% 81.0% 84.0% 92.0% 83.0%

T 790.2 566.3 527.3 437.8 538.2

PPT 0.0% 0.1% 0.1% 8.4% 6.35%

RT 6.7s 4.0s 3.5s 3.3s 4.9s

S15 Default Q-L SARSA DDPG PPO

SR 32% 50% 59% 67% 60%

S 393.8 458.6 435.7 457.8 350.2

BF 65.5% 74.83% 79.1% 83.5% 80.0%

T 806.0 729.3 667.0 636.7 610.1

PPT 0.0% 0.1% 0.1% 8.7% 7.1%

RT 13.1s 7.3s 6.1s 6.0s 6.5s

the environment. This highlights the computational

cost of querying a neural network as opposed to tab-

ular methods, which action selection represents be-

tween 0.17% and 0.24% of the total runtime (RQ2).

Still, DDPG produces faster runs on average than the

rest of conﬁgurations thanks to the higher success

rate.

The policy of the best performing algorithm,

DDPG, can be visualized by averaging the crossover

and mutation probability at each generation of the 100

randomly initialized test runs on the largest N-Queen

problem - see Figures 1 and 2.

Figure 1: DDPG’s crossover

policy on 15-Queen.

Figure 2: DDPG’s mutation

policy on 15-Queen.

There is a clear pattern in the agent’s behavior in-

dicating that both parameters need to be adjusted in

the same direction as if they were determined by a

logarithmic function. Assuming this is the optimal

policy to the problem, we could state that an appro-

priate set of ﬁxed parameters for a vanilla genetic al-

gorithm are the average mutation and crossover rate

of the policy. For this particular case, the crossover

probability is 65.64% and the mutation probability

is 5.11%. Towards measuring the performance gain

from applying Reinforcement Learning for contin-

uous parameter control, the baseline genetic algo-

rithm with default parameters can be updated with the

average crossover and mutation rate extracted from

DDPG’s policy.

Table 4: Parameter tuning on 15-Queen using DDPG’s av-

erage crossover (65.64%) and mutation (5.11%) rate.

SR S BF T PPT RT

55% 520.6 75.33% 736.3 0.0% 7.2s

The results in Table 4 suggest that controlling the

parameters of a genetic algorithm in an online fashion

contributes positively to enhancing the overall per-

formance of the optimizer on the N-Queen problem

(RQ3). Additionally, it also conﬁrms that the ini-

tial default crossover and mutation rates of 80% and

1% are not optimal for this problem - the success

rate of the genetic algorithm increased from 32% to

55%. Despite the additional computational resources

required for querying the neural network’s policy, the

optimizer using DDPG for continuous control has

proven to run faster than the conﬁguration with tuned

parameters.

Figure 3: Success rate of Reinforcement Learning con-

trollers trained on the N-Queen problem of size 8 and tested

on instances up to 15.

With regard to the agents’ generalization ability,

we have observed that the controllers trained on the

8-queen problem failed considerably at solving in-

stances of larger sizes (RQ4) - see Figure 3.

One can infer that a policy can not be extended

to search spaces other than the one it was origi-

nally trained. This not only showcases how well

control policies can ﬁt a speciﬁc problem but also

highlights the limitations of Reinforcement Learn-

ing agents with respect to developing applications at

scale.

Continuous Parameter Control in Genetic Algorithms using Policy Gradient Reinforcement Learning

119

3.2 OneMax

The OneMax problem has shown to be a task that

is highly sensitive to crossover and mutation rates

for different problem sizes. The genetic algorithm

with default parameters drastically reduced its perfor-

mance on larger instances of the problem while the

controllers maintained a reasonable level of conver-

gence - the results are presented in Table 5.

These experiments have also shined some light on

the improved performance of policy gradient meth-

ods over value-based algorithms. Speciﬁcally, both

DDPG and PPO have performed signiﬁcantly better

than Q-Learning and SARSA overall, showing higher

rates of success and taking fewer steps to ﬁnd the op-

timal solution (RQ1). In this regard, PPO is the most

suited controller for this task.

Table 5: Averaged performance results across 100 randomly

initialized test instances of the OneMax problem for sizes

30, 35 and 40. SR: Success Rate, S: Steps, BF: Best Fitness,

PPT: Policy Processing Time, RT: Runtime.

S30 Default Q-L SARSA DDPG PPO

SR 99% 99% 100% 100% 100%

266.2 238.6 211.9 257.7 249.8

BF 99.9% 99.9% 100% 100% 100%

T 273.6 243.3 211.9 257.7 249.8

PPT 0.0% 0.2% 0.2% 8.3% 10.9%

RT 2.1s 2.1s 2.0s 2.3s 2.1s

S35 Default Q-L SARSA DDPG PPO

SR 63% 83% 85% 91% 96%

S 486.7 477.1 441.3 486.2 432.2

BF 98.9% 99.5% 99.6% 99.7% 99.8%

T 676.6 589.1 571.2 501.6 454.8

PPT 0.0% 0.1% 0.1% 8.1% 9.3%

RT 5.9s 5.3s 5.0s 4.8s 4.1s

S40 Default Q-L SARSA DDPG PPO

SR 6% 61% 53% 66% 78%

S 397.7 510.4 492.6 460.9 522.7

BF 96.6% 98.7% 98.1% 98.8% 99.3%

T 963.9 723.4 756.3 698.1 627.7

PPT 0.0% 0.1% 0.1% 6.4% 10.2%

RT 9.3s 7.9s 8.4s 7.1s 6.9s

The policy processing time of controllers using

function approximation ranges values between 6%

and 10% depending on the problem size and algo-

rithm (RQ2). In larger environments, the operators

are expected to process more genetic information,

consequently, the relative time spent selecting an ac-

tion gets progressively reduced. Nevertheless, our re-

sults show that PPO has the lowest runtimes and high-

est rates of success, followed by DDPG.

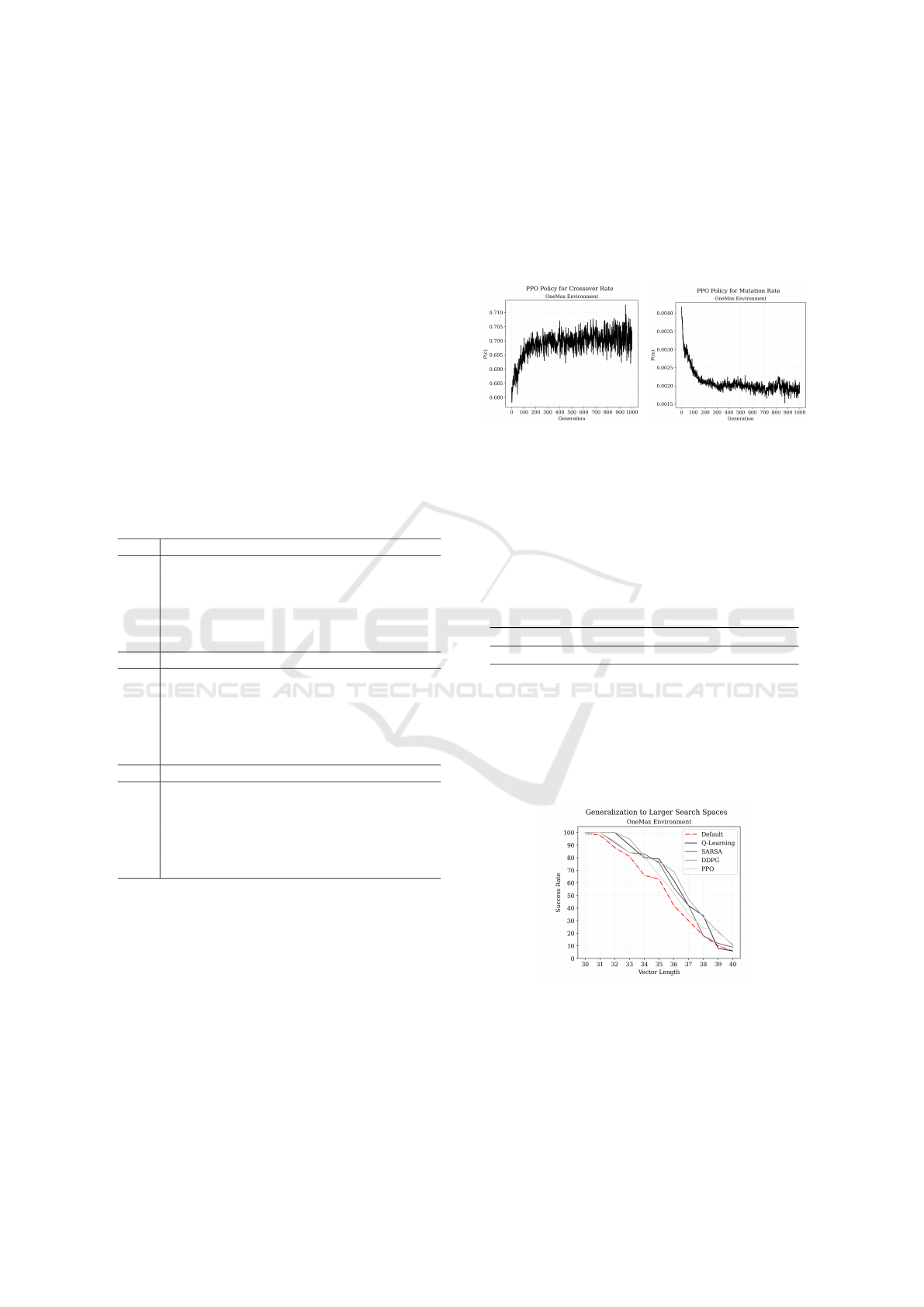
PPO’s policy can be approximated by averaging

the crossover and mutation rate for each time step of

the 100 test runs performed on the OneMax problem

of largest size - see Figure 4 and 5.

The agent updates both parameters in opposite di-

rections following a different strategy from the one

we described in the previous section. In this case,

the mutation rate shows exponential decay while the

crossover rate experiences logarithmic growth. The

overall average of these parameters are 0.20% and

60.89%, respectively.

Figure 4: PPO’s crossover

policy on OneMax-40.

Figure 5: PPO’s mutation

policy on OneMax-40.

Assuming these are the optimal ﬁne tuned values

for a genetic algorithm without parameter control, we

can compare the performance of the traditional ap-

proach to the hybrid optimizer enhanced with Rein-

forcement Learning.

Table 6: Parameter tuning on OneMax-40 using PPO’s av-

erage crossover (60.89%) and mutation (0.20%) rate.

SR S BF T PPT RT

69% 533.8 99.2% 637.6 0.0% 6.2s

The results in table Table 6 indicate that this new

set of parameters are better suited for the task - the

rate of success of the genetic algorithm increased con-

siderably from 6% to 69%. Still, it doesn’t outperform

the algorithm using PPO for online parameter control,

which ﬁnds the optimal solution more frequently with

little added runtime (RQ3).

Figure 6: Success rate of Reinforcement Learning con-

trollers trained on the OneMax problem of size 30 and

tested on instances up to 40.

From the scalability stand point, according to the

results in Figure 6, the policies learnt for the smallest

task were not able to successfully solve larger opti-

mization landscapes (RQ4). Nevertheless, as opposed

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

120

to the N-Queen problem, the genetic algorithm with

default parameters experienced a similar drop in per-

formance to the controllers.

3.3 Password Cracker

The Password Cracker is the task with the largest

search space among the benchmark problems pro-

posed

Table 7: Averaged performance results across 100 randomly

initialized test instances of the Password Cracker problem

for sizes 8, 10 and 12. SR: Success Rate, S: Steps, BF: Best

Fitness, PPT: Policy Processing Time, RT: Runtime.

S8 Default Q-L SARSA DDPG PPO

SR 95% 100% 100% 100% 100%

S 456.3 143.2 211.6 303.6 176.5

BF 99.2% 100% 100% 100% 100%

T 483.5 143.2 211.6 303.6 176.5

PPT 0% 0.3% 0.3% 13.7% 15.3%

RT 2.2s 0.4s 0.5s 1.7s 1.0s

S10 Default Q-L SARSA DDPG PPO

SR 48% 90% 73% 93% 90%

S 680.1 480.0 610.6 429.6 557.9

BF 93.5% 98.4% 97.3% 99.3% 98.9%

T 849.6 532.0 715.7 469.6 606.6

PPT 0.0% 0.3% 0.3% 13.0% 14.6%

RT 4.4s 3.0s 3.5s 2.8s 3.7s

S12 Default Q-L SARSA DDPG PPO

SR 21% 37% 12% 44% 50%

S 796.5 645.6 757.7 726.2 640.4

BF 90.2% 93.4% 92.2% 94.0% 94.8%

T 957.3 868.9 970.9 879.5 820.2

PPT 0.0% 0.2% 0.2% 12.3% 12.6%

RT 5.4s 5.0s 5.0s 5.6s 5.4s

From the very ﬁrst conﬁguration of size 8, the

vanilla genetic algorithm performs comparably worse

than the algorithms enhanced with Reinforcement

Learning - see Table 7. Additionally, most parame-

ter control policies resulted in less than 50% rate of

success on the largest problem size except for PPO

(RQ1). It is also worth mentioning that SARSA is

the worst performing controller on this problem. In

fact, the genetic algorithm with default parameters re-

ported better results than SARSA on the 12-character

long password.

The state and action processing steps by policy

gradient algorithms takes around 12% to 15% of the

total runtime (RQ2). This is the highest contribution

recorded so far considering the benchmark problems

presented earlier. The reason is the reduced number of

The target passwords for the experiments were gen-

erated randomly using an online generator at https://

passwordsgenerator.net/.

computations performed by the genetic operators due

to the smaller chromosome size for this speciﬁc task,

which makes the learning overhead relatively more

costly.

In the light of the results, PPO is considered the

best performing controller on the Password Cracker.

Consequently, we evaluate further the policy that was

applied to the largest problem by computing the aver-

age of the crossover and mutation rate at each gener-

ation across 100 test runs - see Figures 7 and 8.

Figure 7: PPO’s crossover

policy on Password-12.

Figure 8: PPO’s mutation

policy on Password-12.

The agent sets lower crossover rates and higher

mutation probabilities at the beginning of the op-

timization to build diversity within the population.

As new generations of individuals are created, it re-

duces the probability of mutation exponentially and

increases the rate of crossover logarithmically. This

translates into more candidate solutions generated by

chromosomes recombination and less stochasticity in

the environment. Ultimately, the algorithm is trying

to balance the level of exploration and exploitation at

each time step.

The average parameter values extracted from the

policy for crossover and mutation rate are 71.19% and

1.70%, respectively. As it has been shown on pre-

vious sections, running the vanilla genetic algorithm

on this set of values can reveal information about the

controller’s contribution to the performance of the op-

timizer.

Table 8: Parameter tuning on Password-12 using PPO’s av-

erage crossover (71.19%) and mutation (1.70%) rate.

SR S BF T PPT RT

32% 684.2 93.2% 898.9 0.0% 5.1s

Considering the results in Table 8, PPO’s control

policy handles the optimization process more effec-

tively than parameter tuning (RQ3). Moreover, run-

time statistics show that it does not achieve such per-

formance at the cost of substantial longer runs, but

rather improves the algorithm’s search strategy. The

agent’s ability to generalize has been assessed us-

ing the shortest password containing 8 characters for

training and applying the resulting policy on larger in-

Continuous Parameter Control in Genetic Algorithms using Policy Gradient Reinforcement Learning

121

stances up to 12 characters including - see Figure 9.

Figure 9: Success rate of Reinforcement Learning con-

trollers trained on the Password Cracker problem of size 8

and tested on instances up to 12.

The performance degradation of Reinforcement

Learning controllers (RQ4) strengthens the idea that

small changes in the search space greatly contribute

to the dynamics of the environment, which are usu-

ally described as problem-dependent. It also demon-

strates that policy gradient algorithms driven by func-

tion approximation aren’t especially useful for ex-

panding policies to new optimization landscapes.

4 CONCLUSIONS

Reinforcement Learning controllers have proven to be

effective methods for boosting the rate at which Ge-

netic Algorithms ﬁnd the optimal solution to a given

problem, resulting in hybrid optimizers with reduced

running times and faster convergence. This is par-

ticularly noticeable in our novel contribution with

DDPG and PPO continuous policy gradient algo-

rithms, which outperformed Q-Learning and SARSA

discrete value-based approaches in the vast majority

of test environments despite the associated learning

overhead of querying a neural network. Moreover,

this work also suggested that even a ﬁne tuned ge-

netic algorithm with appropriate crossover and muta-

tion rates may not perform optimally as long as these

remain ﬁxed throughout the generations.

Lastly, this study highlighted the fact that Rein-

forcement Learning agents do not generalize well to

larger instances of the problem they were initially

trained on. Conversely, a genetic algorithm with de-

fault parameter values performed comparatively bet-

ter on larger search spaces of the same task. Regard-

less, with respect to the traditional approach to param-

eter control, the successful application of continuous

policy gradient methods opens the door to a branch

of hybrid optimization algorithms that can deal with

the dynamics of a stochastic process optimally in an

effortless manner, bringing together two ﬁelds of Ar-

tiﬁcial Intelligence that could determine the next gen-

eration of Evolutionary Algorithms.

REFERENCES

Aleti, A. and Moser, I. (2016). A systematic literature re-

view of adaptive parameter control methods for evolu-

tionary algorithms. ACM Computing Surveys (CSUR),

49(3):1–35.

Dayan, P. and Watkins, C. (1992). Q-learning. Machine

learning, 8(3):279–292.

Drugan, M. M. (2019). Reinforcement learning versus

evolutionary computation: A survey on hybrid al-

gorithms. Swarm and evolutionary computation,

44:228–246.

Dulac-Arnold, G., Evans, R., van Hasselt, H., Sunehag,

P., Lillicrap, T., Hunt, J., Mann, T., Weber, T., De-

gris, T., and Coppin, B. (2015). Deep reinforcement

learning in large discrete action spaces. arXiv preprint

arXiv:1512.07679.

E.Borel (1913). M

ecanique statistique et irr

eversibilit

pages 189–196.

Eiben,

A. E., Hinterding, R., and Michalewicz, Z. (1999).

Parameter control in evolutionary algorithms. IEEE

Transactions on evolutionary computation, 3(2):124–

141.

ohn, C. and Reeves, C. (1996). The crossover landscape

for the onemax problem.

Karafotias, G., Eiben, A. E., and Hoogendoorn, M. (2014a).

Generic parameter control with reinforcement learn-

ing. Proceedings of the 2014 Annual Conference on

Genetic and Evolutionary Computation.

Karafotias, G., Hoogendoorn, M., and Eiben,

A. E. (2014b).

Parameter control in evolutionary algorithms: Trends

and challenges. IEEE Transactions on Evolutionary

Computation, 19(2):167–187.

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,

Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-

uous control with deep reinforcement learning. arXiv

preprint arXiv:1509.02971.

Olson, A. T. (1993). The eight queens problem. Journal

of Computers in Mathematics and Science Teaching,

12(1):93–102.

Pygad (2021). pygad Module — PyGAD 2.13.0 documen-

tation.

Rummery, G. A. and Niranjan, M. (1994). On-line Q-

learning using connectionist systems, volume 37. Uni-

versity of Cambridge, Department of Engineering

Cambridge, UK.

Sakurai, Y., Takada, K., Kawabe, T., and Tsuruta, S. (2010).

A method to control parameters of evolutionary algo-

rithms by using reinforcement learning. pages 74–79.

IEEE.

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and

Klimov, O. (2017). Proximal policy optimization al-

gorithms. arXiv preprint arXiv:1707.06347.

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

122