An Effective Resistance based Genetic Algorithm for Community

Detection

Clara Pizzuti

and Annalisa Socievole

National Research Council of Italy (CNR), Institute for High Performance Computing and Networking (ICAR),

Via Pietro Bucci, 8-9C, 87036 Rende (CS), Italy

Keywords:

Community Detection, Genetic Algorithm, Effective Resistance, Moore-Penrose Pseudoinverse.

Abstract:

This work presents a new approach based on genetic algorithms (GAs) and the concept of effective resistance

for detecting communities within an undirected graph. The method considers the equivalent electric network

of the input graph, where edges are weighted with their effective resistance, a measure of electrical resistance

between nodes, whose square root has been shown to be a Euclidean metric. The algorithm computes the

similarity between nodes by using the effective resistance values and generates a weighted and sparse graph

by adopting a thresholding sparsiﬁcation strategy based on the nearest neighbors of each node. Experiments

over synthetic and real-world networks demonstrate the effectiveness of our approach when compared to other

benchmark methods.

1 INTRODUCTION

The community detection problem in complex net-

works plays a fundamental role in several ﬁelds, in-

cluding telecommunications, sociology, physics, and

biology. Many real-world systems, in fact, can be rep-

resented through networks where nodes correspond to

the objects of the system and edges model the rela-

tionships between such objects. The task of ﬁnding

communities in networks has attracted a lot of atten-

tion in the last years since the presence of commu-

nities indicates the existence of group organization

which could be interesting to uncover for a better un-

derstanding of the system.

The problem of ﬁnding a community structure

can be generally formalized as an optimization prob-

lem where a criterion function, catching the intu-

itive concept of group, is deﬁned and optimized. To

date, many community detection algorithms, based

on different approaches, such as consensus clus-

tering, spectral methods, statistical inference-based,

optimization-based, dynamics-based methods, have

been proposed (Fortunato and Hric, 2016).

Real-world networks generally have a very high

density of edges and, often, their edges are weighted

(Barrat et al., 2004). As observed in (Yan et al., 2018),

https://orcid.org/0000-0001-7297-7126

https://orcid.org/0000-0001-5420-9959

analyzing these networks with computational meth-

ods is very hard, thus preprocessing techniques need

to be applied in order to reduce the number of con-

nections and make the problem tractable.

An approach to eliminate edges is graph sparsiﬁ-

cation (Tumminello et al., 2005; Radicchi et al., 2011;

Spielman and Srivastava, 1996). In particular, (Spiel-

man and Srivastava, 1996) proposed to build a sparse

graph H from the original one G by including in H

edges of G with a probability proportional to their ef-

fective resistance.

The effective resistance (Klein and Randi

c, 1993;

Ghosh et al., 2008) of an edge is equal to the proba-

bility that the edge appears in a random spanning tree

of G (Doyle and Snell, 1989), and it was proven to

be proportional to the commute-time between its end-

points (Chandra et al., 1996). Moreover, (Klein and

Randi

c, 1993) showed that the square root of the ef-

fective resistance between any couple of nodes (i, j)

is a Euclidean metric, in particular it measures the dis-

tance between nodes i and j. Thus, the computation

of the effective resistance for each edge of G provides

a distance matrix between each couple of nodes of G.

In this paper, given a network G = (V, E), where

V is the set of nodes and E of edges, we propose an

evolutionary algorithm to detect communities by ex-

ploiting the concept of effective resistance. The main

idea is to apply a Genetic Algorithm (GA) (Goldberg,

1989) to ﬁnd communities on the weighted graph

Pizzuti, C. and Socievole, A.

An Effective Resistance based Genetic Algorithm for Community Detection.

DOI: 10.5220/0010644300003063

In Proceedings of the 13th International Joint Conference on Computational Intelligence (IJCCI 2021), pages 28-36

ISBN: 978-989-758-534-0; ISSN: 2184-3236

= (V,W ) obtained from G by computing the ef-

fective resistance of all the node pairs of G. G

has

the same set V of nodes of G, while the set W of

edges consists of the effective resistance between any

couple of nodes (i, j) of V . However, the adjacency

matrix Ω corresponding to G

is a full matrix, thus

a sparsiﬁcation procedure is necessary to reduce the

number of edges and make clear the original network

structure.

The simplest way to obtain a sparse graph is the

weight thresholding (Yan et al., 2018), i.e. removing

the edges whose weight is above a ﬁxed threshold.

Deleting as many edges as possible without altering

the original system is a key point.

Our approach considers for each node i only a

ﬁxed number nn of the most similar nodes and re-

moves from Ω all the edges between i and the nodes

not included in this set of nn nearest neighbors to ob-

tain a sparse weighted adjacency matrix

Ω. We there-

fore run the GA over the sparsiﬁed weighted adja-

cency matrix

Ω by evolving a population of individ-

uals and minimizing the concept of modularity of a

partition, the most popular quality function of com-

munity structure introduced by Girvan and Newman

(Girvan and Newman, 2002).

A comparison with a baseline genetic algorithm

optimizing modularity and running on the original

graph G, along with two of the best-known commu-

nity detection methods Louvain (Blondel et al., 2008)

and Infomap (Rosvall and Bergstrom, 2008) shows

that the proposed algorithm obtains results better than

the contestant methods both over synthetically gener-

ated and real-world networks.

The paper is organized as follows. The next sec-

tion describes some measures proposed for comput-

ing node similarity and how these measures are used

for the community detection task. Section 3 recalls

the concept of effective resistance, deﬁnes the com-

munity detection problem we tackle and describes our

method. Section 4 describes the datasets used and the

experiments performed to validate the proposed algo-

rithm. Finally, Section 5 concludes the paper and dis-

cusses the future directions.

2 RELATED WORK

Distances and similarity measures between the nodes

of a graph are widely used in data analysis and es-

pecially in clustering tasks. Many measures have

been proposed so far including the widely investi-

gated Shortest Path distance (Dijkstra et al., 1959),

the Resistance (Klein and Randi

c, 1993), the loga-

rithmic Walk measure, the Forest measure related to

Resistance, and many others (Deza and Deza, 2009)

(Avrachenkov et al., 2017).

In their pioneering work, Klein and Randic (Klein

and Randi

c, 1993) proposed the use of the effective

resistance, also named resistance distance, between

two nodes as a meaningful distance measure. Indeed,

it has been shown that this measure is a Euclidean

distance.

The close link between the effective resistance and

the commute-time of a random walker on a graph

has been studied in (Chandra et al., 1996). More-

over, the relationship between the Laplacian matrix

of the graph and the commute-time was investigated

in (Saerens et al., 2004). For this reason, the effective

resistance is also named commute-time distance.

In (Avrachenkov et al., 2019), a set of similar-

ity measures on graphs based on three fundamental

graph matrices, the adjacency matrix, the Laplacian

matrix, and the stochastic Markov matrix are analyt-

ically studied and compared. For each measure, the

work investigates if it is (a) a kernel, (b) a proximity

measure, and (c) a transitional measure.

In (Yen et al., 2007), the commute-time kernel

is used for clustering the nodes of a weighted undi-

rected graph. The method is based on a two-step pro-

cedure that initially computes the sigmoid commute-

time kernel matrix from the adjacency matrix of the

graph, providing a similarity measure between nodes,

and then, clusters the nodes by exploiting a kernel-

based k-means or fuzzy k-means on the obtained ker-

nel matrix. The proposed methodology combining

commute-time kernel and kernel clustering outper-

forms standard k-means, as well as spectral cluster-

ing, on a difﬁcult graph clustering problem.

A comprehensive study on graph nodes clustering

with the sigmoid commute-time kernel can be found

in (Yen et al., 2009). In (Sommer et al., 2016), six dif-

ferent distance measures are transformed into kernels

and tested on kernel k-means and a weighted version

of it. A comparison with the Louvain method shows

the effectiveness of the distance-based algorithms.

The impact of network topology on the efﬁciency

of proximity measures for community detection is in-

vestigated in (Aynulin, 2019). Speciﬁcally, the work

checks wether the advantage of using one measure

is kept for different network topologies. The au-

thors showed that there are measures behaving well

for most topologies.

In the next section the concept of effective resis-

tance metric is recalled and how it is exploited for de-

tecting effective community structure is described.

An Effective Resistance based Genetic Algorithm for Community Detection

3 COMMUNITY DETECTION

BASED ON EFFECTIVE

RESISTANCE

In this section, we ﬁrst introduce the concept of ef-

fective resistance as distance metric and then describe

the proposed method.

3.1 Effective Resistance

Klein and Randic, in their seminal work (Klein and

Randi

c, 1993), proposed the theory of resistive elec-

trical networks to deﬁne a new distance function be-

tween vertices. They suggested that if ﬁxed resis-

tors are assigned to the edge of a connected graph,

the effective resistance between couples of nodes is a

graphical distance.

Given an undirected and connected graph G =

(V,E), an equivalent electric network can be associ-

ated with G by weighting each edge (i, j) ∈ E with

positive weights w

i j

representing the conductance, i.e.

the inverse of the electrical resistance ω

i j

of a resistor,

so that ω

i j

ohm (Klein and Randi

c, 1993). As

described in (Klein and Randi

c, 1993; Van Mieghem

et al., 2017), for any edge of the graph G, a distance

function can be deﬁned as follows.

The effective resistance ω

i j

between any pair of

nodes i and j is deﬁned as the voltage developed be-

tween i and j when a unit current is injected at node i

and is withdrawn at node j. The corresponding N ×N

matrix including all the ω

i j

between each node pair i

and j is denoted Ω.

The interesting feature is that ω

i j

is upper

bounded by the shortest path distance in a graph

(Van Mieghem, 2010). Moreover, the communte-time

distance C

i j

between two nodes i and j, i.e. the ex-

pected number of steps needed during a random walk

from i to j, is C

i j

= u

Au ω

i j

, where u is the all

one vector and u

Au is the double of the sum of all

the edge weights in the weighted adjacency matrix

(Chandra et al., 1996).

In (Klein and Randi

c, 1993), it is shown that the

square root

√

i j

of the effective resistance is a Eu-

clidean metric. More precisely, the effective resis-

tance matrix Ω is a distance matrix, in which for any

triple of non-negative elements, ω

= 0, and the tri-

angle inequality, ω

i j

≤ ω

+ ω

k j

is satisﬁed.

Moreover, Ω can be deﬁned (Doyle and Snell,

1989; Klein and Randi

c, 1993; Van Mieghem, 2010)

Ω = ζu

+ uζ

−2L

(1)

where the vector

ζ =



,.. .,L



(2)

contains the diagonal elements of the Moore-Penrose

pseudoinverse matrix L

of the weighted Laplacian

matrix

L of the graph G.

Recall that, given ∆ = diag(d

) the N ×N diago-

nal degree matrix, where d

∑

j=1

i j

, the Laplacian

matrix L of the graph G is deﬁned as the N ×N sym-

metric matrix L = ∆ −A, with elements

i j







if i = j

−1 if the edge (i, j) ∈ E

0 otherwise

(3)

The effective resistance between two nodes x and

y equals

= (e

−e

)

−e

) = l

+ l

−2l

(4)

where e

is the basic vector with the m-th component

equal to (e

)

= δ

and δ

is the Kronecker-delta:

= 1 if m = k, otherwise δ

= 0.

3.2 Problem Deﬁnition

Given a graph G, let Ω be the resistance matrix as-

sociated with G, nn the number of nearest neighbors

to consider, and

Ω the matrix obtained from Ω with

elements







if y is among the nn

nearest neighbors of x

0 otherwise

(5)

The community detection problem is deﬁned as:

ﬁnd a partition C = {C

,...,C

}of the nodes of G such

that the weighted modularity of C is maximized.

The weighted modularity Q is computed as

Q =

∑

i j



i j

−



δ(C

) (6)

where m is the sum of the edge weights, k

and k

the sum of the weights of the edges attached to nodes

i and j respectively, and δ is the Kronecker function

which yields one if i and j are in the same community,

i.e. C

= C

, zero otherwise. Modularity measures the

expected number of edges within the communities of

a random graph with the same degree distribution.

Basically, we look for a community structure

where both intra-community weighted modularity

and similarity between nodes is high (thus the overall

distance between the nodes of the same community is

low).

3.3 Method Description

In this section, a detailed description of the method is

given. OmeGAnet is a method based on Genetic Algo-

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

rithms (GA) (Goldberg, 1989), an evolutionary com-

putation technique which revealed very efﬁcacious

for the task of community detection (Pizzuti, 2018).

The algorithm creates a population of individuals

(i.e. a network division in communities) that are ini-

tially randomly generated, and then evolves the pop-

ulation through variation and selection operators by

optimizing the value of the objective function while

exploring the search space.

Each individual is represented with the locus-

based adjacency representation (Park and Song,

1998) for which an individual I is a vector of N genes

(i.e. nodes). Each gene can assume a value k from 1

to N. When a value k is assigned to the i-th gene, it

means that nodes i and k are connected. A decod-

ing step identiﬁes all the connected components of

the graph which correspond to the network division

in communities.

As crossover operator, OmeGAnet exploits the

uniform crossover which generates a random binary

mask of length equal to the number of nodes. The

offspring is then generated by selecting from the ﬁrst

parent the genes where the mask is 0, and from the

second parent the genes where the mask is 1.

Finally, the mutation operator randomly assigns

the value of a i-th gene to one of its neighbors.

The steps performed by OmeGAnet are the fol-

lowing. It receives in input the graph G = (V,E), the

number of nearest neighbors nn to consider, and per-

forms the following steps:

1. compute the Laplacian L of G;

2. compute the Moore-Penrose pseudoinverse ma-

trix L

of L;

3. compute the effective resistance matrix Ω from

as ω

= l

+ l

−2l

;

4. make Ω a distance matrix by substituting each el-

ement as ω

√

;

5. normalize the elements of Ω and make Ω a sym-

metric matrix Ω = 0.5[

Ω

max(Ω)

+ (

Ω

max(Ω)

)

];

6. generate the sparse similarity weighted matrix

Ω

from Ω by maintaining for each node x only the nn

entries ω

having the minimum distance value,

i.e the connections with the nodes y having the

highest similarity values with x;

7. run the Genetic Algorithm on

Ω for a number of

iterations by using modularity as ﬁtness function

to maximize, uniform crossover and neighbor mu-

tation as variation operators;

8. obtain the partition C = {C

,.. .,C

} correspond-

ing to the solution with the highest ﬁtness value.

Table 1: LFR-128 parameters setting.

Parameter Value

Number of nodes 128

Node average degree 8

Node maximal degree 9

Exponent for power law creating degree sequence 2

Exponent for power law creating community sizes 1

Mixing parameter µ [0.1; 0.6]

Maximal community size 40

Minimal community size 20

Average density 0.062

In the next section, we compare OmeGAnet with

three community detection methods and compare

the results they obtain on synthetic and real-world

datasets.

4 EXPERIMENTAL EVALUATION

For validating OmeGAnet, we performed several sim-

ulations using Matlab 2020a and the Global Opti-

mization Toolbox.

Regarding the input parameters to our approach,

we experimentally set them by performing a trial and

error procedure.

In the following subsections we describe the

datasets, the evaluation measures used, the algorithms

in comparison and ﬁnally the results obtained.

4.1 Datasets

4.1.1 Synthetic Networks

To create synthetic networks with realistic commu-

nity structures, the Lancichinetti-Fortunato-Radicchi

(LFR) benchmark (Lancichinetti et al., 2008) has

been used.

This well-known and widely used network gen-

erator is able to control the structure of the commu-

nities by properly setting the mixing parameter µ.

The lower the µ, the clearer the resulting community

structure with much more intra-community links than

inter-cluster links. On the contrary, when µ has high

values, the community structure is not clear.

The parameters used for generating the LFR net-

works are shown in Table 1. In particular, for each µ

value we generated 10 network instances.

4.1.2 Real-world Networks

We considered four real-world networks for which the

ground-truth division is known.

• Zachary Karate Club. This well-known dataset

contains the data of the friendship social network

An Effective Resistance based Genetic Algorithm for Community Detection

(a) (b)

Figure 1: (a) A 128-nodes LFR network generated with µ = 0.2 and (b) its reduced graph with nn = 5.

of 34 members of a karate club, collected by

Wayne Zachary in 1977. The group has been ob-

served for two years, splitting in two communities

almost of the same size due to disagreements be-

tween the members.

• Amazon US Politics Books. The second dataset

contains the data of books co-purchased on Ama-

zon.com by customers during the US political

elections in 2004. The network was collected by

Krebs and contains 105 nodes and 374 edges. The

books were later classiﬁed into the three political

groups liberal, neutral and conservative by New-

man.

• American College Football. This dataset con-

tains the network of 115 American football teams

extracted from the Fall 2000 regular season

games. The teams were linked during a game with

a resulting number of 616 edges/games and parti-

tioned in 12 communities.

• Bottlenose Dolphins. The last dataset con-

tains the network of 62 Bottlenose dolphins from

Doubtful Sound in New Zealand. Linked through

159 edges, the edges represent frequent associa-

tions observed between dolphins. Here, the dol-

phins are partitioned into two communities.

4.2 Evaluation Measure

We evaluate the quality of the solutions by using the

Normalized Mutual Information (NMI).

Given two divisions A and B of a network, and C

the confusion matrix whose element C

i j

is the number

of nodes of community i of the partition A that are

also in the community j of the partition B, the NMI

between A and B is deﬁned as:

NMI(A,B) =

−2

∑

i=1

∑

j=1

i j

log(C

i j

n/C

. j

)

∑

i=1

log(C

/n) +

∑

j=1

. j

log(C

. j

/n)

(7)

where c

) is the number of groups in the par-

tition A (B), C

. j

) is the sum of the elements of C

in row i (column j), and n is the number of nodes.

If A = B, NMI(A,B) = 1. If A and B are completely

different, NMI(A,B) = 0.

4.3 Algorithms in Comparison

We ﬁrst compare OmeGAnet with a baseline GA-

based algorithm, denoted GA-mod, adopting the same

locus-based representation, initialization, crossover

and mutation operators which optimizes the modular-

ity value. In particular, population initialization con-

nects a node with one of its nn nearest neighbors, in-

stead of a random neighbor.

We also compare OmeGAnet to two benchmarks:

Louvain (Blondel et al., 2008) and Infomap (Rosvall

and Bergstrom, 2008).

The Louvain method is based on a greedy mod-

ularity optimization approach. First, the algorithm

identiﬁes small communities by locally optimizing

modularity. Then, it builds a new network whose

nodes are the communities previously found, and

these steps are repeated until a hierarchy of high-

modularity communities is obtained.

Infomap exploits the principles of information the-

ory by deﬁning the community detection problem as

the problem of ﬁnding a description of minimum in-

formation of a random walk on the graph. The method

maximizes the Minimum Description Length as ob-

jective function by quickly providing an approxima-

tion of the optimal solution.

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

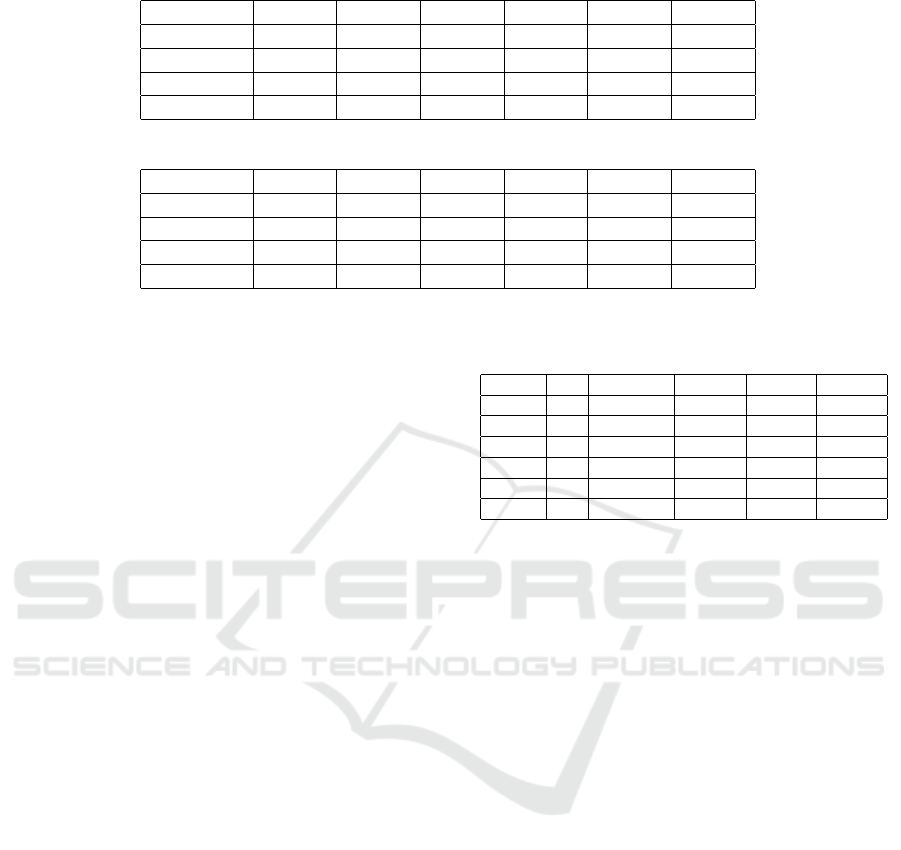
Table 2: NMI results for the LFR-128 networks.

µ = 0.1 µ = 0.2 µ = 0.3 µ = 0.4 µ = 0.5 µ = 0.6

OmeGAnet 1 1 0.8049 0.3308 0.1314 0.0698

GA-mod 1 1 0.6967 0.2988 0.117 0.06

Louvain 0.8793 0.8716 0.5555 0.3228 0.0865 0.055

In f omap 1 1 0.6728 0.2875 0.1162 0.0624

Table 3: Modularity results for the LFR-128 networks.

µ = 0.1 µ = 0.2 µ = 0.3 µ = 0.4 µ = 0.5 µ = 0.6

OmeGAnet 0.7038 0.5446 0.3983 0.3308 0.2999 0.2854

GA-mod 0.7038 0.5446 0.3908 0.3104 0.3223 0.3035

Louvain 0.6268 0.4661 0.3733 0.314 0.3356 0.3086

In f omap 0.7038 0.5446 0.4101 0.2875 0.3386 0.3289

4.4 Results

The ﬁrst experiment has been carried out on a pool of

synthetic network with 128 nodes.

Figure 1 shows an instance of a network gener-

ated with a mixing parameter µ = 0.2. Figure 1 (a)

shows the community structure of the ground-truth

composed by four communities colored in red, green,

magenta and blue. Figure 1 (b), shows the reduced

graph with nn=5, the value for this parameter able to

produce the better results.

It is worth pointing out that, by considering the

subset of neighbors having the highest similarity (i.e.

the lowest distance), the underlying communities are

more visible and the structure is clearer. Here, the

few interlinks between communities make, for exam-

ple, more visible the communities in green and in red.

Table 2 shows the NMI results for the LFR-128 net-

works.

For the genetic algorithms OmeGAnet and GA-

mod we have set maximum number of generations

100, population size 700, nn=5, crossover fraction 0.9

and mutation rate 0.1. Each value has been averaged

over 10 runs of the method. For communities with

clear structure (µ = 0.1 and µ = 0.2), the two genetic

algorithms and Infomap match the ground-truth cor-

rectly identifying the underlying communities.

Louvain, on the contrary, achieves only 0.8793

and 0.8716 for µ = 0.1 and µ = 0.2, respectively.

As µ increases and the structure of the communi-

ties changes becoming less clear, OmeGAnet always

outperforms all the other contestant methods. From

µ = 0.3 to µ = 0.6 the NMI signiﬁcantly decreases

achieving very low values for µ = 0.6.

In Table 3, the modularity values are reported. For

µ = 0.1 and µ = 0.2 the modularity value achieved

with NMI=1 is 0.7038, as can be observed for

OmeGAnet, GA-mod, and Infomap. For µ = 0.3,

µ = 0.5 and µ = 0.6 the highest modularity is ob-

Table 4: Number of communities for the LFR-128 net-

works.

GT OmeGAnet GA-mod Louvain Infomap

µ = 0.1 4 4 4 5 4

µ = 0.2 4 4 4 3 4

µ = 0.3 4 4 5 5 7

µ = 0.4 4 4 7 7 9

µ = 0.5 4 4 7 7 6

µ = 0.6 4 4 7 7 9

tained by In f omap while for the other approaches op-

timizing modularity the highest value is obtained by

OmeGAnet for mu = 0.4.

We point out that our focus is to obtain the high-

est NMI value for the community partition found and

this not always corresponds to the highest modularity

value as can be observed.

In Table 4, we ﬁnally show the number of com-

munities obtained for a single run of a network. In

the second column, the number of classes for the

ground- truth (GT) is reported. For each µ the ground-

truth is composed by 4 communities. OmeGAnet is

always able to split the network in 4 groups while

the other schemes fragment the communities result-

ing in a higher number of communities from µ = 0.3

to µ = 0.6. For µ = 0.4, for example, GA-mod and

Louvain ﬁnd 7 communities, while Infomap even 9.

In the second experiment, we tested OmeGAnet

on the real-world networks described above for which

the true number of communities is known.

Table 5 shows the NMI results obtained by setting

for the genetic algorithms maximum number of gen-

erations 100, population size 500, nn = 4, crossover

fraction 0.9 and mutation rate 0.1.

In Tables 6 and 7 the modularity and the number

of communities are reported. Also for this experi-

ment, the NMI and the modularity values are aver-

aged over 10 runs while the number of communities

refers to a single run.

In terms of NMI, OmeGAnet outperforms the

An Effective Resistance based Genetic Algorithm for Community Detection

Figure 2: The Zachary Karate Club (a) and its reduced graph with nn = 4 (b).

Figure 3: The Bottlenose Dolphins (a) and its reduced graph with nn = 4 (b).

other contestant methods also in the real-world net-

working scenarios considered. For Karate, for ex-

ample, the two communities are correctly identiﬁed

while GA-mod achieves only 0.5485, Louvain 0.5195

and Infomap 0.6995 of NMI.

Figure 2 shows the Karate original graph (a) and

its reduced version (b) where we can observe that the

communities are much more clear than in the original

network. Also for the Dolphins dataset, OmeGAnet

signiﬁcantly outperforms the other methods.

Figure 3 shows how the reduction of the initial

graph better separates the communities. The modular-

ity results, show again that a high modularity does not

correspond always to a high NMI. In fact, for Karate,

for example, the modularity value giving the ground-

truth is the one found by OmeGAnet, 0.3715, which

is the lowest.

Looking at the number of communities, it is worth

pointing out that OmeGAnet matches the number of

underlying communities in most of the cases. The

other algorithms, on the contrary, produce partitions

with a higher number of communities. For Dolphins,

for example, where the network is divided into two

groups, GA-mod, Louvain and Infomap ﬁnd 4, 10 and

6 communities, respectively.

Table 5: NMI results for the real-world networks with max-

Gen=100, popSize=500 and nn=4.

OmeGAnet GA-mod Louvain Infomap

Karate 1 0.5485 0.5195 0.6995

Books 0.6313 0.5338 0.4142 0.5369

Football 0.9326 0.9151 0.9269 0.9242

Dolphins 0.8888 0.5749 0.5169 0.5197

Table 6: Modularity results for the real-world networks.

OmeGAnet GA-mod Louvain Infomap

Karate 0.3715 0.4033 0.402 0.402

Books 0.4546 0.4793 0.4833 0.5268

Football 0.5976 0.6008 0.601 0.6005

Dolphins 0.3787 0.5124 0.4952 0.5146

Table 7: Number of communities for the real-world net-

works.

GT OmeGAnet GA-mod Louvain Infomap

Karate 2 2 4 3 3

Books 3 2 3 8 5

Football 12 12 11 12 12

Dolphins 2 2 4 10 6

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

5 CONCLUSIONS

We proposed OmeGAnet, a new method based on ge-

netic algorithms for dividing the nodes of an undi-

rected and connected graph in communities.

We considered the graph as an electric circuit and

computed for each couple of connected nodes the ef-

fective resistance. We then exploited this distance for

weighting the graph and searching communities with

high weighted modularity.

By performing several experiments on both syn-

thetic and real-world networks, the results show

that the proposed methodology is promising since it

clearly outperforms both a standard GA-based algo-

rithm running on the original adjacency matrix of

the graph, and the state-of-the-art approaches Louvain

and Infomap.

It is worth pointing out that the choice of the

parameter nn plays an important role on the perfor-

mance of OmeGAnet. In the current implementation

we experimentally set it and found that low values of

nn allow to obtain good results.

However, more study is necessary to ﬁnd a general

criterion which allows a good setting of this parame-

ter. In fact, the network sparsiﬁcation is crucial for

improving the quality of the community division ob-

tained by the approach.

(Yan et al., 2018) proposed a measure that esti-

mates the variation of spectral properties of the graph

when edges are removed. They showed that the struc-

ture of real weighted networks is very robust under

weight thresholding when edges are removed if their

weight is below a threshold value computed with such

a measure.

This research line could be a starting point deserv-

ing deeper investigation which could be beneﬁcial for

determining the minimum number of nearest neigh-

bors to consider when building the sparse similarity

weighted matrix

Ω.

REFERENCES

Avrachenkov, K., Chebotarev, P., and Rubanov, D. (2017).

Kernels on graphs as proximity measures. In Inter-

national workshop on algorithms and models for the

web-graph, pages 27–41. Springer.

Avrachenkov, K., Chebotarev, P., and Rubanov, D. (2019).

Similarities on graphs: Kernels versus proximity mea-

sures. European Journal of Combinatorics, 80:47–56.

Aynulin, R. (2019). Impact of network topology on ef-

ﬁciency of proximity measures for community de-

tection. In International Conference on Complex

Networks and Their Applications, pages 188–197.

Springer.

Barrat, A., Barthelemy, M., Pastor-Satorras, R., and Vespig-

nani, A. (2004). The architecture of complex weighted

networks. In Proc. National Academy of Science,

pages 101,3747.

Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Lefeb-

vre, E. (2008). Fast unfolding of communities in large

networks. Journal of statistical mechanics: theory

and experiment, 2008(10):P10008.

Chandra, A. K., Raghavan, P., Ruzzo, W. L., Smolensky,

R., and Tiwari, P. (1996). The electrical resistance of

a graph captures its commute and cover times. Com-

putational Complexity, 6(4):312–340.

Deza, M. M. and Deza, E. (2009). Encyclopedia of dis-

tances. In Encyclopedia of distances, pages 1–583.

Springer.

Dijkstra, E. W. et al. (1959). A note on two problems

in connexion with graphs. Numerische mathematik,

1(1):269–271.

Doyle, P. and Snell, J. (1989). Random walks and electric

networks. Mathematical Association of America.

Fortunato, S. and Hric, D. (2016). Community detection in

networks: A user guide. Physics reports, 659:1–44.

Ghosh, A., Boyd, S., and Saberi, A. (2008). Minimizing

effective resistance of a graph. SIAM Rev., 50(1):37–

66.

Girvan, M. and Newman, M. E. (2002). Community struc-

ture in social and biological networks. Proceedings of

the national academy of sciences, 99(12):7821–7826.

Goldberg, D. E. (1989). Genetic algorithms in search. Op-

timization, and MachineLearning.

Klein, D. J. and Randi

c, M. (1993). Resistance distance.

Journal of mathematical chemistry, 12(1):81–95.

Lancichinetti, A., Fortunato, S., and Radicchi, F. (2008).

Benchmark graphs for testing community detection

algorithms. Physical review E, 78(4):046110.

Park, Y. and Song, M. (1998). A genetic algorithm for clus-

tering problems. In Proceedings of the third annual

conference on genetic programming, volume 1998,

pages 568–575.

Pizzuti, C. (2018). Evolutionary computation for commu-

nity detection in networks: a review. IEEE Transac-

tions on Evolutionary Computation, 22(3):464–483.

Radicchi, F., Ramasco, J. J., and Fortunato, S. (2011). Infor-

mation ﬁltering in complex weighted networks. Phys-

ical Review E, E83:046101.

Rosvall, M. and Bergstrom, C. T. (2008). Maps of random

walks on complex networks reveal community struc-

ture. Proceedings of the National Academy of Sci-

ences, 105(4):1118–1123.

Saerens, M., Fouss, F., Yen, L., and Dupont, P. (2004). The

principal components analysis of a graph, and its re-

lationships to spectral clustering. In European confer-

ence on machine learning, pages 371–383. Springer.

Sommer, F., Fouss, F., and Saerens, M. (2016). Compari-

son of graph node distances on clustering tasks. In In-

ternational Conference on Artiﬁcial Neural Networks,

pages 192–201. Springer.

Spielman, D. A. and Srivastava, N. (1996). Graph spar-

siﬁcation by effective resistances. Siam Journal on

Computing, (40):1913.

An Effective Resistance based Genetic Algorithm for Community Detection

Tumminello, M., Aste, T., Matteo, T. D., , and Mantegna,

R. N. (2005). A tool for ﬁltering information in com-

plex systems. In Proc. National Academy of Science,

pages 102,10421.

Van Mieghem, P. (2010). Graph spectra for complex net-

works. Cambridge University Press.

Van Mieghem, P., Devriendt, K., and Cetinay, H. (2017).

Pseudoinverse of the laplacian and best spreader node

in a network. Physical Review E, 96(3):032311.

Yan, X., Jeub, L. G. S., Flammini, A., Radicchi, F., and

Fortunato, S. (2018). Weight thresholding on complex

networks. Physical Review E, E98:042304.

Yen, L., Fouss, F., Decaestecker, C., Francq, P., and

Saerens, M. (2007). Graph nodes clustering based

on the commute-time kernel. In Paciﬁc-Asia Con-

ference on Knowledge Discovery and Data Mining,

pages 1037–1045. Springer.

Yen, L., Fouss, F., Decaestecker, C., Francq, P., and

Saerens, M. (2009). Graph nodes clustering with the

sigmoid commute-time kernel: A comparative study.

Data & Knowledge Engineering, 68(3):338–

361.

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications