An Evaluation of Hubness Reduction Methods for Entity Alignment with

Knowledge Graph Embeddings

Daniel Obraczka

and Erhard Rahm

ScaDS.AI/Database Group, Leipzig University, Germany

Keywords:

Hubness Reduction, Nearest Neighbor Search, Knowledge Graph Embedding, Entity Alignment.

Abstract:

The heterogeneity of Knowledge Graphs is problematic for conventional data integration frameworks. A

possible solution to this issue is using Knowledge Graph Embeddings (KGEs) to encode entities into a lower-

dimensional embedding space. However, recent ﬁndings suggest that KGEs suffer from the so-called hubness

phenomenon. A dataset that suffers from hubness has a few popular entities that are nearest neighbors of a

highly disproportionate amount of other entities. Because the calculation of nearest neighbors is an integral

part of entity alignment with KGEs, hubness reduces the accuracy of the matching result. We therefore investi-

gate a variety of hubness reduction techniques and utilize approximate nearest neighbor (ANN) approaches to

offset the increase in time complexity stemming from the hubness reduction. Our results suggest, that hubness

reduction in combination with ANN techniques improves the quality of nearest neighbor results signiﬁcantly

compared to using no hubness reduction and exact nearest neighbor approaches. Furthermore, this advantage

comes without losing the speed advantage of ANNs on large datasets.

1 INTRODUCTION

Knowledge Graphs (KGs) contain information

in structured machine-readable form as triples

(sub ject, predicate,ob ject). Integrating multiple

KGs is a necessary step for a plethora of downstream

tasks such as question answering (Usbeck et al.,

2019), recommender systems (Sun et al., 2020a) and

many more. The heterogeneous nature of KGs poses

a challenge to many data integration frameworks.

In recent years Knowledge Graph Embeddings

(KGEs) have seen a surge of attention from the

research community as a possible solution to tackle

the heterogeneous nature of this data structure (Ali

et al., 2020; Sun et al., 2020b). While numerous

models have been devised to obtain KGEs, little

consideration has been given to reﬁning their use in

the alignment step of the data integration pipeline.

A recent study (Sun et al., 2020b) has discovered,

that KGEs suffer from a problem called hubness,

which refers to an unequal distribution of k-nearest

neighbors (kNN) between points. In data that suffers

from hubness a few hubs are the kNN of a lot of

data points, while many data points are the nearest

https://orcid.org/0000-0002-0366-9872

https://orcid.org/0000-0002-2665-1114

neighbors of no other points. Hubness can be found

in many high-dimensional datasets (Feldbauer et al.,

2018) and given the importance of kNN in a diverse

range of tasks this ﬁnding has been determined as a

problem in applications such as recommender sys-

tems (Hara et al., 2015a),speech recognition (Vincent

et al., 2014), image classiﬁcation (Toma

sev and

Buza, 2015) and many more. For a data integration

setting where usually an entity only has one true

match in another dataset hubness is detrimental for

the alignment quality. To investigate the effects

of hubness on data integration tasks we used 15

different Knowledge Graph Embedding approaches

on 16 alignment tasks containing samples of KGs

with varying properties. This procedure resulted in

240 KGEs as input for our study. We examine six

different hubness reduction methods and six different

(approximate) nearest neighbor algorithms with

regards to accuracy and execution time.

The contributions of our work are as follows:

• We provide the ﬁrst (to our knowledge) extensive

evaluation of hubness reduction techniques for en-

tity alignment with knowledge graph embeddings.

• The result of our work suggests, that using ap-

proximate nearest neighbor algorithms with hub-

ness reduction improves kNN results for align-

Obraczka, D. and Rahm, E.

An Evaluation of Hubness Reduction Methods for Entity Alignment with Knowledge Graph Embeddings.

DOI: 10.5220/0010646400003064

In Proceedings of the 13th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2021) - Volume 2: KEOD, pages 28-39

ISBN: 978-989-758-533-3; ISSN: 2184-3228

ment signiﬁcantly in terms of accuracy and for

large datasets also with regards to execution time.

We ensure the signiﬁcance of our ﬁndings with

statistical tests.

• We present the ﬁrst framework for entity align-

ment, that makes a wide array of hubness reduc-

tion methods available https://github.com/dobra

czka/kiez. Furthermore we make all our results

and conﬁgurations freely available in a seperate

benchmarking repository https://github.com/dob

raczka/kiez-benchmarking.

We start by giving an overview of related work,

followed by a synopsis of hubness reduction for the

problem of entity alignment in Section 3. Our exten-

sive evaluation follows in Section 4 and we close with

a conclusion.

2 RELATED WORK

We start by motivating the hubness problem and the

related research. Subsequently, we present different

methods to mitigate hubness. Finally, we give a brief

overview over different KGE approaches.

2.1 Hubness

First noticed in music recommendation (Pachet

and Aucouturier, 2004) the phenomenon of hub-

ness has been shown to occur in high-dimensional

data (Radovanovic et al., 2009). A facet of the so-

called curse of dimensionality is that distances be-

tween all points in high-dimensional data become

very similar. The reason for this distance concentra-

tion, is that with increasing dimensions the volume of

a unit hypercube grows faster than the volume of a

unit hyperball. Correspondingly, numerous distance

metrics (e.g. the euclidean distance) lose their rel-

ative contrast, i.e. given a query point the distance

between the nearest and farthest neighbor decreases

almost entirely (Aggarwal et al., 2001). Related to

nearest neighbors (NN) is the problem of hubness.

Deﬁnition 1 (k-occurence). Given a non-empty

dataset D ⊆ R

with n objects in an m-dimensional

space. We can count how often an object x ∈ D oc-

curs in the k-nearest neighbors of all other objects

D\x. This count is referred to as k-occurrence O

(x).

Hubness now refers to the problem, that with

increasing dimensionality the distribution of the k-

occurence is skewed to the right, which signiﬁes the

occurence of hubs, i.e. ”popular” nearest neighbors,

that occur more frequently in k-NN lists than other

points (Feldbauer et al., 2018). The hubness phe-

nomenon is not yet well understood. While some em-

pirical results indicate, that hubness arises with high

intrinsic dimensionality of the data (Radovanovi

et al., 2010), a later study suggests, that density gra-

dients are the reason for hubness (Low et al., 2013).

Density gradients are spatial variations in density in

an area, in this case over an empirical data distribu-

tion (Feldbauer and Flexer, 2019).

2.2 Hubness Reduction

Several different approaches have been proposed to

reduce hubness. Given two objects x and y the near-

est neighbor relation between them is symmetric if

x is a nearest neighbor of y and vice versa. Hub-

ness leads to an asymmetry in NN relations, be-

cause hubs are NNs of many data points, while only

one data point can be the nearest neighbor of a

hub (Feldbauer and Flexer, 2019). One category of

hubness reduction methods therefore tries to mend

asymmetric relations by transforming these relations

to secondary distance spaces from primary distance

spaces (e.g. euclidean). While for example mu-

tual proximity (Schnitzer et al., 2012) was developed

speciﬁcally to reduce hubness, other methods such

as local scaling (Zelnik-Manor and Perona, 2004)

and the (non-iterative) contextual dissimilarity mea-

sure (J

egou et al., 2007) were later found to reduce

hubness (Schnitzer et al., 2012). Spatial centrality

refers to the fact, that objects closer to the mean of

a data distributions are more likely to to become hubs

with increasing dimensionality (Radovanovi

c et al.,

2010). Accordingly, another category of hubness re-

duction techniques aims to reduce spatial centrality

by subtracting the centroid of the data (Suzuki et al.,

2013) or localized centering (Hara et al., 2015b). Sub-

sequent works argue that variants of these centering

approaches work in reducing hubness by ﬂattening

the density gradient (Hara et al., 2016). For a more

comprehensive overview of hubness reduction tech-

niques we refer to (Feldbauer et al., 2018; Feldbauer

and Flexer, 2019). In Section 3.3 we will present a

more detailed view of the mentioned approaches with

regards to entity alignment.

2.3 Knowledge Graph Embedding

Knowledge Graph Embedding approaches aim to en-

code KG entities into a lower-dimensional space.

This alleviates the heterogeneity present across differ-

ent KGs and makes it usable for downstream machine

learning tasks.

An Evaluation of Hubness Reduction Methods for Entity Alignment with Knowledge Graph Embeddings

Translational models encode relations as trans-

lations from the embedding of the head entity to

tail entity embedding. The pioneering approach

TransE (Bordes et al., 2013) relies on the distance be-

tween h + r and t, where h, r and t are the respec-

tive embedding vectors of the head and tail entity h,t

and the relation r of the triple (h,r,t). TransE has

problems modeling 1 −n or n −n relations. To ad-

dress this shortcoming several different methods were

devised which encode relations in their own hyper-

plane (Wang et al., 2014) or even relation-speciﬁc

spaces (Lin et al., 2015).

Another category of embedding approaches re-

lies on tensor-factorization. RESCAL (Nickel et al.,

2011) models a KG as a 3D binary tensor X ∈R

n×n×m

with n and m being the number of entities and rela-

tions respectively. Each relation therefore is a matrix

∈ R

n×n

, with the weights w

i, j

capturing the inter-

action between the i-th latent factor of h and j-th la-

tent factor of t. The plausibility of a triple (h,r,t) is

therefore scored by

f (h,r,t) = h

t. (1)

Several methods (Sun et al., 2019; Nickel et al., 2016;

Kazemi and Poole, 2018) build on this idea by using

different scoring functions.

With the success of deep learning techniques in

other ﬁelds, they were applied to KGEs as well.

ConvE (Dettmers et al., 2018) relies on a set of

2-dimensional convolutional ﬁlters to capture in-

teractions between h and r. The approach GC-

NAlign (Wang et al., 2018) uses attribute embeddings

with graph convolutions to embed cross-lingual KG

entities into a uniﬁed vector space.

Path-based approaches incorporate information of

multi-hop neighbors of nodes. For example IP-

TransE (Zhu et al., 2017) relies on an extension of

TransE to incorporate multi-step paths.

2.4 Entity Alignment

Extensive research has been done to devise meth-

ods that aid in the matching of entities across dif-

ferent data sources. While most methodologies cen-

ter around aligning tabular data (Christen, 2012), the

ﬁeld of collective entity resolution exploits relational

information in the alignment process (Bhattacharya

and Getoor, 2007). For example (Pershina et al.,

2015) use Personalized PageRank to propagate sim-

ilarities in their graph of potential matches. (Huang

et al., 2020) utilize a human-in-the-loop approach

to make high-quality alignments leveraging relational

information.

A plethora of approaches have been devised to

tackle entity alignment via KGE. These techniques

usually rely on a given seed alignment containing en-

tity pairs, which are known to refer to the same real-

world object. MultiKE learns entity embeddings by

using different views for different aspects of an en-

tity (Zhang et al., 2019). AttrE (Trisedya et al., 2019)

relies on an attribute encoding function to encode the

entity attributes of the different KGs into the same

space. Both MultiKE and AttrE rely on a translational

approach to encode relationship information.

For a more detailled overview over KGEs we refer

the reader to these surveys (Ali et al., 2020; Dai et al.,

2020). A synopsis and benchmarking study of KGE

approaches that are used for entity alignment can be

found in (Sun et al., 2020b). This study also discov-

ered, that KGEs suffer from hubness. However, to our

knowledge, no systematic study on hubness reduction

methods for entity alignment with knowledge graph

embeddings has been published.

3 HUBNESS REDUCTION FOR

ENTITY ALIGNMENT

In the following, we illustrate the task of entity align-

ment, present ways to measure hubness and provide

some details of our framework and the hubness re-

duction methods we implemented for the use case of

entity alignment. Finally, we give an overview of the

approximate nearest neighbor approaches we utilize.

3.1 Entity Alignment

For our purposes a KG is a tuple K G = (E, P,L, T ),

where E is the set of entities, P the set of properties,

L the set of literals and T the set of triples. KGs

consist of triples (h, r,t) ∈ T , with h ∈ E, r ∈ P and

t ∈ {E, L}. Given two KGs the goal of entity align-

ment lies in ﬁnding the mapping M = {(e

) ∈

×E

≡ e

}, where ≡ refers to the equivalence

relation. E

and E

are the entity sets of the respective

KGs.

3.2 Hubness

There are several ways to measure hubness. The old-

est approach (Radovanovi

c et al., 2010) measures the

skewness in the k-occurence O

= E[(O

−µ

)

]/σ

. (2)

In this equation E is the expected value, µ indicates

the mean and σ the standard deviation. Because this

k-skewness is difﬁcult to interpret (Feldbauer et al.,

KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development

2018) adapted an income inequality measure called

Robin Hood index to calculate k-occurence inequality

∑

x∈D

(x) −µ

(

∑

x∈D

(x)) −k)

∑

x∈D

(x) −k|

2k(n −1)

(3)

where D is a dataset of size n. The authors point out

that this measure is easily interpretable, since it an-

swers the question: ”What share of ’nearest neighbor

slots’ must be redistributed to achieve k-occurence

equality among all objects?” (Feldbauer et al., 2018).

3.3 Hubness Reduction

For aligning two KGs we are interested in ﬁnding the

most similar entities between the KGs. Let K

the embeddings of the two KGs we want to align.

Given a distance measure d

x,y

, where x ∈ K

and

y ∈ K

we will refer to the k points with the lowest

distance to x as it’s k-nearest neighbors.

In the following we will present our open-source

framework for hubness reduction for entity align-

ment. Our implementation relies on an adaptation

of (Feldbauer et al., 2020) for our use-case. An

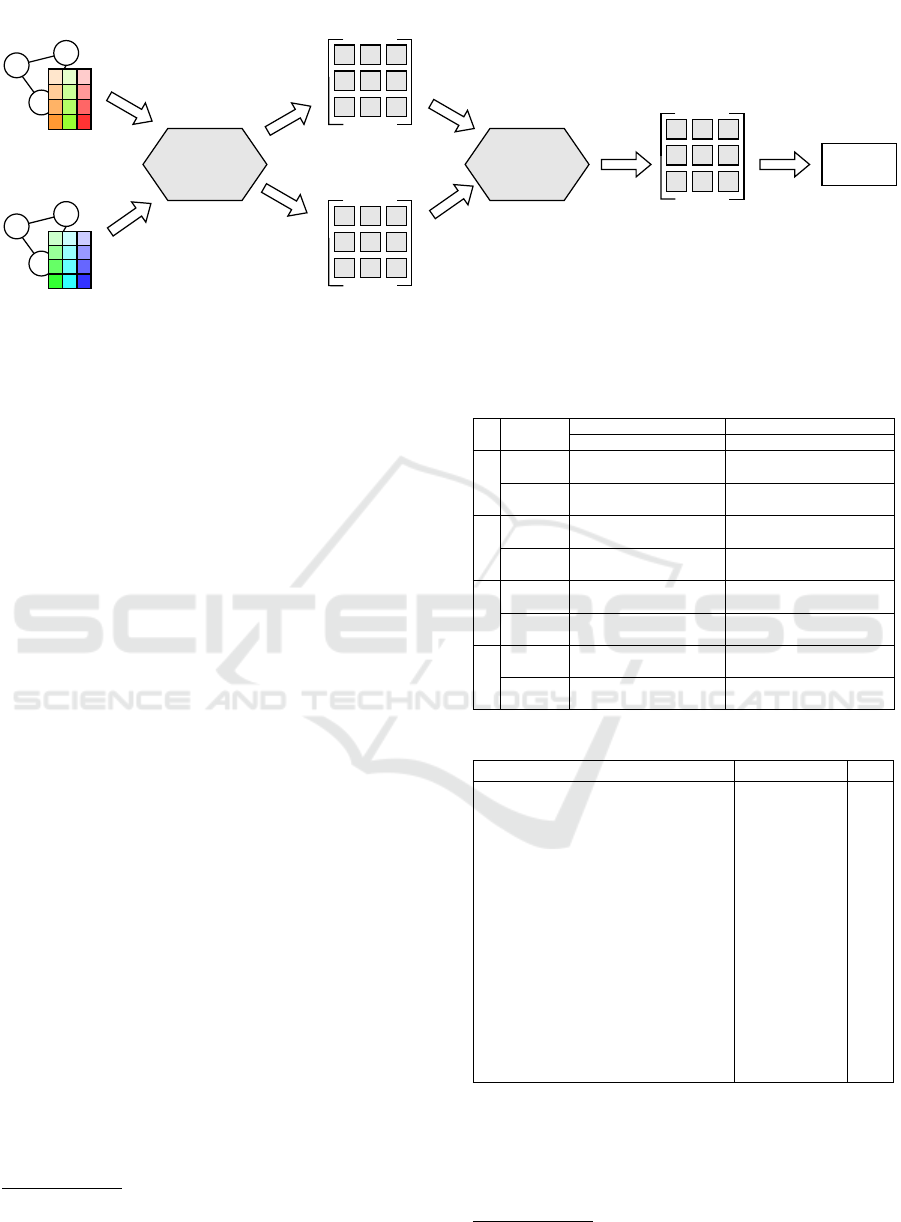
overview of the workﬂow of our framework is shown

in Figure 1. Given two KGEs of the data sources we

wish to align, we ﬁrst retrieve a number of kNN can-

didates using a primary distance measure (e.g. eu-

clidean). We need kNN candidates for all x ∈ K

, as

well as y ∈ K

. Bear in mind, that while the distance

between such two points x and y is the same no matter

whether x is a kNN candidate of y or vice versa, due to

hubness x might be a kNN candidate of y but not the

other way round. Using these primary distances we

can apply hubness reduction methods to obtain sec-

ondary distances. These secondary distances are used

to obtain the ﬁnal kNN from the kNN candidates. We

implemented the possibility to use approximate near-

est neighbor libraries to obtain the primary distances.

As we will see in Section 4, this gives a speed advan-

tage on larger datasets. More information about the

ANN approaches is given in Section 3.4.

In the following we present the hubness reduc-

tion approaches we implemented, which were the

best performing techniques reported in (Feldbauer

and Flexer, 2019). Local Scaling (LS) was ﬁrst intro-

duced in (Zelnik-Manor and Perona, 2004) and later

discovered to reduce hubness (Schnitzer et al., 2012).

Given a distance d

x,y

it calculates the pairwise sec-

ondary distance

LS(d

x,y

) = 1 −exp

−

x,y

(4)

where σ

(or resp. σ

) is the distance between x (resp.

y) and their kth-nearest neighbor

Closely related to local scaling is the non-iterative

contextual dissimilarity measure (NICDM) (J

egou

et al., 2007) which was ﬁrst applied to hubness reduc-

tion in the same study as LS (Schnitzer et al., 2012):

NICDM(d

x,y

) =

x,y

√

,µ

, (5)

with µ

being the mean distance to the k-nearest

neighbors of x and analogously for y and µ

Cross-domain similarity local scaling (CSLS) (Lam-

ple et al., 2018) was introduced to reduce hubness in

word embeddings. As the previous approaches it re-

lies on scaling locally:

CSLS(d

x,y

) = 2 ·d

x,y

−µ

(6)

with µ

being the mean distance from x to its k-nearest

neighbors. This measure was shown in (Sun et al.,

2020b) to successfully reduce hubness in knowledge

graph embeddings.

Mutual Proximity (MP) (Schnitzer et al., 2012)

counts the distances of entities whose distances to

both x and y are larger than d

x,y

emp

x,y

) =

|{j : d

x, j

> d

x,y

}∩{j : d

y, j

> d

y,x

n −2

(7)

The version in Equation 7 was adapted by (Feldbauer

and Flexer, 2019) to normalize the range to [0,1].

Since this measure is computationally expensive an

approximation can be used, that relies on estimating

the sample mean ˆµ

and variance

of the distances

of all other objects to x:

Gauss

x,y

) = SF(d

x,y

, ˆµ

) ·SF(d

x,y

, ˆµ

(8)

In this equation SF is the complement to the cumula-

tive density function at d

x,y

The ﬁnal hubness reduction method we implemented

is DSL (Hara et al., 2016). This technique relies on

ﬂattening the density gradient, by estimating the local

centroids c

(x) =

∑

∈kNN(x)

, with kNN(x) being

the set of k-nearest neighbors of x. This leads to the

following formula:

DSL(x,y) = kx −yk

−kx −c

(x)k

−kx −c

(y)k

(9)

3.4 Approximate Nearest Neighbors

Due to the relatively high time complexity of hubness

reduction methods and the successful use of approxi-

mate nearest neighbor (ANN) approaches to mitigate

this problem (Feldbauer et al., 2018), we utilize three

ANN algorithms for our study:

• HNSW (Malkov, 2018) is an extension of naviga-

ble small world graphs, that exploits a hierarchical

structure of proximity graphs.

An Evaluation of Hubness Reduction Methods for Entity Alignment with Knowledge Graph Embeddings

Obtain kNN

candidates

Primary Distances

S ➝ T

Primary Distances

T ➝ S

Hubness

reduction

kNN

Source KGE

Target KGE

SecondaryDistances

S ➝ T

Figure 1: Overview of our framework.

• NGT (Iwasaki, 2016) relies on the kNN graph for

indexing and greedy search.

• Annoy

is a tree-based approach, which splits

the dataset subsequently into smaller sections for

each node.

For a general benchmark of ANN algorithms

see (Aum

uller et al., 2020).

4 EVALUATION

The evaluation section begins with an overview of

our experimental setup including the datasets and em-

bedding approaches as well as conﬁgurations. After-

wards, we present our results in detail.

4.1 Evaluation Setup

The 16 alignment tasks we use for evaluation were

presented in (Sun et al., 2020b) and consist of sam-

ples from DBpedia (D), Wikidata (W) and Yago (Y).

These fragments of KGs contain a wide range of dif-

ferent relationships and entity types, as well as cover-

ing cross-lingual settings (EN-DE & EN-FR). There

are two sizes of datasets, depending on the number

of entitites: 15K and 100K. More information about

the datasets is shown in Table 1. The number of en-

tities in the respective datasets is equal to the size of

the respective M , which means the task consists of

ﬁnding a 1-1 alignment of entities between the two

datasets. Be aware, that we use an updated version

of the datasets

, which explains different results be-

tween our evaluation and the ﬁndings of (Sun et al.,

https://github.com/spotify/annoy

https://github.com/nju-websoft/OpenEA#dataset-ove

rview

Table 1: Statistics of datasets.

15K 100K

|T | |P | |L| |T | |P | |L|

D-W

D 90399 589 28237 628901 905 133931

W 180992 818 118515 939568 1135 542921

D 125361 341 25690 977153 645 137483

W 259051 578 146977 1466422 999 682367

D-Y

D 82384 421 25297 654603 665 101386

Y 143752 62 105710 1050305 69 497633

D 117665 161 22561 951332 506 97433

Y 177121 40 104546 1620426 66 578596

EN-DE

DE 184195 324 35630 922447 447 199527

EN 110079 500 28973 759025 831 147142

DE 253947 211 33185 1285853 358 200356

EN 144378 339 23831 1053340 648 139867

EN-FR

EN 104498 574 30281 693855 865 145103

FR 95265 613 28760 599010 818 157791

EN 148714 381 22761 1046052 742 145382

FR 136226 386 21645 904159 754 157564

Table 2: Embedding approaches used in the evaluation.

Approach Method Lit.

AttrE (Trisedya et al., 2019) Translation yes

BootEA (Sun et al., 2018) Translation -

ConvE (Dettmers et al., 2018) Neural -

GCNAlign (Wang et al., 2018) Neural yes

HolE (Nickel et al., 2016) Factorization -

IMUSE (He et al., 2019) Translation yes

IPTransE (Zhu et al., 2017) Path -

JAPE (Sun et al., 2017) Translation yes

MultiKE (Zhang et al., 2019) Translation yes

ProjE (Shi and Weninger, 2017) Neural -

RSN4EA (Guo et al., 2019) Path -

RotatE (Sun et al., 2019) Factorization -

SimplE (Kazemi and Poole, 2018) Factorization -

TransD (Ji et al., 2015) Translation -

TransH (Wang et al., 2014) Translation -

2020b). We however used the same hyperparameter

settings to create the KGEs as said study.

To create the KGEs of these datasets we used a

wide range of embedding approaches implemented in

the framework OpenEA

. Table 2 shows a summary

https://github.com/nju-websoft/OpenEA

KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development

of the 15 embedding approaches. With the 16 align-

ment tasks and 15 embedding approaches we there-

fore have 240 KGE pairs for our study.

For the exact nearest neighbor search we used the

scikit-learn (Pedregosa et al., 2011) implementations

of Ball Tree (Omohundro, 1989), KD-Tree (Bent-

ley, 1975) and their brute-force variant which does

not exploit metric space advantages. The approxi-

mate nearest neighbor algorithms used were Annoy,

NGT and HNSW. For all algorithms we found, that

their default settings gave the best results, except

for HNSW where the hyperparameters M = 96 and

e fConstruction = 500 showed the best results. More

details can be found in our benchmarking repository

https://github.com/dobraczka/kiez-benchmarking.

Our experiment setting consists of doing a full

alignment between the data sources, i.e. ﬁnding the

k nearest neighbors of all the source entities in the

target entity embeddings. We choose k = 50 and al-

lowed 100 kNN candidates to obtain the primary dis-

tances. The primary distance was euclidean for all

algorithms, except for HNSW, where it was cosine.

For all experiments we used a single machine

running CentOS 7 with 4 AMD EPYC 7551P 32-

Core CPUs. For the small dataset experiments we al-

lowed 10GB of RAM. The experiments with the large

datasets were provided 30GB of RAM.

To evaluate the retrieval quality of the different

techniques we use the hits@k metric:

hits@k(kNN) =

|{t : y ∈ kNN(x) ∧(x,y) ∈ M }|

|M |

(10)

where kNN are the calculated nearest neighbors and

kNN(x) returns the k nearest neighbors of x. This

metric simply counts the proportion of true matches

t in the k nearest neighbors. While precision and re-

call are the most common metrics for data integration

tasks we choose hits@k, because it is the common

metric for entity alignment tasks and is a better mea-

sure of quality for neighbor-based tasks. In our case

we present hits@50, since we wanted the 50 nearest

neighbors.

Our evaluation is driven by three major questions:

): Does hubness reduction improve the alignment

accuracy?

): Does hubness reduction offset loss in retrieval

quality by ANN algorithms?

): Can hubness reduction be used with ANN al-

gorithms without loss of the speed advantage of

ANNs?

4.2 Results

4.2.1 Hubness Reduction with Exact Nearest

Neighbors

The initial quality of the KGEs plays a major role in

the absolute hits@k value. To address (Q

) we will

therefore look at the hits@k improvement of hubness

reduction methods compared to the baseline of using

no hubness reduction. We present a boxplot repre-

sentation of the results in Figure 2, which summa-

rizes the results over all embedding approaches per

alignment task. It is evident, that all hubness re-

duction methods tend to improve the results. There

are however differences between the approaches. We

can see for example that the two Mutual Proximity

variants perform the worst. In order to make statisti-

cally sound statements about differences between ap-

proaches we rely on the statistical analysis presented

by Dem

sar (Dem

sar, 2006) and the Python package

Autorank (Herbold, 2020), which makes these best

practices readily available. Since we have more than

two hubness reduction methods this means we ﬁrst

test if the average ranks of the methods are signiﬁ-

cantly different using the Friedman test. We do this

for the results across all datasets and embedding ap-

proaches. If we can determine signiﬁcant differences

in the results we perform a post-hoc Nemenyi test

to make a pairwise comparison of hubness reduction

methods. The resulting critical distance diagram is

shown in Figure 3. The lower the rank of the approach

the better. Connected groups are not signiﬁcantly dif-

ferent at signiﬁcance level α = 0.05. With excep-

tion of DSL and CSLS all approaches perform sig-

niﬁcantly different from another. We can especially

see that NICDM is signiﬁcantly better than all other

approaches. Our (Q

) is therefore answered.

Given the large variance seen in Figure 2 the im-

provements are very different between embedding ap-

proaches. We therefore take a closer look at some se-

lected approaches in Figure 4. First of all we can see

that there is a large difference in the hubness produced

by the three selected embedding approaches. While

BootEA has relatively low hubness even without hub-

ness reduction, SimplE has a Robin Hood index of

almost 75% percent. This means that for the latter

almost 75% of nearest neighbor slots would have to

be redistributed to obtain k-occurence equality. Since

BootEA’s hits@50 score is already very high there is

little room for improvement through hubness reduc-

tion. However for the two other approaches we can

see that hubness reduction can improve the hits@50

noticeably.

An Evaluation of Hubness Reduction Methods for Entity Alignment with Knowledge Graph Embeddings

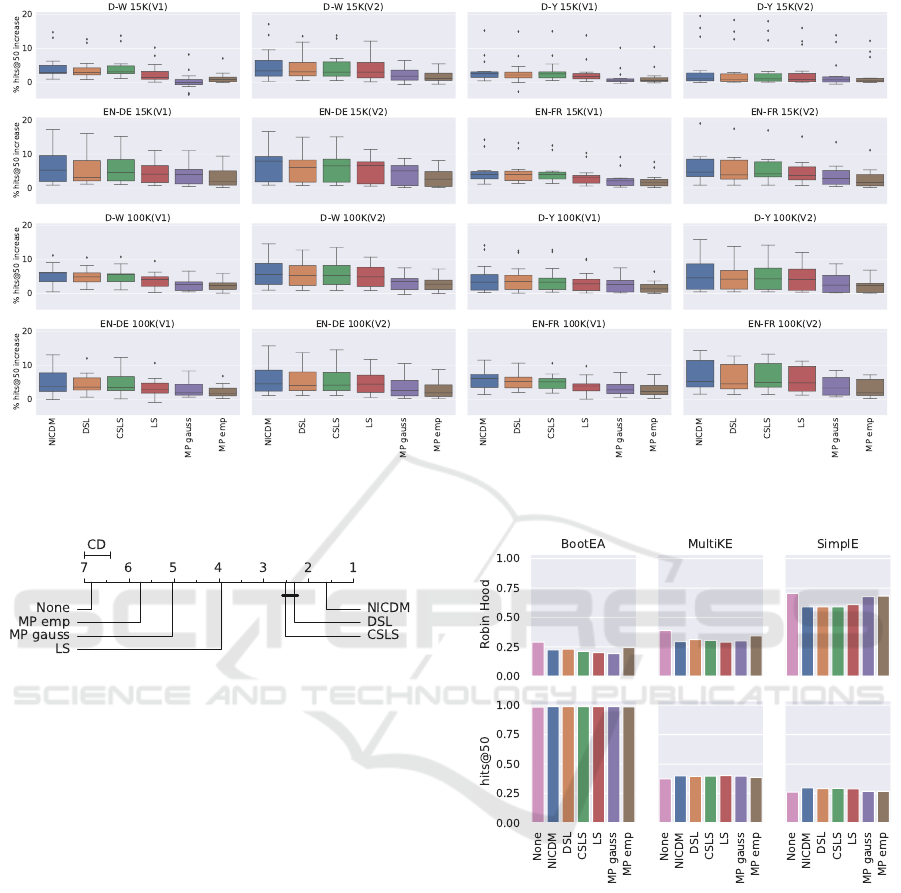
Figure 2: Improvement in hits@50 compared to no hubness reduction. Results are aggregated over different embedding

approaches.

Figure 3: Critical distance diagram for different hubness

reduction techniques w.r.t hits@50. Approaches that are not

signiﬁcantly different at α = 0.05 are connected. Low ranks

are better.

4.2.2 Hubness Reduction with Approximate

Nearest Neighbors

To answer (Q

) we compare the improvement of

hits@50 relative to the baseline with the same base-

line as before (exact NN search without hubness re-

duction). Figure 5 again summarizes these results

over all embedding approaches as boxplot. In con-

trast to Figure 2 we can see that there are many cases,

were the results are worse than the baseline, i.e. neg-

ative improvement. Especially Annoy tends to per-

form worse than the baseline and it has the highest

variance of all three approaches. HNSW seems to

perform the best with almost all results staying in the

positive range. To make more substantial statements

we will again use our aforementioned statistical test-

ing procedure. To make the critical distance diagram

less cluttered we only compare the the three best hub-

ness reduction methods from Figure 3 with the base-

line. The resulting critical distance diagram is shown

in Figure 6. There is no signiﬁcant difference be-

Figure 4: Robin Hood index and hits@50 for selected em-

bedding approaches on D-Y 100K(V2) dataset.

tween Annoy and the baseline. NGT with DSL and

CSLS is also not signiﬁcantly different from the base-

line. HNSW with DSL and NICDM performs the

best and is signiﬁcantly different from all other ap-

proaches. The answer to (Q

) is therefore nuanced:

While not all ANN algorithms can achieve the same

quality as the baseline, given the right algorithm and

hubness reduction technique we can not only match

the performance of exact NN algorithms, but we can

signiﬁcantly outperform them.

KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development

Figure 5: Improvement in hits@50 compared to using no hubness reduction with an exact NN algorithm. Results are aggre-

gated over different embedding approaches.

Figure 6: Critical distance diagram for different algorithms

and hubness reduction techniques with regards to hits@50.

Approaches that are not signiﬁcantly different at α = 0.05

are connected. Low ranks are better.

4.2.3 Execution Time

To answer our last research question we investigate

the difference in execution time for the large and

small datasets seperately. The results are shown in

Figure 7. Generally we can see that Annoy is the

fastest approach, however, as mentioned before, the

low accuracy in terms of hits@50 disqualiﬁes it for

our use case. Surprisingly, the brute approach is the

fastest exact algorithm on all our datasets. On the

small datasets Brute is the fastest hiqh-quality ap-

proach without hubness reduction and has similar ex-

ecution time as HNSW, when hubness reduction is

used. Looking at the 100K datasets, we see the clear

speed advantage of the ANN algorithms. For our sig-

niﬁcance test we are interested to determine speed ad-

vantages of high-quality algorithm/hubness reduction

combinations. We therefore ignore Annoy in the crit-

ical distacnce diagram shown in Figure 8. We can

see that except for NGT with DSL all approaches are

signiﬁcantly faster than the baseline (Exact/None).

HNSW with NICDM is signiﬁcantly faster than all

other approaches except HNSW with CSLS.

4.2.4 Additional Results

Given our results for the 50 nearest neighbors we

are also able to determine hits@k scores for dif-

ferent k values. In Figure 9 we show results for

hits@{1,10,25}. For space reasons we show box-

plots, that aggregate the results over all datasets and

embedding approaches. For a more granular presenta-

tion we refer to a report in our benchmark repository

We can see in the boxplots, that the quality in-

crease tends to be higher the lower k gets. For exam-

ple the median increase of HNSW with the hubness

reduction method NICDM is:

• 5.5% w.r.t hits@25

• 8.43% w.r.t hits@10

• 12.41% w.r.t hits@1

This makes sense because entities that are hubs tend

to occupy the most important nearest neighbor slots.

The increased variance with lower k is due to the fact,

that hits@k values tend get lower the lower k gets,

because it is a more difﬁcult task. This leaves more

room for possible improvement.

The biggest change we can see between different k

values is the performance of the DSL hubness reduc-

tion technique. We suppose that the reason for this is

https://github.com/dobraczka/kiez-benchmarking/blo

b/main/results/additional report.pdf

An Evaluation of Hubness Reduction Methods for Entity Alignment with Knowledge Graph Embeddings

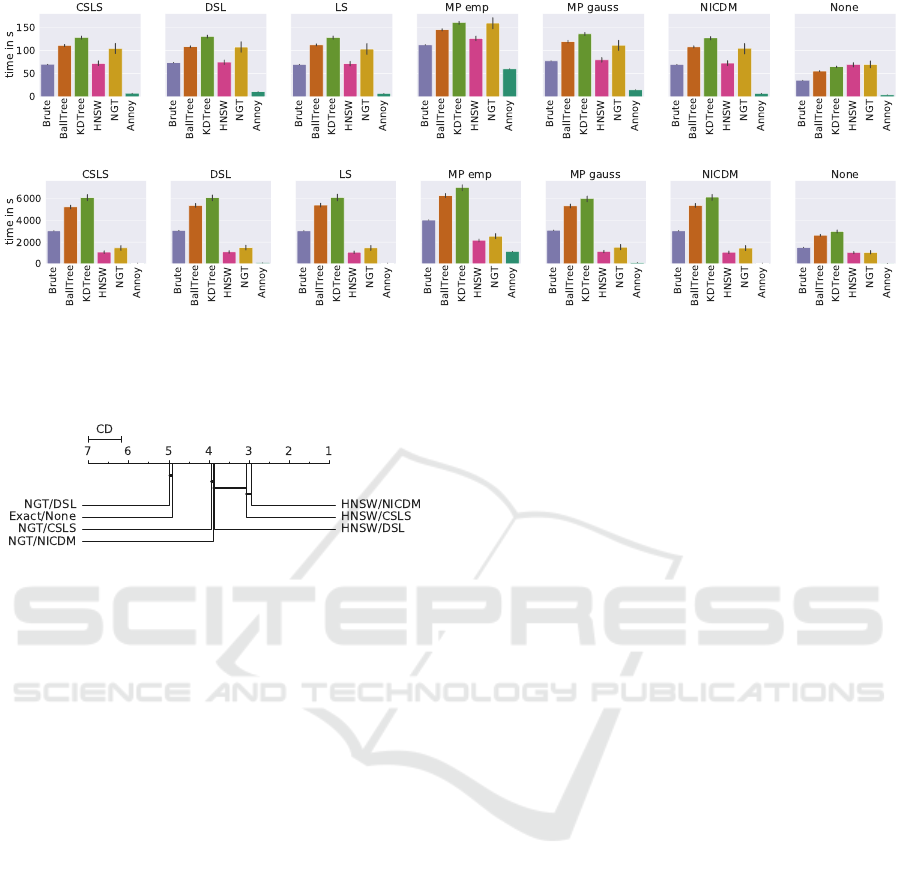
(a) 15K datasets

(b) 100K datasets

Figure 7: Time in seconds for different (A)NN algorithms and hubness reduction methods. Results are averaged over datasets

with black bar showing variance.

Figure 8: Critical distance diagram for different algorithms

and hubness reduction techniques with regards to execution

time. Approaches that are not signiﬁcantly different at α =

0.05 are connected. Low ranks are better.

that we ran our experiments for k=50 and set DSL’s k

parameter accordingly (see Eq. 9).

Another important observation is the improved

performance of Annoy w.r.t hits@1 in contrast to

hits@50. While Annoy still has a higher variance than

HNSW it’s results are comparable, but as stated be-

fore Annoy is much faster. Our general recommenda-

tions are therefore to use NICDM as hubness reduc-

tion technique and depending on the desired number

of kNN either HNSW for k > 1 or Annoy for k = 1.

5 CONCLUSION & FUTURE

WORK

In this study we investigated the advantages of us-

ing hubness reduction techniques for entity alignment

with knowledge graph embeddings. Our results sug-

gest that using methods to mitigate hubness improves

alignment results signiﬁcantly. This is also true when

comparing ANN algorithms to the baseline of using

no hubness reduction and exact NN algorithms. Us-

ing the ANN algorithm HNSW together with the hub-

ness reduction technique NICDM gives a median im-

provement in hits@50 of 3.18% and for large datasets

a median speedup of 1.88x. For small datasets the ex-

ecution time of HNSW with NICDM is similar to the

brute-force variant with NICDM.

We noticed even higher improvements in hits@1,

e.g. for HNSW with NICDM a median improvement

of 12.41% compared to the baseline. Given the high

improvements in terms of hits@1 it could be beneﬁ-

cial to utilize the hubness reduced distances as input

for clustering-based matchers (Saeedi et al., 2017).

Since KGEs are usually generated with the help

of known entity matches a worthwhile future investi-

gation could be the utilization of this training data in

the hubness reduction as well as to calculate the near-

est neighbors. Because KGEs are commonly trained

with the aid of GPUs investigating ANN libraries that

make use of this available resource could further in-

crease the speed advantage of ANN algorithms on the

task of entity alignment with KGEs.

ACKNOWLEDGEMENTS

This work was supported by the German Fed-

eral Ministry of Education and Research (BMBF,

01/S18026A-F) by funding the competence center

for Big Data and AI ”ScaDS.AI Dresden/Leipzig”.

Some computations have been done with resources of

Leipzig University Computing Center.

KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development

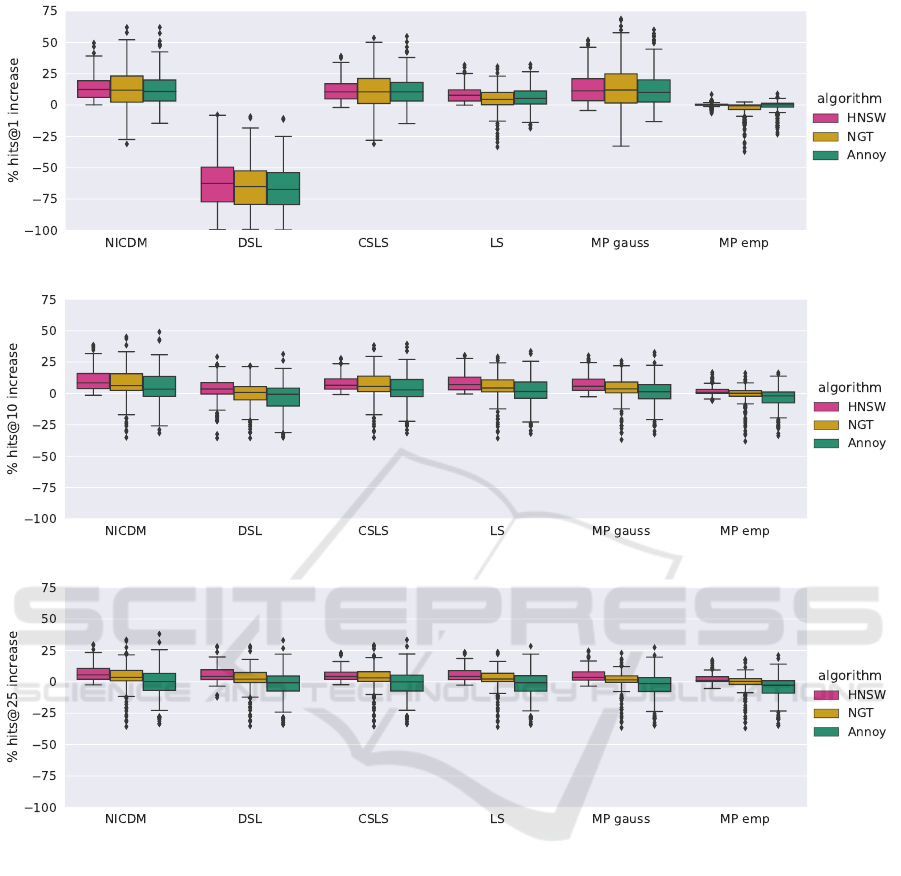
(a) % increase for hits@1

(b) % increase for hits@10

Figure 9: Increase in hits@{1,10,25} compared to baseline (exact NN algorithm without hubness reduction). Boxplot pre-

sentation shows aggregated results over different embedding approaches and all datasets.

REFERENCES

Aggarwal, C. C., Hinneburg, A., and Keim, D. A. (2001).

On the surprising behavior of distance metrics in

high dimensional space. Lecture Notes in Computer

Science (including subseries Lecture Notes in Artiﬁ-

cial Intelligence and Lecture Notes in Bioinformatics),

1973:420–434.

Ali, M., Berrendorf, M., Hoyt, C. T., Vermue, L., Galkin,

M., Sharifzadeh, S., Fischer, A., Tresp, V., and

Lehmann, J. (2020). Bringing light into the dark:

A large-scale evaluation of knowledge graph em-

bedding models under a uniﬁed framework. CoRR,

abs/2006.13365.

Aum

uller, M., Bernhardsson, E., and Faithfull, A. (2020).

ANN-Benchmarks: A benchmarking tool for approx-

imate nearest neighbor algorithms. Information Sys-

tems, 87.

Bentley, J. L. (1975). Multidimensional binary search

trees used for associative searching. Commun. ACM,

18(9):509–517.

Bhattacharya, I. and Getoor, L. (2007). Collective entity

resolution in relational data. ACM Trans. Knowl. Dis-

cov. Data, 1(1):5.

Bordes, A., Usunier, N., Garc

ıa-Dur

an, A., Weston, J., and

Yakhnenko, O. (2013). Translating embeddings for

modeling multi-relational data. In Advances in Neu-

An Evaluation of Hubness Reduction Methods for Entity Alignment with Knowledge Graph Embeddings

ral Information Processing Systems 26: 27th Annual

Conference on Neural Information Processing Sys-

tems 2013. Proceedings of a meeting held December

5-8, 2013, Lake Tahoe, Nevada, United States, pages

2787–2795.

Christen, P. (2012). Data Matching - Concepts and Tech-

niques for Record Linkage, Entity Resolution, and Du-

plicate Detection. Data-Centric Systems and Applica-

tions. Springer.

Dai, Y., Wang, S., Xiong, N. N., and Guo, W. (2020). A sur-

vey on knowledge graph embedding: Approaches, ap-

plications and benchmarks. Electronics (Switzerland),

9(5):1–29.

Dem

sar, J. (2006). Statistical comparisons of classiﬁers

over multiple data sets. Journal of Machine Learning

Research, 7:1–30.

Dettmers, T., Minervini, P., Stenetorp, P., and Riedel, S.

(2018). Convolutional 2d knowledge graph embed-

dings. In Proc. of AAAI, pages 1811–1818. AAAI

Press.

Feldbauer, R. and Flexer, A. (2019). A comprehensive

empirical comparison of hubness reduction in high-

dimensional spaces. Knowledge and Information Sys-

tems, 59(1):137–166.

Feldbauer, R., Leodolter, M., Plant, C., and Flexer, A.

(2018). Fast approximate hubness reduction for large

high-dimensional data. Proceedings - 9th IEEE Inter-

national Conference on Big Knowledge, ICBK 2018,

pages 358–367.

Feldbauer, R., Rattei, T., and Flexer, A. (2020). scikit-

hubness: Hubness reduction and approximate neigh-

bor search. Journal of Open Source Software,

5(45):1957.

Guo, L., Sun, Z., and Hu, W. (2019). Learning to ex-

ploit long-term relational dependencies in knowledge

graphs. In Proceedings of the 36th International Con-

ference on Machine Learning, ICML 2019, 9-15 June

2019, Long Beach, California, USA, volume 97 of

Proceedings of Machine Learning Research, pages

2505–2514. PMLR.

Hara, K., Suzuki, I., Kobayashi, K., and Fukumizu, K.

(2015a). Reducing hubness: A cause of vulnerabil-

ity in recommender systems. In Proc. of SIGIR, pages

815–818. ACM.

Hara, K., Suzuki, I., Kobayashi, K., Fukumizu, K., and

Radovanovic, M. (2016). Flattening the density gra-

dient for eliminating spatial centrality to reduce hub-

ness. In Proc. of AAAI, pages 1659–1665. AAAI

Press.

Hara, K., Suzuki, I., Shimbo, M., Kobayashi, K., Fukumizu,

K., and Radovanovic, M. (2015b). Localized center-

ing: Reducing hubness in large-sample data. In Proc.

of AAAI, pages 2645–2651. AAAI Press.

He, F., Li, Z., Qiang, Y., Liu, A., Liu, G., Zhao, P., Zhao, L.,

Zhang, M., and Chen, Z. (2019). Unsupervised entity

alignment using attribute triples and relation triples.

In Lecture Notes in Computer Science (including sub-

series Lecture Notes in Artiﬁcial Intelligence and Lec-

ture Notes in Bioinformatics), volume 11446 LNCS,

pages 367–382.

Herbold, S. (2020). Autorank: A python package for auto-

mated ranking of classiﬁers. Journal of Open Source

Software, 5(48):2173.

Huang, J., Hu, W., Bao, Z., and Qu, Y. (2020). Crowd-

sourced collective entity resolution with relational

match propagation. In Proc. of ICDE, pages 37–48.

IEEE.

Iwasaki, M. (2016). Pruned Bi-directed K-nearest neigh-

bor graph for proximity search. In Lecture Notes in

Computer Science (including subseries Lecture Notes

in Artiﬁcial Intelligence and Lecture Notes in Bioin-

formatics), volume 9939 LNCS, pages 20–33.

egou, H., Harzallah, H., and Schmid, C. (2007). A con-

textual dissimilarity measure for accurate and efﬁcient

image search. In 2007 IEEE Computer Society Con-

ference on Computer Vision and Pattern Recognition

(CVPR 2007), 18-23 June 2007, Minneapolis, Min-

nesota, USA. IEEE Computer Society.

Ji, G., He, S., Xu, L., Liu, K., and Zhao, J. (2015). Knowl-

edge graph embedding via dynamic mapping matrix.

In Proc. of ACL, pages 687–696, Beijing, China. As-

sociation for Computational Linguistics.

Kazemi, S. M. and Poole, D. (2018). Simple embedding

for link prediction in knowledge graphs. In Advances

in Neural Information Processing Systems 31: An-

nual Conference on Neural Information Processing

Systems 2018, NeurIPS 2018, December 3-8, 2018,

Montr

eal, Canada, pages 4289–4300.

Lample, G., Conneau, A., Ranzato, M., Denoyer, L., and

egou, H. (2018). Word translation without parallel

data. In Proc. of ICLR. OpenReview.net.

Lin, Y., Liu, Z., Sun, M., Liu, Y., and Zhu, X. (2015).

Learning entity and relation embeddings for knowl-

edge graph completion. In Proc. of AAAI, pages 2181–

2187. AAAI Press.

Low, T., Borgelt, C., Stober, S., and N

urnberger, A. (2013).

The hubness phenomenon: Fact or artifact? Studies in

Fuzziness and Soft Computing, 285:267–278.

Malkov, Y. A. (2018). Efﬁcient and robust approximate

nearest neighbor search using Hierarchical Navigable

Small World graphs. IEEE Transactions on Pattern

Analysis and Machine Intelligence, pages 31–33.

Nickel, M., Rosasco, L., and Poggio, T. A. (2016). Holo-

graphic embeddings of knowledge graphs. In Proc. of

AAAI, pages 1955–1961. AAAI Press.

Nickel, M., Tresp, V., and Kriegel, H. (2011). A three-way

model for collective learning on multi-relational data.

In Proceedings of the 28th International Conference

on Machine Learning, ICML 2011, Bellevue, Wash-

ington, USA, June 28 - July 2, 2011, pages 809–816.

Omnipress.

Omohundro, S. M. (1989). Five balltree construction al-

gorithms. Technical report, International Computer

Science Institute.

Pachet, F. and Aucouturier, J.-J. (2004). Improving timbre

similarity: How high is the sky. Journal of negative

results in speech and audio sciences, 1(1).

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Pershina, M., Yakout, M., and Chakrabarti, K. (2015).

Holistic entity matching across knowledge graphs. In

2015 IEEE International Conference on Big Data,

Big Data 2015, Santa Clara, CA, USA, October 29

- November 1, 2015, pages 1585–1590. IEEE Com-

puter Society.

Radovanovic, M., Nanopoulos, A., and Ivanovic, M.

(2009). Nearest neighbors in high-dimensional data:

the emergence and inﬂuence of hubs. In Proceed-

ings of the 26th Annual International Conference on

Machine Learning, ICML 2009, Montreal, Quebec,

Canada, June 14-18, 2009, volume 382 of ACM Inter-

national Conference Proceeding Series, pages 865–

872. ACM.

Radovanovi

c, M., Nanopoulos, A., and Ivanovi

c, M.

(2010). Hubs in space: Popular nearest neighbors in

high-dimensional data. Journal of Machine Learning

Research, 11.

Saeedi, A., Peukert, E., and Rahm, E. (2017). Comparative

evaluation of distributed clustering schemes for multi-

source entity resolution. In Advances in Databases

and Information Systems - 21st European Confer-

ence, ADBIS 2017, Nicosia, Cyprus, September 24-

27, 2017, Proceedings, volume 10509 of Lecture

Notes in Computer Science, pages 278–293. Springer.

Schnitzer, D., Flexer, A., Schedl, M., and Widmer, G.

(2012). Local and global scaling reduce hubs in space.

Journal of Machine Learning Research, 13.

Shi, B. and Weninger, T. (2017). Proje: Embedding pro-

jection for knowledge graph completion. In Proc. of

AAAI, pages 1236–1242. AAAI Press.

Sun, R., Cao, X., Zhao, Y., Wan, J., Zhou, K., Zhang,

F., Wang, Z., and Zheng, K. (2020a). Multi-modal

knowledge graphs for recommender systems. In

CIKM ’20: The 29th ACM International Conference

on Information and Knowledge Management, Virtual

Event, Ireland, October 19-23, 2020, pages 1405–

1414. ACM.

Sun, Z., Deng, Z., Nie, J., and Tang, J. (2019). Rotate:

Knowledge graph embedding by relational rotation in

complex space. In Proc. of ICLR. OpenReview.net.

Sun, Z., Hu, W., and Li, C. (2017). Cross-lingual entity

alignment via joint attribute-preserving embedding.

Lecture Notes in Computer Science (including sub-

series Lecture Notes in Artiﬁcial Intelligence and Lec-

ture Notes in Bioinformatics), 10587 LNCS:628–644.

Sun, Z., Hu, W., Zhang, Q., and Qu, Y. (2018). Bootstrap-

ping entity alignment with knowledge graph embed-

ding. In Proceedings of the Twenty-Seventh Inter-

national Joint Conference on Artiﬁcial Intelligence,

IJCAI 2018, July 13-19, 2018, Stockholm, Sweden,

pages 4396–4402. ijcai.org.

Sun, Z., Zhang, Q., Hu, W., Wang, C., Chen, M., Akrami,

F., and Li, C. (2020b). A benchmarking study

of embedding-based entity alignment for knowledge

graphs. Proc. VLDB Endow., 13(11):2326–2340.

Suzuki, I., Hara, K., Shimbo, M., Saerens, M., and Fuku-

mizu, K. (2013). Centering similarity measures to re-

duce hubs. In Proc. of EMNLP, pages 613–623, Seat-

tle, Washington, USA. Association for Computational

Linguistics.

Toma

sev, N. and Buza, K. (2015). Hubness-aware knn clas-

siﬁcation of high-dimensional data in presence of la-

bel noise. Neurocomputing, 160:157–172.

Trisedya, B. D., Qi, J., and Zhang, R. (2019). Entity Align-

ment between Knowledge Graphs Using Attribute

Embeddings. Proc. of AAAI, 33:297–304.

Usbeck, R., R

oder, M., Hoffmann, M., Conrads, F., Huth-

mann, J., Ngomo, A. N., Demmler, C., and Unger, C.

(2019). Benchmarking question answering systems.

Semantic Web, 10(2):293–304.

Vincent, E., Gkiokas, A., Schnitzer, D., and Flexer, A.

(2014). An investigation of likelihood normalization

for robust ASR. In INTERSPEECH 2014, 15th Annual

Conference of the International Speech Communica-

tion Association, Singapore, September 14-18, 2014,

pages 621–625. ISCA.

Wang, Z., Lv, Q., Lan, X., and Zhang, Y. (2018). Cross-

lingual knowledge graph alignment via graph convo-

lutional networks. In Proc. of EMNLP, pages 349–

357, Brussels, Belgium. Association for Computa-

tional Linguistics.

Wang, Z., Zhang, J., Feng, J., and Chen, Z. (2014). Knowl-

edge graph embedding by translating on hyperplanes.

In Proc. of AAAI, pages 1112–1119. AAAI Press.

Zelnik-Manor, L. and Perona, P. (2004). Self-tuning spec-

tral clustering. In Advances in Neural Information

Processing Systems 17 [Neural Information Process-

ing Systems, NIPS 2004, December 13-18, 2004,

Vancouver, British Columbia, Canada], pages 1601–

1608.

Zhang, Q., Sun, Z., Hu, W., Chen, M., Guo, L., and Qu,

Y. (2019). Multi-view knowledge graph embedding

for entity alignment. In Proceedings of the Twenty-

Eighth International Joint Conference on Artiﬁcial In-

telligence, IJCAI 2019, Macao, China, August 10-16,

2019, pages 5429–5435. ijcai.org.

Zhu, H., Xie, R., Liu, Z., and Sun, M. (2017). Iter-

ative entity alignment via joint knowledge embed-

dings. In Proceedings of the Twenty-Sixth Interna-

tional Joint Conference on Artiﬁcial Intelligence, IJ-

CAI 2017, Melbourne, Australia, August 19-25, 2017,

pages 4258–4264. ijcai.org.

An Evaluation of Hubness Reduction Methods for Entity Alignment with Knowledge Graph Embeddings