Exhaustive Solution for Mining Frequent Conceptual Links in Large

Networks using a Binary Compressed Representation

Hadjer Djahnit

and Malika Bessedik

Laboratoire des Méthodes de Conception de Systèmes (LMCS), Ecole Nationale Supérieure d’Informatique (ESI),

BP 68M -16 270 Oued Smar, Alger, Algeria

Keywords: Social Network Analysis, Data Mining, Graph Mining, Frequent Conceptual Links, Frequent Itemset Mining.

Abstract: In the domain of social network analysis, the frequent pattern mining task gives large opportunities for

knowledge discovery. One of the most recent variations of the pattern definition applied to social networks is

the frequent conceptual links (FCL). A conceptual link represents a set of links connecting groups of nodes

such as nodes of each group share common attributes. When the number of these links exceeds a predefined

threshold, it is referred to as a frequent conceptual link and it aims to describe the network in term of the most

connected type of nodes while exploiting structural and semantic information of the network. Since the

inception of this technique, a number of improvements were achieved in the search process in order to

optimise its performances. In this paper, we propose a new algorithm for extracting frequent conceptual links

from large networks. By adopting a new compressed structure for the network, the proposed approach reaches

up to 90% of gain in the execution time.

1 INTRODUCTION

Complex networks are a set of many connected nodes

that interact in different ways. In the context of

network theory, a complex network is a graph

(network) with non-trivial topological features that do

not occur in simple networks such as lattices or

random graphs but often occur in networks

representing real systems (Mata, 2020).

In the last decades, the study of complex networks

has become a very active research field with a strong

interdisciplinary character. Many different

phenomena in the physical, biological and social

world can be understood as network based, i.e. a

collection of objects connected by a number of links.

(Barabási, 2002). Indeed, these different kinds of

networks share fundamental properties that allow

researchers to study various problems such as

influence, propagation, terrorism and the spread of

infectious diseases in the same way (Barabasi, 2002).

They are based on a complex and evolving pattern of

bilateral connections between entities, whereby the

overall performance of the system is largely

https://orcid.org/0000-0002-8071-7057

https://orcid.org/0000-0002-1007-9096

determined by the intricate architecture of these

connections.

Among the most studied complex networks in

recent years, we find social networks. A social

network is defined as a network of interactions or

relationships, where the nodes consist of actors or

entities, and the edges consist of the relationships or

interactions between these actors (Aggarwal, 2011).

Social Network Analysis (SNA) studies the

underlying conditions of such social networks to

identify patterns of interaction between the network’s

actors to analyse and explain social phenomena using

graph theory metrics (Tabassum et al., 2018). This

analysis has been referred to as structural as it focuses

on the structure (links) of the network in order to

highlight some patterns and features, nodes with high

concentration of links, densely or weakly connected

regions, etc.

Nowadays, social networks, especially online

one, get larger and richer both with relational and

content data. This situation makes the SNA handling

new real world applications and facing new

challenges like scalability, dynamism and streaming.

Thus, data mining techniques appear as a very

180

Djahnit, H. and Bessedik, M.

Exhaustive Solution for Mining Frequent Conceptual Links in Large Networks using a Binary Compressed Representation.

DOI: 10.5220/0010654800003064

In Proceedings of the 13th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2021) - Volume 1: KDIR, pages 180-190

ISBN: 978-989-758-533-3; ISSN: 2184-3228

efficient tools in the social data analysis and provide

researchers with large opportunities for the

knowledge data discovery (Adedoyin, 2014).

Data mining functions include, inter alia,

clustering, classification, link prediction, and

frequent pattern mining, witch explicitly consider

links when building predictive or descriptive models

of the linked data (Getoor, 2005). Moreover, they

have the ability to exploit information about nodes

(attributes) or relationships between nodes (links) to

extract the maximum knowledge from the network.

One of the most recent approaches combining

both information on the structure and attributes of

nodes is the frequent conceptual links (FCL)

(Stattner, 2012; Stattner, 2012c). The FCL is a

descriptive data mining technique which aims to

extract, from a social network, knowledge about the

most connected type of nodes. It gathers, for

accomplishing this task, concepts from the

community detection, the frequent pattern mining and

the formal concept analysis techniques (Stattner,

2012b). In fact, this new pattern exploits the

community structure property of networks and starts

by grouping nodes into clusters or modules with

homogenous attributes (Fortunato, 2009). Then, as

for the frequent pattern mining problem (Agrawal,

1994; Luna, 2019; Agrawal, 2014; Cafaro, 2019), it

defines a support threshold and eliminate all the

groups (clusters) but those with a number of links

between their nodes more than a predefined

threshold. The result is a set of links called Frequent

Conceptual Links, connecting groups of nodes such

as nodes of each group share common attributes.

Hence, each part of the conceptual link is composed

by a set of attributes and the nodes verifying these

attributes, this is what is called a concept by the

concept theory (Kumar, 2011; Sumangali, 2017) in

the formal concept analysis (FCA). The advantage of

this kind of analysis is that the set of the conceptual

links of a network forms a concept lattice as defined

by the formal concept analysis and preserves all its

properties (Stattner, 2012b).

Moreover, a conceptual view of the network is

extracted. It consists of a reduced representation of

the original network which facilitates the task of

extracting knowledge from the network, chiefly for

larger networks. The nodes, or meta-nodes in this

view are groups of nodes in the original network

sharing common attributes and a link between two

meta-nodes represents the whole links between these

two groups (Stattner, 2012b).

The conceptual view is a key aspect of the

frequent conceptual links pattern, as it synthesizes

and summarizes the knowledge acquired from the

network in one visualisation tool allowing the

researcher to directly read the most connected

features of the network.

Figure 1: Application of FCLs to the amazon co-purshasing

network.

Figure 1 presents an extract of the conceptual

view extracted by the application of the FCLs

approach to the amazon co-purshasing network

(Leskovec, 2007). This summarized visualisation

depicts the type of products frequently co-purshased

by customers relatively to a support threshold. Every

node in the conceptual view corresponds to a group

of nodes in the original network characterised all by

the attributes that label the node. For instance, the

node (book, science) designates all the books of the

science category. Furthermore, a link between a

couple of nodes in the conceptual view represents the

whole links between the nodes of each group in the

original network. For instance, the link between the

nodes labelled (book, science) and (book, computers

& internet) designates all the books of the science

category that are co-purchased with the books of the

computers & internet category. The appearance of

this link on the conceptual view means that these

types of products are frequently co-purshased by the

amazon customers.

The FCL problem has been proven NP-hard

(Stattner, 2012a) since the search process depends on

the number of attributes, their valence (the sum of

possible number of attribute values), and the network

size (Stattner, 2012b) which leads to the explosion of

the search space over large networks. The challenge

is, then, to get the solution in a reasonable time. Thus

several attempts were driven in the literature to

optimize the search process, each trying to exploit

properties of the network in order to prune a part of

the search space. Accordingly, several efficient and

tailored exhaustive search methods are proposed to

overcome this difficulty. Each of them tries to achieve

Exhaustive Solution for Mining Frequent Conceptual Links in Large Networks using a Binary Compressed Representation

181

a good trade-off between the runtime and the number

of extracted FCLs relatively to the predefined

threshold. Indeed, the number of the FCLs depends

on the threshold set in the beginning of the algorithm.

A higher threshold allows extracting the FCLs in a

short time, but the result is not significant enough,

since most of the links will be rejected and significant

latent information may be omitted in this case, while

a lower threshold will extract more frequent links at

the expense of performance.

FLMin (Stattner, 2012d), uses a bottom-up search

and the Apriori principle (Samatova, 2014) by

browsing only the itemsets that all of their

subitemsets are frequents. Using the same principle

as well as the frequency property (Stattner, 2012b),

MFCLMin (Stattner, 2012c) looks for the maximal

frequent conceptual links i.e. those which are not

included in other frequent conceptual links.

Subsequently, authors in (Stattner, 2013) and

(Tabatabaee, 2017) proposed respectively the

algorithms H-MFCLMin and D-MFCLMin that

implement the concepts of filtering threshold and

itemset dependency to reduce the search space, thus

significantly improving the performance of the search

process with the trade-off of loss of searched patterns.

Comparing with the results of the complete research

process, the authors have shown that the loss is

admissible from a certain support threshold. Finally,

PALM (Stattner, 2017) is a parallel implementation

that tries to improve performance of the extraction

process by simultaneously exploring several parts of

the search space.

To the best of our knowledge, these are

exhaustively the list of works addressing the FCL

extraction problem. While the last one constitutes a

parallel implementation, the former are sequential

and they adopt an apriori based approach, i.e.,

scanning the database for each FCL candidate and

computing the relative support. Furthermore, each

one of the sequential implementations improves the

performances of the previous, by exploiting more

properties of the network. At this stage, we should

notice that despite that the solution space given by the

MFCLMin and the D-MFCLMin algorithms is

smaller than that obtained by FLMin, this doesn’t

cause any loss in the solution space because as for the

itemset mining problem, from the maximum FCLs we

can reach all the FCLs in the network.

Contrariwise, the H-MFCLMin sacrifices some

solutions for a performance gain. Finally, MFCLMin

and D-MFCLMin remain the only sequential

implementations that list all the maximal FCLS for a

given network. Despite all the properties exploited by

these two algorithms (frequency property,

downward-closure property and the dependency

property) in order to maximize the extraction process

performances, the main problem of them and of any

apriori based algorithm is the multiple scan of the

database. Indeed, MFCLMin and D-MFCLMin

proceed in a breadth first manner, generate all

conceptual links candidates of size k, scan the

network for each candidate and eliminate all but those

frequent before moving to larger candidate

conceptual links. This may induce heavy charge on

the process for large networks.

In this paper, we present a new solution for the

maximum FCLs extraction problem, namely the Bin-

MFCLMin, it constitutes a sequential implementation

that looks for all the maximum FCLs within a social

network, and uses a compressed binary representation

of the social network in order to reduce the time of

extracting frequent conceptual links. As we will see

through this paper, the compressed representation

transforms the input network data into an integer

matrix whose size is reduced by a factor more than 60

than the original network, which allows a gain in run

time up to 91%. The paper is organized as follows:

section 2 gives details about the problem modelling,

section 3 explains the proposed solution and section

4 shows and discusses the obtained results, we finally

conclude and present our perspectives in the last

section.

2 PROBLEM MODELLING

In order to model the FCL extraction problem, we

consider a social network represented by a graph G =

(V;E) where V is the set of nodes and E is the set of

relations between the nodes.

We use a set of attributes A (a1,…, am) and a set

of attribute values (a11,… .a1j

a21,…,a2j

….am1,… .., amj

) where j

the number

of values that can take the attribute ak.

Each node is described by a set of pairs (attribute,

value), each attribute = value pair is said to be an item

and the set of (attributes, values) describing a node(s)

constitutes an itemset.

An itemset which contains one pair (attribute,

value) is called 1-itemset, while an itemset containing

t pairs (attribute, value), it is called t-itemset.

If m1 and m2 are two itemsets, then the set of ties

linking the nodes satisfying the itemset m1 and the

nodes satisfying the itemset m2 constitutes a

conceptual link noted (m1, m2):

(m1, m2) = {e ∈E, e = (a, b) a satisfy m1

and b satisfy m2, a, b ∈ V}

(1)

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

182

In the conceptual link (m1, m2), m1 is called the left

itemset while m2 represents the right itemset.

The support of a conceptual link (m1, m2)

represents the number of links connecting the nodes

verifying m1, m2:

Support((m1, m2)) = | {e ∈E, e = (a, b) a

satisfy m1 and b satisfy m2, a, b ∈ V} |

(2)

Let be a social network where the nodes are

constituted of individuals and a link between two

nodes describes a relation between the corresponding

individuals. Furthermore, each individual is

described by three attributes: age class (age/10),

gender (male/ female) and the work status (employee,

unemployed). According to the above definitions,

(gender=male), (work-status = unemployed) are

items and the set (age=3, gender=female, work-status

= employee) is un itemset. Hence, the conceptual

links ((age=3, gender=female, work-status =

employee), (age=4, gender=male, work-status =

employee)) describes all the links between female

workers aged between 30 and 39 years and male

workers aged between 40 and 49 years old.

The number of these links constitutes the support

of the conceptual link.

A conceptual link is said to be frequent if its

support is greater than a predefined threshold β.

(m1, m2) frequent ≡ Support((m1, m2)) ≥

(3)

A conceptual link (m1, m2) is included in another

conceptual link (m1’, m2’) if: m1⊆ m1’ and m2⊆m2’,

thus:

• (m1, m2) is a sub-conceptual link of (m1’, m2’)

• (m1’, m2’) is a super-conceptual link of (m1, m2).

From this definition, we can deduce two properties

whose proofs are detailed in (Stattner, 2012c):

• If a conceptual link is frequent, all its sub-

conceptual links are frequent.

• If a conceptual link is infrequent, all its super-

conceptual inks are infrequent.

Finally, a frequent conceptual link is said to be

maximal if it is not included in any other frequent

conceptual link.

3 THE PROPOSED SOLVING

APPROACH, BIN-MFCLMIN

We propose in this work, a new solution for

extracting maximum FCLs from a social network,

namely the Bin-MFCL algorithm. It is based on a

bottom-up search using the Apriori principle to

gradually prune the search space. The main novelty

of the proposed solution is in the data structure.

Indeed, we use in this work a compressed binary

presentation of the network (Leon, 2008) in order to

decrease the number of processing operations during

the extraction of FCLs. In this representation, the

entire network (nodes and links) is represented by a

matrix of integers of size m X n, where n is the

number of all possible attribute values and m is the

number of links in the original network divided by a

compression factor, thus, reducing the complexity of

the input data and reducing the search time. The next

section gives more detail about the input structure

construction process.

3.1 The Compressed Binary

Representation

The frequent conceptual link extraction technique

proceeds on an attributed social network which is

depicted through two 2-dimensional array: the profile

array lists all the nodes with their attributes, and the

relation array lists all the existed links between nodes.

Figure 2, and table 1 give an example of an

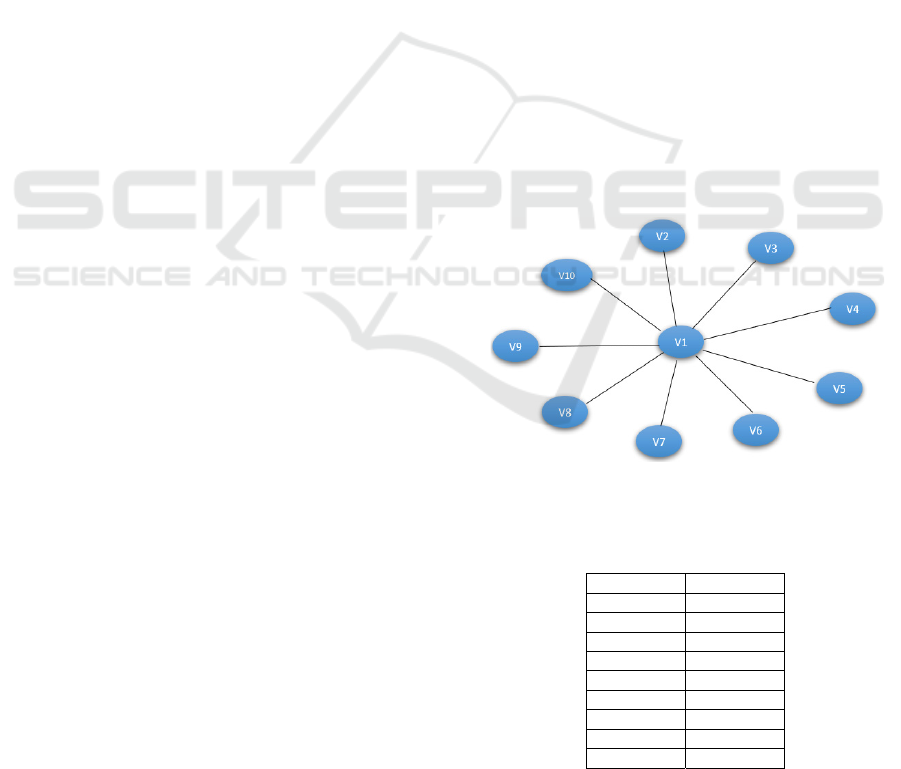
attributed social network. The nodes in this network

are individuals described by the five attributes listed

in the table 2.

Figure 2: Example of a social network with 10 nodes related

by 9 links.

Table 1: Link matrix of the social network example.

Id user 1 Id user 2

110

Exhaustive Solution for Mining Frequent Conceptual Links in Large Networks using a Binary Compressed Representation

183

Table 2: Attribute matrix of the social network example.

User i

Profile privacy Completion rate of

rofile gende

Registration yea

Age class (Age/10)

1 Public < 30% Male <2007 2

2 Public >=60% Female >=2007 1

3 Private >=30% and <60% Male >=2007 2

4 Public <30% Female >=2007 2

5 Public >=60% Male <2007 2

6 Private <30% Female >=2007 3

7 Public <30% Female <2007 2

8 Private <30% Male <2007 2

9 Private <30% Female <2007 1

10 Public >=60% Female <2007 2

Table 3: Merge the attribute and link matrices.

Profile privacy

Completion rate

of profile

gender

Registration

year

Age class

(Age/10)

Id user 1

Id user 2

Profile privacy

Completion rate

of profile

gender

Registration

year

Age class

(Age/10)

ublic < 30% Male <2007 2 1 2 Public >=60% Female >=2007 1

public < 30% Male <2007 2 1 3 Private

>=30% and

<60%

Male >=2007 2

ublic < 30% Male <2007 2 1 4 Public <30% Female >=2007 2

ublic < 30% Male <2007 2 1 5 Public >=60% Male <2007 2

ublic < 30% Male <2007 2 1 6 Private <30% Female >=2007 3

ublic < 30% Male <2007 2 1 7 Public <30% Female <2007 2

ublic < 30% Male <2007 2 1 8 Private <30% Male <2007 2

ublic < 30% Male <2007 2 1 9 Private <30% Female <2007 1

ublic < 30% Male <2007 2 1 10 Public >=60% Female <2007 2

Table 4: The attribute link matrix in one-hot encoding and the extraction of the compressed representation.

Profile privacy = public

Profile privacy = private

Completion rate of profile < 30%

Completion rate of profile >= 30% and < 60%

Completion rate of profile >= 60%

Gender = male

Gender = female

Registration year < 2007

Registration year >= 2007

Age class = 1

Age class = 2

Age class = 3

Id user 1

Id user 2

Profile privacy = public

Profile privacy = private

Completion rate of profile < 30%

Completion rate of profile >= 30% and < 60%

Completion rate of profile >= 60%

Gender = male

Gender = female

Registration year < 2007

Registration year >= 2007

Age class = 1

Age class = 2

Age class = 3

1 0 1 0 0 1 0 1 0 0 1 0 1 2 1 0 0 0 1 0 1 0 1 1 0 0

1 0 1 0 0 1 0 1 0 0 1 0 1 3 0 1 0 1 0 1 0 0 1 0 1 0

1 0 1 0 0 1 0 1 0 0 1 0 1 4 1 0 1 0 0 0 1 0 1 0 1 0

1 0 1 0 0 1 0 1 0 0 1 0 1 5 1 0 0 0 1 1 0 1 0 0 1 0

1 0 1 0 0 1 0 1 0 0 1 0 1 6 0 1 1 0 0 0 1 0 1 0 0 1

1 0 1 0 0 1 0 1 0 0 1 0 1 7 1 0 1 0 0 0 1 1 0 0 1 0

1 0 1 0 0 1 0 1 0 0 1 0 1 8 0 1 1 0 0 1 0 1 0 0 1 0

1 0 1 0 0 1 0 1 0 0 1 0 1 9 0 1 1 0 0 0 1 1 0 1 0 0

1 0 1 0 0 1 0 1 0 0 1 0 1

1 0 0 0 1 0 1 1 0 0 1 0

……………………………..

1023

722

301

188

257

578

328

695

928

516

475

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

184

The transformation of this network into an

integer matrix is described in the following steps:

1. Merge the profile and the link data in the same

matrix [Table 3].

2. Transform the merged matrix into a binary array

using the one-hot encoding (Potdar, 2017). This

is made by transforming each attribute column

with d possible values into d binary columns, the

value of an attribute for each node is indicated by

the presence (1) or absence (0) of the binary

variable [Table 4]. For our social network

example, the attribute profile privacy is divided

into two columns, one indicates if the attribute

value is public and the other indicates the private

value of the attribute.

3. Finally, If F is the compression factor, convert for

each column, F rows into an integer [Table 4]. For

instance, if we take F = 9, the original link-profile

matrix is transformed into a matrix with one row and

24 columns which represent the number of all

possible attribute values.

In general, the result of the compression process

is an MXN matrix where N is the number of items

and M is the number of links in the original network

divided by the compression factor. It is important to

note that this compression is done without any loss

of data and it is possible to revert to the original

network entirely. Moreover, the operation of

searching links satisfying an itemset turns into an

operation of logical ANDs between the columns

corresponding to each item in the itemset in question.

At this stage, the compressed data structure can

be exploited by the proposed algorithm, in order to

optimize the MFCL extraction process in large

networks. The pseudocode of the Bin-MFCLMin

algorithm is given below [Algorithm 1]. As it is

depicted in the listing code, the algorithm

implements a buttom-up search by looking for the

frequent conceptual links involving itemsets of size

1 at first (lines 4-15). After that, every frequent

itemset will generate longer candidate itemsets by a

join operation (lines 18-19).

Again, these itemsets constitute candidate

conceptual links to be checked according to a

predefined threshold (lines 20-31).

This process is repeated until no more candidate

can be generated (while loop line 17)

Algorithm 1: The Bin-MFCLMin algorithm.

Generation of the 1-frequent conceptual links

1. LeftFreqItemset  list of 1-itemsets m where CountItemSupport (m) >= β * S

2. RightFreqItemset  list of 1-itemsets m where CountItemSupport (m) >= β * S

3. For each leftItem in LeftFreqItemset

4. For each rightItem in RightFreqItemset

5. Support = countConceptualLinkSupport((leftItem, rightItem), data)

6. If(Support >= β * S)

7. Add the conceptual link (leftItem, rightItem) to listMFCL

8. Add leftItem to t-leftItemSetCand

9. Add rightItem to t-rightItemSetCand

10. End if

11. End for

12. End for

Generation of the t-frequent conceptual links

1. t = 2

2. While (t-leftItemSetCand ≠ Φ OR t-rightItemSetCand ≠ Φ)

3. t-leftItemSetCand  list of t-itemsets constructed from (t-1)-frequent left itemsets by

a join operation

4. t-rightItemSetCand  list of t-itemsets constructed from (t-1)-frequent right itemsets

by a join operation

5. for each leftItemSet in t-leftItemSetCand

6. for each rightItemSet in t-rightItemSetCand

7. support = countConceptualLinkSupport((leftItemSet, rightItemSet), data)

8. if(support>= β * S)

9. Add the conceptual link (leftItem, rightItem) to listMFCL

10. Add leftItem to t-leftItemSetCand

11. Add rightItem to t-rightItemSetCand

12. Remove all sub-conceptual links of the newly added frequent conceptual link

13. End if

14. End if

15. End for

16. End for

17. t = t+1

18. End while

19. Return listMFCL

Exhaustive Solution for Mining Frequent Conceptual Links in Large Networks using a Binary Compressed Representation

185

The main benefit of the compressed input

structure is in the support counting implemented in

the three following algorithms [Algorithm 2,

Algorithm3, Algorithm4].

Algorithm 2 is the first called by the principal

algorithm for the sake of computing the support of

each single item. This allows us to discard the non-

frequent items as early as possible and use solely the

frequent items for generating longer candidate

itemset in the subsequent iterations. Since each item

is represented by a column in the compressed input

data (line 2), the support counting is done by scanning

all the rows of this column (number of rows = M =

number of Links in the original network /

compression factor) and adding the number of bits set

to 1 in the binary representation of each row data (line

3-4). The support of every couple 1-itemset is then,

counted using the algorithm 3 in order to determine

the list of one frequent conceptual link.

Algorithm 2: CountItemSupport.

The support counting of a one conceptual link,

involves two columns of the input data, the one which

corresponds to the left itemset and the one which

corresponds to the right itemset (lines 2-5). The

algorithm 3 performs an and operation between these

two columns in order to retain only the links where

the two itemsets are satisfied (line 7), before counting

the number of bits set to 1 in the binary representation

just obtained (line 8).

Furthermore, in the case of a of a t-conceptual link

(t>1), the left and right itemsets involved in the

conceptual link correspond to more than column in

the compressed input data. Thus, before counting the

number of links where the left and the right itemset

are satisfied, the algorithm 4 allows us to obtain the

column associated to each itemset. In the lines 3-6,

the algorithm constructs a matrix where each column

correspond to an item of the itemset. Then, it

performs an AND operation within this matrix to

obtain the column representation of the whole itemset

(line 7-11). Finally the support counting is made with

the columns associated to the left and right itemset

similarly to the one conceptual link support counting.

Algorithm 3: CountConceptualLinkSupport.

Input : conceptualLink, network data

in binary compressed representation

Output : support of the conceptual

link

1. Support = 0

2. leftItemSet  left ItemSet of the

conceptual link

3. rightItemSet  right ItemSet of

the conceptual link

4. LeftItemSetColumn =

CountItemSetSupport(leftItemSet)

5. rightItemSetColumn =

CountItemSetSupport(rightItemSet)

6. for each row i in

LeftItemSetColumn,

rightItemSetColumn

7. binaryRepresentationRow =

LeftItemSetColumn[i] AND

rightItemSetColumn[i]

8. support = support + number of 1

in the binaryRepresentationRow

9. End for

10. return support

Algorithm 4: CountItemSetSupport.

Input : itemset, network data in binary

compressed representation

Output : support of itemset,

itemSetColumn

1. itemSetMatrix  []

2. support = 0

3. for each item in itemset

4. itemColumn  the integer array

corresponding to the item in the

input data

5. add the itemColumn to

itemSetMatrix

6. End for

7. for each row in itemSetMatrix

8. for each column N in row

9. binaryRepresentationRow =

binaryRepresentationRow AND

itemSetMatrix [row][N]

10. add the current

binaryRepresentationRow to the

itemSetColumn

11. End for

12. support = support + number of 1 in

the binaryRepresentationRow

13. End for

14. return support, itemSetColumn

Input : item, network data in binary

compressed representation

Output : support of item

1. Support = 0

2. itemColumn  the integer array

corresponding to the item in the

input data

3. for each row in itemColumn

4. support = support + number of

1 in the binary representation of

row

5. end

6. return support

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

186

4 EXPERIMENTAL RESULTS

AND DISCUSSION

In this section, we present the experiments performed

to validate our proposed new solution for solving the

FCL problem. We will first justify the choice of

MFCLMin for the comparison, then, we will present

the dataset used in the tests. Finally, the results will

be compared and discussed in term of the execution

time for both the algorithms.

The table 5 resumes the main characteristics of the

previous implementations and compares them with

our proposed solution. From this table, we can notice

that the MFCLMin and D-MFCL-Min algorithms

have the same properties of our solution and are

consequently the most suitable for the comparison.

Nevertheless, the experiments accomplished with the

D-MFCLMin algorithm on the pokec network

, stated

that the execution time increases up to 15% and this

lost in the search process performances was

justified

by the absence of dependency in the assessed

network. Hence, for a fair comparison, the MFCLMin

algorithm

will be used in the experiments with the

same data and the same min sup threshold.

The input dataset is a Slovak online social

network (Tabatabaee, 2017) which includes one

million nodes and 31 million links, the nodes are

described by a set of 51 attributes which are not all

filled in. A task of cleaning and preparation is

therefore necessary and consists essentially of

discarding null values, transforming the values of

some attributes in the suitable classes (see below the

age, comp and the reg attributes) and preparing the

input data structure.

The number of attributes considered is equal to 5,

with a total valence of 13. Table 6 below describes

the attributes and their possible values.

All tests are carried out on several instances by

varying each time the number of nodes and links and

calculating the execution time taken by the two

algorithms. This is done with four possible support

thresholds.

Figures 6 and 7 show respectively the runtime of

both the MFCLMin and Bin-MFCLMin algorithms

and the gain achieved by the proposed solution. The

results were obtained by a compression factor of 63

while varying support threshold between: 0.1, 0.15,

0.2 and 0.25. One can notice here that the smaller the

threshold, the more tedious the task of detecting

frequent links is, and therefore more time consuming

since the number of frequent links become large.

Firstly, we can observe that the gain on runtime is

at least of 43% which confirms the positive impact of

the input structure on the search process performance.

The second remark that can be done is that while the

performances of Bin-MFCLMin remains relatively

stable for bigger instances, the MFCLMin algorithm

runtime increases considerably, thus proving the

superiority of our data structure compared to the one

used in MFCLMin algorithm. Indeed, the later uses a

vertical layout representation for the network where

it associates to each node, input and output links, then

it calculates the itemset supports by intersecting the

links list associated with each itemset (Stattner,

2012b), whereas, our solution looks for all the

maximum FCLs, by scanning a reduced input data to

a compression factor of 63 in the assessed instance

and uses the AND logic operation to count the support

of each itemset. Hence, this reduces the support

counting process complexity.

To support this result, we also considered the

results of a well-known algorithm in the field of

frequent pattern mining, namely, ECLAT algorithm

(Zaki, 2000). It should be noted that the data structure

employed in the MFCLMin algorithm is similar to

that used by ECLAT while looking for frequent

itemsets in the context of association rules mining. In

fact, the author of this work implements a vertical

layout representation of the input data where it

associates to each item, the list of transactions where

it appeared then, the support of an itemset is defined

by the size of the intersection list of all the lists

associated with each item constituting the itemset.

Table 5: Characteristics of FCLS extraction algorithms.

Solution space Type of implementation Type of search

FLMin FCLs Sequential Exhaustive

MFCLMin Maximum FCLs Sequential Exhaustive

H-MFCLMin Maximum FCLs Sequential Non Exhaustive

D-MFCLMin Maximum FCLs Sequential Exhaustive/non Exhaustive

PALM Maximum FCLs Parallel Exhaustive

Bin-MFCLMin Maximum FCLs Sequential Exhaustive

This is the same network used in our experiments

Exhaustive Solution for Mining Frequent Conceptual Links in Large Networks using a Binary Compressed Representation

187

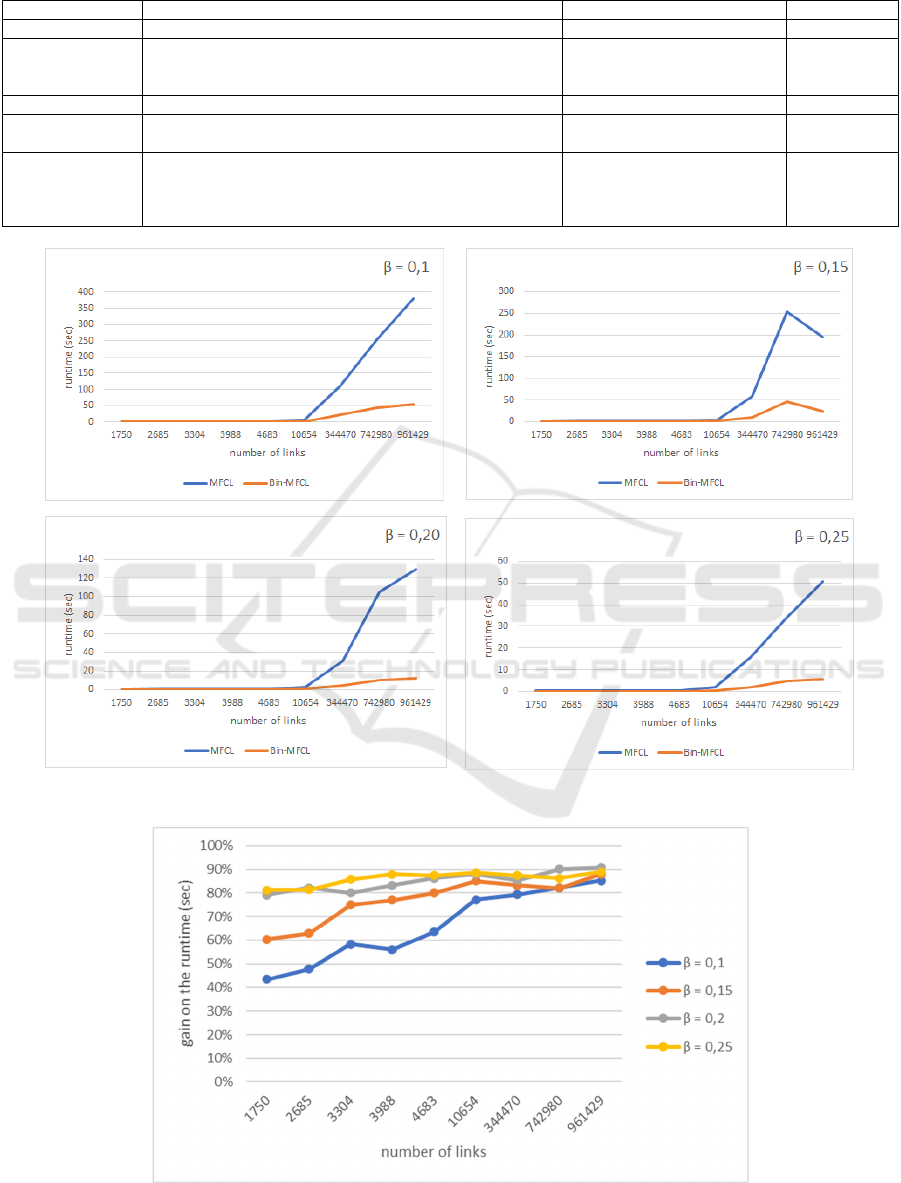
Table 6: Pokec social network attributes.

Attribute Description Possible values Valence

Public Indicates if the user profile is public or private Public / private 2

Comp The completion rate of the user profile

<30%

>=30% and <60%

>=60%

Gende

Indicates the user gende

Male / female 2

Reg Indicates the registration year in the network

<2007

>=2007

Age class The class age of the user

<10

>=11 and <20

>=20 and <30

>=30

Figure 3: Runtime of the MFCLMin and Bin-MFCLMin algorithms.

Figure 4: Gain on the runtime obtained by Bin-MFCLMin algorithm.

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

188

We note that although ECLAT is more efficient

than many leading algorithms in the area, it is

known to be unsuitable for items with large lists of

transactions to be intersected (Luna, 2019). This

proves the superiority of our proposed data structure

especially in that case, which is emphasized by the

gain in runtime, which reaches 91% for the last

network.

5 CONCLUSION

With the proliferation of social networks in recent

years, data mining techniques have become

essential for the knowledge extraction process. The

pattern presented in this paper plays a dual role to

accomplishing this task, on the one hand, it

exploits

the structural and attributed information of the

network in order to extract a more relevant

information which seems, hence, to be very

promising in the analysis of real world application

like the spread of diseases or the recommendation

systems. On the other hand, the conceptual view

provided by this approach summarizes the extracted

knowledge in one simple and content-rich

visualisation.

We proposed in this work a new algorithm for

extracting frequent conceptual links from large

networks, by adopting a new binary compressed

structure for the network, hence reducing the input

data complexity. The proposed approach allows

extracting the FCLs in a shorter time comparing to

MFCLMin for all the used instances. The

improvement reaches up to 90% of gain in the

execution time for items with large lists of

transactions to cross-reference.

Nevertheless, some network instances are so

large that makes approximated methods inevitable

for dealing with the computational challenges that

this problem reveals. Thus, the data structure

presented in this work, may be used within a

heuristic solution as an alternative to tackle this

problem in the future.

REFERENCES

Mata, A. S. (2020). Complex Networks: a Mini-review.

Brazilian Journal of Physics, 1-15.

Albert-'Laszlo Barabasi. (2002). the new science of

networks. Perseus Publishing.

Charu C. Aggarwal (eds.). (2011). Social Network Data

Analytics, Springer US.

L. Getoor, C. Diehl. (2005). Link mining: a survey.

SIGKDD Explor.

M. Adedoyin-Olowe, M. M. Gaber, and F. T. Stahl.

(2014). A survey of data mining techniques for social

media analysis. J. Data Min. Digit. Humanit.

Erick Stattner and Martine Collard. (2012). Frequent

links: An approach that combines attributes and

structure for extracting frequent patterns in social

networks. 16th East-European Conference on

Advances in Databases and Information Systems.

E. Stattner and M. Collard. (2012a). Social-based

conceptual links: Conceptual analysis applied to

social networks. International Conference on

Advances in Social Networks Analysis and Mining.

S. Fortunato. (2009). Community detection in graphs.

ArXiv.

J. M. Luna, P. Fournier-Viger, S. Ventura. (2019).

Frequent itemset mining: A 25 years review. WIREs

Data Mining Knowl Discov.

R. Agrawal et R. Srikant. (1994). Fast Algorithms for

Mining Association Rules in Large Databases. In

Proceedings of the 20th International Conference on

Very Large Data Bases.

Aswani Kumar Ch. (2011). Mining Association Rules

Using Non-Negative Matrix Factorization and Formal

Concept Analysis. International Conference on

Information Processing.

K. Sumangali, Ch. Aswani Kumar. (2017). A

comprehensive overview on the foundations of formal

concept analysis. Knowledge Management & E-

Learning.

E. Stattner. (2012b). «Contributions à l’étude des réseaux

sociaux: propagation, fouille, collecte de données».

Thèse pour obtenir le titre de Docteur en Sciences de

l’Université des Antilles et de la Guyane.

Erick Stattner and Martine Collard. (2012c). Social-based

conceptual links: Conceptual analysis applied to

social networks». International Conference on

Advances in Social Networks Analysis and Mining.

E. Stattner and M. Collard. (2012d). «FLMin: An

Approach for Mining Frequent Links in Social

Networks». International Conference on Networked

Digital Technologies.

Nagiza F. Samatova; W. Hendrix; J. Jenkins; K.

Padmanabhan. (2014). A.Chakraborty. «Practical

graph mining with R». CRC Press.

E. Stattner and M. Collard. (2013). «Towards a hybrid

algorithm for extracting maximal frequent conceptual

links in social networks». IEEE International

Conference on Research Challenges in Information

Science.

H. Tabatabaee. (2017). DMFCLMin: A New Algorithm

for Extracting Frequent Conceptual Links from Social

Networks. International Journal of Advanced

Computer Science and Applications.

E. Stattner, R. Eugenie, and M.Collard. (2017). «PALM:

A Parallel Mining Algorithm for Extracting Maximal

Frequent Conceptual Links from Social Networks».

International Conference on Database and Expert

Systems Applications.

Exhaustive Solution for Mining Frequent Conceptual Links in Large Networks using a Binary Compressed Representation

189

Raudel Hernandez Leon, Airel Perez Suarez, Claudia

Feregrino Uribe, Zobeida Jezabel Guzman Zavaleta.

(2008). An Algorithm for Mining Frequent Itemsets.

5th International Conference on Electrical

Engineering, Computing Science and Automatic

Control (CCE), 2008.

Kedar Potdar, Taher S. Pardawala, Chinmay D. Pai.

(2017). A Comparative Study of Categorical Variable

Encoding Techniques for Neural Network Classifiers.

International Journal of Computer Applications.

J. Leskovec, L. Adamic and B. Adamic. (2007). The

Dynamics of Viral Marketing. ACM Transactions on

the Web (ACM TWEB), 1(1).

S. Tabassum, F S. F. Pereira, S. Fernandes, J. Gama.

(2018). Social network analysis: an overview. Wiley

Interdisciplinary Reviews: Data Mining and

Knowledge Discovery.

Zaki, M. J. (2000). Scalable algorithms for association

mining. IEEE Transactions on Knowledge and Data

Engineering, 2000.

C. C. Aggarwal, J. Han (eds.): Frequent Pattern Mining,

Springer International Publishing Switzerland, 2014.

M. Cafaro and M. Pulimeno: Frequent Itemset Mining.

Springer Nature Switzerland, 2019.

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

190