A Scalable Approach for Distributed Reasoning over
Large-scale OWL Datasets
Heba Mohamed
1,2 a
, Said Fathalla
1,2 b
, Jens Lehmann
1,3 c
and Hajira Jabeen
4 d
1
Smart Data Analytics (SDA), University of Bonn, Bonn, Germany
2
Faculty of Science, University of Alexandria, Alexandria, Egypt
3
NetMedia Department, Fraunhofer IAIS, Dresden Lab, Germany
4
Cluster of Excellence on Plant Sciences (CEPLAS), University of Cologne, Cologne, Germany
Keywords:
Big Data, Distributed Computing, In-Memory Computation, Parallel Reasoning, OWL Horst Rules, OWL
Axioms.
Abstract:
With the tremendous increase in the volume of semantic data on the Web, reasoning over such an amount of
data has become a challenging task. On the other hand, the traditional centralized approaches are no longer
feasible for large-scale data due to the limitations of software and hardware resources. Therefore, horizontal
scalability is desirable. We develop a scalable distributed approach for RDFS and OWL Horst Reasoning over
large-scale OWL datasets. The eminent feature of our approach is that it combines an optimized execution
strategy, pre-shuffling method, and duplication elimination strategy, thus achieving an efficient distributed rea-
soning mechanism. We implemented our approach as open-source in Apache Spark using Resilient Distributed
Datasets (RDD) as a parallel programming model. As a use case, our approach is used by the SANSA frame-
work for large-scale semantic reasoning over OWL datasets. The evaluation results have shown the strength
of the proposed approach for both data and node scalability.
1 INTRODUCTION
The past decades have seen advances in artificial in-
telligence techniques for enabling various sorts of rea-
soning. The two primary forms of reasoning per-
formed by inference engines are Forward Chain-
ing and Backward Chaining. Forward chaining
(also called data-driven or bottom-up approach) ap-
proaches use available data and inference rules to
infer implicit information until a goal is reached
(Sharma et al., 2012). Contrary, backward chaining
(also called goal-driven or up-down approach) ap-
proaches use the goal and inference rules to move
backward until determining the facts that satisfy the
goal (Sharma et al., 2012). Forward chaining tech-
niques can generate a large amount of information
from a small amount of data (Al-Ajlan, 2015). As a
consequence, it has become the key approach in rea-
soning systems. RDFS and OWL mainly permit the
a
https://orcid.org/0000-0003-3146-1937
b
https://orcid.org/0000-0002-2818-5890
c
https://orcid.org/0000-0001-9108-4278
d
https://orcid.org/0000-0003-1476-2121
description of the relationships between the classes
and properties used to structure and define entities us-
ing rich formal semantics, providing a declarative and
extensible space of discourse. RDFS and OWL both
define a set of rules which allow new data to be in-
ferred from the original input. The volume of seman-
tic data available on the Web is expanding precipi-
tously, e.g., the English version of DBpedia describes
approximately 4.5 million things
1
. A plethora of new
information can be inferred from such large-scale se-
mantic data with the help of RDFS/OWL reasoning
rules. However, reasoning over such a vast amount of
data presents a series of challenges when developing
algorithms that can run in a distributed manner (Gu
et al., 2015). Owing to the limitations of software and
hardware infrastructures, as well as the complex data
flow models, conventional single-node strategies are
no longer appropriate for such large-scale semantic
data. The limitations of the traditional centralized ap-
proaches (i.e., software and hardware resources) for
large-scale data have motivated us to develop a dis-
tributed approach that is capable of reasoning over
1
https://wiki.dbpedia.org/about
Mohamed, H., Fathalla, S., Lehmann, J. and Jabeen, H.
A Scalable Approach for Distributed Reasoning over Large-scale OWL Datasets.
DOI: 10.5220/0010656800003064
In Proceedings of the 13th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2021) - Volume 2: KEOD, pages 51-60
ISBN: 978-989-758-533-3; ISSN: 2184-3228
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
51

large amount of data being produced regularly to gain
implicit knowledge. Therefore, we introduce an at-
tempt of developing a scalable distributed approach
for RDFS and OWL Horst Reasoning over large-
scale OWL datasets. In addition, we found that se-
lecting the optimum rule execution order greatly im-
proves the performance. The eminent feature of our
approach is that it combines an optimized execution
strategy, pre-shuffling method, and duplication elimi-
nation strategy, thus achieving an efficient distributed
reasoning mechanism.
The Spark framework is an in-memory distributed
framework using Resilient Distributed Dataset
(RDD) as the primary abstraction for parallel pro-
cessing provided by Spark. There are many benefits
of using RDDs, including in-memory computation,
fault-tolerance, partitioning, and persistence across
worker nodes. Our approach uses Apache Spark
for distributed and scalable in-memory processing.
We aim at answering the question: (RQ) How can
we infer implicit knowledge from large-scale Linked
Data distributed across various nodes? The proposed
approach is capable of reasoning over ontologies
partitioned across various nodes concurrently. Our
experiments showed that the proposed approach is
scalable with respect to data, as well as nodes. We
affirm that the formal semantics specified by the
input ontology are not violated. The sustainability of
our approach is demonstrated through SANSA-Stack
contributors
2
, whereas our approach constitutes
the inference layer in the SANSA-Stack, which is
about reasoning over a very large number of axioms.
The SANSA framework
3
uses Apache Spark
4
as its
big data engine for scalable large-scale RDF data
processing.
Furthermore, SANSA has tools for representing,
querying, inference, and analysing semantic data. A
new release is published almost every six months
since 2016. In addition, bugs and improvement sug-
gestions can be submitted through the issue tracker on
its GitHub repository.
This paper is organized as follows: Section 2 gives
a brief overview of the related work on RDF seman-
tic data reasoning. The proposed methodology for
axiom-based RDFS/OWL Horst parallel reasoning is
presented in Section 3. The experimental setup and
discussion of the results are presented in Section 4.
Finally, we conclude and the potential extension of
the proposed approach in Section 5.
2
http://sansa-stack.net/community/#Contributors
3
http://sansa-stack.net/
4
https://spark.apache.org/
2 RELATED WORK
For many years, the developments of large-scale rea-
soning systems were based on the P2P self-organizing
networks, which are neither efficient nor scalable (Gu
et al., 2015). Distributed in-memory computation sys-
tems, such as Apache Spark or Flink, are used to
perform inferences over large-scale OWL datasets.
These frameworks are robust and can operate on a
cluster of multiple nodes, i.e., the workload is dis-
tributed over multiple machines.
Several existing approaches can perform reason-
ing over RDF data, but none of them can reason over
large-scale axiom-based OWL data. Jacopo et al. (Ur-
bani et al., 2010) have proposed WebPIE, an inference
engine built on top of the Hadoop platform for paral-
lel OWL Horst forward inference. WebPIE has been
evaluated using real-world, large-scale RDF datasets
(i.e., over 100 billion triples). Results have shown
that WebPIE is scalable and significantly outperforms
the state-of-the-art systems in terms of language ex-
pressivity, data size, and inference performance. In
2012, an optimized version of WebPIE (Urbani et al.,
2012) was proposed, which loads the schema triples
in memory and, when possible, executes the join on-
the-fly instead of in the reduce phase, uses the map
function to group the triples to avoid duplicates and
execute the RDFS rules in a specific order to mini-
mize the number of MapReduce jobs. Gu et al. (Gu
et al., 2015) have proposed Cichlid, a distributed rea-
soning algorithm for RDFS and OWL Horst rule set
using Spark. Several design issues have been consid-
ered when developing the algorithm, including a data
partitioning model, the execution order of the rules,
and eliminating duplicate data. The prominent feature
of Cichlid is that the inner Spark execution mecha-
nism is optimized using an off-heap memory storage
mechanism for RDD. Liu et al. (Liu et al., 2016) have
presented an approach for enhancing the performance
of rule-based OWL inference by analyzing the rule
interdependence of each class to find the optimal ex-
ecutable strategies. They have implemented a proto-
type called RORS using Spark. Compared with Ci-
chlid, RORS can infer more implicit triples than Ci-
chlid in less execution time. Yu and Peter (Liu and
McBrien, 2017) have presented a Spark-based OWL
(SPOWL) reasoning approach that maps axioms in
the T-Box to RDDs in order to conclude the reasoning
results entailed by the ontology using a tableaux rea-
soner. SPOWL efficiently caches data in distributed
memory to reduce the amount of I/O used, which sig-
nificantly improves the performance. Furthermore,
they have proposed an optimized order of rule execu-
tion by analyzing the dependencies between RDDs.
KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development
52

Figure 1: RDFS parallel reasoning approach.
Kim and Park (Kim and Park, 2015) have presented
an approach for scalable OWL ontology reasoning in
a Hadoop-based distributed computing cluster using
SPARK. They have overcome the limitation of I/O de-
lay (i.e., disk-based MapReduce approach) by loading
data into the memory of each node. In comparison
with WebPIE, this approach outperforms the WebPIE
performance when the LUBM dataset is used in the
evaluation.
What additionally distinguishes our work from the
related work mentioned above is the utilization of the
optimal execution strategy proposed by Liu et al. (Liu
et al., 2016) and the pre-shuffling method proposed
by Gu et al. (Gu et al., 2015) with our duplication
elimination strategy (more details in the next section).
3 PARALLEL REASONING
In this section, we present the methodology of
the proposed approach for axiom-based RDFS/OWL
Horst parallel reasoning. Our methodology comprise
two tasks; 1) RDFS Parallel Reasoning, in which
RDFS rules are applied until no new data is derived,
and 2) OWL Parallel Reasoning, in which reasoning
over the OWL Horst rule set is performed.
3.1 RDFS Parallel Reasoning
RDFS reasoning is an iterative reasoning process
where RDFS rules are applied to the input data un-
til no new data is derived. The RDFS rule set con-
sists of 13 rules, as listed in (Hayes, 2004). The
rules with one clause are removed from the reason-
ing process because they do not influence the reason-
ing process. Table 1 illustrates the RDFS ruleset (in
axiom-based structure) used in this paper. All reason-
ing steps are implemented using the following RDD
operations: map, filter, join, and union operations.
Figure 1 shows the distributed RDFS reasoning
approach using Spark RDD operations. First, the ap-
proach starts with the input OWL dataset, then con-
verts it to the corresponding RDD of axioms. Next,
the approach selects one rule to filter and combine the
input RDD based on the semantics of this rule. Next,
the derived results (i.e., the inferred axioms after ap-
plying the reasoning rule from the previous step) are
merged with the original input data (i.e., the initial
RDD[axioms]). Finally, the resulting dataset is used
as input for the next reasoning rule. All rules are ap-
plied iteratively until a fixed-point iteration, in which
no new data is produced, and then the reasoning pro-
cess is terminated.
In many parallel RDFS reasoning approaches,
each rule is applied through join operations, and the
related data is read from various nodes. Consequently,
due to the massive volume of data traffic between
nodes, we encounter high network overhead. We can
broadcast the schema axioms to every node before
conducting the reasoning process, as the number of
schema axioms is minimal and conserves constants
in the real world (Heino and Pan, 2012; Gu et al.,
2015). The use of broadcast variables avoids network
communication overhead, whereas the corresponding
data used by the join operation is now available in
each node. Algorithm 1 illustrates the usage of the
broadcast variables to optimize the execution of a rule
R
6
. Line 2 extracts all the OWLClassAssertion ax-
ioms from the ax RDD. Next, the algorithm extracts
all the OWLSubClassOf axioms and converts it to the
corresponding Map (lines 3-5). Line 6 broadcasts the
OWLSubClassOf map to all the nodes of the cluster.
Finally, the OWLClassAssertion axioms are filtered
A Scalable Approach for Distributed Reasoning over Large-scale OWL Datasets
53

Table 1: RDFS rule set in terms of OWL Axioms. The following notation conventions are used: "C" is an OWLClass, "R"
is an OWLObjectProperty, "P" is OWLDataProperty, "A" is an OWLAnnotationProperty, "i" is an OWLIndividual, "v" is
OWLLiteral, "s" is an OWLAnnotationSubject, and "u", "w", "x" and "y" are instances. All names may have subscripts (i
1
... i
n
).
Rule Condition Axiom to Add
R1
SubClassOf (C, C
1
) . SubClassOf (C
1
, C
2
)
SubClassOf (C, C
2
)
R2(a)
SubDataPropertyOf (P, P
1
) .
SubDataPropertyOf (P
1
, P
2
)
SubDataPropertyOf (P, P
2
)
R2(b)
SubObjectPropertyOf (R, R
1
) .
SubObjectPropertyOf (R
1
, R
2
)
SubObjectPropertyOf (R, R
2
)
R2(c)
SubAnnotationPropertyOf (A, A
1
) .
SubAnnotationPropertyOf (A
1
, A
2
)
SubAnnotationPropertyOf (A, A
2
)
R3(a)
DataPropertyAssertion (P i v) .
SubDataPropertyOf (P, P
1
)
DataPropertyAssertion(P
1
i v)
R3(b)
ObjectPropertyAssertion (R i
1
i
2
) .
SubObjectPropertyOf (R, R
1
)
ObjectPropertyAssertion (R
1
i
1
i
2
)
R3(c)
AnnotationAssertion (A s v) .
SubAnnotationPropertyOf (A, A
1
)
AnnotationAssertion (A
1
s v)
R4(a)
DataPropertyDomain (P C) .
DataPropertyAssertion (P i v)
ClassAssertion (C i)
R4(b)
ObjectPropertyDomain (R C) .
ObjectPropertyAssertion (R i
1
i
2
)
ClassAssertion (C i
1
)
R5(a)
DataPropertyRange (P C) .
DataPropertyAssertion (P i v)
ClassAssertion (C i)
R5(b)
ObjectPropertyRange (R C) .
ObjectPropertyAssertion (R i
1
i
2
)
ClassAssertion (C i
2
)
R6
SubClassOf (C, C
1
) . ClassAssertion (C i)
ClassAssertion (C
1
i)
Algorithm 1: Parallel reasoning algorithm of rule R
6
using
broadcast variables.
Input : ax: RDD of OWL Axioms
Output: Inferred axioms from rule R
6
1 begin
2 val ta = extract(ax,
AxiomType.ClassAssertion)
3 val sc = extract(ax, AxiomType.SubClassOf)
4 .map(a => (a.SubClass, a.SuperClass))
5 .collect().toMap
6 val scBC = sc.broadcast(sc)
7 val R6 = ta.filter(a=>
scBc.value.contains(a.ClassExpression))
8 .flatMap(a => scBC.value(a.ClassExpression)
9 .map(s =>
10 ClassAssertionAxiom(s, a.getIndividual)))
11 end
out using the OWLSubClassOf broadcast variable
scBC and mapped to get the inferred axioms based
on the semantics of R
6
(lines 7-11).
3.2 OWL Horst Parallel Reasoning
In addition to RDFS reasoning, there is another more
powerful and complex rule set called OWL Horst rea-
soning rule set. Reasoning over the OWL Horst rule
set is known as OWL reasoning (Ter Horst, 2005).
Table 2 lists the set of OWL Horst rules.
3.2.1 Rule Analysis
The rules of OWL Horst are more complicated than
those of RDFS, and we need to conduct more jobs to
evaluate the complete closure (Urbani et al., 2009).
The OWL datasets contain several OWL Axioms
structures. In this approach, we divide the OWL Ax-
ioms into three main categories: 1) SameAs axioms,
which are OWLSameIndividual axioms, 2) Type ax-
ioms, which are OWLCLassAssertion axioms, and 3)
SPO, which are the remaining axioms. Due to the
complexity of the OWL Horst rules, we have anal-
ysed the set of rules and divide them into four main
rule categories:
− SameAs rules: Rules whose antecedent or con-
sequence include OWLSameIndividual axiom.
Those rules include O
1
, O
2
, O
5
, O
6
, O
8
, O
9
, and
O
10
. According to (Kim and Park, 2015; Gu et al.,
2015), rules O
8
and O
9
are used for ontology
merging and can be excluded from the reasoning
process.
− Type rules: Rules whose antecedent or con-
sequence include OWLClassAssertion axiom.
Those rules include R
4
, R
5
, R
6
, O
13
, O
14
, O
15
, and
O
16
.
− SPO rules: Rules whose antecedent or conse-
quence include axioms from SPO category. Those
rules include R
3
, O
3
, O
4
, and O
7
.
− Schema rules: The remaining rules which are
R
1
, R
2
, O
11
, and O
12
.
KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development
54

Table 2: OWL-Horst rule set in terms of OWL Axioms.
Rule Condition Axiom to Add
O1
FunctionalObjectProperty (R) .
ObjectPropertyAssertion (R i u) .
ObjectPropertyAssertion (R i w)
SameIndividual (u w)
O2
InverseFunctionalObjectProperty(R) .
ObjectPropertyAssertion (R u i) .
ObjectPropertyAssertion (R w i)
SameIndividual (u w)
O3
SymmetricObjectProperty(R) .
ObjectPropertyAssertion (R u w)
ObjectPropertyAssertion (R w u)
O4
TransitiveObjectProperty(R) .
ObjectPropertyAssertion (R i u) .
ObjectPropertyAssertion (R u w)
ObjectPropertyAssertion (R i w)
O5 SameIndividual (u w) SameIndividual (w u)
O6 SameIndividual (i u) . SameIndividual (u w) SameIndividual (i w)
O7(a)
InverseObjectProperties (R
1
R
2
) .
ObjectPropertyAssertion (R
1
u w)
ObjectPropertyAssertion (R
2
w u)
O7(b)
InverseObjectProperties (R
1
R
2
) .
ObjectPropertyAssertion (R
2
u w)
ObjectPropertyAssertion (R
1
w u)
O8 Declaration(Class(C
1
)) . SameIndividual (C
1
, C
2
) SubClassOf (C
1
, C
2
)
O9(a)
Declaration(DataProperty (P
1
)) .
SameIndividual (P
1
, P
2
)
SubDataPropertyOf (P
1
, P
2
)
O9(b)
Declaration(ObjectProperty (R
1
)) .
SameIndividual(R
1
, R
2
)
SubObjectPropertyOf (R
1
, R
2
)
O10(a)
DataPropertyAssertion (P u w) .
SameIndividual (u x) .SameIndividual (w y)
DataPropertyAssertion (P x y)
O10(b)
ObjectPropertyAssertion (R u w) .
SameIndividual (u x) . SameIndividual (w y)
ObjectPropertyAssertion (R x y)
O11(a) EquivalentClasses (C
1
C
2
) SubClassOf (C
1
C
2
)
O11(b) EquivalentClasses (C
1
C
2
) SubClassOf (C
2
C
1
)
O11(c) SubClassOf (C
1
C
2
) . SubClassOf (C
2
C
1
) EquivalentClasses (C
1
C
2
)
O12(a1) EquivalentDataProperty (P
1
P
2
) SubDataPropertyOf (P
1
P
2
)
O12(b1) EquivalentDataProperty (P
1
P
2
) SubDataPropertyOf (P
2
P
1
)
O12(c1)
SubDataPropertyOf (P
1
P
2
) .
SubDataPropertyOf (P
2
P
1
)
EquivalentDataProperty (P
1
P
2
)
O12(a2) EquivalentObjectProperty (R
1
R
2
) SubObjectPropertyOf (R
1
R
2
)
O12(b2) EquivalentObjectProperty (R
1
R
2
) SubObjectPropertyOf (R
2
R
1
)
O12(c2)
SubObjectPropertyOf (R
1
R
2
) .
SubObjectPropertyOf (R
2
R
1
)
EquivalentObjectProperty (R
1
R
2
)
O13(a1)
EquivalentClasses (C, DataHasValue (P v)) .
DataPropertyAssertion (P i v)
ClassAssertion(C i)
O13(b1)
SubClassOf (C, DataHasValue (P v)) .
DataPropertyAssertion (P i v)
ClassAssertion(C i)
O13(a2)
EquivalentClasses (C, ObjectHasValue (R v)) .
ObjectPropertyAssertion (R i v)
ClassAssertion(C i)
O13(b2)
SubClassOf (C, ObjectHasValue (R v)) .
ObjectPropertyAssertion (R i v)
ClassAssertion(C i)
O14(a1) ClassAssertion (DataHasValue (P v), i) DataPropertyAssertion (P i v)
O14(b1)
SubClassOf (C, DataHasValue (P v)) .
ClassAssertion (C i)
DataPropertyAssertion (P i v)
O14(c1)
EquivalentClasses (C, DataHasValue (P v)) .
ClassAssertion (C i)
DataPropertyAssertion (P i v)
O14(a2) ClassAssertion (ObjectHasValue (R v), i) ObjectPropertyAssertion (R i v)
O14(b2)
SubClassOf (C, ObjectHasValue (R v)) .
ClassAssertion (C i)
ObjectPropertyAssertion (R i v)
O14(c2)
EquivalentClasses (C, ObjectHasValue (R v)) .
ClassAssertion (C i)
ObjectPropertyAssertion (R i v)
O15
ObjectSomeValuesFrom (R C) .
ObjectPropertyAssertion (R u w)) .
ClassAssertion (C w)
ClassAssertion (C u)
O16
ObjectAllValuesFrom (R C) .
ObjectPropertyAssertion (R u w)) .
ClassAssertion (C u)
ClassAssertion (C w)
A Scalable Approach for Distributed Reasoning over Large-scale OWL Datasets
55

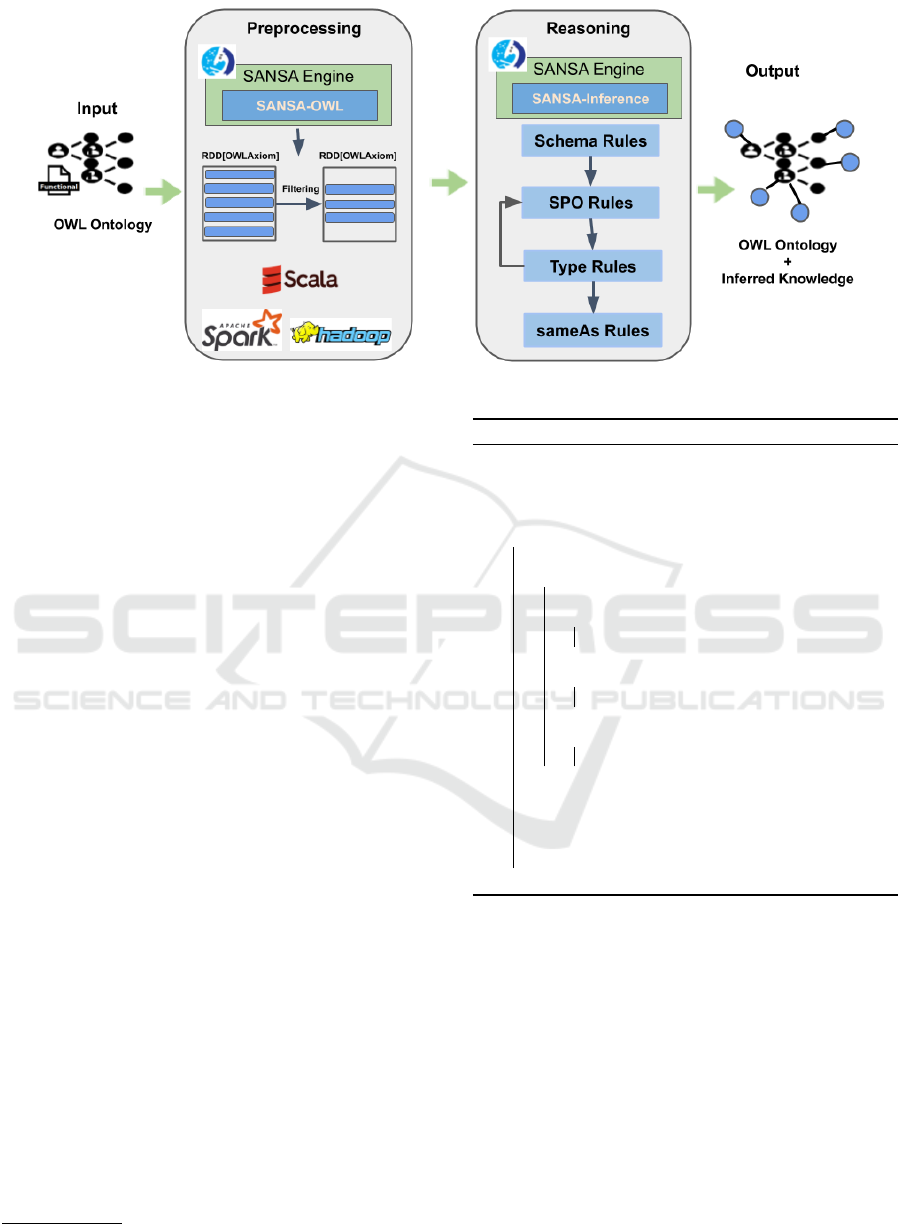
Figure 2: The architecture of the proposed approach.
Figure 2 illustrates the architecture of the pro-
posed approach. In the beginning, SANSA frame-
work (SANSA-OWL layer
5
) is used to convert the
input functional syntax ontology to the correspond-
ing RDD[OWLAxiom]. Afterwards, the filter() transfor-
mation is applied on the input RDD based on the se-
mantic of each rule (i.e., extract the intended axioms
for each specific rule). Then, the execution rule or-
der is performed, as illustrated in the reasoning step.
Relying on the interdependence of rules in each cate-
gory, we selected the optimum rule execution strategy
based on the order proposed in (Liu et al., 2016). The
execution order for schema category is O
11a
, O
11b
→
R
1
→ O
11c
→ O
12a
, O
12b
→ R
2
→ O
12c
. After apply-
ing the schema rules, we choose the rule execution
order for SPO category as O
3
→ R
3
→ O
7
→ O
4
. Af-
terwards, comes the rule execution order for Type rule
category which is R
4
→ R
5
→ R
6
→ O
14
→ O
13
→
O
15
→ O
16
. Finally, we ended with SameAs rule ex-
ecution order which is O
1
→ O
10
→ O
2
→ O
6
→ O
5
.
Ultimately, the inferred OWL axioms are merged with
the input ontology.
Algorithm 2 describes the parallel OWL Horst
reasoning approach. The algorithm starts by apply-
ing the schema rules over the input axioms (line 2).
Then, the reasoning process repeatedly applies rules
over the input data (lines 3-12). After each step, the
derived data is merged with the original data, i.e., the
output of one rule is input to the next one. Next,
sameAs rules are applied over the output (lines 13-
14). Finally, before returning the inferred axioms, we
apply distinct() transformations to eliminate the du-
plicated axioms (line 15), in which the degree of par-
allelism is passed. The degree of parallelism is speci-
fied based on the number of cores in the cluster.
5
https://github.com/SANSA-Stack/SANSA-OWL
Algorithm 2: Parallel OWL-Horst reasoning algorithm.
Input : ax: RDD of OWL Axioms,
rule_set: OWL Horst rule set
Output: The inferred axioms merged with the
original input data
1 begin
2 schema_inferred = ax.apply(schema_rules)
3 while true do
4 SPO_inferred = ax.apply(SPO_rules)
5 if SPO_inferred.count != 0 then
6 ax = ax.union(SPO_inferred)
7 type_inferred = ax.apply(type_rules)
8 if type_inferred.count != 0 then
9 ax = ax.union(type_inferred)
10 if SPO_inferred.count=0 &&
type_inferred.count=0 then
11 break
12 end
13 sameAs_inferred = ax.apply(sameAs_rules)
14 ax = ax.union(sameAs_inferred)
15 ax.distinct(parallelism)
16 return rdd
17 end
3.2.2 Optimization for Join Reasoning
In OWL Horst rules, there is more than one rule that
requires multiple join operations. Such rules con-
tain more than one OWLAssertionAxiom. Since the
schema axioms are usually small, the optimization al-
gorithm (using broadcast variables) is also used to op-
timize the OWL Horst reasoning.
3.2.3 Eliminating Duplicate Axioms
The pre-shuffle optimization method (proposed in (Gu
et al., 2015)) is used to eliminate the duplicated ax-
ioms using distinct operation over the resultant Spark
KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development
56

RDD. In the pre-shuffle strategy, an RDD is parti-
tioned and cached in memory before invoking the
distinct operation on it, to optimize the wide depen-
dencies among RDDs against the narrow dependen-
cies. Wide dependencies can generally be avoided
when constructing distributed algorithms to prevent
overhead communication. After studying the state of
the art, we observed that almost all of them elimi-
nate duplicate data after the reasoning process, which
greatly increases the running time. Therefore, in the
proposed approach, we eliminate the duplicated data
from the derived results of each set of rules in each
category, i.e., SameAs, Type, SPO, and Schema cate-
gories. Therefore, pre-shuffle method is applied be-
fore performing the duplicate elimination strategy.
We found that the elimination of duplication before
performing reasoning of the rules from the next cat-
egory has reduced the number of axioms used in the
next process, which decreases the reasoning time dra-
matically. Experiment 3 (in subsection 4.2) illustrates
the performance improvement with and without using
the proposed duplicate elimination strategy.
3.2.4 Transitive Rules
To conduct the transitive closure, a self-join opera-
tion is needed on the set of transitive pairs. Perform-
ing the self-join over the transitive pairs is not ef-
ficient because it requires a large amount of redun-
dant work. Moreover, it performs too many itera-
tive processes which significantly increases the run-
ning time. For example, consider the transitive chain
a → b → c → d → e. The implicit transitive pair (a, e),
can be produced multiple times, such as computed
from (a, c) and (c, e), or from (a, b) and (b, e), ... etc.
To enhance the reasoning performance, we adopt the
transitive closure algorithm proposed in (Liu et al.,
2016).
Algorithm 3 describes in detail the essential steps
carried out by the parallel transitive closure algo-
rithm. The transitive pairs tc are passed as input to
the algorithm. For example, to compute the transi-
tive rule R
1
, we pass all pairs of OWLSubClassOf ax-
ioms as input. Consider that we have the two axioms
OWLSubClassOf(a,b) and OWLSubClassOf(b,c),
then the pairs RDD will contains the two pairs
[(a, b), (b, c)]. In the beginning, the transitive pairs are
cached in memory for further computations (line 3).
Then, the pairs are swapped (y = [(b, a), (c, b)]) and
partitioned across the cluster using p, which is a de-
fined hash partitioner (lines 5-6). Line 9 performs the
join operation on the original and swapped pairs. For
example, we perform join over the pairs (a, b).(b, c)
to get RDD of (b = b, (a, c)) then map the output to
get the new (a, c) paths. After that, line 11 gets only
Algorithm 3: Parallel transitive closure algorithm.
Input : pairs: RDD of transitive pairs
Output: tc: transitive closure
1 begin
2 var nextCount = 1L
3 var tc = pairs.cache()
4 var x = tc
5 var y = x.map(a => a.swap)
6 .partitionBy(p).cache()
7 do
8 val z = x.partitionBy(p).cache()
9 val x1 = y.join(z)
10 .map(a => (a._2._1, a._2._2))
11 x = x1.subtract(tc, parallelism).cache()
12 nextCount = x.count()
13 if nextCount != 0 then
14 y = x.map(a => a.swap)
15 .partitionBy(p).cache()
16 val s = tc.partitionBy(p).cache()
17 val tc1 = s.join(y)
18
.map(a=>(a._2._2,a._2._1)).cache()
19 tc = tc1.union(tc).union(x).distinct()
20 while nextCount != 0;
21 return tc
22 end
the new inferred pair which is (a, c) pair. If we get
at least one new pair, then the process is repeated
to get the new pair in the transitive chain (lines 14-
18). Finally, line 19 adds the inferred pairs to the
original RDD of transitive pairs (i.e., tc) and hence
tc = [(a, b), (b, c), (a, c)]. The process is continued
until no new pairs are inferred. In Algorithm 3, the
cache() operation is invoked over the joined RDDs.
Caching the data before the join operation substan-
tially enhances the performance of the algorithm. The
transitive closure algorithm can also be used to com-
pute O
6
.
4 EVALUATION
In this section, we describe the evaluation of the pro-
posed approach. We conducted three types of exper-
iments; 1) Experiment 1: we evaluate the reasoning
time of our distributed approach with different data
sizes to analyze the data scalability and the perfor-
mance of the reasoning process, 2) Experiment 2: we
measure the speedup performance by increasing the
number of working nodes (i.e., machines) in the clus-
ter environment to evaluate the horizontal node scala-
bility, and 3) Experiment 3: we measure the reasoning
time of our approach with and without the proposed
duplicate elimination strategy to analyze the perfor-
mance of the reasoning process in both cases. We
start with the experimental setup, then we present and
A Scalable Approach for Distributed Reasoning over Large-scale OWL Datasets
57

discuss the results. The objective is to answer the fol-
lowing evaluation questions (EQs):
• EQ1) How does the runtime of the proposed ap-
proach be influenced with and without caching?
• EQ2) How does the distribution of the workload
over multiple machines affect the runtime?
• EQ3) How does the speedup ratio vary regarding
the number of worker nodes?
• EQ4) How efficient is the proposed approach
when the reasoning is distributed over multiple
machines?
Metrics. Two metrics are used to measure the perfor-
mance of parallel algorithms; Speedup ratio and Effi-
ciency. The speedup ratio (S) is a significant metric
for measuring the performance of parallel algorithms
against serial ones. Mathematically, the speedup ra-
tio is defined as S =
T
L
T
N
, where T
L
is the execution
time of the algorithm in local mode, and T
N
is the
time of N workers. Efficiency (E =
S
N
) represents how
well parallel algorithms utilize the computational re-
sources by measuring the speedup per worker. It is
the time taken to run the algorithm on N workers in
comparison with the time to run it on a local machine.
4.1 Experimental Setup
System Configuration. All distributed experiments
have been run on a cluster with five nodes. Among
these nodes, one is reserved to act as the master,
and the other four nodes are the computing work-
ers. Each node has AMD Opteron 2.3 GHz proces-
sors (64 Cores) with 250 GB of memory, and the con-
figured capacity is 1.7 TB. The nodes are connected
with 1 Gb/s Ethernet. Furthermore, Spark v2.4.4 and
Hadoop v2.8.1 with Java 1.8.0 are installed on this
cluster. All local-mode experiments are carried out
on a single cluster instance. All distributed experi-
ments have been run three times, and we reported the
average execution time.
Benchmark. Lehigh University (LUBM) (Guo et al.,
2005) synthetic benchmark has been used for the ex-
periment. For the evaluation of Semantic Web repos-
itories, LUBM is used to assess systems with var-
ious reasoning and storage process capacities over
large datasets. The benchmark is expressed in OWL
Lite language. We used the LUBM data generator in
our experiment to generate five datasets with differ-
ent sizes: LUBM-5, LUBM-10, LUBM-20, LUBM-
50, and LUBM-100, where the number attached to
the benchmark name, e.g., 20 in LUBM-20, is the
number of generated universities. In addition, to eval-
uate the efficiency of the proposed approach with
more complex OWL languages, we used the Univer-
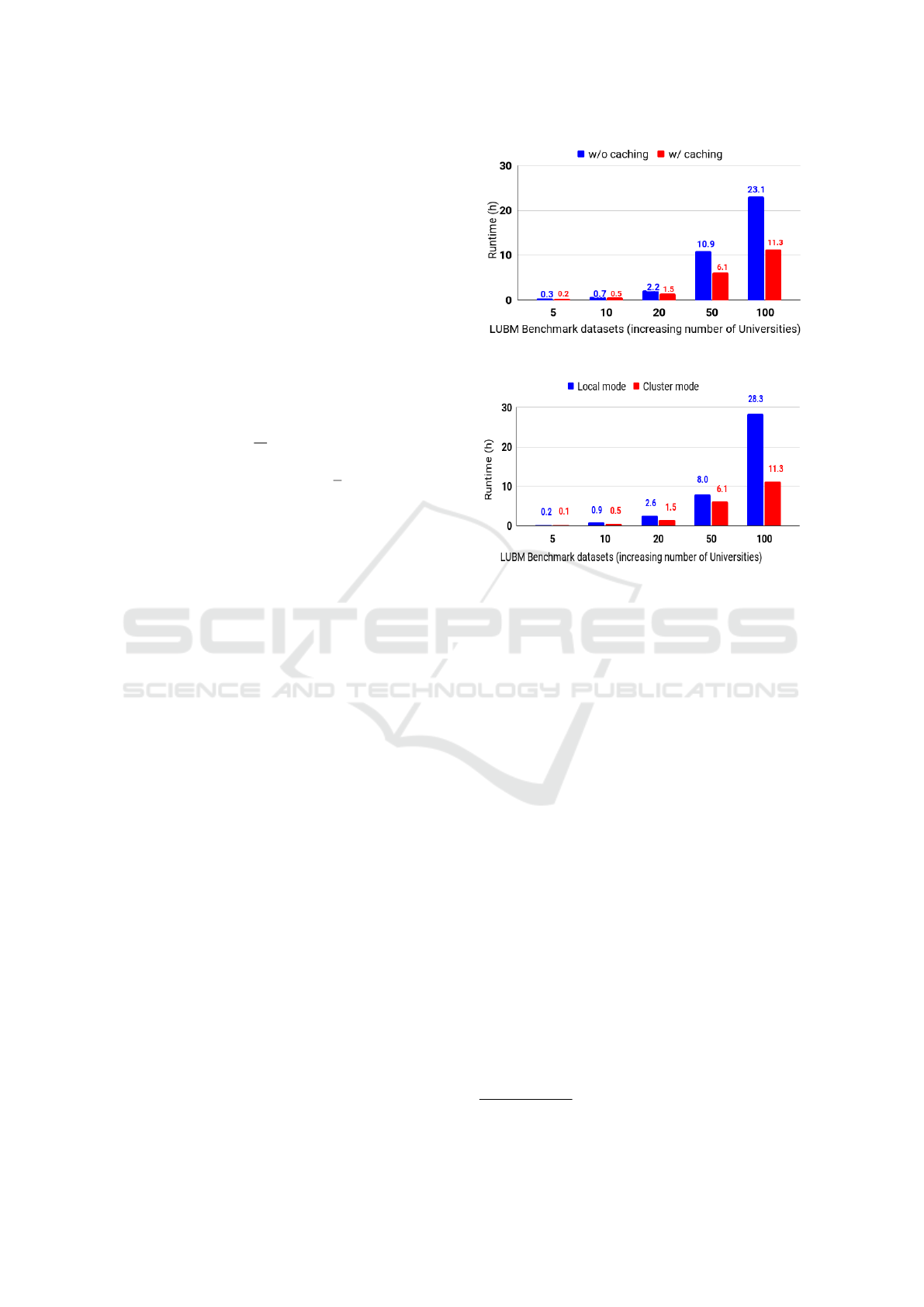
Figure 3: Sizeup evaluation with and without caching.
Figure 4: Evaluation in cluster and local environments.
sity Ontology Benchmark (UOBM)
6
. UOBM extends
LUBM (Guo et al., 2005) and generates more realis-
tic datasets. UOBM covers a complete set of OWL 2
constructs by including both OWL Lite and OWL DL
ontologies. UOBM generates three different data sets:
one, five, and ten universities. Properties of the gener-
ated datasets, loading time to the HDFS, the number
of axioms of each dataset, and the number of inferred
axioms are listed in Table 3.
4.2 Results and Discussion
Experiment 1 (Data Scalability): In this experi-
ment, we increase the size of the input OWL datasets
to measure the effectiveness of the proposed reason-
ing approach. In the cluster environment, we pre-
serve a constant number of nodes (workers) at five and
raise the size of datasets to determine whether larger
datasets can be processed by the proposed approach.
We run the experiments on five different datasets from
the LUBM benchmark to measure the data scalability.
We start by creating a dataset of five universities (i.e.,
LUBM-5), then we increase the number of universi-
ties (i.e., scaling up the size).
Figure 3 indicates the run time of the proposed ap-
proach with and without caching mechanism for each
dataset. Caching is a technique for speeding up pro-
6
https://www.cs.ox.ac.uk/isg/tools/UOBMGenerator/
KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development
58

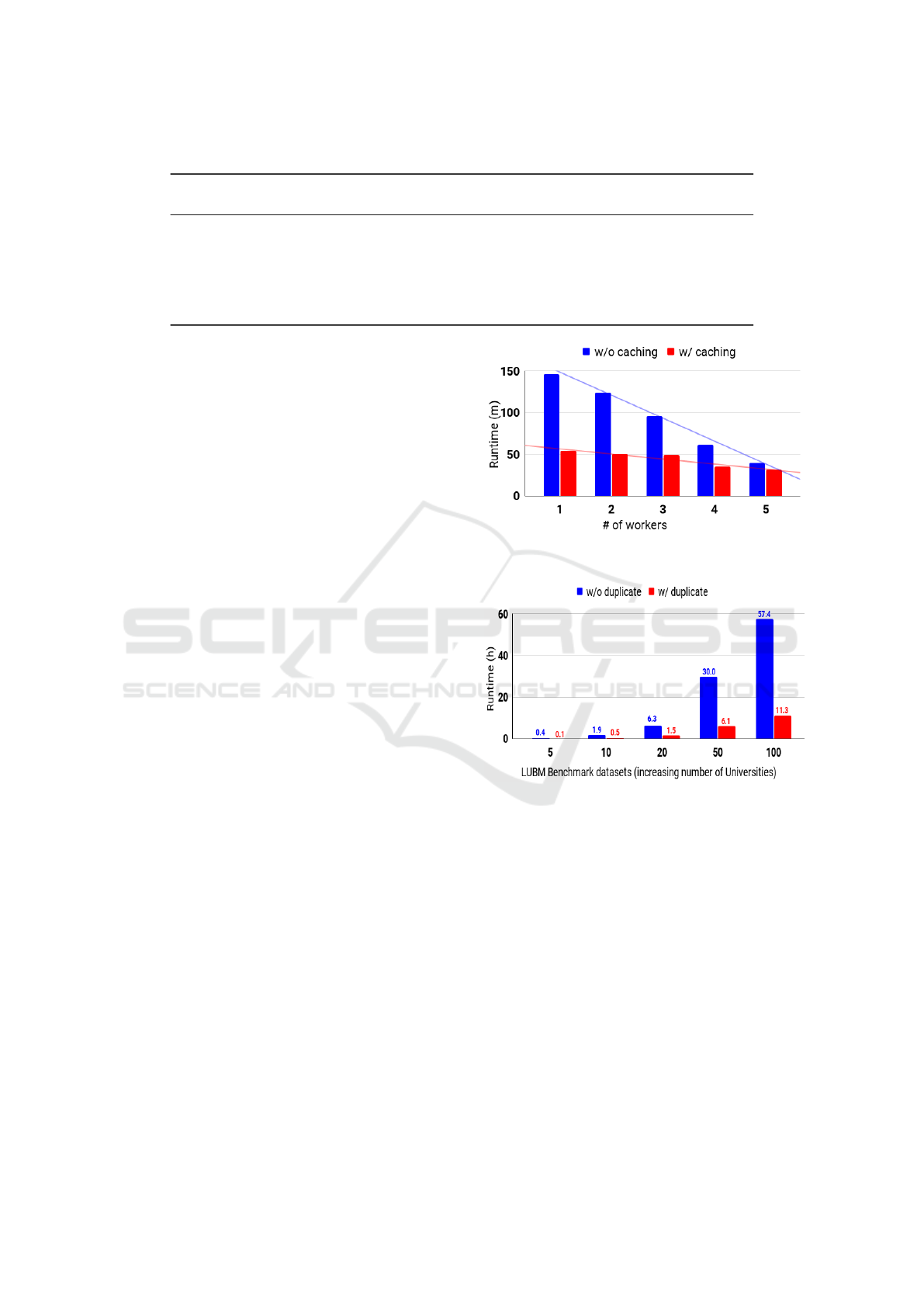
Table 3: LUBM benchmark datasets (functional syntax).
Dataset Size Load
time (sec)
#Axioms #Inferred Speedup Efficiency
LUBM-5 118 MB 3 636,446 274,563 1.4x 0.3
LUBM-10 284 MB 9 1,316,517 559,873 1.7x 0.3
LUBM-20 514 MB 10 2,781,477 1,182,585 1.8x 0.4
LUBM-50 1.3 GB 17 6,654,755 2,924,925 2.1x 0.4
LUBM-100 2.7 GB 48 13,310,784 6,204,835 2.5x 0.5
UOBM-10 282 MB 8 1,475,832 494,143 1.9x 0.5
cesses with multiple access to the same RDD, which
holds the data in memory and speeds up the compu-
tations. The x-axis represents the produced LUBM
datasets with an increase in the number of universi-
ties, while the y-axis represents the time of execu-
tion in hours. As illustrated in Figure 3, the reduc-
tion in execution time between the proposed approach
(blue columns) and without caching (red ones) is clear
(response to EQ1). For instance, OWL Horst rea-
soning on LUBM-100 costs around 23 hours with-
out caching, while the time is decreased by 52%
(i.e., becomes 11.3 hours) after the caching was trig-
gered. Therefore, we conclude that the proposed ap-
proach is scalable in terms of data scalability. Fig-
ure 4 displays the performance of the proposed ap-
proach obtained in a cluster environment compris-
ing five worker machines. For example, consider the
LUBM-100 dataset; the execution time in a single
(local) machine environment is decreased from 28.3
hours to 11.3 hours compared to the cluster environ-
ment. The reason is the distribution of the computa-
tions across multiple machines. The usage of clus-
ter mode has decreased the running time by 60% for
LUBM-100 (response to EQ2).
Experiment 2 (Node Scalability): In this experiment,
we vary the number of nodes in the cluster (with one
node each time from one to five) with an eye towards
affirming the node scalability. Figure 5 illustrates the
scalability performance of our approach by increasing
the number of worker nodes from one to five for the
LUBM-10 dataset. The execution time was dramati-
cally decreased from 146 to 40 minutes, i.e., approxi-
mately one-third. It is apparent that the time of execu-
tion drops linearly as the number of workers increases
(response to EQ3). The speedup and efficiency ratios
for the five datasets are shown in Table 3. Concerning
the number of workers, the speed of the selected data
is improved sequentially (response to EQ4). In con-
clusion, the results illustrate that the proposed OWL
Horst reasoning approach has achieved near-linear
output scalability in the context of speedup.
Experiment 3 (Duplicate Elimination): In this exper-
iment, we study the effect of eliminating duplicates
on the performance using our strategy. This strat-
Figure 5: Run time in the cluster with various number of
nodes for LUBM-10.
Figure 6: Evaluation with and without our duplicate elim-
ination strategy.
egy aims to reduce the amount of data that potential
jobs can handle by removing duplicates as early as
possible. To do so, we recorded the execution time
with and without the proposed duplicate elimination
strategy, i.e., eliminating duplicates after the comple-
tion of the reasoning process. As shown in Figure 6,
the execution time is dramatically decreased when our
elimination strategy is applied.
5 CONCLUSION AND FUTURE
WORK
We proposed a novel approach for performing dis-
tributed reasoning using RDFS and OWL Horst rules.
A Scalable Approach for Distributed Reasoning over Large-scale OWL Datasets
59

Surprisingly, after reviewing the literature, we found
no tool that can reason over large-scale OWL datasets.
The proposed approach is implemented as an open-
source distributed system for reasoning large-scale
OWL datasets using Spark. Compared to Hadoop
MapReduce, Spark enables efficient distributed pro-
cessing by supporting running multiple jobs at the
same node simultaneously as well as the ability to
cache data required for computations in the mem-
ory. The use of data storage in memory greatly
decreases the average time spent on network com-
munication (i.e., communication overhead) and data
read/write using disk-based approaches. We exploit
these advantages for supporting Semantic Web rea-
soning. Furthermore, the proposed approach com-
bines the contributions introduced by state-of-the-art
(i.e., the optimized execution strategy and the pre-
shuffling method). Besides, we proposed a novel du-
plicate elimination strategy that drastically reduces
the reasoning time. These tasks are considered the
most time-consuming tasks in the reasoning process.
The experiments proved that the proposed approach
is scalable in terms of both data and node scalabil-
ity. Our approach has successfully inferred around six
million axioms in 11 hours using only five nodes. In
conclusion, our approach achieved near-linear scala-
bility of output in the sense of speedup. We have suc-
cessfully integrated the proposed approach into the
SANSA framework, which ensures its sustainability
and usability.
To further our research, we plan to perform several
improvements, including code optimization, such as
using different persisting strategies, and build an op-
timal execution strategy based on the statistics of the
input OWL dataset using OWLStats (Mohamed et al.,
2020) approach from the SANSA framework. More-
over, we aim to design more reasoning profiles, such
as OWL EL and OWL RL.
ACKNOWLEDGEMENTS
This work has been supported by the following EU
Horizon2020 projects: LAMBDA project (GA no.
809965), CLEOPATRA project (GA no. 812997),
and PLATOON project (GA no. 872592).
REFERENCES
Al-Ajlan, A. (2015). The comparison between forward and
backward chaining. International Journal of Machine
Learning and Computing, 5(2):106.
Gu, R., Wang, S., Wang, F., Yuan, C., and Huang, Y. (2015).
Cichlid: efficient large scale rdfs/owl reasoning with
spark. In 2015 IEEE International Parallel and Dis-
tributed Processing Symposium, pages 700–709, Hy-
derabad, India. IEEE.
Guo, Y., Pan, Z., and Heflin, J. (2005). Lubm: A bench-
mark for owl knowledge base systems. Web Seman-
tics: Science, Services and Agents on the World Wide
Web, 3(2-3):158–182.
Hayes, P. (2004). Rdf semantics. https://www.w3.org/TR/
rdf-mt/#RDFRules.
Heino, N. and Pan, J. Z. (2012). Rdfs reasoning on mas-
sively parallel hardware. In International Seman-
tic Web Conference, pages 133–148, Boston, USA.
Springer.
Kim, J.-M. and Park, Y.-T. (2015). Scalable owl-horst on-
tology reasoning using spark. In 2015 International
Conference on Big Data and Smart Computing (BIG-
COMP), pages 79–86, Jeju, South Korea. IEEE.
Liu, Y. and McBrien, P. (2017). Spowl: Spark-based owl
2 reasoning materialisation. In Proceedings of the 4th
ACM SIGMOD Workshop on Algorithms and Systems
for MapReduce and Beyond, pages 1–10, Chicago,
USA. ACM.
Liu, Z., Feng, Z., Zhang, X., Wang, X., and Rao, G.
(2016). Rors: enhanced rule-based owl reasoning on
spark. In Asia-Pacific Web Conference, pages 444–
448, Suzhou, China. Springer.
Mohamed, H., Fathalla, S., Lehmann, J., and Jabeen, H.
(2020). OWLStats: Distributed computation of owl
dataset statistics. In IEEE/WIC/ACM International
Joint Conference on Web Intelligence and Intelligent
Agent Technology (WI-IAT), page In press. IEEE.
Sharma, T., Tiwari, N., and Kelkar, D. (2012). Study of dif-
ference between forward and backward reasoning. In-
ternational Journal of Emerging Technology and Ad-
vanced Engineering, 2(10):271–273.
Ter Horst, H. J. (2005). Completeness, decidability and
complexity of entailment for rdf schema and a seman-
tic extension involving the owl vocabulary. Journal of
web semantics, 3(2-3):79–115.
Urbani, J., Kotoulas, S., Maassen, J., Van Harmelen, F., and
Bal, H. (2010). Owl reasoning with webpie: calcu-
lating the closure of 100 billion triples. In Extended
Semantic Web Conference, pages 213–227, Greece.
Springer.
Urbani, J., Kotoulas, S., Maassen, J., Van Harmelen, F., and
Bal, H. (2012). Webpie: A web-scale parallel infer-
ence engine using mapreduce. Journal of Web Seman-
tics, 10:59–75.
Urbani, J., Kotoulas, S., Oren, E., and Van Harmelen, F.
(2009). Scalable distributed reasoning using mapre-
duce. In International semantic web conference, pages
634–649, Chantilly, VA, USA. Springer.
KEOD 2021 - 13th International Conference on Knowledge Engineering and Ontology Development
60