Substitution of the Fittest: A Novel Approach for Mitigating

Disengagement in Coevolutionary Genetic Algorithms

Hugo Alcaraz-Herrera

and John Cartlidge

University of Bristol, Bristol, U.K.

Keywords:

Coevolution, Disengagement, Genetic Algorithms.

Abstract:

We propose substitution of the ﬁttest (SF), a novel technique designed to counteract the problem of disengage-

ment in two-population competitive coevolutionary genetic algorithms. The approach presented is domain-

independent and requires no calibration. In a minimal domain, we perform a controlled evaluation of the

ability to maintain engagement and the capacity to discover optimal solutions. Results demonstrate that the

solution discovery performance of SF is comparable with other techniques in the literature, while SF also

offers beneﬁts including a greater ability to maintain engagement and a much simpler mechanism.

1 INTRODUCTION

While attempting the problem of designing optimal

sorting networks using a genetic algorithm (GA),

Hillis decided that rather than use randomly gener-

ated input lists to evaluate sorting networks, he would

instead co-evolve a population of input lists that are

evaluated on their ability to not be sorted (Hillis,

1990). By coupling the evolution of input lists with

the evolution of the networks to sort those lists, Hillis

attempted to create an “arms race” dynamic such

that input lists consistently challenge networks that

are sorting them. As networks improve their abil-

ity to sort, so lists become more difﬁcult to sort, etc.

This coevolutionary approach signiﬁcantly improved

results and generated wide interest amongst evolu-

tionary computation (EC) practitioners. In particular,

coevolution offers EC the ability to tackle domains

where an evaluation function is unknown or difﬁ-

cult to operationally deﬁne; and through self-learning,

coevolutionary systems offer potential for the “holy

grail” of open-ended evolutionary progress.

However, it soon emerged that coevolution can

suffer from some “pathologies” that cause the system

to behave in an unwanted manner, and prevent contin-

ual progress towards some desired goal. For instance,

coevolving populations may continually cycle with no

overall progress; populations may progress in an un-

intended and unwanted direction; or populations may

https://orcid.org/0000-0002-9991-662X

https://orcid.org/0000-0002-3143-6355

disengage and stop progressing entirely (Watson and

Pollack, 2001). These pathologies have been studied

in depth and a variety of techniques have been intro-

duced as remedy (Popovici et al., 2012). However,

there is still much to be understood, and no panacea

has been discovered.

Contribution: We propose substitution of the ﬁttest

(SF), a novel domain-independent method designed

to tackle the problem of disengagement in two-

population competitive coevolutionary systems. We

explore and evaluate SF in the deliberately simple

“greater than” domain, speciﬁcally designed for elab-

orating the dynamics of coevolution (Watson and Pol-

lack, 2001). We compare performance and system

dynamics against autonomous virulence adaptation

(AVA), a technique that has been shown to reduce the

likelihood of disengagement and improve optimisa-

tion in various domains (Cartlidge and Ait-Boudaoud,

2011). Initial results suggest that SF has some bene-

ﬁts over AVA. We evaluate and discuss the reasons

why, and present avenues for future investigation.

2 BACKGROUND

Coevolutionary genetic algorithms with two distinct

populations are often described using terminology

that follows the biological literature. As such, and fol-

lowing Hillis’ original formulation, the populations

are often named as “hosts” and “parasites” (Hillis,

1990). In such cases, the host population tends to

Alcaraz-Herrera, H. and Cartlidge, J.

Substitution of the Fittest: A Novel Approach for Mitigating Disengagement in Coevolutionary Genetic Algorithms.

DOI: 10.5220/0010661200003063

In Proceedings of the 13th International Joint Conference on Computational Intelligence (IJCCI 2021), pages 59-67

ISBN: 978-989-758-534-0; ISSN: 2184-3236

denote the population of candidate “solutions” that

we are interested in optimising (e.g., the sorting net-

works), while the parasite population tends to denote

the population of test “problems” for the solution pop-

ulation to solve (e.g., the lists to sort); i.e., the hosts

are the models and the parasites are the training set;

or alternatively the hosts are the learners and the para-

sites are the teachers. Throughout this paper, we tend

to use the host-parasite terminology to distinguish co-

evolving populations. However, while this terminol-

ogy is meaningful in asymmetric systems where one

population (the model) is of most interest, it should

be noted that in symmetric systems, such as games of

self-play where both coevolving populations are mod-

els with the same encoding scheme, the two popula-

tions become interchangeable and the names host and

parasite have less meaning.

In an ideal scenario, two-population competitive

coevolution will result in an arms race such that both

populations continually evolve beneﬁcial adaptions

capable of outperforming competitors. As a result,

there is continual system progress towards some de-

sired optimum goal. However, this ideal scenario

rarely materialises. In practice, coevolutionary sys-

tems tend to exhibit pathologies that restrict progress

(Watson and Pollack, 2001). These include cycling,

where populations evolve through repeated trajecto-

ries like players in an endless game of rock-paper-

scissors; and while short-term evolution exhibits con-

tinual progress, there is no long-term global progress

(Cartlidge and Bullock, 2004b). Alternatively, popu-

lations may start to overspecialise on sub-dimensions

of the game, such that evolved solutions are brittle

and do not generalise (Cartlidge and Bullock, 2003).

Furthermore, one population may begin to dominate

the other to such an extent that populations disen-

gage and evolutionary progress fails altogether, with

populations left to drift aimlessly (Cartlidge and Bul-

lock, 2004a). The likelihood of suffering from these

pathologies can be exacerbated by the problem do-

main. Cycling is more likely when the problem ex-

hibits intransitivity; overspecialisation is more likely

in multi-objective problems; and disengagement is

more likely if the problem has an asymmetric bias that

favours one population (Watson and Pollack, 2001).

Numerous techniques have been proposed for mit-

igating the pathologies that prevent continual coevo-

lutionary progress (for detailed reviews, see (Popovici

et al., 2012; Miguel Antonio and Coello Coello,

2018)). We can roughly group these approaches into

three broad categories; although in practice many

techniques straddle more than one category.

First, there are archive methods, which are de-

signed to preserve potentially valuable adaptations

from being “lost” during the evolutionary process.

The ﬁrst coevolutionary archiving technique is the

Hall of Fame (HoF) (Rosin and Belew, 1997). Ev-

ery generation, the elite member of each population

is stored in the HoF archive. Then, individuals in

the current population are evaluated against current

competitors and also against members of the HoF.

This ensures that later generations are evaluated on

their capacity to beat earlier generations as well as

their contemporaries. However, as the archive grows

each generation, simple archiving methods like the

HoF can become unwieldy over time. To counter

this, more sophisticated and efﬁcient archiving meth-

ods have been introduced to simultaneously minimise

archive size while maximising archive “usefulness”.

An efﬁcient example is the Layered Pareto Coevo-

lutionary Archive (LAPCA), which only stores in-

dividuals that are non-dominated and unique; while

the archive itself is pruned over time to keep the size

within manageable bounds (de Jong, 2007). More

recent variations on Pareto archiving approaches in-

clude rIPCA, which has been applied to the problem

of network security through the coevolution of adver-

sarial network attack and defence dynamics (Garcia

et al., 2017). Pareto dominance has also been em-

ployed for selection without the use of an archive,

for example the Population-based Pareto Hill Climber

(Bari et al., 2018); and Pareto fronts have been incor-

porated into an “extended elitism” framework, where

offspring are selected only if they Pareto dominate

parents when evaluated against the same opponents

(Akinola and Wineberg, 2020).

A second popular class of approaches attempt

to maintain a diverse set of evolutionary challenges

through the use of spatial embedding and multiple

populations. Spatially embedded algorithms – where

populations exist on an n-dimensional plane and in-

dividuals only interact with other individuals in the

local neighbourhood – have been shown to succeed

where other non-spatial coevolutionary approaches

fail. Explanations for how spatial models can help

combat disengagement through challenge diversity

have been explored in several works (Wiegand and

Sarma, 2004; Williams and Mitchell, 2005). Chal-

lenge diversity can also be maintained through the

use of multiple genetically-distinct populations (i.e.,

with no interbreeding or migration). Examples in-

clude the friendly competitor, where two model pop-

ulations (one “friendly” and one “hostile”) are coe-

volved against one test population (Ficici and Pollack,

1998). Tests are rewarded if they are both easy to be

defeated by a friendly model and hard to be beaten

by a hostile model; thereby ensuring pressure on tests

to evolve at a challenge-level consistent with the abil-

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

ity of models. Recently, a new method incorporat-

ing the periodic spawning of sub-populations, and

then re-integration of individuals that perform well

across multiple sub-populations back into the main

population has been shown to encourage continual

progress in predator-prey robot coevolution (Simione

and Nolﬁ, 2021).

Finally, there are approaches that focus on adapt-

ing the mechanism for selection such that individuals

are not selected in direct proportion to the number of

competitions that they win; i.e., selection favours in-

dividuals that are not unbeatable. An early endeavour

in this area is the phantom parasite, which marginally

reduces the ﬁtness of an unbeatable competitor, while

all other ﬁtness values remain unchanged (Rosin,

1997). Later, the Φ function was introduced for

the density classiﬁcation task to coevolve cellular au-

tomata rules that classify the density of an initial con-

dition (Pagie and Mitchel, 2002). The Φ function

translates all ﬁtness values such that individuals are

rewarded most highly for being equally difﬁcult and

easy to classify (i.e., by being classiﬁed correctly half

of the time); while individuals that are always classi-

ﬁed or always unclassiﬁed are punished with low ﬁt-

ness. However, while Φ worked well, it was limited

by being domain-speciﬁc.

More generally applicable is the reduced vir-

ulence technique (Cartlidge and Bullock, 2002;

Cartlidge and Bullock, 2004a). Inspired by the be-

haviour of biological host-parasite systems, where the

virulence of pathogens evolves over time, reduced vir-

ulence is the ﬁrst domain-independent technique with

tunable parameters that can be conﬁgured. After gen-

erating a parasite score through competition, reduced

virulence applies the following non-linear function to

generate a ﬁtness for selection:

f (x

,υ) =

−

(1)

where 0 ≤ x

≤ 1 is the relative (or subjective) apti-

tude of individual i and 0.5 ≤ υ ≤ 1 represents the

virulence of the parasite population. When υ = 1,

equation (1) preserves the original ranking of para-

sites (i.e., the ranking of competitive score, x) and

is equivalent to the canonical method of rewarding

parasites for all victories over hosts. When υ = 0.5,

equation (1) rewards maximum ﬁtness to parasites

that win exactly half of all competitions. Therefore,

in domains where there is a bias in favour of one

population (the “parasites”), setting a value of υ < 1

for the advantaged population reduces the bias dif-

ferential in order to preserve coevolutionary engage-

ment. Reduced virulence demonstrated improved per-

formance, but is limited by requiring υ to be deter-

mined in advance. In many domains, bias may be

difﬁcult to determine and may change over time. To

tackle this problem, reduced virulence has been in-

corporated into a human-in-the-loop system enabling

a human controller to steer coevolution during run-

time by observing the system behaviour and altering

the value of υ in real time (Bullock et al., 2002).

Later, autonomous virulence adaptation (AVA) –

a machine learning approach that automatically up-

dates υ during coevolution – was proposed (Cartlidge

and Ait-Boudaoud, 2011). Each generation t, AVA

updates υ using:

t+1

= υ

+ ∆

(2)

∆

= µ∆

t−1

+ α(1 − µ)(τ − X

) (3)

where 0 ≤ α,µ,τ ≤ 1 are learning rate, momentum,

and target value, respectively; and X

is the nor-

malised mean subjective score of the population.

Rigorous calibration of AVA settings demonstrated

that values α = 0.0125, µ = 0.3, and τ = 0.56 can

be applied successfully in a number of diverse do-

mains. In particular, it was shown that AVA can co-

evolve high performing sorting networks and maze

navigation agents with much greater computational

efﬁciency than archive techniques such as LAPCA

(Cartlidge and Ait-Boudaoud, 2011).

3 SUBSTITUTION OF THE

FITTEST

We introduce substitution of the ﬁttest (SF), a novel

technique designed to combat disengagement that

is domain-independent and requires no calibration.

Disengagement tends to occur when one population

“breaks clear” of the competing population such that

all individuals in the leading population outperform

all individuals in the trailing population. Therefore,

in simple terms, SF is designed to apply a “brake” to

the population evolving more quickly; while for the

population trying to keep pace, SF applies an “accel-

eration”. Consequently, the advantage of the leading

population over the trailing population is reduced. In

this way, SF is designed to keep populations engaged.

Unlike standard evolutionary algorithms, where

individuals are evaluated using an “absolute” ﬁtness

function that is exogenous to the evolutionary pro-

cess, competitive coevolutionary GAs utilise a “rel-

ative” (or “subjective”) ﬁtness evaluation, where ﬁt-

ness ψ

of an individual i is endogenously assigned

For the initial t < 5 generations, to avoid immediate

disengagement in cases of extreme bias differential, equa-

tion (3) is replaced by ∆

= (0.5 − X

)/t; so virulence can

immediately adapt to high (υ = 1) or low (υ = 0.5) values.

Substitution of the Fittest: A Novel Approach for Mitigating Disengagement in Coevolutionary Genetic Algorithms

based on performance against other evolving individ-

uals. Usually, score ψ

is simply the proportion of

“victories” that i secures across a series of competi-

tions against evolving opponents. These competitive

interactions between coevolving populations describe

a coupled system that has potential to develop into

an arms-race of continual progress. However, when

the populations decouple, i.e., when disengagement

occurs, all information regarding the relative differ-

ences in performance of individuals is lost, such that

∀i, j : ψ

= ψ

. This is problematic and causes the

coevolving populations to drift.

The current state of a population can be measured

by the population mean subjective aptitude:

pop

∑

i=1

(4)

where n is the number of individuals in the population

and 0 ≤ σ ≤ 1. Then, σ values for each population

can be used to measure the level of disengagement,

deﬁned as:

δ = |σ

popA

− σ

popB

| (5)

where 0 ≤ δ ≤ 1. When populations have similar σ,

then disengagement δ has a low value close to zero.

When populations are fully disengaged, i.e., when

popA

= 1 and σ

popB

= 0, or when σ

popA

= 0 and

popB

= 1, then δ = 1. During the coevolutionary pro-

cess, δ

is calculated and stored each generation t. If

t+1

≤ δ

, disengagement did not increase; otherwise,

disengagement did increase and so SF is triggered.

When SF is triggered, we ﬁrst calculate the num-

ber of individuals to be substituted, κ, deﬁned as:

κ = nδ

(6)

where n is the number of individuals in the popula-

tion and the result is rounded up to the nearest inte-

ger. The value of κ increases non-linearly as a func-

tion of δ. As populations approach disengagement (δ

near 1), the number of substitutions tends to n. It is

important to point out that if κ >

, then effectively

only n − κ substitutions occur. For instance, given a

population with n = 6 parasites whose aptitudes are

[0.8,0.6,0.4,0.2,0.1,0.0] and κ = 4, after the substitu-

tion, their aptitudes will be [0.0,0.1,0.2,0.4,0.1,0.0].

In this example, half the population was not modiﬁed

and the two ﬁttest individuals were substituted by the

two worst individuals. Furthermore, if δ = 1, popu-

lations would not be modiﬁed as the number of indi-

viduals to be substituted is the same as the population

size (i.e., κ = n). On the contrary, when δ < 0.3, κ

tends to 0. During these times, populations are sufﬁ-

ciently engaged and substitutions are not necessary.

The next step in the SF process consists of com-

paring σ

popA

and σ

popB

and then substituting κ indi-

viduals in each population using the following rules:

• Population with lowest σ: Rank all individuals by

subjective aptitude ψ

. Then, the κ individuals

with the highest ψ

replace the κ individuals with

the lowest ψ

. Finally, the subjective aptitude of

every individual is increased by:

= min(ψ

+ δ,1) (7)

taking minimum value to ensure 0 ≤ ψ

≤ 1.

• Population with highest σ: Rank all individuals by

. Then κ individuals with the lowest ψ

replace

the κ individuals with the highest ψ

; following

replacement, the subjective aptitude of every indi-

vidual is decreased using:

= max(ψ

− δ,0) (8)

taking maximum value to ensure 0 ≤ ψ

≤ 1.

As described, SF affects each population in a dif-

ferent manner. For the population that evolves more

quickly, the proportion of individuals to be randomly

selected is increased. For instance, if the highest

ranked individual whose ψ < δ, then the κ individ-

uals would be selected at random because they would

have ψ

= 0. On the other hand, for the population

which evolves slower than the other, the effect is the

opposite, i.e., if the lowest ranked individual whose

ψ + δ ≥ 1, then all κ individuals would have ψ

= 1

and hence those individuals would have high proba-

bility of being selected.

Following SF, selection is performed and genetic

operators are applied as usual. In the minimal exper-

iments we present in the following sections, we use

tournament selection and apply mutation, i.e., popu-

lations are asexual and recombination is not used.

4 EXPERIMENTAL METHOD

4.1 The “Greater Than” Game

The greater than game (Watson and Pollack, 2001)

was introduced as a minimal (and analytically

tractable) substrate capable of demonstrating some of

the pathological dynamics of coevolution; in partic-

ular disengagement. The game consists of maximis-

ing scalar values through a comparison-based func-

tion where given two scalar values, α and γ, the

function operates as score(α,γ) = 1 if α > γ, 0 oth-

erwise. Here, we use a slightly modiﬁed “greater

than or equals” game that rewards draws; such that

score(α,γ) = 1 if α > γ; 0.5 if α = γ; 0 otherwise.

The coevolutionary set-up consists of two isolated

populations, each with n individuals. Each individual

is represented by a binary string with l = 100 bits and

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

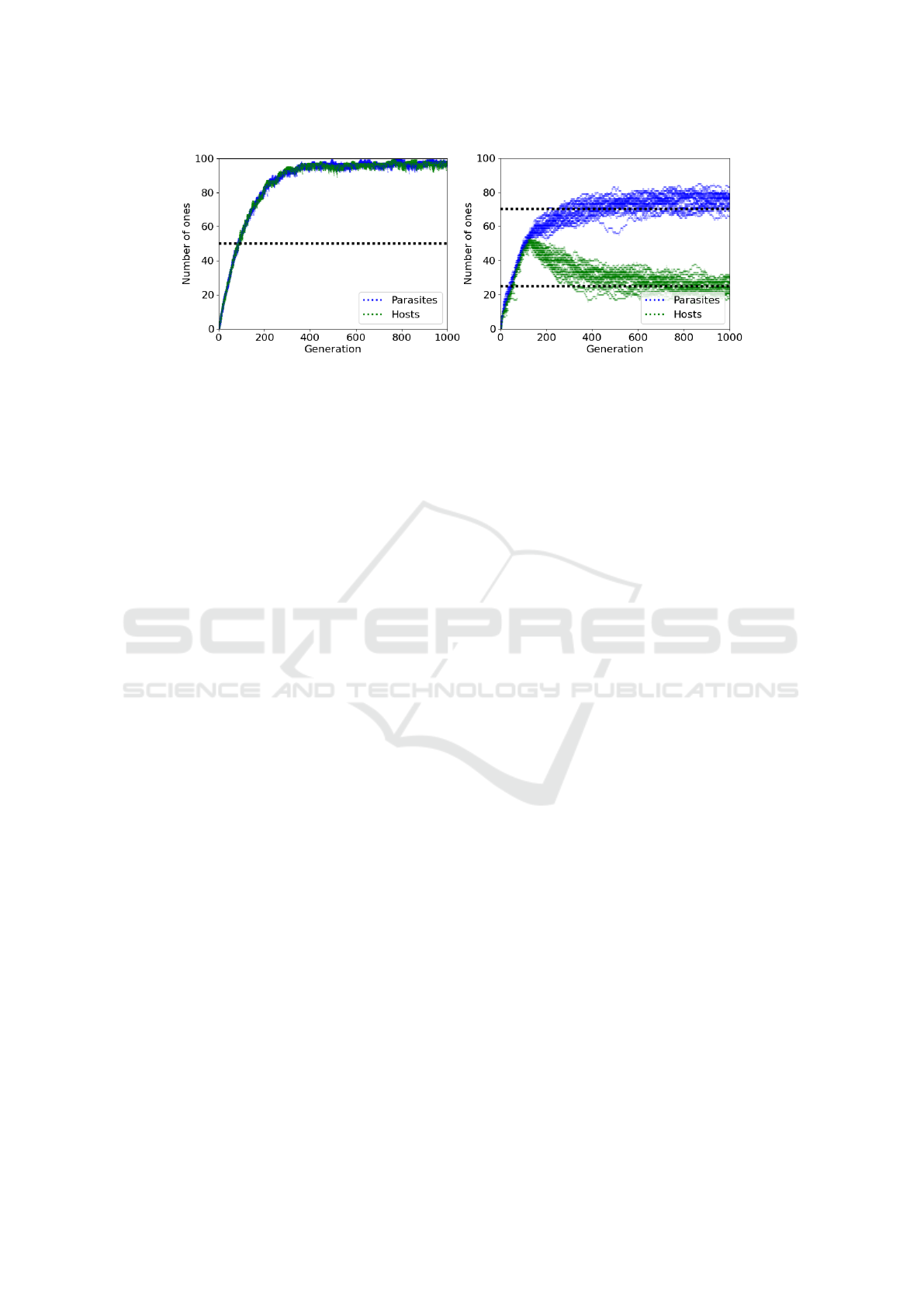
Figure 1: Coevolution: (left) equal bias β

= β

= 0.5; and (right) differential bias β

= 0.25, β

= 0.75.

the “objective” purpose of the coevolutionary system

is to evolve individuals with bit-strings containing all

ones (i.e., scalar values of l = 100). Every genera-

tion, to generate a subjective aptitude score, each in-

dividual plays the greater than game against a sam-

ple of S opponents. Tournament selection is used to

select individuals for reproduction, and the only ge-

netic operator is mutation (i.e., reproduction is asex-

ual). Mutation has a bias controlled by parameter β,

where 0 ≤ β ≤ 1. For each bit, there is a probability

m of mutation occurring. When it occurs, the bit is

assigned a new value at random, with probability β of

assigning a 1, and probability 1 − β of assigning a 0;

i.e., when β = 0.5, mutation has an equal chance of

assigning the bit to 1 or 0; when β = 0 mutation will

always assign the bit to 0; and when β = 1 mutation

will always assign the bit to 1. This bias parameter β

allows the simple game to emulate the intrinsic asym-

metry of real and more complex domains, where it is

often easier for one population to outperform another.

Under mutation bias alone, i.e., when populations are

disengaged and left to drift under the absence of se-

lection pressure, we expect the population to tend to-

wards having β×l ones. Therefore, for a bias β = 0.5,

we would expect the population to drift towards scalar

values of 50.

In our two-population competitive set up, we label

the populations as as hosts and parasites. Each popu-

lation has an independent bias value β, which controls

the problem difﬁculty for each population. We use

to label the bias value of the host population and

to label the bias value of the parasite population.

When bias differential is high, i.e., when the value of

is much larger than the value of β

(or vice versa),

disengagement becomes more likely as the game is

much easier for the parasites (alternatively, the hosts)

to succeed. In more complex domains, there is often

asymmetry in problem difﬁculty for coevolving pop-

ulations. By varying β

and β

, we are able to control

the asymmetry of problems in the simple greater than

game.

Our experimental set up is detailed as follows. We

coevolve two isolated populations, each with 25 indi-

viduals (n = 25). The length of the binary array (an

individual) is 100 (l = 100) and each bit is initialised

to 0. For generating a competitive score, we use a

sample size of 5 (S = 5). Tournament size for selec-

tion is 2. The probability of mutation per bit is 0.005

(m = 0.005). Finally, each evolutionary run lasts for

1000 generations.

4.2 Disengagement

The effect of disengagement can most clearly be elab-

orated by visualising what happens when it occurs.

Figure 1 (left) presents the coevolution of two popu-

lations, each with equal bias β

= β

= 0.5. We see

that populations remain engaged throughout the evo-

lutionary run. This engagement provides a continual

gradient for selection and encourages an “arms race”

of increasing performance. As a result, both popula-

tions reach optimal performance of 100 ones. This is

far higher than 50 ones (dotted line) that both popu-

lations would be expected to reach if drifting through

space under mutation alone, i.e., when selection pres-

sure is removed.

In contrast, Figure 1 (right) demonstrates the

pathology of disengagement. Here, there is a differen-

tial bias in favour of parasites, such that β

= 0.75 and

= 0.25. Initially, both populations remain engaged

and selection drives evolutionary progress, with both

populations reaching approximately 50 ones by gen-

eration 150. However, the impact of differential bias

in favour of parasites then leads to a disengagement

event such that all parasites have more ones than their

competing hosts; resulting in a subjective score of

zero for all hosts and a subjective score of one for

all parasites. At this point selection pressure is re-

moved as all individuals have an equal (and there-

fore random) chance of selection, leaving the popu-

lations to drift under mutation alone. As expected,

the parasite population drifts to the parasite mutation

Substitution of the Fittest: A Novel Approach for Mitigating Disengagement in Coevolutionary Genetic Algorithms

Figure 2: Number of runs with no disengagement; AVA (left) and SF (right) across all bias levels (50 trials).

Figure 3: Number of runs where hosts reached optimum; AVA (left) and SF (right) across all bias levels (50 trials).

Figure 4: Mean number of ones of best host; AVA (left) and SF (right) across all bias levels (50 trials).

bias (dotted line) of 75, while hosts degrade to the

host mutation bias of 25. The high bias differential

between populations (β

− β

= 0.5) not only causes

the initial disengagement event, but ensures that post-

disengagement populations drift through different re-

gions of genotype/phenotype space and will never re-

engage through chance alone.

In general, the greater the bias differential be-

tween populations, the greater the likelihood of dis-

engagement occurring. As shown, disengagement

severely hinders coevolutionary progress.

5 SF VS AVA: A COMPARISON

To measure the performance of SF, we perform a

thorough comparison against AVA (Cartlidge and Ait-

Boudaoud, 2011), which has been previously shown

to dramatically reduce the effects of disengagement

in the greater than game and also in several more

complex and realistic domains, including design-

ing minimal-length sorting networks and discovering

classiﬁer systems for maze navigation. To understand

how the two approaches are likely to perform in more

complex domains, where population asymmetries are

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

more likely, we trial both SF and AVA in simulations

where mutation bias is varied across all possible levels

(β

≥ β

) in the range [0.1, 1.0]. The mutation bias

was conﬁgured in favour of parasites (except when

= β

); although this decision is arbitrary and re-

sults where bias is in favour of hosts would yield sym-

metrically similar results. For each bias scenario, we

performed 50 experimental trials. To analyse perfor-

mance of SF and AVA, we utilise three metrics: (i) the

reliability of the technique to maintain population en-

gagement; (ii) the capacity to discover optimal hosts

containing all ones; and (iii) the mean number of ones

that hosts reach before disengagement occurs. The

following sections describe our ﬁndings.

5.1 Maintaining Engagement

Since the main objective of AVA and SF is to main-

tain engagement during coevolution, regardless of

bias ﬂuctuations that may arise, it is fundamental to

study their response under diverse bias levels. Fig-

ure 2 presents a heatmap showing the number of runs

where AVA and SF maintained population engage-

ment during the full coevolutionary process (regard-

less of whether an optimal host is found).

Overall, we see that SF is able to maintain en-

gagement more successfully than AVA across a di-

verse range of bias differentials. For 38 of the 50 bias

pairings, SF maintains engagement for the full coevo-

lutionary run of 1000 generations across all 50 trials.

For AVA, however, this number is only 12. Moreover,

SF maintains engagement for the full coevolutionary

run in at least 40 out of 50 trials across 49 bias pair-

ings, while for AVA this number is 42.

Relative to SF, results suggest that AVA tends to

struggle in scenarios (i) where the bias of both popu-

lations are either the same (symmetrical systems) or

similar; and (ii) where parasite bias is very high (e.g.,

= 1.0) and there is a large bias differential between

parasites and hosts. In comparison, although SF also

fails in scenarios where parasites have very high bias,

SF is capable of maintaining engagement where AVA

is not.

Regarding the result obtained by AVA, in the orig-

inal research (Cartlidge and Ait-Boudaoud, 2011), it

was calibrated to only handle bias levels in the range

[0.5, 1.0]. Moreover, in the original experiments the

number of generations is 750 whereas in these exper-

iments, the number of generations is 1000. The du-

ration of experimental trials is a key factor inasmuch

AVA, in a number of bias scenarios, tends to allow

disengagement after optimal hosts are found. For in-

stance, when β

= 0.5, β

= 1.0, populations tend to

ﬁrst reach the optimum, but then later, around genera-

tions 850-900, the populations disengage. This unex-

pected behaviour suggests that AVA parameters may

require recalibration to maintain engagement over

long time periods when there is a high bias differ-

ential. It also demonstrates an advantage of SF over

AVA, as SF has no parameter settings to calibrate.

5.2 Reaching the Optimum

Another essential aspect to analyse is the capability

to reach the optimal zone. Figure 3 presents the num-

ber of runs where hosts (more precisely, at least one

host) reached the optimal, regardless of whether or

not populations disengage after this point. We see a

similar pattern for both SF and AVA. AVA reached

the optimal zone at least 40 times under 21 bias lev-

els, where as SF was capable of reaching 40 times or

more under 20 bias levels. Furthermore, both AVA

and SF reached the optimal zone a maximum of 50

times (i.e., every time) under 18 bias scenarios.

As expected, in multiple bias scenarios hosts were

not capable of reaching the optimum when hosts have

a very low mutation bias (β

< 0.5).

5.3 General Performance

Figure 4 shows the mean maximum number of ones

of the best host across all bias conﬁgurations, regard-

less of whether or not populations disengage or hosts

reach the optimum. Again, performance of SF and

AVA is similar. AVA reaches at least 90 ones under

36 bias scenarios, whereas SF reaches 90 ones in 35

scenarios. Furthermore, AVA and SF both reach 100

ones under 18 possible bias scenarios.

Results suggest that AVA and SF tend to behave

similarly across most bias levels. However, when

there is a signiﬁcant bias differential (e.g., β

0.1,β

= 0.9), AVA enables populations to reach a

greater performance (closer to the optimum) than SF.

5.4 Coevolutionary Dynamics

Figures 5 and 6 present example runs to highlight the

effects of AVA (left) and SF (right) during the coevo-

lutionary process. When bias differential is relatively

large (Figure 5; β

= 0.3 and β

= 0.7) both AVA

and SF maintain engagement throughout. However,

when bias differential is very large (Figure 6; β

= 0.2

and β

= 1.0), disengagement occurs under both tech-

niques, but tends to occur earlier (around generation

410 for AVA, compared with generation 550 for SF).

Interestingly, in Figure 6 we see that SF induces

different population dynamics with respect to AVA.

Under SF, in the early generations, parasites exhibit

Substitution of the Fittest: A Novel Approach for Mitigating Disengagement in Coevolutionary Genetic Algorithms

Figure 5: Example coevolutionary runs under AVA (left) and SF (right) with β

= 0.3, β

= 0.7.

Figure 6: Example coevolutionary runs under AVA (left) and SF (right) with β

= 0.2, β

= 1.0.

Figure 7: Initial generations of one run (β

= 0.1, β

= 1.0)

using SF, showing absolute ﬁtness of parasites and hosts

(left axis) and δ value of disengagement (right axis).

lots of variation, with some outliers drifting far from

the engaged populations. Then, around generations

90 and 170, these outlier lineages suddenly disappear.

A similar “cull” effect is not observed with AVA.

To further investigate the cull effect in SF and its

direct relation with disengagement value δ, Figure 7

presents the initial generations of one example run

with very high bias differential (β

= 0.1, β

= 1.0).

Around generation 30, we see that there is a single

outlier parasite containing around 40 ones. As a con-

sequence, δ ≈ 0.81 and κ = 25(0.81

1/0.81

) = 19 (see

Equation 6). Since 19 >

, the effective substitu-

tions are 6 (see example given in Section 3). There-

fore, the 6 ﬁttest parasites, including the outlier, are

substituted by the 6 worst parasites. Consequently,

the subsequent generations do not present outliers and

δ (and therefore κ) decreases. Other outlier lineages

later begin to emerge and the process repeats. In con-

trast, AVA tends to keep both populations more tightly

coupled throughout.

6 CONCLUSIONS

This research has introduced SF as an alternative tech-

nique to mitigate disengagement in competitive co-

evolutionary genetic algorithms. Using a minimal

problem domain to enable exposition, we compared

the performance of SF with AVA, a technique in the

literature that has been shown to combat disengage-

ment in a variety of domains. Experimental results

suggest that, in general, SF has similar performance to

AVA in terms of discovery of optimal solutions. How-

ever, SF is also shown to have better performance than

AVA in terms of consistently maintaining engagement

across a wide variety of bias differentials, i.e., where

there is a large inherent advantage in favour of one co-

evolving population. The mechanism of SF is deliber-

ECTA 2021 - 13th International Conference on Evolutionary Computation Theory and Applications

ately designed to be simple and domain independent,

requiring no domain knowledge or speciﬁc calibra-

tion. This makes SF more easy to implement than

other techniques and offers the possibility of being

more generally applicable.

However, one of the potential weaknesses ob-

served in SF is the highly-ﬂuctuating behaviour in-

duced in populations (i.e., the “cull” effect), which

might lead to sudden disengagement in other more re-

alistic domains. Thus, we believe that SF deserves

further exploration; although it has shown suitable

performance in a simple domain, experiments in more

complex domains such as maze navigation or sort-

ing networks (Cartlidge and Ait-Boudaoud, 2011) are

necessary to demonstrate its reliability. Furthermore,

a robust comparison against other state-of-art tech-

niques will be performed. Finally, we intend to ex-

plore the effects that SF has on other coevolutionary

pathologies, such as overspecialisation and cycling.

ACKNOWLEDGEMENTS

Hugo Alcaraz-Herrera’s PhD is supported by The

Mexican Council of Science and Technology (Con-

sejo Nacional de Ciencia y Tecnolog

ıa - CONACyT).

John Cartlidge is sponsored by Reﬁnitiv.

REFERENCES

Akinola, A. and Wineberg, M. (2020). Using implicit multi-

objectives properties to mitigate against forgetfulness

in coevolutionary algorithms. In Genetic and Evo-

lutionary Computation Conference, GECCO, pages

769–777.

Bari, A. G., Gaspar, A., Wiegand, R. P., and Bucci, A.

(2018). Selection methods to relax strict acceptance

condition in test-based coevolution. In Congress on

Evolutionary Computation, CEC, pages 1–8.

Bullock, S., Cartlidge, J., and Thompson, M. (2002).

Prospects for computational steering of evolutionary

computation. In Workshop Proceedings 8th Int. Conf.

on Artiﬁcial Life, ALIFE, pages 131–137.

Cartlidge, J. and Ait-Boudaoud, D. (2011). Autonomous

virulence adaptation improves coevolutionary opti-

mization. IEEE Transactions on Evolutionary Com-

putation, 15(2):215–229.

Cartlidge, J. and Bullock, S. (2002). Learning lessons from

the common cold: How reducing parasite virulence

improves coevolutionary optimization. In Congress

on Evolutionary Computation, CEC, pages 1420–

1425 vol.2.

Cartlidge, J. and Bullock, S. (2003). Caring versus shar-

ing: How to maintain engagement and diversity in

coevolving populations. In Banzhaf, W., Ziegler, J.,

Christaller, T., Dittrich, P., and Kim, J. T., editors, Ad-

vances in Artiﬁcial Life, pages 299–308, Berlin, Hei-

delberg. Springer Berlin Heidelberg.

Cartlidge, J. and Bullock, S. (2004a). Combating coevolu-

tionary disengagement by reducing parasite virulence.

Evolutionary Computation, 12(2):193–222.

Cartlidge, J. and Bullock, S. (2004b). Unpicking tartan

CIAO plots: Understanding irregular coevolutionary

cycling. Adaptive Behavior, 12(2):69–92.

de Jong, E. D. (2007). A monotonic archive for pareto-

coevolution. Evolutionary Computation, 15(1):61–93.

Ficici, S. G. and Pollack, J. B. (1998). Challenges in

coevolutionary learning: Arms-race dynamics, open-

endedness, and mediocre stable states. In Interna-

tional Conference on Artiﬁcial Life, ALIFE, pages

238–247.

Garcia, D., Lugo, A. E., Hemberg, E., and O’Reilly, U.-

M. (2017). Investigating coevolutionary archive based

genetic algorithms on cyber defense networks. In

Genetic and Evolutionary Computation Conference

Companion, GECCO, pages 1455–1462.

Hillis, W. D. (1990). Co-evolving parasites improve simu-

lated evolution as an optimization procedure. Phys. D,

42(1–3):228–234.

Miguel Antonio, L. and Coello Coello, C. A. (2018). Co-

evolutionary multiobjective evolutionary algorithms:

Survey of the state-of-the-art. IEEE Transactions on

Evolutionary Computation, 22(6):851–865.

Pagie, L. and Mitchel, M. (2002). A comparison of evo-

lutionary and coevolutionary search. International

Journal of Computational Intelligence and Applica-

tion, 2(1):53–59.

Popovici, E., Bucci, A., Wiegand, R. P., and De Jong, E. D.

(2012). Coevolutionary principles. In Handbook of

Natural Computing, pages 987–1033. Springer Berlin

Heidelberg, Berlin, Heidelberg.

Rosin, C. D. (1997). Coevolutionary Search Among Adver-

saries. PhD thesis, Department of Computer Science,

University of California, San Diego, California.

Rosin, C. D. and Belew, R. K. (1997). New methods for

competitive coevolution. Evolutionary Computation,

5(1):1–29.

Simione, L. and Nolﬁ, S. (2021). Long-term progress and

behavior complexiﬁcation in competitive coevolution.

Artiﬁcial Life, 26(4):409–430.

Watson, R. A. and Pollack, J. B. (2001). Coevolutionary

dynamics in a minimal substrate. In Genetic and Evo-

lutionary Computation Conference, GECCO, pages

702–709.

Wiegand, R. P. and Sarma, J. (2004). Spatial embedding

and loss of gradient in cooperative coevolutionary al-

gorithms. In Parallel Problem Solving from Nature,

PPSN, pages 912–921.

Williams, N. and Mitchell, M. (2005). Investigating the suc-

cess of spatial coevolution. In Genetic and Evolution-

ary Computation Conference, GECCO, pages 523–

530.

Substitution of the Fittest: A Novel Approach for Mitigating Disengagement in Coevolutionary Genetic Algorithms