Explainability and Continuous Learning with Capsule Networks

Janis Mohr

, Basil Tousside

, Marco Schmidt

and J

org Frochte

Interdisciplinary Institute for Applied Artiﬁcial Intelligence and Data Science Ruhr,

Bochum University of Applied Science, 42579 Heiligenhaus, Germany

Center Robotics (CERI), University of Applied Sciences Wuerzburg-Schweinfurt, 97421 Schweinfurt, Germany

marco.schmidt@fhws.de

Keywords:

Explainability, Continuous Learning, Capsule Networks, Data Privacy, Image Recognition.

Abstract:

Capsule networks are an emerging technique for image recognition and classiﬁcation tasks with innovative

approaches inspired by the human visual cortex. State of the art is that capsule networks achieve good ac-

curacy for future image recognition tasks and are a promising approach for hierarchical data sets. In this

work, it is shown that capsule networks can generate image descriptions representing detected objects in im-

ages. This visualisation in combination with reconstructed images delivers strong and easily understandable

explainability regarding the decision-making process of capsule networks and leading towards trustworthy AI.

Furthermore it is shown that capsule networks can be used for continuous learning utilising already learned

basic geometric shapes to learn more complex objects. As shown by our experiments, our approach allows for

distinct explainability making it possible to use capsule networks where explainability is required.

1 INTRODUCTION

Convolutional neural networks (CNNs) are very suc-

cessful in recognition and classiﬁcation in computer

vision tasks. However, adopting machine learning

today is facing two major challenges. On the one

side, there is an ever-increasing demand for privacy-

preserving AI. On the other side, there is a need for

constantly evolving neural networks which can learn

continually. Conventional ML approaches based on

centralised data collection cannot meet these chal-

lenges. How to solve the problem of data isolation

while complying with the privacy-protection laws and

regulations is a major challenge for ML researchers

and practitioners.

On the legal front, lawmakers and regulatory bod-

ies are coming up with new laws ruling how data shall

be managed and used. One prominent example is

the adoption of the General Data Protection Regula-

tion (GDPR) by the European Union in 2018 which

makes high demands on data protection and privacy

including the requirement to delete data after a given

time. Some countries decided in a follow-up to en-

act laws that give the right to require an explanation

for every algorithmic decision (Malgieri, 2019). The

ethics guidelines for trustworthy AI of the EU assess

explainability as one of the key requirements for AI.

In the United States, the California Consumer Pri-

vacy Act will be enacted in 2020. China’s Cyber

Security Law which came into effect in 2017, im-

posed strict controls on data collection and transac-

tions. The sensitivity nature of certain data (for exam-

ple, ﬁnancial transactions and medical records) pro-

hibits free data circulation. In the context of explain-

ability and transparency it is important to avoid black

boxes in decision-making processes. Therefore an up-

ward trend for explainability in neural networks ex-

ists, which makes it necessary to come up with novel

ideas and special architectures for neural networks

like capsule networks.

Capsule networks aspire to become an all-round

solution to challenges in computer vision while abid-

ing by the restraints of laws and challenging classic

CNNs in terms of accuracy. The process of trans-

ferring information between layers is called routing.

A pooling operation is conducted after the convolu-

tion operation of each layer is completed. Pooling

can be seen as a special form of routing in neural net-

works. Most information about the image gets lost

during pooling including vital information like orien-

tation and position of an object. Processing an im-

age with several facial features in it will make a CNN

guess that the image shows a face (picasso-problem).

It does not integrate the relative position of speciﬁc

264

Mohr, J., Tousside, B., Schmidt, M. and Frochte, J.

Explainability and Continuous Learning with Capsule Networks.

DOI: 10.5220/0010681300003064

In Proceedings of the 13th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2021) - Volume 1: KDIR, pages 264-273

ISBN: 978-989-758-533-3; ISSN: 2184-3228

features to one another into its decision-making pro-

cess. (Sabour et al., 2017) proposed a novel CNN

(capsule network) with a dynamic routing algorithm

as a solution for this problem.

Capsule networks arise from the idea of inverse

computer graphics and models of the human visual

cortex. They can detect if facial features are just ran-

domly spread through an image or if they form a face.

A variety of attributes can be recognised by a capsule

including pose (position, size, direction), deforma-

tion, hue, texture, and so on. This makes capsule net-

works especially effective on hierarchical data. The

capsules contain different tiers of image information.

The higher the level of a capsule the more information

it contains. Different tiers of capsules are connected

through a routing algorithm.

The image information contained in a capsule can

be presented to a user (even non experts) to gain ex-

plainability. Furthermore it is possible to generate im-

age descriptions (captions) with a stage-wise trained

capsule network based on the learned objects. This

can be combined with a network that has learned to

generate images purely from the image information

of a capsule to achieve a strong set of easy to under-

stand visual clues about what the network has learned

and how it makes a decision.

We studied the performance of capsule networks

for MNIST, Fashion-MNIST, Omniglot and a newly

proposed classiﬁcation task. The objective of this

work is to visualise the decision-making process util-

ising the image information contained in capsules and

effectively gain explainability. We also enhanced cap-

sule networks in a way that they are capable of gener-

ating descriptions for images based on what the cap-

sules have learned. Additionally, it is shown that

it is possible to use capsule networks for resource-

effective continuous learning exploiting the possibil-

ity to reconstruct images which also abides by laws of

data privacy.

Overall, the main contributions of our work are

twofold:

• A set of enhancements is developed which of-

fer the opportunity to generate image descriptions

and preserve vital image information with capsule

networks without affecting the accuracy. Both can

be used to gain explainability regarding the rea-

soning behind the predictions of capsule networks

used in computer vision tasks.

• A framework is developed that utilises the abil-

ity of capsule networks to generate images and

therefore does not need the original training data

to achieve competitive accuracy.

1.1 Related Work

Initial work related to a mathematical representation

of the human visual cortex led to (Geoffrey E. Hinton,

1981a) identifying that some of the processes in the

human brain related to vision have similarities to

the concept of inverse computer graphics. In inverse

computer graphics an image is analysed and the

task is to locate entities in this image in such a way

that complex objects are broken down into several

simple geometric shapes like squares and triangles.

(Geoffrey E. Hinton, 1981b)

The idea of inverse computer graphics led to

the insight that the latest CNNs are not working

in this way and are therefore not close to human

vision (Tielenman, 2014). (Geoffrey E. Hinton et al.,

2011) showed a ﬁrst approach to develop neural

networks which utilise inverse computer graphics.

Further development lead to a fully working capsule

network with dynamic routing in which neurons are

grouped into capsules and vectors are shared between

layers (Sabour et al., 2017). (Hinton et al., 2018)

extended the approach to capsule networks with the

Expectation-Maximisation algorithm and matrices.

Several teams study the performance and pos-

sibilities of capsule networks. (Rajasegaran et al.,

2019) developed a deeper network with capsules

achieving better accuracies on key-benchmark

datasets like Fashion-MNIST and CIFAR-10. The

optimal parameter set and architecture to achieve

an optimal test error on CIFAR-10 was analysed

by (Xi et al., 2017). (Renkens and van hamme,

2018) show that capsule networks can outperform

baseline models for understanding spoken language

in command-and-control applications. Capsule

networks have been generalised to work with 3D

inputs for action detection in videos (Duarte et al.,

2018). Several papers work out that capsule networks

surpass baseline CNNs in image classiﬁcation tasks

across several domains (Afshar et al., 2018; Mobiny

and van Nguyen, 2018; Iesmantas and Alzbutas,

2018; Kumar, 2018; Gagana et al., 2018; Abeysinghe

et al., 2021). All these works proof that capsule

networks are a valuable and promising technique

which is used in a vast array of domains. This makes

it indispensable to research continuous learning and

explainability methods.

(Zhang et al., 2019) proposes to add interpretable

convolutional ﬁlters to CNNs which encode a speciﬁc

part of an object which can help to explain the

logic of a CNN. These ﬁlters are close to the image

Explainability and Continuous Learning with Capsule Networks

265

information contained in a capsule though they have

to be added to the network and need to be speciﬁcally

trained on speciﬁc parts of an object while the cap-

sules simply learn and contain information of objects

in an image. (Simonyan et al., 2013; Mundhenk

et al., 2019) propose that saliency maps (or heatmaps)

can be used to highlight areas in an image that a

convolutional neural network has looked at to make

a decision. The proposed framework to use capsule

networks to generate image descriptions is a more

intuitive way to explain the decision of a network.

(Alqaraawi et al., 2020) reports that users get some

insight into speciﬁc features the CNN uses for its

decision from saliency maps but could not anticipate

the networks decision for new images.

Generative Adversarial Networks (GAN) as pro-

posed by (Goodfellow et al., 2014) have the ability to

generate images that could be used to generate images

for continuous learning. But they are not a classiﬁca-

tor themselves contrary to capsule networks.

Continuous Learning is an ongoing and heavily

discussed topic in machine learning. CNNs tend to

catastrophic forgetting and it is still unclear how to

selectively forget. In the recent years several different

approaches (Kirkpatrick et al., 2017; K

ading et al.,

2017) to overcome catastrophic forgetting have been

researched.

2 CAPSULE NETWORKS

Capsule networks arise from the basic idea to create a

neural network capable of inverse computer graphics.

In other words the network should be able to decon-

struct a scene into co-related parts. Thus, the archi-

tecture of a neural network needs to be changed to

reﬂect the idea of an entity. Every entity gets its own

part of the network, encapsulating a number of neu-

rons. These groups of neurons are called capsules.

2.1 Capsules

A layer of neurons can be divided into many capsules.

These capsules contain the neurons. Therefore, a cap-

sule is a wrapper around a dedicated group of neu-

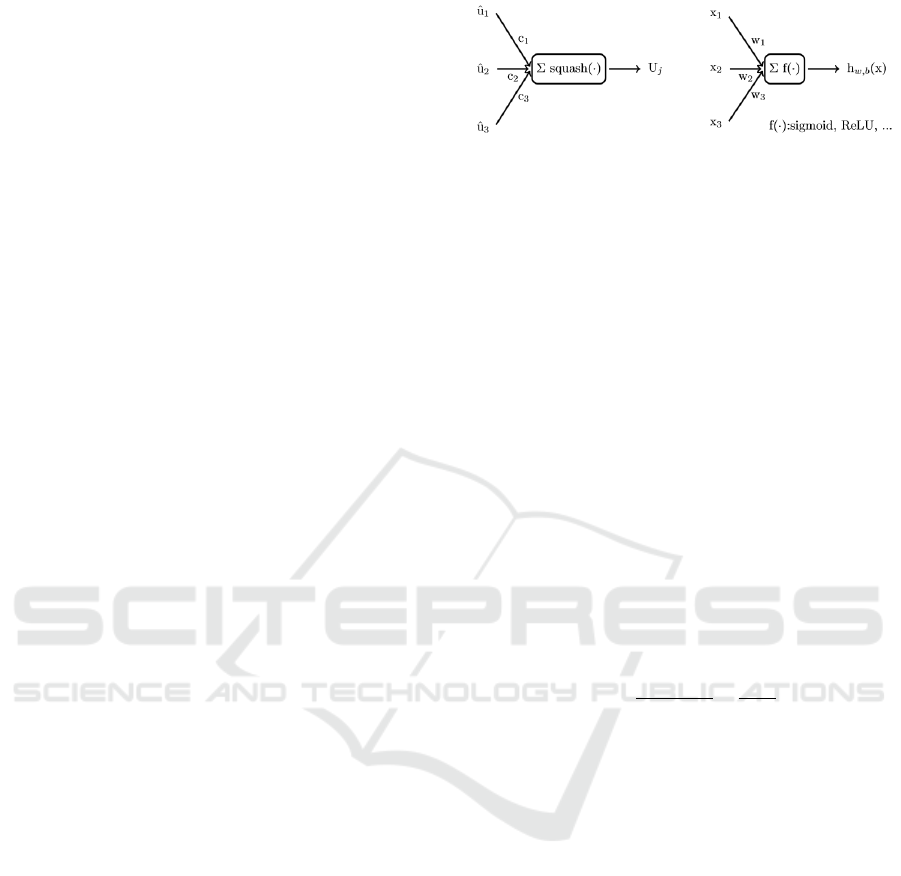
rons. Fig. 1 shows a simpliﬁed comparison between

a capsule and a neuron.

Neurons handle scalar values as input and out-

put. Capsules however encase a group of neurons

and compute vectors as in- and output. The usage

of vectors enables capsule networks to save image

information like location, colour, etc. The length of

Figure 1: On the left-hand side a capsule can be seen which

has in-going vectors and uses the squashing function to get

an output vector. On the right-hand side a neuron in the way

it is currently used in CNNs can be seen which has an input

of scalar values and an activation function (sigmoid, ReLU,

...) to form an output.

the vector represents the probability for feature exis-

tence, while not losing the important image informa-

tion. A n-dimensional capsule can learn n parameters

and outputs a n-dimensional vector. For the output

vector to model a probability, its length has to stay

between 0 and 1. A novel non-linear squashing func-

tion (see Equation 1) was introduced, where v

is the

vector output of capsule j and s

is its total input.

(Sabour et al., 2017) A capsule network should have a

last layer with as many capsules as there are different

classes in the dataset. Figure 8 in section 4.2 shows

a capsule network. The output vector of every cap-

sule represents the image information of every class

and the probability that it is part of the input image.

The various dimensions of the output vectors repre-

sent different attributes for every class.

||s

1 + ||s

||s

(1)

2.2 Routing-by-Agreement

In the scope of inverse graphics a way to connect e.

g. a detected eye to a possible face and not to a car

is needed. This is done by a novel dynamic routing

technique called routing-by-agreement. With routing-

by-agreement the output of a capsule is directed to

a higher-level capsule where it agrees with other in-

puts. For example several detected facial features like

a mouth and a nose should be routed to a capsule

that detects faces. Instead, a detected mouth and tire

should not be directed to the same high-level capsule

and therefore not agree with each other. It is very

unlikely for agreements to lie close to another in a

high dimensional space (coincidence ﬁltering). Thus

an accumulation can not be a coincidence and there-

for strengthens the decision of the network (Sabour

et al., 2017).

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

266

3 EXPLAINABILITY THROUGH

IMAGE DESCRIPTIONS AND

CONTINUOUS LEARNING

WITH IMAGE

RECONSTRUCTION

The capsules contain image information. These infor-

mation can be interpreted as various attributes of each

entity. For example shape, thickness, rotation and so

on. Every capsule delivers a vector. The length of the

vector is the probability that the speciﬁc entity can be

seen at a speciﬁc part of the image. The orientation

of the vector is the information contained in it. The

more dimensions a capsule has the more dimensions

the vector has and therefore more information is con-

tained. The output vector of a capsule can be visu-

alised. These vectors if placed on the original image

give information where the capsule network locates

an entity as can be seen simpliﬁed in Figure 2.

We will demonstrate that it is possible to train a

network to reconstruct the original images out of the

output vectors of the capsules in the last layer. This

generative capability can be used to reconstruct data

while only requiring vectors as input. These vectors

can efﬁciently be generated if the capsule network and

its dimensions and weights are known. The output

of the capsules is fed into a decoder network during

training consisting of 3 fully connected layers that re-

construct images. Aforementioned reconstruction can

be utilised for example to generate data in cases where

a task requires continuous learning without the orig-

inal training data. The need to retrain without orig-

inal training data arises in cases where it is impor-

tant to abide by the laws of data privacy (for example

GDPR).

Figure 3 shows how the reconstructed images

change when only one dimension of the output vector

of the ﬁnal layer of capsules is perturbed. As a con-

sequence it is possible to deﬁne which attribute every

dimension represents and therefore allows to under-

stand how a capsule network makes its decisions. The

ﬁgure was generated with a capsule network trained

on the MNIST dataset (see section 4.1) An output vec-

tor of the capsule of the last layer which represents the

number 8 was fed into the generative network to re-

construct images. A mutated version of this vector

was fed several times into the generative network and

the resulting images where saved. At every new it-

eration one entry in the vector was perturbed slightly

which resulted in images as shown in Figure 3. The

four selected dimensions represent the circle diame-

ter of the two circles that an eight consists out of, the

rotation of the number, the separation of the two cir-

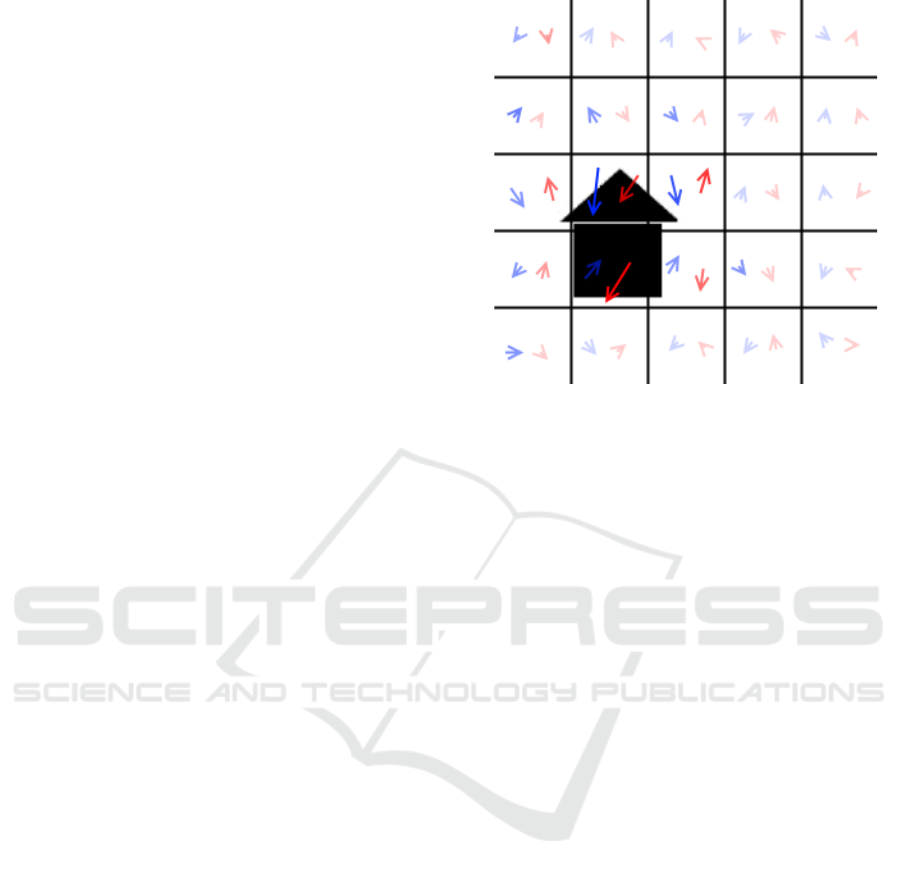
Figure 2: The ﬁgure shows an image of a simpliﬁed house

from the dataset described in section 4.2. It has an overlay

of vector arrows. These arrows represent vectors from cap-

sules in a layer of a capsule network trained on the boat

and house dataset. The blue arrows represent a capsule

looking for triangles and the red arrows capsules looking

for rectangles. The aforementioned technique is an easy-to-

understand way to visualise where the network ﬁnds which

basic geometric shape.

cles and the slant respectively. These images show the

wide variety of different hand-writings present in the

MNIST dataset.

Humans and animals have the ability to acquire

and transfer knowledge throughout their life. This is

called lifelong learning. Continuous learning is an

adaption of this mechanic (K

ading et al., 2017). In

this paper, continuous learning is considered to be a

technique which allows a complete model to be able

to predict a new dataset with the same or other fea-

tures. Therefore, it must be retrained or expanded.

An algorithm that supports the time efﬁcient retrain-

ing was developed. It abides by the laws of GDPR re-

garding data privacy as it does not require to save any

of the data originally used to train the network. The

aforementioned generative network is used to gener-

ate images that are added to a new dataset to repre-

sent the original training data and avoid catastrophic

forgetting.

A capsule network CN is trained on a dataset X

This model reaches a certain quality of its predictions

until the training is stopped. A second dataset X

available after training. For example this could be

data that was gathered after the training on the origi-

nal data was ﬁnished.

In scenarios where it is for example due to data

protection laws not possible to use the original data

anymore capsule networks can be used. Their abil-

Explainability and Continuous Learning with Capsule Networks

267

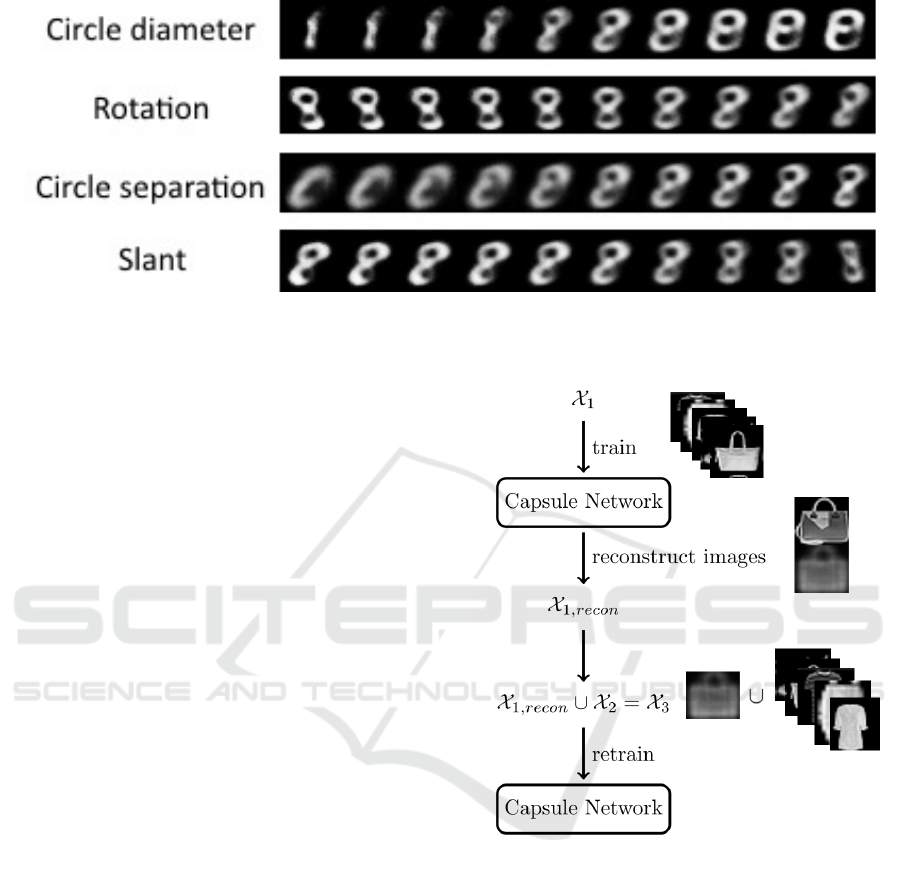
Figure 3: Examples of reconstructed images where only one dimension is perturbed. It can be seen that the changed dimen-

sions can be interpreted as the diameter of the two circles that form an eight, the rotation of the number, the separation of the

two circles and the slant of the whole number.

ity to reconstruct images comes in handy and is use-

ful to overcome catastrophic forgetting which would

otherwise cause a reduction in the accuracy for the

initial trained classes. The part of the network that

is responsible for the reconstruction is fed with sev-

eral randomly generated vectors that have the same

dimensions as the output vectors of the last layer of

capsules. That will make the network generate im-

ages which are reconstructed and share their features

with the original dataset X

. The new dataset is called

1,recon

. The capsule network is already prepared for

continuous learning as it already has spare output cap-

sules. If the number of ﬁnal outputs is unknown it is

advisable to already add plenty of additional capsules

which are not used during initial training.

1,recon

can be combined with X

to form a new

dataset X

. The capsule network can now be retrained

on X

without catastrophic forgetting. It is advisable

to generate at least ten percent of the size of the origi-

nal dataset. In case that the size of the original dataset

is unknown it is indicated to reconstruct as many im-

ages as the new dataset contains. If a new dataset X

exists and the network is to be retrained again then

the framework can be used again starting with recon-

structing images. See section 4.2 for experimental re-

sults of the proposed framework and ﬁgure 4 for a

sketch of the framework.

4 EXPERIMENTS

In the following section three different experiments

are described. The experiments show how the pro-

posed framework can be used effectively for contin-

uous learning while paying regard to the needs of

data protection. Furthermore, the aptitude to increase

explainability through image descriptions is demon-

Figure 4: Diagrammatic overview of the proposed frame-

work for continuous learning with capsule networks. A

capsule network is trained on a dataset X

. The network is

then used to generate images and combine these with a new

dataset X

which was not available during the ﬁrst training.

Then the capsule network is retrained on the union of the

generated images and X

to overcome catastrophic forget-

ting.

strated. An academic implementation of capsule net-

works is used for the experiments. The reconstruc-

tion of complex real-life images and their use in mak-

ing users more conﬁdent in the classiﬁcation of neu-

ral networks by increasing the level of transparency is

shown with Fashion-MNIST. The handwritten num-

bers of MNIST are used to demonstrate how capsule

networks can generate image descriptions based on

simple geometries. The continuous learning frame-

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

268

work with support of reconstructed images is shown

with the proposed boat and house dataset and the on-

miglot dataset of written characters.

4.1 MNIST and Fashion-MNIST

Fashion-MNIST was introduced by (Xiao et al., 2017)

as an alternative for the popular MNIST dataset which

was introduced by (Y. LeCun et al., 1998). The im-

ages are of size 28 × 28 pixels and are greyscale.

Fashion-MNIST consists out of 70.000 images of

fashion items like trousers or shoes separated into

10 categories. The dataset is split into a training

set of 60.000 images and a test set of 10.000 im-

ages. It is freely available at https://github.com/

zalandoresearch/fashion-mnist. The capsule network

architecture used for MNIST and Fashion-MNIST

has 10 20-dimensional capsules in the last layer and

128 9 × 9 convolutional kernels with ReLu activation.

After training for 20 epochs with no preprocessing

(augmentation) of the images it achieves an accuracy

on Fashion-MNIST of 94.6% and 99.7% on MNIST.

This is an average accuracy of 20 cross-validations.

It can be seen that the achieved average accuracy

for MNIST is close to state-of-the-art approaches and

even better then some of them on Fashion-MNIST.

This shows that Capsule Networks are competitive

with these neural networks while also adding the ca-

pabilities of continuous learning and explainability. It

also indicates that no accuracy is lost through these

enhancements. The capsule network has 8.7 M pa-

rameters. Comparable CNNs have much more and up

to 40 M ((Hirata and Takahashi, 2020)) parameters

without a signiﬁcant advantage in accuracy. Further-

more the other models are speciﬁcally tailored for the

MNIST and Fashion-MNIST datasets.

Figure 5 shows a number of original and recon-

structed images of the Fashion-MNIST dataset. It can

be seen that the main features are preserved after re-

construction. This allows a user to match original and

reconstructed images. A user could be shown a selec-

tion of reconstructed images and the user could guess

which classes the network has learned to distinguish

without any further information. Thus boosting the

conﬁdence the user has in decisions of the capsule

network.

Furthermore it is possible to train a capsule net-

work in a stage-wise manner. At ﬁrst the network is

trained with images of basic geometric shapes that

will be present in the target dataset. For MNIST

these shapes are vertical and horizontal lines, circles

and semicircles (This was used to generate the cap-

tions shown in Figure 6). After training on these ba-

sic shapes the weights of the layers are frozen and

Figure 5: A juxtaposition of original inputs sourced from

the Fashion-MNIST dataset and the reconstructed images

with the original image on top of the reconstructed one. All

reconstructions keep the main features of the piece of fash-

ion and even if mixed up it would be easy to match them.

Figure 6: Image descriptions generated by a capsule net-

work. The network was ﬁrst trained on four basic geometric

shapes. vertical lines, horizontal lines, circles and semicir-

cles. Afterwards the network was trained on MNIST. The

route an image takes through the network can be tracked

and therefore it is possible to generate captions based on

the information which basic shapes the capsule network has

found.

the network is expanded with two additional capsule

layers. This network is then trained on the MNIST

dataset. The new capsule layers learn high-level and

abstract features of the images to classify them. This

time no generated images are used. It is not necessary

to achieve ﬁnal predictions of these basic geometric

shapes. They are just trained to achieve meaningful

image descriptions. The network is used to predict

images from the MNIST dataset which show hand-

written numbers. The output of the network is the

classiﬁcation of the image and the way through the

capsules the image has taken. According to the rout-

ing by agreement this allows to comprehend the basic

geometric shapes which the capsule network detects

in the image. An example can be seen in Figure 6.

Explainability and Continuous Learning with Capsule Networks

269

Table 1: Achieved accuracies on MNIST and Fashion-MNIST with the used capsule network compared to a variety of state-

of-the-art approaches.

Model MNIST Fashion-MNIST

Capsule Network (ours) 99.70% 94.60%

TextCaps (Jayasundara et al., 2019) 99.71% 93.71%

Branching & Merging CNN w/HFCs (Byerly et al., 2020) 99.76% 93.66%

EnsNet (Hirata and Takahashi, 2020) 99.84% 95.30%

VGG8B + LocalLearning + CO (Nøkland and Eidnes, 2019) 99.74% 95.47%

Table 2: Achieved accuracies on the single-head and multi-

head scenarios of split MNIST with the used capsule net-

work compared to a variety of state-of-the-art continuous

learning approaches.

Model multi-head single-head

Capsule Network 98.37% 93.52%

EWC 98.64% 20.01%

DGR 99.50% 90.79%

4.1.1 Results for Continuous Learning

MNIST becomes a substantially more difﬁcult prob-

lem if it is split up into multiple tasks that must be

learned in sequence. Splitting MNIST up into sev-

eral parts is simply called split MNIST (Zenke et al.,

2017). Split MNIST is a popular benchmark for con-

tinual learning algorithms. It can be set up in two

different ways giving vastly different tasks. For both

options the dataset is split into 5 separate sequences.

Each containing the data for two digits; zero and one,

two and three and so on. The task incremental learn-

ing scenario (van de Ven and Tolias, 2019) or the

multi-headed setup (Farquhar and Gal, 2019) describe

a scenario in which only two digits need to be distin-

guished at a time. It is always clear that the network

only needs to output which reﬂect the two classes of

the current scenario. For example in the last step it

is only required to distinguish between the numbers

eight and nine. The class incremental learning prob-

lem or single-headed setup means that the network

must learn a 10-way classiﬁer. But it still only gets

data referring to two different classes in every step.

This scenario is probably more realistic and much

more complicated.

Both setups are tested with capsule networks and

state-of-the-art continuous learning approaches. For

capsule networks generated images as described in

this paper were used. All state-of-the-art approaches

were used with the setups (EWC (Kirkpatrick et al.,

2017), DGR (Kamra et al., 2017)) described in the re-

spective paper. The resulting accuracies can be seen

in table 2. The accuracies are calculated as average

test accuracies over all tasks. It can be seen that cap-

sule networks work reasonably well in both scenarios.

4.2 Boat And House Dataset

In the following section the boat and house dataset

is proposed and explained including experimental re-

sults of a capsule network on this dataset.

Figure 7: The ﬁgure shows random examples out of the

dataset presented in section 4.2. The top row shows a rect-

angle on the left and a triangle on the right. The bottom row

shows a house on the left and a boat on the right.

4.2.1 Description of the Dataset

This dataset is newly proposed in this paper. It is

freely available at placeholder. The dataset consists

out of 2000 greyscale images with size 28px × 28px.

These 2000 images are split into 1000 images with

two categories, rectangles and triangles. Each 500 in

various positions, sizes and rotations. And another

subset with 1000 boats and houses split equally which

are a combination of the basic geometric shapes rect-

angles and triangles. For this dataset houses and boats

are deﬁned as follows. A house is a triangle that sits

with its longest side on top of one of the long sides

of a rectangle. A triangle sitting with one of its tips

on the long side of a rectangle is considered a boat.

The images are procedural generated. This dataset

was speciﬁcally designed to show off our approach to

explainability with capsule networks and continuous

learning.

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

270

Figure 8: The capsule network architecture used for the boat

and house dataset.

A simple capsule network is used for this dataset

with a shallow architecture consisting out of only one

convolutional layer and one fully connected layer.

The convolutional layer has 256 9×9 convolution ker-

nels with a stride of 1 and ReLU activation. The ﬁrst

capsule layer (caps1) has 16 capsules with 2 dimen-

sions each (every capsule contains 2 convolutional

units). Each capsule in this ﬁrst capsule layer sees

the outputs of all convolutional units whose receptive

ﬁelds overlap with the location of the centre of the

capsule. The ﬁnal layer (caps2) has only 4 capsules

which receive input from all the layers below. One

for every class with 4 dimensions each. The archi-

tecture can be seen in ﬁgure 8. This capsule network

achieves an accuracy of 91.6% on the dataset.

4.2.2 Results For Continuous Learning

At ﬁrst a capsule network is trained on the dataset

with rectangles and triangles in the aforementioned

way (except having 4 capsules in the last layer as

preparation for the continuous learning). Retraining

this capsule network on new data from the dataset

with boats and houses leads to an underwhelming ac-

curacy of only 62.8%. The network can not sufﬁ-

ciently learn without old data. As proposed in this

paper (see section 3) it is possible to reconstruct im-

ages which can be used to generate an arbitrary num-

ber of images of rectangles and triangles. In this case

100 images of rectangles and 100 images of triangles

were created. If these are added to the new data the

network trains much more effectively and overcomes

catastrophic forgetting with an accuracy of 91.2%.

This is a big step towards continuous learning with-

out catastrophic forgetting and without any need for

the original data. Even capsule networks that were

not trained with the option of continuous learning in

mind have the in-built ability to do so. Table 3 gives

an overview over the achieved accuracies.

Table 3: Achieved accuracies on the boat and house dataset

with and without retraining. The retraining was done with

only the new data and with additional generated images.

only new data generated images whole dataset

62.8% 91.2% 91.6%

4.3 Omniglot

The Omniglot dataset is a popular task and bench-

mark for continuous and incremental learning. It was

proposed by (Lake et al., 2015) and consists of images

of 50 different alphabets originating from a variety of

languages and cultures. Each letter was handwritten

by 20 different persons. To harness the strength of

the capsule networks to learn hierarchical data and to

increase the amount of available images the dataset

was enhanced with datasets that consist of images of

some basic alphabets. Chinese MNIST (https://www.

kaggle.com/gpreda/chinese-mnist), CoMNIST (https:

//github.com/GregVial/CoMNIST) and MNIST were

used. Subsequently this dataset will be referred to

as extended omniglot. Extended omniglot comes

with two tasks. The ﬁrst task is to learn on Chinese

MNIST, CoMNISt and MNIST ﬁrst and afterwards

on omniglot in a transfer learning (tl) manner. This

means all data is available through the whole training.

The second continuous learning task in is to continu-

ally learn on the MNIST datasets and afterwards on

omniglot. During the training of omniglot no images

of the MNIST datasets can be used. These datasets

are used in a ﬁrst iteration of training to initially learn

basic shapes that are part of commonly used alpha-

bets. With this ﬁrst step capsules are formed which

learn a common ground for all alphabets with geome-

tries present in basic shapes. Afterwards the network

is trained on omniglot. For the second task images

of the MNIST datasets are generated by the capsule

networks and added to the omniglot dataset for con-

tinuous training.

The results are summarised in table 4 in compari-

son to state-of-the-art approaches. Capsule Networks

achieve an accuracy of 69.8%, 80.4% and 81.3%

respectively. TapNet, DCN6-E and MAML++ are

CNNs speciﬁcally designed to perform well on the

omniglot dataset and have a vast amount of param-

eters. They are one-purpose networks. In spite of

that capsule networks are on par with their published

results. As shown in the other experiments capsule

networks are able to achieve competitive accuracy

on several different datasets and can handle a variety

of different tasks. Also they have the additional

ability to support explainability without losing any

accuracy. This makes a strong point that capsule net-

Explainability and Continuous Learning with Capsule Networks

271

Table 4: Achieved accuracies on the plain omniglot as proposed by (Lake et al., 2015) and the omniglot dataset extended with

several most widely used alphabets. tl is the transfer learning task on omniglot and cl is the continuous learning task.

Model Plain Omniglot Extended Omniglot(tl) Extended Omniglot(cl)

Capsule Network (ours) 69.8% 80.4% 81.3%

TapNet (Yoon et al., 2019) 71.4% 78.7% 72.1%

DCN6-E (Liu et al., 2019) 68.9% 80.6% 67.5%

MAML++ (Antoniou et al., 2018) 69.6% 76.2% 69.7%

works are an all-round solution to computer vision

tasks while also being capable of learning continually

and being explainable. The results on the continuous

learning task for extended omniglot shows the suc-

cess of the continuous learning capabilities of capsule

networks especially in comparison to the other ap-

proaches which only achieve accuracies close to their

accuracy on plain omniglot.

5 CONCLUSION AND FUTURE

PROSPECTS

This paper showed that it is possible to effectively

visualise the image information contained in a cap-

sule as deﬁned by the emerging capsule networks. In

combination with the reconstructed images and im-

age descriptions this gives vast information about the

decision-making process of an artiﬁcial neural net-

work. Therefore, explainability and transparency is

increased by our work. With capsule networks it is

possible to get closer to the demands regarding ex-

plainability established in game-changing laws. The

part-whole correlation capsule networks are able to

learn, give them the ability to explore new paths of

continuous learning possibly leading to a solution for

catastrophic forgetting and training with limited re-

sources and no access to original training data. Espe-

cially our proposed framework for continuous learn-

ing with reconstructed images is a novel and promis-

ing approach to tackle the main challenges in machine

learning today. For further improvements it would

make sense to use capsule networks as base learner in

a modularised architecture. The capabilities of cap-

sule networks to explain their decision-making pro-

cess and continuous learning ability make them es-

pecially interesting to enhance novel approaches to

continuous learning like Tree-CNN proposed by (Roy

et al., 2018). Scenarios like household robots re-

quire resource efﬁcient training and continuous learn-

ing methods that require as few old data and process-

ing time as possible. Being able to explain where

and why a neural network makes mistakes allows for

very speciﬁc retraining. The ability to generate im-

ages without need for the original data is a stable and

data protection compliant way to achieve resource ef-

ﬁcient training.

ACKNOWLEDGEMENTS

This work was funded by the federal state of North

Rhine-Westphalia and the European Regional Devel-

opment Fund FKZ: ERFE-040021.

REFERENCES

Abeysinghe, C., Perera, I., and Meedeniya, D. (2021). Cap-

sule networks for character recognition in low re-

source languages. Machine Vision Inspection Systems,

Volume 2: Machine Learning-Based Approaches,

pages 23–46.

Afshar, P., Mohammadi, A., and Plataniotis, K. N. (2018).

Brain Tumor Type Classiﬁcation via Capsule Net-

works. 25th IEEE International Conference on Image

Processing ICIP.

Alqaraawi, A., Schuessler, M., Weiß, P., Costanza, E.,

and Berthouze, N. (2020). Evaluating Saliency Map

Explanations for Convolutional Neural Networks: A

User Study. International Conference on Intelligent

User Interfaces.

Antoniou, A., Edwards, H., and Storkey, A. (2018). How

to train your MAML. International Conference on

Learning Representations.

Byerly, A., Kalganova, T., and Dear, I. (2020). A Branch-

ing and Merging Convolutional Network with Homo-

geneous Filter Capsules.

Duarte, K., Rawat, Y. S., and Shah, M. (2018). VideoCap-

suleNet: A Simpliﬁed Network for Action Detection.

Advances in Neural Information Processing Systems.

Farquhar, S. and Gal, Y. (2019). Towards robust evaluations

of continual learning.

Gagana, B., Athri, H. U., and Natarajan, S. (2018). Activa-

tion function optimizations for capsule networks. In

2018 International Conference on Advances in Com-

puting, Communications and Informatics (ICACCI),

pages 1172–1178. IEEE.

Geoffrey E. Hinton (1981a). A Parallel Computation that

Assigns Canonical Object-Based Frames of Refer-

ence. Seventh International Joint Conference on Arti-

ﬁcial Intelligence.

KDIR 2021 - 13th International Conference on Knowledge Discovery and Information Retrieval

272

Geoffrey E. Hinton (1981b). Shape Representation in Par-

allel Systems. Seventh International Joint Conference

on Artiﬁcial Intelligence.

Geoffrey E. Hinton, A. Krizhevsky, and S. Wang (2011).

Transforming Auto-Encoders. International Confer-

ence on Artiﬁcial Neural Networks.

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative Adversarial Networks.

Neural Information Processing Systems NIPS.

Hinton, G. E., Sabour, S., and Frosst, N. (2018). Matrix

capsules with EM routing. International Conference

on Learning Representations.

Hirata, D. and Takahashi, N. (2020). Ensemble learning in

CNN augmented with fully connected subnetworks.

Iesmantas, T. and Alzbutas, R. (2018). Convolutional cap-

sule network for classiﬁcation of breast cancer histol-

ogy images.

Jayasundara, V., Jayasekara, S., Jayasekara, H., Ra-

jasegaran, J., Seneviratne, S., and Rodrigo, R. (2019).

TextCaps: Handwritten Character Recognition With

Very Small Datasets. In 2019 IEEE Winter Confer-

ence on Applications of Computer Vision, pages 254–

262. IEEE Computer Society, Conference Publishing

Services.

ading, C., Erik Rodner, Alexander Freytag, and Joachim

Denzler (2017). Fine-Tuning Deep Neural Networks

in Continuous Learning Scenarios. Asian Conference

on Computer Vision, pages 588–605.

Kamra, N., Gupta, U., and Liu, Y. (2017). Deep generative

dual memory network for continual learning.

Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J.,

Desjardins, G., Rusu, A. A., Milan, K., Quan, J.,

Ramalho, T., Grabska-Barwinska, A., Hassabis, D.,

Clopath, C., Kumaran, D., and Hadsell, R. (2017).

Overcoming catastrophic forgetting in neural net-

works. Proceedings of the National Academy of Sci-

ences, 114(13):3521–3526.

Kumar, A. D. (2018). Novel Deep Learning Model for Traf-

ﬁc Sign Detection Using Capsule Networks. Interna-

tional Journal of Pure and Applied Mathematics Vol-

ume 118 No. 20.

Lake, B. M., Salakhutdinov, R., and Tenenbaum, J. B.

(2015). Human-level concept learning through proba-

bilistic program induction. Science (New York, N.Y.),

350(6266):1332–1338.

Liu, J., Chao, F., Yang, L., Lin, C.-M., and Shen, Q. (2019).

Decoder Choice Network for Meta-Learning.

Malgieri, G. (2019). Automated decision-making in the

EU Member States: The right to explanation and

other “suitable safeguards” in the national legislations.

Computer Law & Security Review, 35(5):105327.

Mobiny, A. and van Nguyen, H. (2018). Fast CapsNet for

Lung Cancer Screening.

Mundhenk, T. N., Chen, B. Y., and Friedland, G. (2019).

Efﬁcient Saliency Maps for Explainable AI.

Nøkland, A. and Eidnes, L. H. (2019). Training Neural Net-

works with Local Error Signals.

Rajasegaran, J., Jayasundara, V., Jayasekara, S., Jayasekara,

H., Seneviratne, S., and Rodrigo, R. (2019). Deep-

Caps: Going Deeper with Capsule Networks.

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition CVPR.

Renkens, V. and van hamme, H. (2018). Capsule Networks

for Low Resource Spoken Language Understanding.

Proc. Interspeech 2018.

Roy, D., Panda, P., and Roy, K. (2018). Tree-CNN: A Hier-

archical Deep Convolutional Neural Network for In-

cremental Learning.

Sabour, S., Frosst, N., and Hinton, G. E. (2017). Dynamic

Routing Between Capsules.

Simonyan, K., Vedaldi, A., and Zisserman, A. (2013). Deep

Inside Convolutional Networks: Visualising Image

Classiﬁcation Models and Saliency Maps. Interna-

tional Conference on Learning Representations ICLR.

Tielenman, T. (2014). Optimizing Neural Networks That

Generate Images. Dissertation, University of Toronto,

Toronto.

van de Ven, G. M. and Tolias, A. S. (2019). Three scenarios

for continual learning. CoRR.

Xi, E., Bing, S., and Jin, Y. (2017). Capsule Network Per-

formance on Complex Data. International Joint Con-

ference on Neural Networks (IJCNN).

Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-

MNIST: a Novel Image Dataset for Benchmarking

Machine Learning Algorithms.

Y. LeCun, L. Bottou, Yoshua Bengio, and P. Haffner (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE.

Yoon, S. W., Seo, J., and Moon, J. (2019). TapNet: Neu-

ral Network Augmented with Task-Adaptive Projec-

tion for Few-Shot Learning. Proceedings of the 36th

International Conference on Machine Learning.

Zenke, F., Poole, B., and Ganguli, S. (2017). Improved mul-

titask learning through synaptic intelligence. CoRR.

Zhang, Q., Wang, X., Wu, Y. N., Zhou, H., and Zhu, S.-C.

(2019). Interpretable CNNs for Object Classiﬁcation.

Explainability and Continuous Learning with Capsule Networks

273