A Data Quality Assessment Approach in the SmartWork Project’s

Time-series Data Imputation Paradigm

Georgios Papoulias

, Otilia Kocsis

and Konstantinos Moustakas

Department of Electrical and Computer Engineering, University of Patras, Greece

Keywords:

Data Quality, Missing Data, Time-series Imputation.

Abstract:

The plethora of collected data streams of the SmartWork project’s sensing system is often accompanied by

missing values, yielding the need for estimating these missing values through imputation, which may prove

unnecessary or computationally expensive in relation to the outcome. This work introduces a data quality

assessment approach that allows for decision making regarding the need/efﬁciency of data completion in order

to save system computational resources and ensure quality of imputed data. Preliminary validation of the

proposed approach is performed by assessing the correlation between the proposed data quality assessment

scores and the normalized mean square error of the imputation on various simulated missing patterns. The

results reinforce our initial hypothesis that the suggested score is a suitable data quality indicator, correlating

well with the potential errors introduced by imputation in the case of a given batch of input data.

1 INTRODUCTION

The continuous collection of large data

amounts(Labrinidis and Jagadish, 2012)(Sagiroglu

and Sinanc, 2013)(George et al., 2014) coming

from heterogeneous sources (i.e. devices) is often

accompanied by missing entries, which need to be

handled owing to the uncertainty they introduce in

decision-making systems(Zhang, 2015). In such

cases, an imputation algorithm responsible for

estimating the missing values is required, especially

when the time-series acting as input are employed

for the derivation of other crucial parameters or in

predictive tasks. However, the imputation might

prove to be unreliable in certain cases and, given

the additional computational cost, it is important to

establish whether it is efﬁcient or not to perform

data imputation(Cai and Zhu, 2015). In particular,

in the scope of the SmartWork project (Kocsis et al.,

2019b)(Kocsis et al., 2019a), in which the risk factor

investigation (Fazakis et al., 2021)) and subsequent

robust estimation of ofﬁce workers’ work ability

(Kocsis et al., 2021) is conducted by using contin-

uous data acquired by various monitoring devices

(e.g. FitBit activity tracker, a smart mouse, ofﬁce

environment quality sensors, etc.), the quality of data

https://orcid.org/0000-0003-2518-1904

https://orcid.org/0000-0001-6937-6442

https://orcid.org/0000-0001-7617-227X

estimated through imputation may be critically im-

portant for decision making(Nousias et al., 2018). In

other words, poor quality of the input data might lead

to low data imputation accuracy and, subsequently,

render the system prone to serious decision-making

mistakes(Guan and Stephens, 2008). Thus, the

motivation behind the introduction of the proposed

algorithm is two-fold: ﬁrst, to guarantee that, as long

as it has been performed, imputation is reliable and,

second, to save us from spending rather useless com-

putational time performing imputation on suspicious

data quality.

In the context of the SmartWork project imple-

mentation, a data quality assessment module was in-

troduced as part of the Data Imputation module in or-

der to support decision making on whether the exe-

cution of an imputation algorithm on a given batch

of input data is worth to be performed and to provide

a quality score for the data values estimated through

imputation. Data quality, though, is a multidimen-

sional concept, as elaborated on in the next section,

thus difﬁcult to evaluate from a plethora of viewing

aspects, such as completeness, consistency and accu-

racy as deﬁned in (Batini et al., 2009)(Pipino et al.,

2002). Hence, the compound nature of data quality

led us to decide not to evaluate it as an entity but

to adapt and target our assessment algorithm at the

singularities of the data completion paradigm. De-

pending on the imputation approach selected, namely

Papoulias, G., Kocsis, O. and Moustakas, K.

A Data Quality Assessment Approach in the SmartWork Project’s Time-series Data Imputation Paradigm.

DOI: 10.5220/0010719000003063

In Proceedings of the 13th International Joint Conference on Computational Intelligence (IJCCI 2021), pages 453-459

ISBN: 978-989-758-534-0; ISSN: 2184-3236

453

a single-channel or a multi-channel imputation algo-

rithm, the suggested algorithm performs data quality

assessment either for each data channel individually

or for all input channels combined, respectively. Both

approaches derive a single quality score for the input

data, reﬂecting their imputability.

2 RELATED WORK

Data quality was summarized from ISO 25012 as ’the

capability of data to satisfy stated and implied needs

when used under speciﬁc conditions’(Taleb et al.,

2016) and, in simpler words, as ’ﬁtness for use’ in

(Cai and Zhu, 2015), whom postulate data quality de-

pends on a plethora of factors, including (at least) the

purpose for which the data are being used, the user,

the time etc. In different settings, data quality may

depend on various factors such as accuracy, timeli-

ness, completeness, relevancy, objectivity, believabil-

ity, understandability, consistency, conciseness, avail-

ability and veriﬁability. All these quality dimensions,

also known as characteristics of the dataset, affect-

ing data quality assessment are directly relevant to the

consumer or, otherwise, the purpose of use.

In the Big Data era, measuring data quality has

turned into a compound process. A quantitative as-

sessment method, is a formal, objective and system-

atic process in which numerical data are utilized to

obtain information. Therefore, objectivity, general-

izability and numbers are features often associated

with this type of methods, whose evaluation results

are more intuitive and concrete.

The data quality assessment involves measuring

the quality dimensions(Pipino et al., 2002) that are

relevant to the user and comparing the assessment

results with the users’ quality requirements. Each

quality dimension needs different measurement tech-

niques, which leads to differences in assessment times

and costs. After having explicitly deﬁned the data di-

mensions of interest, a data quality assessment metric

is opted for each dimension, or more of them simulta-

neously. However, the literature does not provide an

exhaustive set of easily applicable metrics (Cappiello

et al., 2004). Additionally, the algorithms concerned

with these metrics’ calculation focus exclusively on

data values but do not consider the specialized use of

data. However, owing to the fact that data quality is an

abstract concept (Pipino et al., 2002), thus feasible to

assess only in a speciﬁc context, it is difﬁcult and un-

necessary to examine it from all aspects at the same

time. Thus, these metrics are heuristics designed to

ﬁt a speciﬁc assessment situation. Therefore, when

it comes to data quality assessment, it is essential to

explicitly deﬁne the context of the evaluation.

To this end, metrics are categorized in Task-

dependent metrics, namely a metric developed in spe-

ciﬁc application contexts, satisfying constraints im-

posed by the database architecture as conceptualized

in (Taleb et al., 2016) as opposed to Task-independent

metrics, which reﬂect states of the data without the

contextual knowledge of the application, and can be

applied to any dataset.

In the modern era, extra challenges arise from the

huge data size and speed of generation such as the

reduction of the assessments’ computational burden.

Thus, evaluation schemes applying sampling strate-

gies on large datasets were introduced (Taleb et al.,

2016), while maintaining completeness and accu-

racy(Zaveri et al., 2016), dimensions considered crit-

ical for medical applications as postulated by (Cai

and Zhu, 2015). In the data imputation paradigm,

we are mostly interested in ‘property completeness’,

which reﬂects the measure of the missing values for a

speciﬁc property. Our hypothesis that the quality is-

sues emerging from the data missingness as concep-

tualized in (Batini et al., 2009) are mostly related to

those two data quality dimensions, namely accuracy

and completeness, is clearly conﬁrmed in (Taleb et al.,

2016).

To develop an illustrative metric for important

data quality dimensions in practice, three principal

functional forms can be employed: simple ratio, min

or max operators and weighted average as described

in (Pipino et al., 2002). Additionally, the type of

data to be evaluated equally affects the quality eval-

uation metrics. The contingent types of data could be

Content-based, Context-based and Rating-based. In

Content-based metrics, the information itself is used

as quality indicators, while in Context-based metrics

meta-data is employed for this purpose. Finally, in

Rating-based metrics, both the information and the

sources of information are exploited (Taleb et al.,

2016). In the data completion paradigm, the type of

data is purely Content-based.

3 PROPOSED APPROACH

We aimed to establish an objective Task-dependent

data quality metric, the conceptualization of which

is based on principles of data imputation, especially

when it comes to multi-channel imputation schemes,

taking advantage of the correlation observed between

timeseries coming from different data channels. The

principal data quality indicator taken into considera-

tion for the calculation of the suggested score is com-

pleteness ((Zaveri et al., 2016), (Pipino et al., 2002)),

SmartWork 2021 - 2nd International Workshop on Smart, Personalized and Age-Friendly Working Environments

454

expressed primarily by the missingness percentage, in

the single channel paradigm, and by additional esti-

mated quantities in the multi-channel paradigm. Ow-

ing to the different kind of information available in

each of those two individual cases, a different formula

for each paradigm is proposed.

Considering the profound dependence of the data

quality score on the percentage of missing values de-

tected in a given temporal sequence of data as well as

the maximum number of consecutive missing values

observed in the time-series, the formulas employed

for the data quality score include all terms required to

express this dependency.

3.1 The Single-channel Imputation Case

For the single-channel imputation case, it is important

to provide a deﬁnition for the term ‘single channel

score’. Single channel score refers to an evaluation

connected to a single channel imputation approach.

To assess whether the imputation process is meaning-

ful for a given set of input data consisted of a number

of distinct channels, the imputability of each distinct

data channel is evaluated individually and is estimated

through the formula:

IS =

missPerc

timeseriesLength

maxCons

(1)

where missPerc stands for the number of missing val-

ues of the input data compared to the overall length

of the timeseries, maxCons stands for the maximum

number of consecutive missing values of the time-

series and IS stands for the imputability score. This

approach was adopted due to the fact that imputa-

tion methods struggle to deal with big blocks of miss-

ing data, thus we penalize large blocks of missing

data through the data quality score. The greater the

missing block of maximum size is, the lower the im-

putability score is. Additionally, the smaller the per-

centage of missing data is in the data channel, the

higher its imputability score is.

3.2 The Multi-channel Imputation Case

For the multi-channel imputation paradigm, we

adopted a slightly different approach owing to the fact

that imputation methods of this type are capable of

exploiting the correlations observed across different

data channels in order to perform the imputation more

effectively. R

is a zero-diagonal symmetric correla-

tion matrix where r

i j

is the correlation between i-th

and j-th channel.







. . . r







(2)

Let (X

, ≤) be the ordered set X

= { x|x ∈ R

} con-

taining the elements or R

. Then X

(n) is the correla-

tion of channel i with the highest correlated of the rest

of the channels and X

(n − 1) correlation of channel

i with the second highest correlated of the rest of the

channels.

Hence, the formula employed to assess the ex-

pected quality of the results a multiple-channel im-

putation method yields is the one that follows

IS =

∑

i=1

(

+ 200 · X

(n) ×

Tot

+100 · X

(n − 1) ×

Tot

)

(3)

where c is the number of channels, m

is the percent-

age of missing values, N

is the number of missing

values of the reference channel i corresponding to le-

git values in the channel with which it is the most cor-

related among the other channels and N

is the sec-

ond highest number of missing values of the reference

channel i corresponding to legit values in the channel

with which it is the most correlated among the other

channels. N

Tot

stands for the overall number of miss-

ing values recorded in channel i.

In this way, apart from the missingness percentage

of each channel, we exploit the knowledge provided

by the inter-correlations between data channels as it

is certain that a channel with a given number of miss-

ing values will be more efﬁciently imputed in a multi-

channel imputation setting when the highest corre-

lated channel’s values corresponding to the missing

values of the reference channel are not missing. Us-

ing the same line of reasoning, we also included in the

calculation of the score a respective term for the sec-

ond highest correlated channel, only with a reduced

value for the weighting term since it is only rational

that the highest correlated channel of each reference

channel outweighs the second one.

4 EXPERIMENTAL EVALUATION

Regardless of the selected imputation approach (i.e.

single or multi-channel imputation) and the corre-

sponding type of quality assessment, namely all

A Data Quality Assessment Approach in the SmartWork Project’s Time-series Data Imputation Paradigm

455

data channels altogether or each channel individu-

ally, a score threshold is set in order to support de-

cision making to avoid meaningless data completion.

Hence, the imputation is permitted on the condition

that the input data quality has been evaluated with

a score exceeding the pre-deﬁned score threshold by

the Data Quality Assessment module. The threshold

value was set to 5.0 in logarithmic scale through trial

and error.

Taking into account that the input data quality is

expected to have a conspicuous impact on imputation

accuracy, the normalized mean squared error the im-

putation process yields ought to be inversely propor-

tional to the data quality score of the input data. Thus,

in order to validate the proposed data quality assess-

ment score, a series of experiments were conducted,

aiming at conﬁrming this hypothesis.

4.1 Experimental Setup

The three types of data missingness patterns analyzed

in our experiments are: Missing Completely at Ran-

dom (MCAR), Missing Blocks, as well as a Mixed

type of missingness combining both of the former

types. To clarify, the Mixed pattern of missingness is

practically a combination of the two former patterns

of missingness, which are explicitly deﬁned.

MCAR is the most common type observed in a

timeseries and the easiest kind to perform imputa-

tion on since very few instances of a large num-

ber of consecutive missing values are observed in

this setting, compared to Missing Blocks and Mixed

missingness where entire blocks of consecutive miss-

ing values raise the degree of difﬁculty in the con-

text of data completion as elaborated in (Nousias

et al., 2019). Additionally, in the SmartWork project’s

scope, MCAR missingness is more prevalent com-

pared to the other two missingness types due to the na-

ture of the sensing devices. These two types, though,

are also employed in our experiments in order to con-

ﬁrm that our score displays lower values in the lat-

ter types while the missingness percentage remains

the same. Missing Blocks and Mixed missingness

types in a given timeseries are highly likely to yield

a considerably larger maximum in terms of consecu-

tive missing entries, thus resulting in lower score val-

ues. In order to accomplish this goal, actual heart rate

data recorded over a timespan of 5 consecutive days

by 1 user were employed. This timeseries normally

contained missing data entries, forcing us to detect

the longest complete timeseries in the total data to ex-

periment on as the NRMSE (Normalized Root Mean

Square Error) the imputation introduces could not be

quantiﬁed for a timeseries containing missing entries.

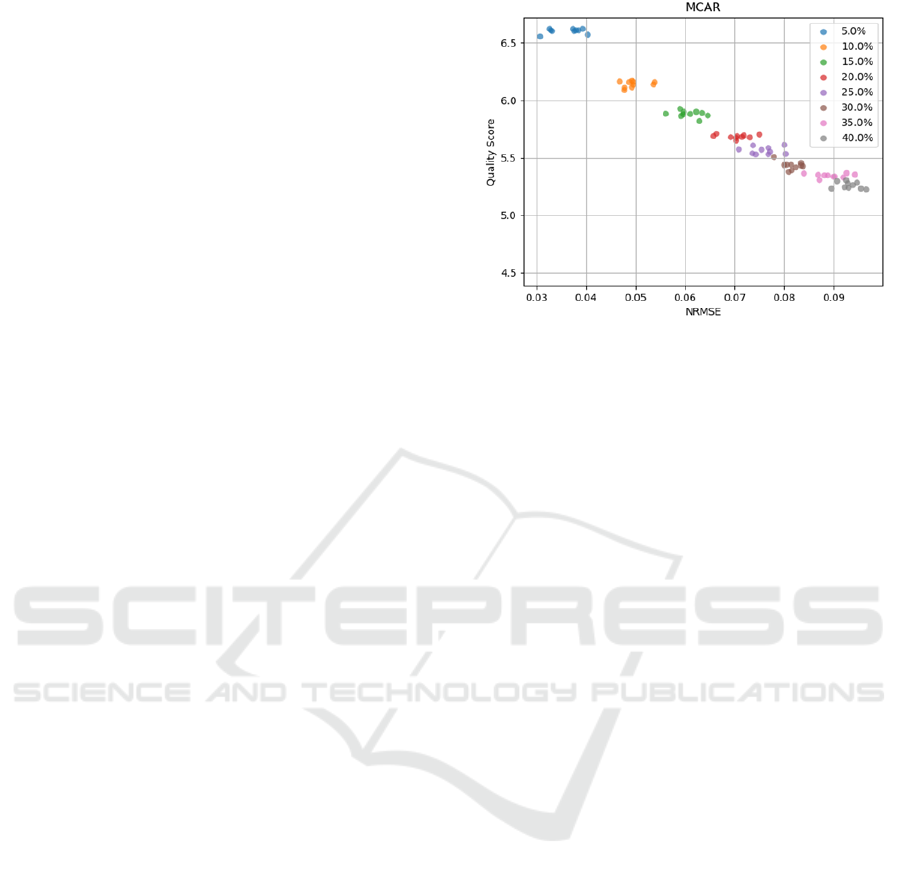
Figure 1: Data Quality Score WRT NRMSE – MCAR

Paradigm.

Thus, taking a complete timeseries as ground truth, a

large number of timeseries characterized of the miss-

ingness patterns mentioned above with a missingness

percentage ranging from 5% to 40% were artiﬁcially

generated. In further detail, 10 permutations were

generated for each missing percentage, and consid-

ering the number of distinct missingness percentages

was 8, there were 80 permutations for each pattern

of missingness, namely MCAR, Missing Blocks and

Mixed patterns. In total, 240 permutations of a time-

series each consisting of 1476 heart rate samples were

generated. The results these experiments yielded are

displayed and analysed in the following section.

4.2 Results

4.2.1 Imputation Quality for MCAR

Missingness

Figure 1 shows the the data quality assessment score

variation in relation to the NRMSE calculated for

each imputed artiﬁcially generated permutation. It is

important to point out that the score has been trans-

lated into a logarithmic scale so as to be more visually

perceivable.

As expected, the score is inversely proportional to

the NRMSE, and the relationship between the two

quantities is nearly linear. Each data point corre-

sponds to a different permutation of the original heart

rate timeseries. Permutations characterized of the

same missingness percentage have been colored simi-

larly in order to additionally highlight the importance

of the missingness percentage of the unimputed time-

series in terms of the expected quality of the imputa-

tion.

The decrease of the quality score from a missing-

ness percentage to the next one is much steeper in low

SmartWork 2021 - 2nd International Workshop on Smart, Personalized and Age-Friendly Working Environments

456

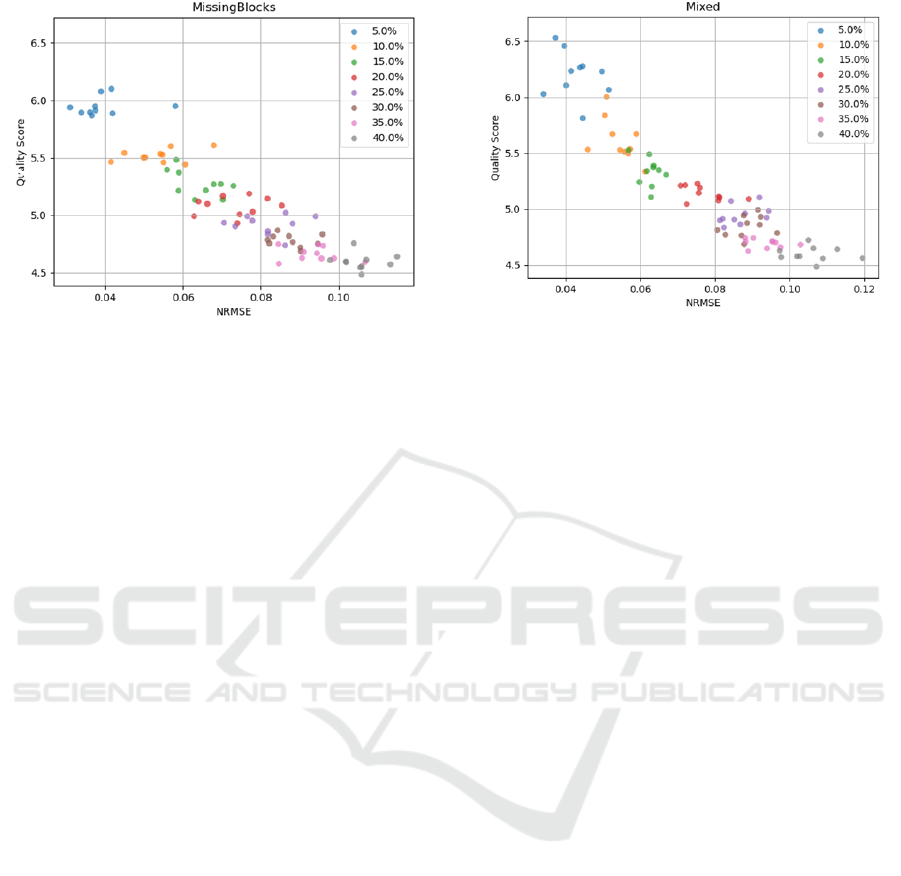
Figure 2: Data Quality Score WRT NRMSE – Missing

Blocks Paradigm.

missingness percentages and becomes almost negligi-

ble in the highest ones. Moreover, the permutations

characterized of the same missing percentage cover

a wider range in the y-axis which becomes apparent

from the fact that almost no data points corresponding

to a permutation of the same missingness percentage

coincide.

4.2.2 Imputation Quality for Missing Blocks

Missingness

In Figure 2 below, the behaviour of the data quality as-

sessment score with respect to the values of NRMSE

after the imputation of the original timeseries we gen-

erated is plotted, in the same manner we demonstrated

our results for the MCAR pattern of missingness for

the sake of comparability.

In this paradigm, results change to a noticeable ex-

tent due to the fact that imputation is highly tough-

ened when missing blocks are included into the mix

which becomes apparent by the lower values of the

quality score in these permutations. The decrease is

considerable when taking into account the data qual-

ity score scale is logarithmic. What is more, the

NRMSE displays slightly higher values compared to

the MCAR paradigm. It is clear that the relationship

between the exhibited quantities has started to diverge

from being linear while still seeming to be inversely

proportional, which is only anticipated.

What is noticeable concerns the overlap in the y-

axis between data point groups corresponding to dif-

ferent values of missingness percentage. However,

it could be interpreted by the effect of the extensive

missing blocks in the imputation process. This hy-

pothesis is conﬁrmed by the fact this effect is even

more prevalent when the missingness percentage ex-

ceeds the value of 20%. The relationship between the

Figure 3: Data Quality Score WRT NRMSE – Mixed

Paradigm.

quantities is close to linear, but the variance of the

score values for data points corresponding to the same

missingness percentage is considerably higher. This

observation leads us to the conclusion that the sug-

gested score is less representative -in terms of data

quality- when large missing blocks are contained in

the timeseries compared to the MCAR paradigm.

4.2.3 Imputation Quality for Mixed Missingness

Patterns

In Figure 3, the relationship between the data qual-

ity assessment score and the NRMSE recorded after

the imputation has been performed is demonstrated,

for permutations of the actual timeseries created us-

ing the Mixed pattern of missingness. This graph

displays trends similar to those observed in the re-

spective graph of the Missing Blocks missingness

paradigm. The score values are higher than those in

the Missing Blocks case while the NRMSE error is

also higher – and expectedly lower compared to those

observed in the MCAR paradigm. It is observed that

the variance observed in the groups of data points cor-

responding to the same missingness percentage de-

creases to a considerable extent as the missingness

percentage decreases. Lastly, it is important to notice

the overlaps of data points in the y-axis corresponding

to different missingness percentages’ permutations,

also described in the Missing Blocks paradigm’s sec-

tion. In spite of the fact these overlaps still exist, they

are limited compared to the Missing Blocks case, es-

pecially for permuations with lower missingness per-

centage, not only in the sense that they are not that nu-

merous but also less intense than those observed in the

Missing Blocks’ pattern. By the term ‘less intense’, it

is implied that there are no data points correspond-

ing to higher missingness percentage displaying sig-

A Data Quality Assessment Approach in the SmartWork Project’s Time-series Data Imputation Paradigm

457

niﬁcantly higher data quality assessment score values

than data points corresponding to lower missingness

percentage.

5 CONCLUSIONS - FUTURE

WORK

The work presented in this paper introduces a data

quality assessment approach that allows for decision

making regarding the need/efﬁciency of data comple-

tion in order to save system computational resources

and ensure quality of imputed data. To the best of

our knowledge, this is the ﬁrst method deriving a pre-

dictive quantitative metric for data quality in the data

imputation paradigm, providing a yes or no answer

for the question: Would data completion about to per-

formed in a given batch of data is meaningful and re-

liable? The dearth of similar known works approach-

ing the data quality assessment in data imputation set-

tings in the same way deprives us of the potential to

perform extensive comparative evaluation.

Further experiments backing the validity of the

suggested score, while optimizing the score’s hyper-

parameters, in a variety of data missingness settings

will be addressed in our future work. Additionally,

we aim at expanding our validation experiments in the

multi-channel imputation setting, expecting for even

clearer evidence for our method’s utility and under-

stability. Moreover, we perform cross-validation to

demonstrate the proposed metric is insusceptible to

the selection of different data completion techniques.

Finally, although data quality has been assessed in

other setups, its application in the context of data im-

putation optimization has not been studied, thus not

being possible for us to perform more extensive com-

parative evaluation of the proposed approach.

The presented results seem to conﬁrm the valid-

ity of the newly introduced data quality assessment

score since, as the data quality score assigned to a

given batch of input data is inversely proportional to

the value of the NRMSE yielded by the imputation

performed on that particular batch. Therefore, the ex-

ported results reinforce our initial hypothesis that the

suggested score is a suitable indicator regarding the

imputability of a given batch of data, allowing to as-

sess the potential outcome (e.g. errors introduced) of

the imputation processes, thus, saving us from unnec-

essary computational cost.

ACKNOWLEDGEMENTS

This work has been partially supported by the Smart-

Work project (GA 826343), EU H2020, SC1-DTH-

03-2018 - Adaptive smart working and living envi-

ronments supporting active and healthy ageing.

REFERENCES

Batini, C., Cappiello, C., Francalanci, C., and Maurino, A.

(2009). Methodologies for data quality assessment

and improvement. ACM computing surveys (CSUR),

41(3):1–52.

Cai, L. and Zhu, Y. (2015). The challenges of data quality

and data quality assessment in the big data era. Data

science journal, 14.

Cappiello, C., Francalanci, C., and Pernici, B. (2004). Data

quality assessment from the user’s perspective. In Pro-

ceedings of the 2004 international workshop on Infor-

mation quality in information systems, pages 68–73.

Fazakis, Nikos & Kocsis, Otilia & Dritsas, Elias & Alexiou,

Sotiris & Fakotakis, Nikos & Moustakas, Konstanti-

nos. (2021). Machine Learning Tools for Long-Term

Type 2 Diabetes Risk Prediction. IEEE Access. PP. 1-

1. 10.1109/ACCESS.2021.3098691.

George, G., Haas, M. R., and Pentland, A. (2014). Big data

and management.

Guan, Y. and Stephens, M. (2008). Practical issues in

imputation-based association mapping. PLoS genet-

ics, 4(12):e1000279.

Kocsis, O., Moustakas, K., Fakotakis, N., Hermens, H. J.,

Cabrita, M., Ziemke, T., and Kovordanyi, R. (2019a).

Conceptual architecture of a multi-dimensional mod-

eling framework for older ofﬁce workers. In Pro-

ceedings of the 12th ACM International Conference

on PErvasive Technologies Related to Assistive Envi-

ronments, PETRA ’19, page 448–452, New York, NY,

USA. Association for Computing Machinery.

Kocsis, O., Moustakas, K., Fakotakis, N., Vassiliou, C.,

Toska, A., Vanderheiden, G. C., Stergiou, A., Amax-

ilatis, D., Pardal, A., Quintas, J. a., Hermens, H. J.,

Cabrita, M., Dantas, C., Hansen, S., Ziemke, T.,

Tageo, V., and Dougan, P. (2019b). Smartwork: De-

signing a smart age-friendly living and working envi-

ronment for ofﬁce workers. In Proceedings of the 12th

ACM International Conference on PErvasive Tech-

nologies Related to Assistive Environments, PETRA

’19, page 435–441, New York, NY, USA. Association

for Computing Machinery.

Kocsis, O., Papoulias, G., Fakotakis, N., and Moustakas, K.

(2021). An approach to determine short- and long-

term work ability in smart work system. In Russo,

D., Ahram, T., Karwowski, W., Di Bucchianico, G.,

and Taiar, R., editors, Intelligent Human Systems Inte-

gration 2021, pages 388–394, Cham. Springer Inter-

national Publishing.

SmartWork 2021 - 2nd International Workshop on Smart, Personalized and Age-Friendly Working Environments

458

Labrinidis, A. and Jagadish, H. V. (2012). Challenges and

opportunities with big data. Proceedings of the VLDB

Endowment, 5(12):2032–2033.

Nousias, S., Papoulias, G., Kocsis, O., Cabrita, M., La-

los, A. S., and Moustakas, K. (2019). Coping with

missing data in an unobtrusive monitoring system for

ofﬁce workers. In 2019 International Conference

on Biomedical Innovations and Applications (BIA),

pages 1–4. IEEE.

Nousias, S., Tselios, C., Bitzas, D., Lalos, A. S., Mous-

takas, K., and Chatzigiannakis, I. (2018). Uncer-

tainty management for wearable iot wristband sen-

sors using laplacian-based matrix completion. In

2018 IEEE 23rd International Workshop on Computer

Aided Modeling and Design of Communication Links

and Networks (CAMAD), pages 1–6. IEEE.

Pipino, L. L., Lee, Y. W., and Wang, R. Y. (2002). Data

quality assessment. Communications of the ACM,

45(4):211–218.

Sagiroglu, S. and Sinanc, D. (2013). Big data: A review. In

2013 international conference on collaboration tech-

nologies and systems (CTS), pages 42–47. IEEE.

Taleb, I., El Kassabi, H. T., Serhani, M. A., Dssouli, R., and

Bouhaddioui, C. (2016). Big data quality: A quality

dimensions evaluation. In 2016 Intl IEEE Conferences

on Ubiquitous Intelligence & Computing, Advanced

and Trusted Computing, Scalable Computing and

Communications, Cloud and Big Data Computing,

Internet of People, and Smart World Congress

(UIC/ATC/ScalCom/CBDCom/IoP/SmartWorld),

pages 759–765. IEEE.

Zaveri, A., Rula, A., Maurino, A., Pietrobon, R., Lehmann,

J., and Auer, S. (2016). Quality assessment for linked

data: A survey. Semantic Web, 7(1):63–93.

Zhang, Z. (2015). Missing values in big data research: some

basic skills. Annals of translational medicine, 3(21).

A Data Quality Assessment Approach in the SmartWork Project’s Time-series Data Imputation Paradigm

459