Numerical Study of the Drag Reduction and the Electronics

Composites Cooling by using the Three Flat Plates

Youssef Admi

, Jaouad Benhamou, El Bachir Lahmer

, Mohammed Amine Moussaoui,

Mohammed Jami and Ahmed Mezrhab

Mechanics & Energetics Laboratory, Faculty of Sciences, Mohammed First University, 60000 Oujda, Morocco

moussaoui.amine@gmail.com, amezrhab@yahoo.fr

Keywords: Lattice Boltzmann method, flow control, the drag reduction, heat exchange, flat plates.

Abstract: The objective of this research is to study the flow control allowing the reduction of the aerodynamic drag and

at the same time the cooling of the electronic components. To this end, a numerical study was carried out on

the effect of the length of three parallel flat plates on the control of vortex shedding behind a heated square

block located in a two-dimensional channel at Reynolds number fixe (Re = 150). The numerical approach

used to simulate these physical problems is the lattice Boltzmann method (LBM). The results obtained are

illustrated in terms of velocity contours and isotherms. These results present a reduction of more than 67% of

the drag coefficient for a critical length of the control plates (Lp = 2D). In addition, a large and regular heat

exchange for the same length is observed.

1 INTRODUCTION

Nowadays, the technology of electronic components

has progressed strongly. However, despite this

development, the successive increase in temperature

and the high vortex shedding leads to a decrease in

the operating performance and sometimes to the

breakdown of these electronic components

(processors, high-performance servers, etc.). In order

to avoid these impediments, the protection of the

performance of these electronic systems and the

improvement of their efficiency is the greatest

challenge facing researchers and companies in the

electronics industry (El Omari, Kousksou, and Le

Guer 2011; Ali and Arshad 2017; De Césaro Oliveski,

Krenzinger, and Vielmo 2003; Seyyedi et al. 2012;

Nazari and Ramzani 2014)

(El Omari, Kousksou, and Le Guer 2011)

presented a numerical study on the analysis of a

passive cooling system. They employed various

geometries of enclosures filled with phase change

material (PCM) with enhanced thermal conductivity.

The authors evaluated five geometric shapes that

https://orcid.org/ 0000-0003-0920-0618

https://orcid.org/ 0000-0001-5435-1429

contained the same volume of PCM while cooling the

same surface. Their calculation results show the

significant effect of changing the geometry. Indeed,

they found a maximum temperature difference of up

to 40°C between two of the enclosures. An enclosure

offset vertically from the cooled surface represented

a better performance. (Seyyedi et al. 2012)applied the

Boltzmann lattice method (LBM) to investigate the

influence of a separator plate and an inclined square

cylinder (with 45°). They used a horizontal channel

filled with air with a blocking ratio (𝛽=0.25) as study

geometry. The effects of the plate and cylinder were

examined on the two-dimensional unsteady laminar

flow and on the heat transfer within the channel. Their

numerical results found that there is an excellent

position for the separator plate. This is demonstrated

by a maximum value of the ratio between the Nusselt

number and the drag coefficient. They also showed

that there are particular points where there is a sharp

jump in drag coefficient and average Nusselt number.

This research presents work aimed at

controlling the flow around electronic systems to

improve their performance and increase their

efficiency, as well as improving the quality of heat

Admi, Y., Benhamou, J., Lahmer, E., Moussaoui, M., Jami, M. and Mezrhab, A.

Numerical Study of the Drag Reduction and the Electronics Composites Cooling by using the Three Flat Plates.

DOI: 10.5220/0010727600003101

In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 21-26

ISBN: 978-989-758-559-3

transference around these systems. For this purpose, a

numerical study of the flow around a heated square

block controlled by three flat plates parallels located

in a bi-dimensional channel was performed. The

simulations were carried out by the double multiple

lattice Boltzmann method. The influence of the length

of the control plates on the temporal and average

variation of the drag coefficient and on the heat

exchange was presented.

CONFIGURATION DESCRIPTION

AND BOUNDARY CONDITIONS

2.1 Configuration Domain and Initial

Conditions

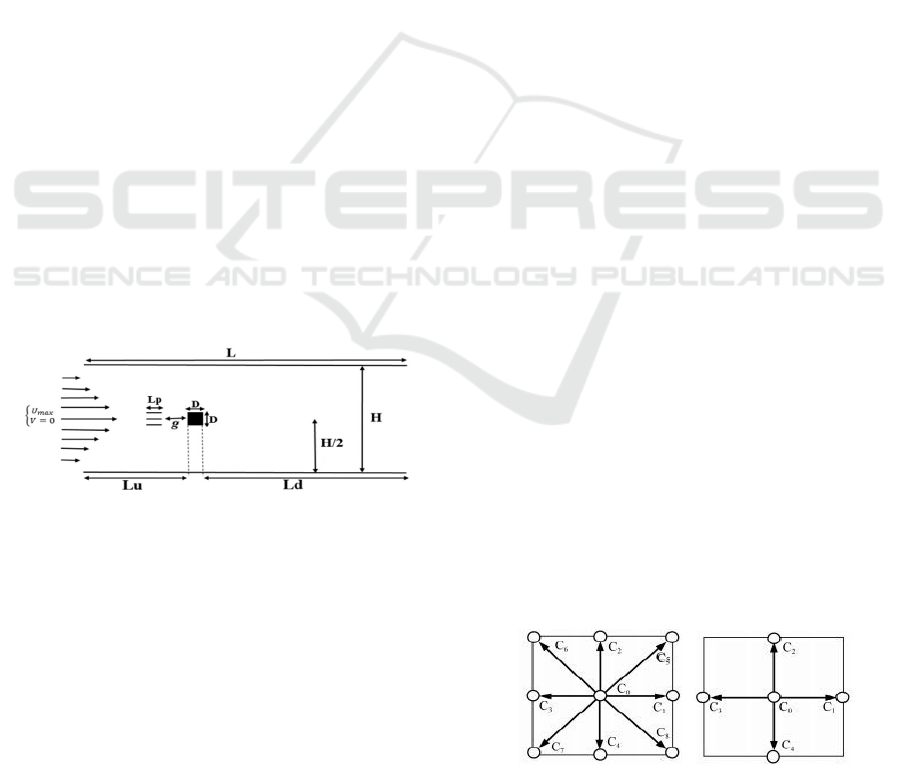
Figure 1 illustrates the geometry employed to study

the flow past a heated square cylinder controlled by

three control partitions placed in a horizontal

bidimensional channel. The square cylinder

positioned in an upstream distance Lu =6D and a

downstream length sufficiently wide Ld = 31D, and a

height H =11D (see Fig. 1) where the "D" represents

the dimension of the square cylinder. The controlling

partitions are arranged successively downstream the

principal square cylinder, having the same length

"Lp" and height "h=0.02D". Moreover, g designates

the gap spacing between the square cylinder and

partitions (see Fig. 1). The fluid entering with a

dimensionless temperature 𝜃



0,5 and the block

is considered heated with a dimensionless

temperature 𝜃



 0,5.

Figure 1: The structure of the computational domain.

At the channel input, the flow is created based on

a parabolic velocity profile (u = 1.5 *U

max

(1- (y/H));

v = 0), where U

max

is the maximal entrance velocity,

and y is the vertical dimension from the centerline,

and u and v are the components of velocity vectors.

As well as at the outlet, the parabolic velocity profile

is imposed and the gradients of velocity and pressure

are considered to be zero.

2.2 Boundary Conditions

In LBM, the most well-known type of boundary

conditions in the literature, are the Bounce-Back

boundary conditions(Bouzidi, Firdaouss, and

Lallemand 2001). These conditions are used in the

present work to define the solid walls of the channel.

In the inlet and outlet of the channel, the flow is

completely expanded with a parabolic velocity profile,

so the implementation of the boundary conditions of

Zou and He is the most preferred(Zou and He 1997)

The conditions suggested by (Mezrhab et al.

2010) are used to treat the heat flow boundary

conditions. thus The adiabatic boundary conditions

are applied for the channel walls.

3 NUMERICAL SCHEME

As already mentioned, this paper uses the LB method

as the numerical approach to simulate the physical

phenomenon studied in this work.

Two models are widely used for this method, the

LBM a single relaxation time (BGK-SRT) scheme

(Bhatnagar, Gross, and Krook 1954; Lallemand and

Luo 2000) and the multiple relaxation time (MRT)

scheme (Moussaoui et al. 2021; Admi, Moussaoui,

and Mezrhab 2020; Benhamou et al. 2020;

Moussaoui et al. 2019).

In this paper, the MRT model is used since it is

more stable, precise and presents a good convergence

compared to the SRT model.

3.1 The D2Q9 Model

Thanks to reasons of convergence and compatibility

with the model used in thermic, the D2Q9 model was

used to treat the distribution of the density of fluid

particles. This model is illustrated in figure 1. For

more information, see my previous work(Admi,

Moussaoui, and Mezrhab 2020).

3.2 The D2Q5 Model

For reasons of compatibility and reduction of

calculation time, the D2Q5 model is used to treat the

thermal problem. The motion of the fluid particles, in

this model (D2Q5), is carried out by the discrete

velocities which are given by (Admi et al., 2020):

(a) 𝐷2𝑄9 (b) 𝐷2𝑄5

Figure 2: D2Q9 and D2Q5 LBM schemes.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

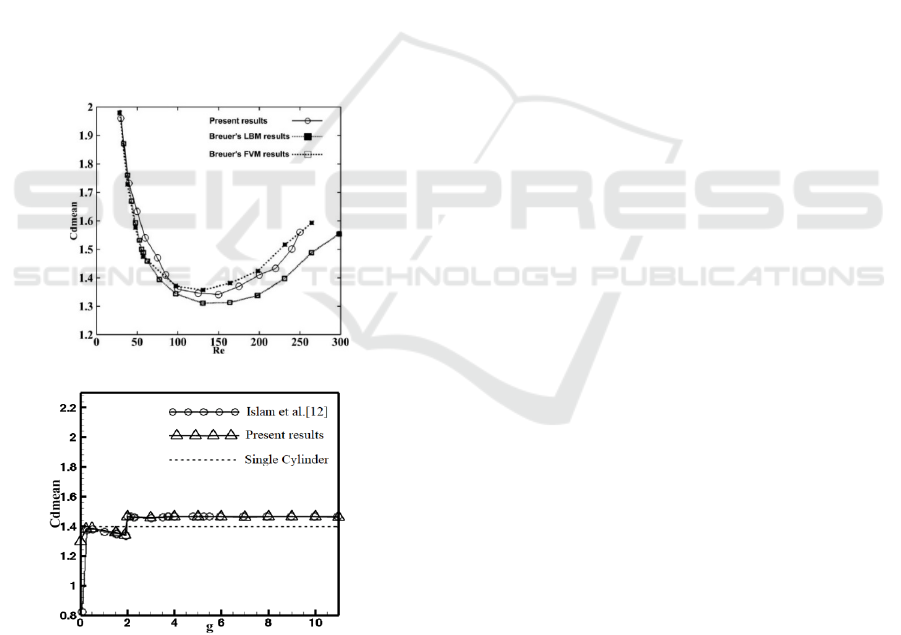
4 CODE VALIDATION

In this work, we have two validation cases with two

different problems. First, we validated our numerical

code with the work of (Breuer et al. 2000) using both

methods: LBM and FVM (finite volume method),

where we examined the flow around a square cylinder

installed inside a horizontal channel with a blocking

ratio of 1/8. Fig. 3-a shows the graph showing the

temporal variation of the drag coefficient as a

function of Reynolds. An agreement existing between

our results and those of Breuer is observed. The small

differences between the two results may be

due to the

mesh size used. Next, we validated our numerical

results with those found numerically by (Islam et al.

2015) or experimentally by (Okajima A 1982) for a

flow around a square obstacle controlled by a single

flat plate (fig. 3-b). Figure 4 shows the variation of

the mean value of the drag coefficient as a function of

the spacing between the square block and the control

plate. A good correspondence is noted between our

results and the reference results.

(a)

(b)

Figure 3: Comparison of our results for the average drag

coefficient with previous works for a single obstacle: (a)

without control partition; (b) with control partition.

5 NUMERICAL RESULTS AND

DISCUSSION

The present section presents the obtained numerical

results of the effect of the length of the three flat

plates on the velocity contours of the flow patterns,

the isotherm contours and on the mean and time drag

coefficient. To avoid the effect of the location

between the plates and the block, a study was carried

out to find the optimal location for which we have a

maximum reduction of the drag coefficient and large

and regular heat exchange. The results obtained in

this study show that the optimal position of the

partitions is g=1.5. In the present work, we have

placed the plates at this critical distance (g = 1.5) and

we have varied their lengths (1D < Lp < 5.5D).

5.1 Streamline Structures and

Isotherms

Figure 5 illustrates the velocity contours (5-a,c,e,g)

and isotherms (5-b,d,f,h) around the square cylinder,

heated and controlled by three parallel flat plates

placed horizontally upstream. In this figure (fig.5), an

alternate Van Karman vortex street is seen in the

wake area downstream of the square cylinder. The

wake can be considered as periodically undulating in

the case where the control partitions are not

implemented (no control case). This undulation

decreases with the increasing plate length until a

critical length Lp=2.5D (Fig.5-e,f). After this critical

length, the wake becomes strongly undulated (see fig.

5-g,h).

Likewise, an alternation of positive and negative

vortices is observed in the uncontrolled case and in

the cases where the plate length exceeds the critical

length, whereas in the cases at or approaching the

critical length only negative vortices are apparent.

Also, the size of detached vortexes behind the square

cylinder decreases with the increasing length until

Lp-critical=2.5D where the vortexes are smaller in

size. Then, this size increases strongly with the

increase of the length of the plates.

We also observe that the number of vortexes

shedding behind the square cylinder in the

uncontrolled case than in the controlled cases. This is

justified by the direct exposure of the frontal surface

of the cylinder to the entering fluid in the uncontrolled

case. Whereas in the case where the three control

plates are inserted, the incoming fluid strikes the

plates firstly before the block. This decreases the

fluidic forces acting on the square cylinder compared

to the uncontrolled case. Similarly, in the case where

the plates are present, part of the front face of the

Numerical Study of the Drag Reduction and the Electronics Composites Cooling by using the Three Flat Plates

cylinder is exposed directly to the incoming fluid

while the other part is controlled by these three plates.

Thus, in the case where Lp varies from Lp = 1D to Lp

= 3D (case tested: g=1; 1.3; 1.5; 2; 2.2; 2.5; 2.7; 3) the

length of the control plates is small, the fluid

considers the whole (square cylinder + three

partitions) as one bluffing body. For these lengths,

the shear layers produced by the edges of the

partitions jump up and down behind the square

cylinder. This decreases the number and size of

vortices released behind the square cylinder (the

fluidic forces acting on the square cylinder also

decrease). Whereas, in the case where the length is

large (Lp > 3D), the shear layers are stuck from the

bottom and top surface of the plates and then partially

or completely hit the front face of the square cylinder,

which again increases the size of the vortices

shedding behind the square cylinder.

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Figure 4: Velocity & Isotherms contours visualisation :

Velocity contours (a, c, e, g);Isotherms contours (b, d, f, h)

5.2 Drag Coefficient

In this section, the effect of the length of the plates on

the time-averaged drag force acting on the square

cylinder. Table 1 gives the average values of the drag

coefficient Cdmean and the length of the control

plates while fixing the spacing between the partitions

and the square cylinder. Figure 5 illustrates the time

variation of the drag coefficient in the case with and

without control plates. From this figure, it can be

noted that the drag coefficient varies periodically and

that the average value of the drag coefficient is

𝐶𝑑𝑚𝑒𝑎𝑛0  1.1. A comparison between Cdmean0

and the average values presented in Table 1 shows

that the drag acting on the cylinder decreases

significantly when the control partitions are

implemented. This decrease (drag reduction) is

caused by changing the flow input that hits the square

cylinder. In this work, the control plates are located

before the cylinder, so the cylinder will be in the wake

of the plates. This will decrease the pressure forces

applied in this wake area, resulting in a decrease in

drag force (also, an increase in lift force).

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

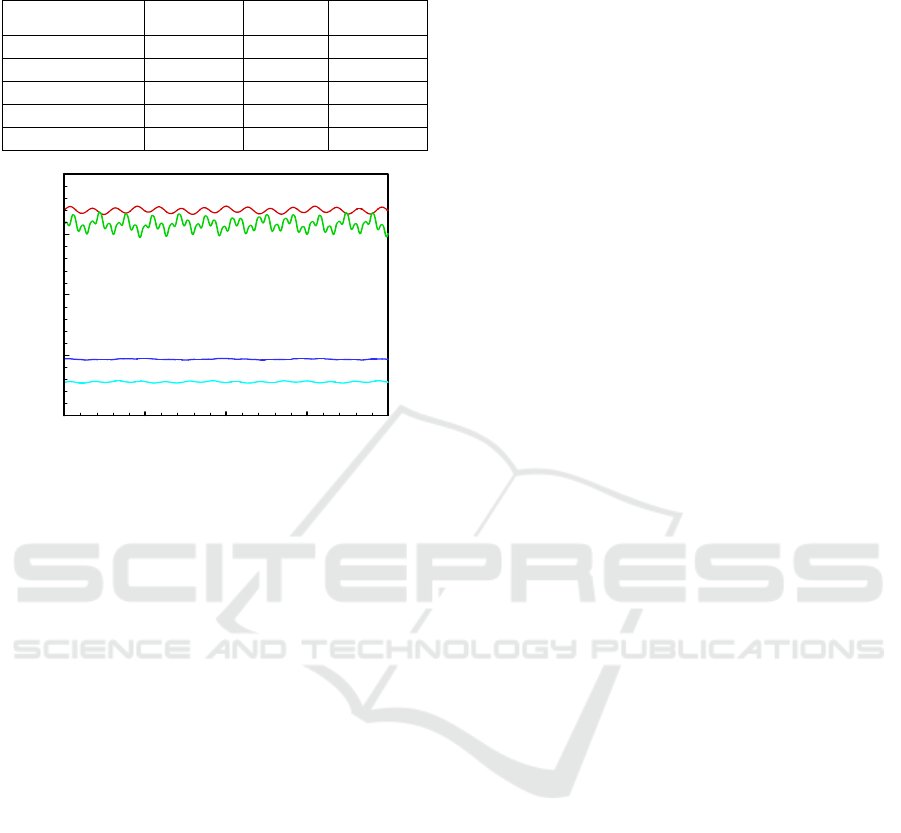
Table1: The average drag coefficient in function of the flat

plates length.

Cdmean Lp Cdmean

Without control 1.0998 2.2D 0.3905

1D 0.4831 2.5D 0.3892

1.3D 0.4453 3D 0.4078

1.5D 0.4268 4D 0.6948

2D 0.3969 5.5D 1.0384

Figure 5. The temporal drag coefficient visualisation

Similarly, Table 1 shows that the highest Cdmean

value appears for the uncontrolled case, then a

reduction in Cdmean values is observed until it

reaches a minimum in the case where the length of the

plates becomes equal Lp

= 2.5. At this critical

length, an effective vortex suppression was observed.

After this critical length, the average drag coefficient

increases again with increasing plate length. The front

face of the square cylinder is partially or totally

exposed to the shear layers detached by the edges of

the control plates. This increases the pressure forces

applied on the cylinder and consequently increases

the drag force. The optimal length of the control

plates (Lp=2.5) corresponds to a minimum Cdmean

value and a high and even heat exchange. A

maximum reduction of the average drag coefficient

reaches about 64.6% for Lp=2.5D (critical length).

Therefore, in the other cases (Lp varies from 1D to

3D), the incoming fluid considers the control plates

and the cylinder as a single bluff body. This reduces

the fluidic forces applied on the cylinder and the

amplitude of the vortex shedding.

6 CONCLUSIONS

The present research presents a numerical

investigation that had been performed to study the

vortex suppression (drag reduction) and to study the

heat transfer characteristics on a heated square

cylinder placed in a horizontal 2D channel and

controlled by three partitions arranged in parallel

upstream of the square cylinder.

The numerical results obtained show that the drag

acting on the square cylinder reduces in all the cases

studied compared to the uncontrolled case. This

shows the importance and the necessity of flow

control. The maximum reduction of the drag is

observed in the case where the length of the partitions

becomes a critical length Lpcr = 2.5D. At this length,

important and regular heat exchange is observed.

Also, the size of the thermal vortices and the width of

the Von Karman street decreases at this critical

position. Therefore, for beneficial use of the control

partitions, for example, in the cooling of electronic

components, it is preferable to use three parallel

partitions of length Lp = 2.5D placed upstream of the

square cylinder at a critical distance g = 1,5.

REFERENCES

Admi, Y., Moussaoui, M.A., Mezrhab. A., 2020. “Effect of

a Flat Plate on Heat Transfer and Flow Past a Three

Side-by-Side Square Cylinders Using Double MRT-

Lattice Boltzmann Method.” In 2020 IEEE 2nd

International Conference on Electronics, Control,

Optimization and Computer Science, ICECOCS 2020.

Ali, H.M., Adeel, A., 2017. “Experimental Investigation of

N-Eicosane Based Circular Pin-Fin Heat Sinks for

Passive Cooling of Electronic Devices.” International

Journal of Heat and Mass Transfer.

Benhamou, J., Jami, M., Mezrhab, A., Botton, V., Henry,

D., 2020. “Numerical Study of Natural Convection and

Acoustic Waves Using the Lattice Boltzmann Method.”

Heat Transfer.

Bhatnagar, P. L., Gross, E.P., Krook, M., 1954. “A Model

for Collision Processes in Gases. I. Small Amplitude

Processes in Charged and Neutral One-Component

Systems.” Physical Review.

Bouzidi, M., Firdaouss, M., Lallemand, P., 2001.

“Momentum Transfer of a Boltzmann-Lattice Fluid

with Boundaries.” Physics of Fluids.

Breuer, M., Bernsdorf, J., Zeiser, T., Durst, F., 2000.

“Accurate Computations of the Laminar Flow Past a

Square Cylinder Based on Two Different Methods:

Lattice-Boltzmann and Finite-Volume.” International

Journal of Heat and Fluid Flow.

Césaro, O., Rejane, D., Arno K.., Horácio, A. Vielmo.

2003. “Cooling of Cylindrical Vertical Tanks

Submitted to Natural Internal Convection.”

International Journal of Heat and Mass Transfer.

Islam, S. Ul., Rahman, H., Abbasi, W. S., Shahina, T.,

2015. “Lattice Boltzmann Study of Wake Structure and

Force Statistics for Various Gap Spacings Between a

Square Cylinder with a Detached Flat Plate.” Arabian

Journal for Science and Engineering 40 (8): 2169–82.

580000 585000 590000 595000 600000

0.25

0.5

0.75

1.25

no control

Lp = 2. 5D

Lp = 5.5D

Lp = 1D

Numerical Study of the Drag Reduction and the Electronics Composites Cooling by using the Three Flat Plates

Lallemand, P., Li, S.L., 2000. “Theory of the Lattice

Boltzmann Method: Dispersion, Dissipation, Isotropy,

Galilean Invariance, and Stability.” Physical Review E

- Statistical Physics, Plasmas, Fluids, and Related

Interdisciplinary Topics.

Mezrhab, A., Moussaoui, M.A., Jami, M., Naji, H.,

Bouzidi, M., 2010. “Double MRT Thermal Lattice

Boltzmann Method for Simulating Convective Flows.”

Physics Letters, Section A: General, Atomic and Solid

State Physics.

Moussaoui, M. A., Admi, Y., Lahmer, E.B., Mezrhab, A.,

2021. “Numerical Investigation of Convective Heat

Transfer in Fluid Flow Past a Tandem of Triangular and

Square Cylinders in Channel.” IOP Conference Series:

Materials Science and Engineering.

Moussaoui, M. A., Lahmer, E.B., Admi, Y., Mezrhab, A.,

2019. “Natural Convection Heat Transfer in a Square

Enclosure with an inside Hot Block.” In 2019

International Conference on Wireless Technologies,

Embedded and Intelligent Systems, WITS 2019.

Nazari, M., Ramzani, S., 2014. “Cooling of an Electronic

Board Situated in Various Configurations inside an

Enclosure: Lattice Boltzmann Method.” Meccanica.

Okajima A. 1982. “Strouhal Number of Rectangular

Cylinders.” Journal of Fluid Mechanics.

Omari, K.E., Kousksou, T., Guer, Y. L., 2011. “Impact of

Shape of Container on Natural Convection and Melting

inside Enclosures Used for Passive Cooling of

Electronic Devices.” Applied Thermal Engineering.

Seyyedi, S.M., Bararnia, H., Ganji, D.D., Gorji-Bandpy,

D.D, Soleimani, S., 2012. “Numerical Investigation of

the Effect of a Splitter Plate on Forced Convection in a

Two Dimensional Channel with an Inclined Square

Cylinder.” International Journal of Thermal Sciences.

Zou, Q., He, X., 1997. “On Pressure and Velocity Boundary

Conditions for the Lattice Boltzmann BGK Model.”

Physics of Fluids.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)