Tuning Convolutional Neural Networks Hyperparameters

for Offline Handwriting Recognition

Ahmed Remaida

, Aniss Moumen

, Younes El Bouzekri El Idrissi

and Benyoussef Abdellaoui

Laboratory of Engineering Sciences, National School of Applied Sciences,

Ibn Tofaïl University, Kenitra, Morocco

Keywords: EMNIST, Deep Learning, Convolutional Neural Networks, Handwriting Letters Recognition.

Abstract: Deep Learning Artificial Neural Networks has pushed forward researches in the field of image recognition,

furthermore in handwriting recognition. In writing or writer identification, segmentation, or features

extraction applications, many ANNs models are applied in the process. This paper presents a comparative

study of one of the most widely used ANNs for offline handwriting recognition, known as Deep

Convolutional Neural Networks. We describe the challenging benchmark Dataset entitled EMNIST

introduced in 2017 as an extended version of the well-known MNIST to fill the gap of handwritten letters

characters. The accuracies obtained in this work for the letters dataset compares favourably with many other

approaches in the literature. The effect of the choice of hyperparameters related to our network architecture

and capabilities are explored and detailed, like the number of layers, neurons, optimizers, learning rates and

other parameters.

https://orcid.org/0000-0002-2981-8936

https://orcid.org/0000-0001-5330-0136

https://orcid.org/0000-0003-4018-437X

https://orcid.org/0000-0002-5950-0187

1 INTRODUCTION

Convolutional Neural Networks (CNNs) have

proven their incredible ability for feature extraction

leading to outstanding classification performances in

several application areas, such as object detection,

language processing, image recognition, and many

more. Nevertheless, their performance is affected by

small changes in the network hyperparameters like

the number of convolutional layers, dense layers,

activation functions, optimizers, learning rates… etc.

For the last decade, researchers have made great

efforts to automatically tune hyperparameters

seeking to enhance the CNNs performances for

different applications. Although these methods

exceeded most of the manually generated

architectures, the searching process requires greater

computational resources and implies time to train all

possibilities during the search for the best

architecture. Here in this paper, we intend to

compare different CNNs performances based on

hyperparameters changes when applied for EMNIST

letters recognition. It is structured as the following:

Section two where we give a non-exhaustive

description of the benchmarked handwriting

datasets. After that, in section 3 where we describe a

comprehensive explanation of the Convolutional

Neural Networks architecture. Finally, in section 4

where we present our results and findings.

2 HANDWRITING DATASETS

BENCHMARK

Many handwritten datasets have been developed

across the years, building a solid background for

evaluating numerous recognition tasks. These

datasets could be classified based on different

dimensions: Online or Offline data acquisition

method, script, size, and types of supported tasks

(Hussain et al., 2015). This section highlights some

Remaida, A., Moumen, A., El Bouzekri El Idrissi, Y. and Abdellaoui, B.

Tuning Convolutional Neural Networks Hyperparameters for Ofﬂine Handwriting Recognition.

DOI: 10.5220/0010728600003101

In Proceedings of the 2nd Inter national Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 71-76

ISBN: 978-989-758-559-3

of the Benchmarks used in offline handwriting

recognition for validating novel techniques and

algorithms.

2.1 NIST SD 19

Since the beginning of the 90s, the National Institute

of Standards and Technology (NIST) developed a

series of image databases intended for handprint

document processing and OCR research. In 1995

they introduced the Special Database 19 (Grother,

1995), composed of handwriting samples forms of

3600 writers and 810,000 isolated character images

in addition to ground-truth information. Even if it

was available since 1995, it remained mostly unused

because of difficulties in both accessing and using

for modern computers, due to the way it was stored.

2.2 MNIST

The Mixed National Institute of Standards and

Technology dataset, or simply (MNIST) was

introduced in 1998 by LeCun et al., it is a

handwriting digit database derived from a small

subset of the numerical digits contained within the

larger database NIST (Le Cun et al., 1989). It is

constructed based on two different sources: The

NIST SD 1 collected among high-school students

and the NIST SD 3 retrieved from Census Bureau

employees. We could describe the MNIST as a

labelled images database that contains handwritten

digits, with a separate training dataset (60,000

samples) and test dataset (10,000 samples), making

it easy to use and allows a fast comparison between

different techniques. Initially, black and white

images from NIST were sized to fit in a 20*20

pixels box with aspect ratio preservation and then

normalized to grey-scale with anti-aliasing

technique. As a final result, images were centred in a

28*28 image by computing the pixel’s centre of

mass. The MNIST dataset remained the most known

and used dataset in the computer vision and neural

networks community and was widely used as the

“hello-world” of machine and deep learning

tutorials.

2.3 EMNIST

Considering that MNIST dataset has becomes a non-

challenging benchmark, Cohen et al. introduced in

April 2017 the extended version of the MNIST

(EMNIST) consisting of both handwritten letters and

digits with the same structure as the MNIST database

(Cohen et al., 2017), offering new challenges for

researchers on computer vision. The EMNIST was

constructed with the NIST Special Database 19

(NIST SD 19), where original images were stored as

28*28-pixel binary images and with using the bi-

cubic interpolation with a Gaussian filter to soften

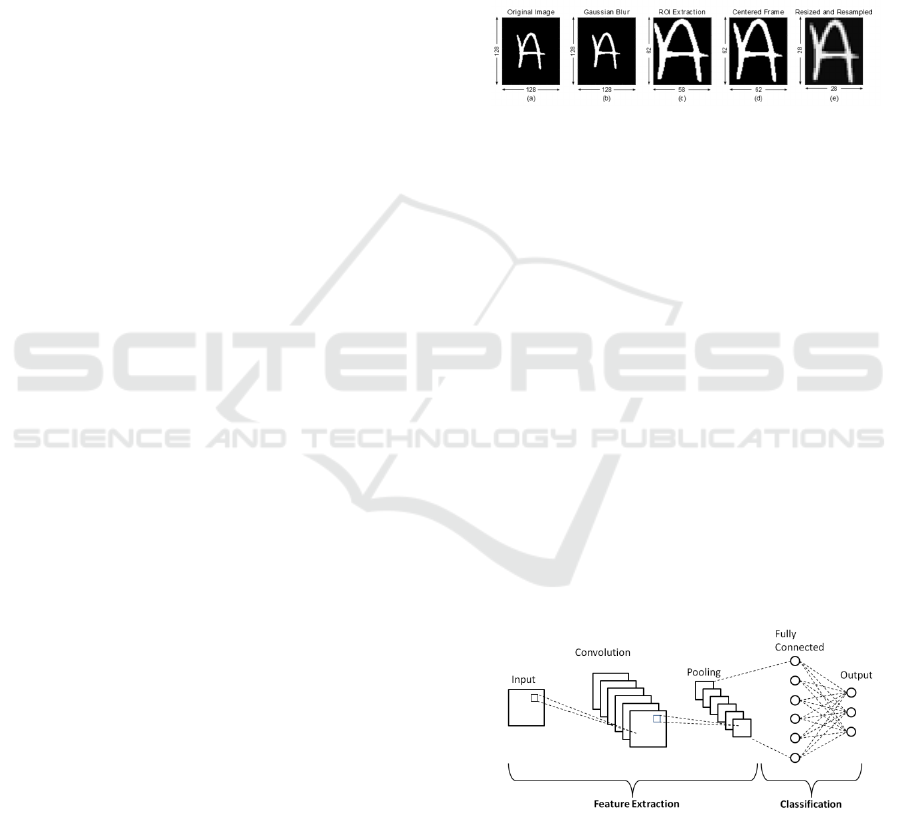
the edges with aspect ratio preservation. In the Figure

below, the process of transforming NIST SD 19

images into the EMNIST. The EMNIST database is

growing more interest among researchers in the

Neural Networks community. Like the MNIST it is

now known as the “hello-world 2” of machine and

deep learning tutorials.

Figure 1: Diagram of the conversion process used to

convert the NIST dataset into EMNIST

(Cohen et al., 2017)

3 CONVOLUTIONAL NEURAL

NETWORKS

In general, CNN's architecture comprises two parts:

the first one is composed of alternate layers of

convolution and pooling that extract features from

imputed data. The second one is composed of one or

more fully connected layers leading to classification.

Different regulating units like batch normalization or

dropout can be incorporated with the different

mapping functions in order to optimize CNN

performances. Therefore, the arrangement of

components in a CNN is considered fundamental to

designing new architectures for enhancing

performances. Here in the following, we describe

each one of those components:

Figure 2: A Typical Convolutional Neural Networks

Architecture

3.1 Convolutional Layer

The existing neurons in the convolutional layer act

as filters that aim to divide the image into small

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

parts known as kernels or receptive fields. By sliding

those filters over the inputted image, we calculate

the product between the parts of the input image and

the filter respecting the size of the filter (M*M). As

a result, we get a feature map that provides the

classification part of the network with relevant

information about the image, such as edges and

corners, leading to enhancing the features extraction

process and classification performances.

3.2 Pooling Layer

Pooling, also referred to as down-sampling, is a

great local operation that allows summing a number

of similar information in the neighbourhood of the

kernels leading to output the dominant response

within this local region. It also reduces the size of

resulted feature maps from the convolutional layer

which regulates the network complexity. Different

formulas of pooling exist such as max, average,

overlapping, spatial pyramid, L2… etc. When using

a max-pooling layer the resulted map would contain

the most prominent features in the previous feature

map generated in the convolutional layer.

3.3 Fully Connected Layer

The fully connected layer represents the

classification part at the end of the Convolutional

Neural Network. It takes the pooled feature maps as

inputs and performs non-linear combinations in

order to classify the data. In some cases, we replace

the fully connected layer with a global-average-

pooling layer.

3.4 Dropout Layer

Dropout is a technique that introduces regularization

within the network by skipping some of the units or

connections (randomly) with a predefined

probability. In a CNN, multiple connections that

learn a non-linear relation are sometimes co-adapted,

which causes over-fitting (Srivastava et al., 2014).

Randomly dropping some connections or units

produces several thinned network architectures, and

as a result, the one representative network with small

weights is selected to be considered as an

approximation of all proposed networks.

3.5 Activation Functions Layer

The Activation function is one of the main

hyperparameters of the CNNs model. It adds the

non-linearity aspect to the model, allowing it to

decide which information is fired in the forward

direction and which ones are not at the network's

end. Several activation functions are commonly

used, such as tanH, Sigmoid, ReLU, Softmax, and

most recently Mish (Misra, 2019). Each of these

functions has a specific usage: Sigmoid and Softmax

are more used in a binary classification, ReLU is

generally used in multi-class classification.

3.6 Normalization Layer

Data normalization ensures similar data distribution

for each input parameter. It is a process that makes

convergence faster while the network is training.

Many normalization layers types have been used in

CNNs architectures like Batch Normalization,

Weight Normalization, Layer Normalization and

Group Normalization.

3.7 Optimizers Algorithms

Optimizers are algorithms used to change a CNN’s

attributes like the weights and learning rate with the

purpose of reducing the losses. Changing the

optimizers and learning rates reduces the losses, so

they are a key factor for reducing the losses and

providing the most accurate results possible. There

are various choices of optimizers such as Adam

(Kingma & Ba, 2017), RMSprop (Hinton, 2012),

GD and SGD (Ruder, 2017).

4 EXPERIMENT

METHODOLOGY

There is an important number of hyperparameters in

a Convolutional Neural Network. Changing all those

parameters would result in a more significant

number of cases. Thus, we only chose

hyperparameters like the number of layers,

activation functions, optimizers, learning rates,

dropout rates and the number of neurones.

Combining nine possible architectures with three

different optimizers and four learning rates, we

generated 108 CNNs architecture. We trained and

tested all of them on the EMNIST Letter dataset

after grouping existing samples and splitting them

randomly into training and testing sets with a ratio of

80% to 20%. The training was for 50 epochs with a

fixed batch size equal to 512 batches and took nearly

three and a half-hour. We have automated

implementing, training and testing all the possible

models in Python 3.7 using Keras, a well-known

high-level neural networks API that runs on top of

the TensorFlow Framework. We carried out our

Tuning Convolutional Neural Networks Hyperparameters for Ofﬂine Handwriting Recognition

experiments on the Kaggle, a cloud-based

workbench for Data Science and Deep Machine

Learning. It offers a free virtual notebook powered

by a 2-core of Intel Xeon CPU @ 2.30GHz, 16GB

of RAM, 16GB of the NVidia K80 GPUs and 73 GB

of Storage access. Here below in Table 1, we give a

detailed description of all the hyperparameters

choices:

Table 1: Hyperparameters choice description.

arameters Value

Number of convolution la

ers 1-3

Number of filters respectivel

32-64-128

Kernel sizes 3x3

Pool size in MaxPooling laye

2x2

Dropout rates

0.2-0.5

(0.05 steps)

Number of dense layers 1-3

Number of neurons per dense

512-1024

(

2 ste

)

Activation function for all

convolutional and dense la

ers

Mish

Optimizer

Adam , SGD,

RMSprop

Number of E

ochs 50

Batch size 512

5 RESULTS AND DISCUSSION

We have noticed that the choice of learning rates is

remarkably affecting the efficiency of the

optimizer’s algorithm. We have noticed that with the

SGD optimizer, there is stability using all the

learning rates, it take more time for the network to

learn, and the smaller is the learning rate, the slower

the learning is getting. However, the best

performances were with the bigger learning rates

like 1e-2. As for Adam and RMSprop optimizers, it

seems that they are unstable when used with bigger

learning rates. Nevertheless, all nine CNNs

architectures showed faster learning with accurate

performances when used with the learning rate 1e-4,

whichever optimizer is chosen. The use of three

convolutional layers with one or two dense layers

marked the best results in all cases. A summary of

the results can be found in Tables 2 and 3 below:

Table 2: Top 3 CNN’s Architectures with highest Testing

Accuracy.

CNN Architectures Optimizer (L R) Accuracy

3 Conv, 2 Dense Adam

(

1e-3

)

94.681 %

3 Conv, 2 Dense Adam

(

1e-4

)

94.517 %

3 Conv, 2 Dense RMS

(

1e-4

)

94.517 %

Table 3: Top 3 CNN’s Architectures with highest Testing

Error rate.

CNN Architectures Optimizer (L R)

Error

Rate

3 Conv, 1 Dense Adam

(

1e-4

)

16.706 %

3 Conv, 1 Dense RMSprop (1e-4) 17.043 %

3 Conv, 2 Dense Adam (1e-4) 17.323%

The highest accuracy was achieved by a CNN model

with three convolutional and two dense layers. A full

description of this model’s architecture is presented

in the following Figure:

Figure 3: Architecture of the best CNN model.

Here in Figures 4 and 5, we give more details

about the best CNN model with the highest accuracy

rates, an illustration of monitoring the training and

validation for the 50 epochs:

Figure 4: Top CNN’s Training and Validation Accuracy

across different learning Epochs

Figure 5: Top CNN’s Training and Validation Loss

across different learning Epochs.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

There is an apparent absence of the phenomena of

neither overfitting nor underfitting across the

training and validation process. The main factor of

such achievement is the choice of the Mish

activation function (Misra, 2019) in addition to the

use of the batch normalization layer (Ioffe &

Szegedy, 2015). We strongly believe that further

training for this model could lead to better results.

Satisfied with what we had achieved, we chose to

present only those results. In the following table, we

compare our best achievement to the existing works

under the same scope:

Table 4: Our best achievement compared to the state of

art.

CNNs for EMNIST Letters Accuracy

(Peng & Yin, 2017) 95.44%

(

Baldominos et al., 2019

)

95.35%

This wor

94.68 %

(Sen Sharma et al., 2018) 94.36%

(Cavalin & Oliveira, 2019) 93.63%

(

esan et al., 2011

)

92.42%

6 CONCLUSION

In this paper, we have described the EMNIST

benchmark dataset alongside Deep Convolutional

Neural Networks architectures and hyperparameters.

By tuning hyperparameters of CNNs, we have

achieved excellent results that compare favourably

with other work under the same scope. We believe

that further tuning would lead to better outcomes.

Thus we intend to evaluate deeper architectures of

the CNNs with larger hyperparameters tuning to

enhance performances even further.

REFERENCES

Baldominos, A., Saez, Y., & Isasi, P. (2019). Hybridizing

Evolutionary Computation and Deep Neural

Networks: An Approach to Handwriting Recognition

Using Committees and Transfer Learning.

Complexity, 2019, 1–16.

https://doi.org/10.1155/2019/2952304

Cavalin, P., & Oliveira, L. (2019). Confusion Matrix-

Based Building of Hierarchical Classification. In R.

Vera-Rodriguez, J. Fierrez, & A. Morales (Eds.),

Progress in Pattern Recognition, Image Analysis,

Computer Vision, and Applications (Vol. 11401, pp.

271–278). Springer International Publishing.

https://doi.org/10.1007/978-3-030-13469-3_32

Ciresan, D. C., Meier, U., Gambardella, L. M., &

Schmidhuber, J. (2011). Convolutional Neural

Network Committees for Handwritten Character

Classification. 2011 International Conference on

Document Analysis and Recognition, 1135–1139.

https://doi.org/10.1109/ICDAR.2011.229

Cohen, G., Afshar, S., Tapson, J., & van Schaik, A.

(2017). EMNIST: An extension of MNIST to

handwritten letters. ArXiv:1702.05373 [Cs].

http://arxiv.org/abs/1702.05373

Grother, P. (1995). NIST Special Database 19

Handprinted Forms and Characters Database.

/paper/NIST-Special-Database-19-Handprinted-

Forms-and-

Grother/1ea788f1f4334095d215afd4c137936ff89d7f6

Hinton, G. (2012). Lecture Notes On RMSprop.

http://www.cs.toronto.edu/~hinton/coursera/lecture6/le

c6.pdf

Hussain, R., Raza, A., Siddiqi, I., Khurshid, K., & Djeddi,

C. (2015). A comprehensive survey of handwritten

document benchmarks: Structure, usage and

evaluation. EURASIP Journal on Image and Video

Processing, 2015(1), 46.

https://doi.org/10.1186/s13640-015-0102-5

Ioffe, S., & Szegedy, C. (2015). Batch Normalization:

Accelerating Deep Network Training by Reducing

Internal Covariate Shift. ArXiv:1502.03167 [Cs].

http://arxiv.org/abs/1502.03167

Khan, A., Sohail, A., Zahoora, U., & Qureshi, A. S.

(2020). A survey of the recent architectures of deep

convolutional neural networks. Artificial Intelligence

Review, 53(8), 5455–5516.

https://doi.org/10.1007/s10462-020-09825-6

Kingma, D. P., & Ba, J. (2017). Adam: A Method for

Stochastic Optimization. ArXiv:1412.6980 [Cs].

http://arxiv.org/abs/1412.6980

Le Cun, Y., Jackel, L. D., Boser, B., Denker, J. S., Graf,

H. P., Guyon, I., Henderson, D., Howard, R. E., &

Hubbard, W. (1989). Handwritten digit recognition:

Applications of neural network chips and automatic

learning. IEEE Communications Magazine, 27(11),

41–46. https://doi.org/10.1109/35.41400

Misra, D. (2019). Mish: A Self Regularized Non-

Monotonic Activation Function. ArXiv:1908.08681

[Cs, Stat]. https://doi.org/1908.08681

Peng, Y., & Yin, H. (2017). Markov Random Field Based

Convolutional Neural Networks for Image

Classification. In H. Yin, Y. Gao, S. Chen, Y. Wen, G.

Cai, T. Gu, J. Du, A. J. Tallón-Ballesteros, & M.

Zhang (Eds.), Intelligent Data Engineering and

Automated Learning – IDEAL 2017 (Vol. 10585, pp.

387–396). Springer International Publishing.

https://doi.org/10.1007/978-3-319-68935-7_42

Ruder, S. (2017). An overview of gradient descent

optimization algorithms. ArXiv:1609.04747 [Cs].

http://arxiv.org/abs/1609.04747

Sen Sharma, A., Ahmed Mridul, M., Jannat, M.-E., &

Saiful Islam, M. (2018). A Deep CNN Model for

Student Learning Pedagogy Detection Data Collection

Using OCR. 2018 International Conference on Bangla

Tuning Convolutional Neural Networks Hyperparameters for Ofﬂine Handwriting Recognition

Speech and Language Processing (ICBSLP), 1–6.

https://doi.org/10.1109/ICBSLP.2018.8554701

Simonyan, K., & Zisserman, A. (2015). Very Deep

Convolutional Networks for Large-Scale Image

Recognition. ArXiv:1409.1556 [Cs].

http://arxiv.org/abs/1409.1556

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,

& Salakhutdinov, R. (2014). Dropout: A Simple Way

to Prevent Neural Networks from Overﬁtting. 30.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)