Incremental Subsequence Clustering Algorithm from Multiple Data

Streams

Zaher Al Aghbari

, Ayoub Al-Hamadi

and Thar Baker

Department of Computer Science, University of Sharjah, UAE

IIKT, Otto-von-Guericke-University Magdeburg, Germany

Keywords: Clustering subsequences, Data streams, Incremental clustering, Big Data.

Abstract: Clustering subsequences of continuous data streams have a wide range of applications, such as stock market

data, social data, and wireless sensor data. Due to the continuous nature of data streams, finding evolving

clusters is a challenging task. This paper proposes ISsC, which is an incremental clustering algorithm of

subsequences in multiple data streams. The ISsC algorithm employs a window buffer to collect and process

the continuous data. Clusters found in previous windows are kept in a global List. Then, the List of clusters

is updated incrementally by clusters found in the current without the need to recompute the clusters from the

entire historical streams. If the number of cluster members (e.g., subsequences) is above a certain threshold,

the cluster is deemed a frequent subsequence. Old clusters are tracked through a decay parameter and removed

from the global List once this parameter is decayed to a negative value. Extensive experiments are conducted

on multiple data streams to show the feasibility of the ISsC algorithm.

1 INTRODUCTION

Due to the abundance of generated data streams in

recent years, many new applications benefited from

mining these data streams. These data streams are

continuously generated and are affecting many

aspects of our life. The Internet of Things (IoT)

devices, social media, stock markets, online services,

etc., are generating continuous data streams (Islam et

al. 2019) (Tareq et al. 2021) (Alkouz et al. 2019).

Sensors have been utilized by several applications

and industries, such as health services, transportation,

and environment, where these IoT devices transmit

massive data streams (Al-Aghbari et al. 2019).

Processing data streams to find clusters of

subsequences within them requires careful algorithm

design that considers the characteristics of these data

streams. The first requirement is that the algorithm

should pass through the data only once due to the

continuous nature of the stream. This requirement can

be solved by employing a window buffer to collect

the incoming data. Moreover, the requirement of one-

pass only through data stream is imposed due to other

https://orcid.org/0000-0003-2285-953X

https://orcid.org/0000-0002-3632-2402

https://orcid.org/0000-0002-5166-4873

characteristics, such as unboundedness and high

arrival rate of the data. Therefore, a data stream would

be processed in chunks of data, where each chunk is

a group of buffered m data values that fills one

window. Processing chunks of data is known as a

sliding window model (Al-Aghbari et al. 2012)

(Dinges et al. 2011). Another requirement of data

stream processing is that the task (e.g., clustering)

should be mined incrementally. Clustering the data at

the current window should not require recomputing

the whole historical data stream, but rather the found

clusters in the current window should be added and

update the existing clusters that were computed in

previous windows.

This paper proposes an incremental algorithm

called ISsC to discover clusters in multiple data

streams. Each cluster contains a group of similar

subsequences of the data stream. One of the

subsequences in the cluster acts as a representative

subsequence of the cluster. The ISsC algorithm

computes these clusters efficiently, and they can be

extracted at any time. To dynamically update

clusters, involves adding new subsequences to active

Al Aghbari, Z., Al Hamadi, A. and Baker, T.

Incremental Subsequence Clustering Algorithm from Multiple Data Streams.

DOI: 10.5220/0010729000003101

In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 92-96

ISBN: 978-989-758-559-3

clusters and removing old clusters from the global

List of clusters, ISsC utilized a delay parameter for

every cluster. This parameter increments if the cluster

is still active in the current window and decreases

otherwise.

Several applications could benefit from clustering

subsequences, such as finding correlated stocks

behaviours in financial markets, discovering buying

patterns of customers, and mining website search

behaviour of online users that can be utilized by web

admins in making their websites more efficient

through predicting and pre-fetching certain pages

(Alkouz et al. 2020). System administrators may use

such clusters of subsequences in creating efficient

load-balancing strategies. The benefits of clustering

subsequences as well as the fact that this topic has not

been fully addressed by the research community are

the motivations behind the proposed ISsC.

Plenty of research work was conducted on

discovering frequent itemsets from transactional data

streams. However, very few research works were

published on finding clusters of subsequences of

continuous data streams. Moreover, existing research

work on clustering subsequences processes a single

data stream. Therefore, the main contributions of the

ISsC algorithm are:

 It is an efficient and incremental algorithm that

finds clusters of subsequences by passing

through the data stream only once.

 It employs a decay parameter to incrementally

update existing clusters and remove decayed

old clusters.

 It processes multiple data streams in parallel to

find clusters of subsequences, and thus, our

algorithm is scalable.

The rest of this paper is organized as follows. The

related work is presented in Section 2. Section 3

discusses the problem of clustering subsequences

from multiple data streams and presents the ISsC

algorithm. Extesive experiments are presented and

discussed in Section 4. The paper is concluded in

Section 5.

2 RELATED WORKS

Clustering subsequences of data streams has attracted

several research works. A fundamental clustering

algorithm called DBSCAN (Ester et. al 1996) finds

density-based clusters; however, it does not cope with

high dimensionality. DenStream (Cao et. al 2006) is

a density-based algorithm to find clusters in the data

stream; however, this algorithm suffers from high

processing time. A similar density-based clustering

algorithm is called CluStream (Aggarwal et al. 2003)

was proposed to find clusters from data streams, but

it does not support non-circular clusters.

Maintaining stream summaries using a tree index

structure that is leveraged to find clusters is proposed

by (Kranen et al. 2018). The Piece-wise Aggregate

Approximation algorithm was combined with the

density-based spatial clustering to find clusters from

medical data streams to group and monitor patients

with similar symptoms (Al-Shammari et al. 2019).

(Gong et al. 2017) propose an algorithm called

EDMStream to discover clusters from data streams

and address the concept of the drift problem.

However, this algorithm does not consider the

temporal relationships between the data values in the

stream. On the other hand, (Zoumpatianos et al. 2014)

propose an index to help find clusters incrementally

in time series data. However, this method adopts a

distance function to compute the clusters, which

hinders extracting information about the dynamicity

of frequent subsequences.

A method to find clusters of similar subsequences

whose length are variable is called StreamScan

(Matsubara et al. 2014) was proposed. This method

uses HMM to compute the clusters of subsequences

from the data stream.

Most of the research mentioned above, provided

solutions to find clusters of subsequences from data

streams; however, they do not satisfy all the

requirements, such as an incremental and scalable

algorithm.

3 CLUSTERING SUBSEQUENCES

Data streams are inherently continuous and infinite

(Al-Aghbari et al. 2013). Although a data stream can

contain any type of data (e.g. social media data

streams can be textual, images, and audio), in this

paper, we consider data streams that consist of real

numbers. Assume S

, S

, …, S

are given data

streams, the ISsC clusters subsequences over these

data streams incrementally. These clusters represent

frequent subsequences in the data streams.

Since the proposed ISsC algorithm mines clusters

from multiple data streams, the arrival rate r of the

data values of a stream is assumed to be fixed among

all data streams (i.e. synchronized data streams).

3.1 Incremental Clustering Parameter

Data values of a stream are arriving at a specified rate

in all considered streams. Therefore, clusters of

subsequences appear and grow during a number of

Incremental Subsequence Clustering Algorithm from Multiple Data Streams

windows, and then shrink and disappear during

another set of windows. Therefore, ISsC tracks

clusters at every window. That is ISsC determines

whether each of the existing clusters is active or

inactive at each window. Here, a cluster is considered

active at the current window if a new subsequence is

found to be similar to the subsequences that are

already in the cluster and thus added to the cluster.

Otherwise, a cluster is considered inactive.

For a certain cluster C

, if the number of member

subsequences,



, is greater than or equal to the

support threshold, τ, (  τ), then C

is active, and its

decaying parameter δ is incremented. Otherwise, if C

is inactive, the δ is decremented. The inactive cluster

whose decaying parameter δ reaches -1 is removed

from the global List. That is because it is thought to

contain infrequent subsequences.

3.2 IScC Clustering Algorithm

Each cluster in the global List represents a frequent

subsequence, where the member subsequences in the

cluster are similar. Each cluster is represented by one

of its member subsequences, and usually, the first

member of the cluster is selected as the

representative. The Incremental Subsequence

Clustering (ISsC) algorithm initializes the number of

member subsequences,



, in the current window w

for every cluster to 0. In the current window, the ISsC

algorithm iterates over all variable lengths

subsequences l within a range between h and m. That

is, every subsequence l is in the range: h ≤ l ≤ m. The

length of an obtained subsequence should not be

smaller than the minimum h and should not exceed

the maximum m, where h and m are set based on the

application under consideration. Then, for every

obtained subsequence l, the ISsC algorithm verifies

whether one of its subsets s

. is frequent. If so, the

ISsC algorithm verifies whether the global List of

existing clusters contains a cluster (representative

subsequence) similar to the found frequent subset s

of the current subsequence l. This similarity check is

performed by computing the distance d

min

between s

and every cluster C

in List.

If d

min

is greater than a certain threshold Θ and

there is no overlap between s

and the subsequences

in the cluster C

, then the current s

belongs to C

Therefore, s

is included in C

, and the number of

cluster members



of C

is incremented by one.

Otherwise, if s

is not similar to any of the

representative subsequences of clusters in List, then

creates a new cluster C

Note that the ISsC

algorithm does not consider overlapping

subsequences since they lead to trivial matches

(Keogh et al. 2005).

For every cluster C

if the number of cluster

members



is less than the support threshold τ, (



τ), cluster C

is considered inactive, and its decaying

parameter δ is decremented. However, if



is greater

than or equal to the support threshold τ, (



 τ), then

cluster C

is considered active and its decaying

parameter δ is incremented. If a cluster is inactive for

several recent windows, its δ value decreases to -1,

and thus, this cluster will be removed by ISsC.

Moreover, to parallelize finding clusters from the

different data streams, the ISsC algorithm executes

each data stream using a separate JAVA thread.

Algorithm: Incremental Subsequence Clustering

Input: w, List, Θ

Output: Lis

Set



of every cluster (subsequence) in w

to zero.

for every subsequence l: h ≤ l ≤ m do

if a subset s

of l is frequent,

Compute d

min

with every C

in List

if (d

min

> Θ AND s

no overlap with C

)

include

Increment



else

creates a new cluster

end if

end for

for every cluster in List do

if (



< τ)

decrease the decay value δ by one

remove clusters with δ = -1

end if

end fo

4 EXPERIMENTS

The ISsC algorithm was evaluated by conducting a

set of experiments. First, the ISsC is assessed on how

well it discovers the clusters of subsequences from

multiple data streams as we modify the density of

clusters in the stream. Second, we evaluated how the

three parameters (window size, support threshold and

the number of cluster members of each sequence)

affect the system’s performance in terms of speed.

That is to what extent the data arrival rate r can be

increased under certain values of the measured

parameters. Note that the higher the value of r, the

slower the performance.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

To obtain a dataset for the experiments, we built a

data generator to create continuous data values for

each of the data streams used in the experiment. The

data values are real numbers and generated around

selected prototype values, which will act as cluster

centres. Each cluster centre value and data values that

belong to this cluster are generated randomly within

a predefined range [value1, value2].

4.1 Evaluating Clustering Purity

We used Equation 1 to measure the clustering purity

of the ISsC algorithm. To validate the result of this

experiment, we use a ground truth of labelled clusters

and their member subsequences in the different data

streams. Then, for every cluster, the purity of cluster

is computed by Equation 1.

𝐶𝑖 𝑝𝑢𝑟𝑖𝑡𝑦 



𝑇𝑜𝑡𝑎𝑙 𝑚𝑒𝑚𝑏𝑒𝑟𝑠 𝑖𝑛 𝑎𝑙𝑙 𝑐𝑙𝑢𝑠𝑡𝑒𝑟𝑠

1

Assume that the number of clusters in the data

streams is n at the current window w

, then the total

purity of clustering the clusters in w

is given by

Equation 2.

𝑡𝑜𝑡𝑎𝑙 𝑝𝑢𝑟𝑖𝑡𝑦  𝐶𝑖 𝑝𝑢𝑟𝑖𝑡𝑦 2





The reported result of the total purity is the

average of 100 runs of the experiment. Each run

includes clusters of five consecutive windows.

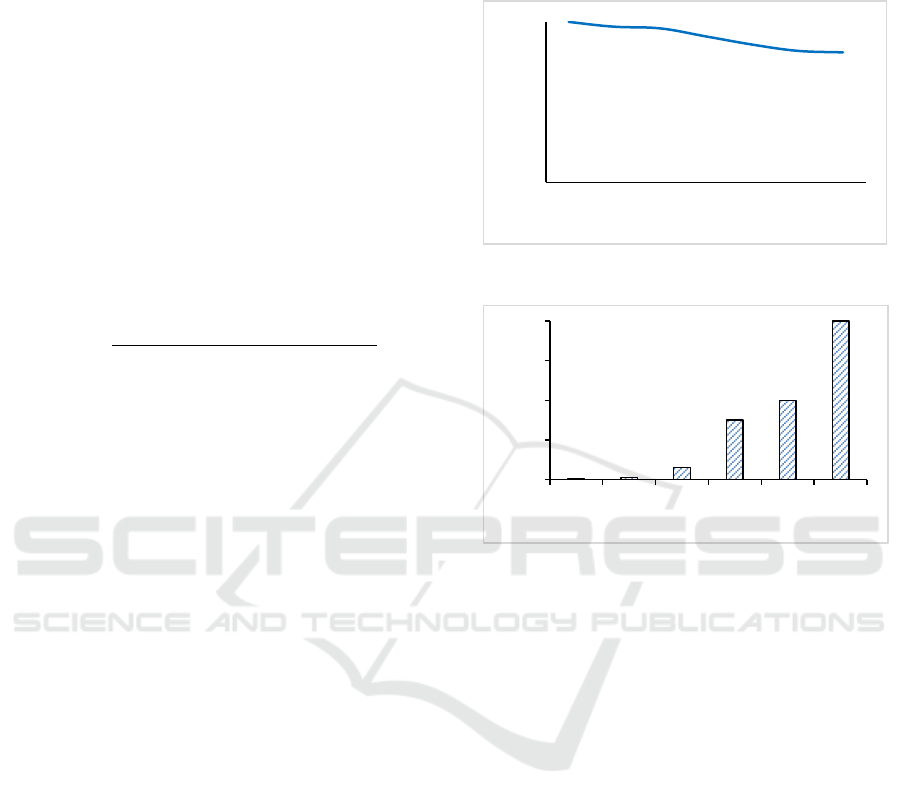
Figure 1 illustrates the effect of modifying the

range [value1, value2] from which cluster member

subsequences are generated (referred to as density



)

on the total purity of the clusters. In these

experiments, we fixed the other parameters, which are

α = 60%, τ = 3, number of clusters = 4 and the window

size to 120. We notice from Figure 1 that as the

density



of subsequences in the clusters decreases,

which means the range [value1, value2] increases, the

purity of clusters decreases. This is expected as bigger

ranges make the clusters sparse, which cause clusters

to overlap. When clusters are sparse, the possibility

of false-positive subsequences to become members of

clusters increases.

In Figure 2, the performance of the ISsC is

assessed by measuring the data arrival rate r as we

modify the size of window buffers. During this

experiment, we fixed the other parameters at α = 50%,

τ = 3, number of clusters = 4 and the density



= 1.5.

Thus, in Figure 2, we measure the effect of modifying

the size of the window on the maximum speed of r at

which the ISsC algorithm can still process and

discover the intended clusters from the multiple data

streams. Note that the bigger the window size, the

slower the ISsC, which means the slower the required

Figure 1: Effect of cluster density  on total purity

Figure 2: Effect of the size of w on r

Another parameter that affects the ISsC

performance is the support threshold τ. In Figure 3,

we measure the maximum speed of the data arrival

rate r as we increase the value of τ. The other

parameters are set at α = 50%,



= 1.5, number of

clusters = 4, and w = 120. In this experiment, which

is shown in Figure 3, we compare two versions of

ISsC: applying the Monotonicity Property (MP) in

one and without MP in the other. The behaviour of

both versions is that r decreases as τ increases since

less number of subsequences will be selected to be

processed. Note that the ISsC algorithm (with MP)

can deal with faster r.

Similarly, in Figure 4 we measure the effect of the

number of clusters on the performance of ISsC

(required speed of r) using the two versions of ISsC

as in Figure 3. In this experiment, we set  = 1.5, τ =

3, w = 120, and α = 50%. For the ISsC algorithm (with

monotonicity property, MP), the performance

improves (required r decreases) as we increase the

number of clusters. That is because the infrequent

subsequences are skipped when using the

monotonicity property. That is, the ISsC algorithm

tolerates high r of data streams.

0,2

0,4

0,6

0,8

0,5 1 2 4 6 8 10

TotalPurity

ClusterDensity

100

200

300

400

60 120 180 240 300 360

ArrivalRate(ms)

WindowSize

Incremental Subsequence Clustering Algorithm from Multiple Data Streams

Figure 3: Effect of the support threshold on τ.

Figure 4: Effect of the number of clusters on r.

5 CONCLUSION

The proposed ISsC is an incremental algorithm that

discovers clusters in multiple data streams. By using

the monotonicity property, the ISsC reduces the

number of processed subsequences. That is by

excluding the non-frequent subsets, which do not

contribute to finding the clusters of subsequences

(non-frequent subsequences). By employing a decay

factor of subsequences, the ISsC can remove older

uninteresting subsequences. We noticed that, as the

cluster density is increased, the total purity of

clustering improved. Moreover, we noted that using

the monotonicity property improved the performance

over not using this property.

REFERENCES

Al Aghbari, Z., Kamel, I., & Awad, T. (2012). On clustering

large number of data streams. Intelligent Data Analysis,

16(1), 69-91.

Islam, M. K., Ahmed, M. M., & Zamli, K. Z. (2019). A

buffer-based online clustering for evolving data stream.

Information Sciences, 489, 113-135.

Tareq, M., Sundararajan, E. A., Mohd, M., & Sani, N. S.

(2020). Online Clustering of Evolving Data Streams

Using a Density Grid-Based Method. IEEE Access, 8,

166472-166490.

Alkouz, B., Al Aghbari, Z., & Abawajy, J. H. (2019).

Tweetluenza: Predicting flu trends from twitter data.

Big Data Mining and Analytics, 2(4), 273-287.

Al Aghbari, Z., Khedr, A. M., Osamy, W., Arif, I., &

Agrawal, D. P. (2019). Routing in wireless sensor

networks using optimization techniques: A survey.

Wireless Personal Communications, 1-28.

Ester M., Kriegel H.-P., Sander J., Xu X.: “A Density-

Based Algorithm for Discovering Clusters in Large

Spatial Databases with Noise”, KDD, 1996, vol. 96, no.

34, 226–231.

Cao F., Estert M., Qian W., and Zhou A., ‘‘Density-based

clustering over an evolving data stream with noise,’’ in

Proc. SIAM Int. Conf. Data Mining, Apr. 2006, 328–

339.

Aggarwal C. C., Han J., Wang J., and Yu P. S., ‘‘A

framework for clustering evolving data streams,’’ in

Proc. 29th Int. Conf. Very Large Data Bases, 29, 2003,

81–92

Kranen, P., Assent, I., Baldauf, C., & Seidl, T. (2011). The

ClusTree: indexing micro-clusters for anytime stream

mining. Knowledge and information systems, 29(2),

249-272.

Al-Shammari, A., Zhou, R., Naseriparsaa, M., & Liu, C.

(2019). An effective density-based clustering and

dynamic maintenance framework for evolving medical

data streams. International journal of medical

informatics, 126, 176-186.

Gong, S., Zhang, Y., & Yu, G. (2017). Clustering stream

data by exploring the evolution of density mountain.

Proceedings of the VLDB Endowment, 11(4), 393-405.

Zoumpatianos, K., Idreos, S., & Palpanas, T. (2014, June).

Indexing for interactive exploration of big data series.

In Proceedings of the 2014 ACM SIGMOD

international conference on Management of data (pp.

1555-1566).

Matsubara, Y., Sakurai, Y., Ueda, N., & Yoshikawa, M.

(2014, December). Fast and exact monitoring of co-

evolving data streams. In 2014 IEEE International

Conference on Data Mining (pp. 390-399). IEEE.

Keogh, E., & Lin, J. (2005). Clustering of time-series

subsequences is meaningless: implications for previous

and future research. Knowledge and information

systems, 8(2), 154-177.

Al Aghbari, Z., Kamel, I., & Elbaroni, W. (2013). Energy-

efficient distributed wireless sensor network scheme for

cluster detection. International Journal of Parallel,

Emergent and Distributed Systems, 28(1), 1-28.

Alkouz, B., & Al Aghbari, Z. (2020). SNSJam: Road traffic

analysis and prediction by fusing data from multiple

social networks. Information Processing &

Management, 57(1), 102139.

Dinges, L., Al-Hamadi, A., Elzobi, M., Al Aghbari, Z., &

Mustafa, H. (2011). Offline automatic segmentation

based recognition of handwritten Arabic words.

International Journal of Signal Processing, Image

Processing and Pattern Recognition, 4(4), 131-143.

23456

ArrivalRate(ms)

SupportThreshold

withMP

withoutMP

246810

ArrivalRate(ms)

NumberofClusters

withMP

withoutMP

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)