Lattice Boltzmann Simulation of the Three-dimensional Natural
Convection with a Regularly Heated Cavity Slab
El Bachir Lahmer
1a
, Jaouad Benhamou
1
, Youssef Admi
1b
, Mohammed Amine Moussaoui
1
,
Mohammed Jami
1
and Ahmed Mezrhab
1
1
Mechanics & Energetics Laboratory, Faculty of Sciences, Mohammed First University, 60000 Oujda, Morocco.
Keywords: Lattice Boltzmann Method, Heated Cavity, Cubical cavity, Nusselt Number Calculation, Heat Transfer,
LBM-MRT.
Abstract: In this paper, the Lattice Boltzmann method (LBM) associated with the Multi-Relaxation Times (MRT) is
performed to investigate the three-dimensional (3D) natural convection of the air in a cubical cavity for
various values of the Rayleigh number ranged between 10
3
<Ra<10
5
. The main 3D-LBM-MRT code was
compared and validated with the experimental and numerical work for different cases. The main objective of
this work is to analyze the heat transfer between the two cold vertical walls and the hot cavity base by using
the D3Q7 model for thermal field, and the evolution of the velocity field employing the D3Q19 model.
Furthermore, the effects of the conjugate heat transfer also take into consideration to investigate the heat
transfer rate by using different values of the thermal conductivity.
1 INTRODUCTION
The natural convection in a cubical cavity within a
heat generation source is commonly used to
investigate the fluid flow and heat transfer
enhancement for the various fields. This prototype
system is considered one of the main subjects of many
researchers because of its privileges in many
industrial and engineering applications related to the
thermal insulation of buildings, cooling the electronic
chips, etc. (Admi, 2020; Li, 2019). The study of
natural convection heat transfer using a three-
dimensional for complex configuration presents a
great challenge to understand the mechanism and the
behavior of the flow of fluid and heat transfer from
numerical simulations related to real physical
problems. Time and cost for experimental studies are
some of the main problems which oriented most
researchers to find alternative solutions to reduce the
time and lack of the experimental equipment. The
numerical simulation enables to solve concrete
problems masterly and efficiently, where it offers
valuable solutions by providing a clear view of
complex systems.
a
https://orcid.org/0000-0001-5435-1429
b
https://orcid.org/0000-0003-0920-0618
In this context, the lattice Boltzmann method
(LBM), as a numerical simulation, allows to
describing the fluid behavior and the heat transfer
using different models. Moussaoui et al. (Moussaoui,
2019) analyzed the effect of the Rayleigh number of
two-dimensional heated obstacle inside a square
enclosure by using the double MRT-LBM, they
conclude that the increase of obstacle dimension
enhances the heat transfer by increasing the surface
exchange. The recirculation zone loses its symmetric
when the position of the heated obstacle varied, and
the isotherm field also disturbs because of this
variation in the local heating. Chavez-Modena et al.
(Chávez-Modena, 2020) realized the under-resolved
turbulent flow simulation using the D3Q19 model
with multi-relaxation time with the central moment.
They interpret that the model used to obtain a
satisfactory result compared with the results BGK and
MRT-CM model for the under-resolved systems.
Wang et al. (Wang, 2017) performed a numerical
investigation of a three-dimensional heated cubical
cavity for a high Rayleigh number. This study focuses
on the evolution of the heat transfer and fluid
behavior inside the differential heated cavity, where
Lahmer, E., Benhamou, J., Admi, Y., Moussaoui, M., Jami, M. and Mezrhab, A.
Lattice Boltzmann Simulation of the Three-dimensional Natural Convection with a Regularly Heated Cavity Slab.
DOI: 10.5220/0010730500003101
In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 175-180
ISBN: 978-989-758-559-3
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
175

the obtained numerical results conclude that the
thermal and velocity contour formed close to the
adiabatic walls, and the thickness of the contour
layers narrowness near these walls for high values of
Rayleigh number. Liu et al. (Liu, 2019) also
investigate 3D convection heat transfer in porous
media at the REV scale. They found that the model
employed for studying the porous channel is suitable
to investigate the heat transfer and the fluid flow.
The present work was performed to analyze the
heated cavity slab with different values of thermal
conductivity which is related to the nature and
thickness of the heating source.
2 NUMERICAL STATEMENT
DETAILS
2.1 Configuration System
The configuration system studied is a cubical cavity
consist of two vertical cold walls and a heated floor
as shown in Figure 1. The cavity base undergoes a
dimensionless temperature T
h
=1 according to
different values of the thermal conductivity (Ks).
While the cold surfaces kept fixed cold dimensionless
temperatures Tc=0. The front, rear, and top cavity
surfaces are insulated. The thickness of the cavity
base characterized by a different thermal conductivity
(ks) compared to the thermal conductivity of the
airflow (kf). The continuity of the temperature and
heat flux is taken into account for the interface
solid/fluid (See Figure 1).
Figure 1: 3D Geometry system of a cubical cavity.
2.2 Discrete Numerical Model
In this study, The Natural convection of the air in a
cubical cavity was performed using the three-
dimensional lattice Boltzmann method including the
D3Q19 and D3Q7 model to define the velocity and
the thermal field (Liu, 2019; Wang, 2017),
respectively as illustrate in Figure 2.
Figure 2: a) Discrete Velocities for D3Q19 model b)
discrete temperature for D3Q7 model.
The above figure describes the nineteen discrete
speeds for the D3Q19 model
⟨
𝑒

|
𝑖0,….,18
⟩
such
as the speed coordinate was proposed as below:
𝑒

𝑐
0 1 1 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0
0 0 0 1 1 0 0 1 1 1 1 0 0 0 0 1 1 1 1
0 0 0 0 0 1 1 0 0 0 0 1 1 1 1 1 1 1 1

(1)
The quantity c considers the lattice speed related
to the speed of sound where:
𝑐

3𝑐


(2)
Furthermore, the seven discrete speed was
proposed for this investigation for the D3Q7 scheme
where the temperature direction is correspondent to
seven speed direction of the D3Q19 scheme (Liu,
2019).
2.3 Numerical Approach
Recently, the lattice Boltzmann method associated
with multi-relaxation times (LBM-MRT) consider
one of the powerful numerical estimation to describe
the physics phenomena, the precision, and the
simplicity of the implementation in the code allows to
define of most physics and engineering problem for
various complex geometries. This approach makes it
possible to found satisfactory results with a reduced
computation time and for weak grids compared with
the other numerical approaches.
The lattice Boltzmann equation (LBE) defines
two main parts: the propagation and the collision
process of the fluid popularity, such that the study of
complete fluid is done in such a way that the fluid
discretized into a finite set of particles, namely the
distribution function or the probability of finding a
group of particles in a position x
i
with velocity e
i
at
time t (Lahmer, 2019; Admi, 2020; Li, 2019;
Moussaoui, 2017).
BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)
176

2.3.1 Lattice Boltzmann Equation for the
Flow Field
The LBM-MRT equation related to the D3Q19 model
for the velocity field is expressed as follows:
𝒇

𝒙𝒆𝒊 ∆𝒕,𝒕

𝒇

𝒙,𝒕

𝑴
𝟏
𝑺

𝒎

𝒙,𝒕

𝒎
𝒆𝒒

𝒙,𝒕


𝑭
(3)
Where M and S denote the 19×19 transformation
matrix and the relaxation matrix, respectively, which
is related to the moment m and the equilibrium
moment m
eq
. The quantity F is the body force related
to the gravity aspect.
The numerical resolution of this equation makes it
possible to describe the fluid flow behavior from the
macroscopic quantities (Lahmer, 2019).
2.3.2 Lattice Boltzmann Equation for the
Thermal Field
The thermal LBE-MRT equation is adopted to
simulate the temperature field using the D3Q7 model
as shown in the following expression:
𝒈

𝒙𝒆𝒊 ∆𝒕,𝒕

𝒈

𝒙,𝒕

𝑵
𝟏
𝑸

𝒏

𝒙,𝒕

𝒏
𝒆𝒒

𝒙,𝒕


(4)
The quantities N and Q define the 7×7
transformation matrix and the relaxation matrix,
respectively. During the numerical computation, the
data obtained from the thermal Boltzmann equation
allow modelling the temperature field at each point of
the computation domain. This process was performed
by the transformation of obtained data to macroscopic
quantities which is the temperature.
All the parameters used for this study have been
presented in detail in the reference (Liu, 2019; Wang,
2017).
2.4 Boundary Conditions
2.4.1 Velocity Boundary Condition
The boundary conditions used in the numerical
calculation procedure correspond to the Boltzmann
equation considered as conditions easy to implement
in the calculation code.
Regarding the fluid flow, the “bounce-back”
scheme was employed to describe the cavity walls as
shown in the expression below:
𝑓


𝑥,𝑦,𝑧

𝑓

̃

𝑥,𝑦,𝑧

𝑖0,…,18 (5)
Where i denotes the direction of the discrete
velocity, and 

defines the opposite speed direction.
The positions x, y, and z describe the position of each
cubical cavity walls.
2.4.2 Thermal Boundary Condition
For the thermal problem, the boundary conditions
adopted to define the cold and hot walls which are
expressed by the equation related to the macroscopic
quantity:
𝑇
∑
𝑔



(6)
From the equation above, the boundary conditions
can be expressed for the hot bottom wall and the cold
vertical walls by the following expressions:
⎩
⎪
⎨
⎪
⎧
𝑧0 → 𝑔


𝑥,𝑦

𝑇


∑
𝑔




𝑦0 → 𝑔


𝑥,𝑧

𝑇


∑
𝑔




𝑔


𝑥,𝑧

𝑇


∑
𝑔




(7)
Concerning the adiabatic walls, Neumann
Boundary Condition was executed by the following
expressions:

𝑧𝐻
→ 𝑔


𝑥,𝑦

𝑔


𝑥,𝑦

𝑥0
→ 𝑔


𝑦,𝑧

𝑔


𝑦,𝑧

𝑥𝐻
→ 𝑔


𝑦,𝑧

𝑔


𝑦,𝑧

(8)
3 VALIDATION AND
NUMERICAL RESULTS
To cognize the consistency and accuracy of our
simulation code, we executed Intensive studies in
order to know that the current code used is more
suitable for studying the fluid flow and convective
heat transfer in various geometries.
3.1 Validation Code for Double
MRT-LBM
In this context, the developed code is compared to the
literature results (Corvaro, 2008). The first
comparison was made with the experimental results
of the isotherm and velocity contour obtained by
Corvaro and Paroncini. The results showed a good
agreement with the reference (Corvaro, 2008) for
Rayleigh number equal Ra=2.02×10
5
and δ=0.5. (See
Figures 3 and 4). The interest of studying the Ra
number is to characterize the heat transfer within a
fluid during its flow.
Lattice Boltzmann Simulation of the Three-dimensional Natural Convection with a Regularly Heated Cavity Slab
177

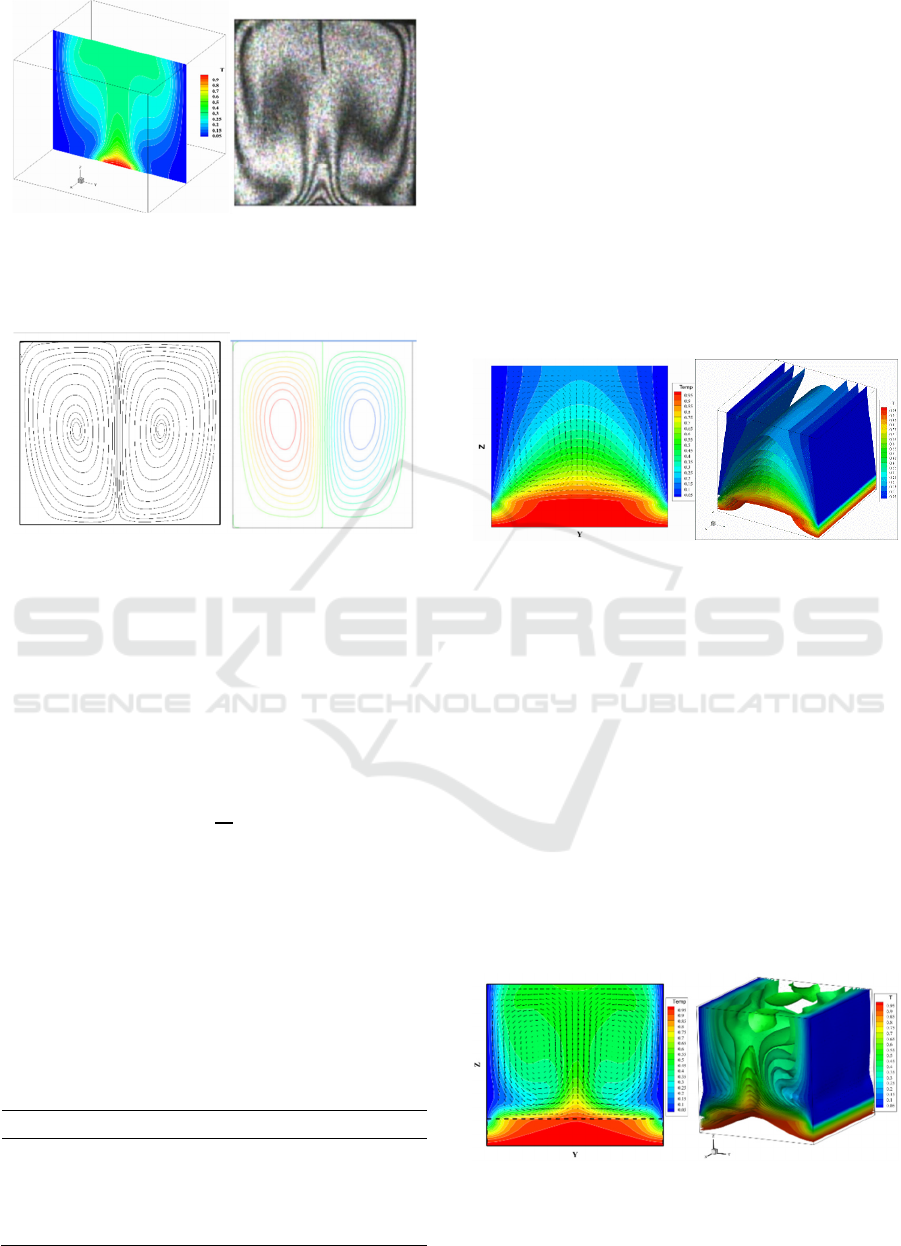
Figure 3: Comparison between the 3D and 2D projection of
LBM-MRT simulation result, and the experimental
measurement using the double-exposure interferogram
(Corvaro, 2008) For Ra=2.02×10
5
, δ=0.5.
Figure 4: Comparison study between the 3D projection of
LBM-MRT simulation results, and the numerical
simulation of the streamline For Ra=2×10
5
, δ=0.5.
To reinforce the reliability of our simulation code,
the Nusselt number is carried out for different values
of the Rayleigh number where δ=0.5. Note that the
role of the Nusselt number is to characterize the
nature of thermal transfer involved between the hot
cavity base and the two vertical cold walls as shown
in the expression below:
𝑁𝑢𝐿




|

(9)
Where Lc denotes the characteristic length
correspond to the heated part of the cubical cavity.
The experimental and numerical results obtained by
the literature (Corvaro, 2008) are converged towards
the results obtained by the numerical simulation
carried out by the double MRT-LBM as illustrate in
Table 1.
Table 1: Comparison of the average Nusselt number
between the experimental (Corvaro,2008) and numerical
results for δ=0.5.
Ra Nu (exp) Nu (num)
|∆|[%]
1.71E+05 6.3 6.306 0.095
1.98E+05 6.45 6.488 0.59
2.32E+05 6.65 6.697 0.70
2.50E+05 6.81 6.8 0.15
Furthermore, the maximum deviation of each
average Nusselt number results under 1%. Therefore,
the code used in the current study able to make
numerical simulations that correspond to real physical
problems of the fluid flow and thermal transfer.
3.2 Results and Discussion
Isotherm contours, velocity fields, and average
Nusselt number for different values of the thermal
conductivity ratio (Kr=K
s
/Kf) and Rayleigh number
are investigated in this section. The objective
proposed in this study is the analysis of the heat
transfer evolution by the air cooling of the electronic
equipment inside a cubical box.
Figure 5: 2D projection for isotherms, velocity field and the
3D isosurfaces temperature for Ra=3.10
3
, Kr=10.
Figures 5 and 6 present the evolution of the fluid
flow and heat transfer by natural convection for two
different values of Rayleigh number with fixed
thermal conductivity ratio. The results show that the
energy transport increase promptly upwards of the
cavity such that the fluid flows symmetrically relative
to the cavity mid-length. Two recirculation zone
appear clockwise and anticlockwise. Furthermore,
the isotherms field evolves symmetrically where the
heat transfer enhances in the left and right of the cold
cavity walls. This explains that the fluid flow and
convective heat transfer behavior refer to the thermal
exchange between the cold walls and the heated slab,
where the magnitude of heat transfer more enhanced
at the two corners of the cavity slab.
Figure 6: 2D projection of isotherm and velocity pattern,
and 3D isosurface of the thermal field for Ra=5.10
5
, Kr=10.
BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)
178

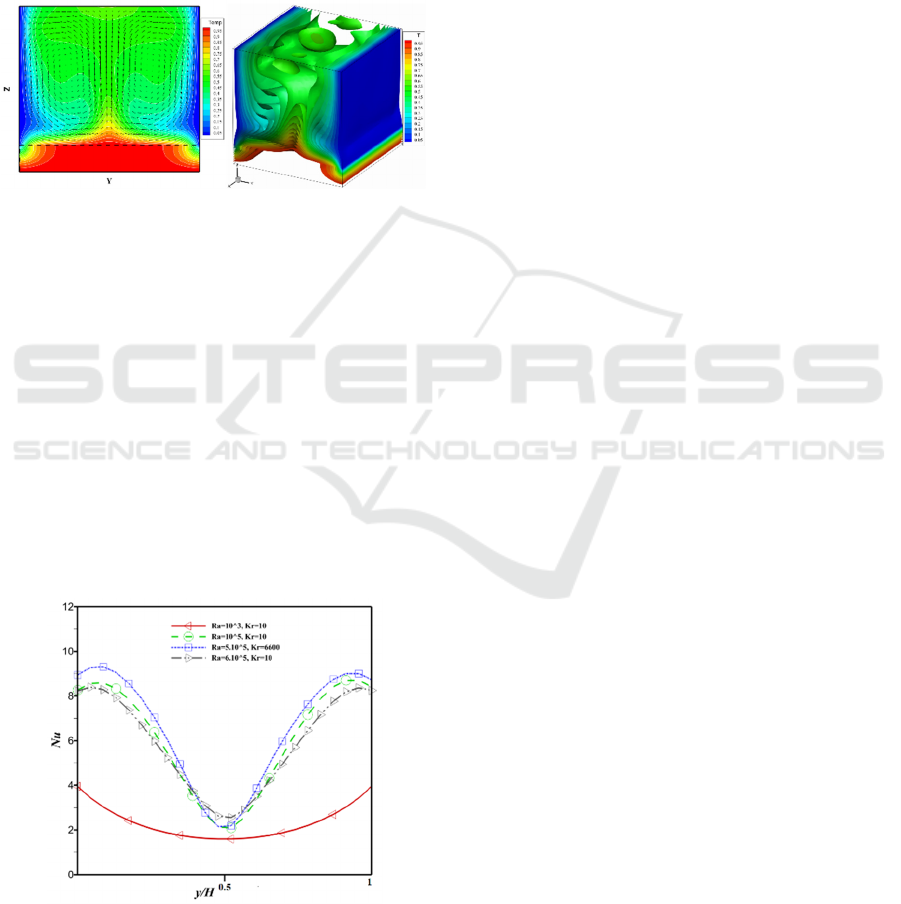
The evaluation of the thermal transfer and fluid
flow was also investigated for two various values of
thermal conductivity ratio (Kr=10 and Kr=6600) with
fixed Ra. As shown in Figures 6 and 7, the slab
became almost isothermal as the thermal conductivity
ratio increases. In addition, the energy transport of the
heated air near the slab propagates rapidly upward of
the cavity. The presence of the cold walls in the
vicinity of the heated base provokes an efficient
cooling compared with the center of the heated slab.
Figure 7: 2D projection of isotherm and velocity pattern,
and 3D isosurface of thermal field for Ra=5.10
5
, Kr=6600.
To understand substantially the mechanisms of
heat transfer involved in this work, the local Nusselt
number evolution was realized for several values of
Ra and Kr for the heated cavity base (see Figure 8).
The thermal exchange increases as Ra increases from
3.10
3
to 5.10
5
. While the heat exchange reduced from
5.10
5
to 6.10
5
. This diminishes of the Nu refers to the
fact that the fluid receives more heat through
convective heat transfer, and the buoyancy forces
increase, and in turn, thermal boundary layer
thickness near the hot wall decreases. In order to
enhance the heat transfer in this case, for a high
thermal conductivity ratio, the heat exchange
improves for Ra=5×10
5
, Kr=6600.
Figure 8: Local Nusselt number evolution.
4 CONCLUSION
In this work, the examination of the three-
dimensional natural convection heat transfer with a
regularly heats cubical cavity slab is illustrated. The
results obtained using the double MRT-LBM method
had a good agreement with the experimental
investigation which gives credibility to our
simulation code. To achieve the perfect cooling of
electronic components whatever its nature in a
cubical enclosure, one can reconsider that the effects
of introducing a large Rayleigh number provoke a
decrease in heat exchange if it exceeds the critical
point which is equal to 6.10
5
. On the other hand, the
increase in thermal conductivity considers a strong
point to reinforce the heat exchange for the case
where the high Rayleigh number.
REFERENCES
Admi, Y.., MOUSSAOUI, M.A. and MEZRHAB, A., 2020,
December. Effect of a flat plate on heat transfer and
flow past a three side-by-side square cylinders using
double MRT-lattice Boltzmann method. In 2020 IEEE
2nd International Conference on Electronics, Control,
Optimization and Computer Science (ICECOCS) (pp.
1-5). IEEE.
Chávez-Modena, M., Martínez-Cava, A., Rubio, G. and
Ferrer, E., 2020. Optimizing free parameters in the
D3Q19 Multiple-Relaxation lattice Boltzmann methods
to simulate under-resolved turbulent flows. Journal of
Computational Science, 45, p.101170.
Corvaro, F., Paroncini, M.,2008, A numerical and
experimental analysis on the natural convective heat
transfer of a small heating strip located on the floor of
a square cavity, Applied Thermal Engineering, Volume
28.
Lahmer, E.B., Moussaoui, M.A. and Mezrhab, A., 2019,
April. Investigation of laminar flow and convective
heat transfer in a constricted channel based on double
MRT-LBM. In 2019 International Conference on
Wireless Technologies, Embedded and Intelligent
Systems (WITS) (pp. 1-6). IEEE.
Li, Z., Yang, M. and Zhang, Y., 2019. Hybrid LBM-FVM
and LBM-MCM Methods for Fluid Flow and Heat
Transfer Simulation. arXiv preprint arXiv:1908.08386.
Liu, Q., Feng, X.B., He, Y.L., Lu, C.W. and Gu, Q.H., 2019.
Three-dimensional multiple-relaxation-time lattice
Boltzmann models for single-phase and solid-liquid
phase-change heat transfer in porous media at the REV
scale. Applied Thermal Engineering, 152, pp.319-337.
Moussaoui, M.A., Lahmer, E.B., Admi, Y. and Mezrhab,
A., 2019, April. Natural convection heat transfer in a
square enclosure with an inside hot block. In 2019
International Conference on Wireless Technologies,
Lattice Boltzmann Simulation of the Three-dimensional Natural Convection with a Regularly Heated Cavity Slab
179

Embedded and Intelligent Systems (WITS) (pp. 1-6).
IEEE.
Wang, P., Zhang, Y. and Guo, Z., 2017. Numerical study of
three-dimensional natural convection in a cubical
cavity at high Rayleigh numbers. International Journal
of Heat and Mass Transfer, 113, pp.217-228.
BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)
180