Deep Neural Networks for Forecasting Build Energy Load

Chaymae Makri

, Said Guedira

, Imad El Harraki

and Soumia El Hani

Team of Energy Optimization, Diagnostics and Control, National School of Arts and Crafts of Rabat, Morocco

Laboratory of Control, Piloting and Monitoring of Electrical Energy, National Higher School of Mines of Rabat, Morocco

Laboratory of Applied Mathematics and Business Intelligence, National Higher School of Mines of Rabat, Morocco

Keywords: Energy consumption prediction, residential sector, deep learning, long short-term memory (LSTM).

Abstract: The consumption of electric power is progressing rapidly with the increase in the human population and

technology development. Therefore, for a stable power supply, accurate prediction of power consumption is

essential. In recent years, deep neural networks have been one of the main tools in developing methods for

predicting energy consumption. This paper aims to propose a method for predicting energy demand in the

case of the residential sector. This method uses a deep learning algorithm based on long short-term memory

(LSTM). We applied the built model to the electricity consumption data of a house. To evaluate the proposed

approach, we compared the performance of the prediction results with Multilayer Perceptron, Recurrent

Neural Network, and other methods. The experimental results demonstrate that the proposed method has

higher prediction performance and excellent generalization capability.

1 INTRODUCTION

Electric energy consumption accelerating with

economic and demographic growth (Zhao et al.,

2017). International Energy Agency (IEA) published,

according to the World Energy Outlook 2017, that the

world energy consumption rises 28% between 2015

and 2040 (T.-Y. Kim & Cho, 2019b). In addition,

energy consumption increases over the projection for

all fuels (World Energy Outlook 2017 – Analysis, s.

d.). The residential sector is a large consumer of

electrical energy, as it exceeds 27% of global energy

consumption. (Nejat et al., 2015). The production and

consumption of electrical power must be

simultaneously due to its characteristics and its

storage (He, 2017). So, to have a steady supply of

electricity, an efficient forecast of the demand for

electric power is required.

In (Son & Kim, 2020), the authors use a model

based on LSTM to forecast monthly consumption

energy in the residential sector. The authors of

(Wang et al., 2020) are exploited the LSTM method

after a well-determined pre-processing process on the

industrial sector data.

Several models are designed and validated by

using the same database called “Individual household

electricity consumption” to forecast energy

consumption. In (T.-Y. Kim & Cho, 2019a), the

authors associated the CNN (convolutional neural

networks) with LSTM to forecast this electricity

consumption. In (J.-Y. Kim & Cho, 2019), the

proposed model is the combination of RNN (recurrent

neural networks) and LSTM. In (Marino et al., 2016),

the presented method is based on the LSTM auto-

encoder (LSTM-AE). In (Le et al., 2019), the authors

have combined two types of neural networks, CNN,

and bidirectional LSTM (Bi-LSTM). In (Khan et al.,

2020), the authors have formed their models by CNN

and LSTM-AE. We can conclude that all five models

give acceptable results; however, our goal is to

improve this result.

In this paper, we exploit the deep learning

technique for robust forecasting of energy

consumption in the residential sector. The

methodology presented is based on the algorithm of

short-term memory. The model built is tested on the

same benchmark data for a single residential

customer with a one-minute time resolution.

The paper is organized as follows. Section II gives

a general presentation on LSTM algorithms. Section

III shows the methodology used for forecasting

energy demand using LSTM. Section IV explains the

data and presents the experimental results. Section VI

concludes the document.

306

Makri, C., Guedira, S., El Harraki, I. and El Hani, S.

Deep Neural Networks for Forecasting Build Energy Load.

DOI: 10.5220/0010733100003101

In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 306-310

ISBN: 978-989-758-559-3

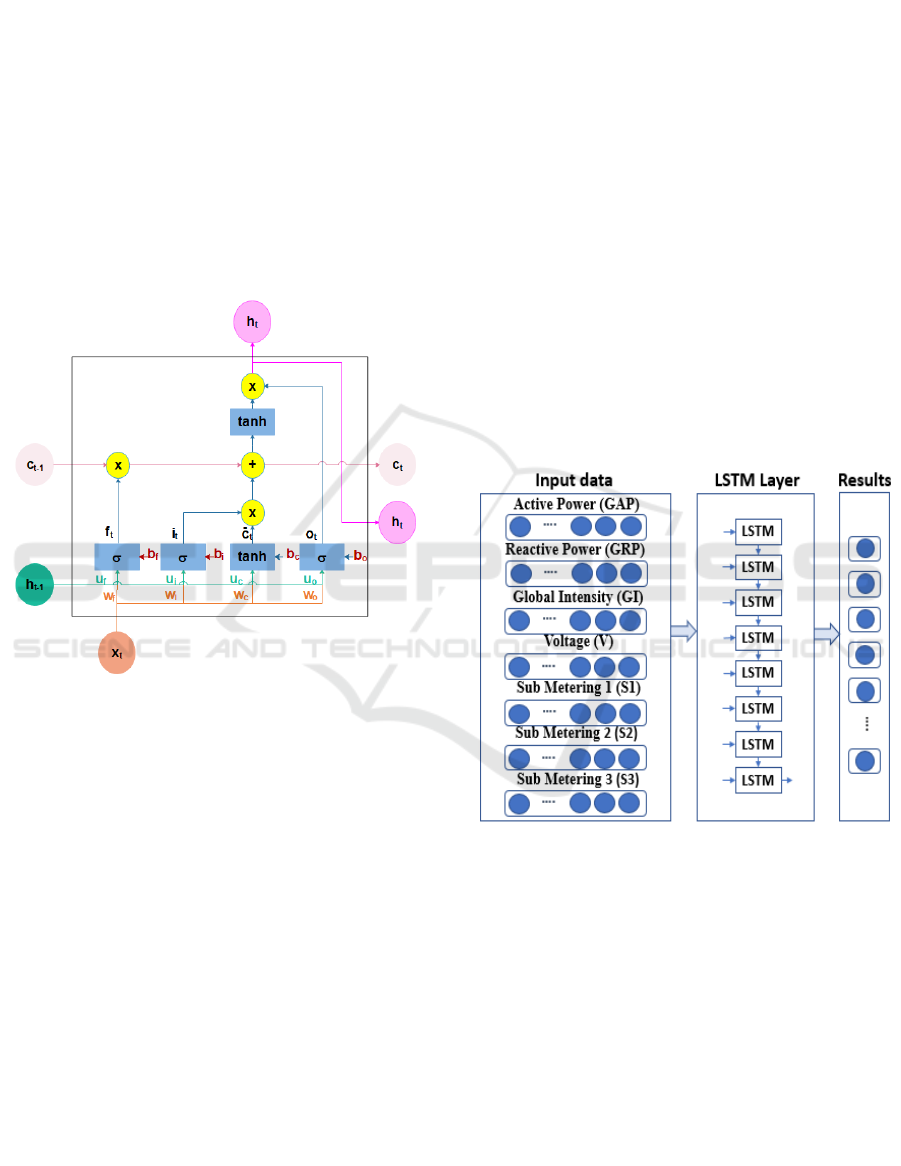
2 LSTM

Recurrent neural networks (RNNs) give the vanishing

gradient problem regardless of the learning algorithm

used, either the Backpropagation algorithm in time or

the real-time recurrent learning algorithm (Taylor et

al., s. d.; Werbos, 1990). Long and short-term

memories (LSTM) are improved recurrent neural

networks (Hochreiter & Schmidhuber, 1997). This

type of network makes it possible to remedy the

vanishing gradient problem and memorize

information for long periods (Marino et al., 2016). An

LSTM network is made up of three gates and a cell,

as shown in Figure 1. The equations (1) – (6) present

the inner workings of a single LSTM cell.

Figure 1: LSTM cell.

= σ



t-1



(1)

= σ



t-1



(2)



=tanh



t-1



3)

= f

t-1



(4)

= σ



t-1



(5)

= o

*tanh (C

) (6)

Where i



, f



, and o



are the input gate, forget gate,

and output gate, respectively. C

is cell state and C





represents candidate cell state. w







,and w



are

weight matrices of the forgetting

gate, the input gate,

the memory cell, and the output gate

respectively. u







,and u



the recurrent

connections of the forgetting gate, the input gate, the

memory cell, and the output gate, respectively.







,and b



are bias vectors of the forgetting

gate, the input gate, the memory cell, and the output

gate, respectively. x



is the current input. h



and h



are the outputs at the present time t and the previous

time t-1, respectively (Zhang et al., 2018).

The role of the input gate is to extract information

from the current data. The forge gate makes it

possible to decide which data should be kept or not.

The output gate its role is to extract the valuable

information for the prediction. The operation of the

three doors is similar. If we take the forget gate, in the

case of the value 𝑓



is close to zero, the information

will be forgotten.

3 LOAD FORECASTING USING

LSTM

This section presents the load forecasting

methodology based on LSTM networks. Figure 2

illustrates the proposed architecture for the electrical

load forecast.

Figure 2: The overview architecture of the LSTM model.

This methodology aims to forecast the global

active power for a time step or several time steps in

the future, considering the historical data of electrical

load. We can be expressed the N available active

power measurements as follow:

h = h

,…,h



Where h is the measurement of the actual load for

the time step t, the predicted load values for the

subsequent time steps 𝑇 - N can be expressed as

follows:

Deep Neural Networks for Forecasting Build Energy Load

307



= h



N+1



N+2

,…,h





As shown in figure 2, to forecast active power for

60 minutes, we use the active power, the reactive

power, the current, the voltage, 𝑆



, 𝑆



, and 𝑆



for the

previous 60 minutes as inputs for the model. We can

be formulated the input matrix as follows:

x =

⎣

⎢

⎡

GAP

1

GRP

-1

... S2

-1

1

GAP

2

GRP

2

... S2

-2

. . . ... . .

GAP

-60

GRP

60

... S2

-60

⎦

⎥

⎤

(7)

The resulting network is a very deep lattice, so to

alleviate the problem of gradient disappearance, we

used the ADAM (Adaptive Moment Estimation)

optimizer (Kingma & Ba, 2017). We can be presented

the minimize loss function as follows:

J =

(h

-h



)²

i=1

(8)

4 DATA AND EXPERIMENTAL

RESULT

4.1 Data

To test and validate the proposed model, we used the

data collected over four years, from 16th of December

2006, until 26th of November, 2010, in a house in

France (Household Electric Power Consumptions.

d.), named “Individual household electric power

consumption”. The data contained 2,075,259

measurements with a resolution of one minute. The

collected variables encompassing the time variables

include day, month, year, hour, and minute. The

variables assembled from sensors include global

active power (GAP), global reactive power (GRP),

global intensity (GI), voltage (V), sub_metering 1

(𝑆



) for the kitchen, sub_metering 2 (𝑆



) for the

laundry room, and sub_metering 3 (𝑆



) for the electric

water heater and air conditioner (T.-Y. Kim & Cho,

2019a).

4.2 Experimental Results

The proposed model consists of planning the

following 60 minutes by introducing 60 minutes of

measurements. During the test, a set of data not used

during training should be used. Therefore, we must

divide the data into two parts, the first part for training

the model and the other for testing.

We evaluate the proposed model by comparing

the performance of the prediction results with Multi-

layer Perceptron (Hamedmoghadam et al., s. d.), the

recurrent neural network (Cho et al., 2014) and the

models used in (Khan et al., 2020; J.-Y. Kim & Ch

o, 2019; T.-Y. Kim & Cho, 2019a; Le et al., 2019;

Marino et al., 2016). Figure 3 shows the actual

demand and the forecasted energy demand results for

the different models. From the figure, we can see that

the models based on LSTM and MPL perform well

the forecast compared to RNN.

The performance measures to evaluate the

models are MSE, RMSE and MAE, which can be

expressed as follows:

MSE =

(y

i=1

-y

)²

(9)

𝑅𝑀𝑆𝐸



(y

i=1

-y

)²

(10)

MAE =

y

-y



i=1

(11)

Where 𝑦



is the actual load value, 𝑦



is the

predicted load value, and N is the number of samples

(Huang & Wang, 2018).

Table 1 summarizes the performance of the

different models used to test the capacity of the

proposed model. We can be concluded that the

electric load forecasting using the LSTM model has

better accuracy in each of the measures considered in

this study. These results demonstrate the ability of the

LSTM to predict accurately. Therefore, we can

conclude that model's accuracy

 is related to the

number of measurements taken as input.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

308

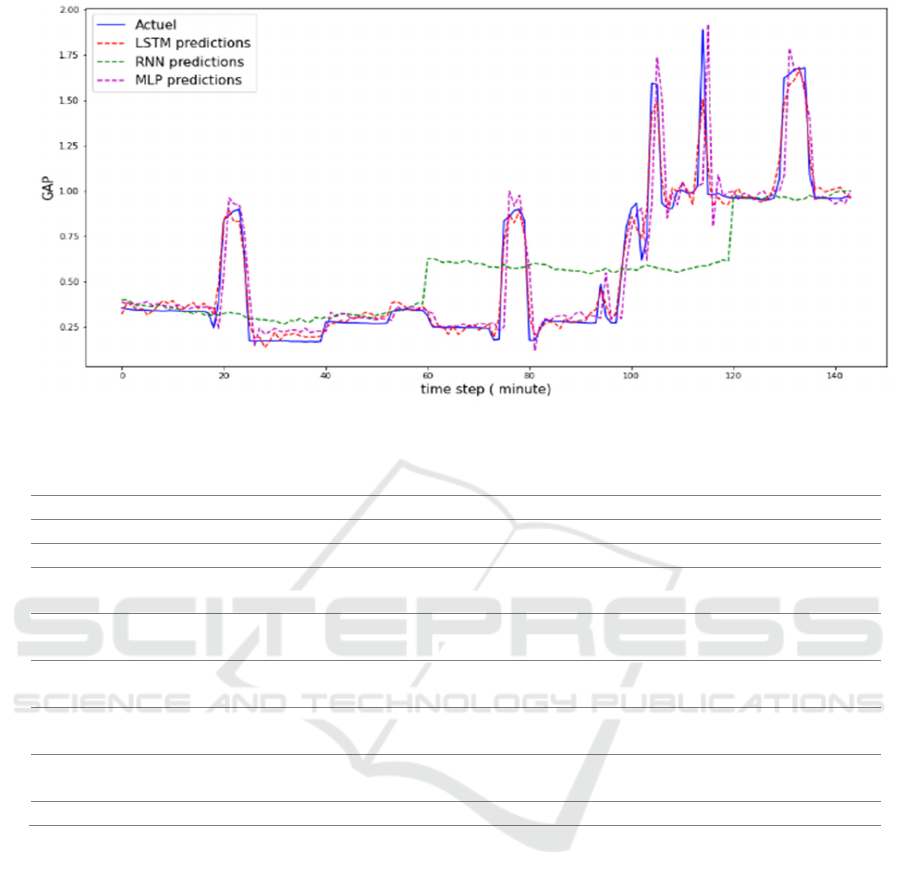
Figure 3: The predicted and actual electric energy consumption demand.

Table 1: The performance of the different models.

Method RMSE MSE MAE

MLP 0.1884 0.0355 0.0846

RNN 0.9396 0.8829 0.7281

Kim and Cho (J.-Y.

Kim & Cho, 2019)

0.3840 0.3953

Kim and Cho (T.-Y.

Kim & Cho, 2019a)

0.6114 0.3738 0.3493

Le et al. (Le et al.,

2019)

0.225 0.051 0.098

Marino et al. (Marino

et al., 2016)

0.667 - -

khan and al. (Khan et

al., 2020)

0.47 0.19 0.31

The proposed method 0.2941 0.0066 0.0482

5 CONCLUSION

The model based on deep neural networks has

demonstrated its efficiency in predicting the energy

load at the building level. This paper presented the

architecture of LSTM-based neural networks to

electricity load prediction. The model built was

trained and tested on data with a temporal resolution

of one minute. The proposed LSTM model has shown

its ability to accurately forecast power consumption

although its simple architecture. The model produced

results comparable to the results presented in (Khan

et al., 2020; J.-Y. Kim & Cho, 2019; T.-Y. Kim &

Cho, 2019a; Le et al., 2019; Marino et al., 2016) for

the same data. In addition, we can be reinforced the

proposed solution, either by adding other inputs such

as temperature, humidity electricity price, and time

variables or by improving deep learning algorithms.

REFERENCES

Cho, K., van Merrienboer, B., Gulcehre, C., Bahdanau, D.,

Bougares, F., Schwenk, H., & Bengio, Y. (2014).

Learning Phrase Representations using RNN Encoder-

Decoder for Statistical Machine Translation.

arXiv:1406.1078 [cs, stat].

http://arxiv.org/abs/1406.1078

Hamedmoghadam, H., Joorabloo, N., & Jalili, M. (s. d.).

Australia’s long-term electricity demand forecasting

using deep neural networks. 14.

Deep Neural Networks for Forecasting Build Energy Load

309

He, W. (2017). Load Forecasting via Deep Neural

Networks. Procedia Computer Science, 122, 308‑314.

https://doi.org/10.1016/j.procs.2017.11.374

Hochreiter, S., & Schmidhuber, J. (1997). Long Short-Term

Memory. Neural Computation, 9(8), 1735‑1780.

https://doi.org/10.1162/neco.1997.9.8.1735

Huang, L., & Wang, J. (2018). Global crude oil price

prediction and synchronization based accuracy

evaluation using random wavelet neural network.

Energy, 151, 875‑888.

https://doi.org/10.1016/j.energy.2018.03.099

Khan, Z., Hussain, T., Ullah, A., Rho, S., Lee, M., & Baik,

S. (2020). Towards Efficient Electricity Forecasting in

Residential and Commercial Buildings : A Novel

Hybrid CNN with a LSTM-AE based Framework.

Sensors, 20(5), 1399.

https://doi.org/10.3390/s20051399

Kim, J.-Y., & Cho, S.-B. (2019). Electric Energy

Consumption Prediction by Deep Learning with State

Explainable Autoencoder. Energies, 12(4), 739.

https://doi.org/10.3390/en12040739

Kim, T.-Y., & Cho, S.-B. (2019a). "Load Forecasting via

Deep Neural Networks. Energy, 182, 72‑81.

https://doi.org/10.1016/j.energy.2019.05.230

Kim, T.-Y., & Cho, S.-B. (2019b). Predicting residential

energy consumption using CNN-LSTM neural

networks. Energy, 182, 72‑81.

https://doi.org/10.1016/j.energy.2019.05.230

Le, T., Vo, M. T., Vo, B., Hwang, E., Rho, S., & Baik, S.

W. (2019). Improving Electric Energy Consumption

Prediction Using CNN and Bi-LSTM. Applied

Sciences, 9(20), 4237.

https://doi.org/10.3390/app9204237

Marino, D. L., Amarasinghe, K., & Manic, M. (2016).

Building energy load forecasting using Deep Neural

Networks. IECON 2016 - 42nd Annual Conference of

the IEEE Industrial Electronics Society, 7046‑7051.

https://doi.org/10.1109/IECON.2016.7793413

Nejat, P., Jomehzadeh, F., Taheri, M. M., Gohari, M., &

Abd. Majid, M. Z. (2015). A global review of energy

consumption, CO2 emissions and policy in the

residential sector (with an overview of the top ten CO2

emitting countries). Renewable and Sustainable Energy

Reviews, 43, 843‑862.

https://doi.org/10.1016/j.rser.2014.11.066

Son, H., & Kim, C. (2020). A Deep Learning Approach to

Forecasting Monthly Demand for Residential–Sector

Electricity. Sustainability, 12(8), 3103.

https://doi.org/10.3390/su12083103

Taylor, G. W., Hinton, G. E., & Roweis, S. T. (s. d.). Two

Distributed-State Models For Generating High-

Dimensional Time Series. 44.

Wang, J. Q., Du, Y., & Wang, J. (2020). LSTM based long-

term energy consumption prediction with periodicity.

Energy, 197, 117197.

https://doi.org/10.1016/j.energy.2020.117197

Werbos, P. J. (1990). Backpropagation through time : What

it does and how to do it. Proceedings of the IEEE,

78(10), 1550‑1560. https://doi.org/10.1109/5.58337

World Energy Outlook 2017 – Analysis. (s. d.). IEA.

Consulté 17 avril 2021, à l’adresse

https://www.iea.org/reports/world-energy-outlook-

2017

Zhang, Q., Liu, B., Zhou, F., Wang, Q., & Kong, J. (2018).

State-of-charge estimation method of lithium-ion

batteries based on long-short term memory network.

IOP Conference Series: Earth and Environmental

Science, 208, 012001. https://doi.org/10.1088/1755-

1315/208/1/012001

Zhao, G. Y., Liu, Z. Y., He, Y., Cao, H. J., & Guo, Y. B.

(2017). Energy consumption in machining :

Classification, prediction, and reduction strategy.

Energy, 133, 142‑157.

https://doi.org/10.1016/j.energy.2017.05.110

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

310