
Lattice Boltzmann Modelling of MHD Rayleigh-Bénard Convection
in a Square Cavity Filled with a Ferrofluid
K. Chtaibi
a
, M. Hasnaoui
b
, Y. Dahani
c
and A. Amahmid
d
LMFE, Department of Physics, Cadi Ayyad University, Faculty of Sciences Semlalia, B.P. 2390, Marrakesh, Morocco
Keywords: Rayleigh-Bénard Convection, Ferrofluid Fe
O
H
O, Magnetic Field, Square Cavity, Lattice Boltzmann
Method.
Abstract: In this study, heat transfer of ferrofluid Fe
O
H
O generated by Rayleigh-Bénard convection in a square
cavity is studied numerically in the presence of a vertical uniform magnetic field. The effect of the governing
parameters, such as the Rayleigh number (𝑅𝑎 10
10
), the volume fraction of nanoparticles (φ0
4%) and the Hartmann number (Ha0 100), is studied using the Lattice Boltzmann Method (LBM). The
results obtained show the existence of up to three different solutions for values of Ha less than some threshold.
The obtained solutions have different ranges of existence and generate different amounts of heat transfer.
1 INTRODUCTION
Magnetohydrodynamic convection (MHD) in
cavities heated from below is one of the most
interesting problems in the literature due to its
specificity. The Rayleigh-Bénard (RB) convection in
the presence of an external magnetic field has been
the object of wide studies by many researchers
worldwide, owing to the importance of the field. The
presence of an imposed magnetic field engenders the
formation of the Lorentz force, whose effect
competes with gravity. By this fact, the magnetic
field, depending on its strength and orientation, may
lead to a substantial modification of the flow structure
and its intensity. In a previous study, (Alchaar et al.
1995) conducted a numerical study of RB convection
in a shallow cavity filled with a conductive fluid,
subject to the effect of an inclined magnetic field. The
results of this study show that the vertical magnetic
field has a significant impact and may bring back the
convective motion to rest. Using a similar approach,
(Rudraiah et al. 1995) performed a numerical
investigation on free convection in a rectangular
chamber confining a conductive fluid under the effect
of an external magnetic field. The effect of the
inclination angle of a cavity with two opposite sides
a
https://orcid.org/ 0000-0001-7138-1179
b
https://orcid.org/ 0000-0002-5045-8840
c
https://orcid.org/ 0000-0002-9497-5655
d
https://orcid.org/ 0000-0002-7174-8265
brought to constant but different temperatures and
filled with liquid gallium and exposed to a horizontal
magnetic field was investigated by (Pirmohammadi
and Ghassemi 2009). They recorded a maximum heat
transfer rate for an inclination angle of 45° both in the
absence and in the presence of a magnetic field.
Many studies were devoted to investigating
experimentally and numerically the effect of the
addition of magnetic nanoparticles (like nickel,
cobalt, magnetite Fe
3
O
4
,
etc.) in a base fluid (such as
water), forming so-called ferrofluids. For instance,
(Wang et al. 2016) studied experimentally the
magnetic field effect on the viscosity of the ferrofluid
Fe
3
O
4
H
2
O. The results of this experiment show
that the ferrofluid viscosity increases with magnetic
induction and volume fraction of nanoparticles but
decreases with temperature. A numerical study of a
periodic magnetic field effect on natural convection
and entropy generation in a square cavity filled with
the ferrofluid Fe
3
O
4
H
2
O has been performed by
(Mehryan et al. 2018). Their results show that the
increase of the magnetic field period amplifies the
vortex intensity inside the cavity. Furthermore, the
addition of nanoparticles may lead to an improvement
or degradation of the total entropy generation,
depending on Ha and the remaining parameters.
Chtaibi, K., Hasnaoui, M., Dahani, Y. and Amahmid, A.
Lattice Boltzmann Modelling of MHD Rayleigh-Bénard Convection in a Square Cavity Filled with a Ferrofluid.
DOI: 10.5220/0010734900003101
In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 381-386
ISBN: 978-989-758-559-3
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
381
(Kefayati 2014) used the LBM to study a problem
dealing with natural convection in a square cavity
filled with ferrofluid in the presence of a magnetic
force. Recently, (Ghasemi and Siavashi 2020)
developed a numerical code based on the MRT-LBM
(multi relaxation time Lattice Boltzmann method) to
study the flow of Cu H
O nanofluid by mixed
MHD convection in a 3D enclosure.
The effect of a vertical magnetic field in cavities
heated from below and filled with the ferrofluid
Fe
3
O
4
H
2
O is poorly documented in the literature.
Therefore, taking advantage of the simplicity and
robustness of the LBM, an appropriate code based on
this method was developed to examine the combined
effects of numerous control parameters, such as
Rayleigh number (Ra), Hartmann number (Ha) and
nanoparticles volume fraction (φ) on multiple steady
solutions describing the flow of the ferrofluid
Fe
3
O
4
H
2
O.
2 MATHEMATICAL
FORMULATION
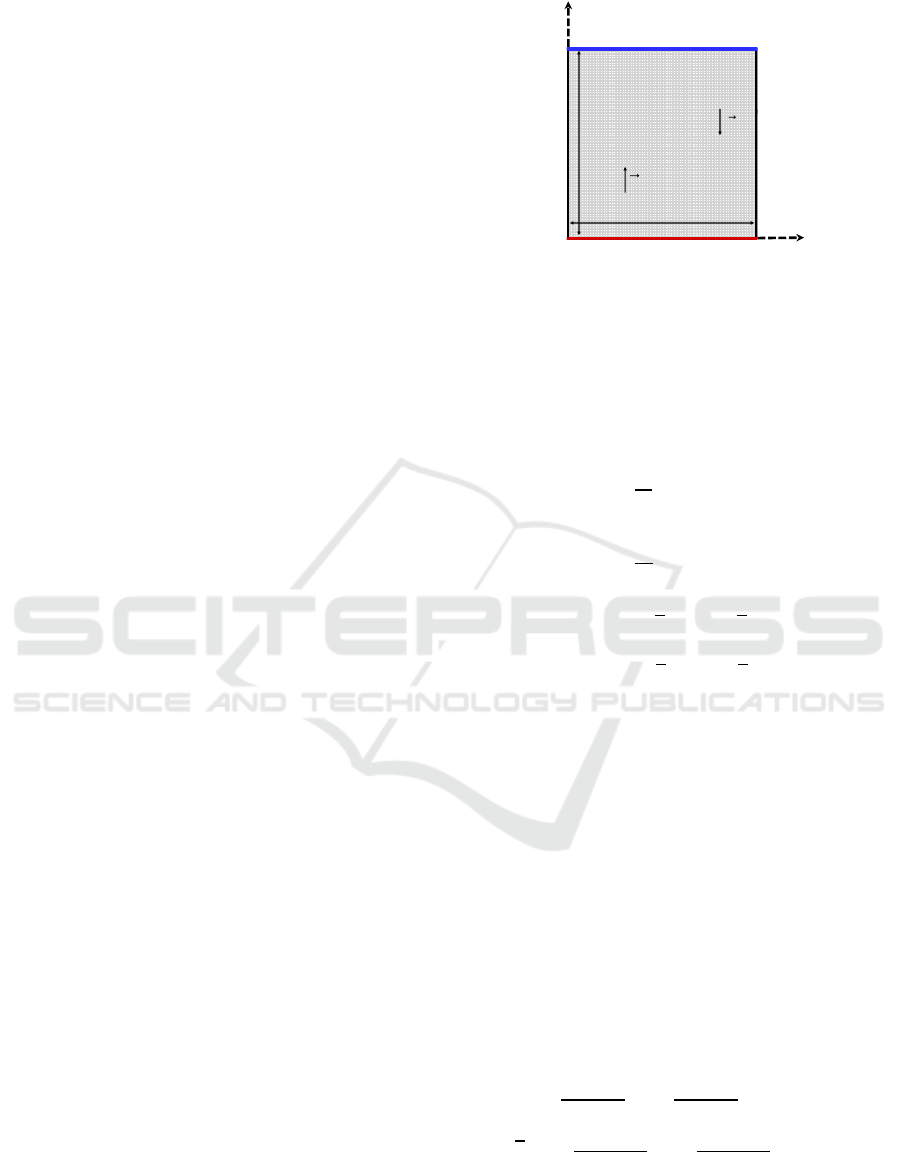
2.1 Rayleigh Bénard Configuration
The two-dimensional physical model considered is
shown in Fig. 1. It consists of a square cavity (LL)
whose horizontal walls are subjected to a vertical
destabilizing thermal gradient, while its vertical walls
are thermally insulated. The bottom wall temperature
(T
) is higher than that of the upper wall (T
). The
square cavity is filled with the ferrofluid Fe
3
O
4
H
2
O and subject to the action of a vertical uniform
magnetic field.
The study was conducted considering that the
ferrofluid is Newtonian, and the resulting flow is
laminar and incompressible. Moreover, the viscous
dissipation and the heating due to the Joule effect
were neglected. All the ferrofluid properties were
considered constant, apart from its density that obeys
the Boussinesq approximation in the buoyancy term.
The data specific to the ferrofluid used in the present
study are listed in Table 1.
2.2 Lattice Boltzmann Method
Essentially, the LBM method is based on two main
steps: collision between the fluid particles
characterized by the left side of Eq. (1), and streaming
to describe the movement of these fluid particles
towards the neighbouring nodes, characterized by the
Figure 1: Schematic of the physical problem.
right side of Eq. (1). Bhatnagar-Gross-Krook (BGK)
approximation was used for both local distribution
functions 𝑓 and 𝑔 for the momentum and energy
equations, respectively. The lattice Boltzmann
equation (LBE) with external forces can be expressed
at the position r and time t as follows:
𝑓
𝑟𝑐
∆𝑡,𝑡 ∆𝑡
𝑓
𝑟,𝑡
1
𝜏
𝑓
𝑟,𝑡
𝑓
𝑟,𝑡
𝐹
(1)
𝑔
𝑟𝑐
∆𝑡,𝑡 ∆𝑡
𝑔
𝑟,𝑡
1
𝜏
𝑔
𝑟,𝑡
𝑔
𝑟,𝑡
(2)
𝑓
𝜔
𝜌13𝑐
⃗
𝑢
⃗
9
2
𝑐
⃗
𝑢
⃗
3
2
𝑢
⃗
(3)
𝑔
𝜔
𝑇13𝑐
⃗
𝑢
⃗
9
2
𝑐
⃗
𝑢
⃗
3
2
𝑢
⃗
(4)
𝐹
𝐹𝑥
𝐹𝑦
𝐹𝑥
3𝜔
𝜌𝐴𝑢𝑐
𝐹𝑦
3𝜔
𝜌𝑔𝛽
𝑇𝑇
𝑐
(5)
Where τ
and τ
are respectively the relaxation
coefficients for the momentum and energy equations
and T
T
T
2
⁄
is the reference temperature.
The quantities 𝑓
and 𝑔
are the local equilibrium
distribution functions for density and temperature,
respectively and 𝐹
is the external force, which is
composed of two terms (the buoyancy ( 𝐹𝑦
) and
Lorentz (𝐹𝑥
) forces). The coefficients 𝑐⃗
and 𝜔
are
respectively the discrete velocity and the weighting
coefficients at direction 𝑖, which are defined in D2Q9
lattice arrangement as follows:
𝑐
⎩
⎪
⎨
⎪
⎧
0,0
, 𝑖0
cos
𝜋
𝑖1
2
,sin
𝜋
𝑖1
2
, 𝑖1 4
√
2cos
𝜋
2𝑖 9
4
,sin
𝜋
2𝑖 9
4
,𝑖5 8
(6)
Ferrofluid
Fe
O
H
O
g
B
L
L
y
x
BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)
382

Table 1: Thermal physical properties of H
O (pure water) and Fe
O
(nanoparticles) (Ghaffarpasand 2016).
Properties
𝜌
𝐾𝑔.𝑚
𝑐
𝐽
.𝐾𝑔
.𝐾
𝑘
𝑊.𝑚
.𝐾
𝛽10
𝐾
𝜎
𝑚.𝛺
H
O
997.1 4179 0.613 21 0.05
Fe
O
5200 670 6 1.3 25000
𝜔
⎩
⎪
⎨
⎪
⎧
4
9
, 𝑖0
1
9
, 𝑖1 4
1
36,
𝑖5 8
(7)
Finally, the density𝜌, velocity u
⃗
and temperature
T, are calculated using the local distribution functions
as follows:
𝜌
𝑓
𝑖
8
𝑖0
(8)
𝑢
⃗
1
𝜌
𝑓
𝑖
8
𝑖0
𝑐
⃗
(9)
𝑇𝑔
(10)
The ferrofluid thermo-physical properties, such as
density (𝜌
), coefficient of thermal expansion (𝛽
)
and heat capacity ( 𝜌𝑐
) that appear in the
governing equations, were evaluated using the
following equations (Sheikholeslami and Ganji
2014):
𝜌
1𝜑𝜌
𝜑𝜌
(11)
𝛽
1𝜑𝛽
𝜑𝛽
(12)
𝜌𝑐
1𝜑𝜌𝑐
𝜑𝜌𝑐
(13)
The thermal and electrical conductivities are
estimated by the Hamilton and Crosser (Hamilton
1962) and Maxwell models, respectively.
𝑘
𝑘
𝑘
2𝑘
2𝜑𝑘
𝑘
𝑘
2𝑘
𝜑𝑘
𝑘
(14)
𝜎
𝜎
1
3𝜑
𝜎
𝜎
1
𝜎
𝜎
2𝜑
𝜎
𝜎
1
(15)
The parameter 𝐴 in equation (5) is obtained as
𝐴
.
.
Ha
𝜈𝐿
⁄
, with Ha𝐿𝐵
𝜎
𝜇
⁄
being
the Hartmann number.
The boundary conditions adopted in the present
study are similar to those used by (Kao and Yang
2007).
The heat transfer by convection is evaluated
through the calculation of the Nusselt number that is
evaluated locally on the heated wall, Eq. (16), and
averaged along this boundary, Eq. (17):
𝑁𝑢
𝑘
𝑘
𝜕𝑇
𝜕𝑌
(16)
and
𝑁𝑢
𝑁𝑢
𝑑𝑋
(17)
2.3 Validation of the LBM Code
The validation of the numerical code is an essential
step before carrying out the numerical simulations
specific to the studied problem. Thus, for the
validation tests, the case of natural convection flow of
the nanofluid Al
O
water confined in a
differentially heated cavity subjected to the action of
a magnetic field was considered. This configuration
was the object of a previous numerical investigation
by (Ghasemi et al. 2011). The results presented in Fig.
2 in terms of mean Nusselt number were obtained
with a volume fraction of nanoparticles of 3% and
various Rayleigh and Hartmann numbers. Fig. 2
shows a good agreement between our results and
those obtained by (Ghasemi et al. 2011), the
maximum deviation being within 4.18%. On another
hand, preliminary tests were carried out to appreciate
the sensitivity of the results by varying the mesh size
as illustrated in Table 2 in terms of mean Nusselt
numbers for different solutions of the problem
obtained with 𝑅𝑎 10
, Ha 30 and 𝜑4%.
The inspection of these results shows that the selected
grid of 120 120 is enough to conduct the present
study. In fact, this grid leads to results that differ by
about 0.23% (as maximum deviation) from those
obtained with the finest grid of 160 160.
Table 2: Grid sensitivity in terms of 𝑁𝑢
for 𝑅𝑎 10
,
Ha 30 and 𝜑4%.
80
100
120
140
160
MF 3.020 3.018 3.0164 3.0157 3.0153
BF 3.509 3.495 3.486 3.481 3.478
TF 3.481 3.471 3.467 3.464 3.462
Lattice Boltzmann Modelling of MHD Rayleigh-Bénard Convection in a Square Cavity Filled with a Ferrofluid
383

Figure 2: Numerical code validation against results of
(Ghasemi et al. 2011) in terms of Nu
m
vs. Ha for 𝜑 3%
and various Ra.
3 RESULTS AND DISCUSSION
In the case of cavities heated from below, the
literature review shows that heat transfer depends on
the type of solution for a problem characterized by a
multiplicity of solutions. The present study is part of
these problems since multi-steady state solutions
have been obtained with different ranges of existence.
In fact, the existence of the monocellular, bicellular
and tri-cellular flows has been proved numerically;
they will be noted MF, BF and TF, respectively.
These three types of solution were also obtained by
(Mansour et al. 2006) in a square porous cavity heated
from below and submitted to a horizontal
concentration gradient. The main purpose of this
study is to investigate the influence of a uniform
vertical magnetic field ( Ha0 to 100 ) and
nanoparticles volume fractions (𝜑0 to 4%) on
different thermal and dynamic behaviours for a fixed
value of Rayleigh number (𝑅𝑎10
).
3.1 Effect of Hartmann Number
The effect of Hartmann number on the thermal and
dynamic behaviours of the base fluid (solid lines) and
the Fe
O
H
O ferrofluid (dashed lines) is
illustrated in Figs. 3(a) and 3(b) for 𝑅𝑎 10
. The
inspection of Fig. 3a shows that for Ha 0 and 25,
the three types of solutions previously mentioned are
obtained. The bicellular solution is characterized by a
symmetry regarding the vertical axis passing by the
centre of enclosure, while the monocellular and
tricellular solutions show a symmetry with respect to
the centre of the cavity. The increase of Ha to 25 leads
to a substantial reduction of the flow intensity
characterized by a division by factors of 2.87 / (1.65)
/ (1.28) in the case of the MF / (BF)/ (TF). These
important reductions that accompany the increase of
Ha are expected knowing the damping role
engendered by the increase of the intensity of the
magnetic field. The increase of Ha from 25 to 50
leads to the disappearance of the MF solution and
severely reduces the intensities of the remaining
structures that become 2.08 and 1.80 times less
intense for the BF and TF solutions, respectively. The
addition of the nanoparticles promotes the flow
intensity since the effect of the global improvement
of the ferrofluid conductivity outweighs the increase
of viscosity for the small fraction of nanoparticles
added. It is also observed that the impact of
nanoparticles on the MF flow is more important
compared to the other flow types (BF and TF). More
specifically, for Ha 0, the flow intensity increases
by about 4.2% for the MF, while this increase does
not exceed 2.4% and 1.3% for the BF and TF flows,
respectively. On another side, the flow intensity is
influenced differently by adding nanoparticles in the
presence of a magnetic field, and this influence is
more attenuated in comparison with Ha 0. In fact,
the addition of nanoparticles for Ha 25 leads to an
improvement of the MF and BF flows intensities,
respectively, by about 2.5% and 1.7%, while the
intensity of the TF stays unchanged. By increasing
progressively Ha, the MF flow transits toward the TF
from a threshold value 𝐻𝑎
of this parameter. This
critical value depends strongly on the volume fraction
of the nanoparticles. More exactly, 𝐻𝑎
drops from
45 (case of pure fluid) to 40 (case of ferrofluid with
𝜑4%).
By considering the thermal aspect of the problem,
Fig. 3b shows clearly that the temperature fields
undergo strong changes accompanying the change in
the flow structure, particularly in the central region of
the cavity due to the interaction between the
neighbouring cells. Thus, the number of ripples
revealed by the isotherms increases horizontally as
the flow cells number increases. This behaviour
results from the fact that each cell has one cold
vertical side and one hot vertical side. The presence
of the ripples attests that the changes of temperature
gradients prevail horizontally following the increase
of the number of cells. For the three types of
solutions, the thicknesses of the thermal boundary
layers developed near the horizontal active walls
increase by incrementing Ha.
3.2 Heat Transfer
The effect of the magnetic field on the mean Nusselt
number calculated along the heated wall is
exemplified in Fig. 4 for 𝜑0 and 4%. This figure
shows that the addition of nanoparticles loses its
0 15304560
2
4
6
8
10
Ra = 10
3
Ra = 10
4
Ra = 10
5
Nu
m
Ha
LBM code
Ghasemi et al., 2011
Ra = 10
6
BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)
384

𝐻𝑎0
|
Ψ
|
25.4138
|
Ψ
|
15.1212
|
Ψ
|
7.7362
𝐻𝑎25
|
Ψ
|
8.8548
|
Ψ
|
9.1685
|
Ψ
|
6.0411
𝐻𝑎50
|
Ψ
|
4.4167
|
Ψ
|
3.3508
Figure 3a: Streamlines obtained with 𝜑0 (solid lines)
and 𝜑4% (dashed lines), Ra 10
and different Ha.
𝐻𝑎0
𝐻𝑎25
𝐻𝑎50
Figure 3b: Isotherms obtained with 𝜑0 (solid lines) and
𝜑4% (dashed lines), Ra 10
and different Ha.
advantage from some thresholds of Ha depending on
the type of solution. Moreover, the increase of the
magnetic field strength (which leads to the increase
of Ha) has a negative effect on heat transfer rates
within the cavity since it is accompanied by a
continuous deterioration of the Nusselt numbers
corresponding to each type of solution. The MF is the
least favourable to heat exchange for this
configuration and the most unstable in the sense that
it transits first toward the TF from Ha40/45 for
𝜑0/4%. This transition leads to a substantial
improvement of the heat transfer rate (with an
0 20406080100
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
Nu
m
Ha
MF
BF
TF
Figure 4: Mean Nusselt number vs. Ha for Ra 10
and
different solutions.
increase of about 24%). Globally, the BF dethrones
the TF in terms of heat exchange from some
thresholds values of Ha that depend on 𝜑, and this
limited advantage persists in the whole range of Ha.
Note also that the TF resists to the increase of Ha, and
its transition towards the BF is delayed and occurs in
a regime dominated by conduction.
4 CONCLUSION
In the present study, natural convection heat transfer
of ferrofluid Fe
O
H
O in a Rayleigh-Bénard
square cavity was investigated numerically using the
LBM. The results presented show that up to three
steady-solutions were obtained for relatively low
Hartmann numbers ( Ha19). The MF is less
favourable to heat transfer and transits towards the TF
from this threshold value of Ha. Both BF and TF
resist to the increase of Ha even when the role of
convection vanishes (Ha > 80). Finally, the heat
transfer rates generated by the BF and TF remain
comparable with a slight advantage in favour of the
BF for relatively high values of Ha.
REFERENCES
Alchaar, S., P. Vasseur, and E. Bilgen. 1995. “The Effect of
a Magnetic Field on Natural Convection in a Shallow
Cavity Heated from Below.” Chemical Engineering
Communications 134(1): 195–209.
Ghaffarpasand, Omid. 2016. “Numerical Study of MHD
Natural Convection inside a Sinusoidally Heated Lid-
Driven Cavity Filled with Fe
3
O
4
-Water Nanofluid in
the Presence of Joule Heating.” Applied Mathematical
Modelling 40(21–22): 9165–82.
Ghasemi, B., S. M. Aminossadati, and A. Raisi. 2011.
“Magnetic Field Effect on Natural Convection in a
Lattice Boltzmann Modelling of MHD Rayleigh-Bénard Convection in a Square Cavity Filled with a Ferrofluid
385

Nanofluid-Filled Square Enclosure.” International
Journal of Thermal Sciences 50(9): 1748–56.
Ghasemi, Kasra, and Majid Siavashi. 2020. “Three-
Dimensional Analysis of Magnetohydrodynamic
Transverse Mixed Convection of Nanofluid inside a
Lid-Driven Enclosure Using MRT-LBM.”
International Journal of Mechanical Sciences 165:
105199.
Hamilton, R. L. 1962. “Thermal Conductivity of
Heterogeneous Two-Component Systems.” Industrial
and Engineering Chemistry Fundamentals 1(3): 187–
91.
Kao, P. H., and R. J. Yang. 2007. “Simulating Oscillatory
Flows in Rayleigh-Bénard Convection Using the
Lattice Boltzmann Method.” International Journal of
Heat and Mass Transfer 50(17–18): 3315–28.
Kefayati, G. H.R. 2014. “Natural Convection of Ferrofluid
in a Linearly Heated Cavity Utilizing LBM.” Journal of
Molecular Liquids 191: 1–9.
Mansour, A., A. Amahmid, M. Hasnaoui, and M. Bourich.
2006. “Multiplicity of Solutions Induced by
Thermosolutal Convection in a Square Porous Cavity
Heated from Below and Submitted to Horizontal
Concentration Gradient in the Presence of Soret
Effect.” Numerical Heat Transfer; Part A: Applications
49(1): 69–94.
Mehryan, S. A.M., Mohsen Izadi, Ali J. Chamkha, and
Mikhail A. Sheremet. 2018. “Natural Convection and
Entropy Generation of a Ferrofluid in a Square
Enclosure under the Effect of a Horizontal Periodic
Magnetic Field.” Journal of Molecular Liquids 263:
510–25.
Pirmohammadi, Mohsen, and Majid Ghassemi. 2009.
“Effect of Magnetic Field on Convection Heat Transfer
inside a Tilted Square Enclosure.” International
Communications in Heat and Mass Transfer 36(7):
776–80.
Rudraiah, N., R. M. Barron, M. Venkatachalappa, and C.
K. Subbaraya. 1995. “Effect of a Magnetic Field on
Free Convection in a Rectangular Enclosure.”
International Journal of Engineering Science 33(8):
1075–84.
Sheikholeslami, Mohsen, and Davood Domiri Ganji. 2014.
“Ferrohydrodynamic and Magnetohydrodynamic
Effects on Ferrofluid Flow and Convective Heat
Transfer.” Energy 75: 400–410.
Wang, Lijun et al. 2016. “Investigation on Viscosity of
Fe
3
O
4
Nanofluid under Magnetic Field.” International
Communications in Heat and Mass Transfer 72: 23–28.
BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)
386
