Using the Box-Jenkins ARIMA Approach for Long-term Forecasting

of 𝐂𝐎

𝟐

Emissions in Morocco

Mohammed Jamii, Naima Oumidou and Mohamed Maaroufi

Engineering for Smart and Sustainable System Research Centre, Mohamadia School of Engineers, Mohammed V

University in Rabat 11000, Morocco

Keywords: ARIMA, The Box-Jenkins, Forecasting.

Abstract: The Box-Jenkins ARIMA approach is one of the most essential methods to predict the variable carbon dioxide



value with a proper model to describe the time variation of past data, and ensure security and

environmental protection (Wang, T, 2016). This study aimed to predict carbon dioxide emissions in Morocco

over the period 1928-2020, using the Box-Jenkins methodology, by building an econometric model for

forecasting carbon dioxide (CO



) emissions in Morocco during 1928-2020. Our study concluded that the time

series was stationary at the first difference. After examination, analysis, and comparison according to the Box-

Jenkins methodology through divers statistical tests, we have been proposed and building the best econometric

model to forecasting carbon dioxide (CO



) emissions in Morocco from the form ARIMA (2,1,1), Using the

proposed econometric model, our study concluded an estimate of the yearly forecast of carbon dioxide (CO



)

emissions in Morocco during the period between 2021-2040 which was Continuously increasing.

1 INTRODUCTION

Over the last few years, climate change is a

significant issue on the global political agenda due to

global warming (Nyoni et al. 2019). The CO



emitted

by human activities is primarily due to the

combustion of fossil fuels and deforestation (Daniel

A. Vallero, 2016). Based on international statistics,

the aviation and transport sector are most of the

reasons for the increase in GHGs over the last decade,

while other sectors have shown negative trends:

(Daniel A. Vallero, 2016). Prediction of future

behaviour of time series is one of the crucial topics of

statistical sciences, due to its necessity in all areas of

life, and its importance for the human element,

governments, and organizations in the planning and

implementation of the process of economic

development (Daniel A. Vallero, 2016).

Forecasting CO



emissions is an indispensable

part of a green energy economy (Pao et al, 2012). It is

essential to have a more in-depth view of the past

trajectory of Morocco's CO



emissions to reliably

forecast its future emissions (Pao et al, 2012).

This paper seeks to predict the evolution of carbon

dioxide emissions in Morocco during the next two

decades, 2021-2040 (Daniel A. Vallero, 2016). The

accuracy and validity of the ARIMA forecasting

method were tested by matching actual data with

forecast data (Nyoni et al, 2019).

The rest of the paper is structured as follows:

Section 2 presents a brief review of the literature

relevant to our research. Section 3 introduces the

methodology analysis. Section 4 sums up the data.

Empirical and predictive results are provided in

Section 5. Finally, the last section contains

concluding remarks.

2 LITERATURE REVIEW

In the literature, many articles use different

approaches such as time series econometrics, ANNs,

hybrids, etc. From various fields of engineering,

economics, science and, technology.

(Rahman and Hasan, 2017) used forty-four years

of time series data between 1972 and 2015 through

the use of ARIMA model, and they found that

ARIMA (0, 2, 1) model is the most appropriate model

to predict carbon dioxide in Bangladesh.

In other research on Bangladesh, (Hossain et al,

2017) forecasted the carbon dioxide emissions in

Bangladesh based on Box-Jenkins ARIMA from

496

Jamii, M., Oumidou, N. and Maarouﬁ, M.

Using the Box-Jenkins ARIMA Approach for Long-term Forecasting of CO2 Emissions in Morocco.

DOI: 10.5220/0010737600003101

In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 496-501

ISBN: 978-989-758-559-3

1972 to 2013, and they identified that ARIMA (12, 2,

12), ARIMA (8, 1, 3) are the most appropriate models

for predicting CO



emissions compared to the other

forecasting methods.

In China, (Nyoni. T, Chipo. M; 2019) forecasted



emissions in the period 1960-2017, by using

Jenkins-Box (ARIMA) methodology, and the study

led to the selection of the most suitable model

ARIMA (1,2,1), to predict the total CO



emissions in

China in the coming ten years.

(Jamii and Maaroufi, 2021) predicted electrical

energy consumption using the ARIMA approach. The

most significant results indicate that the ARIMA

(1,1,1) model is the most appropriate model for

predicting electricity consumption in Morocco, and

among the results they found, an expected increase in

electricity consumption in Morocco by the end of

2030.

(Mitkov et al, 2019) predicted the energy

consumption of the Islamic Republic of Afghanistan

from 2001 to 2018, using the linear ARIMA model.

The results showed that energy demand would

continue to increase towards the end of 2024.

(Sangeetha and Amudha, 2018) predicted CO



emissions in India, and their results illustrated that the

PSO method could achieve a very efficient and

accurate estimation compared to the MLR model.

In Morocco, (Nafil et al, 2020) investigate three

forecasting methods, namely; ARIMA, Temporal

causality modelling, and Exponential smoothing, to

calculate the energy demand forecasts of Morocco in

2020.

This study will apply the ARIMA approach to

model and forecast CO



emissions in Morocco.

3 METHODOLOGY

3.1 ARIMA Model

The ARIMA model is a univariate model that tends

to identify a single variable as an autoregressive

integrated moving average process (Awe et al, 2020).

It includes a composition of three kinds of random

processes, the performance of which is expressed as

ARIMA (p, d, q), where p is the order of the

autoregressive process AR (p), d is the degree of

integration of the process I (d), and q is the order of

the moving average MA (q) (Cheikh Sarr et al, 2021).

The ARIMA (p, d, q) model is generally organized as

follows:

𝑌

𝑡1

𝑌

𝑡

 𝐶ℇ

𝑡

(1)

Where, t is a white noise perturbation term. Then, 𝑌

𝑡

is then considered to be generated by an integrated

first-order process, and it is notated as I (1).

Compactly, the model can be written as:

∇𝑌



𝐶ℇ



(2)

Where,

∇ 1𝐵

(3)

Likewise, an integrated process of order d is indicated

by I(d) and can be expressed as follows:

∇

𝑑

𝐶ℇ

𝑡

(4)

The ARIMA process of order p, d, and q is given as

ARIMA (p, d, q), and can be represented compactly

as follows:

𝜑B ∇



𝑌



𝐶 𝜃



𝐵



ℇ



(5)

4 DATA COLLECTION

This study is based on 92 years of observations (i.e.,

1928 - 2020) of CO2 annual emissions (Mt) in

Morocco. All the data used in this study were

extracted from the World Bank's online database.

Figure 1: The annual CO



emissions in Morocco for the

period 1928-2020.

We note that our series is not stationary, as shown by

an upward trend over the period 1928- 2020. This

indicates that the mean and variance of annual CO



emissions change over time. In addition, carbon

dioxide emissions in 2020 dropped by 7% in 2020,

the most significant decrease on record, as countries

worldwide, imposed lockdowns and restrictions on

Using the Box-Jenkins ARIMA Approach for Long-term Forecasting of CO2 Emissions in Morocco

497

movement to curb the spread of the coronavirus

pandemic (IEA, 2021).

4.1 The ADF Test for Stationarity

After applying Augmented Dickey–Fuller test on our

series, we found that the ADF value is 3.713814,

which is superior to the critical value of significance

level of 10%, 5% and 1%, respectively. Hence, it

cannot reject the presence of the unit root.

Based on

the unit root test, the CO



emission series in Morocco

seems to contain a unit root. Indeed, our series is non-

stationery. Indeed, the ADF value at the first

difference is -8.915777, which is below the critical

value of the significance level of 10%, 5% and 1%,

respectively. It is stationary at the 1st difference

(Jamii and Maaroufi, 2021). The specific results are

provided in Table 1.

Table1: Augmented Dickey–Fuller test

Test

critical

values

(%)

Unit Root Test

(Level)

Unit Root Test

(First diff)

T Statistic

3.713814

Prob

1.00

T Statistic

-8.91577

Prob

0.00

1 -3.513 -3.532

5 -2.897 -2.906

10 -2.586 -2.590

Figure 2: The time series plot of the first difference of CO



emissions of Morocco

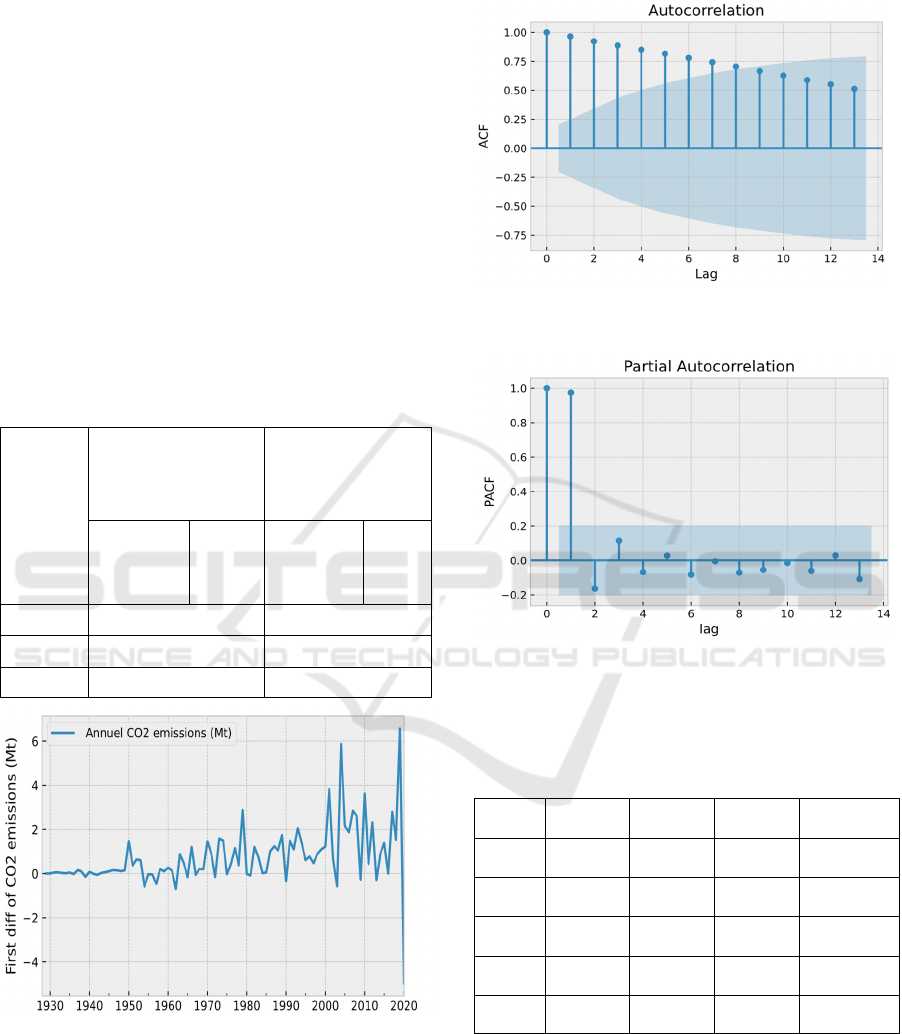
The next step is to simulate the procedure for the



emissions

series. We start by using the correlogram of

the stationary series, and we can obtain from (Fig 3

and Fig 4) the results of the correlation analysis. From

the autocorrelation coefficients and partial

autocorrelation coefficients, we attempt to adjust a

random time series.

Figure 3: The first-order autocorrelation coefficients of

carbon dioxide emissions

Figure 4: The first-order partial autocorrelation coefficients

of carbon dioxide emissions

4.2 Evaluation of ARIMA Models

Table 2: overview of information criteria

Model

AIC

BIC

HQIC

Log

Likelihoo

ARIMA

(1,1,1)

318.430

325.995

321.483

–156.215

ARIMA

(1,1,2)

306.486 316.933 310.917 –149.423

ARIMA

(2,1,1)

305.739* 315.739* 309.727* –148.826*

ARIMA

(2,1,2)

307.198 319.807 312.287 –148.599

ARIMA

(3,1,1)

307.130 319.739 312.219 –148.565

In order to obtain the best ARIMA, we applied

selection criteria such as log-likelihood, AIC (Akaike

information criterion), BIC (Bayesian information

criterion) and HQC (Hannan Quinn information

criterion). The ARIMA (2, 1, 1) model is chosen as

the optimal model due to the lowest value of AIC,

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

498

BIC and HQC and the maximum value of Log-

Likelihood as shown in Table 2.

Figure 5: Residuals diagnostic plots of ARIMA (2,1,1)

5 RESULTS & DISCUSSION

5.1 Descriptive Statistics

We notice from the table below that Jarque-Bera (JB

= 454) indicates a critical probability of 0.52. We

accept H0 of normality of residuals. Therefore,

Homoscedasticity residues are verified. Residues are

white noise processes.

Table 3: Descriptive Statistic from ARIMA Model

Mean Std Skew Kurtosis JB Prob

19.15 21.09 0.58 8.70 454 0.52

5.2 Estimation of ARIMA (2,1,1)

The parameters of ARIMA (2,1,1) are listed in table

3. Thus, the forecasted model can be written as

follows:

𝑌



 0.4956𝑌



 0.4937𝑌



 0.8475ℇ

–

ℇ



(6)

Table 4: ARIMA (2, 1, 1) Final parameter estimates

Variable Coef Std err Z Pb

AR (1) 0.4956 0.075 6.583 0.000

AR (2) 0.4937 0.076 6.483 0.000

MA (1) -0.8475 0.085 -10.006 0.000

A comparison between the actual data obtained from

the dataset and the predicted data based on the

ARIMA model is presented in Fig. 6. It can be seen

that the two graphs match well. The predicted data

follow the shape of the data graph. This shows the

extent of convergence of the model estimated from the

real data.

Figure 6: Actual, fitted plot of CO



emission from model

selected ARIMA (2,1,1)

5.3 Forecast Graph

Based on the estimated model, 𝐶𝑂



emissions are

provided over the next two decades. The results in

Figure 7 show that by 2040, annual CO2 emissions

will continue to increase from 69.18 million tonnes of

carbon dioxide equivalent to 109.25 million tonnes of

carbon dioxide equivalent. However, this increase is

due to the growth of the Moroccan population in

recent years, and consequently, the need for

electricity is increasing. Indeed, the main sources of

carbon dioxide emissions in Morocco are electricity

generation and transport sector. According to the

latest statistics, in 2016, the electricity sector

generated 39% and the transport sector 31% of total

emissions. The rest came from industry (13%),

residential and commercial buildings (12%) and

agriculture (5%). (International Energy Agency,

2019).

Figure 7: Forecast of CO



emissions over the next two

decades (2021 to 2040)

Using the Box-Jenkins ARIMA Approach for Long-term Forecasting of CO2 Emissions in Morocco

499

5.4 Policy Implications

In this paper, we have discussed the forecasting of



emissions in Morocco based on the Jenkins

approach (ARIMA). The results show that the

ARIMA method performs well in predicting CO



emissions for the next 20 years and offers increased



emissions. These results are essential for the

Moroccan government. This knowledge can be used

in the decision-making process, such as energy

control in the transport sector. Some

recommendations can be listed as follows:

- Support the integration of renewable energy sources

in homes for householder self-consumption.

-The adoption of electric cars is also highly

recommended, as it will decrease the transport

sector's emissions, especially if the energy needed to

run them is produced by renewable sources.

-Allowing discounts on the purchase of low

consumption and environmentally friendly household

appliances.

-Initiate policy actions such as increasing taxes on the

polluting companies, particularly those that burn

fossil fuels in their daily production activities.

6 CONCLUSIONS

In this study, we developed an ARIMA model to

forecast CO



emissions in Morocco using the Box-

Jenkins time series approach. The historical CO



emissions data have been used to develop several

models, and the appropriate model selected based on

four performance criteria: AIC, BIC, HQIC, and

maximum likelihood. As a result, we found that the

ARIMA (2,1,1) model is the model that minimizes

the four previous criteria. The results obtained prove

that this model can be used to model and forecast

future CO



emissions over the next two decades in

Morocco.

The results of this study are vital as they can be

used by researchers, stakeholders and, the Moroccan

government to take adequate measures to implement

a sustainable climate policy. In addition, an accurate

forecast of CO



emissions on our territory will help

the country's political leaders to negotiate a climate

fund with the international community.

REFERENCES

Hossain, A., Islam, M. A., Kamruzzaman, M., Khalek, M.

A. & Ali, M. A (2017). Forecasting carbon dioxide

emissions in Bangladesh using Box-Jenkins ARIMA

models, Department of Statistics, University of

Rajshahi.

Vallero, D.A. Air Pollution Monitoring Changes to

Accompany the Transition from a Control to a Systems

Focus. Sustainability 2016, 8. [CrossRef]

Pao, H., Fu, H., & Tseng, C (2012). Forecasting of CO



emissions, energy consumption and economic growth

in China using an improved grey model, Energy, 40

(2012): 400 – 409.

Nyoni, T. (2018i). Box – Jenkins ARIMA Approach to

Predicting net FDI inflows in Zimbabwe, Munich

University Library – Munich Personal RePEc Archive

(MPRA), Paper No. 87737.

Sangeetha, A & Amudha, T (2018). A Novel Bio-Inspired

Framework for CO



emission forecast in India,

Procedia – Computer Science, 125 (2018): 367 – 375.

Rahman, A & Hasan, M. M (2017). Modelling and

forecasting carbon dioxide emissions in Bangladesh

using Autoregressive Integrated Moving Average

(ARIMA) models, Scientific Research Publishing –

Open Journal of Statistics, 7: 560 – 566.

Hossain, A., Islam, M. A., Kamruzzaman, M., Khalek, M.

A. & Ali, M. A (2017). Forecasting carbon dioxide

emissions in Bangladesh using Box-Jenkins ARIMA

models, Department of Statistics, University of

Rajshahi.

A. MITKOV, N (2019)., “Forecasting the Energy

Consumption in Afghanistan with the ARIMA Model,”

in XVI-TH International Conference on Electrical

Machines, Drives and Power Systems ELMA 2019, 6-8

June 2019, Varna, Bulgaria, 2019.

Wang, T. (2016). Forecast of economic growth by time

series and scenario planning method—A case study of

Shenzhen. Modern Economy, 7(02), 212.

R. Bourbonnais, Econometrics, Malakoff: Dunod, 2018.

S. B. Taieb, J. W. Taylor, and R. J. Hyndman, “Hierarchical

probabilistic forecasting of electricity demand with

smart meter data,” 2019.

Nyoni, T., & Bonga, W. G. (2019). Prediction of CO



emissions in India using ARIMA models. DRJ-Journal

of Economics & Finance, 4(2), 01-10.

Nafil, A., Bouzi, M., Anoune, K., & Ettalabi, N. (2020).

Comparative study of forecasting methods for energy

demand in Morocco. Energy Reports, 6, 523-536.

Mpawenimana, I., Pegatoquet, A., Roy, V., Rodriguez, L.,

& Belleudy, C. (2020, March). A comparative study of

LSTM and ARIMA for energy load prediction with

enhanced data pre-processing. In 2020 IEEE Sensors

Applications Symposium (SAS) (pp. 1-6). IEEE.

A. Chater and A. Lasfar, “Detection of image descriptors

and modification of the weighting function for the

estimation of the fundamental matrix using robust

methods,” Journal of Engineering and Applied

Sciences, vol. 13, no. 7, pp. 1835–1843, 2018.

IEA (International Energy Agency) (2018), CO



Emissions

from Fuel Combustion 2018, OECD/IEA, Paris,

www.iea.org/statistics/.

M. Jamii and M. Maaroufi, “The Forecasting of Electrical

Energy Consumption in Morocco with an

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

500

Autoregressive Integrated Moving Average

Approach,” Mathematical Problems Engineering, vol.

2021, Article ID 6623570, 9 pages, 2021

O. Awe, A. Okeyinka and J. O. Fatokun, "An Alternative

Algorithm for ARIMA Model Selection," 2020

International Conference in Mathematics, Computer

Engineering and Computer Science (ICMCECS), 2020,

pp. 1-4, doi: 10.1109/ICMCECS47690.2020.246979.

Cheikh Sarr, Mouhamadou Ndour, Mahdi Haddad, Issa

Sakho. Estimation of Sea Level Rise on the West

African Coasts: Case of Senegal, Mauritania and Cape

Verde. International Journal of Geosciences, Scientific

Research 2021, 12, pp.121-137.

Energy Policies Beyond IEA Countries: Morocco 2019.

Aruna, N. F., Rubel, T. M., Siddiqui, T. A., Karim, T.,

Saika, S., Arifeen, M., ... & Kabir, H. (2021). Time

series analysis of electric energy consumption using an

autoregressive integrated moving average model and

Holt-Winters model. Telkomnika, 19(3).

https://www.iea.org/countries/morocco, visited 04-07-2021

Using the Box-Jenkins ARIMA Approach for Long-term Forecasting of CO2 Emissions in Morocco

501